Measurement of Piezoelectric Amplifiers

1. Effect of a change of capacitance
- 1.1. Cedrat Technology
- 1.2. PI
2. Effect of a change in Voltage level
- 2.1. Cedrat Technology
- 2.2. PI
3. Comparison PI / Cedrat
- 3.1. Results
4. Impedance Measurement
- 4.1. Cedrat Technology
- 4.2. PI

Two voltage amplifiers are tested:

PI E-505.00 (link)
Cedrat Technology LA75B (link)

The piezoelectric actuator under test is an APA95ML from Cedrat technology. It contains three stacks with a capacitance of \(5 \mu F\) each that can be connected independently to the amplifier.

1 Effect of a change of capacitance

1.1 Cedrat Technology

Load Data

piezo1 = load('mat/cedrat_la75b_med_1_stack.mat', 't', 'V_in', 'V_out');
piezo2 = load('mat/cedrat_la75b_med_2_stack.mat', 't', 'V_in', 'V_out');
piezo3 = load('mat/cedrat_la75b_med_3_stack.mat', 't', 'V_in', 'V_out');

Compute Coherence and Transfer functions

Ts = 1e-4;
win = hann(ceil(0.1/Ts));

[tf_1, f_1] = tfestimate(piezo1.V_in, piezo1.V_out, win, [], [], 1/Ts);
[co_1, ~] = mscohere(piezo1.V_in, piezo1.V_out, win, [], [], 1/Ts);


[tf_2, f_2] = tfestimate(piezo2.V_in, piezo2.V_out, win, [], [], 1/Ts);
[co_2, ~] = mscohere(piezo2.V_in, piezo2.V_out, win, [], [], 1/Ts);


[tf_3, f_3] = tfestimate(piezo3.V_in, piezo3.V_out, win, [], [], 1/Ts);
[co_3, ~] = mscohere(piezo3.V_in, piezo3.V_out, win, [], [], 1/Ts);

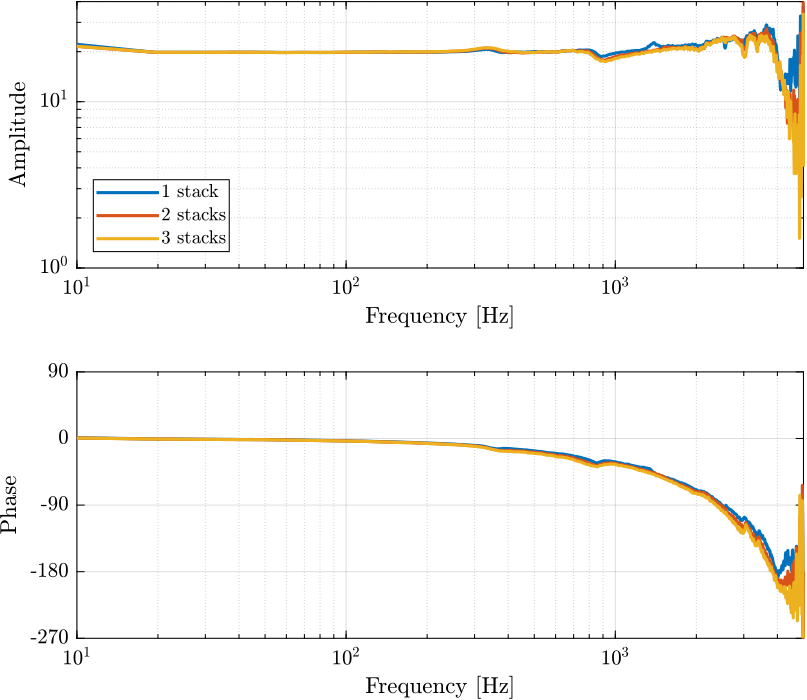
Figure 1: Effect of a change of the piezo capacitance on the Amplifier transfer function

1.2 PI

piezo1 = load('mat/pi_505_high.mat', 't', 'V_in', 'V_out');
piezo2 = load('mat/pi_505_high_2_stacks.mat', 't', 'V_in', 'V_out');
piezo3 = load('mat/pi_505_high_3_stacks.mat', 't', 'V_in', 'V_out');

Ts = 1e-4;
win = hann(ceil(0.1/Ts));

[tf_1, f_1] = tfestimate(piezo1.V_in, piezo1.V_out, win, [], [], 1/Ts);
[co_1, ~] = mscohere(piezo1.V_in, piezo1.V_out, win, [], [], 1/Ts);


[tf_2, f_2] = tfestimate(piezo2.V_in, piezo2.V_out, win, [], [], 1/Ts);
[co_2, ~] = mscohere(piezo2.V_in, piezo2.V_out, win, [], [], 1/Ts);


[tf_3, f_3] = tfestimate(piezo3.V_in, piezo3.V_out, win, [], [], 1/Ts);
[co_3, ~] = mscohere(piezo3.V_in, piezo3.V_out, win, [], [], 1/Ts);

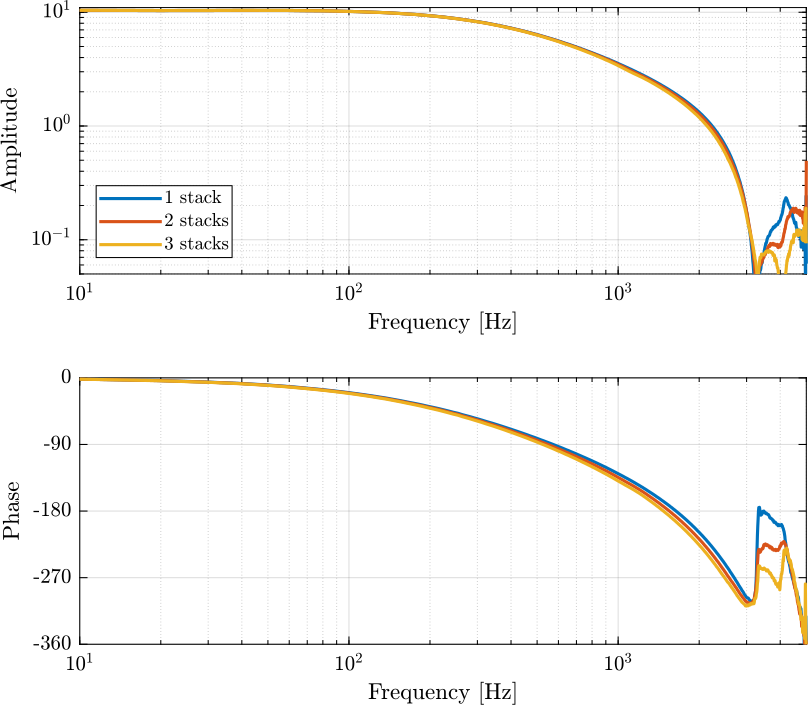
Figure 2: Effect of a change of the piezo capacitance on the Amplifier transfer function

2 Effect of a change in Voltage level

2.1 Cedrat Technology

hi = load('mat/cedrat_la75b_high_1_stack.mat', 't', 'V_in', 'V_out');
me = load('mat/cedrat_la75b_med_1_stack.mat', 't', 'V_in', 'V_out');
lo = load('mat/cedrat_la75b_low_1_stack.mat', 't', 'V_in', 'V_out');

Ts = 1e-4;
win = hann(ceil(0.1/Ts));

[tf_hi, f_hi] = tfestimate(hi.V_in, hi.V_out, win, [], [], 1/Ts);
[co_hi, ~] = mscohere(hi.V_in, hi.V_out, win, [], [], 1/Ts);

[tf_me, f_me] = tfestimate(me.V_in, me.V_out, win, [], [], 1/Ts);
[co_me, ~] = mscohere(me.V_in, me.V_out, win, [], [], 1/Ts);

[tf_lo, f_lo] = tfestimate(lo.V_in, lo.V_out, win, [], [], 1/Ts);
[co_lo, ~] = mscohere(lo.V_in, lo.V_out, win, [], [], 1/Ts);

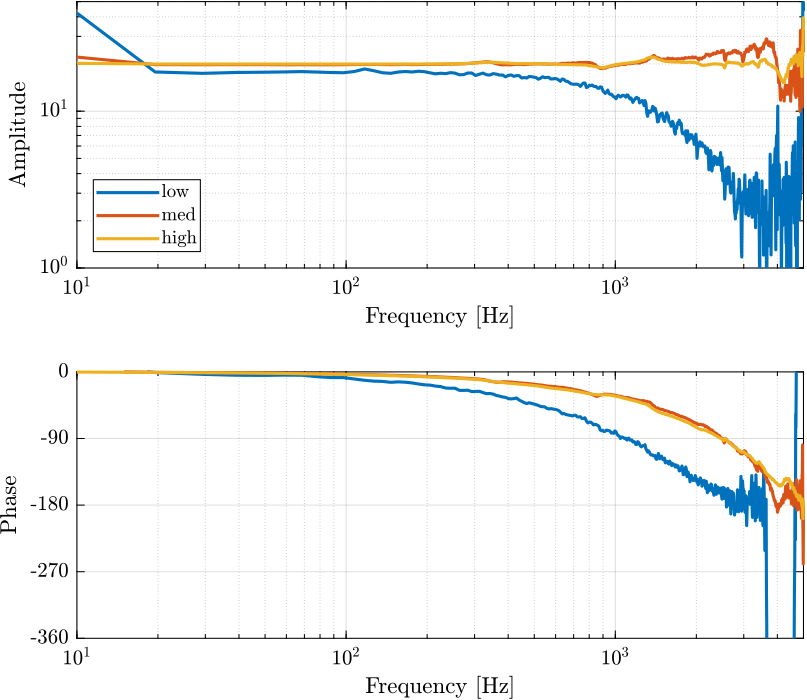
Figure 3: Effect of a change of voltage level on the Amplifier transfer function

2.2 PI

hi = load('mat/pi_505_high.mat', 't', 'V_in', 'V_out');
lo = load('mat/pi_505_low.mat', 't', 'V_in', 'V_out');

Ts = 1e-4;
win = hann(ceil(0.1/Ts));

[tf_hi, f_hi] = tfestimate(hi.V_in, hi.V_out, win, [], [], 1/Ts);
[co_hi, ~] = mscohere(hi.V_in, hi.V_out, win, [], [], 1/Ts);

[tf_lo, f_lo] = tfestimate(lo.V_in, lo.V_out, win, [], [], 1/Ts);
[co_lo, ~] = mscohere(lo.V_in, lo.V_out, win, [], [], 1/Ts);

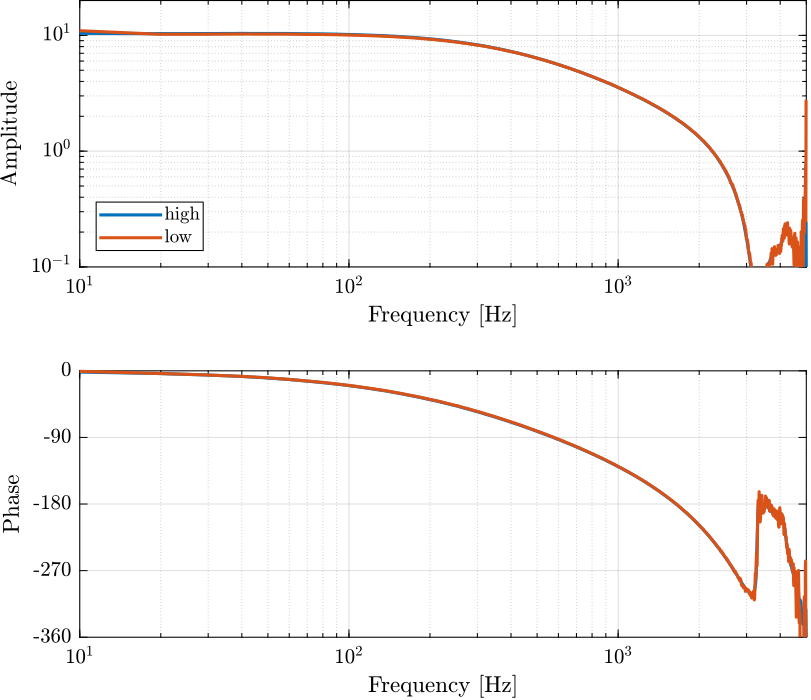
Figure 4: Effect of a change of voltage level on the Amplifier transfer function

3 Comparison PI / Cedrat

3.1 Results

ce_results = load('mat/cedrat_la75b_high_1_stack.mat', 't', 'V_in', 'V_out');
pi_results = load('mat/pi_505_high.mat', 't', 'V_in', 'V_out');

Ts = 1e-4;
win = hann(ceil(0.1/Ts));

[tf_ce, f_ce] = tfestimate(ce_results.V_in, ce_results.V_out, win, [], [], 1/Ts);
[tf_pi, f_pi] = tfestimate(pi_results.V_in, pi_results.V_out, win, [], [], 1/Ts);

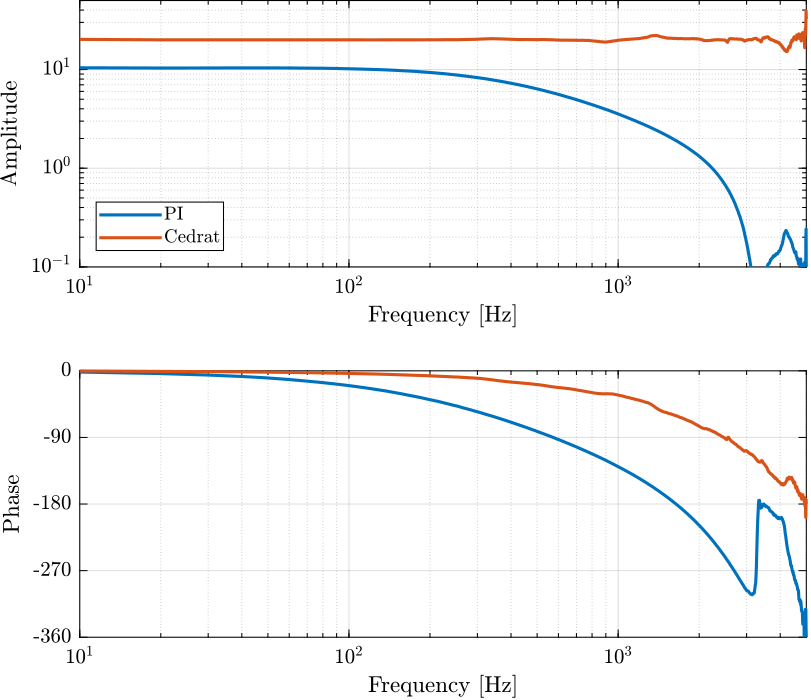
Figure 5: Comparison of the two Amplifier transfer functions

4 Impedance Measurement

The goal is to experimentally measure the output impedance of the voltage amplifiers.

To do so, the output voltage is first measure without any load (\(V\)). It is then measure when a 10Ohm load is used (\(V^\prime\)).

The load (\(R = 10\Omega\)) and the internal resistor (\(R_i\)) form a voltage divider, and thus: \[ V^\prime = \frac{R}{R + R_i} V \]

From the two values of voltage, the internal resistor value can be computed: \[ R_i = R \frac{V - V^\prime}{V^\prime} \]

4.1 Cedrat Technology

R = 10;    % Resistive Load used [Ohm]
V = 10.09; % Output Voltage without any load [V]
Vp = 3.46; % Output Voltage with resistice load [V]

R * (V - Vp)/Vp;

19.162

C = 5e-6; % Capacitance in [F]
Ri = R * (V - Vp)/Vp; % Internal resistance [Ohm]

G_ce = 1/(1+Ri*C*s);

4.2 PI

R = 10;    % Resistive Load used [Ohm]
V = 10.35; % Output Voltage without any load [V]
Vp = 4.14; % Output Voltage with resistice load [V]

R * (V - Vp)/Vp