Voltage Amplifier PD200 - Test Bench
Table of Contents
This report is also available as a pdf.
1 Introduction
2 Voltage Amplifier Requirements
| Specification | |
|---|---|
| Continuous Current | > 50 [mA] |
| Output Voltage Noise (1-200Hz) | < 2 [mV rms] |
| Voltage Input Range | +/- 10 [V] |
| Voltage Output Range | -20 [V] to 150 [V] |
| Small signal bandwidth (-3dB) | > 5 [kHz] |
3 PD200 Expected characteristics
| Characteristics | Manual | Specification |
|---|---|---|
| Input Voltage Range | +/- 10 [V] | +/- 10 [V] |
| Output Voltage Range | -50/150 [V] | -20/150 [V] |
| Gain | 20 [V/V] | |
| Maximum RMS current | 0.9 [A] | > 50 [mA] |
| Maximum Pulse current | 10 [A] | |
| Slew Rate | 150 [V/us] | |
| Noise (10uF load) | 0.7 [mV RMS] | < 2 [mV rms] |
| Small Signal Bandwidth (10uF load) | 7.4 [kHz] | > 5 [kHz] |
| Large Signal Bandwidth (150V, 10uF) | 300 [Hz] |
For a load capacitance of \(10\,\mu F\), the expected \(-3\,dB\) bandwidth is \(6.4\,kHz\) (Figure 2) and the low frequency noise is \(650\,\mu V\,\text{rms}\) (Figure 3).
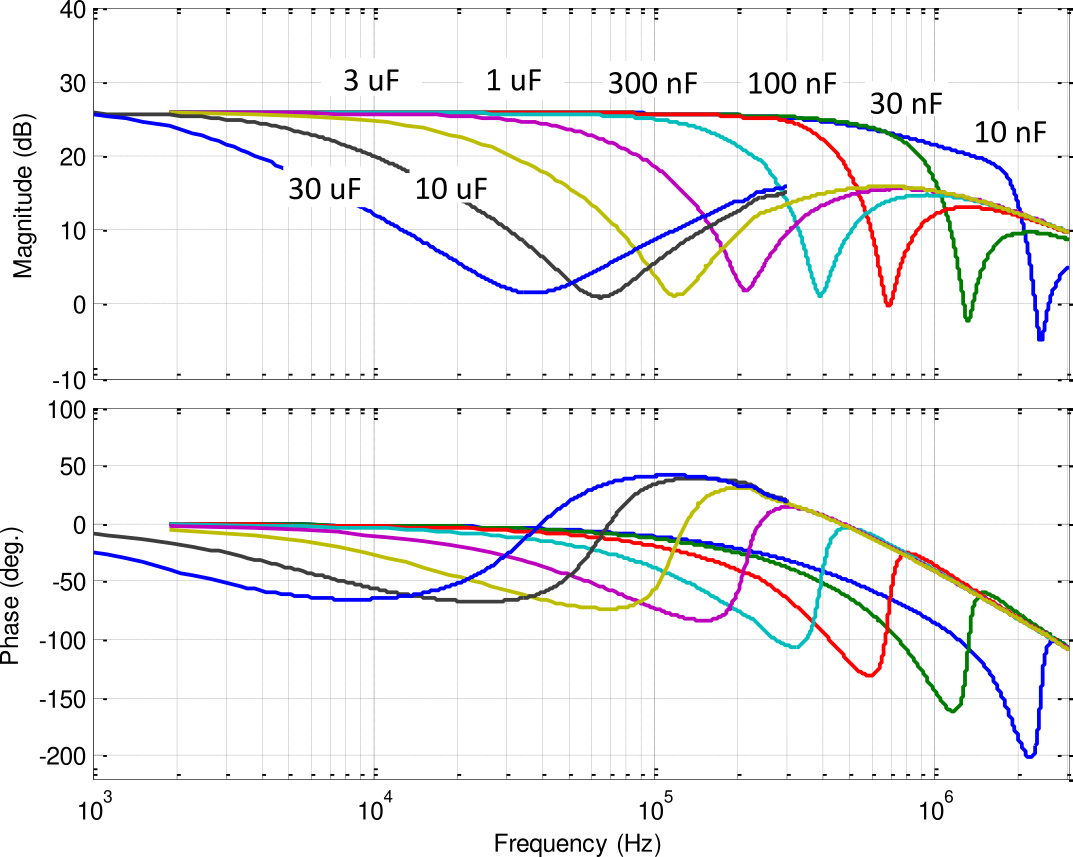
Figure 2: Expected small signal bandwidth
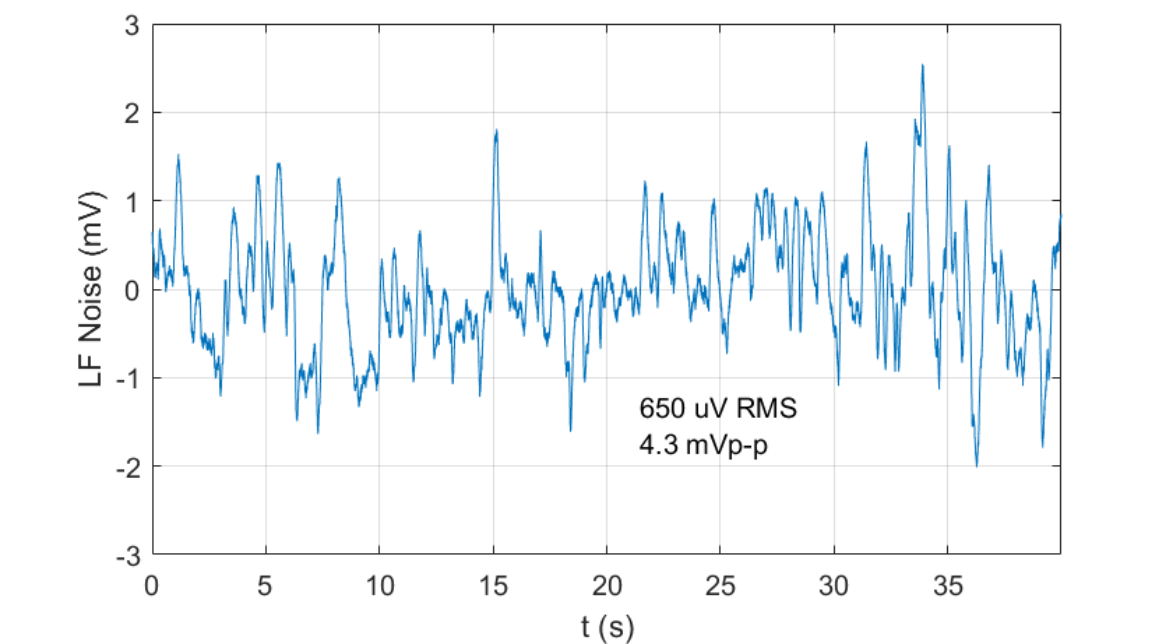
Figure 3: Expected Low frequency noise from 0.03Hz to 20Hz
4 Voltage Amplifier Model
The Amplifier is characterized by its dynamics \(G_p(s)\) from voltage inputs \(V_{in}\) to voltage output \(V_{out}\). Ideally, the gain from \(V_{in}\) to \(V_{out}\) is constant over a wide frequency band with very small phase drop.
It is also characterized by its output noise \(n\). This noise is described by its Power Spectral Density.
The objective is therefore to determine the transfer function \(G_p(s)\) from the input voltage to the output voltage as well as the Power Spectral Density \(S_n(\omega)\) of the amplifier output noise.
As both \(G_p\) and \(S_n\) depends on the load capacitance, they should be measured when loading the amplifier with a \(10\,\mu F\) capacitor.
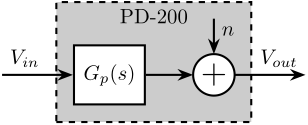
Figure 4: Model of the voltage amplifier
5 Noise measurement
5.1 Setup
Here are the documentation of the equipment used for this test bench:
- Voltage Amplifier PD200
- Load Capacitor EPCOS 10uF Multilayer Ceramic Capacitor
- Low Noise Voltage Amplifier EG&G 5113
- Speedgoat ADC IO313
The output noise of the voltage amplifier PD200 is foreseen to be around 1mV rms in a bandwidth from DC to 1MHz. If we suppose a white noise, this correspond to an amplitude spectral density:
\begin{equation} \phi_{n} \approx \frac{1\,mV}{\sqrt{1\,MHz}} = 1 \frac{\mu V}{\sqrt{Hz}} \end{equation}The RMS noise begin very small compare to the ADC resolution, we must amplify the noise before digitizing the signal. The added noise of the instrumentation amplifier should be much smaller than the noise of the PD200. We use the amplifier EG&G 5113 that has a noise of \(\approx 4 nV/\sqrt{Hz}\) referred to its input which is much smaller than the noise induced by the PD200.
The gain of the low-noise amplifier can be increased until the full range of the ADC is used. This gain should be around 1000.

Figure 5: Schematic of the test bench to measure the Power Spectral Density of the Voltage amplifier noise \(n\)
A low pass filter at 10kHz can be included in the EG&G amplifier in order to limit aliasing. An high pass filter at low frequency can be added if there is a problem of large offset.
5.2 Model of the setup
As shown in Figure 6, there are 4 equipment involved in the measurement:
- a Digital to Analog Convert (DAC)
- the Voltage amplifier to be measured with a gain of 20 (PD200)
- a low noise voltage amplifier with a variable gain and integrated low pass filters and high pass filters
- an Analog to Digital Converter (ADC)
Each of these equipment has some noise:
- \(q_{da}\): quantization noise of the DAC
- \(n_{da}\): output noise of the DAC
- \(n_p\): output noise of the PD200 (what we wish to characterize)
- \(n_a\): input noise of the pre amplifier
- \(q_{ad}\): quantization noise of the ADC

Figure 6: Sources of noise in the experimental setup
5.3 Quantization Noise
The quantization noise is something that can be predicted. The Amplitude Spectral Density of the quantization noise of an ADC/DAC is equal to:
\begin{equation} \Gamma_q(\omega) = \frac{q}{\sqrt{12 f_s}} \end{equation}with:
- \(q = \frac{\Delta V}{2^n}\) the quantization in [V], which is the corresponding value in [V] of the least significant bit
- \(\Delta V\) is the full range of the ADC in [V]
- \(n\) is the number of bits
- \(f_s\) is the sample frequency in [Hz]
adc = struct(); adc.Delta_V = 20; % [V] adc.n = 16; % number of bits adc.Fs = 20e3; % [Hz] adc.Gamma_q = adc.Delta_V/2^adc.n/sqrt(12*adc.Fs); % [V/sqrt(Hz)]
The obtained Amplitude Spectral Density is 6.2294e-07 \(V/\sqrt{Hz}\).
5.4 Pre Amplifier noise measurement
First, we wish to measure the noise of the pre-amplifier. To do so, the input of the pre-amplifier is shunted such that there is 0V at its inputs. Then, the gain of the amplifier is increase until the measured signal on the ADC is much larger than the quantization noise.
The Amplitude Spectral Density \(\Gamma_n(\omega)\) of the measured signal \(n\) is computed. Finally, the Amplitude Spectral Density of \(n_a\) can be computed taking into account the gain of the pre-amplifier:
\begin{equation} \Gamma_{n_a}(\omega) \approx \frac{\Gamma_n(\omega)}{|G_a(\omega)|} \end{equation}This is true if the quantization noise \(\Gamma_{q_{ad}}\) is negligible.
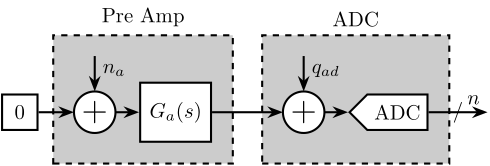
Figure 7: Sources of noise in the experimental setup
The gain of the low noise amplifier is set to 50000.
% Hanning window win = hanning(ceil(0.5/Ts)); % Power Spectral Density [pxx, f] = pwelch(preamp.Vn, win, [], [], Fs); % Save the results inside the struct preamp.pxx = pxx; preamp.f = f;
The obtained Amplitude Spectral Density of the Low Noise Voltage Amplifier is shown in Figure 8. The obtained noise amplitude is very closed to the one specified in the documentation of \(4nV/\sqrt{Hz}\) at 1kHZ.
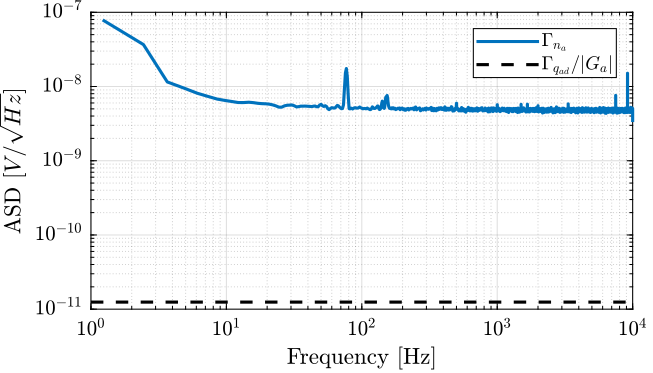
Figure 8: Obtained Amplitude Spectral Density of the Low Noise Voltage Amplifier
5.5 PD200 noise measurement
The input of the PD200 amplifier is shunted such that there is 0V between its inputs. Then the gain of the pre-amplifier is increased in order to measure a signal much larger than the quantization noise of the ADC. We compute the Amplitude Spectral Density of the measured signal \(\Gamma_n(\omega)\). The Amplitude Spectral Density of \(n_p\) can be computed taking into account the gain of the pre-amplifier:
\begin{equation} \Gamma_{n_p}(\omega) = \frac{\Gamma_n(\omega)}{|G_a(\omega)|} \end{equation}And we verify that this is indeed the noise of the PD200 and not the noise of the pre-amplifier by checking that:
\begin{equation} \Gamma_{n_p} \ll \Gamma_{n_a} \end{equation}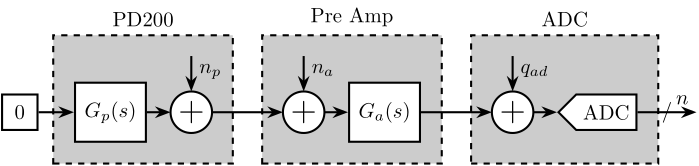
Figure 9: Sources of noise in the experimental setup
The measured low frequency noise \(n_p\) of one of the amplifiers is shown in Figure 10. It is very similar to the one specified in the datasheet in Figure 3.
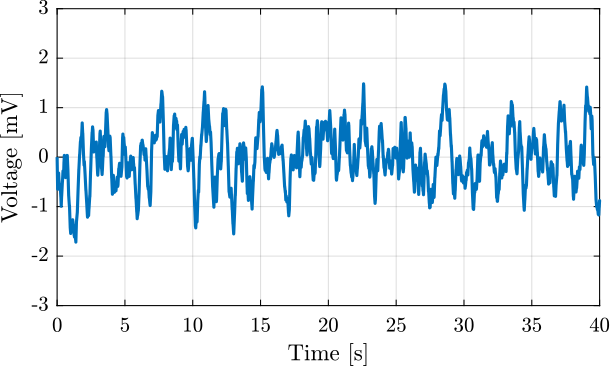
Figure 10: Measured low frequency noise of the PD200 from 0.01Hz to 20Hz
The obtained RMS and peak to peak values of the measured noises are shown in Table 3.
| RMS [uV] | Peak to Peak [mV] | |
|---|---|---|
| Specification [10uF] | 714.0 | 4.3 |
| PD200_1 | 565.1 | 3.7 |
| PD200_2 | 767.6 | 3.5 |
| PD200_3 | 479.9 | 3.0 |
| PD200_4 | 615.7 | 3.5 |
| PD200_5 | 651.0 | 2.4 |
| PD200_6 | 473.2 | 2.7 |
| PD200_7 | 423.1 | 2.3 |
The Amplitude Spectral Density of the measured noise is now computed and shown in Figure 11.
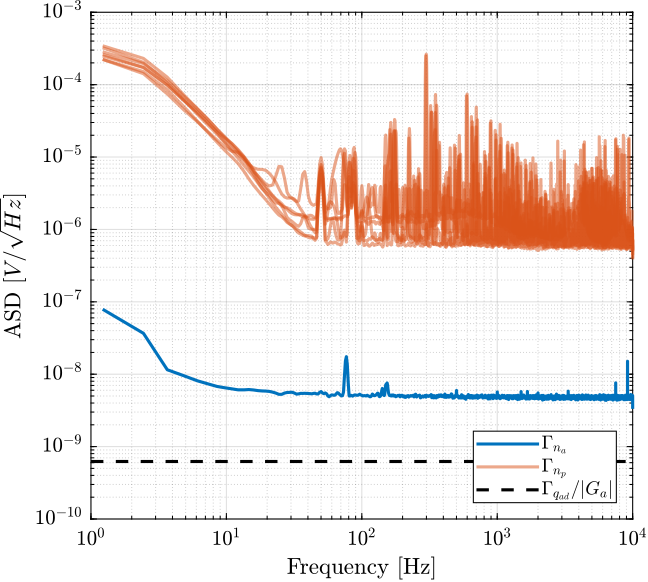
Figure 11: Amplitude Spectral Density of the measured noise
5.6 DAC noise measurement
In order not to have any quantization noise, we impose the DAC to output a zero voltage. The gain of the low noise amplifier is adjusted to
The Amplitude Spectral Density \(\Gamma_n(\omega)\) of the measured signal is computed. The Amplitude Spectral Density of \(n_{da}\) can be computed taking into account the gain of the pre-amplifier:
\begin{equation} \Gamma_{n_{da}}(\omega) = \frac{\Gamma_m(\omega)}{|G_a(\omega)|} \end{equation}And it is verify that the Amplitude Spectral Density of \(n_{da}\) is much larger than the one of \(n_a\):
\begin{equation} \Gamma_{n_{da}} \gg \Gamma_{n_a} \end{equation}
Figure 12: Sources of noise in the experimental setup
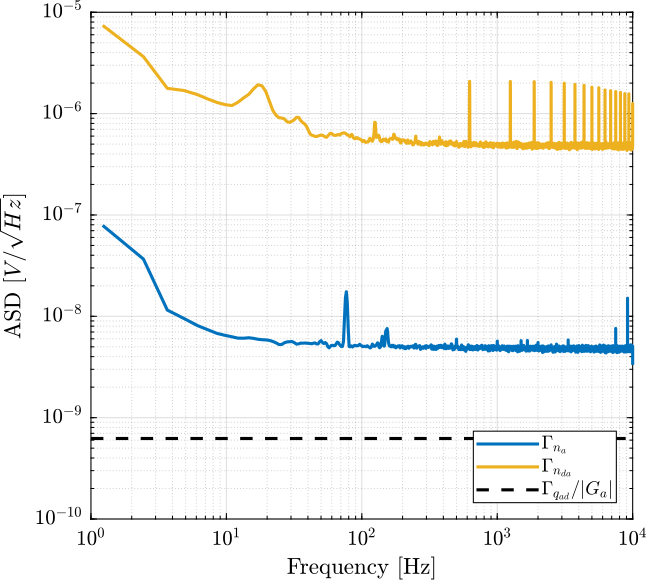
5.7 Total noise measurement
Let’s now analyze the measurement of the setup in Figure 6.
The PSD of the measured noise is computed and the ASD is shown in Figure 14.
win = hanning(ceil(0.5/Ts)); for i = 1:7 [pxx, f] = pwelch(pd200dac{i}.Vn, win, [], [], Fs); pd200dac{i}.f = f; pd200dac{i}.pxx = pxx; end
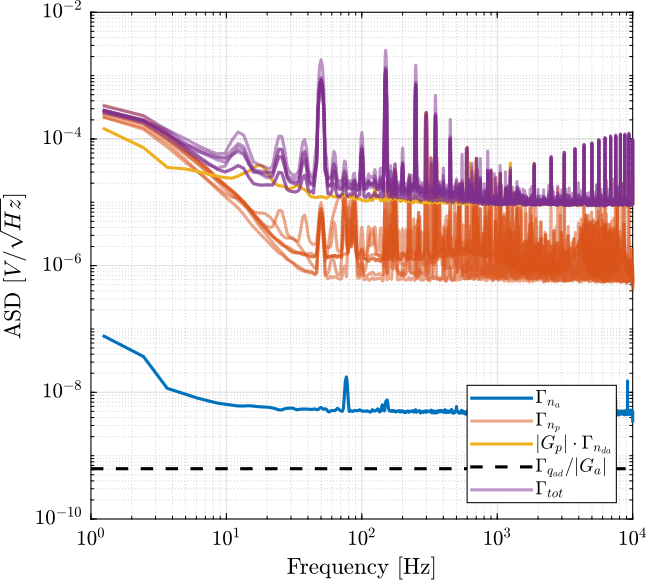
Figure 14: Amplitude Spectral Density of the measured noise and of the individual sources of noise
The output noise of the PD200 amplifier is limited by the noise of the DAC. Having a DAC with lower noise could lower the output noise of the PD200. SSI2V DACs will be used to verify that.
5.8 20bits DAC noise measurement
Let’s now measure the noise of another DAC called the “SSI2V” (doc). It is a 20bits DAC with an output of +/-10.48 V and a very low noise.
The measurement setup is the same as the one in Figure 12.
win = hanning(ceil(0.5/Ts));
[pxx, f] = pwelch(ssi2v.Vn, win, [], [], Fs);
ssi2v.pxx = pxx;
ssi2v.f = f;
The obtained noise of the SSI2V DAC is shown in Figure 15 and compared with the noise of the 16bits DAC. It is shown to be much smaller (~1 order of magnitude).
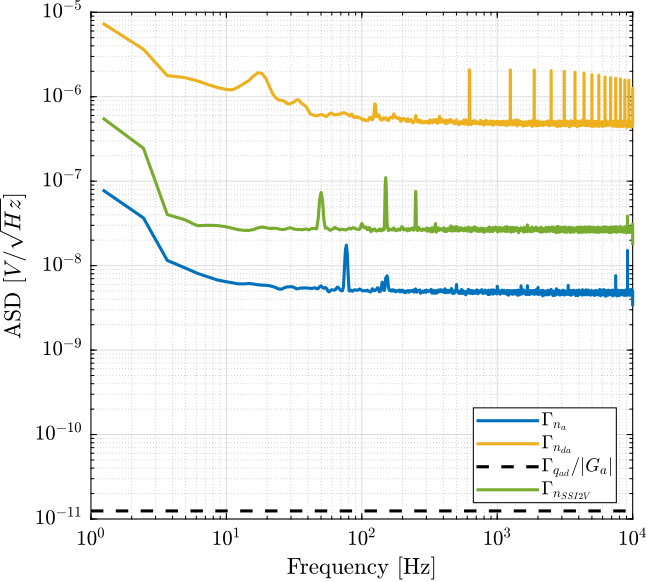
Figure 15: Amplitude Spectral Density of the SSI2V DAC’s noise
Using the SSI2V as the DAC with the PD200 should give much better noise output than using the 16bits DAC. The limiting factor should then be the noise of the PD200 itself.
6 Transfer Function measurement
6.1 Setup
In order to measure the transfer function from the input voltage \(V_{in}\) to the output voltage \(V_{out}\), the test bench shown in Figure 16 is used.
Here are the documentation of the equipment used for this test bench:
- Voltage Amplifier PD200
- Load Capacitor EPCOS 10uF Multilayer Ceramic Capacitor
- Speedgoat DAC/ADC IO313
For this measurement, the sampling frequency of the Speedgoat ADC should be as high as possible.
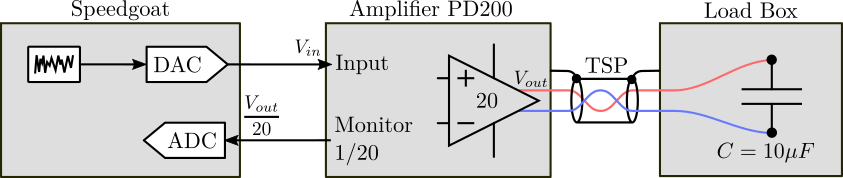
Figure 16: Schematic of the test bench to estimate the dynamics from voltage input \(V_{in}\) to voltage output \(V_{out}\)
6.2 Maximum Frequency/Voltage to not overload the amplifier
The maximum current is 1A [rms] which corresponds to 0.7A in amplitude of the sin wave.
The impedance of the capacitance is: \[ Z_C(\omega) = \frac{1}{jC\omega} \]
Therefore the relation between the output current amplitude and the output voltage amplitude for sinusoidal waves of frequency \(\omega\): \[ V_{out} = \frac{1}{C\omega} I_{out} \]
Moreover, there is a gain of 20 between the input voltage and the output voltage: \[ 20 V_{in} = \frac{1}{C\omega} I_{out} \]
For a specified voltage input amplitude \(V_{in}\), the maximum frequency at which the output current reaches its maximum value is: \[ \omega_{\text{max}} = \frac{1}{20 C V_{in}} I_{out,\text{max}} \]
\(\omega_max\) as a function of \(V_{in}\) is shown in Figure 17.
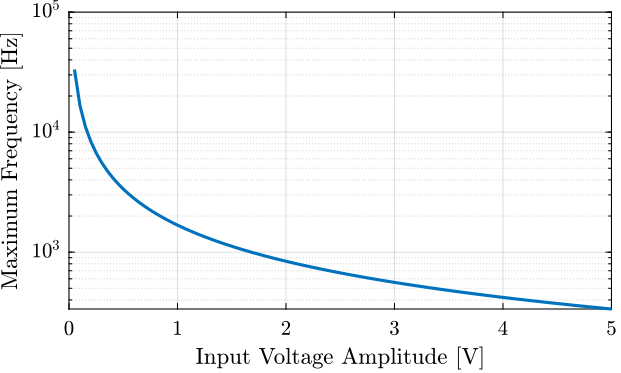
Figure 17: Maximum frequency as a function of the excitation voltage amplitude
6.3 Obtained Transfer Functions
Several identifications using sweep sin were performed with input voltage amplitude ranging from 0.1V to 4V.
The obtained frequency response functions are shown in Figure 18. As the input voltage increases, the voltage drop is increasing.
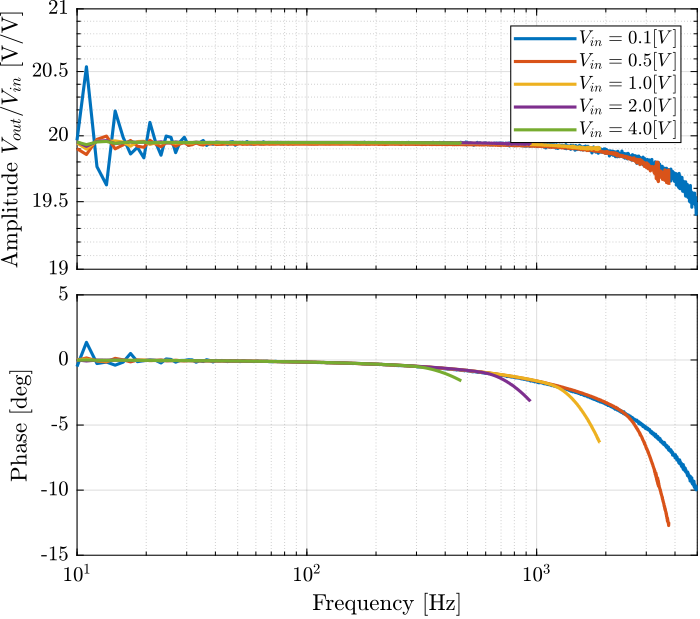
Figure 18: Transfer function for the PD200 amplitude between \(V_{in}\) and \(V_{out}\) for multiple voltage amplitudes
The small signal transfer function of the amplifier can be approximated by a first order low pass filter.
Gp = 19.95/(1 + s/2/pi/35e3);
The comparison from the model and measurements are shown in Figure 19.
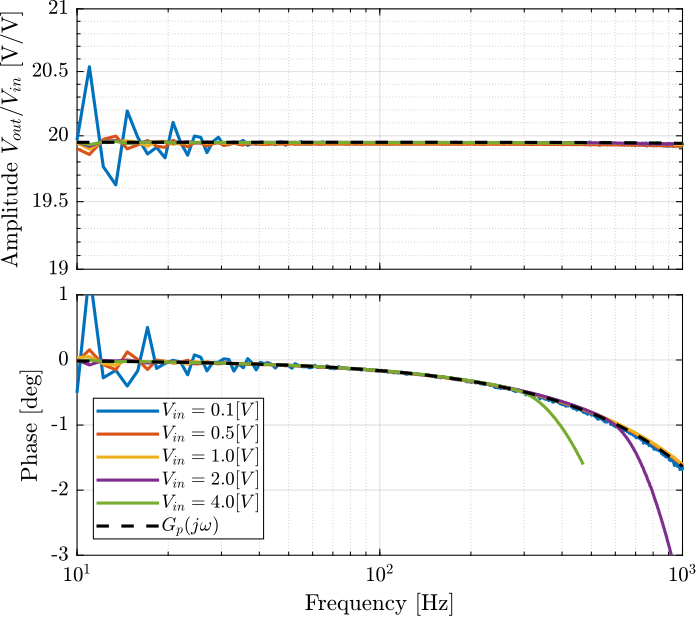
Figure 19: Comparison of the model transfer function and the measured frequency response function
7 Conclusion
| Characteristics | Measurement | Manual | Specification |
|---|---|---|---|
| Input Voltage Range | - | +/- 10 [V] | +/- 10 [V] |
| Output Voltage Range | - | -50/150 [V] | -20/150 [V] |
| Gain | 20 [V/V] | - | |
| Maximum RMS current | 0.9 [A] | > 50 [mA] | |
| Maximum Pulse current | 10 [A] | - | |
| Slew Rate | 150 [V/us] | - | |
| Noise (10uF load) | 0.7 [mV RMS] | < 2 [mV rms] | |
| Small Signal Bandwidth (10uF load) | 7.4 [kHz] | > 5 [kHz] | |
| Large Signal Bandwidth (150V, 10uF) | 300 [Hz] | - |
