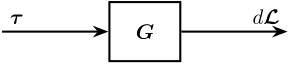Nano-Hexapod - Test Bench
Table of Contents
- 1. Encoders fixed to the Struts - Dynamics
- 1.1. Identification of the dynamics
- 1.2. Comparison with the Simscape Model
- 1.2.1. Load measured FRF
- 1.2.2. Dynamics from Actuator to Force Sensors
- 1.2.3. Dynamics from Actuator to Encoder
- 1.2.4. Effect of a change in bending damping of the joints
- 1.2.5. Effect of a change in damping factor of the APA
- 1.2.6. Effect of a change in stiffness damping coef of the APA
- 1.2.7. Effect of a change in mass damping coef of the APA
- 1.2.8. Using Flexible model
- 1.2.9. Flexible model + encoders fixed to the plates
- 1.3. Integral Force Feedback
- 1.4. Modal Analysis
- 1.5. Conclusion
- 2. Encoders fixed to the plates - Dynamics
- 3. Decentralized High Authority Control with Integral Force Feedback
- 3.1. Reference Tracking - Trajectories
- 3.2. First Basic High Authority Controller
- 3.3. Interaction Analysis and Decoupling
- 3.3.1. Parameters
- 3.3.2. No Decoupling (Decentralized)
- 3.3.3. Static Decoupling
- 3.3.4. Decoupling at the Crossover
- 3.3.5. SVD Decoupling
- 3.3.6. Dynamic decoupling
- 3.3.7. Jacobian Decoupling - Center of Stiffness
- 3.3.8. Jacobian Decoupling - Center of Mass
- 3.3.9. Decoupling Comparison
- 3.3.10. Decoupling Robustness
- 3.3.11. Conclusion
- 3.4. Robust High Authority Controller
- 4. Functions
This report is also available as a pdf.
This document is dedicated to the experimental study of the nano-hexapod shown in Figure 1.

Figure 1: Nano-Hexapod
Here are the documentation of the equipment used for this test bench (lots of them are shwon in Figure 2):

Figure 2: Nano-Hexapod and the control electronics
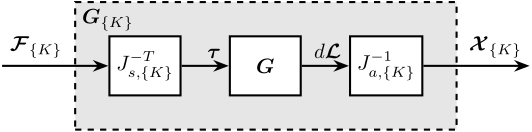
In Figure 3 is shown a block diagram of the experimental setup. When possible, the notations are consistent with this diagram and summarized in Table 1.
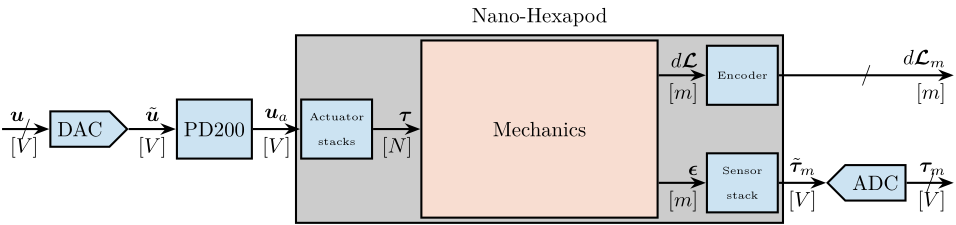
Figure 3: Block diagram of the system with named signals
| Unit | Matlab | Vector | Elements | |
|---|---|---|---|---|
| Control Input (wanted DAC voltage) | [V] |
u |
\(\bm{u}\) | \(u_i\) |
| DAC Output Voltage | [V] |
u |
\(\tilde{\bm{u}}\) | \(\tilde{u}_i\) |
| PD200 Output Voltage | [V] |
ua |
\(\bm{u}_a\) | \(u_{a,i}\) |
| Actuator applied force | [N] |
tau |
\(\bm{\tau}\) | \(\tau_i\) |
| Strut motion | [m] |
dL |
\(d\bm{\mathcal{L}}\) | \(d\mathcal{L}_i\) |
| Encoder measured displacement | [m] |
dLm |
\(d\bm{\mathcal{L}}_m\) | \(d\mathcal{L}_{m,i}\) |
| Force Sensor strain | [m] |
epsilon |
\(\bm{\epsilon}\) | \(\epsilon_i\) |
| Force Sensor Generated Voltage | [V] |
taum |
\(\tilde{\bm{\tau}}_m\) | \(\tilde{\tau}_{m,i}\) |
| Measured Generated Voltage | [V] |
taum |
\(\bm{\tau}_m\) | \(\tau_{m,i}\) |
| Motion of the top platform | [m,rad] |
dX |
\(d\bm{\mathcal{X}}\) | \(d\mathcal{X}_i\) |
| Metrology measured displacement | [m,rad] |
dXm |
\(d\bm{\mathcal{X}}_m\) | \(d\mathcal{X}_{m,i}\) |
This document is divided in the following sections:
- Section 1: the dynamics of the nano-hexapod when the encoders are fixed to the struts is studied.
- Section 2: the same is done when the encoders are fixed to the plates.
- Section 3: a decentralized HAC-LAC strategy is studied and implemented.
1. Encoders fixed to the Struts - Dynamics
In this section, the encoders are fixed to the struts.
It is divided in the following sections:
- Section 1.1: the transfer function matrix from the actuators to the force sensors and to the encoders is experimentally identified.
- Section 1.2: the obtained FRF matrix is compared with the dynamics of the simscape model
- Section 1.3: decentralized Integral Force Feedback (IFF) is applied and its performances are evaluated.
- Section 1.4: a modal analysis of the nano-hexapod is performed
1.1. Identification of the dynamics
1.1.1. Load Measurement Data
%% Load Identification Data meas_data_lf = {}; for i = 1:6 meas_data_lf(i) = {load(sprintf('mat/frf_data_exc_strut_%i_noise_lf.mat', i), 't', 'Va', 'Vs', 'de')}; meas_data_hf(i) = {load(sprintf('mat/frf_data_exc_strut_%i_noise_hf.mat', i), 't', 'Va', 'Vs', 'de')}; end
1.1.2. Spectral Analysis - Setup
%% Setup useful variables % Sampling Time [s] Ts = (meas_data_lf{1}.t(end) - (meas_data_lf{1}.t(1)))/(length(meas_data_lf{1}.t)-1); % Sampling Frequency [Hz] Fs = 1/Ts; % Hannning Windows win = hanning(ceil(1*Fs)); % And we get the frequency vector [~, f] = tfestimate(meas_data_lf{1}.Va, meas_data_lf{1}.de, win, [], [], 1/Ts); i_lf = f < 250; % Points for low frequency excitation i_hf = f > 250; % Points for high frequency excitation
1.1.3. Transfer function from Actuator to Encoder
First, let’s compute the coherence from the excitation voltage and the displacement as measured by the encoders (Figure 4).
%% Coherence coh_dvf = zeros(length(f), 6, 6); for i = 1:6 coh_dvf_lf = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts); coh_dvf_hf = mscohere(meas_data_hf{i}.Va, meas_data_hf{i}.de, win, [], [], 1/Ts); coh_dvf(:,:,i) = [coh_dvf_lf(i_lf, :); coh_dvf_hf(i_hf, :)]; end
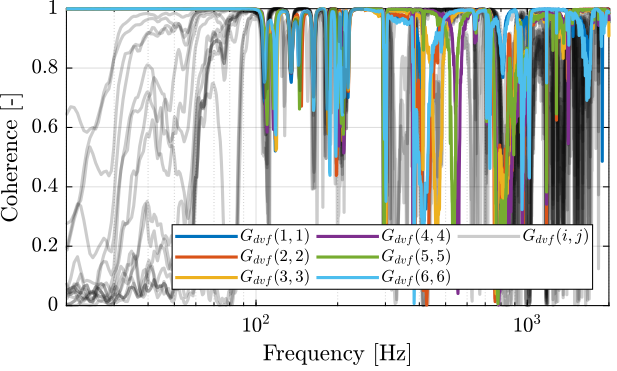
Figure 4: Obtained coherence for the DVF plant
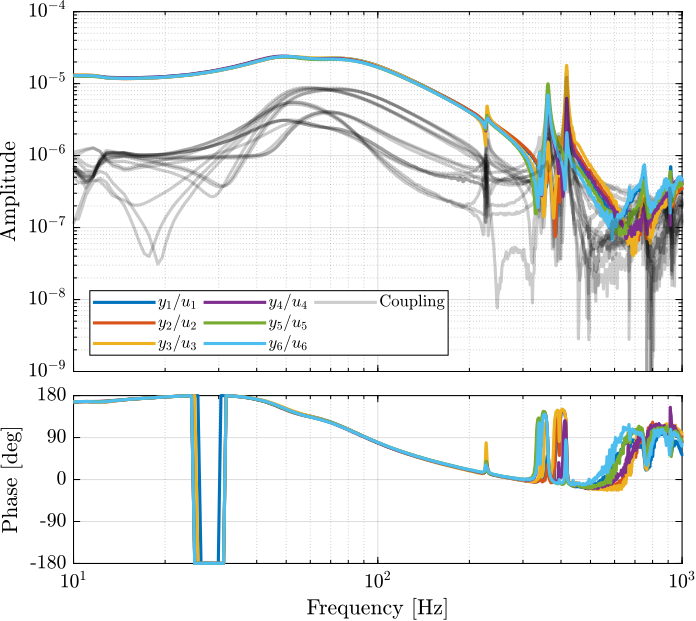
Then the 6x6 transfer function matrix is estimated (Figure 5).
%% DVF Plant (transfer function from u to dLm) G_dvf = zeros(length(f), 6, 6); for i = 1:6 G_dvf_lf = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts); G_dvf_hf = tfestimate(meas_data_hf{i}.Va, meas_data_hf{i}.de, win, [], [], 1/Ts); G_dvf(:,:,i) = [G_dvf_lf(i_lf, :); G_dvf_hf(i_hf, :)]; end
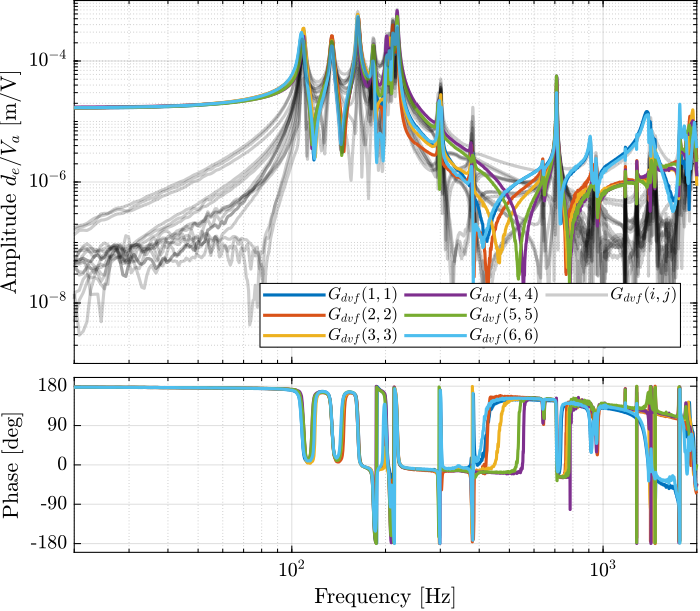
Figure 5: Measured FRF for the DVF plant
1.1.4. Transfer function from Actuator to Force Sensor
First, let’s compute the coherence from the excitation voltage and the displacement as measured by the encoders (Figure 6).
%% Coherence for the IFF plant coh_iff = zeros(length(f), 6, 6); for i = 1:6 coh_iff_lf = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts); coh_iff_hf = mscohere(meas_data_hf{i}.Va, meas_data_hf{i}.Vs, win, [], [], 1/Ts); coh_iff(:,:,i) = [coh_iff_lf(i_lf, :); coh_iff_hf(i_hf, :)]; end
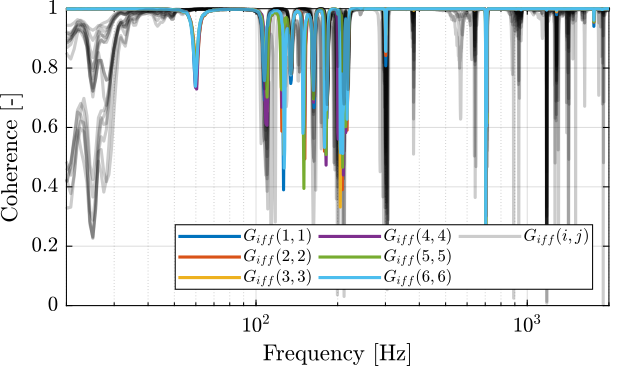
Figure 6: Obtained coherence for the IFF plant
Then the 6x6 transfer function matrix is estimated (Figure 7).
%% IFF Plant G_iff = zeros(length(f), 6, 6); for i = 1:6 G_iff_lf = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts); G_iff_hf = tfestimate(meas_data_hf{i}.Va, meas_data_hf{i}.Vs, win, [], [], 1/Ts); G_iff(:,:,i) = [G_iff_lf(i_lf, :); G_iff_hf(i_hf, :)]; end
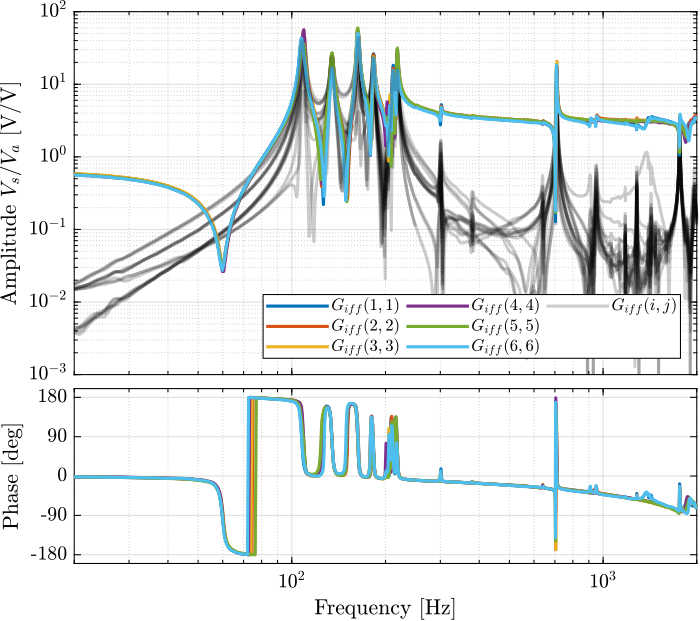
Figure 7: Measured FRF for the IFF plant
1.1.5. Save Identified Plants
save('matlab/mat/identified_plants_enc_struts.mat', 'f', 'Ts', 'G_iff', 'G_dvf')
1.2. Comparison with the Simscape Model
In this section, the measured dynamics is compared with the dynamics estimated from the Simscape model.
1.2.1. Load measured FRF
%% Load data load('identified_plants_enc_struts.mat', 'f', 'Ts', 'G_iff', 'G_dvf')
1.2.2. Dynamics from Actuator to Force Sensors
%% Initialize Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', '2dof');
%% Identify the IFF Plant (transfer function from u to taum) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dum'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
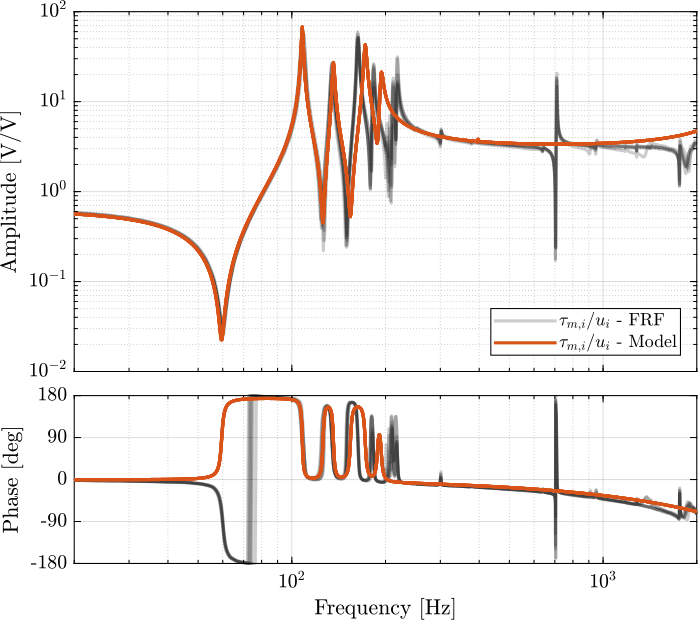
Figure 8: Diagonal elements of the IFF Plant
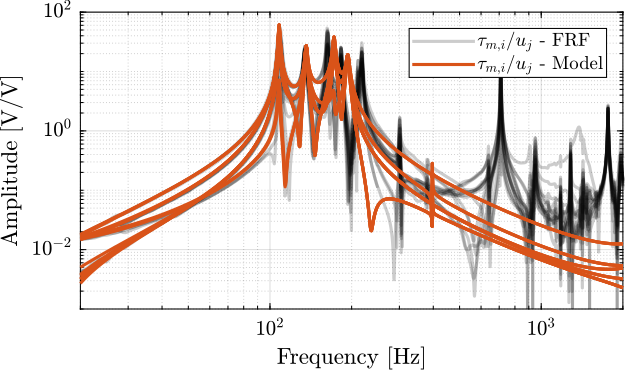
Figure 9: Off diagonal elements of the IFF Plant
1.2.3. Dynamics from Actuator to Encoder
%% Initialization of the Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', 'flexible');
%% Identify the DVF Plant (transfer function from u to dLm) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders Gdvf = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
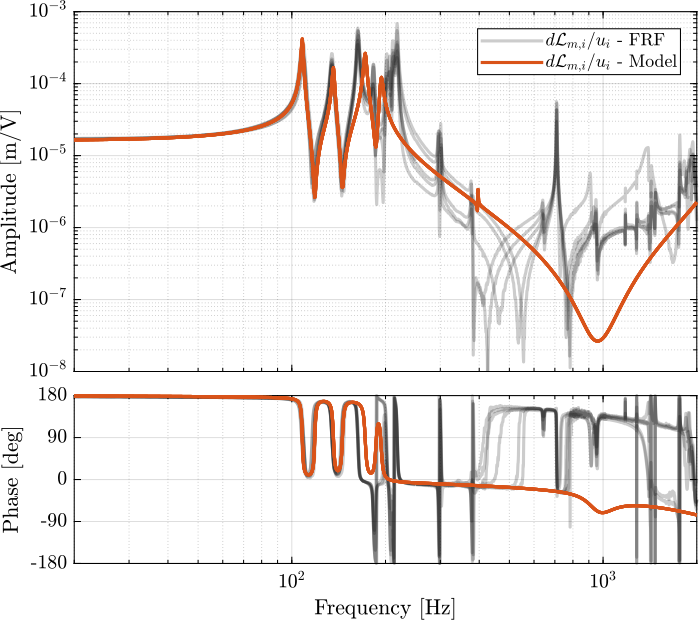
Figure 10: Diagonal elements of the DVF Plant
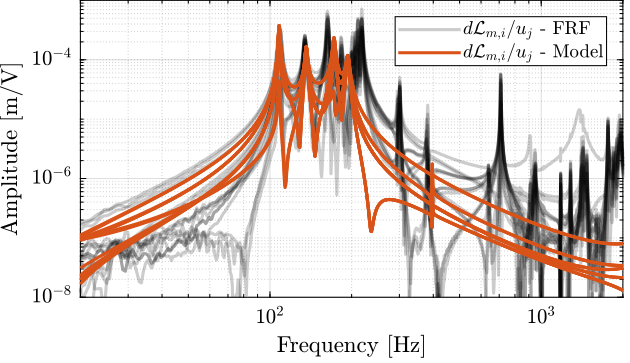
Figure 11: Off diagonal elements of the DVF Plant
1.2.4. Effect of a change in bending damping of the joints
%% Tested bending dampings [Nm/(rad/s)] cRs = [1e-3, 5e-3, 1e-2, 5e-2, 1e-1];
%% Identify the DVF Plant (transfer function from u to dLm) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders
Then the identification is performed for all the values of the bending damping.
%% Idenfity the transfer function from actuator to encoder for all bending dampins Gs = {zeros(length(cRs), 1)}; for i = 1:length(cRs) n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', 'flexible', ... 'flex_bot_cRx', cRs(i), ... 'flex_bot_cRy', cRs(i), ... 'flex_top_cRx', cRs(i), ... 'flex_top_cRy', cRs(i)); G = exp(-s*Ts)*linearize(mdl, io, 0.0, options); G.InputName = {'Va1', 'Va2', 'Va3', 'Va4', 'Va5', 'Va6'}; G.OutputName = {'dL1', 'dL2', 'dL3', 'dL4', 'dL5', 'dL6'}; Gs(i) = {G}; end
- Could be nice
- Actual damping is very small
1.2.5. Effect of a change in damping factor of the APA
%% Tested bending dampings [Nm/(rad/s)] xis = [1e-3, 5e-3, 1e-2, 5e-2, 1e-1];
%% Identify the DVF Plant (transfer function from u to dLm) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders
%% Idenfity the transfer function from actuator to encoder for all bending dampins Gs = {zeros(length(xis), 1)}; for i = 1:length(xis) n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', 'flexible', ... 'actuator_xi', xis(i)); G = exp(-s*Ts)*linearize(mdl, io, 0.0, options); G.InputName = {'Va1', 'Va2', 'Va3', 'Va4', 'Va5', 'Va6'}; G.OutputName = {'dL1', 'dL2', 'dL3', 'dL4', 'dL5', 'dL6'}; Gs(i) = {G}; end
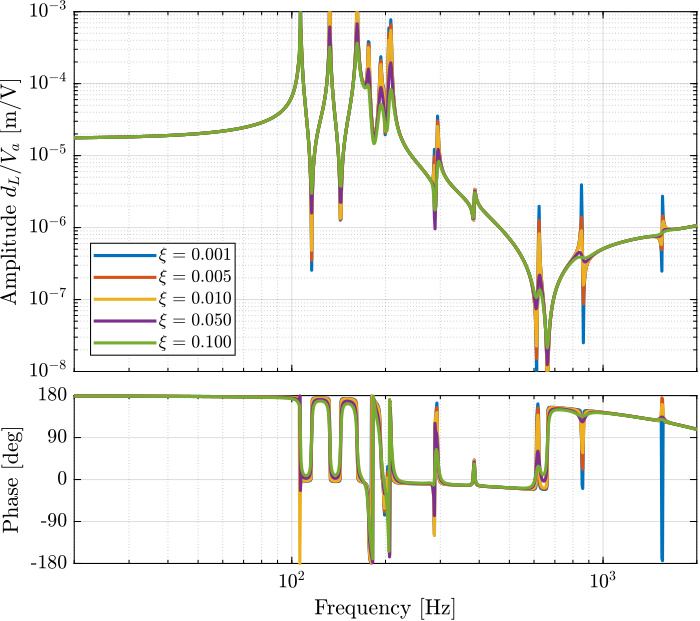
Figure 12: Effect of the APA damping factor \(\xi\) on the dynamics from \(u\) to \(d\mathcal{L}\)
Damping factor \(\xi\) has a large impact on the damping of the “spurious resonances” at 200Hz and 300Hz.
Why is the damping factor does not change the damping of the first peak?
1.2.6. Effect of a change in stiffness damping coef of the APA
m_coef = 1e1;
%% Tested bending dampings [Nm/(rad/s)] k_coefs = [1e-6, 5e-6, 1e-5, 5e-5, 1e-4];
%% Identify the DVF Plant (transfer function from u to dLm) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders
%% Idenfity the transfer function from actuator to encoder for all bending dampins Gs = {zeros(length(k_coefs), 1)}; n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', 'flexible'); for i = 1:length(k_coefs) k_coef = k_coefs(i); G = exp(-s*Ts)*linearize(mdl, io, 0.0, options); G.InputName = {'Va1', 'Va2', 'Va3', 'Va4', 'Va5', 'Va6'}; G.OutputName = {'dL1', 'dL2', 'dL3', 'dL4', 'dL5', 'dL6'}; Gs(i) = {G}; end
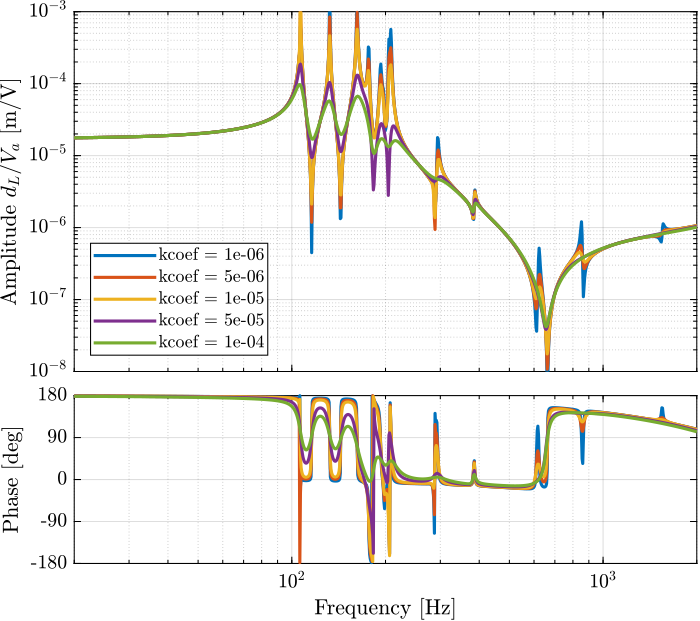
Figure 13: Effect of a change of the damping “stiffness coeficient” on the transfer function from \(u\) to \(d\mathcal{L}\)
1.2.7. Effect of a change in mass damping coef of the APA
k_coef = 1e-6;
%% Tested bending dampings [Nm/(rad/s)]
m_coefs = [1e1, 5e1, 1e2, 5e2, 1e3];
%% Identify the DVF Plant (transfer function from u to dLm) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders
%% Idenfity the transfer function from actuator to encoder for all bending dampins Gs = {zeros(length(m_coefs), 1)}; n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', 'flexible'); for i = 1:length(m_coefs) m_coef = m_coefs(i); G = exp(-s*Ts)*linearize(mdl, io, 0.0, options); G.InputName = {'Va1', 'Va2', 'Va3', 'Va4', 'Va5', 'Va6'}; G.OutputName = {'dL1', 'dL2', 'dL3', 'dL4', 'dL5', 'dL6'}; Gs(i) = {G}; end
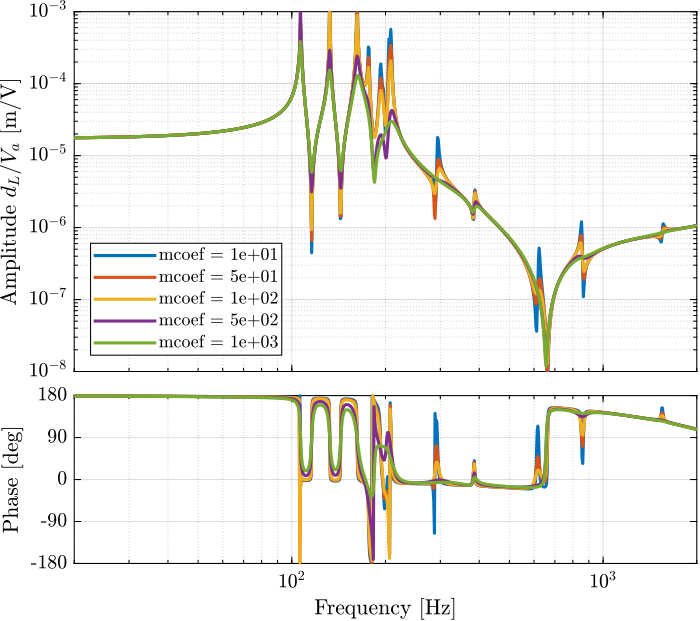
Figure 14: Effect of a change of the damping “mass coeficient” on the transfer function from \(u\) to \(d\mathcal{L}\)
1.2.8. Using Flexible model
d_aligns = [[-0.05, -0.3, 0]; [ 0, 0.5, 0]; [-0.1, -0.3, 0]; [ 0, 0.3, 0]; [-0.05, 0.05, 0]; [0, 0, 0]]*1e-3;
d_aligns = zeros(6,3); % d_aligns(1,:) = [-0.05, -0.3, 0]*1e-3; d_aligns(2,:) = [ 0, 0.3, 0]*1e-3;
%% Initialize Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', 'flexible', ... 'actuator_d_align', d_aligns);
Why do we have smaller resonances when using flexible APA? On the test bench we have the same resonance as the 2DoF model. Could it be due to the compliance in other dof of the flexible model?
%% Identify the DVF Plant (transfer function from u to dLm) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders Gdvf = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
%% Identify the IFF Plant (transfer function from u to taum) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dum'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
1.2.9. Flexible model + encoders fixed to the plates
%% Identify the IFF Plant (transfer function from u to taum) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors
d_aligns = [[-0.05, -0.3, 0]; [ 0, 0.5, 0]; [-0.1, -0.3, 0]; [ 0, 0.3, 0]; [-0.05, 0.05, 0]; [0, 0, 0]]*1e-3;
%% Initialize Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', 'flexible', ... 'actuator_d_align', d_aligns);
Gdvf_struts = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
%% Initialize Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'plates', ... 'actuator_type', 'flexible', ... 'actuator_d_align', d_aligns);
Gdvf_plates = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
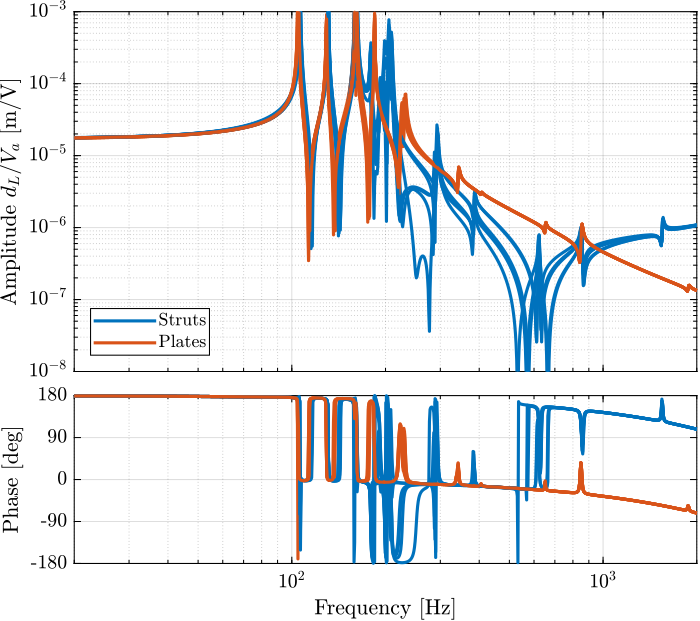
Figure 15: Comparison of the dynamics from \(V_a\) to \(d_L\) when the encoders are fixed to the struts (blue) and to the plates (red). APA are modeled as a flexible element.
1.3. Integral Force Feedback
In this section, the Integral Force Feedback (IFF) control strategy is applied to the nano-hexapod. The main goal of this to add damping to the nano-hexapod’s modes.
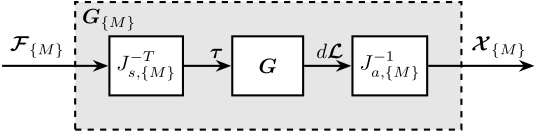
The control architecture is shown in Figure 16 where \(\bm{K}_\text{IFF}\) is a diagonal \(6 \times 6\) controller.
The system as then a new input \(\bm{u}^\prime\), and the transfer function from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) should be easier to control than the initial transfer function from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\).
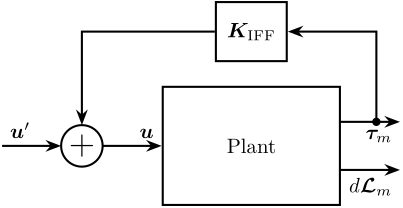
Figure 16: Integral Force Feedback Strategy
This section is structured as follow:
- Section 1.3.1: Using the Simscape model (APA taken as 2DoF model), the transfer function from \(\bm{u}\) to \(\bm{\tau}_m\) is identified. Based on the obtained dynamics, the control law is developed and the optimal gain is estimated using the Root Locus.
- Section 1.3.2: Still using the Simscape model, the effect of the IFF gain on the the transfer function from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) is studied.
- Section 1.3.3: The same is performed experimentally: several IFF gains are used and the damped plant is identified each time.
- Section 1.3.4: The damped model and the identified damped system are compared for the optimal IFF gain. It is found that IFF indeed adds a lot of damping into the system. However it is not efficient in damping the spurious struts modes.
- Section 1.3.5: Finally, a “flexible” model of the APA is used in the Simscape model and the optimally damped model is compared with the measurements.
1.3.1. IFF Control Law and Optimal Gain
Let’s use a model of the Nano-Hexapod with the encoders fixed to the struts and the APA taken as 2DoF model.
%% Initialize Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', '2dof');
The transfer function from \(\bm{u}\) to \(\bm{\tau}_m\) is identified.
%% Identify the IFF Plant (transfer function from u to taum) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dum'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
The IFF controller is defined as shown below:
%% IFF Controller Kiff_g1 = -(1/(s + 2*pi*40))*... % LPF: provides integral action above 40Hz (s/(s + 2*pi*30))*... % HPF: limit low frequency gain (1/(1 + s/2/pi/500))*... % LPF: more robust to high frequency resonances eye(6); % Diagonal 6x6 controller
Then, the poles of the system are shown in the complex plane as a function of the controller gain (i.e. Root Locus plot) in Figure 17. A gain of \(400\) is chosen as the “optimal” gain as it visually seems to be the gain that adds the maximum damping to all the suspension modes simultaneously.
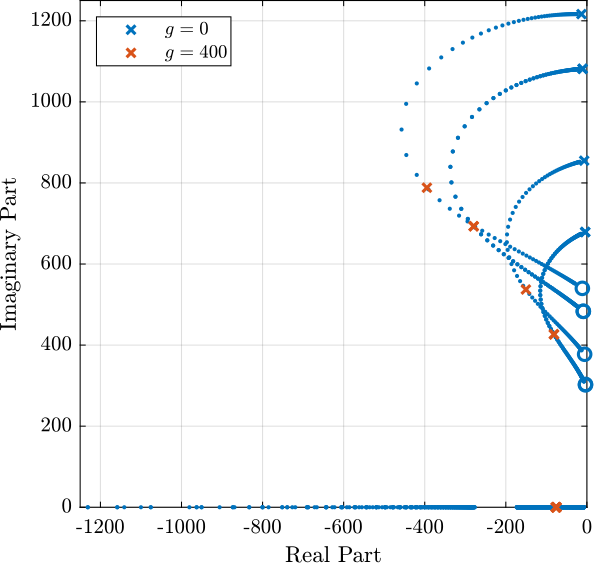
Figure 17: Root Locus for the IFF control strategy
Then the “optimal” IFF controller is:
%% IFF controller with Optimal gain Kiff = 400*Kiff_g1;
And it is saved for further use.
save('mat/Kiff.mat', 'Kiff')
The bode plots of the “diagonal” elements of the loop gain are shown in Figure 18. It is shown that the phase and gain margins are quite high and the loop gain is large arround the resonances.
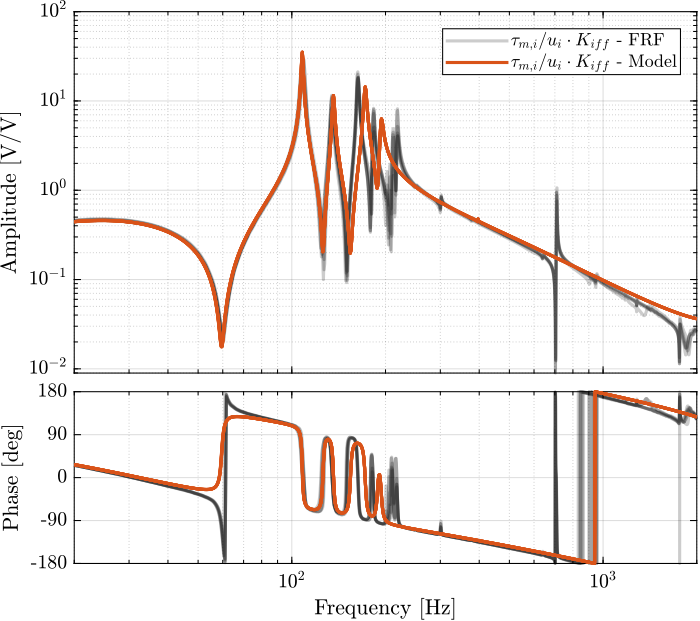
Figure 18: Bode plot of the “decentralized loop gain” \(G_\text{iff}(i,i) \times K_\text{iff}(i,i)\)
1.3.2. Effect of IFF on the plant - Simulations
Still using the Simscape model with encoders fixed to the struts and 2DoF APA, the IFF strategy is tested.
%% Initialize the Simscape model in closed loop n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', '2dof', ... 'controller_type', 'iff');
The following IFF gains are tried:
%% Tested IFF gains
iff_gains = [4, 10, 20, 40, 100, 200, 400];
And the transfer functions from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) are identified for all the IFF gains.
%% Identify the (damped) transfer function from u to dLm for different values of the IFF gain Gd_iff = {zeros(1, length(iff_gains))}; clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Strut Displacement (encoder) for i = 1:length(iff_gains) Kiff = iff_gains(i)*Kiff_g1*eye(6); % IFF Controller Gd_iff(i) = {exp(-s*Ts)*linearize(mdl, io, 0.0, options)}; isstable(Gd_iff{i}) end
The obtained dynamics are shown in Figure 19.
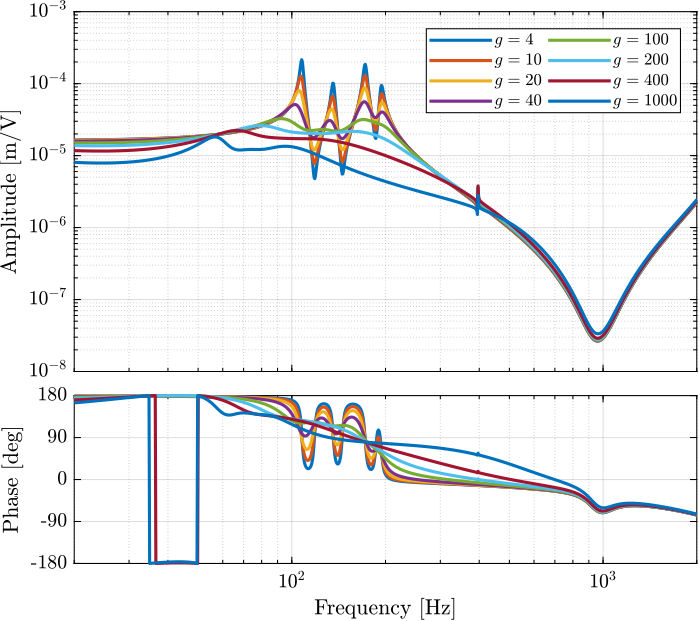
Figure 19: Effect of the IFF gain \(g\) on the transfer function from \(\bm{\tau}\) to \(d\bm{\mathcal{L}}_m\)
1.3.3. Effect of IFF on the plant - Experimental Results
The IFF strategy is applied experimentally and the transfer function from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) is identified for all the defined values of the gain.
1.3.3.1. Load Data
First load the identification data.
%% Load Identification Data meas_iff_gains = {}; for i = 1:length(iff_gains) meas_iff_gains(i) = {load(sprintf('mat/iff_strut_1_noise_g_%i.mat', iff_gains(i)), 't', 'Vexc', 'Vs', 'de', 'u')}; end
1.3.3.2. Spectral Analysis - Setup
And define the useful variables that will be used for the identification using the tfestimate function.
%% Setup useful variables % Sampling Time [s] Ts = (meas_iff_gains{1}.t(end) - (meas_iff_gains{1}.t(1)))/(length(meas_iff_gains{1}.t)-1); % Sampling Frequency [Hz] Fs = 1/Ts; % Hannning Windows win = hanning(ceil(1*Fs)); % And we get the frequency vector [~, f] = tfestimate(meas_iff_gains{1}.Vexc, meas_iff_gains{1}.de, win, [], [], 1/Ts);
1.3.3.3. DVF Plant
The transfer functions are estimated for all the values of the gain.
%% DVF Plant (transfer function from u to dLm) G_iff_gains = {}; for i = 1:length(iff_gains) G_iff_gains{i} = tfestimate(meas_iff_gains{i}.Vexc, meas_iff_gains{i}.de(:,1), win, [], [], 1/Ts); end
The obtained dynamics as shown in the bode plot in Figure 20. The dashed curves are the results obtained using the model, and the solid curves the results from the experimental identification.
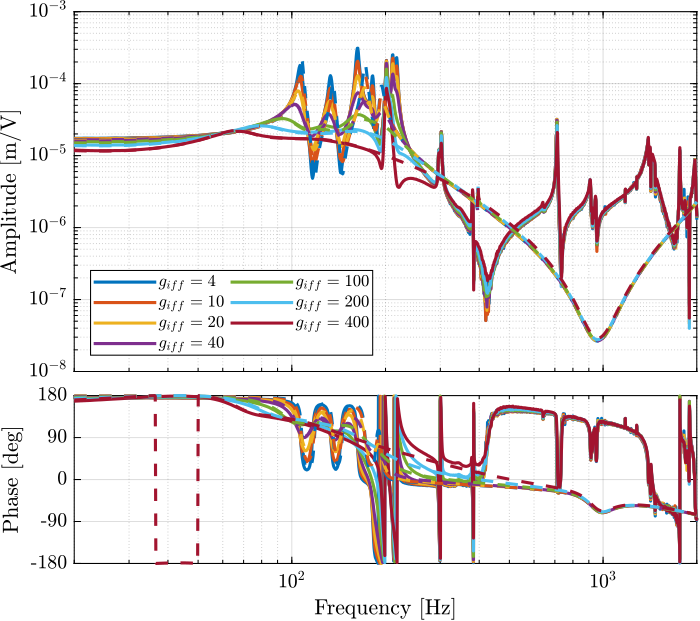
Figure 20: Transfer function from \(u\) to \(d\mathcal{L}_m\) for multiple values of the IFF gain
The bode plot is then zoomed on the suspension modes of the nano-hexapod in Figure 21.
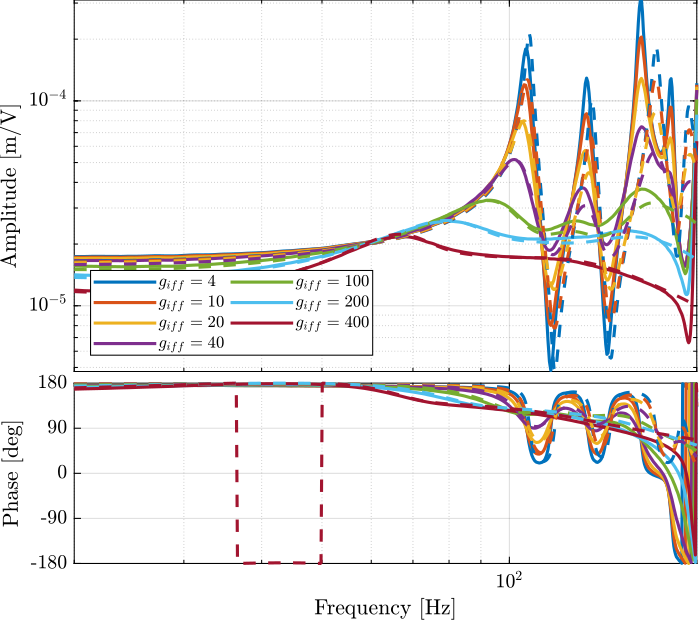
Figure 21: Transfer function from \(u\) to \(d\mathcal{L}_m\) for multiple values of the IFF gain (Zoom)
The IFF control strategy is very effective for the damping of the suspension modes. It however does not damp the modes at 200Hz, 300Hz and 400Hz (flexible modes of the APA).
Also, the experimental results and the models obtained from the Simscape model are in agreement concerning the damped system (up to the flexible modes).
1.3.3.4. Experimental Results - Comparison of the un-damped and fully damped system
The un-damped and damped experimental plants are compared in Figure 22 (diagonal terms).
It is very clear that all the suspension modes are very well damped thanks to IFF. However, there is little to no effect on the flexible modes of the struts and of the plate.
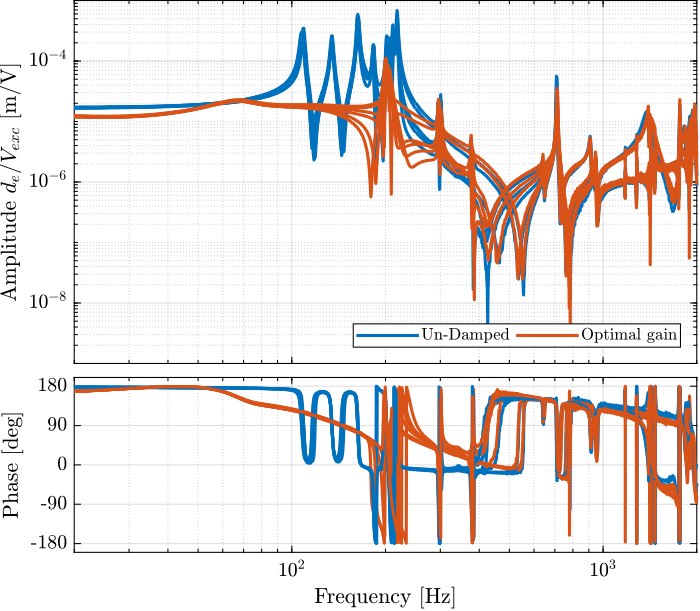
Figure 22: Comparison of the diagonal elements of the tranfer function from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\) without active damping and with optimal IFF gain
1.3.4. Experimental Results - Damped Plant with Optimal gain
1.3.4.1. Load Data
The experimental data are loaded.
%% Load Identification Data meas_iff_struts = {}; for i = 1:6 meas_iff_struts(i) = {load(sprintf('mat/iff_strut_%i_noise_g_400.mat', i), 't', 'Vexc', 'Vs', 'de', 'u')}; end
1.3.4.2. Spectral Analysis - Setup
And the parameters useful for the spectral analysis are defined.
%% Setup useful variables % Sampling Time [s] Ts = (meas_iff_struts{1}.t(end) - (meas_iff_struts{1}.t(1)))/(length(meas_iff_struts{1}.t)-1); % Sampling Frequency [Hz] Fs = 1/Ts; % Hannning Windows win = hanning(ceil(1*Fs)); % And we get the frequency vector [~, f] = tfestimate(meas_iff_struts{1}.Vexc, meas_iff_struts{1}.de, win, [], [], 1/Ts);
1.3.4.3. DVF Plant
Finally, the \(6 \times 6\) plant is identified using the tfestimate function.
%% DVF Plant (transfer function from u to dLm) G_iff_opt = {}; for i = 1:6 G_iff_opt{i} = tfestimate(meas_iff_struts{i}.Vexc, meas_iff_struts{i}.de, win, [], [], 1/Ts); end
The obtained diagonal elements are compared with the model in Figure 23.
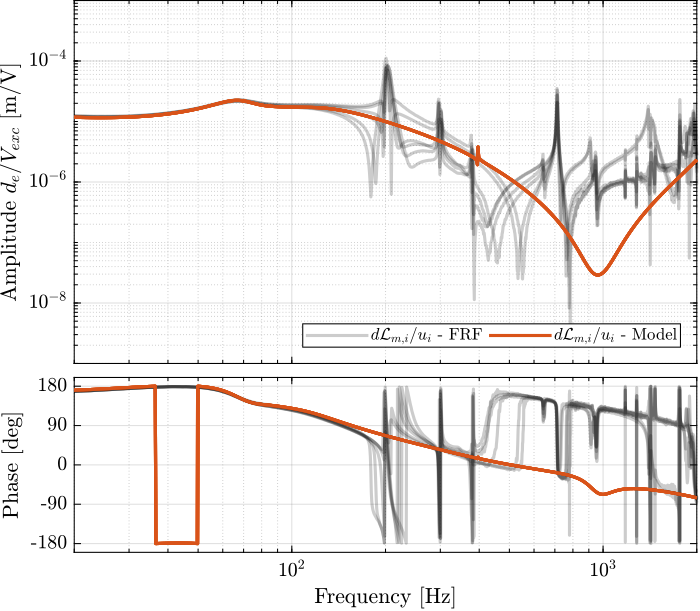
Figure 23: Comparison of the diagonal elements of the transfer functions from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\) with active damping (IFF) applied with an optimal gain \(g = 400\)
And all the off-diagonal elements are compared with the model in Figure 24.
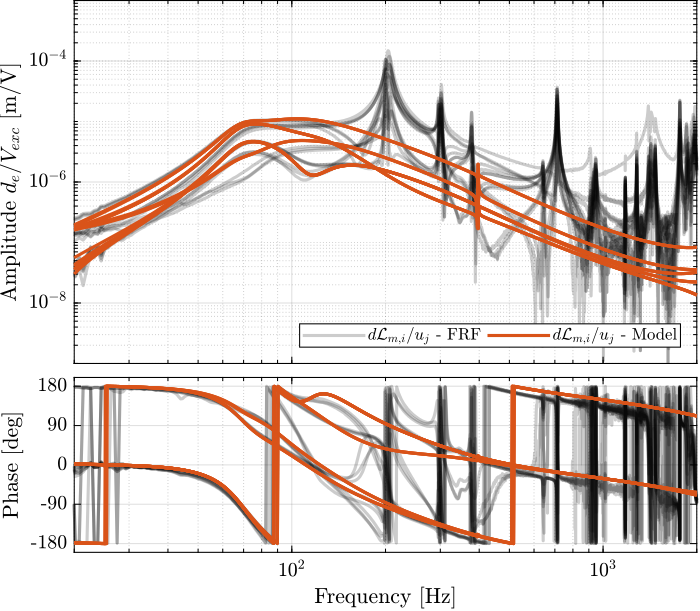
Figure 24: Comparison of the off-diagonal elements of the transfer functions from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\) with active damping (IFF) applied with an optimal gain \(g = 400\)
With the IFF control strategy applied and the optimal gain used, the suspension modes are very well damped. Remains the un-damped flexible modes of the APA (200Hz, 300Hz, 400Hz), and the modes of the plates (700Hz).
The Simscape model and the experimental results are in very good agreement.
1.3.5. Comparison with the Flexible model
When using the 2-DoF model for the APA, the flexible modes of the struts were not modelled, and it was the main limitation of the model. Now, let’s use a flexible model for the APA, and see if the obtained damped plant using the model is similar to the measured dynamics.
First, the nano-hexapod is initialized.
%% Estimated misalignement of the struts d_aligns = [[-0.05, -0.3, 0]; [ 0, 0.5, 0]; [-0.1, -0.3, 0]; [ 0, 0.3, 0]; [-0.05, 0.05, 0]; [0, 0, 0]]*1e-3; %% Initialize Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', 'flexible', ... 'actuator_d_align', d_aligns, ... 'controller_type', 'iff');
And the “optimal” controller is loaded.
%% Optimal IFF controller load('Kiff.mat', 'Kiff');
The transfer function from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) is identified using the Simscape model.
%% Linearized inputs/outputs clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Strut Displacement (encoder) %% Identification of the plant Gd_iff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
The obtained diagonal elements are shown in Figure 25 while the off-diagonal elements are shown in Figure 26.
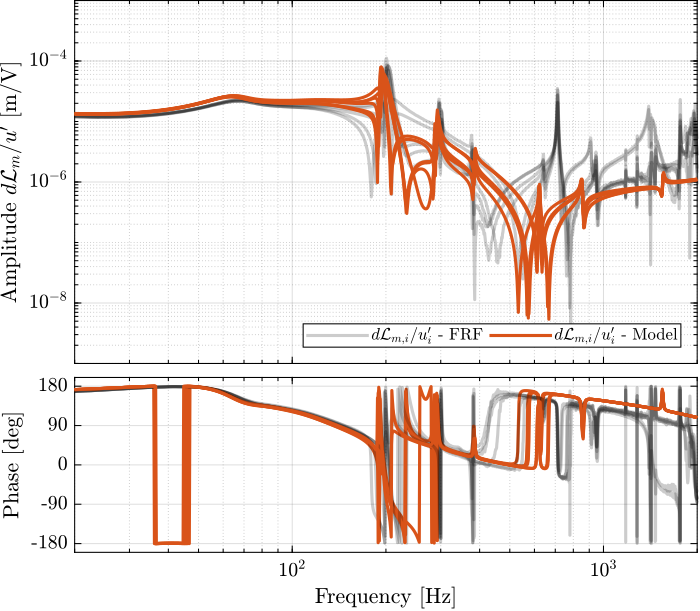
Figure 25: Diagonal elements of the transfer function from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) - comparison of the measured FRF and the identified dynamics using the flexible model
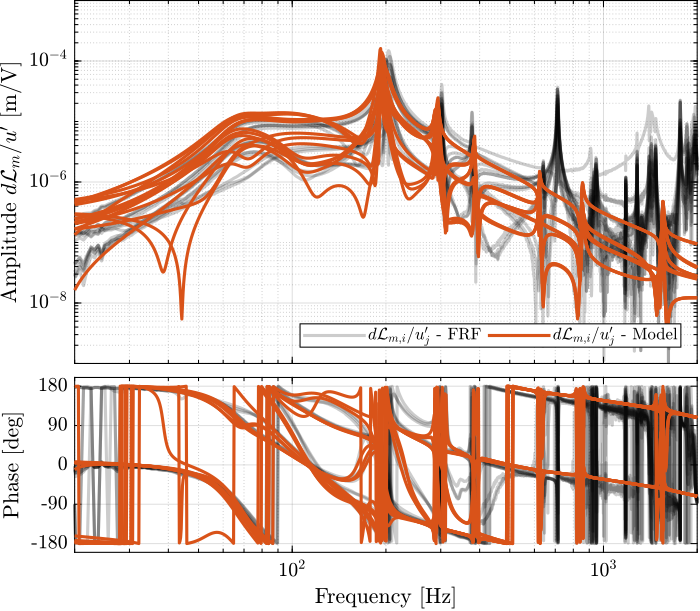
Figure 26: Off-diagonal elements of the transfer function from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) - comparison of the measured FRF and the identified dynamics using the flexible model
Using flexible models for the APA, the agreement between the Simscape model of the nano-hexapod and the measured FRF is very good.
Only the flexible mode of the top-plate is not appearing in the model which is very logical as the top plate is taken as a solid body.
1.3.6. Conclusion
The decentralized Integral Force Feedback strategy applied on the nano-hexapod is very effective in damping all the suspension modes.
The Simscape model (especially when using a flexible model for the APA) is shown to be very accurate, even when IFF is applied.
1.4. Modal Analysis
Several 3-axis accelerometers are fixed on the top platform of the nano-hexapod as shown in Figure 31.

Figure 27: Location of the accelerometers on top of the nano-hexapod
The top platform is then excited using an instrumented hammer as shown in Figure 28.

Figure 28: Example of an excitation using an instrumented hammer
From this experiment, the resonance frequencies and the associated mode shapes can be computed (Section 1.4.1). Then, in Section 1.4.2, the vertical compliance of the nano-hexapod is experimentally estimated. Finally, in Section 1.4.3, the measured compliance is compare with the estimated one from the Simscape model.
1.4.1. Obtained Mode Shapes
We can observe the mode shapes of the first 6 modes that are the suspension modes (the plate is behaving as a solid body) in Figure 29.
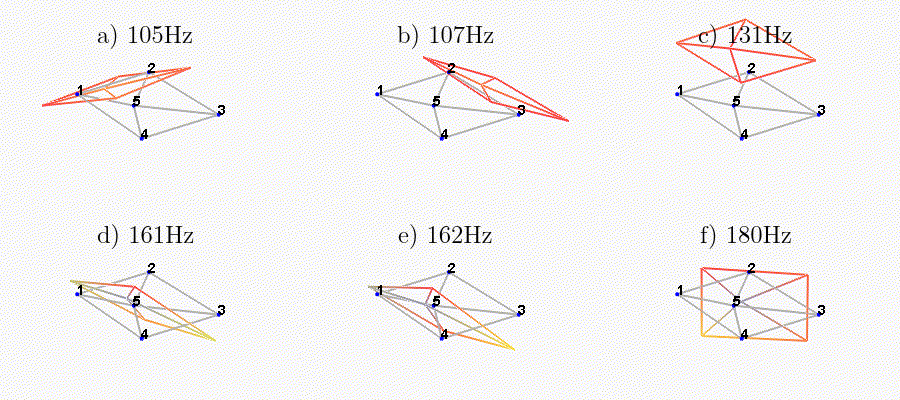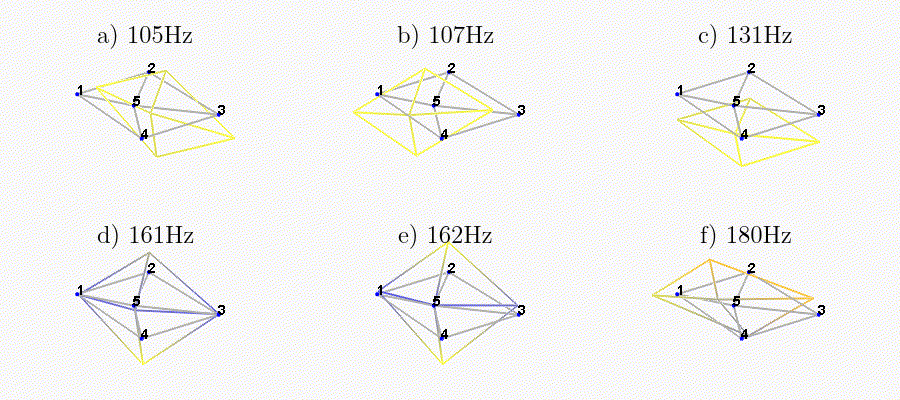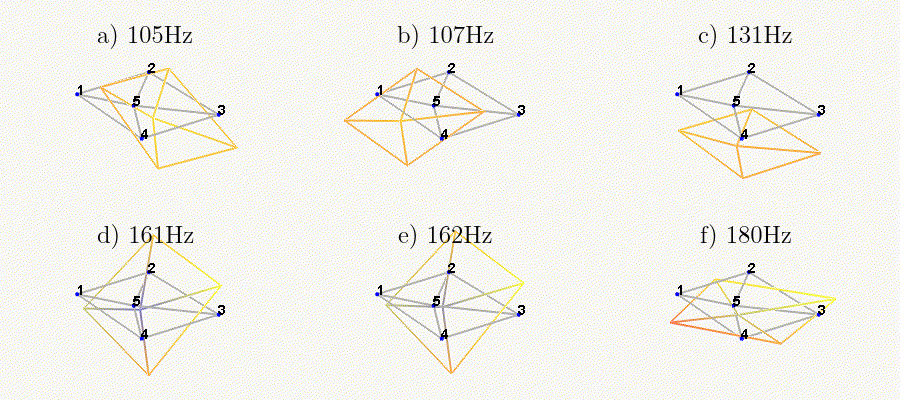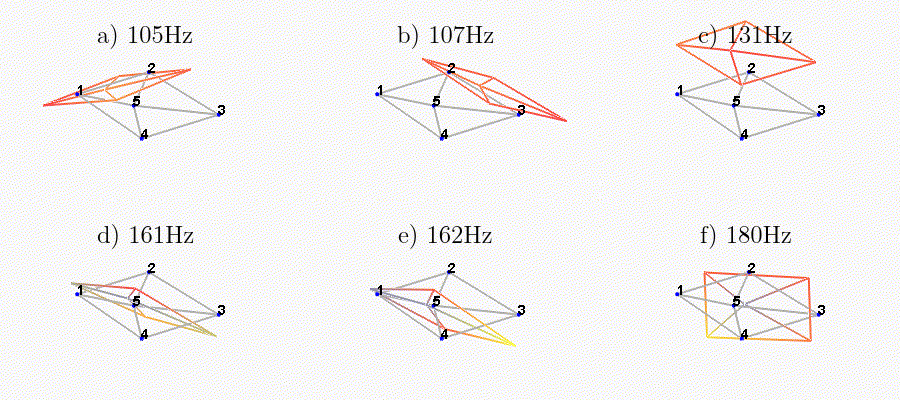
Figure 29: Measured mode shapes for the first six modes
Then, there is a mode at 692Hz which corresponds to a flexible mode of the top plate (Figure 30).
Figure 30: First flexible mode at 692Hz
The obtained modes are summarized in Table 2.
| Mode | Freq. [Hz] | Description |
|---|---|---|
| 1 | 105 | Suspension Mode: Y-translation |
| 2 | 107 | Suspension Mode: X-translation |
| 3 | 131 | Suspension Mode: Z-translation |
| 4 | 161 | Suspension Mode: Y-tilt |
| 5 | 162 | Suspension Mode: X-tilt |
| 6 | 180 | Suspension Mode: Z-rotation |
| 7 | 692 | (flexible) Membrane mode of the top platform |
1.4.2. Nano-Hexapod Compliance - Effect of IFF
In this section, we wish to estimated the effectiveness of the IFF strategy concerning the compliance.
The top plate is excited vertically using the instrumented hammer two times:
- no control loop is used
- decentralized IFF is used
The data is loaded.
frf_ol = load('Measurement_Z_axis.mat'); % Open-Loop frf_iff = load('Measurement_Z_axis_damped.mat'); % IFF
The mean vertical motion of the top platform is computed by averaging all 5 accelerometers.
%% Multiply by 10 (gain in m/s^2/V) and divide by 5 (number of accelerometers) d_frf_ol = 10/5*(frf_ol.FFT1_H1_4_1_RMS_Y_Mod + frf_ol.FFT1_H1_7_1_RMS_Y_Mod + frf_ol.FFT1_H1_10_1_RMS_Y_Mod + frf_ol.FFT1_H1_13_1_RMS_Y_Mod + frf_ol.FFT1_H1_16_1_RMS_Y_Mod)./(2*pi*frf_ol.FFT1_H1_16_1_RMS_X_Val).^2; d_frf_iff = 10/5*(frf_iff.FFT1_H1_4_1_RMS_Y_Mod + frf_iff.FFT1_H1_7_1_RMS_Y_Mod + frf_iff.FFT1_H1_10_1_RMS_Y_Mod + frf_iff.FFT1_H1_13_1_RMS_Y_Mod + frf_iff.FFT1_H1_16_1_RMS_Y_Mod)./(2*pi*frf_iff.FFT1_H1_16_1_RMS_X_Val).^2;
The vertical compliance (magnitude of the transfer function from a vertical force applied on the top plate to the vertical motion of the top plate) is shown in Figure 31.
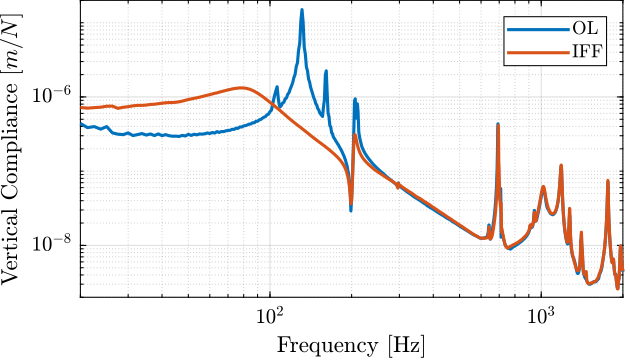
Figure 31: Measured vertical compliance with and without IFF
From Figure 31, it is clear that the IFF control strategy is very effective in damping the suspensions modes of the nano-hexapod. It also has the effect of (slightly) degrading the vertical compliance at low frequency.
It also seems some damping can be added to the modes at around 205Hz which are flexible modes of the struts.
1.4.3. Comparison with the Simscape Model
Let’s now compare the measured vertical compliance with the vertical compliance as estimated from the Simscape model.
The transfer function from a vertical external force to the absolute motion of the top platform is identified (with and without IFF) using the Simscape model. The comparison is done in Figure 32. Again, the model is quite accurate!
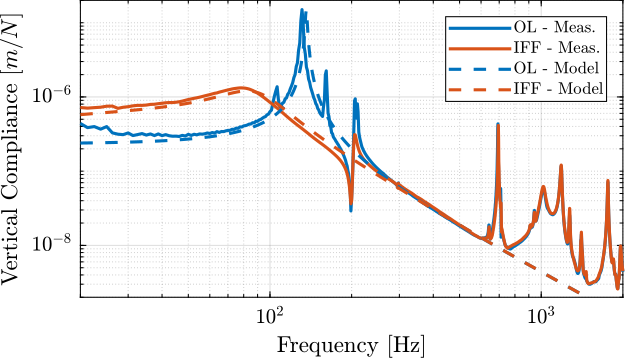
Figure 32: Measured vertical compliance with and without IFF
1.5. Conclusion
From the previous analysis, several conclusions can be drawn:
- Decentralized IFF is very effective in damping the “suspension” modes of the nano-hexapod (Figure 22)
- Decentralized IFF does not damp the “spurious” modes of the struts nor the flexible modes of the top plate (Figure 22)
- Even though the Simscape model and the experimentally measured FRF are in good agreement (Figures 25 and 26), the obtain dynamics from the control inputs \(\bm{u}\) and the encoders \(d\bm{\mathcal{L}}_m\) is very difficult to control
Therefore, in the following sections, the encoders will be fixed to the plates. The goal is to be less sensitive to the flexible modes of the struts.
2. Encoders fixed to the plates - Dynamics
In this section, the encoders are fixed to the plates rather than to the struts as shown in Figure 33.

Figure 33: Nano-Hexapod with encoders fixed to the struts
It is structured as follow:
- Section 2.1: The dynamics of the nano-hexapod is identified.
- Section 2.2: The identified dynamics is compared with the Simscape model.
- Section 2.3: The Integral Force Feedback (IFF) control strategy is applied and the dynamics of the damped nano-hexapod is identified and compare with the Simscape model.
2.1. Identification of the dynamics
In this section, the dynamics of the nano-hexapod with the encoders fixed to the plates is identified.
First, the measurement data are loaded in Section 2.1.1, then the transfer function matrix from the actuators to the encoders are estimated in Section 2.1.2. Finally, the transfer function matrix from the actuators to the force sensors is estimated in Section 2.1.3.
2.1.1. Data Loading and Spectral Analysis Setup
The actuators are excited one by one using a low pass filtered white noise. For each excitation, the 6 force sensors and 6 encoders are measured and saved.
%% Load Identification Data meas_data_lf = {}; for i = 1:6 meas_data_lf(i) = {load(sprintf('mat/frf_exc_strut_%i_enc_plates_noise.mat', i), 't', 'Va', 'Vs', 'de')}; end
2.1.2. Transfer function from Actuator to Encoder
Let’s compute the coherence from the excitation voltage \(\bm{u}\) and the displacement \(d\bm{\mathcal{L}}_m\) as measured by the encoders.
%% Coherence coh_dvf = zeros(length(f), 6, 6); for i = 1:6 coh_dvf(:, :, i) = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts); end
The obtained coherence shown in Figure 34 is quite good up to 400Hz.
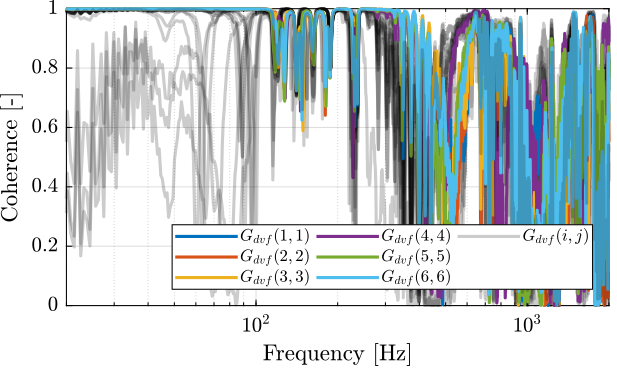
Figure 34: Obtained coherence for the DVF plant
Then the 6x6 transfer function matrix is estimated.
%% DVF Plant (transfer function from u to dLm) G_dvf = zeros(length(f), 6, 6); for i = 1:6 G_dvf(:,:,i) = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts); end
The diagonal and off-diagonal terms of this transfer function matrix are shown in Figure 35.
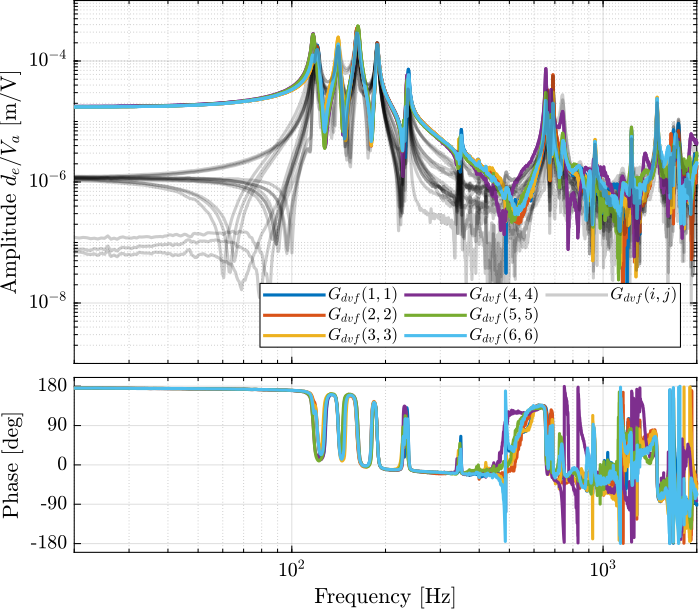
Figure 35: Measured FRF for the DVF plant
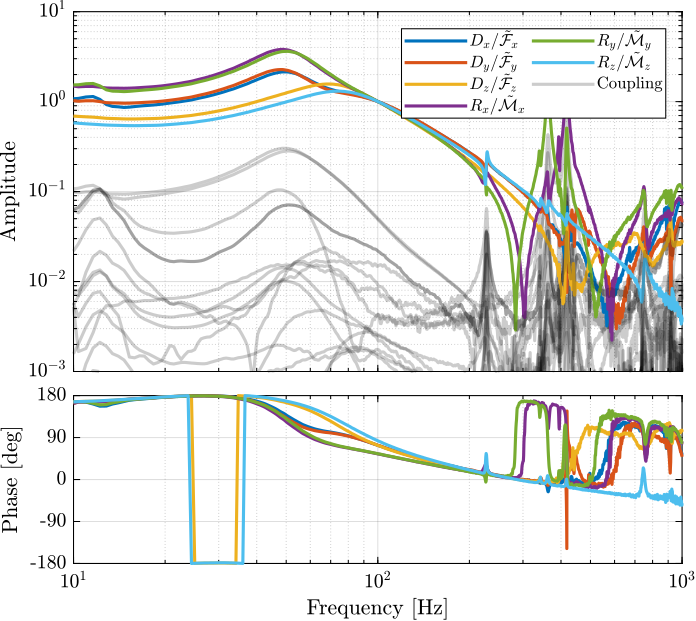
From Figure 35, we can draw few conclusions on the transfer functions from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\) when the encoders are fixed to the plates:
- the decoupling is rather good at low frequency (below the first suspension mode). The low frequency gain is constant for the off diagonal terms, whereas when the encoders where fixed to the struts, the low frequency gain of the off-diagonal terms were going to zero (Figure 5).
- the flexible modes of the struts at 226Hz and 337Hz are indeed shown in the transfer functions, but their amplitudes are rather low.
- the diagonal terms have alternating poles and zeros up to at least 600Hz: the flexible modes of the struts are not affecting the alternating pole/zero pattern. This what not the case when the encoders were fixed to the struts (Figure 5).
2.1.3. Transfer function from Actuator to Force Sensor
Let’s now compute the coherence from the excitation voltage \(\bm{u}\) and the voltage \(\bm{\tau}_m\) generated by the Force senors.
%% Coherence for the IFF plant coh_iff = zeros(length(f), 6, 6); for i = 1:6 coh_iff(:,:,i) = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts); end
The coherence is shown in Figure 36, and is very good for from 10Hz up to 2kHz.
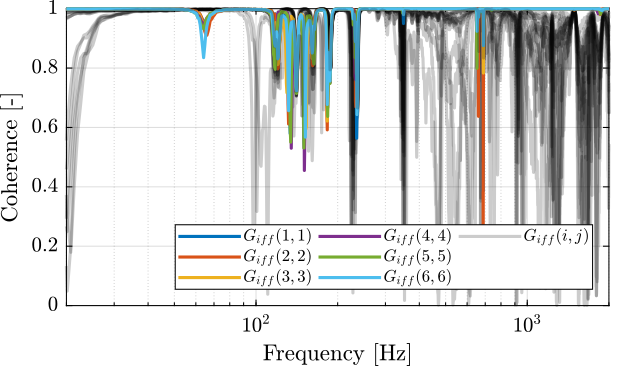
Figure 36: Obtained coherence for the IFF plant
Then the 6x6 transfer function matrix is estimated.
%% IFF Plant G_iff = zeros(length(f), 6, 6); for i = 1:6 G_iff(:,:,i) = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts); end
The bode plot of the diagonal and off-diagonal terms are shown in Figure 37.
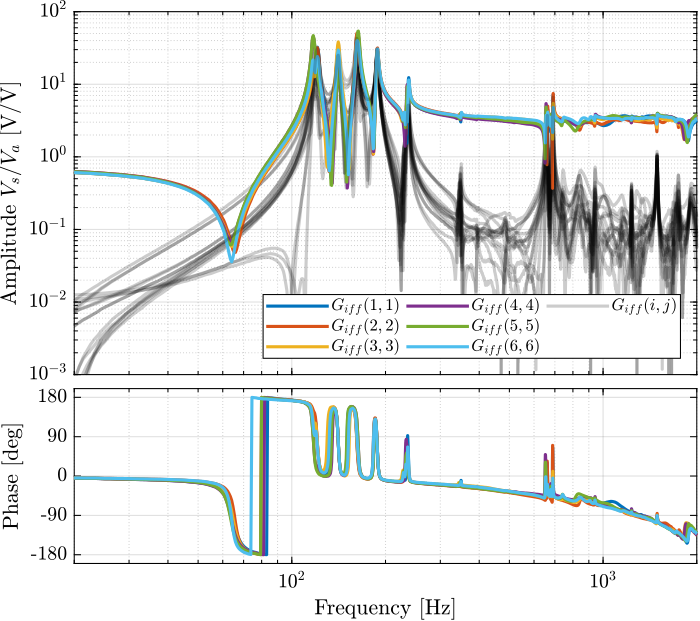
Figure 37: Measured FRF for the IFF plant
It is shown in Figure 38 that:
- The IFF plant has alternating poles and zeros
- The first flexible mode of the struts as 235Hz is appearing, and therefore is should be possible to add some damping to this mode using IFF
- The decoupling is quite good at low frequency (below the first model) as well as high frequency (above the last suspension mode, except near the flexible modes of the top plate)
2.1.4. Save Identified Plants
The identified dynamics is saved for further use.
save('mat/identified_plants_enc_plates.mat', 'f', 'Ts', 'G_iff', 'G_dvf')
2.2. Comparison with the Simscape Model
In this section, the measured dynamics done in Section 2.1 is compared with the dynamics estimated from the Simscape model.
2.2.1. Identification Setup
The nano-hexapod is initialized with the APA taken as flexible models.
%% Initialize Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'plates', ... 'actuator_type', 'flexible');
2.2.2. Dynamics from Actuator to Force Sensors
Then the transfer function from \(\bm{u}\) to \(\bm{\tau}_m\) is identified using the Simscape model.
%% Identify the IFF Plant (transfer function from u to taum) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
The identified dynamics is compared with the measured FRF:
- Figure 38: the individual transfer function from \(u_1\) (the DAC voltage for the first actuator) to the force sensors of all 6 struts are compared
- Figure 39: all the diagonal elements are compared
- Figure 40: all the off-diagonal elements are compared
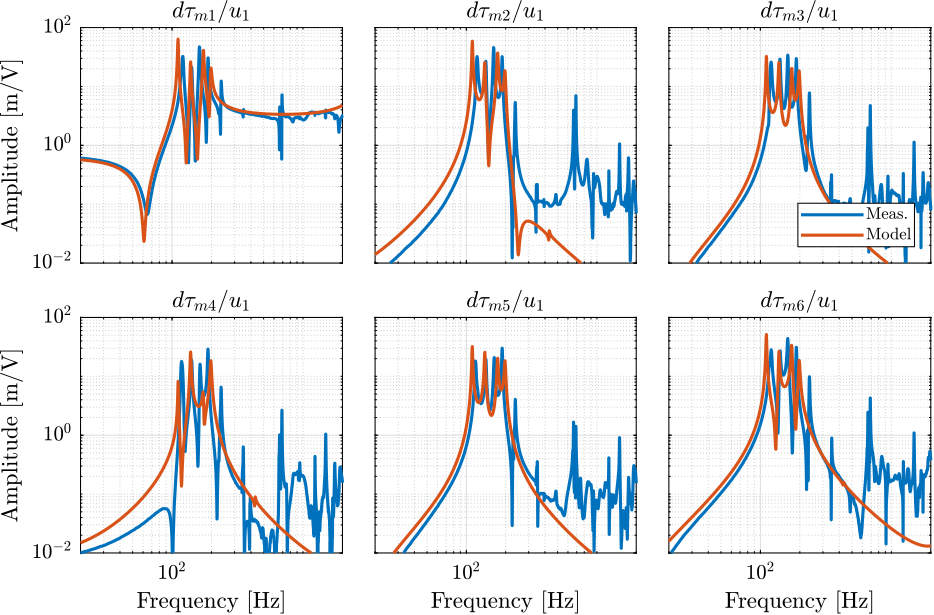
Figure 38: IFF Plant for the first actuator input and all the force senosrs
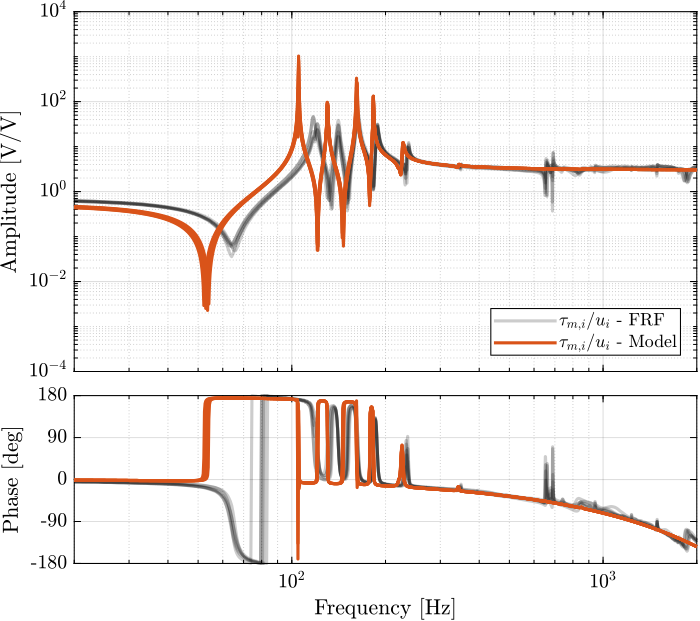
Figure 39: Diagonal elements of the IFF Plant
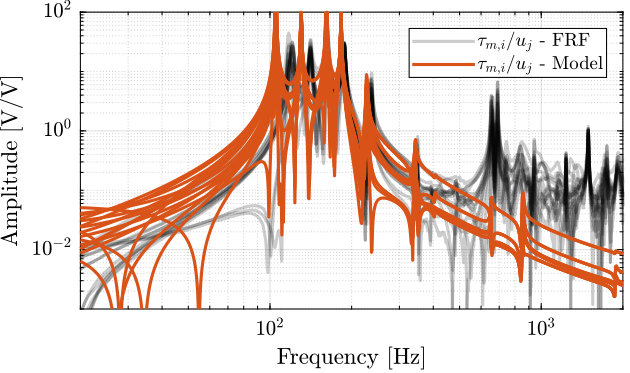
Figure 40: Off diagonal elements of the IFF Plant
2.2.3. Dynamics from Actuator to Encoder
Now, the dynamics from the DAC voltage \(\bm{u}\) to the encoders \(d\bm{\mathcal{L}}_m\) is estimated using the Simscape model.
%% Identify the DVF Plant (transfer function from u to dLm) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Encoders Gdvf = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
The identified dynamics is compared with the measured FRF:
- Figure 41: the individual transfer function from \(u_3\) (the DAC voltage for the actuator number 3) to the six encoders
- Figure 42: all the diagonal elements are compared
- Figure 43: all the off-diagonal elements are compared
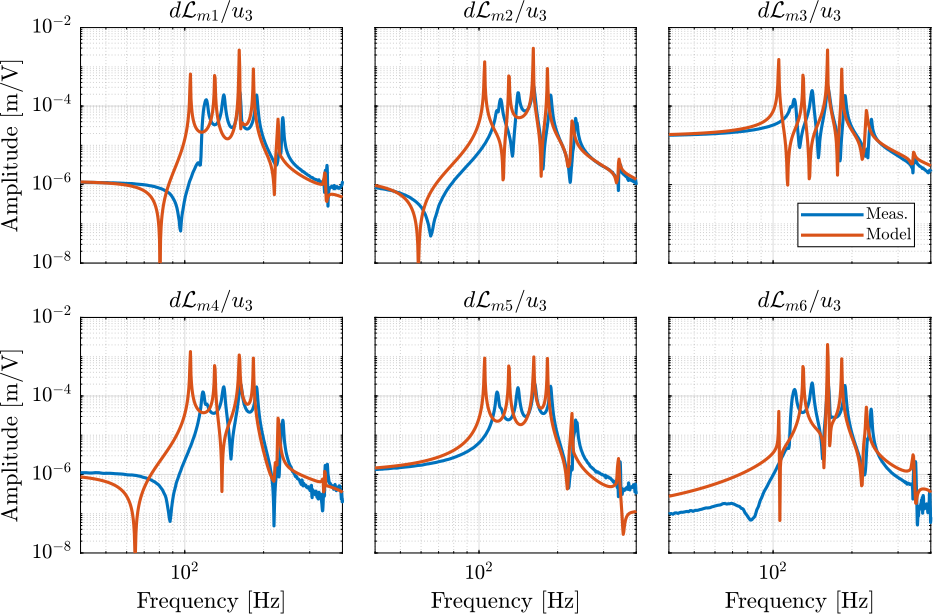
Figure 41: DVF Plant for the first actuator input and all the encoders
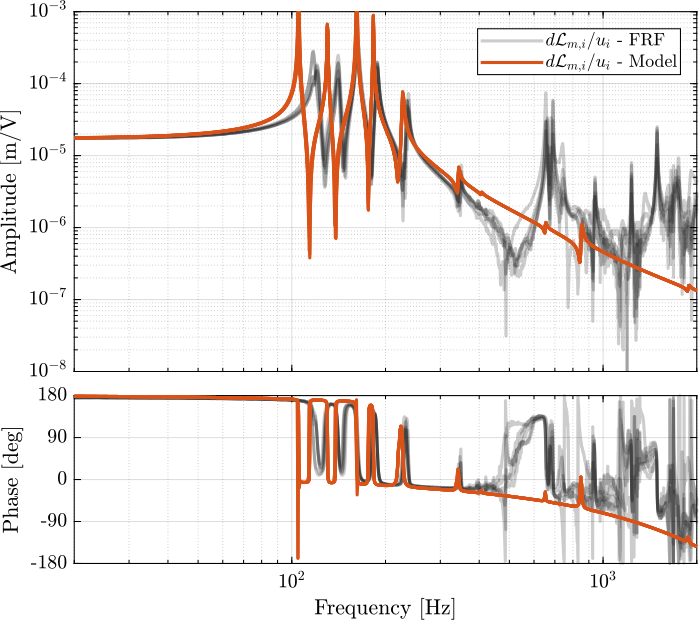
Figure 42: Diagonal elements of the DVF Plant
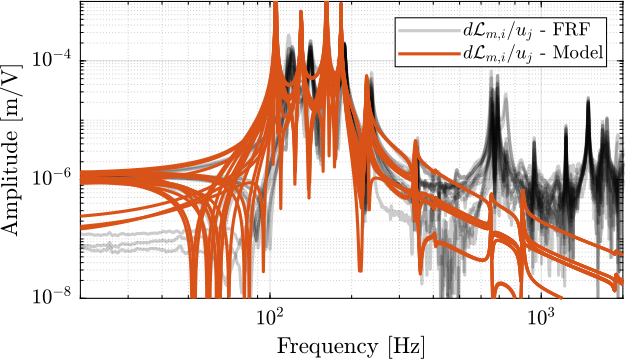
Figure 43: Off diagonal elements of the DVF Plant
2.2.4. Flexible Top Plate
%% Initialize Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '2dof', ... 'flex_top_type', '3dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', '2dof', ... 'top_plate_type', 'rigid');
%% Identify the DVF Plant (transfer function from u to dLm) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Encoders Gdvf = linearize(mdl, io, 0.0, options);
size(Gdvf) isstable(Gdvf)
[sys,g] = balreal(Gdvf); % Compute balanced realization elim = (g<1e-4); % Small entries of g are negligible states rsys = modred(sys,elim); % Remove negligible states size(rsys)
%% Identify the IFF Plant (transfer function from u to taum) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
2.2.5. Conclusion
The Simscape model is quite accurate for the transfer function matrices from \(\bm{u}\) to \(\bm{\tau}_m\) and from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\) except at frequencies of the flexible modes of the top-plate. The Simscape model can therefore be used to develop the control strategies.
2.3. Integral Force Feedback
In this section, the Integral Force Feedback (IFF) control strategy is applied to the nano-hexapod in order to add damping to the suspension modes.
The control architecture is shown in Figure 44:
- \(\bm{\tau}_m\) is the measured voltage of the 6 force sensors
- \(\bm{K}_{\text{IFF}}\) is the \(6 \times 6\) diagonal controller
- \(\bm{u}\) is the plant input (voltage generated by the 6 DACs)
- \(\bm{u}^\prime\) is the new plant inputs with added damping
Figure 44: Integral Force Feedback Strategy
- Section 2.3.1
2.3.1. Effect of IFF on the plant - Simscape Model
The nano-hexapod is initialized with flexible APA and the encoders fixed to the struts.
%% Initialize the Simscape model in closed loop n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'plates', ... 'actuator_type', 'flexible');
The same controller as the one developed when the encoder were fixed to the struts is used.
%% Optimal IFF controller load('Kiff.mat', 'Kiff')
The transfer function from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) is identified.
%% Identify the (damped) transfer function from u to dLm for different values of the IFF gain clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Plate Displacement (encoder)
First in Open-Loop:
%% Transfer function from u to dL (open-loop) Gd_ol = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
And then with the IFF controller:
%% Initialize the Simscape model in closed loop n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'plates', ... 'actuator_type', 'flexible', ... 'controller_type', 'iff'); %% Transfer function from u to dL (IFF) Gd_iff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
It is first verified that the system is stable:
isstable(Gd_iff)
1
The diagonal and off-diagonal terms of the \(6 \times 6\) transfer function matrices identified are compared in Figure 45. It is shown, as was the case when the encoders were fixed to the struts, that the IFF control strategy is very effective in damping the suspension modes of the nano-hexapod.
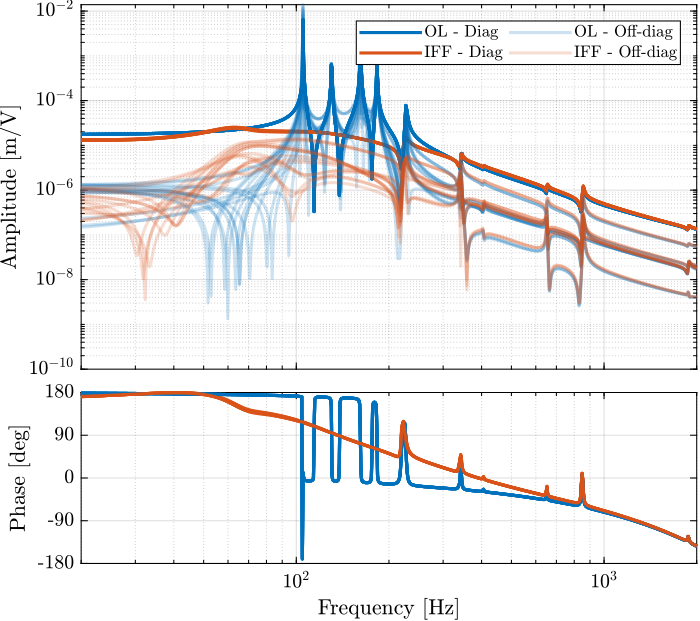
Figure 45: Effect of the IFF control strategy on the transfer function from \(\bm{\tau}\) to \(d\bm{\mathcal{L}}_m\)
2.3.2. Effect of IFF on the plant - FRF
The IFF control strategy is experimentally implemented. The (damped) transfer function from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) is experimentally identified.
The identification data are loaded:
%% Load Identification Data meas_iff_plates = {}; for i = 1:6 meas_iff_plates(i) = {load(sprintf('mat/frf_exc_iff_strut_%i_enc_plates_noise.mat', i), 't', 'Va', 'Vs', 'de', 'u')}; end
And the parameters used for the transfer function estimation are defined below.
% Sampling Time [s] Ts = (meas_iff_plates{1}.t(end) - (meas_iff_plates{1}.t(1)))/(length(meas_iff_plates{1}.t)-1); % Hannning Windows win = hanning(ceil(1/Ts)); % And we get the frequency vector [~, f] = tfestimate(meas_iff_plates{1}.Va, meas_iff_plates{1}.de, win, [], [], 1/Ts);
The estimation is performed using the tfestimate command.
%% Estimation of the transfer function matrix from u to dL when IFF is applied G_enc_iff_opt = zeros(length(f), 6, 6); for i = 1:6 G_enc_iff_opt(:,:,i) = tfestimate(meas_iff_plates{i}.Va, meas_iff_plates{i}.de, win, [], [], 1/Ts); end
The obtained diagonal and off-diagonal elements of the transfer function from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) are shown in Figure 46 both without and with IFF.
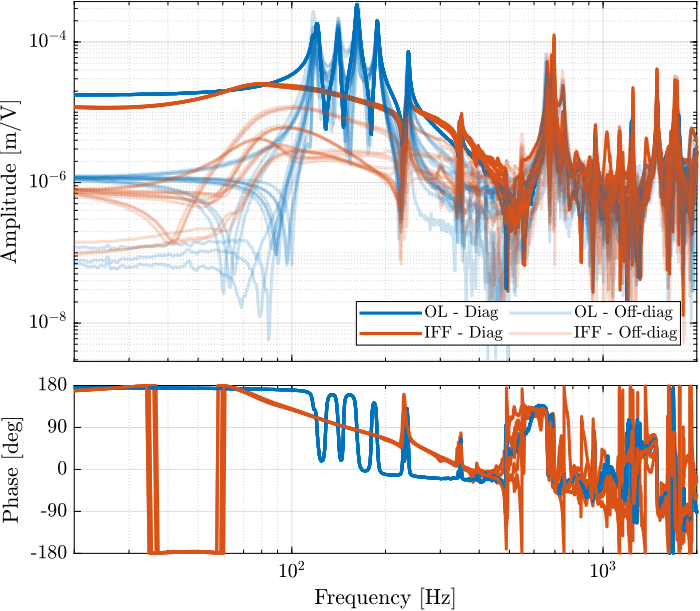
Figure 46: Effect of the IFF control strategy on the transfer function from \(\bm{\tau}\) to \(d\bm{\mathcal{L}}_m\)
As was predicted with the Simscape model, the IFF control strategy is very effective in damping the suspension modes of the nano-hexapod. Little damping is also applied on the first flexible mode of the strut at 235Hz. However, no damping is applied on other modes, such as the flexible modes of the top plate.
2.3.3. Comparison of the measured FRF and the Simscape model
Let’s now compare the obtained damped plants obtained experimentally with the one extracted from Simscape:
- Figure 47: the individual transfer function from \(u_1^\prime\) to the six encoders are comapred
- Figure 48: all the diagonal elements are compared
- Figure 49: all the off-diagonal elements are compared
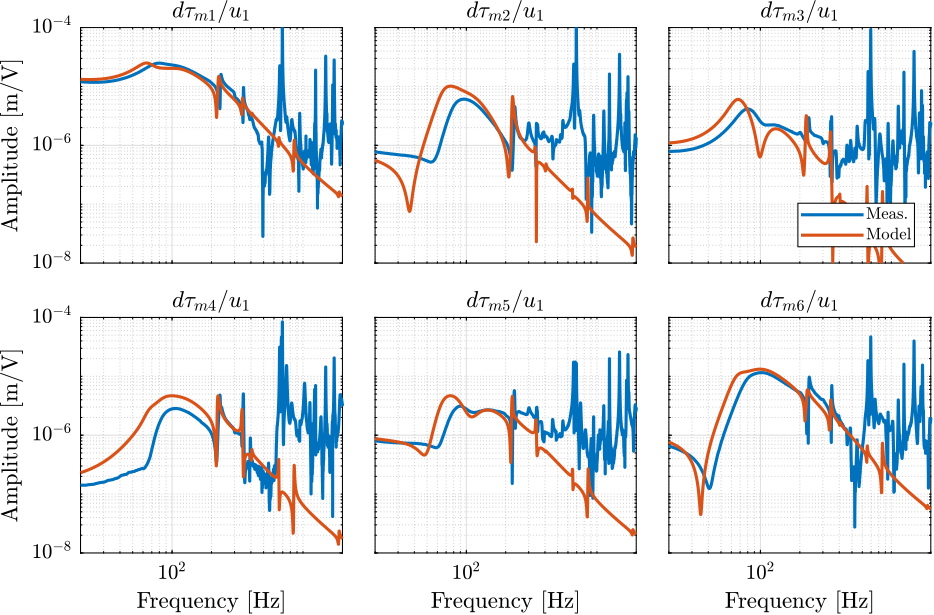
Figure 47: FRF from one actuator to all the encoders when the plant is damped using IFF
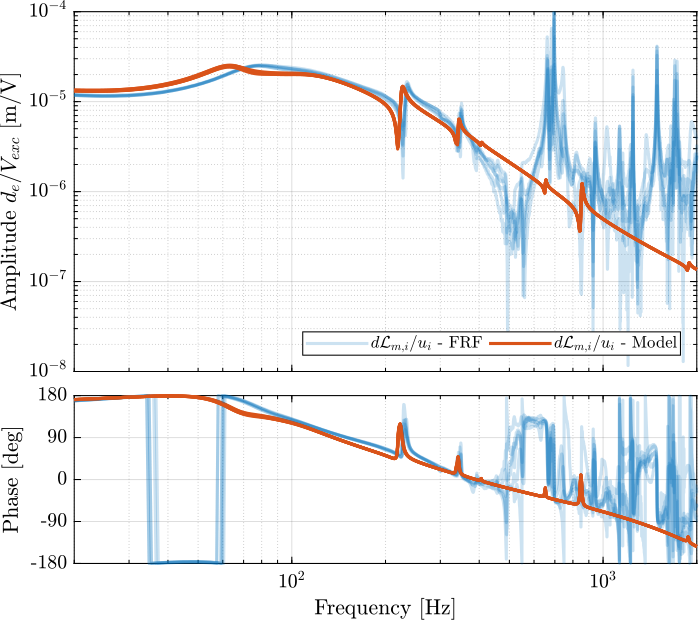
Figure 48: Comparison of the diagonal elements of the transfer functions from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\) with active damping (IFF) applied with an optimal gain \(g = 400\)
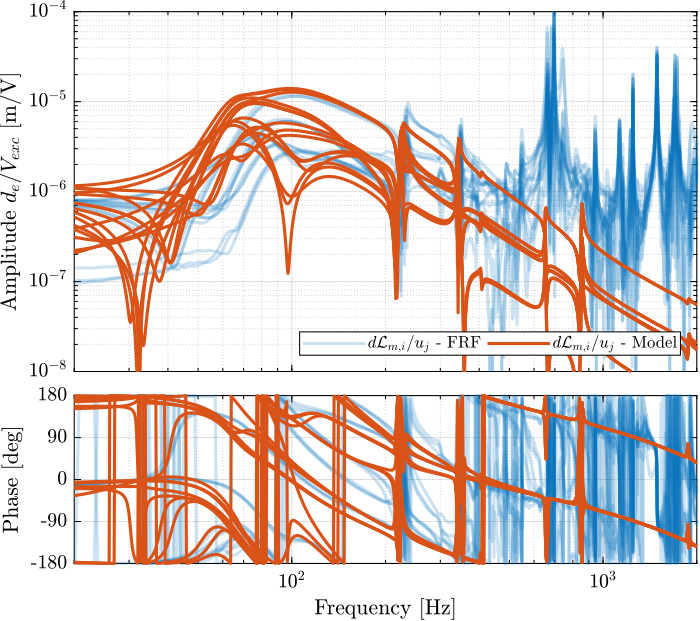
Figure 49: Comparison of the off-diagonal elements of the transfer functions from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\) with active damping (IFF) applied with an optimal gain \(g = 400\)
2.3.4. Save Damped Plant
The experimentally identified plant is saved for further use.
save('matlab/mat/damped_plant_enc_plates.mat', 'f', 'Ts', 'G_enc_iff_opt')
save('mat/damped_plant_enc_plates.mat', 'f', 'Ts', 'G_enc_iff_opt')
2.4. Effect of Payload mass - Robust IFF
In this section, the encoders are fixed to the plates, and we identify the dynamics for several payloads. The added payload are half cylinders, and three layers can be added for a total of around 40kg (Figure 50).

Figure 50: Picture of the nano-hexapod with added mass
First the dynamics from \(\bm{u}\) to \(d\mathcal{L}_m\) and \(\bm{\tau}_m\) is identified. Then, the Integral Force Feedback controller is developed and applied as shown in Figure 51. Finally, the dynamics from \(\bm{u}^\prime\) to \(d\mathcal{L}_m\) is identified and the added damping can be estimated.
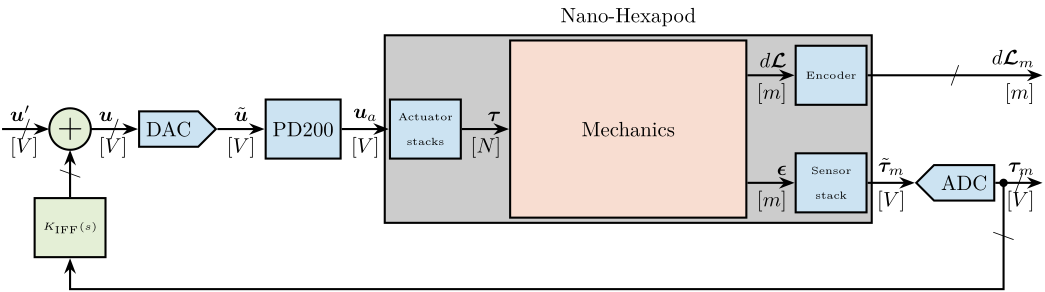
Figure 51: Block Diagram of the experimental setup and model
2.4.1. Measured Frequency Response Functions
2.4.1.1. Compute FRF in open-loop
The identification is performed without added mass, and with one, two and three layers of added cylinders.
i_masses = 0:3;
The following data are loaded:
Va: the excitation voltage (corresponding to \(u_i\))Vs: the generated voltage by the 6 force sensors (corresponding to \(\bm{\tau}_m\))de: the measured motion by the 6 encoders (corresponding to \(d\bm{\mathcal{L}}_m\))
%% Load Identification Data meas_added_mass = {}; for i_mass = i_masses for i_strut = 1:6 meas_added_mass(i_strut, i_mass+1) = {load(sprintf('frf_data_exc_strut_%i_realigned_vib_table_%im.mat', i_strut, i_mass), 't', 'Va', 'Vs', 'de')}; end end
The window win and the frequency vector f are defined.
% Sampling Time [s] Ts = (meas_added_mass{1,1}.t(end) - (meas_added_mass{1,1}.t(1)))/(length(meas_added_mass{1,1}.t)-1); % Hannning Windows win = hanning(ceil(1/Ts)); % And we get the frequency vector [~, f] = tfestimate(meas_added_mass{1,1}.Va, meas_added_mass{1,1}.de, win, [], [], 1/Ts);
Finally the \(6 \times 6\) transfer function matrices from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\) and from \(\bm{u}\) to \(\bm{\tau}_m\) are identified:
%% DVF Plant (transfer function from u to dLm) G_dL = {}; for i_mass = i_masses G_dL(i_mass+1) = {zeros(length(f), 6, 6)}; for i_strut = 1:6 G_dL{i_mass+1}(:,:,i_strut) = tfestimate(meas_added_mass{i_strut, i_mass+1}.Va, meas_added_mass{i_strut, i_mass+1}.de, win, [], [], 1/Ts); end end %% IFF Plant (transfer function from u to taum) G_tau = {}; for i_mass = i_masses G_tau(i_mass+1) = {zeros(length(f), 6, 6)}; for i_strut = 1:6 G_tau{i_mass+1}(:,:,i_strut) = tfestimate(meas_added_mass{i_strut, i_mass+1}.Va, meas_added_mass{i_strut, i_mass+1}.Vs, win, [], [], 1/Ts); end end
The identified dynamics are then saved for further use.
save('mat/frf_vib_table_m.mat', 'f', 'Ts', 'G_tau', 'G_dL')
2.4.2. Transfer function from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\)
The transfer functions from \(u_i\) to \(d\mathcal{L}_{m,i}\) are shown in Figure 52.
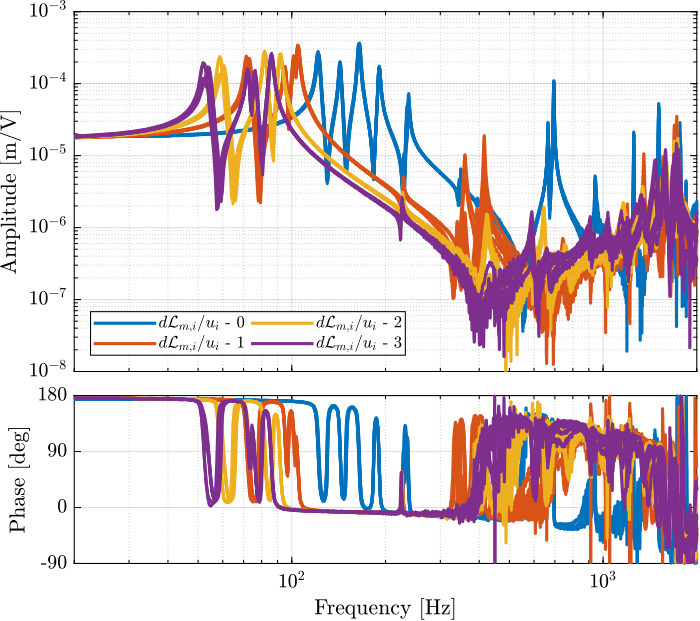
Figure 52: Measured Frequency Response Functions from \(u_i\) to \(d\mathcal{L}_{m,i}\) for all 4 payload conditions
From Figure 52, we can observe few things:
- The obtained dynamics is changing a lot between the case without mass and when there is at least one added mass.
- Between 1, 2 and 3 added masses, the dynamics is not much different, and it would be easier to design a controller only for these cases.
- The flexible modes of the top plate is first decreased a lot when the first mass is added (from 700Hz to 400Hz). This is due to the fact that the added mass is composed of two half cylinders which are not fixed together. Therefore is adds a lot of mass to the top plate without adding a lot of rigidity in one direction. When more than 1 mass layer is added, the half cylinders are added with some angles such that rigidity are added in all directions (see Figure 50). In that case, the frequency of these flexible modes are increased. In practice, the payload should be one solid body, and we should not see a massive decrease of the frequency of this flexible mode.
- Flexible modes of the top plate are becoming less problematic as masses are added.
- First flexible mode of the strut at 230Hz is not much decreased when mass is added. However, its apparent amplitude is much decreased.
2.4.3. Transfer function from \(\bm{u}\) to \(\bm{\tau}_m\)
The transfer functions from \(u_i\) to \(\tau_{m,i}\) are shown in Figure 53.
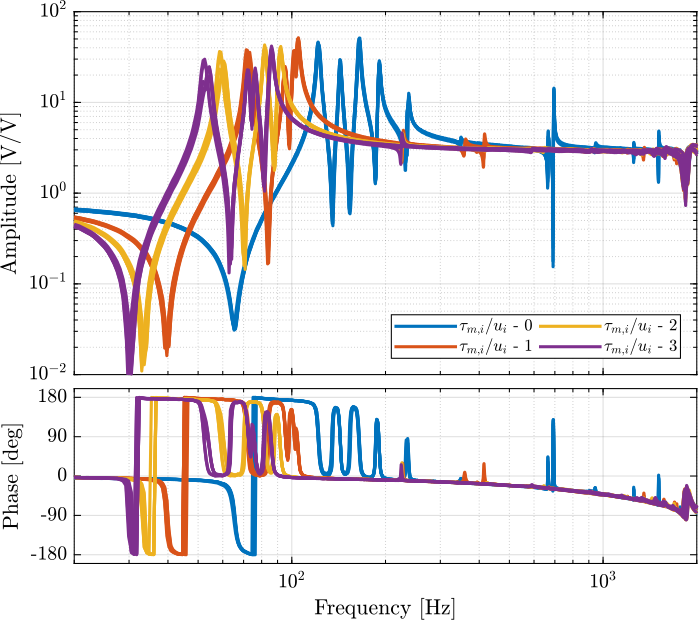
Figure 53: Measured Frequency Response Functions from \(u_i\) to \(\tau_{m,i}\) for all 4 payload conditions
From Figure 53, we can see that for all added payloads, the transfer function from \(u_i\) to \(\tau_{m,i}\) always has alternating poles and zeros.
2.5. Comparison with the Simscape model
2.5.1. System Identification
Let’s initialize the simscape model with the nano-hexapod fixed on top of the vibration table.
support.type = 1; % On top of vibration table
The model of the nano-hexapod is defined as shown bellow:
%% Initialize Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '2dof', ... 'flex_top_type', '3dof', ... 'motion_sensor_type', 'plates', ... 'actuator_type', '2dof');
And finally, we add the same payloads as during the experiments:
payload.type = 1; % Payload / 1 "mass layer"
First perform the identification for the transfer functions from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\):
%% Identify the DVF Plant (transfer function from u to dLm) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Encoders %% Identification for all the added payloads G_dL = {}; for i = i_masses fprintf('i = %i\n', i) payload.type = i; G_dL(i+1) = {exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options)}; end
%% Identify the IFF Plant (transfer function from u to taum) clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors %% Identification for all the added payloads G_tau = {}; for i = 0:3 fprintf('i = %i\n', i) payload.type = i; G_tau(i+1) = {exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options)}; end
The identified dynamics are then saved for further use.
save('mat/sim_vib_table_m.mat', 'G_tau', 'G_dL')
2.5.2. Transfer function from \(\bm{u}\) to \(d\bm{\mathcal{L}}_m\)
The measured FRF and the identified dynamics from \(u_i\) to \(d\mathcal{L}_{m,i}\) are compared in Figure 54. A zoom near the “suspension” modes is shown in Figure 55.
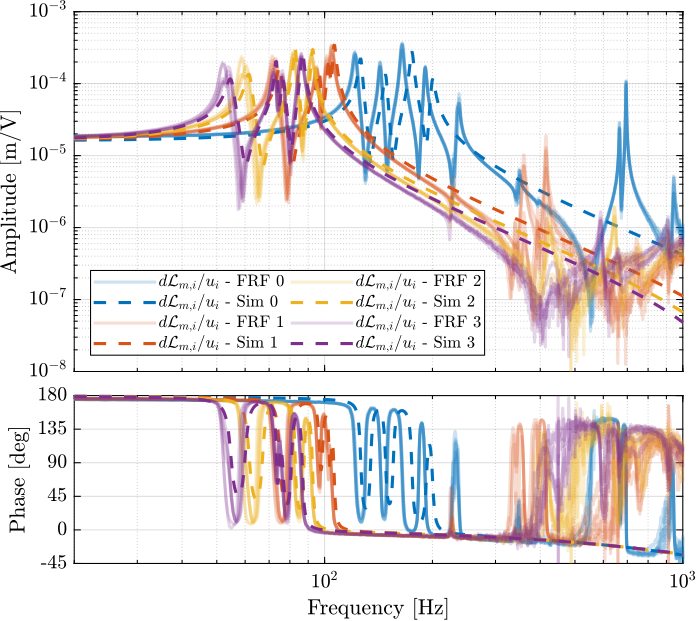
Figure 54: Comparison of the transfer functions from \(u_i\) to \(d\mathcal{L}_{m,i}\) - measured FRF and identification from the Simscape model
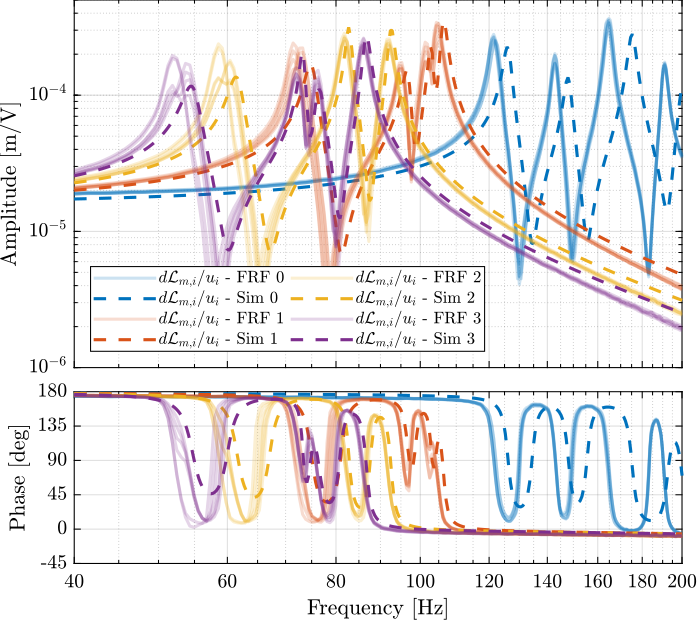
Figure 55: Comparison of the transfer functions from \(u_i\) to \(d\mathcal{L}_{m,i}\) - measured FRF and identification from the Simscape model (Zoom)
The Simscape model is very accurately representing the measured dynamics up. Only the flexible modes of the struts and of the top plate are not represented here as these elements are modelled as rigid bodies.
2.5.3. Transfer function from \(\bm{u}\) to \(\bm{\tau}_m\)
The measured FRF and the identified dynamics from \(u_i\) to \(\tau_{m,i}\) are compared in Figure 56. A zoom near the “suspension” modes is shown in Figure 57.
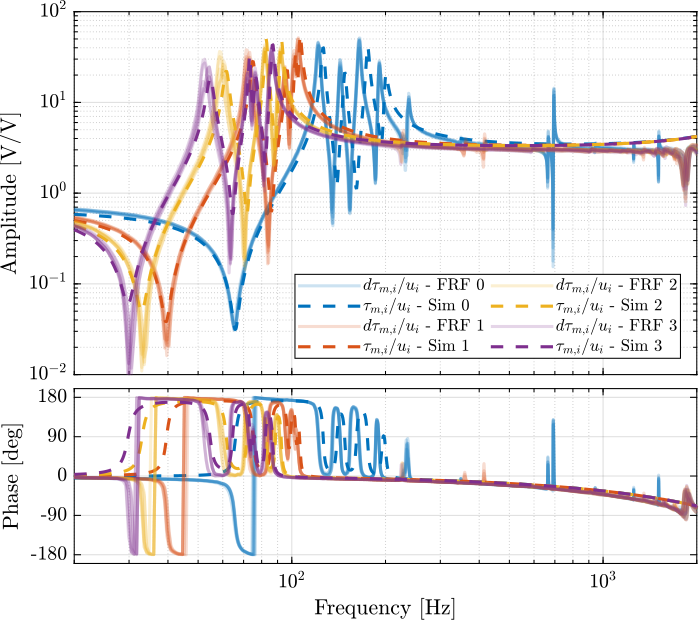
Figure 56: Comparison of the transfer functions from \(u_i\) to \(\tau_{m,i}\) - measured FRF and identification from the Simscape model
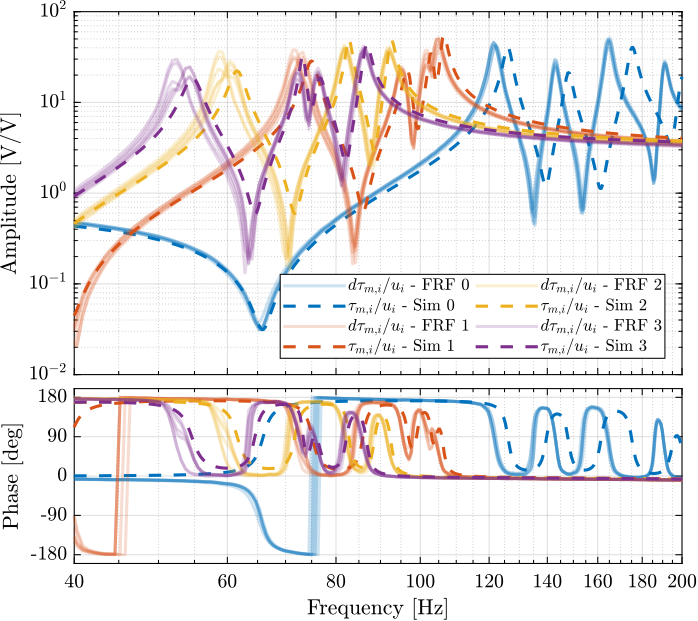
Figure 57: Comparison of the transfer functions from \(u_i\) to \(\tau_{m,i}\) - measured FRF and identification from the Simscape model (Zoom)
2.6. Integral Force Feedback Controller
2.6.1. Robust IFF Controller
Based on the measured FRF from \(u_i\) to \(\tau_{m,i}\), the following IFF controller is developed:
%% IFF Controller Kiff_g1 = (1/(s + 2*pi*20))*... % LPF: provides integral action above 20[Hz] (s/(s + 2*pi*20))*... % HPF: limit low frequency gain (1/(1 + s/2/pi/400)); % LPF: more robust to high frequency resonances
Then, the Root Locus plot of Figure 58 is used to estimate the optimal gain. This Root Locus plot is computed from the Simscape model.
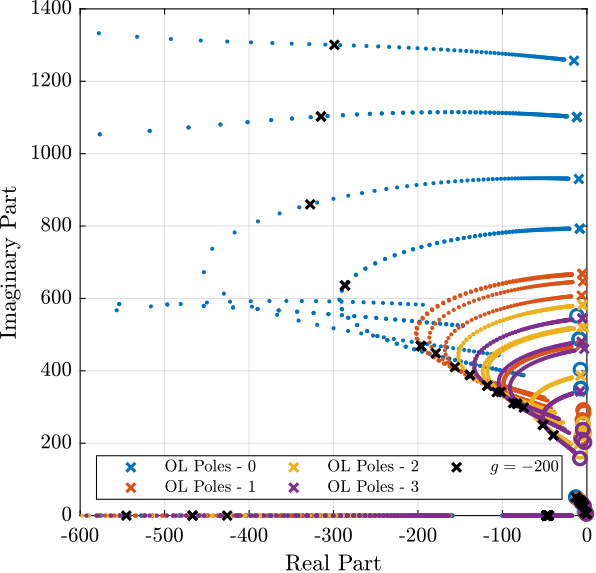
Figure 58: Root Locus for the IFF control strategy (for all payload conditions).
The found optimal IFF controller is:
%% Optimal controller g_opt = -2e2; Kiff = g_opt*Kiff_g1*eye(6);
It is saved for further use.
save('mat/Kiff_opt.mat', 'Kiff')
The corresponding experimental loop gains are shown in Figure 59.
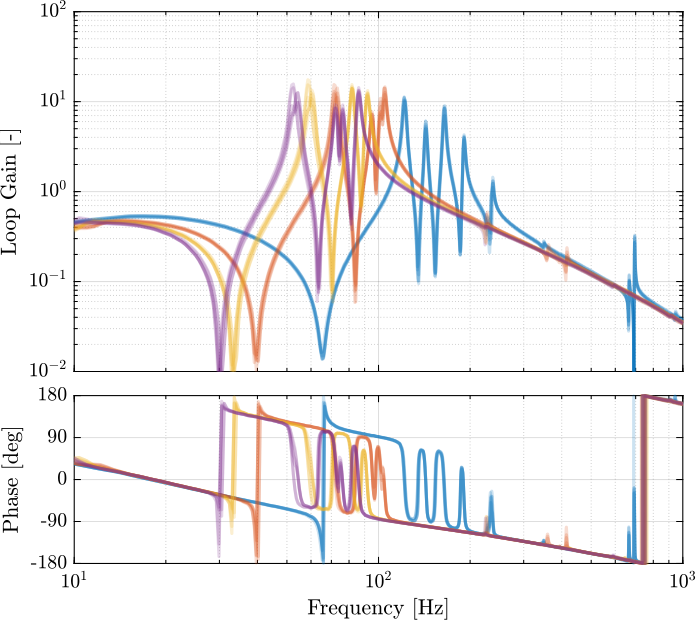
Figure 59: Loop gain for the Integral Force Feedback controller
Based on the above analysis:
- The same IFF controller can be used to damp the suspension modes for all payload conditions
- The IFF controller should be robust
2.6.2. Estimated Damped Plant from the Simscape model
Let’s initialize the simscape model with the nano-hexapod fixed on top of the vibration table.
support.type = 1; % On top of vibration table
The model of the nano-hexapod is defined as shown bellow:
%% Initialize the Simscape model in closed loop n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '2dof', ... 'flex_top_type', '3dof', ... 'motion_sensor_type', 'plates', ... 'actuator_type', '2dof', ... 'controller_type', 'iff');
And finally, we add the same payloads as during the experiments:
payload.type = 1; % Payload / 1 "mass layer"
%% Identify the (damped) transfer function from u to dLm clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Plate Displacement (encoder) %% Identify for all add masses G_dL = {}; for i = i_masses payload.type = i; G_dL(i+1) = {exp(-s*frf_ol.Ts)*linearize(mdl, io, 0.0, options)}; end
The identified dynamics are then saved for further use.
save('mat/sim_iff_vib_table_m.mat', 'G_dL');
sim_iff = load('sim_iff_vib_table_m.mat', 'G_dL');
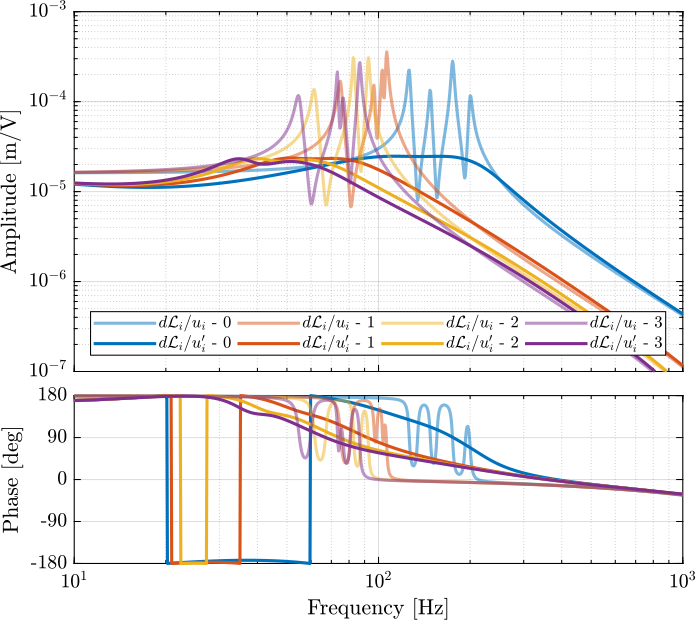
Figure 60: Transfer function from \(u_i\) to \(d\mathcal{L}_{m,i}\) (without active damping) and from \(u^\prime_i\) to \(d\mathcal{L}_{m,i}\) (with IFF)
2.6.3. Compute the identified FRF with IFF
The identification is performed without added mass, and with one, two and three layers of added cylinders.
i_masses = 0:3;
The following data are loaded:
Va: the excitation voltage for the damped plant (corresponding to \(u^\prime_i\))de: the measured motion by the 6 encoders (corresponding to \(d\bm{\mathcal{L}}_m\))
%% Load Identification Data meas_added_mass = {}; for i_mass = i_masses for i_strut = 1:6 meas_iff_mass(i_strut, i_mass+1) = {load(sprintf('frf_data_exc_strut_%i_iff_vib_table_%im.mat', i_strut, i_mass), 't', 'Va', 'de')}; end end
The window win and the frequency vector f are defined.
% Sampling Time [s] Ts = (meas_iff_mass{1,1}.t(end) - (meas_iff_mass{1,1}.t(1)))/(length(meas_iff_mass{1,1}.t)-1); % Hannning Windows win = hanning(ceil(1/Ts)); % And we get the frequency vector [~, f] = tfestimate(meas_iff_mass{1,1}.Va, meas_iff_mass{1,1}.de, win, [], [], 1/Ts);
Finally the \(6 \times 6\) transfer function matrix from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) is estimated:
%% DVF Plant (transfer function from u to dLm) G_dL = {}; for i_mass = i_masses G_dL(i_mass+1) = {zeros(length(f), 6, 6)}; for i_strut = 1:6 G_dL{i_mass+1}(:,:,i_strut) = tfestimate(meas_iff_mass{i_strut, i_mass+1}.Va, meas_iff_mass{i_strut, i_mass+1}.de, win, [], [], 1/Ts); end end
The identified dynamics are then saved for further use.
save('mat/frf_iff_vib_table_m.mat', 'f', 'Ts', 'G_dL');
2.6.4. Comparison of the measured FRF and the Simscape model
The following figures are computed:
- Figure 61: the measured damped FRF are displayed
- Figure 62: the open-loop and damped FRF are compared (diagonal elements)
- Figure 63: the obtained damped FRF is compared with the identified damped from using the Simscape model
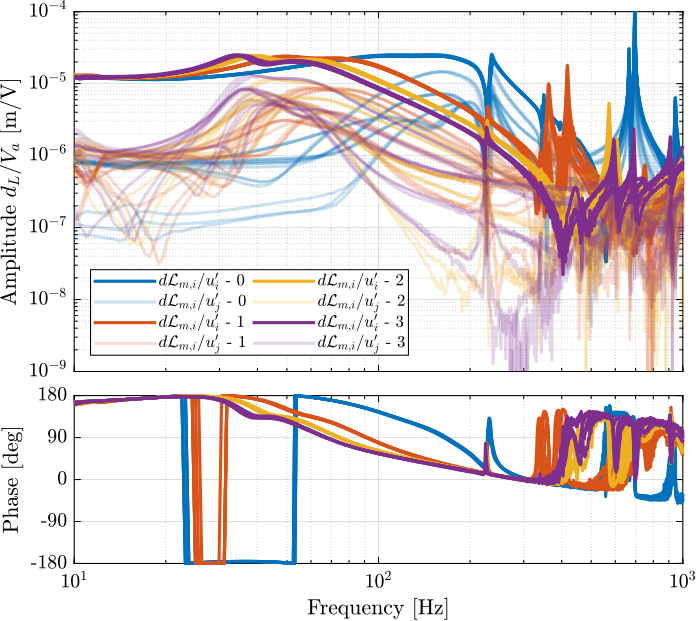
Figure 61: Diagonal and off-diagonal of the measured FRF matrix for the damped plant
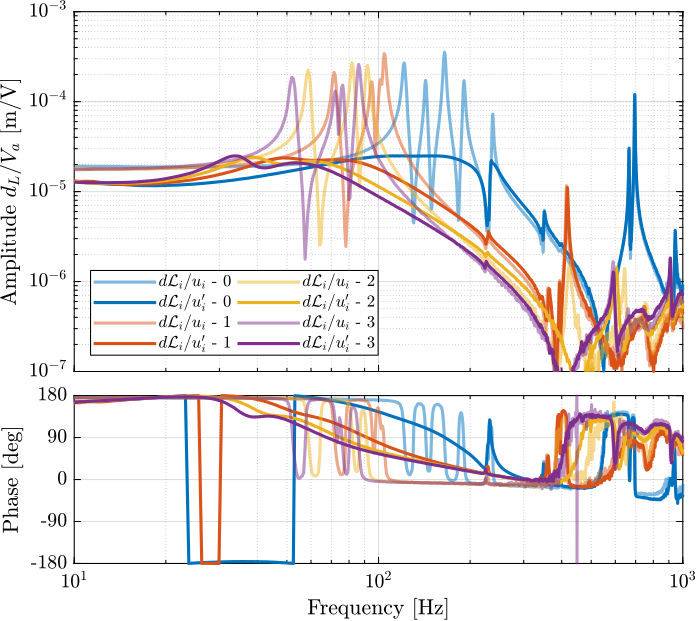
Figure 62: Damped and Undamped measured FRF (diagonal elements)
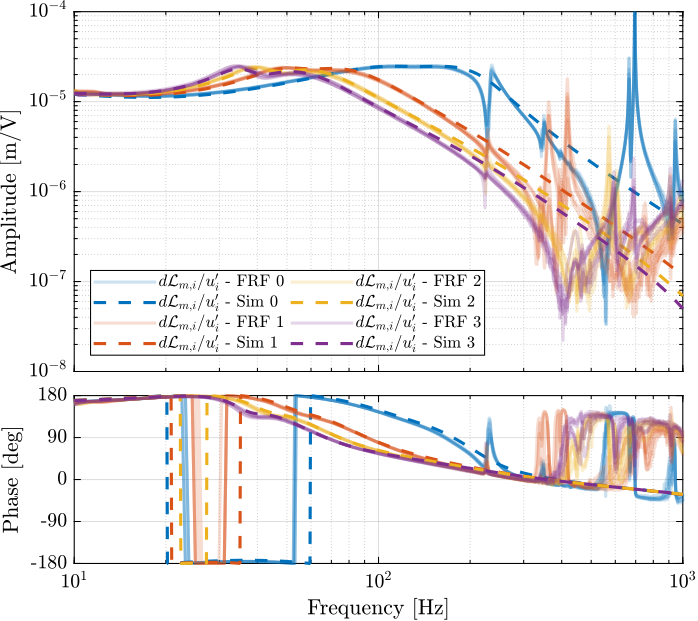
Figure 63: Comparison of the measured FRF and the identified dynamics from the Simscape model
The IFF control strategy effectively damps all the suspensions modes of the nano-hexapod whatever the payload is. The obtained plant is easier to control (provided the flexible modes of the top platform are well damped).
2.6.5. Change of coupling with IFF
The added damping using IFF reduces the coupling in the system near the suspensions modes that are damped. It can be estimated by taking the ratio of the diagonal-term and the off-diagonal term.
This is shown in Figure 64.
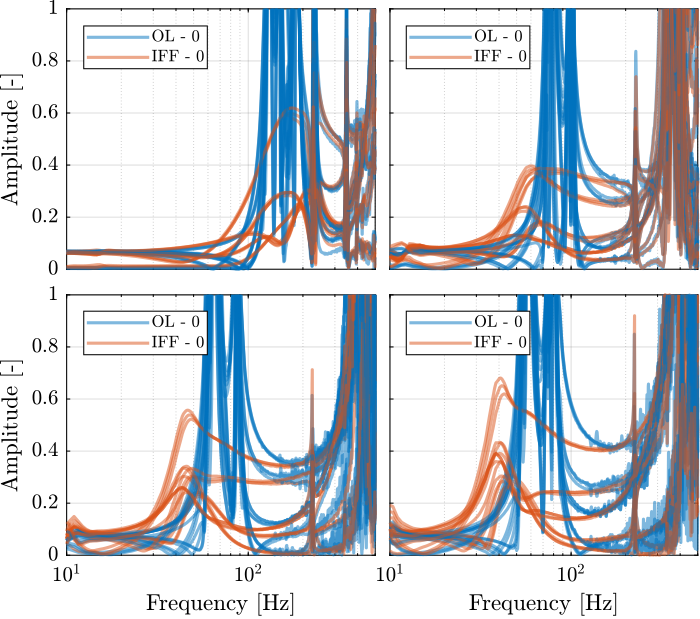
Figure 64: Comparison of the coupling with and without IFF
2.7. Un-Balanced mass
2.7.1. Introduction

Figure 65: Nano-Hexapod with unbalanced payload
2.7.2. Compute the identified FRF with IFF
The following data are loaded:
Va: the excitation voltage for the damped plant (corresponding to \(u^\prime_i\))de: the measured motion by the 6 encoders (corresponding to \(d\bm{\mathcal{L}}_m\))
%% Load Identification Data meas_added_mass = {zeros(6,1)}; for i_strut = 1:6 meas_iff_mass(i_strut) = {load(sprintf('frf_data_exc_strut_%i_iff_vib_table_1m_unbalanced.mat', i_strut), 't', 'Va', 'de')}; end
The window win and the frequency vector f are defined.
% Sampling Time [s] Ts = (meas_iff_mass{1}.t(end) - (meas_iff_mass{1}.t(1)))/(length(meas_iff_mass{1}.t)-1); % Hannning Windows win = hanning(ceil(1/Ts)); % And we get the frequency vector [~, f] = tfestimate(meas_iff_mass{1}.Va, meas_iff_mass{1}.de, win, [], [], 1/Ts);
Finally the \(6 \times 6\) transfer function matrix from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) is estimated:
%% DVF Plant (transfer function from u to dLm) G_dL = zeros(length(f), 6, 6); for i_strut = 1:6 G_dL(:,:,i_strut) = tfestimate(meas_iff_mass{i_strut}.Va, meas_iff_mass{i_strut}.de, win, [], [], 1/Ts); end
The identified dynamics are then saved for further use.
save('mat/frf_iff_unbalanced_vib_table_m.mat', 'f', 'Ts', 'G_dL');
2.7.3. Effect of an unbalanced payload
The transfer functions from \(u_i\) to \(d\mathcal{L}_i\) are shown in Figure 66. Due to the unbalanced payload, the system is not symmetrical anymore, and therefore each of the diagonal elements are not equal. This is due to the fact that each strut is not affected by the same inertia.
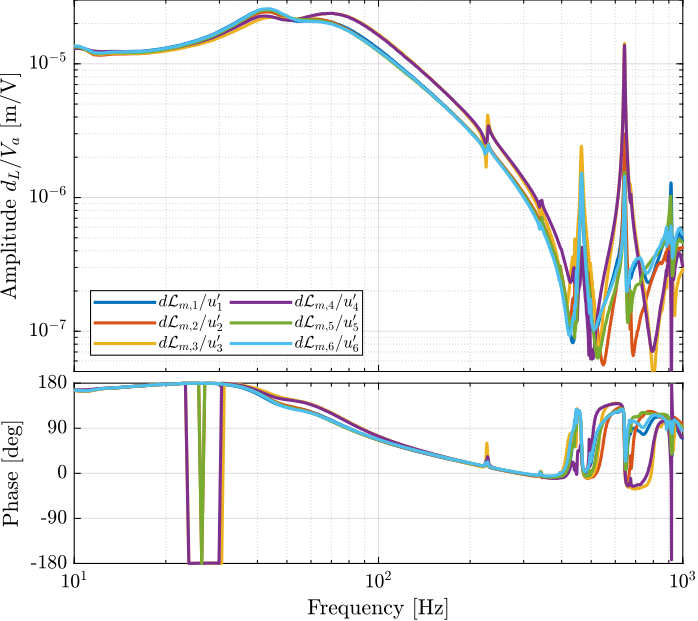
Figure 66: Transfer function from \(u_i\) to \(d\mathcal{L}_i\) for the nano-hexapod with an unbalanced payload
2.8. Conclusion
In this section, the dynamics of the nano-hexapod with the encoders fixed to the plates is studied.
It has been found that:
- The measured dynamics is in agreement with the dynamics of the simscape model, up to the flexible modes of the top plate. See figures 39 and 40 for the transfer function to the force sensors and Figures 42 and 43for the transfer functions to the encoders
- The Integral Force Feedback strategy is very effective in damping the suspension modes of the nano-hexapod (Figure 46).
- The transfer function from \(\bm{u}^\prime\) to \(d\bm{\mathcal{L}}_m\) show nice dynamical properties and is a much better candidate for the high-authority-control than when the encoders were fixed to the struts. At least up to the flexible modes of the top plate, the diagonal elements of the transfer function matrix have alternating poles and zeros, and the phase is moving smoothly. Only the flexible modes of the top plates seems to be problematic for control.
3. Decentralized High Authority Control with Integral Force Feedback
In this section is studied the HAC-IFF architecture for the Nano-Hexapod. More precisely:
- The LAC control is a decentralized integral force feedback as studied in Section 2.3
- The HAC control is a decentralized controller working in the frame of the struts
The corresponding control architecture is shown in Figure 67 with:
- \(\bm{r}_{\mathcal{X}_n}\): the \(6 \times 1\) reference signal in the cartesian frame
- \(\bm{r}_{d\mathcal{L}}\): the \(6 \times 1\) reference signal transformed in the frame of the struts thanks to the inverse kinematic
- \(\bm{\epsilon}_{d\mathcal{L}}\): the \(6 \times 1\) length error of the 6 struts
- \(\bm{u}^\prime\): input of the damped plant
- \(\bm{u}\): generated DAC voltages
- \(\bm{\tau}_m\): measured force sensors
- \(d\bm{\mathcal{L}}_m\): measured displacement of the struts by the encoders
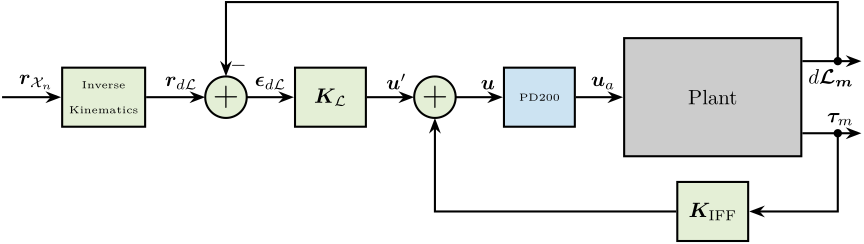
Figure 67: HAC-LAC: IFF + Control in the frame of the legs
This part is structured as follow:
- Section 3.1: some reference tracking tests are performed
- Section 3.2: the decentralized high authority controller is tuned using the Simscape model and is implemented and tested experimentally
- Section 3.3: an interaction analysis is performed, from which the best decoupling strategy can be determined
- Section 3.4: Robust High Authority Controller are designed
3.1. Reference Tracking - Trajectories
In this section, several trajectories representing the wanted pose (position and orientation) of the top platform with respect to the bottom platform are defined.
These trajectories will be used to test the HAC-LAC architecture.
In order to transform the wanted pose to the wanted displacement of the 6 struts, the inverse kinematic is required. As a first approximation, the Jacobian matrix \(\bm{J}\) can be used instead of using the full inverse kinematic equations.
Therefore, the control architecture with the input trajectory \(\bm{r}_{\mathcal{X}_n}\) is shown in Figure 68.
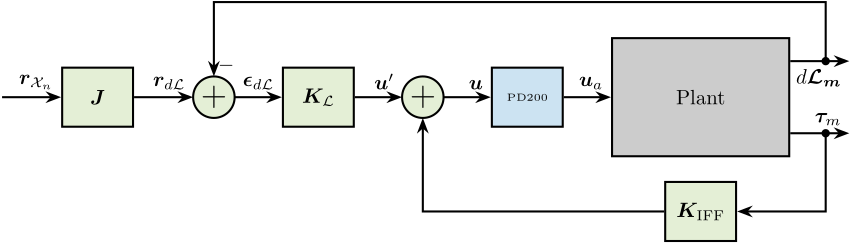
Figure 68: HAC-LAC: IFF + Control in the frame of the legs
In the following sections, several reference trajectories are defined:
3.1.1. Y-Z Scans
A function generateYZScanTrajectory has been developed (accessible here) in order to easily generate scans in the Y-Z plane.
For instance, the following generated trajectory is represented in Figure 69.
%% Generate the Y-Z trajectory scan Rx_yz = generateYZScanTrajectory(... 'y_tot', 4e-6, ... % Length of Y scans [m] 'z_tot', 4e-6, ... % Total Z distance [m] 'n', 5, ... % Number of Y scans 'Ts', 1e-3, ... % Sampling Time [s] 'ti', 1, ... % Time to go to initial position [s] 'tw', 0, ... % Waiting time between each points [s] 'ty', 0.6, ... % Time for a scan in Y [s] 'tz', 0.2); % Time for a scan in Z [s]
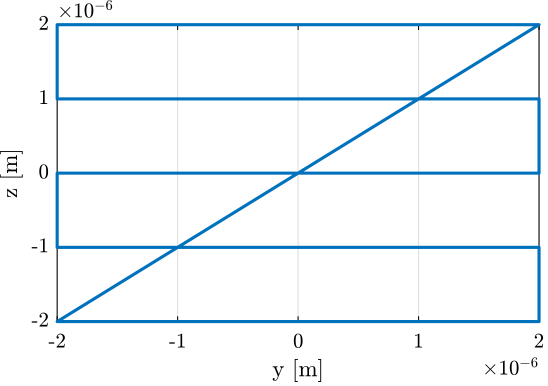
Figure 69: Generated scan in the Y-Z plane
The Y and Z positions as a function of time are shown in Figure 70.
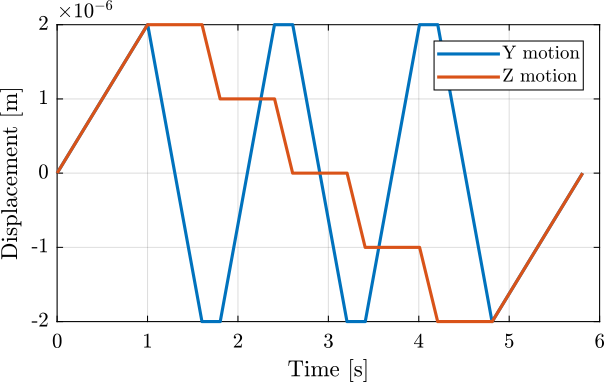
Figure 70: Y and Z trajectories as a function of time
Using the Jacobian matrix, it is possible to compute the wanted struts lengths as a function of time:
\begin{equation} \bm{r}_{d\mathcal{L}} = \bm{J} \bm{r}_{\mathcal{X}_n} \end{equation}%% Compute the reference in the frame of the legs dL_ref = [J*Rx_yz(:, 2:7)']';
The reference signal for the strut length is shown in Figure 71.
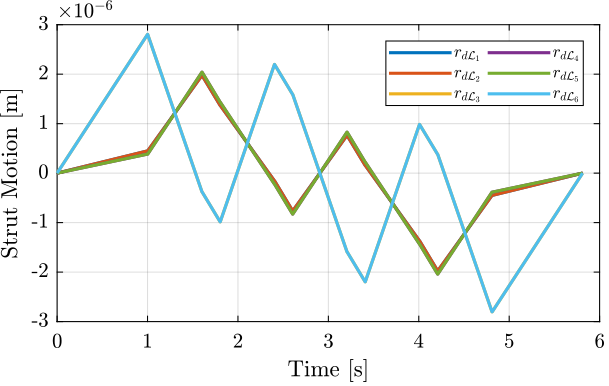
Figure 71: Trajectories for the 6 individual struts
3.1.2. Tilt Scans
A function generalSpiralAngleTrajectory has been developed in order to easily generate \(R_x,R_y\) tilt scans.
For instance, the following generated trajectory is represented in Figure 72.
%% Generate the "tilt-spiral" trajectory scan R_tilt = generateSpiralAngleTrajectory(... 'R_tot', 20e-6, ... % Total Tilt [ad] 'n_turn', 5, ... % Number of scans 'Ts', 1e-3, ... % Sampling Time [s] 't_turn', 1, ... % Turn time [s] 't_end', 1); % End time to go back to zero [s]
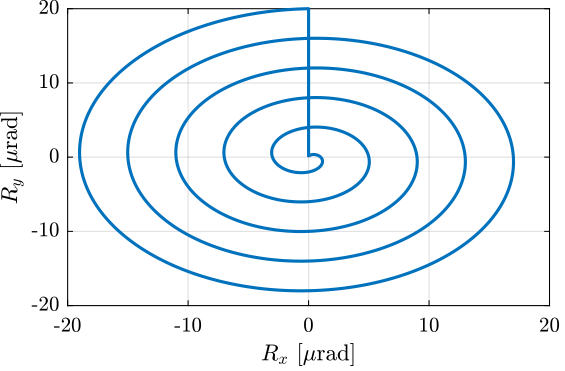
Figure 72: Generated “spiral” scan
The reference signal for the strut length is shown in Figure 73.
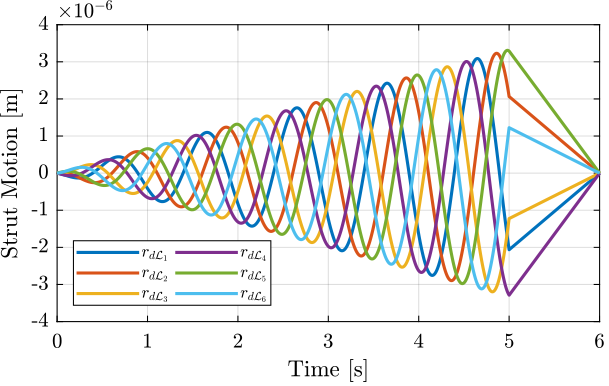
Figure 73: Trajectories for the 6 individual struts - Tilt scan
3.1.3. “NASS” reference path
In this section, a reference path that “draws” the work “NASS” is developed.
First, a series of points representing each letter are defined. Between each letter, a negative Z motion is performed.
%% List of points that draws "NASS" ref_path = [ ... 0, 0,0; % Initial Position 0,0,1; 0,4,1; 3,0,1; 3,4,1; % N 3,4,0; 4,0,0; % Transition 4,0,1; 4,3,1; 5,4,1; 6,4,1; 7,3,1; 7,2,1; 4,2,1; 4,3,1; 5,4,1; 6,4,1; 7,3,1; 7,0,1; % A 7,0,0; 8,0,0; % Transition 8,0,1; 11,0,1; 11,2,1; 8,2,1; 8,4,1; 11,4,1; % S 11,4,0; 12,0,0; % Transition 12,0,1; 15,0,1; 15,2,1; 12,2,1; 12,4,1; 15,4,1; % S 15,4,0; ]; %% Center the trajectory arround zero ref_path = ref_path - (max(ref_path) - min(ref_path))/2; %% Define the X-Y-Z cuboid dimensions containing the trajectory X_max = 10e-6; Y_max = 4e-6; Z_max = 2e-6; ref_path = ([X_max, Y_max, Z_max]./max(ref_path)).*ref_path; % [m]
Then, using the generateXYZTrajectory function, the \(6 \times 1\) trajectory signal is computed.
%% Generating the trajectory Rx_nass = generateXYZTrajectory('points', ref_path);
The trajectory in the X-Y plane is shown in Figure 74 (the transitions between the letters are removed).
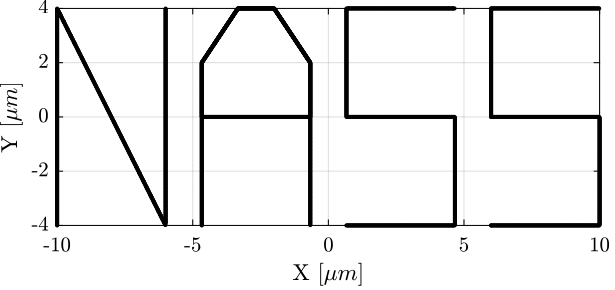
Figure 74: Reference path corresponding to the “NASS” acronym
It can also be better viewed in a 3D representation as in Figure 75.
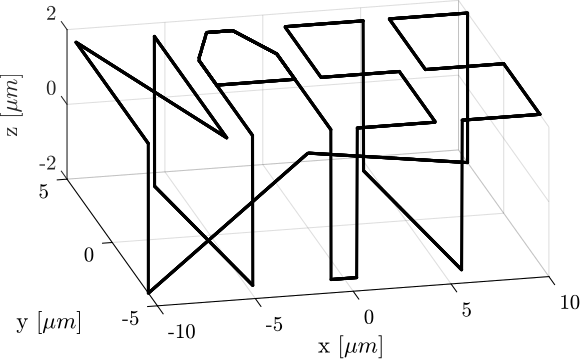
Figure 75: Reference path that draws “NASS” - 3D view
3.2. First Basic High Authority Controller
In this section, a simple decentralized high authority controller \(\bm{K}_{\mathcal{L}}\) is developed to work without any payload.
The diagonal controller is tuned using classical Loop Shaping in Section 3.2.1. The stability is verified in Section 3.2.2 using the Simscape model.
3.2.1. HAC Controller
Let’s first try to design a first decentralized controller with:
- a bandwidth of 100Hz
- sufficient phase margin
- simple and understandable components
After some very basic and manual loop shaping, A diagonal controller is developed. Each diagonal terms are identical and are composed of:
- A lead around 100Hz
- A first order low pass filter starting at 200Hz to add some robustness to high frequency modes
- A notch at 700Hz to cancel the flexible modes of the top plate
- A pure integrator
%% Lead to increase phase margin a = 2; % Amount of phase lead / width of the phase lead / high frequency gain wc = 2*pi*100; % Frequency with the maximum phase lead [rad/s] H_lead = (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a))); %% Low Pass filter to increase robustness H_lpf = 1/(1 + s/2/pi/200); %% Notch at the top-plate resonance gm = 0.02; xi = 0.3; wn = 2*pi*700; H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2); %% Decentralized HAC Khac_iff_struts = -(1/(2.87e-5)) * ... % Gain H_lead * ... % Lead H_notch * ... % Notch (2*pi*100/s) * ... % Integrator eye(6); % 6x6 Diagonal
This controller is saved for further use.
save('mat/Khac_iff_struts.mat', 'Khac_iff_struts')
The experimental loop gain is computed and shown in Figure 76.
L_hac_iff_struts = pagemtimes(permute(frf_iff.G_dL{1}, [2 3 1]), squeeze(freqresp(Khac_iff_struts, frf_iff.f, 'Hz')));
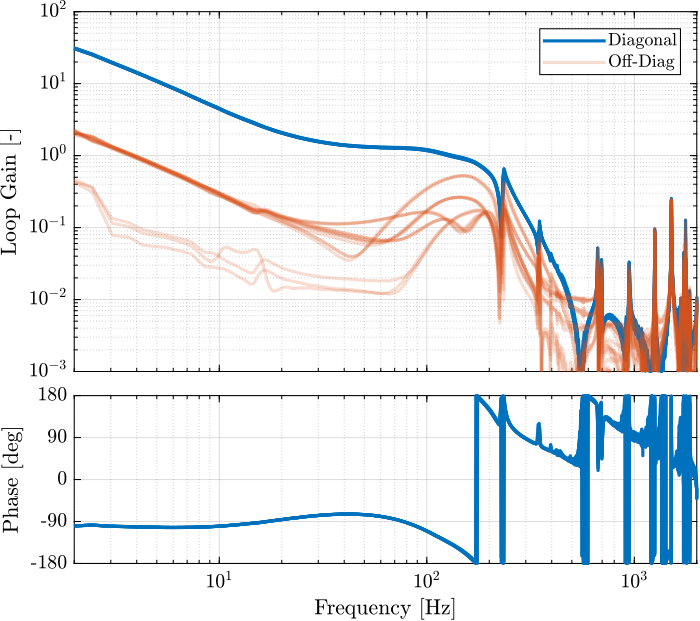
Figure 76: Diagonal and off-diagonal elements of the Loop gain for “HAC-IFF-Struts”
3.2.2. Verification of the Stability using the Simscape model
The HAC-IFF control strategy is implemented using Simscape.
%% Initialize the Simscape model in closed loop n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'plates', ... 'actuator_type', 'flexible', ... 'controller_type', 'hac-iff-struts');
%% Identify the (damped) transfer function from u to dLm clear io; io_i = 1; io(io_i) = linio([mdl, '/du'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Plate Displacement (encoder)
We identify the closed-loop system.
%% Identification
Gd_iff_hac_opt = linearize(mdl, io, 0.0, options);
And verify that it is indeed stable.
%% Verify the stability
isstable(Gd_iff_hac_opt)
1
3.2.3. Experimental Validation
Both the Integral Force Feedback controller (developed in Section 2.3) and the high authority controller working in the frame of the struts (developed in Section 3.2) are implemented experimentally.
Two reference tracking experiments are performed to evaluate the stability and performances of the implemented control.
%% Load the experimental data load('hac_iff_struts_yz_scans.mat', 't', 'de')
The position of the top-platform is estimated using the Jacobian matrix:
%% Pose of the top platform from the encoder values load('jacobian.mat', 'J'); Xe = [inv(J)*de']';
%% Generate the Y-Z trajectory scan Rx_yz = generateYZScanTrajectory(... 'y_tot', 4e-6, ... % Length of Y scans [m] 'z_tot', 8e-6, ... % Total Z distance [m] 'n', 5, ... % Number of Y scans 'Ts', 1e-3, ... % Sampling Time [s] 'ti', 1, ... % Time to go to initial position [s] 'tw', 0, ... % Waiting time between each points [s] 'ty', 0.6, ... % Time for a scan in Y [s] 'tz', 0.2); % Time for a scan in Z [s]
The reference path as well as the measured position are partially shown in the Y-Z plane in Figure 77.
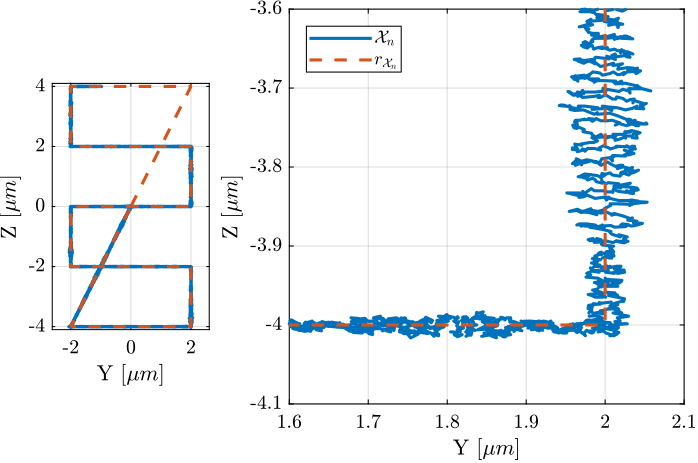
Figure 77: Measured position \(\bm{\mathcal{X}}_n\) and reference signal \(\bm{r}_{\mathcal{X}_n}\) in the Y-Z plane - Zoom on a change of direction
It is clear from Figure 77 that the position of the nano-hexapod effectively tracks to reference signal. However, oscillations with amplitudes as large as 50nm can be observe.
It turns out that the frequency of these oscillations is 100Hz which is corresponding to the crossover frequency of the High Authority Control loop. This clearly indicates poor stability margins. In the next section, the controller is re-designed to improve the stability margins.
3.2.4. Controller with increased stability margins
The High Authority Controller is re-designed in order to improve the stability margins.
%% Lead a = 5; % Amount of phase lead / width of the phase lead / high frequency gain wc = 2*pi*110; % Frequency with the maximum phase lead [rad/s] H_lead = (1 + s/(wc/sqrt(a)))/(1 + s/(wc*sqrt(a))); %% Low Pass Filter H_lpf = 1/(1 + s/2/pi/300); %% Notch gm = 0.02; xi = 0.5; wn = 2*pi*700; H_notch = (s^2 + 2*gm*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2); %% HAC Controller Khac_iff_struts = -2.2e4 * ... % Gain H_lead * ... % Lead H_lpf * ... % Lead H_notch * ... % Notch (2*pi*100/s) * ... % Integrator eye(6); % 6x6 Diagonal
The bode plot of the new loop gain is shown in Figure 78.
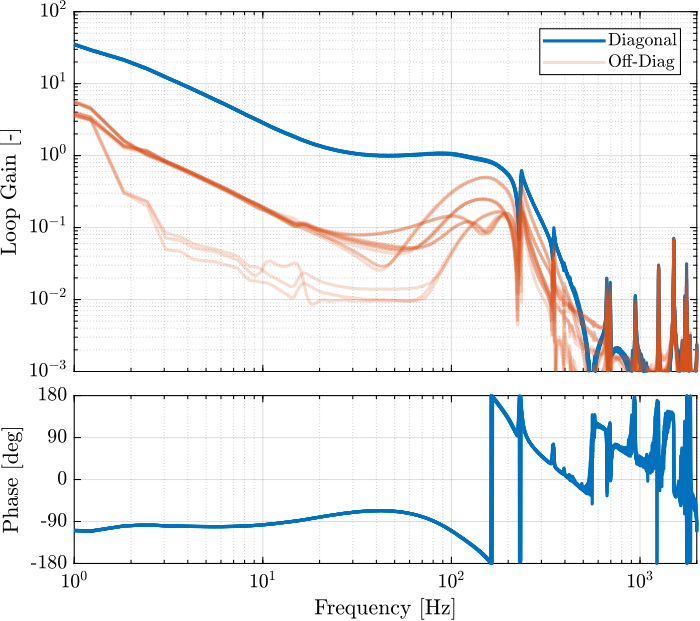
Figure 78: Loop Gain for the updated decentralized HAC controller
This new controller is implemented experimentally and several tracking tests are performed.
%% Load Measurements load('hac_iff_more_lead_nass_scan.mat', 't', 'de')
The pose of the top platform is estimated from the encoder position using the Jacobian matrix.
%% Compute the pose of the top platform load('jacobian.mat', 'J'); Xe = [inv(J)*de']';
The measured motion as well as the trajectory are shown in Figure 79.
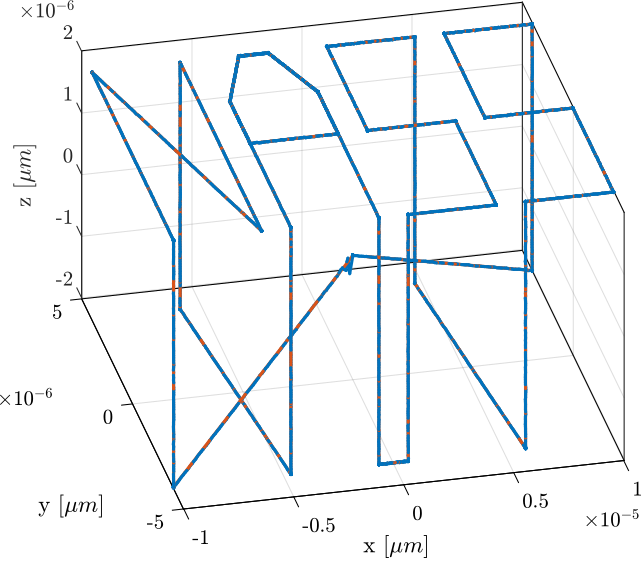
Figure 79: Measured position \(\bm{\mathcal{X}}_n\) and reference signal \(\bm{r}_{\mathcal{X}_n}\) for the “NASS” trajectory
The trajectory and measured motion are also shown in the X-Y plane in Figure 80.
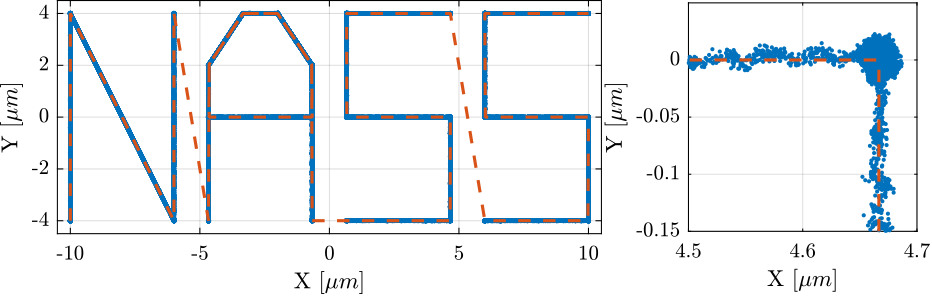
Figure 80: Reference path and measured motion in the X-Y plane
The orientation errors during all the scans are shown in Figure 81.
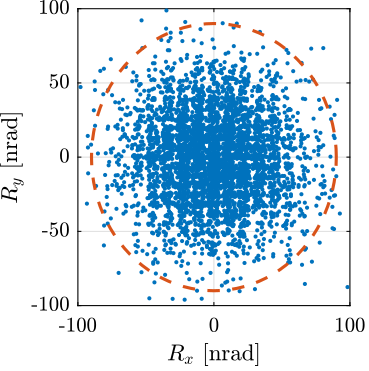
Figure 81: Orientation errors during the scan
Using the updated High Authority Controller, the nano-hexapod can follow trajectories with high accuracy (the position errors are in the order of 50nm peak to peak, and the orientation errors 300nrad peak to peak).
3.3. Interaction Analysis and Decoupling
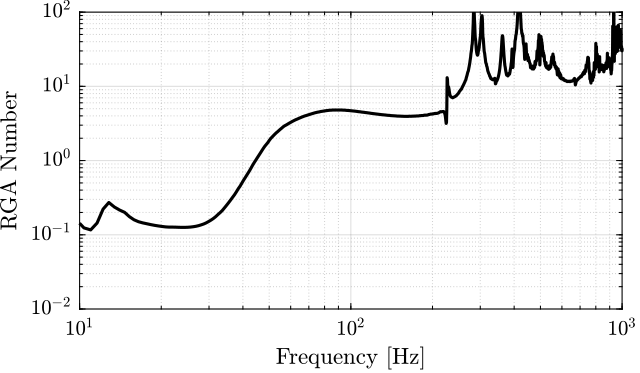
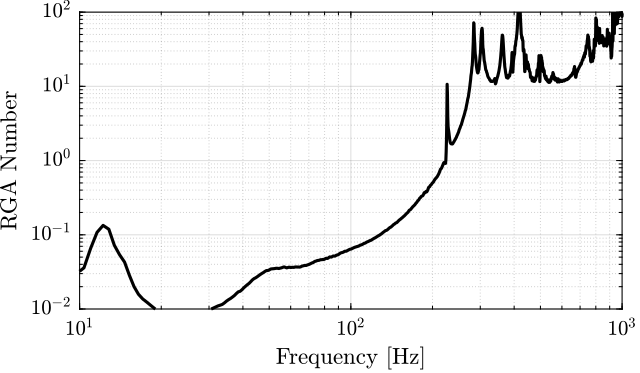
In this section, the interaction in the identified plant is estimated using the Relative Gain Array (RGA) (Skogestad and Postlethwaite 2007, 3.4).
Then, several decoupling strategies are compared for the nano-hexapod.
The RGA Matrix is defined as follow:
\begin{equation} \text{RGA}(G(f)) = G(f) \times (G(f)^{-1})^T \end{equation}Then, the RGA number is defined:
\begin{equation} \text{RGA-num}(f) = \| \text{I - RGA(G(f))} \|_{\text{sum}} \end{equation}In this section, the plant with 2 added mass is studied.
3.3.1. Parameters
wc = 100; % Wanted crossover frequency [Hz] [~, i_wc] = min(abs(frf_iff.f - wc)); % Indice corresponding to wc
%% Plant to be decoupled
frf_coupled = frf_iff.G_dL{2};
G_coupled = sim_iff.G_dL{2};
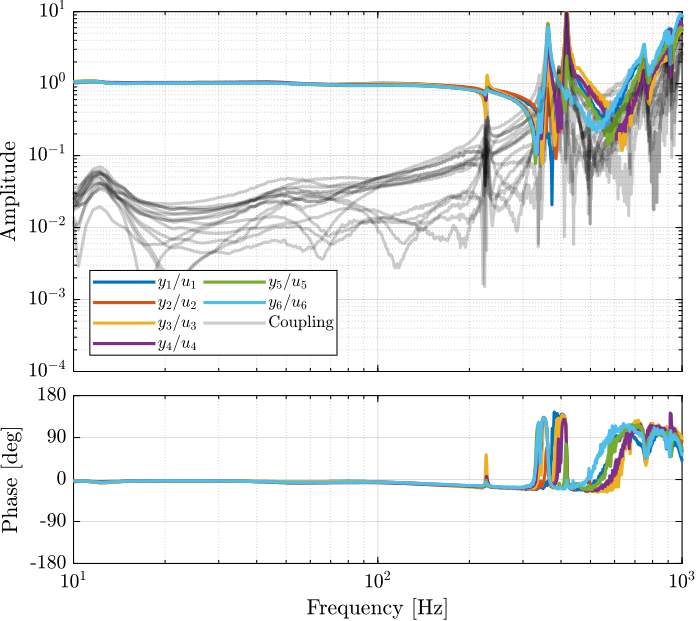
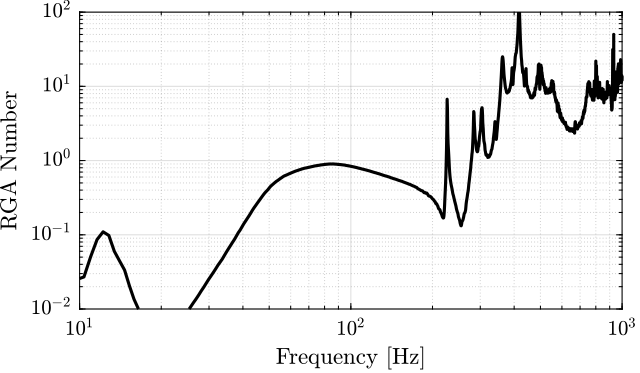
3.3.2. No Decoupling (Decentralized)
3.3.3. Static Decoupling
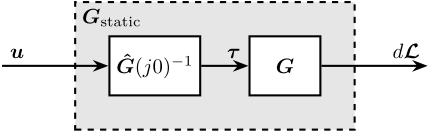
Figure 85: Decoupling using the inverse of the DC gain of the plant
The DC gain is evaluated from the model as be have bad low frequency identification.
| -62011.5 | 3910.6 | 4299.3 | 660.7 | -4016.5 | -4373.6 |
| 3914.4 | -61991.2 | -4356.8 | -4019.2 | 640.2 | 4281.6 |
| -4020.0 | -4370.5 | -62004.5 | 3914.6 | 4295.8 | 653.8 |
| 660.9 | 4292.4 | 3903.3 | -62012.2 | -4366.5 | -4008.9 |
| 4302.8 | 655.6 | -4025.8 | -4377.8 | -62006.0 | 3919.7 |
| -4377.9 | -4013.2 | 668.6 | 4303.7 | 3906.8 | -62019.3 |
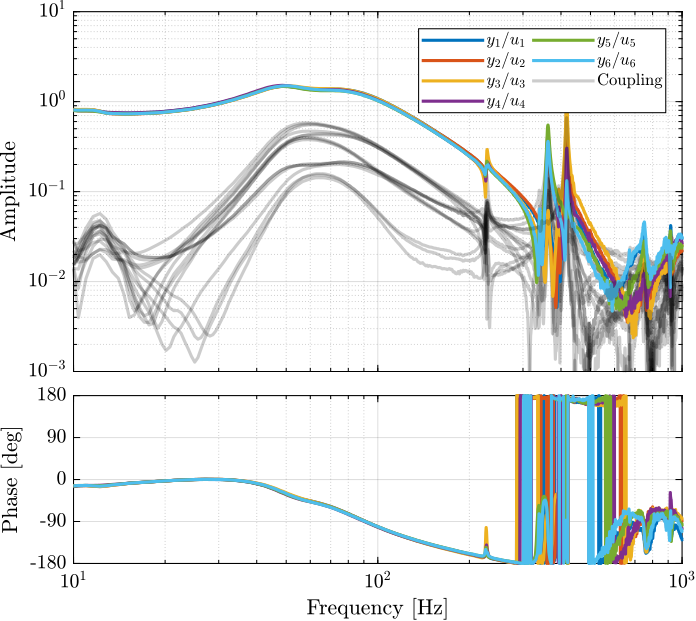
Figure 86: Bode Plot of the static decoupled plant
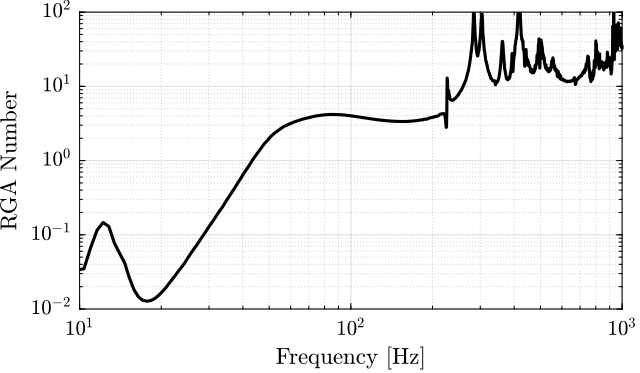
Figure 87: RGA number for the statically decoupled plant
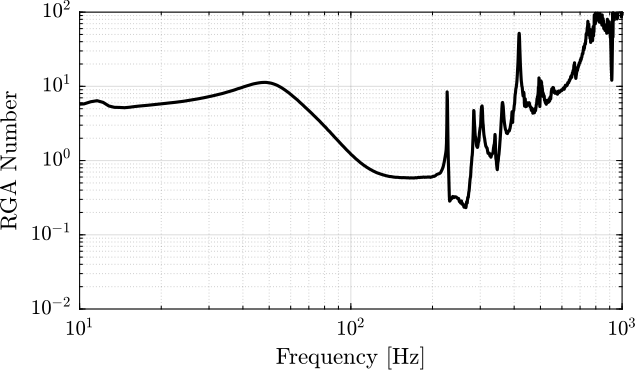
3.3.4. Decoupling at the Crossover
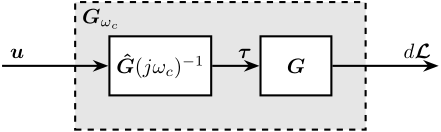
Figure 88: Decoupling using the inverse of a dynamical model \(\bm{\hat{G}}\) of the plant dynamics \(\bm{G}\)
| 67229.8 | 3769.3 | -13704.6 | -23084.8 | -6318.2 | 23378.7 |
| 3486.2 | 67708.9 | 23220.0 | -6314.5 | -22699.8 | -14060.6 |
| -5731.7 | 22471.7 | 66701.4 | 3070.2 | -13205.6 | -21944.6 |
| -23305.5 | -14542.6 | 2743.2 | 70097.6 | 24846.8 | -5295.0 |
| -14882.9 | -22957.8 | -5344.4 | 25786.2 | 70484.6 | 2979.9 |
| 24353.3 | -5195.2 | -22449.0 | -14459.2 | 2203.6 | 69484.2 |
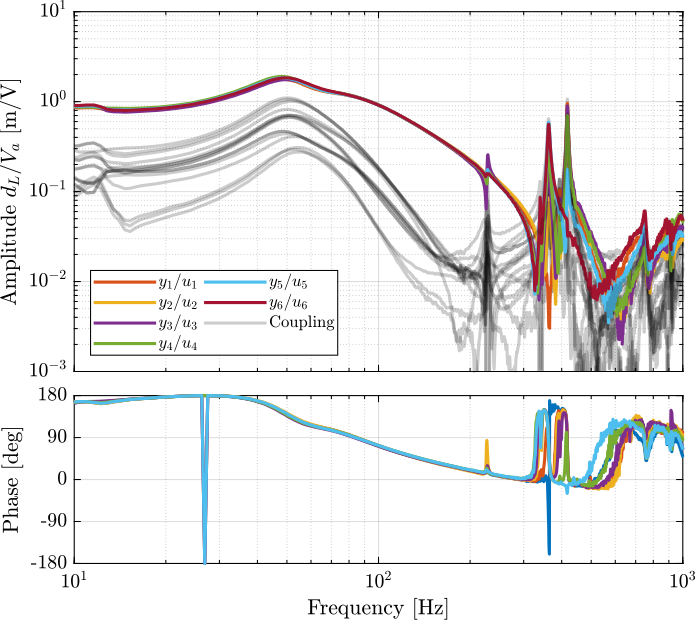
Figure 89: Bode Plot of the plant decoupled at the crossover
%% Compute RGA Matrix RGA_wc = zeros(size(frf_coupled)); for i = 1:length(frf_iff.f) RGA_wc(i,:,:) = squeeze(G_dL_wc(i,:,:)).*inv(squeeze(G_dL_wc(i,:,:))).'; end %% Compute RGA-number RGA_wc_sum = zeros(size(RGA_wc, 1), 1); for i = 1:size(RGA_wc, 1) RGA_wc_sum(i) = sum(sum(abs(eye(6) - squeeze(RGA_wc(i,:,:))))); end
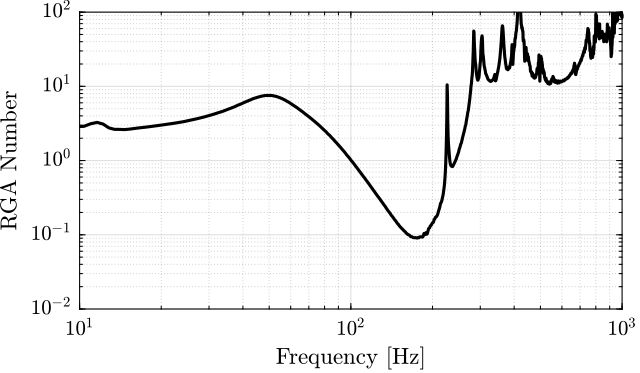
Figure 90: RGA number for the plant decoupled at the crossover
3.3.5. SVD Decoupling
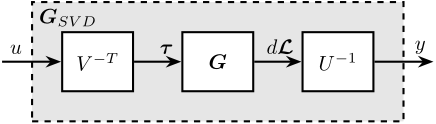
Figure 91: Decoupling using the Singular Value Decomposition
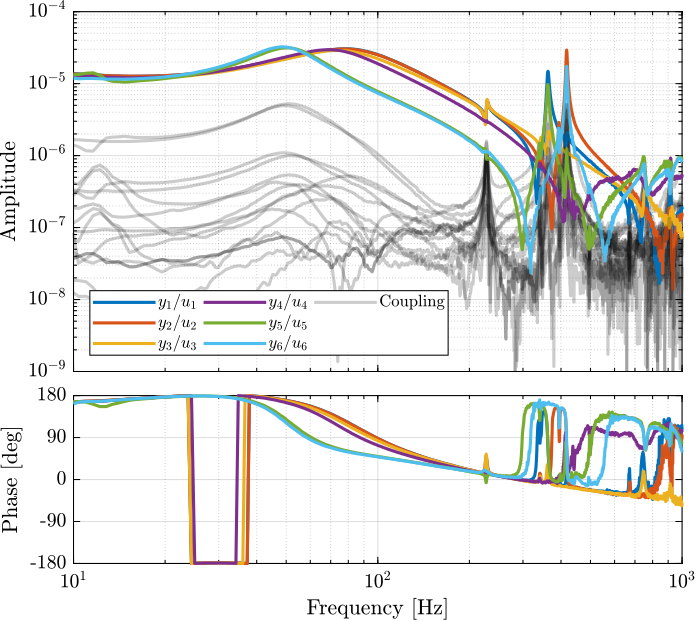
Figure 92: Bode Plot of the plant decoupled using the Singular Value Decomposition
%% Compute the RGA matrix for the SVD decoupled plant RGA_svd = zeros(size(frf_coupled)); for i = 1:length(frf_iff.f) RGA_svd(i,:,:) = squeeze(G_dL_svd(i,:,:)).*inv(squeeze(G_dL_svd(i,:,:))).'; end %% Compute the RGA-number RGA_svd_sum = zeros(size(RGA_svd, 1), 1); for i = 1:length(frf_iff.f) RGA_svd_sum(i) = sum(sum(abs(eye(6) - squeeze(RGA_svd(i,:,:))))); end
%% RGA Number for the SVD decoupled plant figure; plot(frf_iff.f, RGA_svd_sum, 'k-'); set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); xlabel('Frequency [Hz]'); ylabel('RGA Number'); xlim([10, 1e3]); ylim([1e-2, 1e2]);
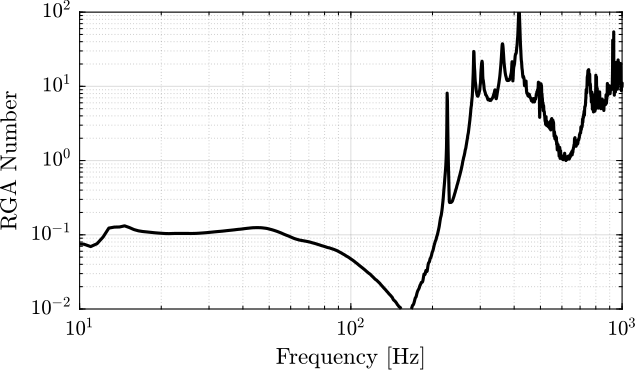
Figure 93: RGA number for the plant decoupled using the SVD
3.3.6. Dynamic decoupling
3.3.7. Jacobian Decoupling - Center of Stiffness
3.3.8. Jacobian Decoupling - Center of Mass
3.3.9. Decoupling Comparison
Let’s now compare all of the decoupling methods (Figure 103).
From Figure 103, the following remarks are made:
- Decentralized plant: well decoupled below suspension modes
- Static inversion: similar to the decentralized plant as the decentralized plant has already a good decoupling at low frequency
- Crossover inversion: the decoupling is improved around the crossover frequency as compared to the decentralized plant. However, the decoupling is increased at lower frequency.
- SVD decoupling: Very good decoupling up to 235Hz. Especially between 100Hz and 200Hz.
- Dynamic Inversion: the plant is very well decoupled at frequencies where the model is accurate (below 235Hz where flexible modes are not modelled).
- Jacobian - Stiffness: good decoupling at low frequency. The decoupling increases at the frequency of the suspension modes, but is acceptable up to the strut flexible modes (235Hz).
- Jacobian - Mass: bad decoupling at low frequency. Better decoupling above the frequency of the suspension modes, and acceptable decoupling up to the strut flexible modes (235Hz).
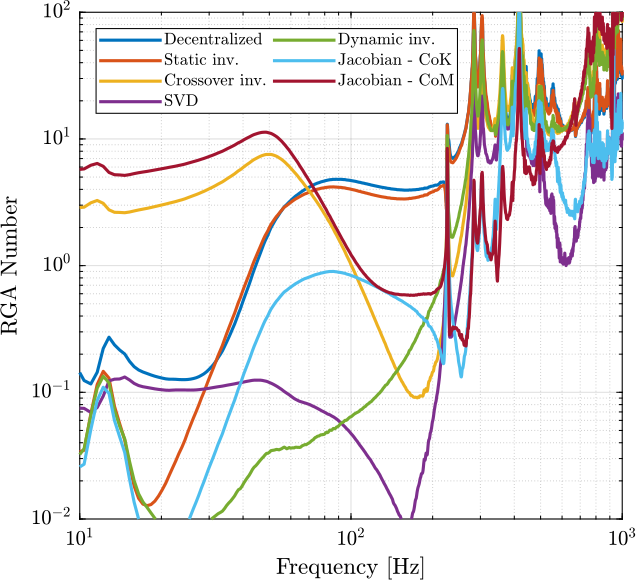
Figure 103: Comparison of the obtained RGA-numbers for all the decoupling methods
3.3.10. Decoupling Robustness
Let’s now see how the decoupling is changing when changing the payload’s mass.
frf_new = frf_iff.G_dL{3};
The obtained RGA-numbers are shown in Figure 104.
From Figure 104:
- The decoupling using the Jacobian evaluated at the “center of stiffness” seems to give the most robust results.
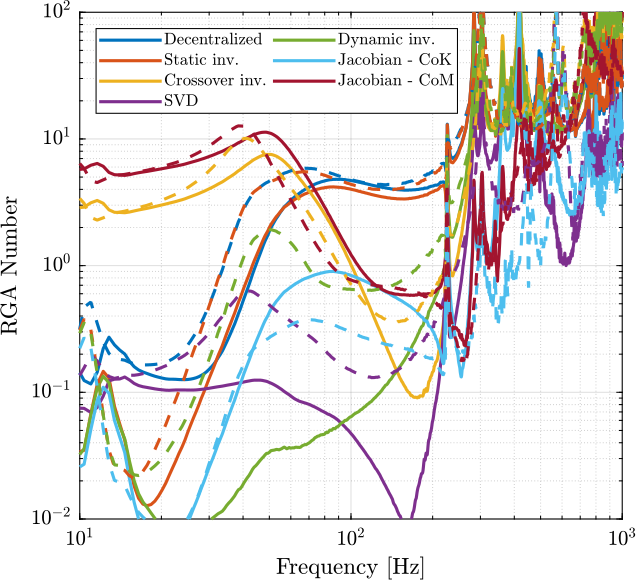
Figure 104: Change of the RGA-number with a change of the payload. Indication of the robustness of the inversion method.
3.3.11. Conclusion
Several decoupling methods can be used:
- SVD
- Inverse
- Jacobian (CoK)
| Method | RGA | Diag Plant | Robustness |
|---|---|---|---|
| Decentralized | -- | Equal | ++ |
| Static dec. | -- | Equal | ++ |
| Crossover dec. | - | Equal | 0 |
| SVD | ++ | Diff | + |
| Dynamic dec. | ++ | Unity, equal | - |
| Jacobian - CoK | + | Diff | ++ |
| Jacobian - CoM | 0 | Diff | + |
3.4. Robust High Authority Controller
In this section we wish to develop a robust High Authority Controller (HAC) that is working for all payloads.
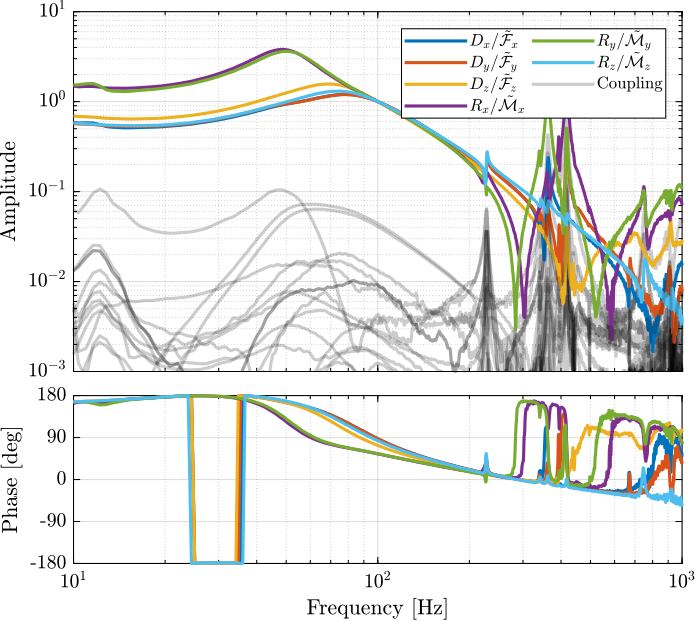
3.4.1. Using Jacobian evaluated at the center of stiffness
3.4.1.1. Decoupled Plant
G_nom = frf_iff.G_dL{2}; % Nominal Plant
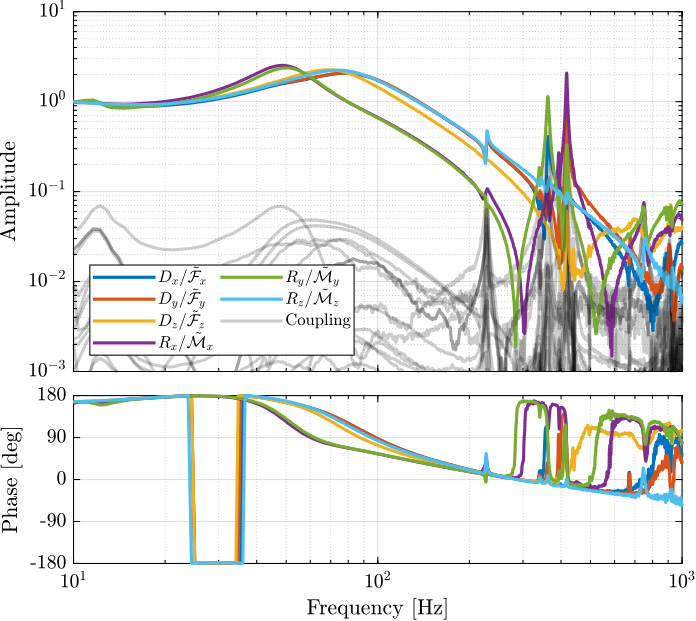
Figure 105: Bode plot of the decoupled plant using the Jacobian evaluated at the Center of Stiffness
3.4.1.2. SISO Controller Design
As the diagonal elements of the plant are not equal, several SISO controllers are designed and then combined to form a diagonal controller. All the diagonal terms of the controller consists of:
- A double integrator to have high gain at low frequency
- A lead around the crossover frequency to increase stability margins
- Two second order low pass filters above the crossover frequency to increase the robustness to high frequency modes
3.4.1.3. Obtained Loop Gain
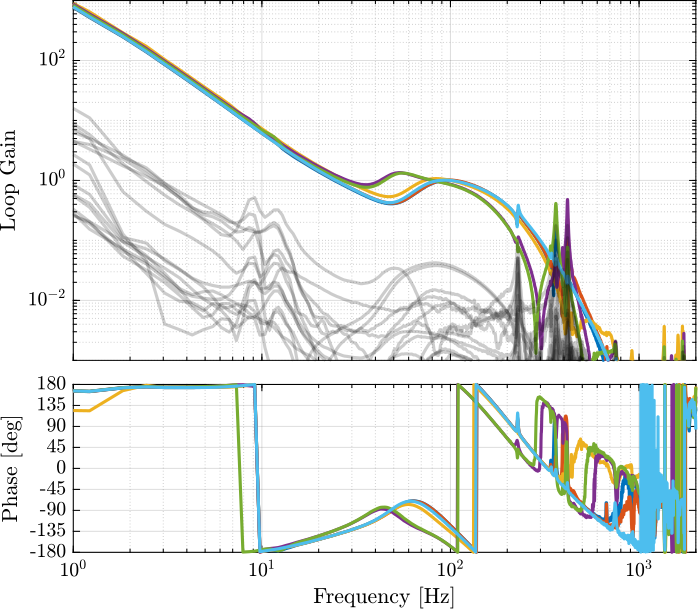
Figure 106: Bode plot of the Loop Gain when using the Jacobian evaluated at the Center of Stiffness to decouple the system
%% Controller to be implemented Kd = inv(J_cok')*input_normalize*ss(Kd_diag)*inv(Js_cok);
3.4.1.4. Verification of the Stability
Now the stability of the feedback loop is verified using the generalized Nyquist criteria.
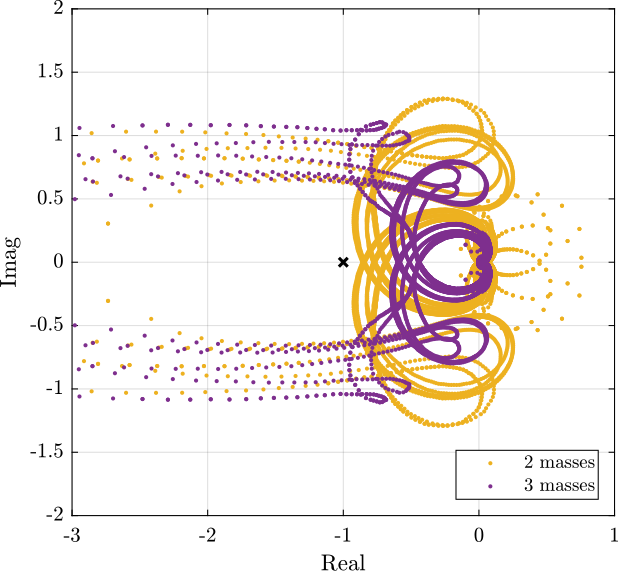
Figure 107: Loci of \(L(j\omega)\) in the complex plane.
3.4.1.5. Save for further analysis
save('mat/Khac_iff_struts_jacobian_cok.mat', 'Kd')
3.4.2. Using Singular Value Decomposition
3.4.2.1. Decoupled Plant
G_nom = frf_iff.G_dL{2}; % Nominal Plant
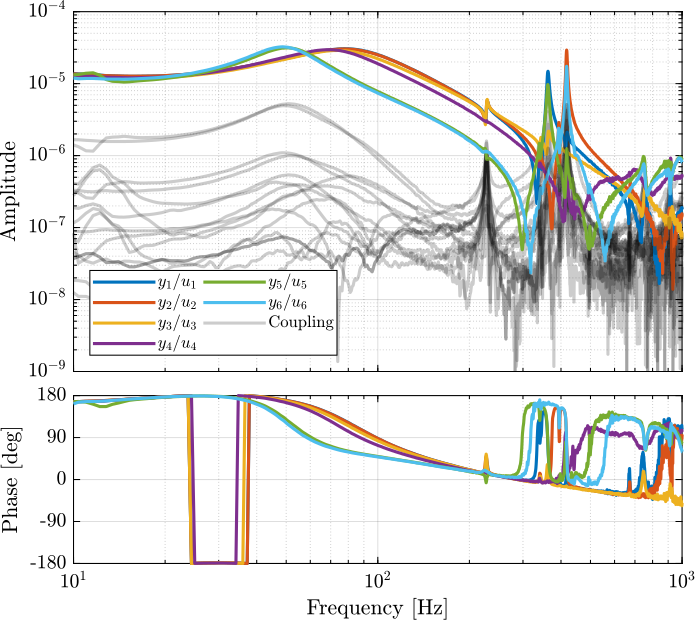
Figure 108: Bode plot of the decoupled plant using the SVD
3.4.2.2. Controller Design
3.4.2.3. Loop Gain
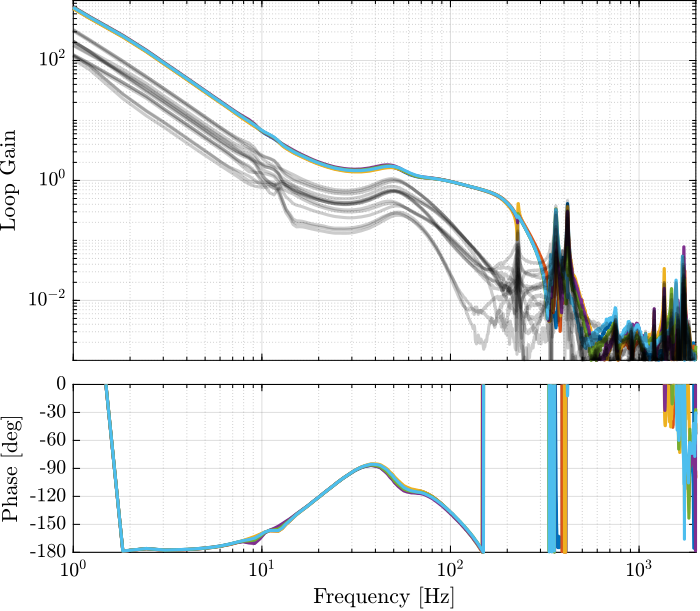
Figure 109: Bode plot of Loop Gain when using the SVD
3.4.2.4. Stability Verification
%% Compute the Eigenvalues of the loop gain Ldet = zeros(3, 6, length(frf_iff.f)); for i = 1:3 Lmimo = pagemtimes(permute(frf_iff.G_dL{i}, [2,3,1]),squeeze(freqresp(Kd, frf_iff.f, 'Hz'))); for i_f = 2:length(frf_iff.f) Ldet(i,:, i_f) = eig(squeeze(Lmimo(:,:,i_f))); end end
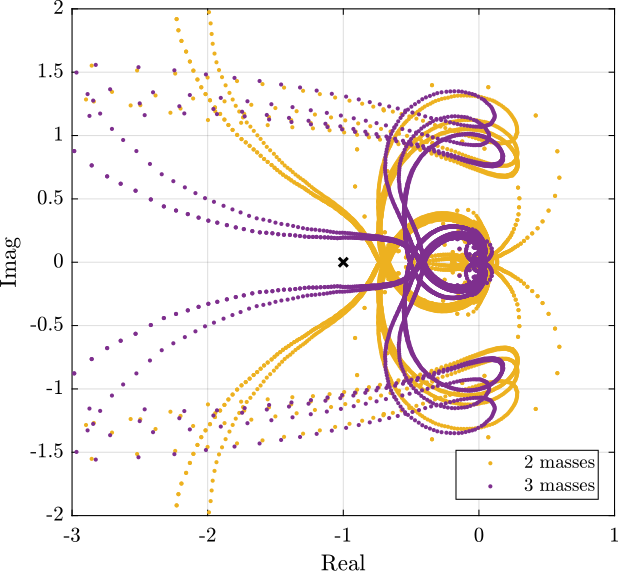
Figure 110: Locis of \(L(j\omega)\) in the complex plane.
3.4.2.5. Save for further analysis
save('mat/Khac_iff_struts_svd.mat', 'Kd')
4. Functions
4.1. generateXYZTrajectory
Function description
function [ref] = generateXYZTrajectory(args) % generateXYZTrajectory - % % Syntax: [ref] = generateXYZTrajectory(args) % % Inputs: % - args % % Outputs: % - ref - Reference Signal
Optional Parameters
arguments
args.points double {mustBeNumeric} = zeros(2, 3) % [m]
args.ti (1,1) double {mustBeNumeric, mustBeNonnegative} = 1 % Time to go to first point and after last point [s]
args.tw (1,1) double {mustBeNumeric, mustBeNonnegative} = 0.5 % Time wait between each point [s]
args.tm (1,1) double {mustBeNumeric, mustBeNonnegative} = 1 % Motion time between points [s]
args.Ts (1,1) double {mustBeNumeric, mustBePositive} = 1e-3 % Sampling Time [s]
end
Initialize Time Vectors
time_i = 0:args.Ts:args.ti; time_w = 0:args.Ts:args.tw; time_m = 0:args.Ts:args.tm;
XYZ Trajectory
% Go to initial position xyz = (args.points(1,:))'*(time_i/args.ti); % Wait xyz = [xyz, xyz(:,end).*ones(size(time_w))]; % Scans for i = 2:size(args.points, 1) % Go to next point xyz = [xyz, xyz(:,end) + (args.points(i,:)' - xyz(:,end))*(time_m/args.tm)]; % Wait a litle bit xyz = [xyz, xyz(:,end).*ones(size(time_w))]; end % End motion xyz = [xyz, xyz(:,end) - xyz(:,end)*(time_i/args.ti)];
Reference Signal
t = 0:args.Ts:args.Ts*(length(xyz) - 1);
ref = zeros(length(xyz), 7); ref(:, 1) = t; ref(:, 2:4) = xyz';
4.2. generateYZScanTrajectory
Function description
function [ref] = generateYZScanTrajectory(args) % generateYZScanTrajectory - % % Syntax: [ref] = generateYZScanTrajectory(args) % % Inputs: % - args % % Outputs: % - ref - Reference Signal
Optional Parameters
arguments
args.y_tot (1,1) double {mustBeNumeric, mustBePositive} = 10e-6 % [m]
args.z_tot (1,1) double {mustBeNumeric, mustBePositive} = 10e-6 % [m]
args.n (1,1) double {mustBeInteger, mustBePositive} = 10 % [-]
args.Ts (1,1) double {mustBeNumeric, mustBePositive} = 1e-4 % [s]
args.ti (1,1) double {mustBeNumeric, mustBeNonnegative} = 1 % [s]
args.tw (1,1) double {mustBeNumeric, mustBeNonnegative} = 1 % [s]
args.ty (1,1) double {mustBeNumeric, mustBeNonnegative} = 1 % [s]
args.tz (1,1) double {mustBeNumeric, mustBeNonnegative} = 1 % [s]
end
Initialize Time Vectors
time_i = 0:args.Ts:args.ti; time_w = 0:args.Ts:args.tw; time_y = 0:args.Ts:args.ty; time_z = 0:args.Ts:args.tz;
Y and Z vectors
% Go to initial position y = (time_i/args.ti)*(args.y_tot/2); % Wait y = [y, y(end)*ones(size(time_w))]; % Scans for i = 1:args.n if mod(i,2) == 0 y = [y, -(args.y_tot/2) + (time_y/args.ty)*args.y_tot]; else y = [y, (args.y_tot/2) - (time_y/args.ty)*args.y_tot]; end if i < args.n y = [y, y(end)*ones(size(time_z))]; end end % Wait a litle bit y = [y, y(end)*ones(size(time_w))]; % End motion y = [y, y(end) - y(end)*time_i/args.ti];
% Go to initial position z = (time_i/args.ti)*(args.z_tot/2); % Wait z = [z, z(end)*ones(size(time_w))]; % Scans for i = 1:args.n z = [z, z(end)*ones(size(time_y))]; if i < args.n z = [z, z(end) - (time_z/args.tz)*args.z_tot/(args.n-1)]; end end % Wait a litle bit z = [z, z(end)*ones(size(time_w))]; % End motion z = [z, z(end) - z(end)*time_i/args.ti];
Reference Signal
t = 0:args.Ts:args.Ts*(length(y) - 1);
ref = zeros(length(y), 7); ref(:, 1) = t; ref(:, 3) = y; ref(:, 4) = z;
4.3. generateSpiralAngleTrajectory
Function description
function [ref] = generateSpiralAngleTrajectory(args) % generateSpiralAngleTrajectory - % % Syntax: [ref] = generateSpiralAngleTrajectory(args) % % Inputs: % - args % % Outputs: % - ref - Reference Signal
Optional Parameters
arguments
args.R_tot (1,1) double {mustBeNumeric, mustBePositive} = 10e-6 % [rad]
args.n_turn (1,1) double {mustBeInteger, mustBePositive} = 5 % [-]
args.Ts (1,1) double {mustBeNumeric, mustBePositive} = 1e-3 % [s]
args.t_turn (1,1) double {mustBeNumeric, mustBePositive} = 1 % [s]
args.t_end (1,1) double {mustBeNumeric, mustBePositive} = 1 % [s]
end
Initialize Time Vectors
time_s = 0:args.Ts:args.n_turn*args.t_turn; time_e = 0:args.Ts:args.t_end;
Rx and Ry vectors
Rx = sin(2*pi*time_s/args.t_turn).*(args.R_tot*time_s/(args.n_turn*args.t_turn)); Ry = cos(2*pi*time_s/args.t_turn).*(args.R_tot*time_s/(args.n_turn*args.t_turn));
Rx = [Rx, 0*time_e]; Ry = [Ry, Ry(end) - Ry(end)*time_e/args.t_end];
Reference Signal
t = 0:args.Ts:args.Ts*(length(Rx) - 1);
ref = zeros(length(Rx), 7); ref(:, 1) = t; ref(:, 5) = Rx; ref(:, 6) = Ry;
4.4. getTransformationMatrixAcc
Function description
function [M] = getTransformationMatrixAcc(Opm, Osm) % getTransformationMatrixAcc - % % Syntax: [M] = getTransformationMatrixAcc(Opm, Osm) % % Inputs: % - Opm - Nx3 (N = number of accelerometer measurements) X,Y,Z position of accelerometers % - Opm - Nx3 (N = number of accelerometer measurements) Unit vectors representing the accelerometer orientation % % Outputs: % - M - Transformation Matrix
Transformation matrix from motion of the solid body to accelerometer measurements
Let’s try to estimate the x-y-z acceleration of any point of the solid body from the acceleration/angular acceleration of the solid body expressed in \(\{O\}\). For any point \(p_i\) of the solid body (corresponding to an accelerometer), we can write:
\begin{equation} \begin{bmatrix} a_{i,x} \\ a_{i,y} \\ a_{i,z} \end{bmatrix} = \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \end{bmatrix} + p_i \times \begin{bmatrix} \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} \end{equation}We can write the cross product as a matrix product using the skew-symmetric transformation:
\begin{equation} \begin{bmatrix} a_{i,x} \\ a_{i,y} \\ a_{i,z} \end{bmatrix} = \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \end{bmatrix} + \underbrace{\begin{bmatrix} 0 & p_{i,z} & -p_{i,y} \\ -p_{i,z} & 0 & p_{i,x} \\ p_{i,y} & -p_{i,x} & 0 \end{bmatrix}}_{P_{i,[\times]}} \cdot \begin{bmatrix} \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} \end{equation}If we now want to know the (scalar) acceleration \(a_i\) of the point \(p_i\) in the direction of the accelerometer direction \(\hat{s}_i\), we can just project the 3d acceleration on \(\hat{s}_i\):
\begin{equation} a_i = \hat{s}_i^T \cdot \begin{bmatrix} a_{i,x} \\ a_{i,y} \\ a_{i,z} \end{bmatrix} = \hat{s}_i^T \cdot \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \end{bmatrix} + \left( \hat{s}_i^T \cdot P_{i,[\times]} \right) \cdot \begin{bmatrix} \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} \end{equation}Which is equivalent as a simple vector multiplication:
\begin{equation} a_i = \begin{bmatrix} \hat{s}_i^T & \hat{s}_i^T \cdot P_{i,[\times]} \end{bmatrix} \begin{bmatrix} \dot{v}_x \\ \dot{v}_y \\ \dot{v}_z \\ \dot{\omega}_x \\ \dot{\omega}_y \\ \dot{\omega}_z \end{bmatrix} = \begin{bmatrix} \hat{s}_i^T & \hat{s}_i^T \cdot P_{i,[\times]} \end{bmatrix} {}^O\vec{x} \end{equation}And finally we can combine the 6 (line) vectors for the 6 accelerometers to write that in a matrix form. We obtain Eq. \eqref{eq:M_matrix}.
The transformation from solid body acceleration \({}^O\vec{x}\) from sensor measured acceleration \(\vec{a}\) is:
\begin{equation} \label{eq:M_matrix} \vec{a} = \underbrace{\begin{bmatrix} \hat{s}_1^T & \hat{s}_1^T \cdot P_{1,[\times]} \\ \vdots & \vdots \\ \hat{s}_6^T & \hat{s}_6^T \cdot P_{6,[\times]} \end{bmatrix}}_{M} {}^O\vec{x} \end{equation}with \(\hat{s}_i\) the unit vector representing the measured direction of the i’th accelerometer expressed in frame \(\{O\}\) and \(P_{i,[\times]}\) the skew-symmetric matrix representing the cross product of the position of the i’th accelerometer expressed in frame \(\{O\}\).
Let’s define such matrix using matlab:
M = zeros(length(Opm), 6); for i = 1:length(Opm) Ri = [0, Opm(3,i), -Opm(2,i); -Opm(3,i), 0, Opm(1,i); Opm(2,i), -Opm(1,i), 0]; M(i, 1:3) = Osm(:,i)'; M(i, 4:6) = Osm(:,i)'*Ri; end
end
4.5. getJacobianNanoHexapod
Function description
function [J] = getJacobianNanoHexapod(Hbm) % getJacobianNanoHexapod - % % Syntax: [J] = getJacobianNanoHexapod(Hbm) % % Inputs: % - Hbm - Height of {B} w.r.t. {M} [m] % % Outputs: % - J - Jacobian Matrix
Transformation matrix from motion of the solid body to accelerometer measurements
Fa = [[-86.05, -74.78, 22.49], [ 86.05, -74.78, 22.49], [ 107.79, -37.13, 22.49], [ 21.74, 111.91, 22.49], [-21.74, 111.91, 22.49], [-107.79, -37.13, 22.49]]'*1e-3; % Ai w.r.t. {F} [m] Mb = [[-28.47, -106.25, -22.50], [ 28.47, -106.25, -22.50], [ 106.25, 28.47, -22.50], [ 77.78, 77.78, -22.50], [-77.78, 77.78, -22.50], [-106.25, 28.47, -22.50]]'*1e-3; % Bi w.r.t. {M} [m] H = 95e-3; % Stewart platform height [m] Fb = Mb + [0; 0; H]; % Bi w.r.t. {F} [m] si = Fb - Fa; si = si./vecnorm(si); % Normalize Bb = Mb - [0; 0; Hbm]; J = [si', cross(Bb, si)'];