Nano-Hexapod - Test Bench
Table of Contents
This report is also available as a pdf.
In this document, the dynamics of the nano-hexapod shown in Figure 1 is identified.
Here are the documentation of the equipment used for this test bench:

Figure 1: Nano-Hexapod

Figure 2: Nano-Hexapod and the control electronics
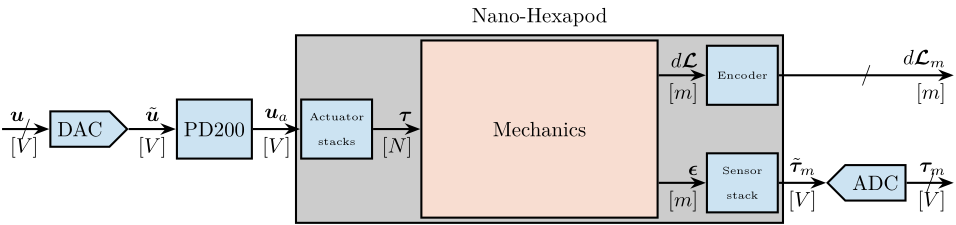
Figure 3: Block diagram of the system with named signals
| Unit | Matlab | Vector | Elements | |
|---|---|---|---|---|
| Control Input (wanted DAC voltage) | [V] |
u |
\(\bm{u}\) | \(u_i\) |
| DAC Output Voltage | [V] |
u |
\(\tilde{\bm{u}}\) | \(\tilde{u}_i\) |
| PD200 Output Voltage | [V] |
ua |
\(\bm{u}_a\) | \(u_{a,i}\) |
| Actuator applied force | [N] |
tau |
\(\bm{\tau}\) | \(\tau_i\) |
| Strut motion | [m] |
dL |
\(d\bm{\mathcal{L}}\) | \(d\mathcal{L}_i\) |
| Encoder measured displacement | [m] |
dLm |
\(d\bm{\mathcal{L}}_m\) | \(d\mathcal{L}_{m,i}\) |
| Force Sensor strain | [m] |
epsilon |
\(\bm{\epsilon}\) | \(\epsilon_i\) |
| Force Sensor Generated Voltage | [V] |
taum |
\(\tilde{\bm{\tau}}_m\) | \(\tilde{\tau}_{m,i}\) |
| Measured Generated Voltage | [V] |
taum |
\(\bm{\tau}_m\) | \(\tau_{m,i}\) |
| Motion of the top platform | [m,rad] |
dX |
\(d\bm{\mathcal{X}}\) | \(d\mathcal{X}_i\) |
| Metrology measured displacement | [m,rad] |
dXm |
\(d\bm{\mathcal{X}}_m\) | \(d\mathcal{X}_{m,i}\) |
1 Encoders fixed to the Struts
1.1 Introduction
In this section, the encoders are fixed to the struts.
1.2 Identification of the dynamics
1.2.1 Load Data
%% Load Identification Data meas_data_lf = {}; for i = 1:6 meas_data_lf(i) = {load(sprintf('mat/frf_data_exc_strut_%i_noise_lf.mat', i), 't', 'Va', 'Vs', 'de')}; meas_data_hf(i) = {load(sprintf('mat/frf_data_exc_strut_%i_noise_hf.mat', i), 't', 'Va', 'Vs', 'de')}; end
1.2.2 Spectral Analysis - Setup
%% Setup useful variables % Sampling Time [s] Ts = (meas_data_lf{1}.t(end) - (meas_data_lf{1}.t(1)))/(length(meas_data_lf{1}.t)-1); % Sampling Frequency [Hz] Fs = 1/Ts; % Hannning Windows win = hanning(ceil(1*Fs)); % And we get the frequency vector [~, f] = tfestimate(meas_data_lf{1}.Va, meas_data_lf{1}.de, win, [], [], 1/Ts); i_lf = f < 250; % Points for low frequency excitation i_hf = f > 250; % Points for high frequency excitation
1.2.3 DVF Plant
First, let’s compute the coherence from the excitation voltage and the displacement as measured by the encoders (Figure 4).
%% Coherence coh_dvf_lf = zeros(length(f), 6, 6); coh_dvf_hf = zeros(length(f), 6, 6); for i = 1:6 coh_dvf_lf(:, :, i) = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts); coh_dvf_hf(:, :, i) = mscohere(meas_data_hf{i}.Va, meas_data_hf{i}.de, win, [], [], 1/Ts); end
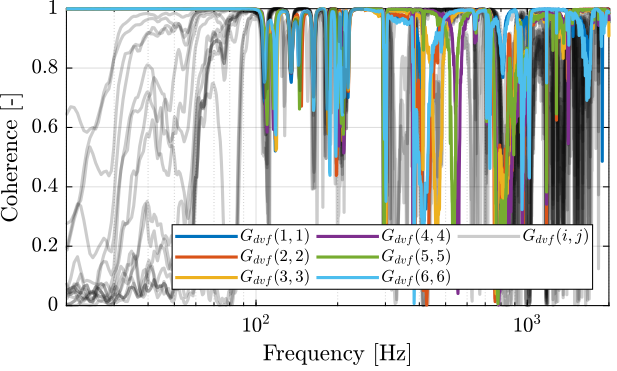
Figure 4: Obtained coherence for the DVF plant
Then the 6x6 transfer function matrix is estimated (Figure 5).
%% DVF Plant (transfer function from u to dLm) G_dvf_lf = zeros(length(f), 6, 6); G_dvf_hf = zeros(length(f), 6, 6); for i = 1:6 G_dvf_lf(:, :, i) = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.de, win, [], [], 1/Ts); G_dvf_hf(:, :, i) = tfestimate(meas_data_hf{i}.Va, meas_data_hf{i}.de, win, [], [], 1/Ts); end
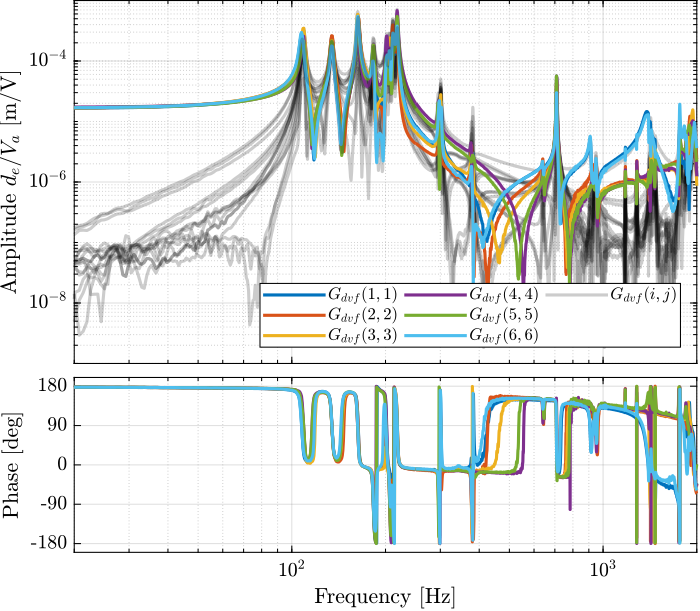
Figure 5: Measured FRF for the DVF plant
1.2.4 IFF Plant
First, let’s compute the coherence from the excitation voltage and the displacement as measured by the encoders (Figure 6).
%% Coherence for the IFF plant coh_iff_lf = zeros(length(f), 6, 6); coh_iff_hf = zeros(length(f), 6, 6); for i = 1:6 coh_iff_lf(:, :, i) = mscohere(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts); coh_iff_hf(:, :, i) = mscohere(meas_data_hf{i}.Va, meas_data_hf{i}.Vs, win, [], [], 1/Ts); end
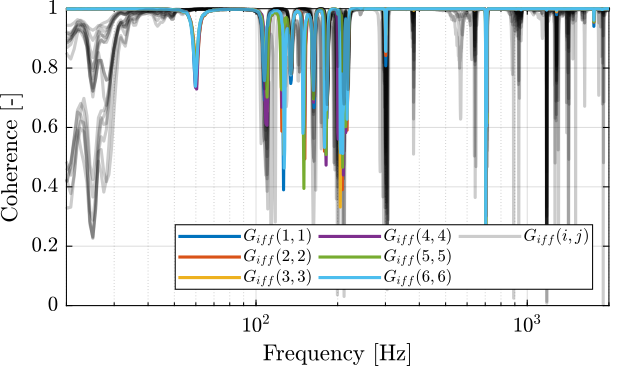
Figure 6: Obtained coherence for the IFF plant
Then the 6x6 transfer function matrix is estimated (Figure 7).
%% IFF Plant G_iff_lf = zeros(length(f), 6, 6); G_iff_hf = zeros(length(f), 6, 6); for i = 1:6 G_iff_lf(:, :, i) = tfestimate(meas_data_lf{i}.Va, meas_data_lf{i}.Vs, win, [], [], 1/Ts); G_iff_hf(:, :, i) = tfestimate(meas_data_hf{i}.Va, meas_data_hf{i}.Vs, win, [], [], 1/Ts); end
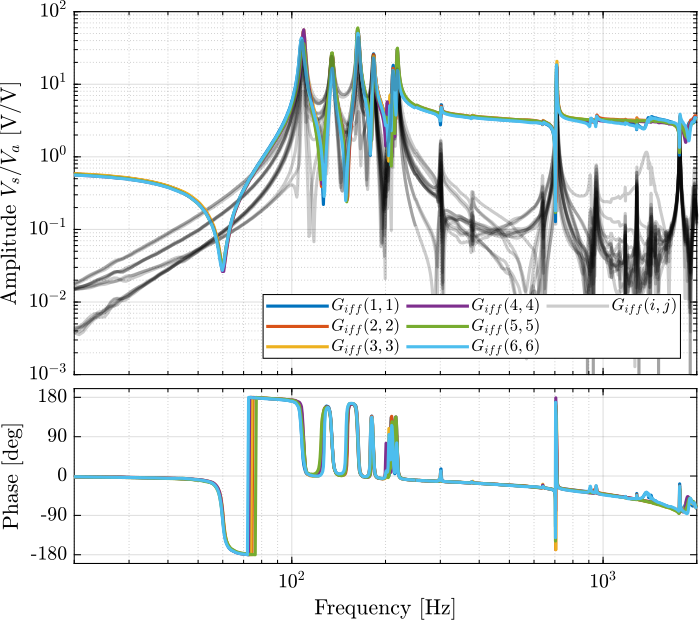
Figure 7: Measured FRF for the IFF plant
1.3 Comparison with the Simscape Model
In this section, the measured dynamics is compared with the dynamics estimated from the Simscape model.
1.3.1 Dynamics from Actuator to Force Sensors
%% Initialize Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', '2dof');
%% Identify the IFF Plant (transfer function from u to taum) clear io; io_i = 1; io(io_i) = linio([mdl, '/F'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/Fm'], 1, 'openoutput'); io_i = io_i + 1; % Force Sensors Giff = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
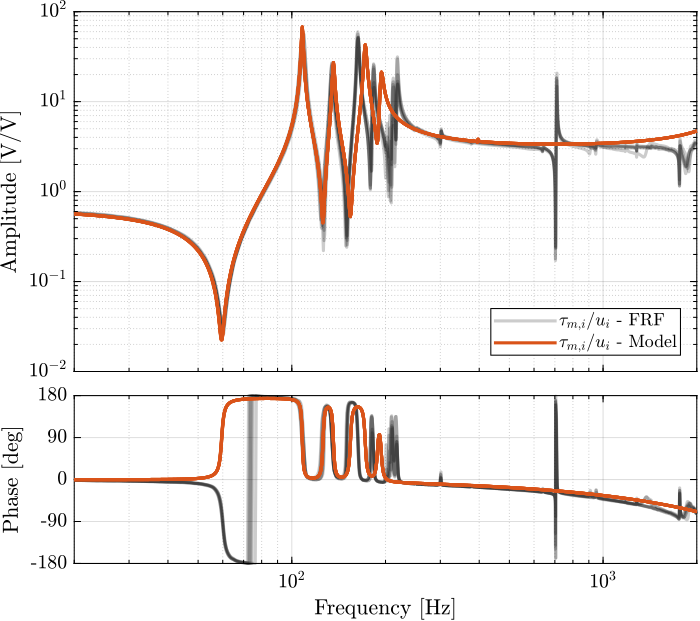
Figure 8: Diagonal elements of the IFF Plant
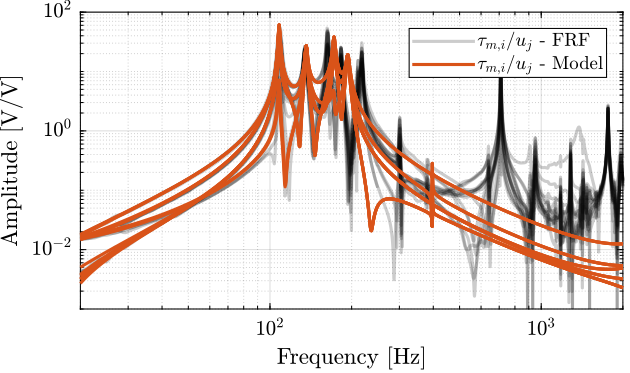
Figure 9: Off diagonal elements of the IFF Plant
1.3.2 Dynamics from Actuator to Encoder
%% Initialization of the Nano-Hexapod n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', '2dof');
%% Identify the DVF Plant (transfer function from u to dLm) clear io; io_i = 1; io(io_i) = linio([mdl, '/F'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Encoders Gdvf = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
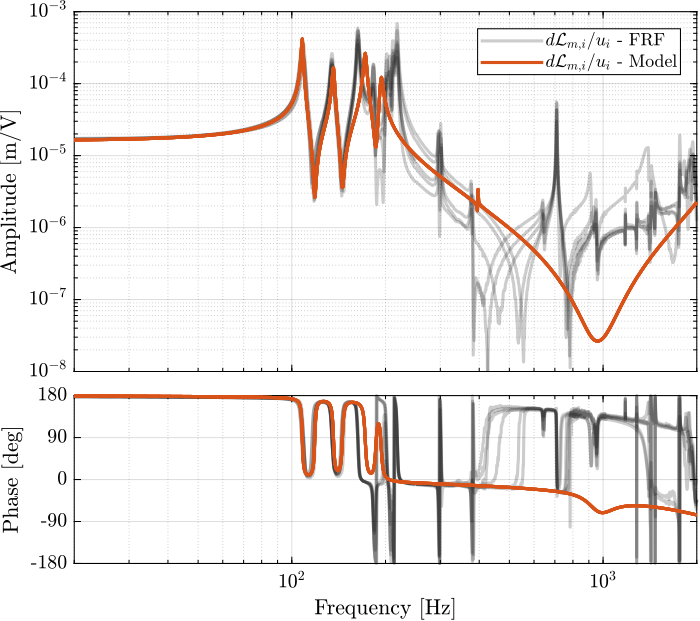
Figure 10: Diagonal elements of the DVF Plant
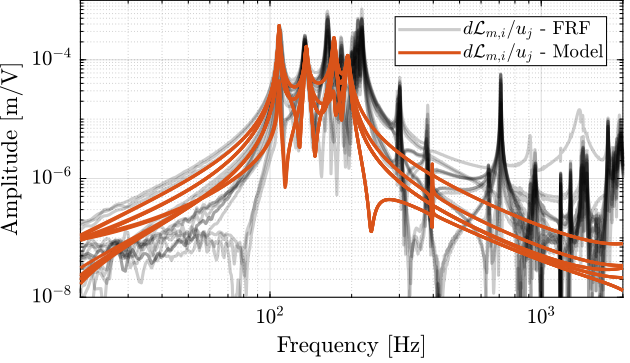
Figure 11: Off diagonal elements of the DVF Plant
1.4 Integral Force Feedback
1.4.1 Root Locus and Decentralized Loop gain
%% IFF Controller Kiff_g1 = (1/(s + 2*pi*40))*... % Low pass filter (provides integral action above 40Hz) (s/(s + 2*pi*30))*... % High pass filter to limit low frequency gain (1/(1 + s/2/pi/500))*... % Low pass filter to be more robust to high frequency resonances eye(6); % Diagonal 6x6 controller
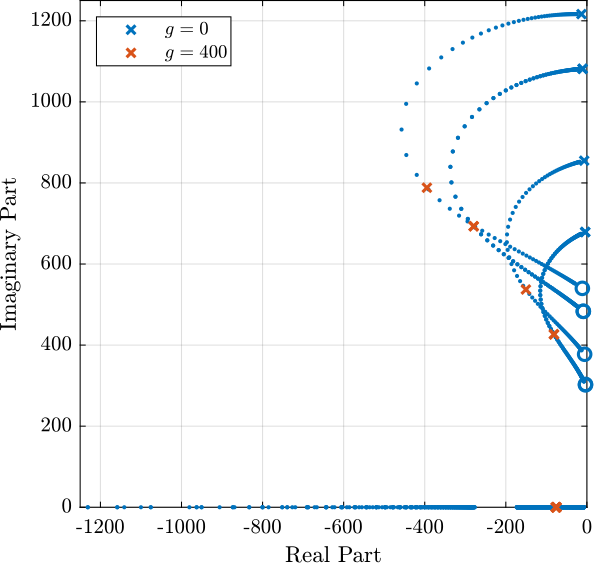
Figure 12: Root Locus for the IFF control strategy
Then the “optimal” IFF controller is:
%% IFF controller with Optimal gain Kiff = g*Kiff_g1;
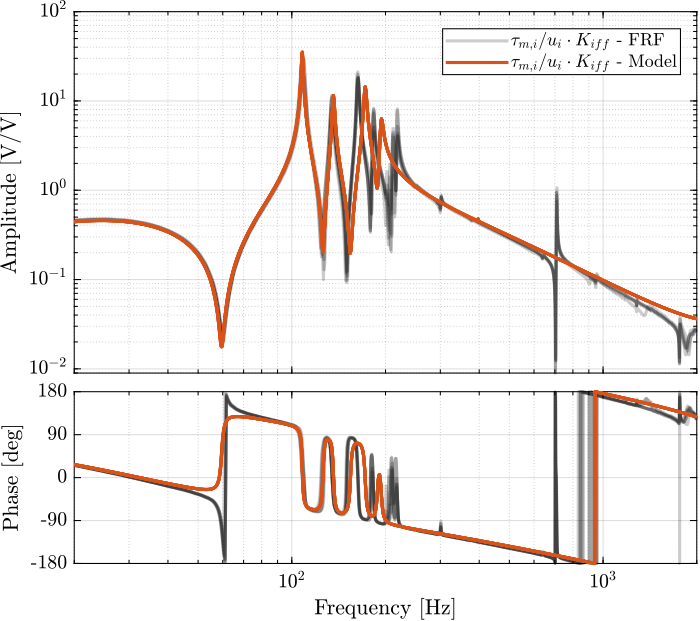
Figure 13: Bode plot of the “decentralized loop gain” \(G_\text{iff}(i,i) \times K_\text{iff}(i,i)\)
1.4.2 Multiple Gains - Simulation
%% Tested IFF gains
iff_gains = [4, 10, 20, 40, 100, 200, 400, 1000];
%% Initialize the Simscape model in closed loop n_hexapod = initializeNanoHexapodFinal('flex_bot_type', '4dof', ... 'flex_top_type', '4dof', ... 'motion_sensor_type', 'struts', ... 'actuator_type', '2dof', ... 'controller_type', 'iff');
%% Identify the (damped) transfer function from u to dLm for different values of the IFF gain Gd_iff = {zeros(1, length(iff_gains))}; clear io; io_i = 1; io(io_i) = linio([mdl, '/F'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/D'], 1, 'openoutput'); io_i = io_i + 1; % Strut Displacement (encoder) for i = 1:length(iff_gains) Kiff = iff_gains(i)*Kiff_g1*eye(6); % IFF Controller Gd_iff(i) = {exp(-s*Ts)*linearize(mdl, io, 0.0, options)}; isstable(Gd_iff{i}) end
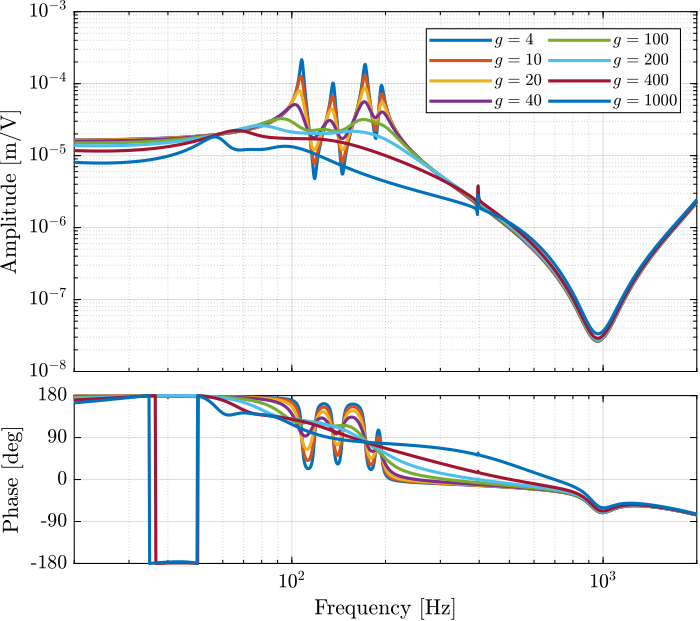
Figure 14: Effect of the IFF gain \(g\) on the transfer function from \(\bm{\tau}\) to \(d\bm{\mathcal{L}}_m\)