UP | HOME

Piezoelectric Force Sensor - Test Bench

Table of Contents

In this document is studied how a piezoelectric stack can be used to measured the force.

1 Change of Stiffness due to Sensors stack being open/closed circuit

1.1 Load Data

oc = load('identification_open_circuit.mat', 't', 'encoder', 'u');
sc = load('identification_short_circuit.mat', 't', 'encoder', 'u');

1.2 Transfer Functions

Ts = 1e-4; % Sampling Time [s]
win = hann(ceil(10/Ts));

[tf_oc_est, f] = tfestimate(oc.u, oc.encoder, win, [], [], 1/Ts);
[co_oc_est, ~] = mscohere(  oc.u, oc.encoder, win, [], [], 1/Ts);

[tf_sc_est, ~] = tfestimate(sc.u, sc.encoder, win, [], [], 1/Ts);
[co_sc_est, ~] = mscohere(  sc.u, sc.encoder, win, [], [], 1/Ts);

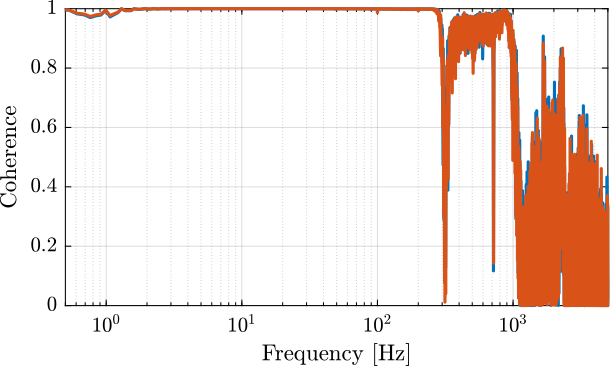
stiffness_force_sensor_coherence.png

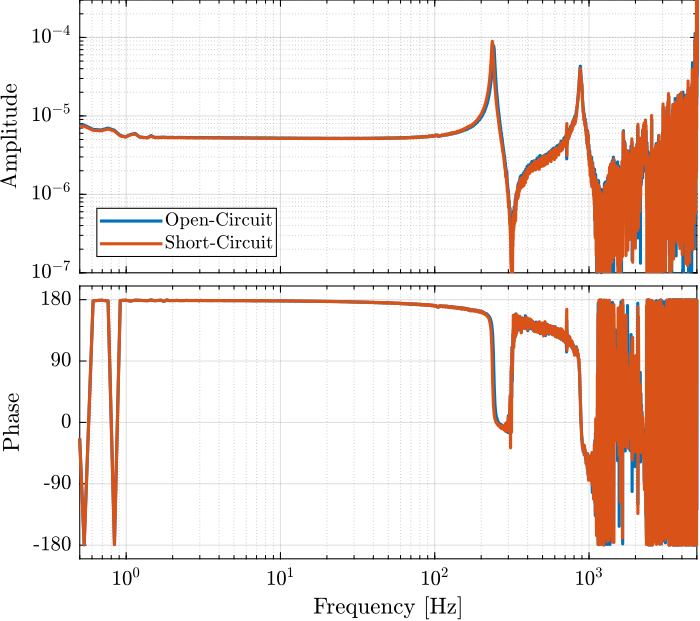
stiffness_force_sensor_bode.png

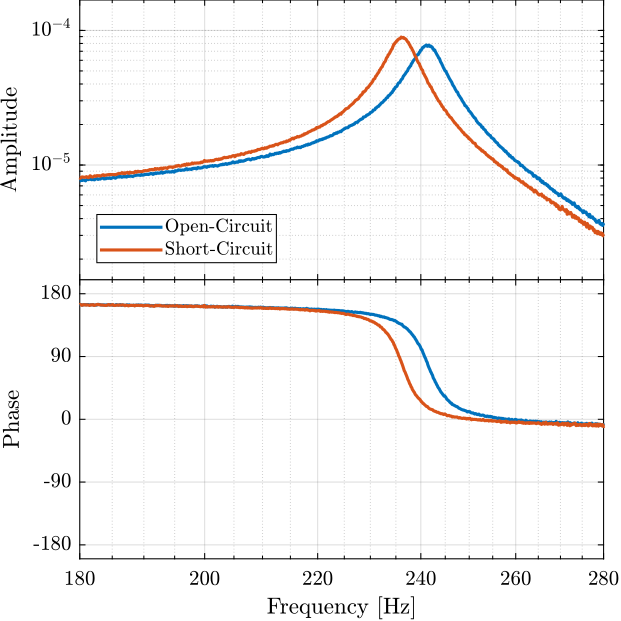
stiffness_force_sensor_bode_zoom.png

Figure 3: Zoom on the change of resonance

The change of resonance frequency / stiffness is very small and is not important here.

2 Generated Number of Charge / Voltage

Two stacks are used as actuator (in parallel) and one stack is used as sensor.

The amplifier gain is 20V/V (Cedrat LA75B).

2.1 Steps

load('force_sensor_steps.mat', 't', 'encoder', 'u', 'v');

figure;
tiledlayout(2, 1, 'TileSpacing', 'None', 'Padding', 'None');
nexttile;
plot(t, v);
xlabel('Time [s]'); ylabel('Measured voltage [V]');
nexttile;
plot(t, u);
xlabel('Time [s]'); ylabel('Actuator Voltage [V]');

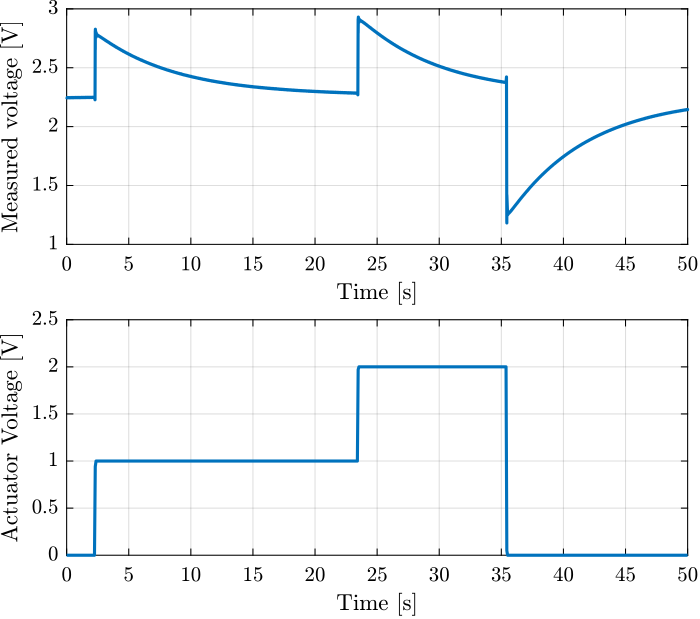
force_sen_steps_time_domain.png

Figure 4: Time domain signal during the 3 actuator voltage steps

Three steps are performed at the following time intervals: 

t_s = [ 2.5, 23;
       23.8, 35;
       35.8, 50];

Fit function: 

f = @(b,x) b(1).*exp(b(2).*x) + b(3);

We are interested by the b(2) term, which is the time constant of the exponential. 

tau = zeros(size(t_s, 1),1);
V0  = zeros(size(t_s, 1),1);

for t_i = 1:size(t_s, 1)
    t_cur = t(t_s(t_i, 1) < t & t < t_s(t_i, 2));
    t_cur = t_cur - t_cur(1);
    y_cur = v(t_s(t_i, 1) < t & t < t_s(t_i, 2));

    nrmrsd = @(b) norm(y_cur - f(b,t_cur)); % Residual Norm Cost Function
    B0 = [0.5, -0.15, 2.2];                        % Choose Appropriate Initial Estimates
    [B,rnrm] = fminsearch(nrmrsd, B0);     % Estimate Parameters ‘B’

    tau(t_i) = 1/B(2);
    V0(t_i)  = B(3);
end
\(tau\) [s] \(V_0\) [V]
6.47 2.26
6.76 2.26
6.49 2.25

With the capacitance being \(C = 4.4 \mu F\), the internal impedance of the Speedgoat ADC can be computed as follows: 

Cp = 4.4e-6; % [F]
Rin = abs(mean(tau))/Cp;

1494100.0

The input impedance of the Speedgoat’s ADC should then be close to \(1.5\,M\Omega\) (specified at \(1\,M\Omega\)).

How can we explain the voltage offset?

As shown in Figure 5 (taken from (Reza and Andrew 2006)), an input voltage offset is due to the input bias current \(i_n\).

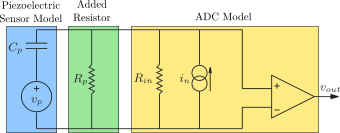
force_sensor_model_electronics.png

Figure 5: Model of a piezoelectric transducer (left) and instrumentation amplifier (right)

The estimated input bias current is then: 

in = mean(V0)/Rin;

1.5119e-06

An additional resistor in parallel with \(R_{in}\) would have two effects:

  • reduce the input voltage offset \[ V_{off} = \frac{R_a R_{in}}{R_a + R_{in}} i_n \]
  • increase the high pass corner frequency \(f_c\) \[ C_p \frac{R_{in}R_a}{R_{in} + R_a} = \tau_c = \frac{1}{f_c} \] \[ R_a = \frac{R_i}{f_c C_p R_i - 1} \]

If we allow the high pass corner frequency to be equals to 3Hz: 

fc = 3;
Ra = Rin/(fc*Cp*Rin - 1);

79804

With this parallel resistance value, the voltage offset would be: 

V_offset = Ra*Rin/(Ra + Rin) * in;

0.11454

Which is much more acceptable.

2.2 Add Parallel Resistor

A resistor \(R_p \approx 100\,k\Omega\) is added in parallel with the force sensor as shown in Figure 6.

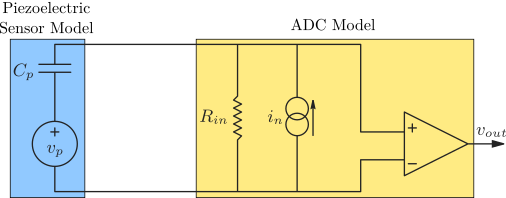
force_sensor_model_electronics_without_R.png

Figure 6: Model of a piezoelectric transducer (left) and instrumentation amplifier (right) with added resistor \(R_p\)

load('force_sensor_steps_R_82k7.mat', 't', 'encoder', 'u', 'v');

figure;
tiledlayout(2, 1, 'TileSpacing', 'None', 'Padding', 'None');
nexttile;
plot(t, v);
xlabel('Time [s]'); ylabel('Measured voltage [V]');
nexttile;
plot(t, u);
xlabel('Time [s]'); ylabel('Actuator Voltage [V]');

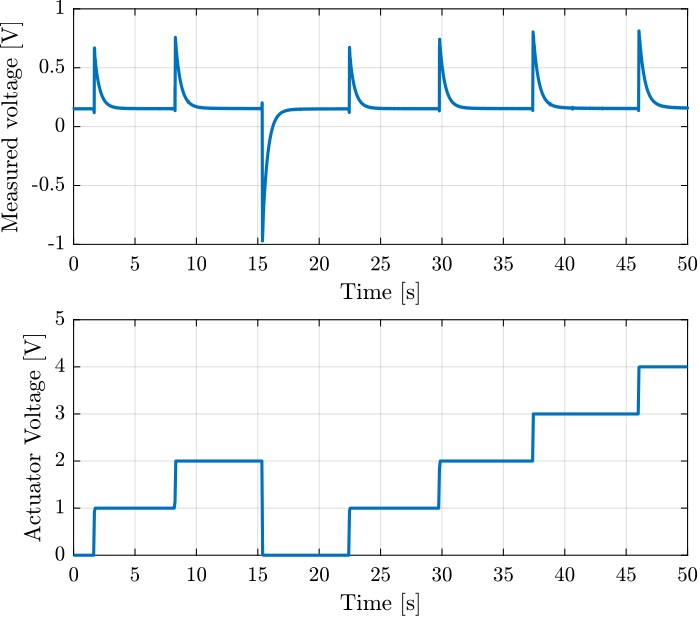
force_sen_steps_time_domain_par_R.png

Figure 7: Time domain signal during the actuator voltage steps

Three steps are performed at the following time intervals: 

t_s = [1.9,  6;
       8.5, 13;
      15.5, 21;
      22.6, 26;
      30.0, 36;
      37.5, 41;
      46.2, 49.5]

Fit function: 

f = @(b,x) b(1).*exp(b(2).*x) + b(3);

We are interested by the b(2) term, which is the time constant of the exponential. 

tau = zeros(size(t_s, 1),1);
V0  = zeros(size(t_s, 1),1);

for t_i = 1:size(t_s, 1)
    t_cur = t(t_s(t_i, 1) < t & t < t_s(t_i, 2));
    t_cur = t_cur - t_cur(1);
    y_cur = v(t_s(t_i, 1) < t & t < t_s(t_i, 2));

    nrmrsd = @(b) norm(y_cur - f(b,t_cur)); % Residual Norm Cost Function
    B0 = [0.5, -0.2, 0.2];                        % Choose Appropriate Initial Estimates
    [B,rnrm] = fminsearch(nrmrsd, B0);     % Estimate Parameters ‘B’

    tau(t_i) = 1/B(2);
    V0(t_i)  = B(3);
end

And indeed, we obtain a much smaller offset voltage and a much faster time constant.

\(tau\) [s] \(V_0\) [V]
0.43 0.15
0.45 0.16
0.43 0.15
0.43 0.15
0.45 0.15
0.46 0.16
0.48 0.16

Knowing the capacitance value, we can estimate the value of the added resistor (neglecting the input impedance of \(\approx 1\,M\Omega\)): 

Cp = 4.4e-6; % [F]
Rin = abs(mean(tau))/Cp;

101200.0

And we can verify that the bias current estimation stays the same: 

in = mean(V0)/Rin;

1.5305e-06

This validates the model of the ADC and the effectiveness of the added resistor.

2.3 Sinus

load('force_sensor_sin.mat', 't', 'encoder', 'u', 'v');

u       = u(t>25);
v       = v(t>25);
encoder = encoder(t>25) - mean(encoder(t>25));
t       = t(t>25);

The driving voltage is a sinus at 0.5Hz centered on 3V and with an amplitude of 3V (Figure 8).

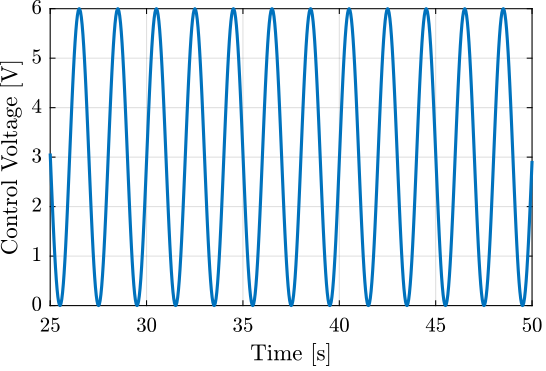
force_sensor_sin_u.png

Figure 8: Driving Voltage

The full stroke as measured by the encoder is: 

max(encoder)-min(encoder)

5.005e-05

Its signal is shown in Figure 9.

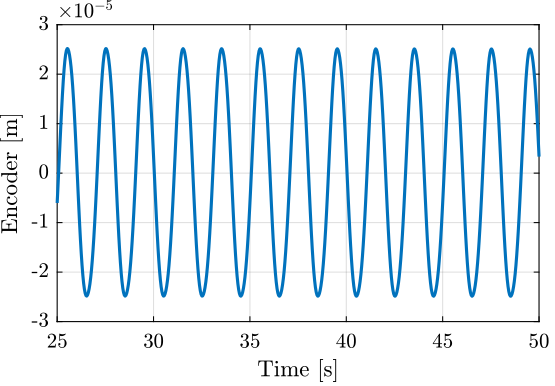
force_sensor_sin_encoder.png

Figure 9: Encoder measurement

The generated voltage by the stack is shown in Figure

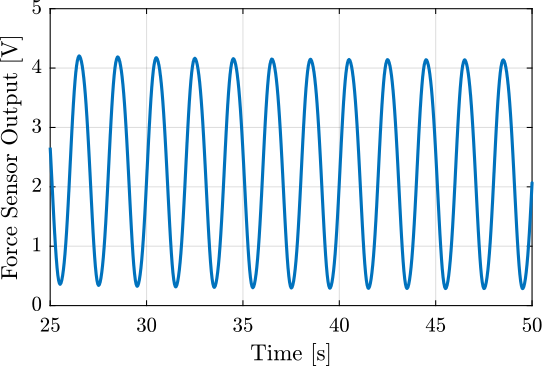
force_sensor_sin_stack.png

Figure 10: Voltage measured on the stack used as a sensor

The capacitance of the stack is 

Cp = 4.4e-6; % [F]

The corresponding generated charge is then shown in Figure 11.

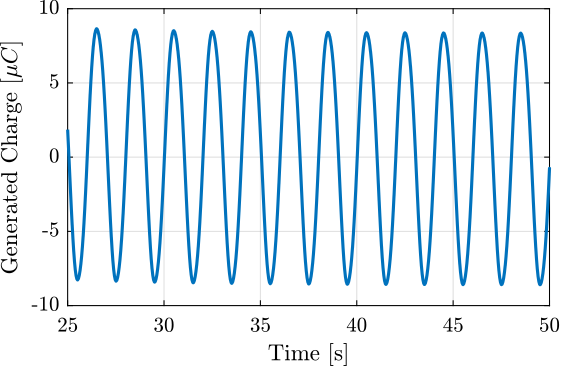
force_sensor_sin_charge.png

Figure 11: Generated Charge

The relation between the generated voltage and the measured displacement is almost linear as shown in Figure 12. 

b1 = encoder\(v-mean(v));

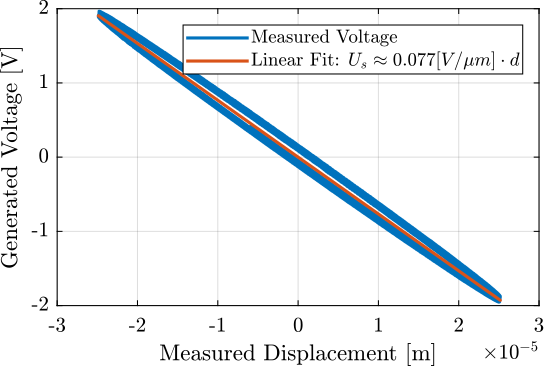
force_sensor_linear_relation.png

Figure 12: Almost linear relation between the relative displacement and the generated voltage

With a 16bits ADC, the resolution will then be equals to (in [nm]): 

abs((20/2^16)/(b1/1e9))

3.9838

Bibliography

Reza, Moheimani, and Fleming Andrew. 2006. Piezoelectric Transducers for Vibration Control and Damping. London: Springer.

Author: Dehaeze Thomas

Created: 2020-11-10 mar. 12:55