<?xml version="1.0" encoding="utf-8"?>
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN"
"http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<!-- 2020-12-16 mer. 11:07 -->
<meta http-equiv="Content-Type" content="text/html;charset=utf-8" />
<title>Amplifier Piezoelectric Actuator APA300ML - Test Bench</title>
<meta name="generator" content="Org mode" />
<meta name="author" content="Dehaeze Thomas" />
<link rel="stylesheet" type="text/css" href="https://research.tdehaeze.xyz/css/style.css"/>
<script type="text/javascript" src="https://research.tdehaeze.xyz/js/script.js"></script>
<script>MathJax = {
tex: {
tags: 'ams',
macros: {bm: ["\\boldsymbol{#1}",1],}
}
};
</script>
<script type="text/javascript" src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js"></script>
</head>
<body>
<div id="org-div-home-and-up">
<a accesskey="h" href="../index.html"> UP </a>
|
<a accesskey="H" href="../index.html"> HOME </a>
</div><div id="content">
<h1 class="title">Amplifier Piezoelectric Actuator APA300ML - Test Bench</h1>
<div id="table-of-contents">
<h2>Table of Contents</h2>
<div id="text-table-of-contents">
<ul>
<li><a href="#org1313e99">1. Model of an Amplified Piezoelectric Actuator and Sensor</a></li>
<li><a href="#org3c114e3">2. Test-Bench Description</a></li>
<li><a href="#orgeef8a7b">3. Measurement Procedure</a>
<ul>
<li><a href="#orgf5f4de4">3.1. Stroke Measurement</a></li>
<li><a href="#orgc6a7f40">3.2. Stiffness Measurement</a></li>
<li><a href="#orgf924c27">3.3. Hysteresis measurement</a></li>
<li><a href="#org8dd84d4">3.4. Piezoelectric Actuator Constant</a></li>
<li><a href="#org133086b">3.5. Piezoelectric Sensor Constant</a></li>
<li><a href="#org6d5e309">3.6. Capacitance Measurement</a></li>
</ul>
</li>
</ul>
</div>
</div>
<p>
The goal of this test bench is to extract all the important parameters of the Amplified Piezoelectric Actuator APA300ML.
</p>
<p>
This include:
</p>
<ul class="org-ul">
<li>Stroke</li>
<li>Stiffness</li>
<li>Hysteresis</li>
<li>Gain from the applied voltage \(V_a\) to the generated Force \(F_a\)</li>
<li>Gain from the sensor stack strain \(\delta L\) to the generated voltage \(V_s\)</li>
</ul>
<div id="outline-container-org1313e99" class="outline-2">
<h2 id="org1313e99"><span class="section-number-2">1</span> Model of an Amplified Piezoelectric Actuator and Sensor</h2>
<div class="outline-text-2" id="text-1">
<p>
Consider a schematic of the Amplified Piezoelectric Actuator in Figure <a href="#org5dd279e">1</a>.
</p>
<p>
A voltage \(V_a\) applied to the actuator stacks will induce an actuator force \(F_a\):
</p>
\begin{equation}
F_a = g_a \cdot V_a
\end{equation}
<p>
A change of length \(dl\) of the sensor stack will induce a voltage \(V_s\):
</p>
\begin{equation}
V_s = g_s \cdot dl
\end{equation}
<p>
We wish here to experimental measure \(g_a\) and \(g_s\).
</p>
<div id="org5dd279e" class="figure">
<p><img src="figs/apa_model_schematic.png" alt="apa_model_schematic.png" />
</p>
<p><span class="figure-number">Figure 1: </span>Amplified Piezoelectric Actuator Schematic</p>
</div>
</div>
</div>
<div id="outline-container-org3c114e3" class="outline-2">
<h2 id="org3c114e3"><span class="section-number-2">2</span> Test-Bench Description</h2>
<div class="outline-text-2" id="text-2">
<div class="note" id="org84f08a9">
<p>
Here are the documentation of the equipment used for this test bench:
</p>
<ul class="org-ul">
<li>Voltage Amplifier: <a href="doc/PD200-V7-R1.pdf">PD200</a></li>
<li>Amplified Piezoelectric Actuator: <a href="doc/APA300ML.pdf">APA300ML</a></li>
<li>DAC/ADC: Speedgoat <a href="doc/IO131-OEM-Datasheet.pdf">IO313</a></li>
<li>Encoder: <a href="doc/L-9517-9678-05-A_Data_sheet_VIONiC_series_en.pdf">Renishaw Vionic</a> and used <a href="doc/L-9517-9862-01-C_Data_sheet_RKLC_EN.pdf">Ruler</a></li>
<li>Interferometer: <a href="https://www.attocube.com/en/products/laser-displacement-sensor/displacement-measuring-interferometer">Attocube IDS3010</a></li>
</ul>
</div>
<div id="org9ba13fa" class="figure">
<p><img src="figs/test_bench_apa_alone.png" alt="test_bench_apa_alone.png" />
</p>
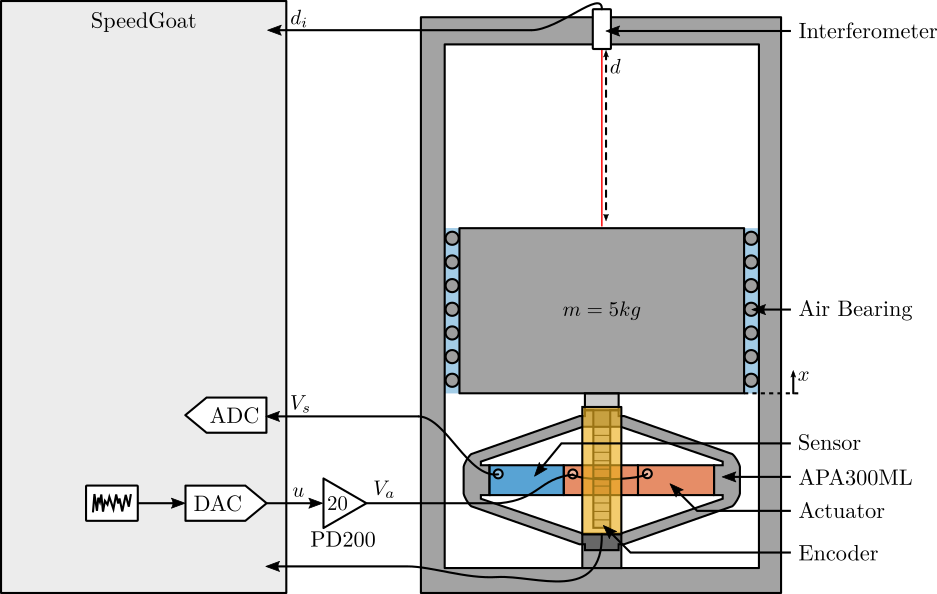
<p><span class="figure-number">Figure 2: </span>Schematic of the Test Bench</p>
</div>
</div>
</div>
<div id="outline-container-orgeef8a7b" class="outline-2">
<h2 id="orgeef8a7b"><span class="section-number-2">3</span> Measurement Procedure</h2>
<div class="outline-text-2" id="text-3">
</div>
<div id="outline-container-orgf5f4de4" class="outline-3">
<h3 id="orgf5f4de4"><span class="section-number-3">3.1</span> Stroke Measurement</h3>
<div class="outline-text-3" id="text-3-1">
<p>
Using the PD200 amplifier, output a voltage:
\[ V_a = 65 + 85 \sin(2\pi \cdot t) \]
To have a quasi-static excitation between -80 and 150V.
</p>
<p>
As the gain of the PD200 amplifier is 20, the DAC output voltage should be:
\[ V_{dac}(t) = 3.25 + 4.25\sin(2\pi \cdot t) \]
</p>
<p>
Verify that the voltage offset is zero!
</p>
<p>
Measure the output vertical displacement \(d\) using the interferometer.
</p>
<p>
Then, plot \(d\) as a function of \(V_a\), and perform a linear regression.
Conclude on the obtained stroke.
</p>
</div>
</div>
<div id="outline-container-orgc6a7f40" class="outline-3">
<h3 id="orgc6a7f40"><span class="section-number-3">3.2</span> Stiffness Measurement</h3>
<div class="outline-text-3" id="text-3-2">
<p>
Add some (known) weight \(\delta m g\) on the suspended mass and measure the deflection \(\delta d\).
This can be tested when the piezoelectric stacks are open-circuit.
</p>
<p>
As the stiffness will be around \(k \approx 10^6 N/m\), an added mass of \(m \approx 100g\) will induce a static deflection of \(\approx 1\mu m\) which should be large enough for a precise measurement using the interferometer.
</p>
<p>
Then the obtained stiffness is:
</p>
\begin{equation}
k = \frac{\delta m g}{\delta d}
\end{equation}
</div>
</div>
<div id="outline-container-orgf924c27" class="outline-3">
<h3 id="orgf924c27"><span class="section-number-3">3.3</span> Hysteresis measurement</h3>
<div class="outline-text-3" id="text-3-3">
<p>
Supply a quasi static sinusoidal excitation \(V_a\) at different voltages.
</p>
<p>
The offset should be 65V, and the sin amplitude can range from 1V up to 85V.
</p>
<p>
For each excitation amplitude, the vertical displacement \(d\) of the mass is measured.
</p>
<p>
Then, \(d\) is plotted as a function of \(V_a\) for all the amplitudes.
</p>
</div>
</div>
<div id="outline-container-org8dd84d4" class="outline-3">
<h3 id="org8dd84d4"><span class="section-number-3">3.4</span> Piezoelectric Actuator Constant</h3>
<div class="outline-text-3" id="text-3-4">
<p>
Using the measurement test-bench, it is rather easy the determine the static gain between the applied voltage \(V_a\) to the induced displacement \(d\).
Use a quasi static (1Hz) excitation signal \(V_a\) on the piezoelectric stack and measure the vertical displacement \(d\).
Perform a linear regression to obtain:
</p>
\begin{equation}
d = g_{d/V_a} \cdot V_a
\end{equation}
<p>
Using the Simscape model of the APA, it is possible to determine the static gain between the actuator force \(F_a\) to the induced displacement \(d\):
</p>
\begin{equation}
d = g_{d/F_a} \cdot F_a
\end{equation}
<p>
From the two gains, it is then easy to determine \(g_a\):
</p>
\begin{equation}
g_a = \frac{F_a}{V_a} = \frac{F_a}{d} \cdot \frac{d}{V_a} = \frac{g_{d/V_a}}{g_{d/F_a}}
\end{equation}
</div>
</div>
<div id="outline-container-org133086b" class="outline-3">
<h3 id="org133086b"><span class="section-number-3">3.5</span> Piezoelectric Sensor Constant</h3>
<div class="outline-text-3" id="text-3-5">
<p>
From a quasi static (1Hz) excitation of the piezoelectric stack, measure the gain from \(V_a\) to \(V_s\):
</p>
\begin{equation}
V_s = g_{V_s/V_a} V_a
\end{equation}
<p>
Using the simscape model, compute the static gain from the actuator force \(F_a\) to the strain of the sensor stack \(dl\):
</p>
\begin{equation}
dl = g_{dl/F_a} F_a
\end{equation}
<p>
Then, the static gain from the sensor stack strain \(dl\) to the general voltage \(V_s\) is:
</p>
\begin{equation}
g_s = \frac{V_s}{dl} = \frac{V_s}{V_a} \cdot \frac{V_a}{F_a} \cdot \frac{F_a}{dl} = \frac{g_{V_s/V_a}}{g_a \cdot g_{dl/F_a}}
\end{equation}
<p>
Alternatively, we could impose an external force to add strain in the APA that should be equally present in all the 3 stacks and equal to 1/5 of the vertical strain.
This external force can be some weight added, or a piezo in parallel.
</p>
</div>
</div>
<div id="outline-container-org6d5e309" class="outline-3">
<h3 id="org6d5e309"><span class="section-number-3">3.6</span> Capacitance Measurement</h3>
<div class="outline-text-3" id="text-3-6">
<p>
Measure the capacitance of the 3 stacks individually using a precise multi-meter.
</p>
</div>
</div>
</div>
</div>
<div id="postamble" class="status">
<p class="author">Author: Dehaeze Thomas</p>
<p class="date">Created: 2020-12-16 mer. 11:07</p>
</div>
</body>
</html>