Amplifier Piezoelectric Actuator APA300ML - Test Bench
Table of Contents
This report is also available as a pdf.
The goal of this test bench is to extract all the important parameters of the Amplified Piezoelectric Actuator APA300ML.
This include:
- Stroke
- Stiffness
- Hysteresis
- Gain from the applied voltage \(V_a\) to the generated Force \(F_a\)
- Gain from the sensor stack strain \(\delta L\) to the generated voltage \(V_s\)
- Dynamical behavior

Figure 1: Picture of the APA300ML
1 Model of an Amplified Piezoelectric Actuator and Sensor
Consider a schematic of the Amplified Piezoelectric Actuator in Figure 2.
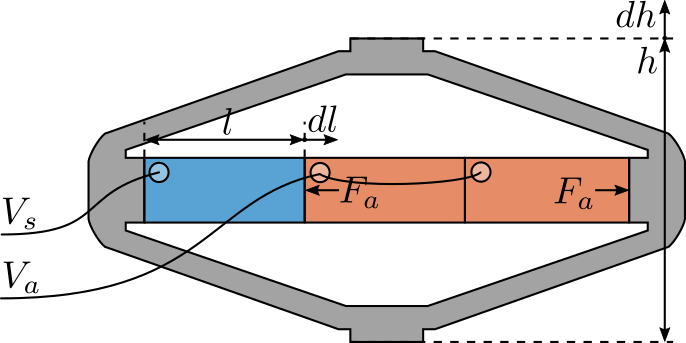
Figure 2: Amplified Piezoelectric Actuator Schematic
A voltage \(V_a\) applied to the actuator stacks will induce an actuator force \(F_a\):
\begin{equation} F_a = g_a \cdot V_a \end{equation}A change of length \(dl\) of the sensor stack will induce a voltage \(V_s\):
\begin{equation} V_s = g_s \cdot dl \end{equation}We wish here to experimental measure \(g_a\) and \(g_s\).
The block-diagram model of the piezoelectric actuator is then as shown in Figure 3.

Figure 3: Model of the APA with Simscape/Simulink
2 Geometrical Measurements
The received APA are shown in Figure 4.

Figure 4: Received APA
2.1 Measurement Setup
The flatness corresponding to the two interface planes are measured as shown in Figure 5.

Figure 5: Measurement Setup
2.2 Measurement Results
The height (Z) measurements at the 8 locations (4 points by plane) are defined below.
apa1 = 1e-6*[0, -0.5 , 3.5 , 3.5 , 42 , 45.5, 52.5 , 46]; apa2 = 1e-6*[0, -2.5 , -3 , 0 , -1.5 , 1 , -2 , -4]; apa3 = 1e-6*[0, -1.5 , 15 , 17.5 , 6.5 , 6.5 , 21 , 23]; apa4 = 1e-6*[0, 6.5 , 14.5 , 9 , 16 , 22 , 29.5 , 21]; apa5 = 1e-6*[0, -12.5, 16.5 , 28.5 , -43 , -52 , -22.5, -13.5]; apa6 = 1e-6*[0, -8 , -2 , 5 , -57.5, -62 , -55.5, -52.5]; apa7 = 1e-6*[0, 19.5 , -8 , -29.5, 75 , 97.5, 70 , 48]; apa7b = 1e-6*[0, 9 , -18.5, -30 , 31 , 46.5, 16.5 , 7.5]; apa = {apa1, apa2, apa3, apa4, apa5, apa6, apa7b};
The X/Y Positions of the 8 measurement points are defined below.
W = 20e-3; % Width [m] L = 61e-3; % Length [m] d = 1e-3; % Distance from border [m] l = 15.5e-3; % [m] pos = [[-L/2 + d; W/2 - d], [-L/2 + l - d; W/2 - d], [-L/2 + l - d; -W/2 + d], [-L/2 + d; -W/2 + d], [L/2 - l + d; W/2 - d], [L/2 - d; W/2 - d], [L/2 - d; -W/2 + d], [L/2 - l + d; -W/2 + d]];
Finally, the flatness is estimated by fitting a plane through the 8 points using the fminsearch command.
apa_d = zeros(1, 7); for i = 1:7 fun = @(x)max(abs(([pos; apa{i}]-[0;0;x(1)])'*([x(2:3);1]/norm([x(2:3);1])))); x0 = [0;0;0]; [x, min_d] = fminsearch(fun,x0); apa_d(i) = min_d; end
The obtained flatness are shown in Table 1.
| Flatness \([\mu m]\) | |
|---|---|
| APA 1 | 8.9 |
| APA 2 | 3.1 |
| APA 3 | 9.1 |
| APA 4 | 3.0 |
| APA 5 | 1.9 |
| APA 6 | 7.1 |
| APA 7 | 18.7 |
3 Electrical Measurements
The capacitance of the stacks is measure with the LCR-800 Meter (doc)

Figure 6: LCR Meter used for the measurements
The excitation frequency is set to be 1kHz.
| Sensor Stack | Actuator Stacks | |
|---|---|---|
| APA 1 | 5.10 | 10.03 |
| APA 2 | 4.99 | 9.85 |
| APA 3 | 1.72 | 5.18 |
| APA 4 | 4.94 | 9.82 |
| APA 5 | 4.90 | 9.66 |
| APA 6 | 4.99 | 9.91 |
| APA 7 | 4.85 | 9.85 |
There is clearly a problem with APA300ML number 3
4 Stiffness measurement
4.1 APA test
load('meas_stiff_apa_1_x.mat', 't', 'F', 'd');
figure;
plot(t, F)
%% Automatic Zero of the force F = F - mean(F(t > 0.1 & t < 0.3)); %% Start measurement at t = 0.2 s d = d(t > 0.2); F = F(t > 0.2); t = t(t > 0.2); t = t - t(1);
i_l_start = find(F > 0.3, 1, 'first'); [~, i_l_stop] = max(F);
F_l = F(i_l_start:i_l_stop); d_l = d(i_l_start:i_l_stop);
fit_l = polyfit(F_l, d_l, 1); % %% Reset displacement based on fit % d = d - fit_l(2); % fit_s(2) = fit_s(2) - fit_l(2); % fit_l(2) = 0; % %% Estimated Stroke % F_max = fit_s(2)/(fit_l(1) - fit_s(1)); % d_max = fit_l(1)*F_max;
h^2/fit_l(1)
figure; hold on; plot(F,d,'k') plot(F_l, d_l) plot(F_l, F_l*fit_l(1) + fit_l(2), '--')
5 Stroke measurement
We here wish to estimate the stroke of the APA.
To do so, one side of the APA is fixed, and a displacement probe is located on the other side as shown in Figure 7.
Then, a voltage is applied on either one or two stacks using a DAC and a voltage amplifier.
Here are the documentation of the equipment used for this test bench:
- Voltage Amplifier: PD200 with a gain of 20
- 16bits DAC: IO313 Speedgoat card
- Displacement Probe: Millimar C1216 electronics and Millimar 1318 probe

Figure 7: Bench to measured the APA stroke
5.1 Voltage applied on one stack
Let’s first look at the relation between the voltage applied to one stack to the displacement of the APA as measured by the displacement probe.
The applied voltage is shown in Figure 8.
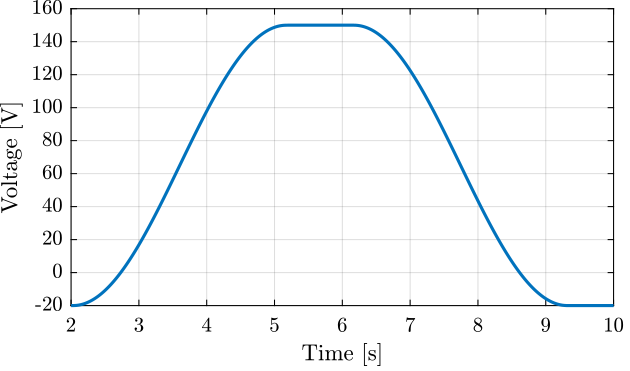
Figure 8: Applied voltage as a function of time
The obtained displacement is shown in Figure 9. The displacement is set to zero at initial time when the voltage applied is -20V.
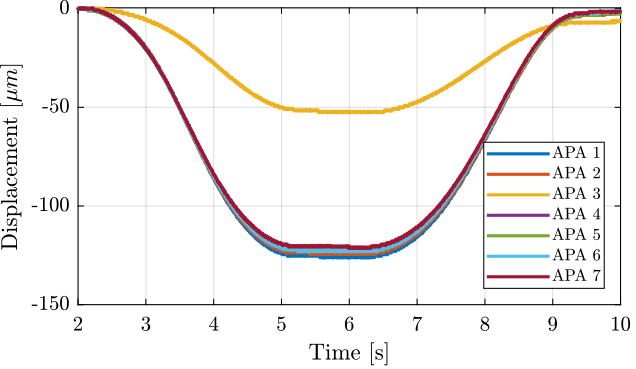
Figure 9: Displacement as a function of time for all the APA300ML
Finally, the displacement is shown as a function of the applied voltage in Figure 10. We can clearly see that there is a problem with the APA 3. Also, there is a large hysteresis.

Figure 10: Displacement as a function of the applied voltage
We can clearly see from Figure 10 that there is a problem with the APA number 3.
5.2 Voltage applied on two stacks
Now look at the relation between the voltage applied to the two other stacks to the displacement of the APA as measured by the displacement probe.
The obtained displacement is shown in Figure 11. The displacement is set to zero at initial time when the voltage applied is -20V.

Figure 11: Displacement as a function of time for all the APA300ML
Finally, the displacement is shown as a function of the applied voltage in Figure 12. We can clearly see that there is a problem with the APA 3. Also, there is a large hysteresis.

Figure 12: Displacement as a function of the applied voltage
5.3 Voltage applied on all three stacks
Finally, we can combine the two measurements to estimate the relation between the displacement and the voltage applied to the three stacks (Figure 13).
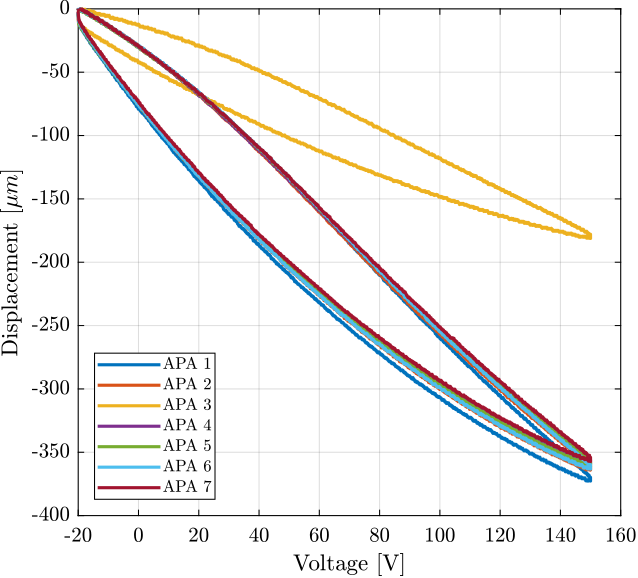
Figure 13: Displacement as a function of the applied voltage
The obtained maximum stroke for all the APA are summarized in Table 3.
| Stroke \([\mu m]\) | |
|---|---|
| APA 1 | 373.2 |
| APA 2 | 365.5 |
| APA 3 | 181.7 |
| APA 4 | 359.7 |
| APA 5 | 361.5 |
| APA 6 | 363.9 |
| APA 7 | 358.4 |
6 Test-Bench Description
Here are the documentation of the equipment used for this test bench:
- Voltage Amplifier: PD200
- Amplified Piezoelectric Actuator: APA300ML
- DAC/ADC: Speedgoat IO313
- Encoder: Renishaw Vionic and used Ruler
- Interferometer: Attocube IDS3010
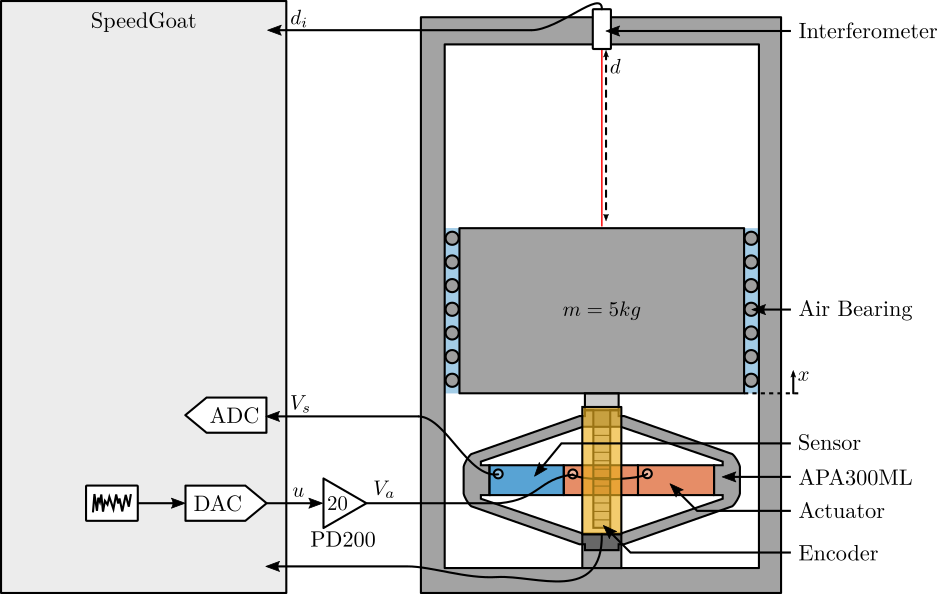
Figure 14: Schematic of the Test Bench
7 Measurement Procedure
7.1 Stroke Measurement
Using the PD200 amplifier, output a voltage: \[ V_a = 65 + 85 \sin(2\pi \cdot t) \] To have a quasi-static excitation between -20 and 150V.
As the gain of the PD200 amplifier is 20, the DAC output voltage should be: \[ V_{dac}(t) = 3.25 + 4.25\sin(2\pi \cdot t) \]
Verify that the voltage offset of the PD200 is zero!
Measure the output vertical displacement \(d\) using the interferometer.
Then, plot \(d\) as a function of \(V_a\), and perform a linear regression. Conclude on the obtained stroke.
7.2 Stiffness Measurement
Add some (known) weight \(\delta m g\) on the suspended mass and measure the deflection \(\delta d\). This can be tested when the piezoelectric stacks are open-circuit.
As the stiffness will be around \(k \approx 10^6 N/m\), an added mass of \(m \approx 100g\) will induce a static deflection of \(\approx 1\mu m\) which should be large enough for a precise measurement using the interferometer.
Then the obtained stiffness is:
\begin{equation} k = \frac{\delta m g}{\delta d} \end{equation}7.3 Hysteresis measurement
Supply a quasi static sinusoidal excitation \(V_a\) at different voltages.
The offset should be 65V, and the sin amplitude can range from 1V up to 85V.
For each excitation amplitude, the vertical displacement \(d\) of the mass is measured.
Then, \(d\) is plotted as a function of \(V_a\) for all the amplitudes.
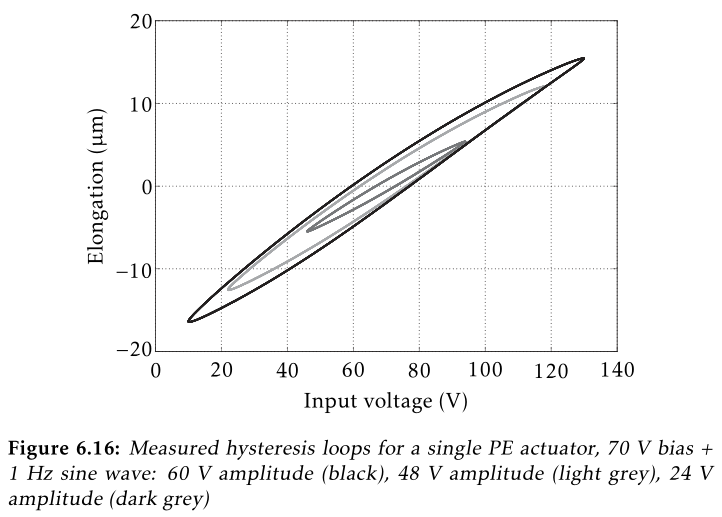
Figure 15: Expected Hysteresis (poel10_explor_activ_hard_mount_vibrat)
7.4 Piezoelectric Actuator Constant
Using the measurement test-bench, it is rather easy the determine the static gain between the applied voltage \(V_a\) to the induced displacement \(d\). Use a quasi static (1Hz) excitation signal \(V_a\) on the piezoelectric stack and measure the vertical displacement \(d\). Perform a linear regression to obtain:
\begin{equation} d = g_{d/V_a} \cdot V_a \end{equation}Using the Simscape model of the APA, it is possible to determine the static gain between the actuator force \(F_a\) to the induced displacement \(d\):
\begin{equation} d = g_{d/F_a} \cdot F_a \end{equation}From the two gains, it is then easy to determine \(g_a\):
\begin{equation} g_a = \frac{F_a}{V_a} = \frac{F_a}{d} \cdot \frac{d}{V_a} = \frac{g_{d/V_a}}{g_{d/F_a}} \end{equation}7.5 Piezoelectric Sensor Constant
From a quasi static excitation of the piezoelectric stack, measure the gain from \(V_a\) to \(V_s\):
\begin{equation} V_s = g_{V_s/V_a} V_a \end{equation}Note here that there is an high pass filter formed by the piezo capacitor and parallel resistor. The excitation frequency should then be in between the cut-off frequency of this high pass filter and the first resonance.
Alternatively, the gain can be computed from the dynamical identification and taking the gain at the wanted frequency.
Using the simscape model, compute the static gain from the actuator force \(F_a\) to the strain of the sensor stack \(dl\):
\begin{equation} dl = g_{dl/F_a} F_a \end{equation}Then, the static gain from the sensor stack strain \(dl\) to the general voltage \(V_s\) is:
\begin{equation} g_s = \frac{V_s}{dl} = \frac{V_s}{V_a} \cdot \frac{V_a}{F_a} \cdot \frac{F_a}{dl} = \frac{g_{V_s/V_a}}{g_a \cdot g_{dl/F_a}} \end{equation}Alternatively, we could impose an external force to add strain in the APA that should be equally present in all the 3 stacks and equal to 1/5 of the vertical strain. This external force can be some weight added, or a piezo in parallel.
7.6 Capacitance Measurement
Measure the capacitance of the 3 stacks individually using a precise multi-meter.
7.7 Dynamical Behavior
Perform a system identification from \(V_a\) to the measured displacement \(d\) by the interferometer and by the encoder, and to the generated voltage \(V_s\).
This can be performed using different excitation signals.
This can also be performed with and without the encoder fixed to the APA.
7.8 Compare the results obtained for all 7 APA300ML
Compare all the obtained parameters for all the test APA.