UP | HOME

Amplifier Piezoelectric Actuator APA300ML - Test Bench

Table of Contents

This report is also available as a pdf.

The goal of this test bench is to extract all the important parameters of the Amplified Piezoelectric Actuator APA300ML.

This include:

apa300ML.png

Figure 1: Picture of the APA300ML

1 Model of an Amplified Piezoelectric Actuator and Sensor

Consider a schematic of the Amplified Piezoelectric Actuator in Figure 2.

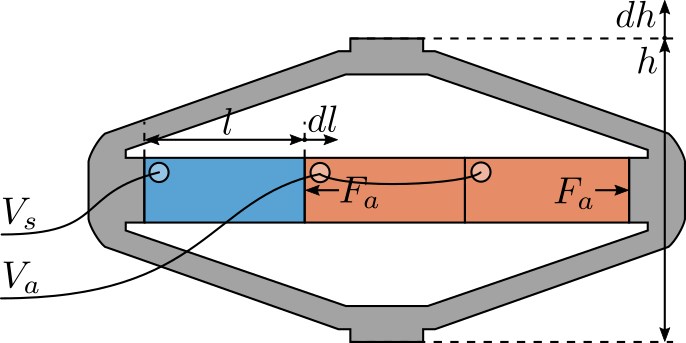
apa_model_schematic.png

Figure 2: Amplified Piezoelectric Actuator Schematic

A voltage \(V_a\) applied to the actuator stacks will induce an actuator force \(F_a\):

\begin{equation} F_a = g_a \cdot V_a \end{equation}

A change of length \(dl\) of the sensor stack will induce a voltage \(V_s\):

\begin{equation} V_s = g_s \cdot dl \end{equation}

We wish here to experimental measure \(g_a\) and \(g_s\).

The block-diagram model of the piezoelectric actuator is then as shown in Figure 3.

apa-model-simscape-schematic.png

Figure 3: Model of the APA with Simscape/Simulink

2 First Basic Measurements

2.1 Geometrical Measurements

The received APA are shown in Figure 4.

IMG_20210224_143500.jpg

Figure 4: Received APA

2.1.1 Measurement Setup

The flatness corresponding to the two interface planes are measured as shown in Figure 5.

IMG_20210224_143809.jpg

Figure 5: Measurement Setup

2.1.2 Measurement Results

The height (Z) measurements at the 8 locations (4 points by plane) are defined below. 

apa1  = 1e-6*[0, -0.5 , 3.5  , 3.5  , 42   , 45.5, 52.5 , 46];
apa2  = 1e-6*[0, -2.5 , -3   , 0    , -1.5 , 1   , -2   , -4];
apa3  = 1e-6*[0, -1.5 , 15   , 17.5 , 6.5  , 6.5 , 21   , 23];
apa4  = 1e-6*[0, 6.5  , 14.5 , 9    , 16   , 22  , 29.5 , 21];
apa5  = 1e-6*[0, -12.5, 16.5 , 28.5 , -43  , -52 , -22.5, -13.5];
apa6  = 1e-6*[0, -8   , -2   , 5    , -57.5, -62 , -55.5, -52.5];
apa7  = 1e-6*[0, 19.5 , -8   , -29.5, 75   , 97.5, 70   , 48];
apa7b = 1e-6*[0, 9    , -18.5, -30  , 31   , 46.5, 16.5 , 7.5];
apa = {apa1, apa2, apa3, apa4, apa5, apa6, apa7b};

The X/Y Positions of the 8 measurement points are defined below. 

W = 20e-3;   % Width [m]
L = 61e-3;   % Length [m]
d = 1e-3;    % Distance from border [m]
l = 15.5e-3; % [m]

pos = [[-L/2 + d; W/2 - d], [-L/2 + l - d; W/2 - d], [-L/2 + l - d; -W/2 + d], [-L/2 + d; -W/2 + d], [L/2 - l + d; W/2 - d], [L/2 - d; W/2 - d], [L/2 - d; -W/2 + d], [L/2 - l + d; -W/2 + d]];

Finally, the flatness is estimated by fitting a plane through the 8 points using the fminsearch command. 

apa_d = zeros(1, 7);
for i = 1:7
    fun = @(x)max(abs(([pos; apa{i}]-[0;0;x(1)])'*([x(2:3);1]/norm([x(2:3);1]))));
    x0 = [0;0;0];
    [x, min_d] = fminsearch(fun,x0);
    apa_d(i) = min_d;
end

The obtained flatness are shown in Table 1.

Table 1: Estimated flatness
  Flatness \([\mu m]\)
APA 1 8.9
APA 2 3.1
APA 3 9.1
APA 4 3.0
APA 5 1.9
APA 6 7.1
APA 7 18.7

2.2 Electrical Measurements

The capacitance of the stacks is measure with the LCR-800 Meter (doc)

IMG_20210312_120337.jpg

Figure 6: LCR Meter used for the measurements

The excitation frequency is set to be 1kHz.

Table 2: Capacitance measured with the LCR meter. The excitation signal is a sinus at 1kHz
  Sensor Stack Actuator Stacks
APA 1 5.10 10.03
APA 2 4.99 9.85
APA 3 1.72 5.18
APA 4 4.94 9.82
APA 5 4.90 9.66
APA 6 4.99 9.91
APA 7 4.85 9.85

There is clearly a problem with APA300ML number 3

The APA number 3 has ben sent back to Cedrat, and a new APA300ML has been shipped back.

2.3 Stroke measurement

We here wish to estimate the stroke of the APA.

To do so, one side of the APA is fixed, and a displacement probe is located on the other side as shown in Figure 7.

Then, a voltage is applied on either one or two stacks using a DAC and a voltage amplifier.

Here are the documentation of the equipment used for this test bench:

CE0EF55E-07B7-461B-8CDB-98590F68D15B.jpeg

Figure 7: Bench to measured the APA stroke

2.3.1 Voltage applied on one stack

Let’s first look at the relation between the voltage applied to one stack to the displacement of the APA as measured by the displacement probe.

The applied voltage is shown in Figure 8.

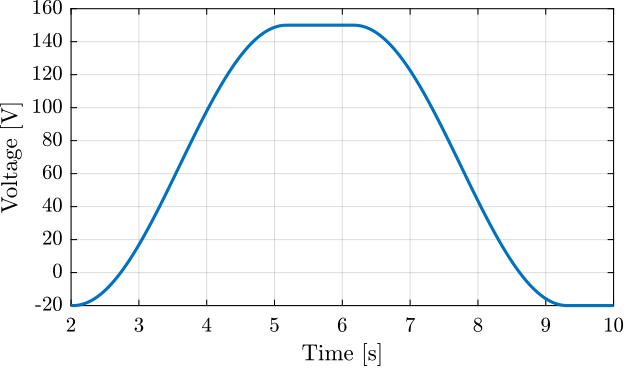
apa_stroke_voltage_time.png

Figure 8: Applied voltage as a function of time

The obtained displacement is shown in Figure 9. The displacement is set to zero at initial time when the voltage applied is -20V.

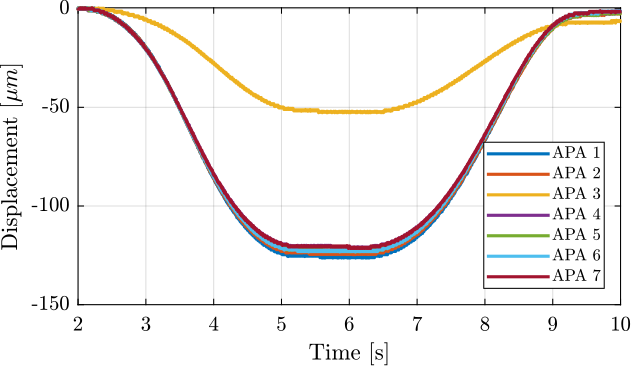
apa_stroke_time_1s.png

Figure 9: Displacement as a function of time for all the APA300ML

Finally, the displacement is shown as a function of the applied voltage in Figure 10. We can clearly see that there is a problem with the APA 3. Also, there is a large hysteresis.

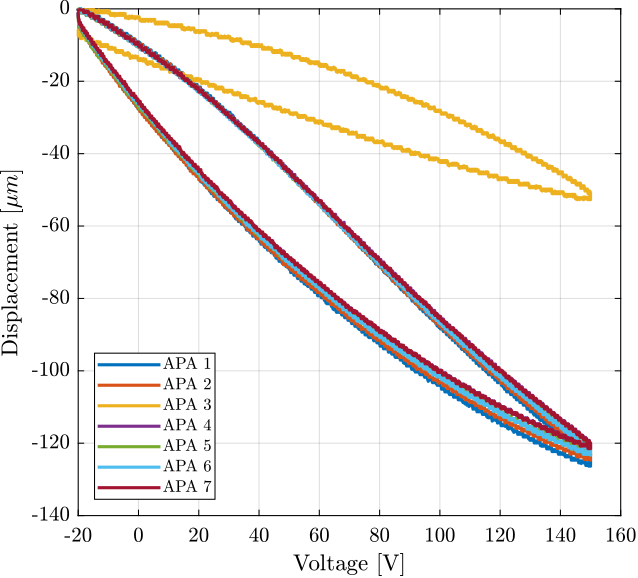
apa_d_vs_V_1s.png

Figure 10: Displacement as a function of the applied voltage

We can clearly see from Figure 10 that there is a problem with the APA number 3.

2.3.2 Voltage applied on two stacks

Now look at the relation between the voltage applied to the two other stacks to the displacement of the APA as measured by the displacement probe.

The obtained displacement is shown in Figure 11. The displacement is set to zero at initial time when the voltage applied is -20V.

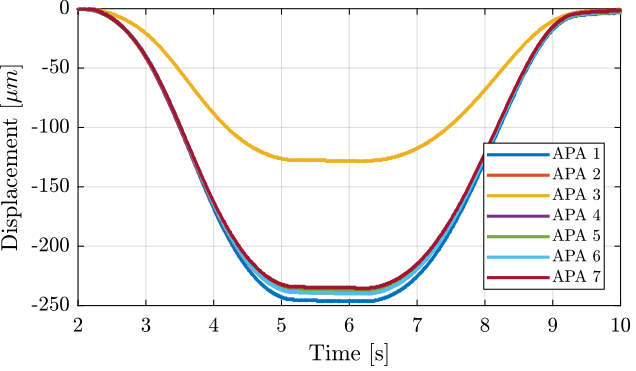
apa_stroke_time_2s.png

Figure 11: Displacement as a function of time for all the APA300ML

Finally, the displacement is shown as a function of the applied voltage in Figure 12. We can clearly see that there is a problem with the APA 3. Also, there is a large hysteresis.

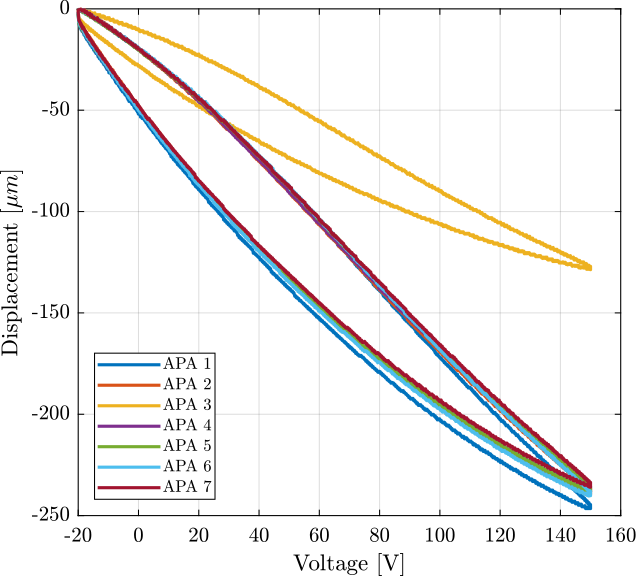
apa_d_vs_V_2s.png

Figure 12: Displacement as a function of the applied voltage

2.3.3 Voltage applied on all three stacks

Finally, we can combine the two measurements to estimate the relation between the displacement and the voltage applied to the three stacks (Figure 13).

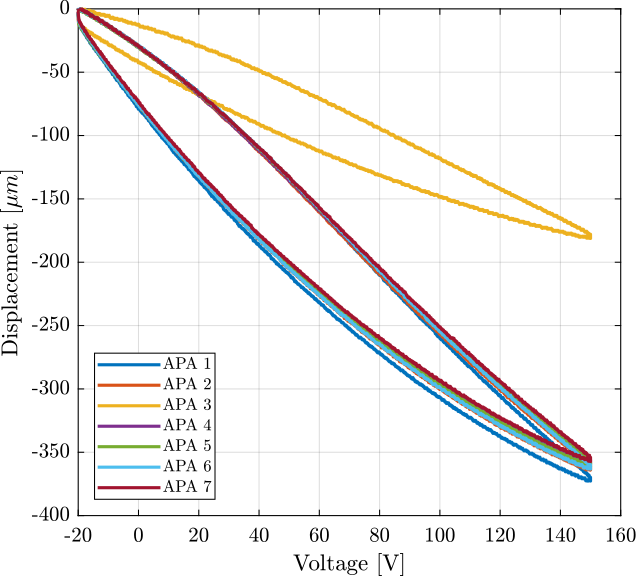
apa_d_vs_V_3s.png

Figure 13: Displacement as a function of the applied voltage

The obtained maximum stroke for all the APA are summarized in Table 3.

Table 3: Measured maximum stroke
  Stroke \([\mu m]\)
APA 1 373.2
APA 2 365.5
APA 3 181.7
APA 4 359.7
APA 5 361.5
APA 6 363.9
APA 7 358.4

2.4 Spurious resonances

2.4.1 Introduction

Three main resonances are foreseen to be problematic for the control of the APA300ML:

  • Mode in X-bending at 189Hz (Figure 14)
  • Mode in Y-bending at 285Hz (Figure 15)
  • Mode in Z-torsion at 400Hz (Figure 16)

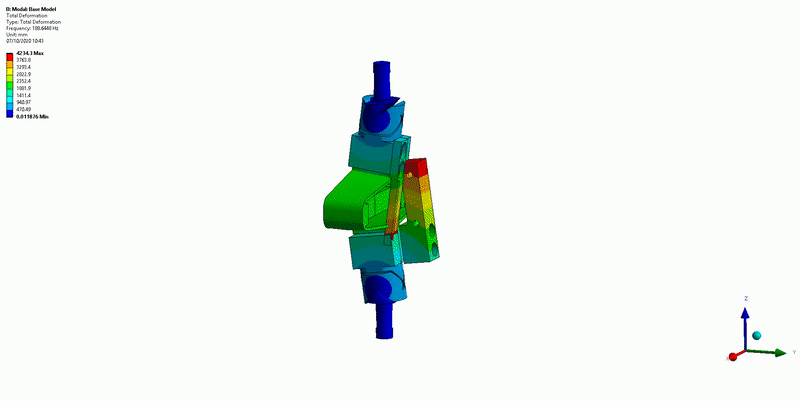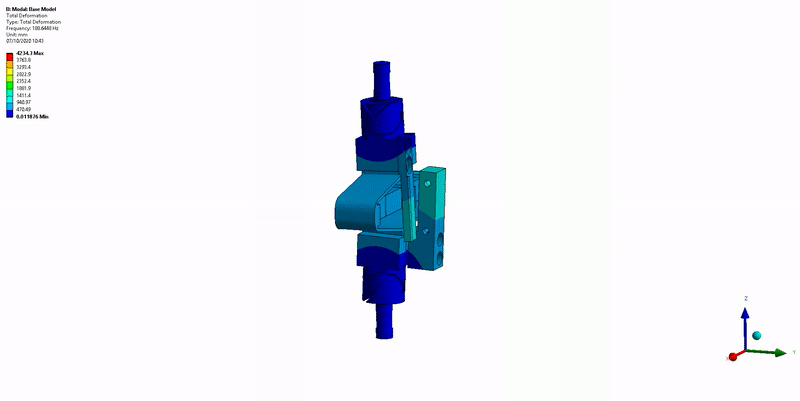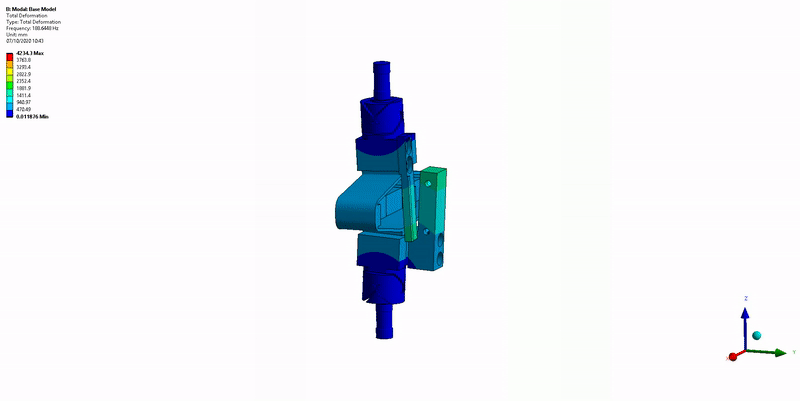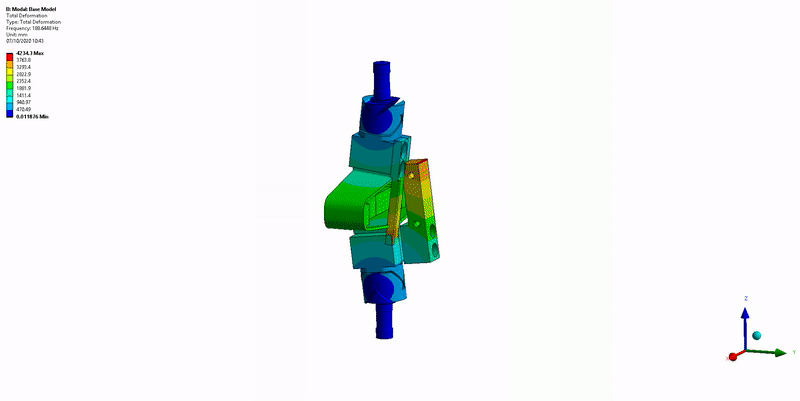
mode_bending_x.gif

Figure 14: X-bending mode (189Hz)

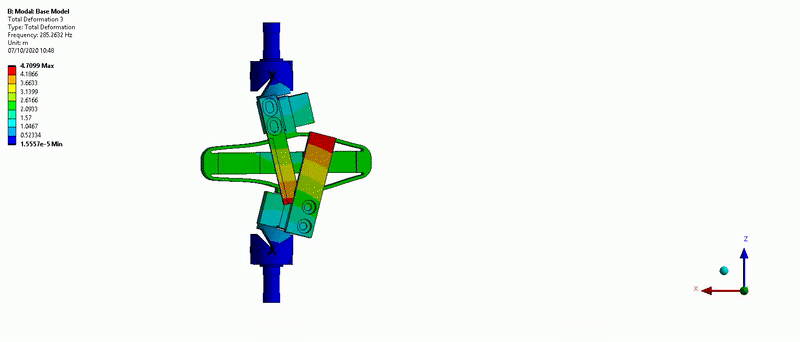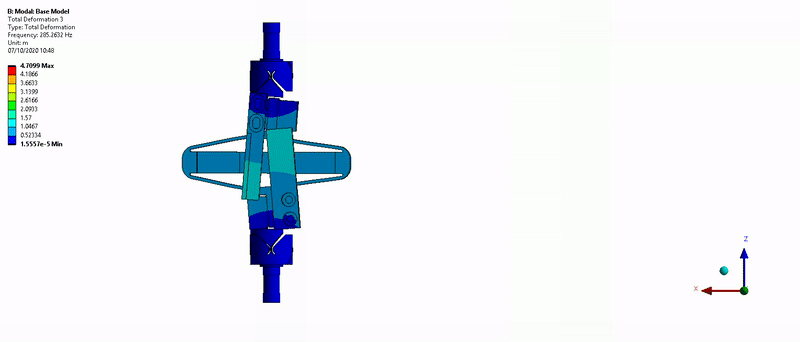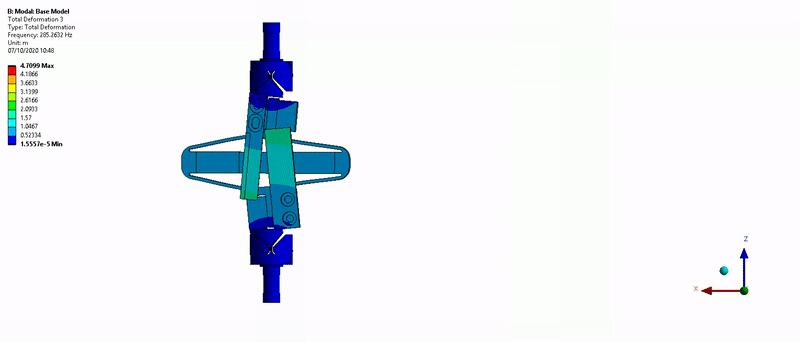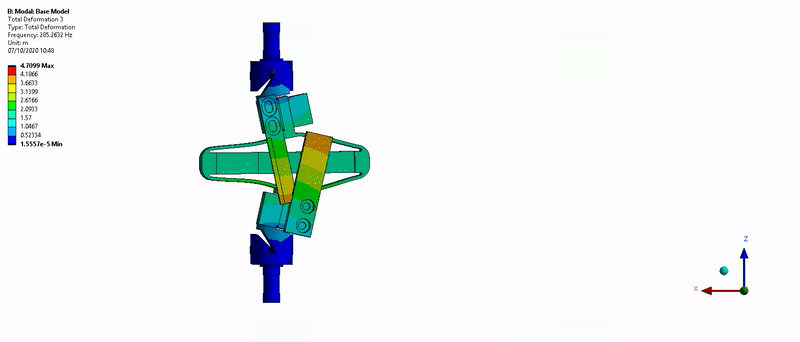
mode_bending_y.gif

Figure 15: Y-bending mode (285Hz)

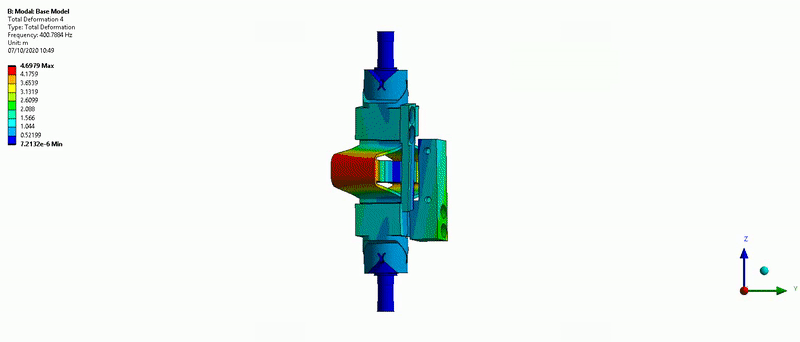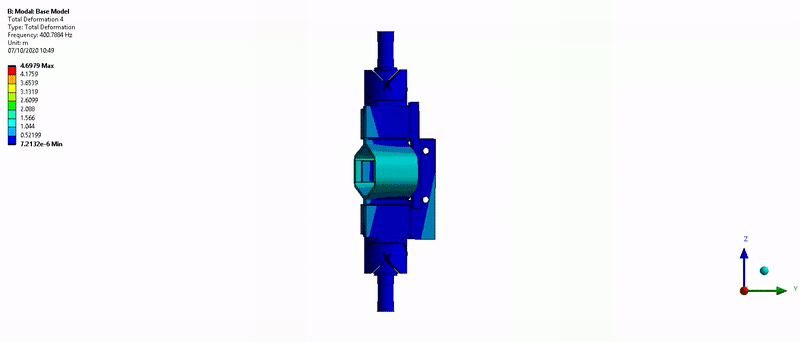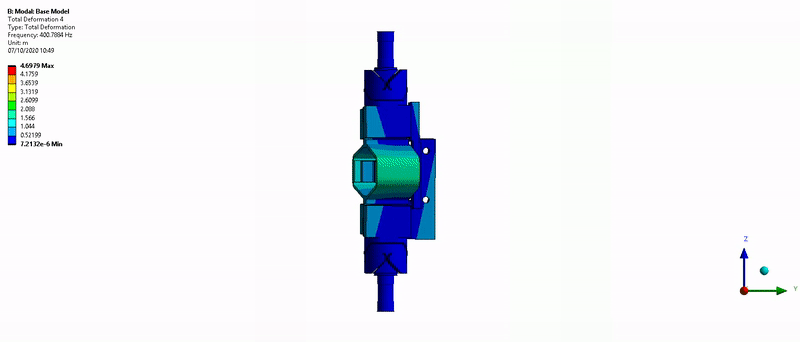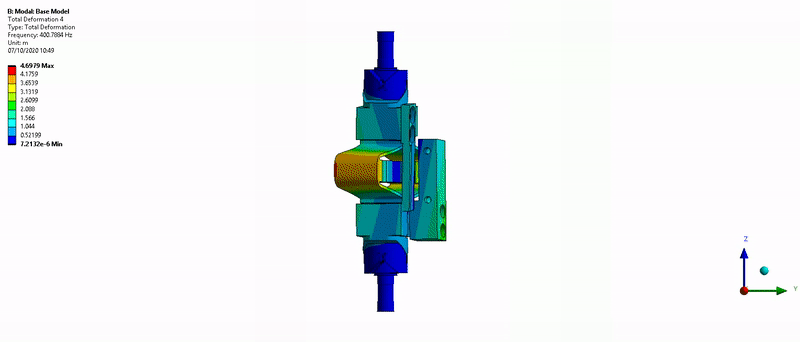
mode_torsion_z.gif

Figure 16: Z-torsion mode (400Hz)

These modes are present when flexible joints are fixed to the ends of the APA300ML.

In this section, we try to find the resonance frequency of these modes when one end of the APA is fixed and the other is free.

2.4.2 Setup

The measurement setup is shown in Figure 17. A Laser vibrometer is measuring the difference of motion of two points. The APA is excited with an instrumented hammer and the transfer function from the hammer to the measured rotation is computed.

  • Laser Doppler Vibrometer Polytec OFV512
  • Instrumented hammer

measurement_setup_torsion.jpg

Figure 17: Measurement setup with a Laser Doppler Vibrometer and one instrumental hammer

2.4.3 Bending - X

The setup to measure the X-bending motion is shown in Figure 18. The APA is excited with an instrumented hammer having a solid metallic tip. The impact point is on the back-side of the APA aligned with the top measurement point.

measurement_setup_X_bending.jpg

Figure 18: X-Bending measurement setup

The data is loaded. 

bending_X = load('apa300ml_bending_X_top.mat');

The config for tfestimate is performed: 

Ts = bending_X.Track1_X_Resolution; % Sampling frequency [Hz]
win = hann(ceil(1/Ts));

The transfer function from the input force to the output “rotation” (difference between the two measured distances). 

[G_bending_X, f]  = tfestimate(bending_X.Track1, bending_X.Track2, win, [], [], 1/Ts);

The result is shown in Figure 19.

The can clearly observe a nice peak at 280Hz, and then peaks at the odd “harmonics” (third “harmonic” at 840Hz, and fifth “harmonic” at 1400Hz).

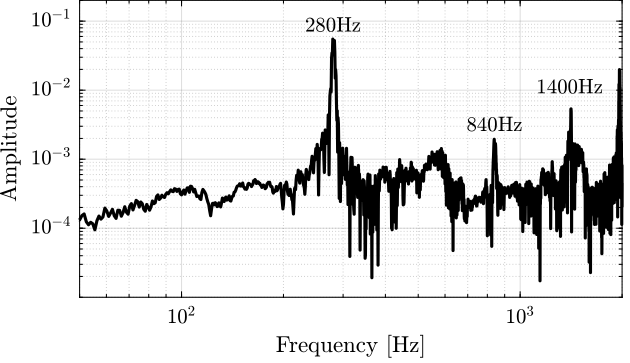
apa300ml_meas_freq_bending_x.png

Figure 19: Obtained FRF for the X-bending

2.4.4 Bending - Y

The setup to measure the Y-bending is shown in Figure 20.

The impact point of the instrumented hammer is located on the back surface of the top interface (on the back of the 2 measurements points).

measurement_setup_Y_bending.jpg

Figure 20: Y-Bending measurement setup

The data is loaded, and the transfer function from the force to the measured rotation is computed. 

bending_Y = load('apa300ml_bending_Y_top.mat');
[G_bending_Y, ~]  = tfestimate(bending_Y.Track1, bending_Y.Track2, win, [], [], 1/Ts);

The results are shown in Figure 21. The main resonance is at 412Hz, and we also see the third “harmonic” at 1220Hz.

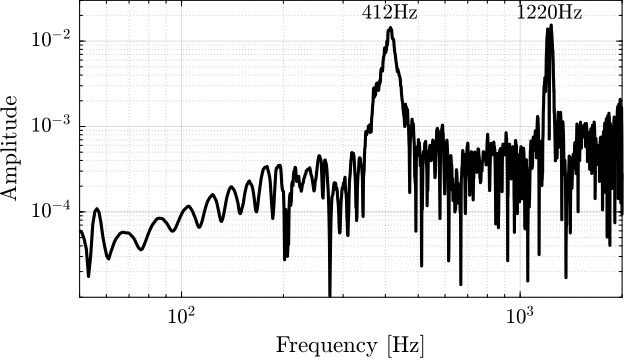
apa300ml_meas_freq_bending_y.png

Figure 21: Obtained FRF for the Y-bending

2.4.5 Torsion - Z

Finally, we measure the Z-torsion resonance as shown in Figure 22.

The excitation is shown on the other side of the APA, on the side to excite the torsion motion.

measurement_setup_torsion_bis.jpg

Figure 22: Z-Torsion measurement setup

The data is loaded, and the transfer function computed. 

torsion = load('apa300ml_torsion_left.mat');
[G_torsion, ~]  = tfestimate(torsion.Track1, torsion.Track2, win, [], [], 1/Ts);

The results are shown in Figure 23. We observe a first peak at 267Hz, which corresponds to the X-bending mode that was measured at 280Hz. And then a second peak at 415Hz, which corresponds to the X-bending mode that was measured at 412Hz. The mode in pure torsion is probably at higher frequency (peak around 1kHz?).

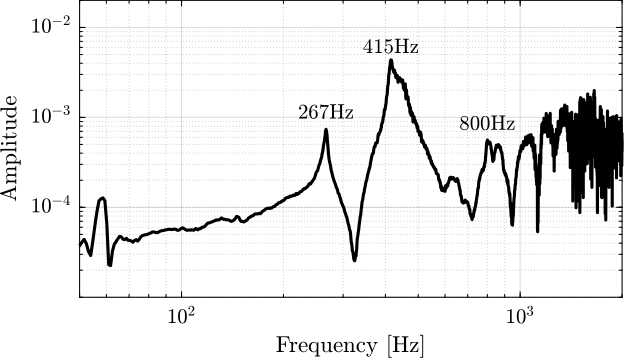
apa300ml_meas_freq_torsion_z.png

Figure 23: Obtained FRF for the Z-torsion

In order to verify that, the APA is excited on the top part such that the torsion mode should not be excited. 

torsion = load('apa300ml_torsion_top.mat');
[G_torsion_top, ~]  = tfestimate(torsion.Track1, torsion.Track2, win, [], [], 1/Ts);

The two FRF are compared in Figure 24. It is clear that the first two modes does not correspond to the torsional mode. Maybe the resonance at 800Hz, or even higher resonances. It is difficult to conclude here.

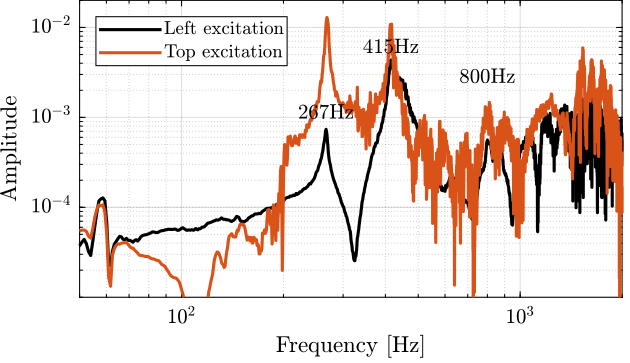
apa300ml_meas_freq_torsion_z_comp.png

Figure 24: Obtained FRF for the Z-torsion

2.4.6 Compare

The three measurements are shown in Figure 25.

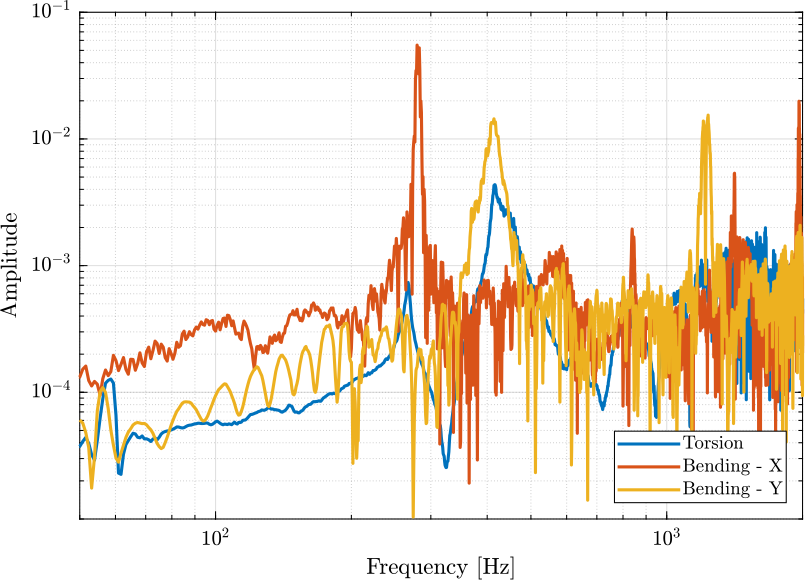
apa300ml_meas_freq_compare.png

Figure 25: Obtained FRF - Comparison

2.4.7 Conclusion

When two flexible joints are fixed at each ends of the APA, the APA is mostly in a free/free condition in terms of bending/torsion (the bending/torsional stiffness of the joints being very small).

In the current tests, the APA are in a fixed/free condition. Therefore, it is quite obvious that we measured higher resonance frequencies than what is foreseen for the struts. It is however quite interesting that there is a factor \(\approx \sqrt{2}\) between the two (increased of the stiffness by a factor 2?).

Table 4: Measured frequency of the modes
Mode Strut Mode Measured Frequency
X-Bending 189Hz 280Hz
Y-Bending 285Hz 410Hz
Z-Torsion 400Hz ?

3 Dynamical measurements - APA

In this section, a measurement test bench is used to identify the dynamics of the APA.

The bench is shown in Figure 26, and a zoom picture on the APA and encoder is shown in Figure 27.

picture_apa_bench.png

Figure 26: Picture of the test bench

picture_apa_bench_encoder.png

Figure 27: Zoom on the APA with the encoder

Here are the documentation of the equipment used for this test bench:

The bench is schematically shown in Figure 28 and the signal used are summarized in Table 5.

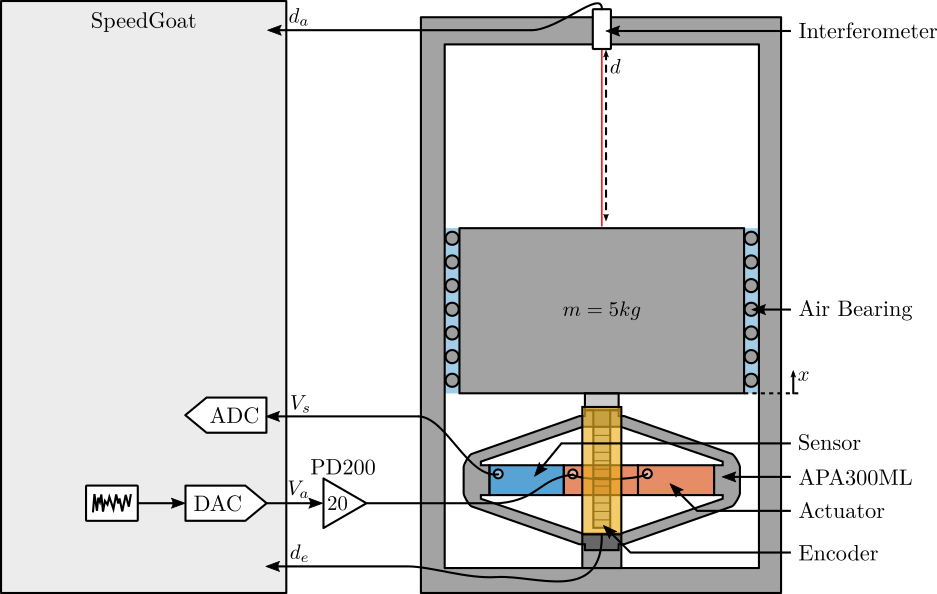
test_bench_apa_alone.png

Figure 28: Schematic of the Test Bench

Table 5: Variables used during the measurements
Variable Description Unit Hardware
Va Output DAC voltage [V] DAC - Ch. 1 => PD200 => APA
Vs Measured stack voltage (ADC) [V] APA => ADC - Ch. 1
de Encoder Measurement [m] PEPU Ch. 1 - IO318(1) - Ch. 1
da Attocube Measurement [m] PEPU Ch. 2 - IO318(1) - Ch. 2
t Time [s]  

This section is structured as follows:

  • Section 3.1: the Speedgoat setup is described (excitation signals, saved signals, etc.)
  • Section 3.2: the measurements are first performed on one APA.
  • Section 3.3: the same measurements are performed on all the APA and are compared.

3.1 Speedgoat Setup

3.1.1 frf_setup.m - Measurement Setup

First is defined the sampling frequency: 

%% Simulation configuration
Fs   = 10e3; % Sampling Frequency [Hz]
Ts   = 1/Fs; % Sampling Time [s]

%% Data record configuration
Trec_start = 5;  % Start time for Recording [s]
Trec_dur   = 100; % Recording Duration [s]

Tsim = 2*Trec_start + Trec_dur;  % Simulation Time [s]

A white noise excitation signal can be very useful in order to obtain a first idea of the plant FRF. The gain can be gradually increased until satisfactory output is obtained. 

%% Shaped Noise
V_noise = generateShapedNoise('Ts', 1/Fs, ...
                              'V_mean', 3.25, ...
                              't_start', Trec_start, ...
                              'exc_duration', Trec_dur, ...
                              'smooth_ends', true, ...
                              'V_exc', 0.05/(1 + s/2/pi/10));

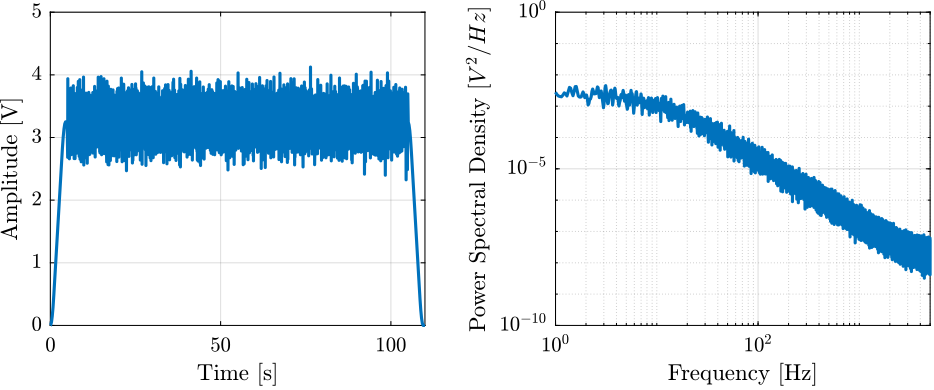
frf_meas_noise_excitation.png

Figure 29: Example of Shaped noise excitation signal

The maximum excitation voltage at resonance is 9Vrms, therefore corresponding to 0.6V of output DAC voltage. 

%% Sweep Sine
gc = 0.1;
xi = 0.5;
wn = 2*pi*94.3;

% Notch filter at the resonance of the APA
G_sweep = 0.2*(s^2 + 2*gc*xi*wn*s + wn^2)/(s^2 + 2*xi*wn*s + wn^2);

V_sweep = generateSweepExc('Ts',      Ts, ...
                           'f_start', 10, ...
                           'f_end',   400, ...
                           'V_mean',  3.25, ...
                           't_start', Trec_start, ...
                           'exc_duration', Trec_dur, ...
                           'sweep_type',   'log', ...
                           'V_exc', G_sweep*1/(1 + s/2/pi/500));

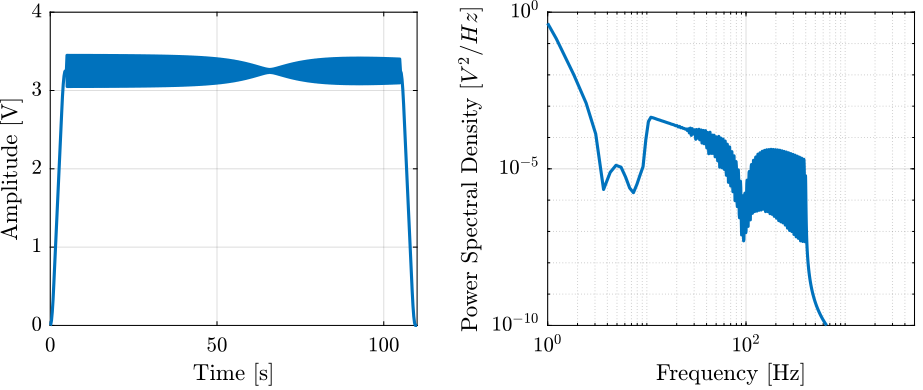
frf_meas_sweep_excitation.png

Figure 30: Example of Sweep Sin excitation signal

In order to better estimate the high frequency dynamics, a band-limited noise can be used (Figure 31). The frequency content of the noise can be precisely controlled. 

%% High Frequency Shaped Noise
[b,a] = cheby1(10, 2, 2*pi*[300 2e3], 'bandpass', 's');
wL = 0.005*tf(b, a);

V_noise_hf = generateShapedNoise('Ts', 1/Fs, ...
                              'V_mean', 3.25, ...
                              't_start', Trec_start, ...
                              'exc_duration', Trec_dur, ...
                              'smooth_ends', true, ...
                              'V_exc', wL);

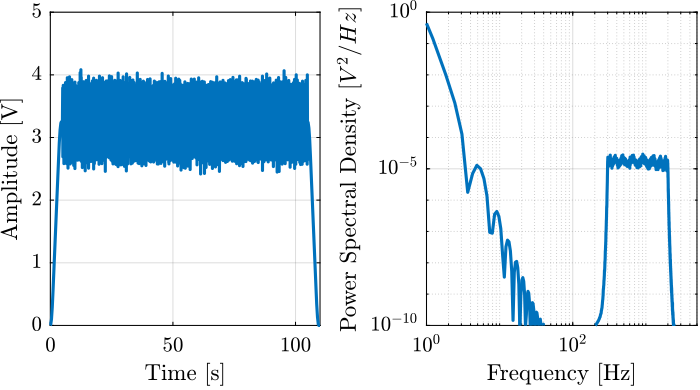
frf_meas_noise_hf_exc.png

Figure 31: Example of band-limited noise excitation signal

Then a sinus excitation can be used to estimate the hysteresis. 

%% Sinus excitation with increasing amplitude
V_sin = generateSinIncreasingAmpl('Ts', 1/Fs, ...
                                  'V_mean', 3.25, ...
                                  'sin_ampls', [0.1, 0.2, 0.4, 1, 2, 4], ...
                                  'sin_period', 1, ...
                                  'sin_num', 5, ...
                                  't_start', Trec_start, ...
                                  'smooth_ends', true);

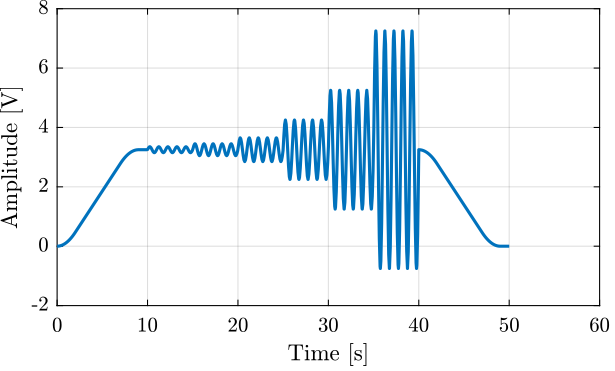
frf_meas_sin_excitation.png

Figure 32: Example of Shaped noise excitation signal

Then, we select the wanted excitation signal. 

%% Select the excitation signal
V_exc = timeseries(V_noise(2,:), V_noise(1,:));

%% Save data that will be loaded in the Simulink file
save('./frf_data.mat', 'Fs', 'Ts', 'Tsim', 'Trec_start', 'Trec_dur', 'V_exc');

3.1.2 frf_save.m - Save Data

First, we get data from the Speedgoat: 

tg = slrt;

f = SimulinkRealTime.openFTP(tg);
mget(f, 'data/data.dat');
close(f);

And we load the data on the Workspace: 

data = SimulinkRealTime.utils.getFileScopeData('data/data.dat').data;

da = data(:, 1); % Excitation Voltage (input of PD200) [V]
de = data(:, 2); % Measured voltage (force sensor) [V]
Vs = data(:, 3); % Measurment displacement (encoder) [m]
Va = data(:, 4); % Measurement displacement (attocube) [m]
t  = data(:, end); % Time [s]

And we save this to a mat file: 

apa_number = 1;

save(sprintf('mat/frf_data_%i_huddle.mat', apa_number), 't', 'Va', 'Vs', 'de', 'da');

3.2 Measurements on APA 1

Measurements are first performed on only one APA. Once the measurement procedure is validated, it is performed on all the other APA.

3.2.1 Excitation Signal

For this first measurement, a basic logarithmic sweep is used between 10Hz and 2kHz.

The data are loaded. 

apa_sweep = load(sprintf('mat/frf_data_%i_sweep.mat', 1), 't', 'Va', 'Vs', 'da', 'de');

The initial time is set to zero. 

%% Time vector
t = apa_sweep.t - apa_sweep.t(1) ; % Time vector [s]

The excitation signal is shown in Figure 33. It is a sweep sine from 10Hz up to 2kHz filtered with a notch centered with the main resonance of the system and a low pass filter.

apa_bench_exc_sweep.png

Figure 33: Excitation voltage

3.2.2 FRF Identification - Setup

Let’s define the sampling time/frequency. 

%% Sampling
Ts = (t(end) - t(1))/(length(t)-1); % Sampling Time [s]
Fs = 1/Ts; % Sampling Frequency [Hz]

Then we defined a “Hanning” windows that will be used for the spectral analysis: 

win = hanning(ceil(1*Fs)); % Hannning Windows

We get the frequency vector that will be the same for all the frequency domain analysis. 

% Only used to have the frequency vector "f"
[~, f] = tfestimate(apa_sweep.Va, apa_sweep.de, win, [], [], 1/Ts);

3.2.3 FRF Identification - Displacement

In this section, the transfer function from the excitation voltage \(V_a\) to the encoder measured displacement \(d_e\) and interferometer measurement \(d_a\).

The coherence from \(V_a\) to \(d_e\) is computed and shown in Figure 34. It is quite good from 10Hz up to 500Hz. 

%% TF - Encoder
[coh_sweep, ~] = mscohere(apa_sweep.Va,    apa_sweep.de,    win, [], [], 1/Ts);

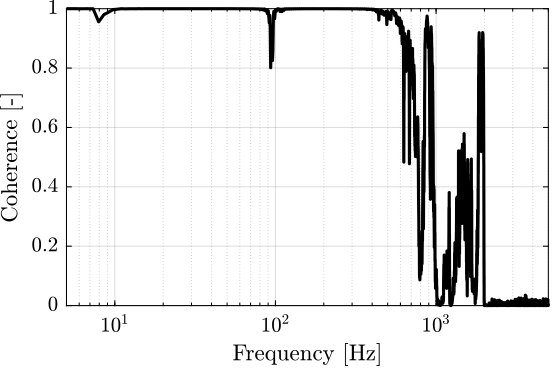
apa_1_coh_dvf.png

Figure 34: Coherence for the identification from \(V_a\) to \(d_e\)

The transfer functions are then estimated and shown in Figure 35. 

%% TF - Encoder
[dvf_sweep, ~] = tfestimate(apa_sweep.Va, apa_sweep.de, win, [], [], 1/Ts);

%% TF - Interferometer
[int_sweep, ~] = tfestimate(apa_sweep.Va, apa_sweep.da, win, [], [], 1/Ts);

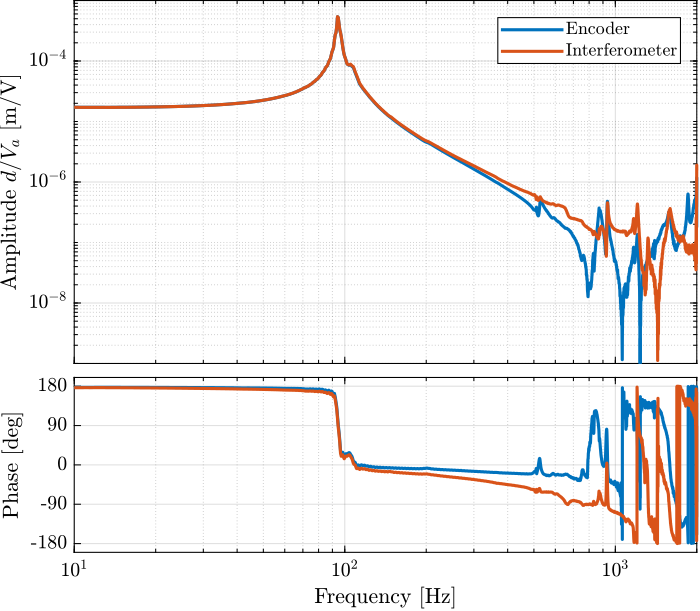
apa_1_frf_dvf.png

Figure 35: Obtained transfer functions from \(V_a\) to both \(d_e\) and \(d_a\)

It seems that using the interferometer, we have a lot more time delay than when using the encoder.

3.2.4 FRF Identification - Force Sensor

Now the dynamics from excitation voltage \(V_a\) to the force sensor stack voltage \(V_s\) is identified.

The coherence is computed and shown in Figure 36 and found very good from 10Hz up to 2kHz. 

%% TF - Encoder
[coh_sweep, ~] = mscohere(apa_sweep.Va, apa_sweep.Vs, win, [], [], 1/Ts);

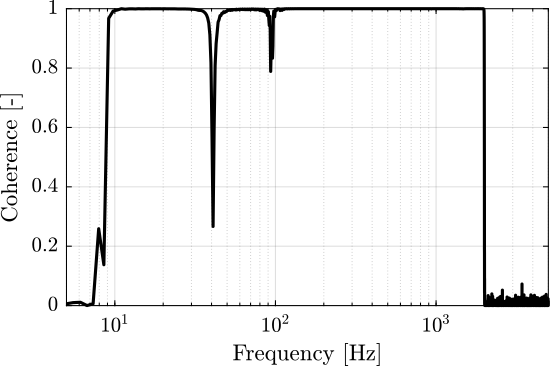
apa_1_coh_iff.png

Figure 36: Coherence for the identification from \(V_a\) to \(V_s\)

The transfer function is estimated and shown in Figure 37. 

%% Transfer function estimation
[iff_sweep, ~] = tfestimate(apa_sweep.Va, apa_sweep.Vs, win, [], [], 1/Ts);

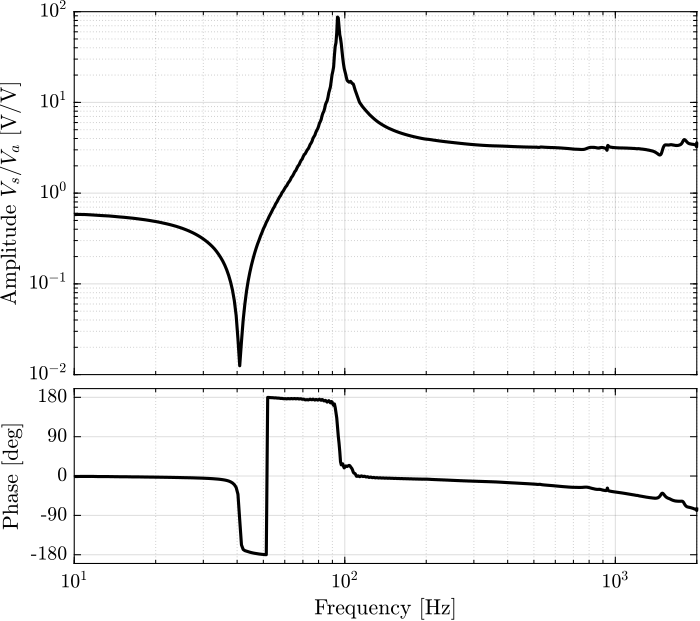
apa_1_frf_iff.png

Figure 37: Obtained transfer functions from \(V_a\) to \(V_s\)

3.2.5 Hysteresis

We here wish to visually see the amount of hysteresis present in the APA.

To do so, a quasi static sinusoidal excitation \(V_a\) at different voltages is used.

The offset is 65V, and the sin amplitude is ranging from 1V up to 80V.

For each excitation amplitude, the vertical displacement \(d\) of the mass is measured.

Then, \(d\) is plotted as a function of \(V_a\) for all the amplitudes.

We expect to obtained something like the hysteresis shown in Figure 38.

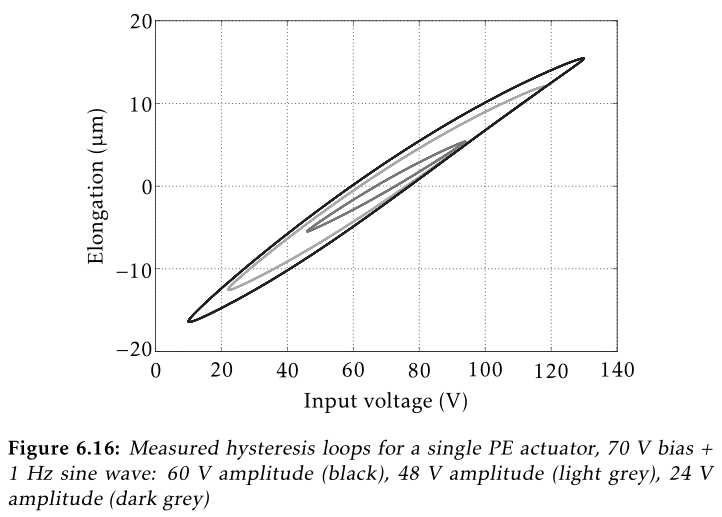
expected_hysteresis.png

Figure 38: Expected Hysteresis poel10_explor_activ_hard_mount_vibrat

The data is loaded. 

apa_hyst = load('frf_data_1_hysteresis.mat', 't', 'Va', 'de');
% Initial time set to zero
apa_hyst.t = apa_hyst.t - apa_hyst.t(1);

The excitation voltage amplitudes are: 

ampls = [0.1, 0.2, 0.4, 1, 2, 4]; % Excitation voltage amplitudes

The excitation voltage and the measured displacement are shown in Figure 39.

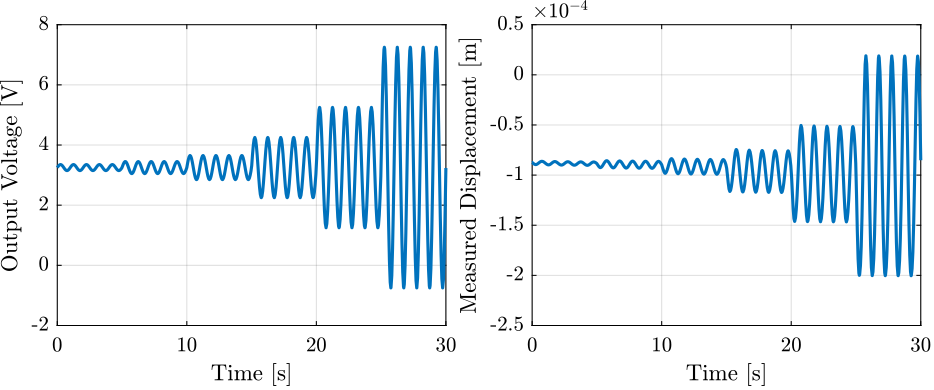
hyst_exc_signal_time.png

Figure 39: Excitation voltage and measured displacement

For each amplitude, we only take the last sinus in order to reduce possible transients. Also, it is centered on zero.

The measured displacement at a function of the output voltage are shown in Figure 40.

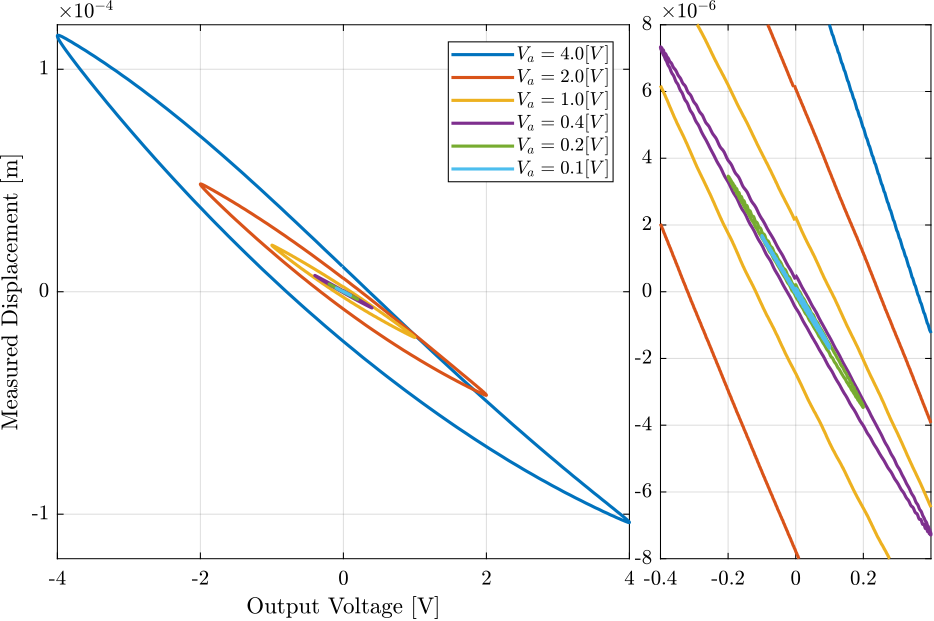
hyst_results_multi_ampl.png

Figure 40: Obtained hysteresis for multiple excitation amplitudes

It is quite clear that hysteresis is increasing with the excitation amplitude.

Also, no hysteresis is found on the sensor stack voltage.

3.2.6 Estimation of the APA axial stiffness

In order to estimate the stiffness of the APA, a weight with known mass \(m_a\) is added on top of the suspended granite and the deflection \(d_e\) is measured using the encoder. The APA stiffness is then:

\begin{equation} k_{\text{apa}} = \frac{m_a g}{d} \end{equation}

Here, a mass of 6.4 kg is used: 

added_mass = 6.4; % Added mass [kg]

The data is loaded, and the measured displacement is shown in Figure 41. 

apa_mass = load(sprintf('frf_data_%i_add_mass_closed_circuit.mat', 1), 't', 'de');
apa_mass.de = apa_mass.de - mean(apa_mass.de(apa_mass.t<11));

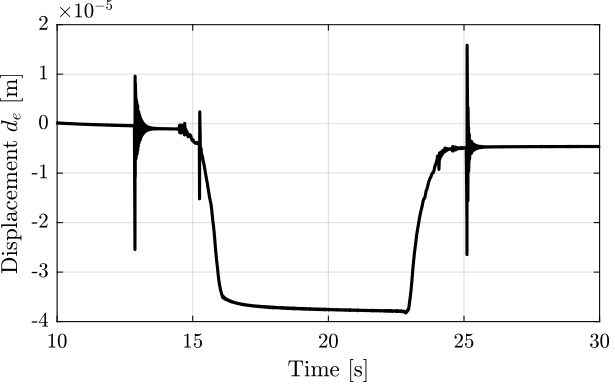
apa_1_meas_stiffness.png

Figure 41: Measured displacement when adding the mass and removing the mass

There is some imprecision in the measurement as there are some drifts that are probably due to some creep.

The stiffness is then computed as follows: 

k = 9.8 * added_mass / (mean(apa_mass.de(apa_mass.t > 12 & apa_mass.t < 12.5)) - mean(apa_mass.de(apa_mass.t > 20 & apa_mass.t < 20.5)));

And the stiffness obtained is very close to the one specified in the documentation (\(k = 1.794\,[N/\mu m]\)). 

k = 1.68 [N/um]

3.2.7 Stiffness change due to electrical connections

We wish here to see if the stiffness changes when the actuator stacks are not connected to the amplifier and the sensor stacks are not connected to the ADC.

Note here that the resistor in parallel to the sensor stack is present in both cases.

First, the data are loaded. 

add_mass_oc = load(sprintf('frf_data_%i_add_mass_open_circuit.mat',   1), 't', 'de');
add_mass_cc = load(sprintf('frf_data_%i_add_mass_closed_circuit.mat', 1), 't', 'de');

And the initial displacement is set to zero. 

add_mass_oc.de = add_mass_oc.de - mean(add_mass_oc.de(add_mass_oc.t<11));
add_mass_cc.de = add_mass_cc.de - mean(add_mass_cc.de(add_mass_cc.t<11));

The measured displacements are shown in Figure 42.

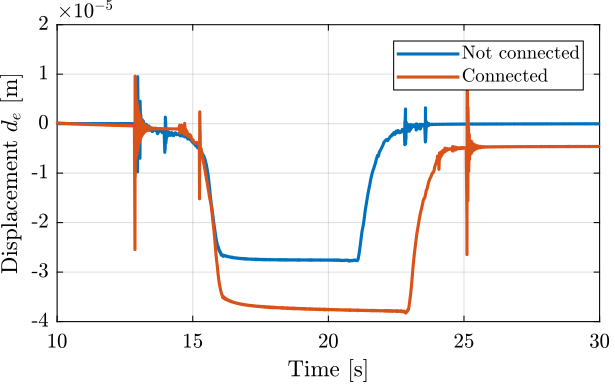
apa_meas_k_time_oc_cc.png

Figure 42: Measured displacement

And the stiffness is estimated in both case. The results are shown in Table 6. 

apa_k_oc = 9.8 * added_mass / (mean(add_mass_oc.de(add_mass_oc.t > 12 & add_mass_oc.t < 12.5)) - mean(add_mass_oc.de(add_mass_oc.t > 20 & add_mass_oc.t < 20.5)));
apa_k_cc = 9.8 * added_mass / (mean(add_mass_cc.de(add_mass_cc.t > 12 & add_mass_cc.t < 12.5)) - mean(add_mass_cc.de(add_mass_cc.t > 20 & add_mass_cc.t < 20.5)));
Table 6: Measured stiffnesses on “open” and “closed” circuits
  \(k [N/\mu m]\)
Not connected 2.3
Connected 1.7

Clearly, connecting the actuator stacks to the amplified (basically equivalent as to short circuiting them) lowers the stiffness.

3.2.8 Effect of the resistor on the IFF Plant

A resistor \(R \approx 80.6\,k\Omega\) is added in parallel with the sensor stack. This has the effect to form a high pass filter with the capacitance of the stack.

We here measured the low frequency transfer function from \(V_a\) to \(V_s\) with and without this resistor. 

% With the resistor
wi_k = load('frf_data_1_sweep_lf_with_R.mat', 't', 'Vs', 'Va');

% Without the resistor
wo_k = load('frf_data_1_sweep_lf.mat',        't', 'Vs', 'Va');

We use a very long “Hanning” window for the spectral analysis in order to estimate the low frequency behavior. 

win = hanning(ceil(50*Fs)); % Hannning Windows

And we estimate the transfer function from \(V_a\) to \(V_s\) in both cases: 

[frf_wo_k, f] = tfestimate(wo_k.Va, wo_k.Vs, win, [], [], 1/Ts);
[frf_wi_k, ~] = tfestimate(wi_k.Va, wi_k.Vs, win, [], [], 1/Ts);

With the following values of the resistor and capacitance, we obtain a first order high pass filter with a crossover frequency equal to: 

C = 5.1e-6; % Sensor Stack capacitance [F]
R = 80.6e3; % Parallel Resistor [Ohm]

f0 = 1/(2*pi*R*C); % Crossover frequency of RC HPF [Hz]

f0 = 0.39 [Hz]

The transfer function of the corresponding high pass filter is: 

G_hpf = 0.6*(s/2*pi*f0)/(1 + s/2*pi*f0);

Let’s compare the transfer function from actuator stack to sensor stack with and without the added resistor in Figure 43.

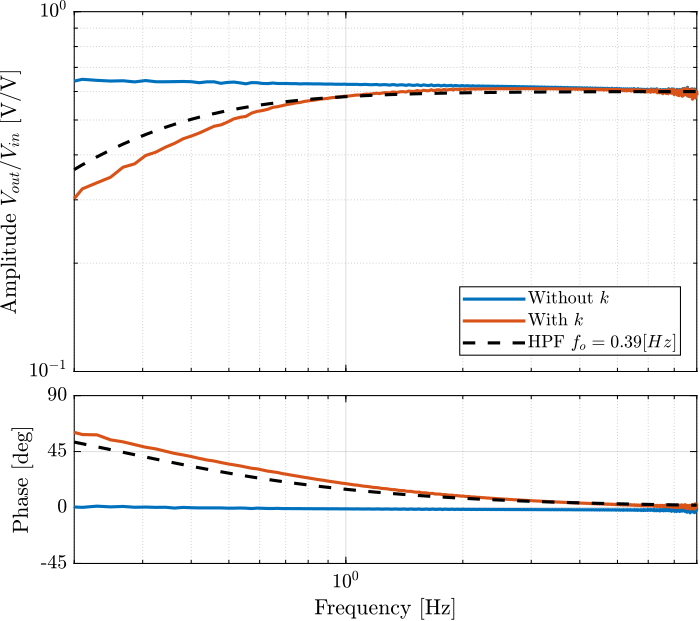
frf_iff_effect_R.png

Figure 43: Transfer function from \(V_a\) to \(V_s\) with and without the resistor \(k\)

The added resistor has indeed the expected effect.

3.3 Comparison of all the APA

The same measurements that was performed in Section 3.2 are now performed on all the APA and then compared.

3.3.1 Axial Stiffnesses - Comparison

Let’s first compare the APA axial stiffnesses.

The added mass is: 

added_mass = 6.4; % Added mass [kg]

Here are the number of the APA that have been measured: 

apa_nums = [1 2 4 5 6 7 8];

The data are loaded. 

apa_mass = {};
for i = 1:length(apa_nums)
    apa_mass(i) = {load(sprintf('frf_data_%i_add_mass_closed_circuit.mat', apa_nums(i)), 't', 'de')};
    % The initial displacement is set to zero
    apa_mass{i}.de = apa_mass{i}.de - mean(apa_mass{i}.de(apa_mass{i}.t<11));
end

The raw measurements are shown in Figure 44. All the APA seems to have similar stiffness except the APA 7 which should have an higher stiffness.

It is however strange that the displacement \(d_e\) when the mass is removed is higher for the APA 7 than for the other APA. What could cause that?

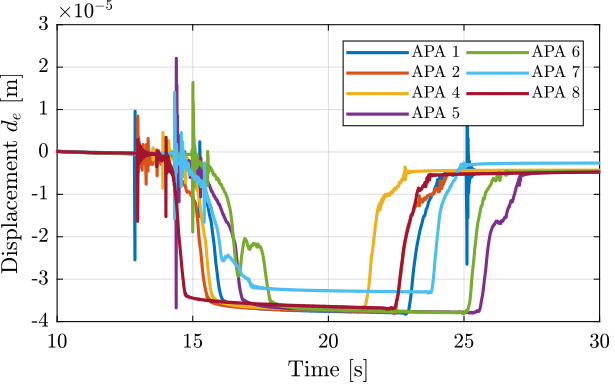
apa_meas_k_time.png

Figure 44: Raw measurements for all the APA. A mass of 6.4kg is added at arround 15s and removed at arround 22s

The stiffnesses are computed for all the APA and are summarized in Table 7.

Table 7: Measured stiffnesses
APA Num \(k [N/\mu m]\)
1 1.68
2 1.69
4 1.7
5 1.7
6 1.7
7 1.93
8 1.73

The APA300ML manual specifies the nominal stiffness to be \(1.8\,[N/\mu m]\) which is very close to what have been measured. Only the APA number 7 is a little bit off.

3.3.2 FRF Identification - Setup

The identification is performed in three steps:

  1. White noise excitation with small amplitude. This is used to determine the main resonance of the system.
  2. Sweep sine excitation with the amplitude lowered around the resonance. The sweep sine is from 10Hz to 400Hz.
  3. High frequency noise. The noise is band-passed between 300Hz and 2kHz.

Then, the result of the second identification is used between 10Hz and 350Hz and the result of the third identification if used between 350Hz and 2kHz.

Here are the APA numbers that have been measured. 

apa_nums = [1 2 4 5 6 7 8];

The data are loaded for both the second and third identification: 

%% Second identification
apa_sweep = {};
for i = 1:length(apa_nums)
    apa_sweep(i) = {load(sprintf('frf_data_%i_sweep.mat', apa_nums(i)), 't', 'Va', 'Vs', 'de', 'da')};
end

%% Third identification
apa_noise_hf = {};
for i = 1:length(apa_nums)
    apa_noise_hf(i) = {load(sprintf('frf_data_%i_noise_hf.mat', apa_nums(i)), 't', 'Va', 'Vs', 'de', 'da')};
end

The time is the same for all measurements. 

%% Time vector
t = apa_sweep{1}.t - apa_sweep{1}.t(1) ; % Time vector [s]

%% Sampling
Ts = (t(end) - t(1))/(length(t)-1); % Sampling Time [s]
Fs = 1/Ts; % Sampling Frequency [Hz]

Then we defined a “Hanning” windows that will be used for the spectral analysis: 

win = hanning(ceil(0.5*Fs)); % Hannning Windows

We get the frequency vector that will be the same for all the frequency domain analysis. 

% Only used to have the frequency vector "f"
[~, f] = tfestimate(apa_sweep{1}.Va, apa_sweep{1}.de, win, [], [], 1/Ts);

3.3.3 FRF Identification - DVF

In this section, the dynamics from excitation voltage \(V_a\) to encoder measured displacement \(d_e\) is identified.

We compute the coherence for 2nd and 3rd identification: 

%% Coherence computation
coh_sweep = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
    [coh, ~] = mscohere(apa_sweep{i}.Va, apa_sweep{i}.de, win, [], [], 1/Ts);
    coh_sweep(:, i) = coh;
end

coh_noise_hf = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
    [coh, ~] = mscohere(apa_noise_hf{i}.Va, apa_noise_hf{i}.de, win, [], [], 1/Ts);
    coh_noise_hf(:, i) = coh;
end

The coherence is shown in Figure 45. It is clear that the Sweep sine gives good coherence up to 400Hz and that the high frequency noise excitation signal helps increasing a little bit the coherence at high frequency.

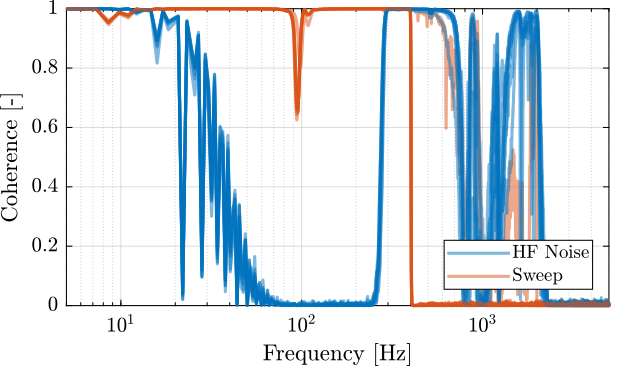
apa_frf_dvf_plant_coh.png

Figure 45: Obtained coherence for the plant from \(V_a\) to \(d_e\)

Then, the transfer function from the DAC output voltage \(V_a\) to the measured displacement by the encoders is computed: 

%% Transfer function estimation
dvf_sweep = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
    [frf, ~] = tfestimate(apa_sweep{i}.Va, apa_sweep{i}.de, win, [], [], 1/Ts);
    dvf_sweep(:, i) = frf;
end

dvf_noise_hf = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
    [frf, ~] = tfestimate(apa_noise_hf{i}.Va, apa_noise_hf{i}.de, win, [], [], 1/Ts);
    dvf_noise_hf(:, i) = frf;
end

The obtained transfer functions are shown in Figure 46. They are all superimposed except for the APA7.

Why is the APA7 off? We could think that the APA7 is stiffer, but also the mass line is off.

It seems that there is a “gain” problem. The encoder seems fine (it measured the same as the Interferometer). Maybe it could be due to the amplifier?

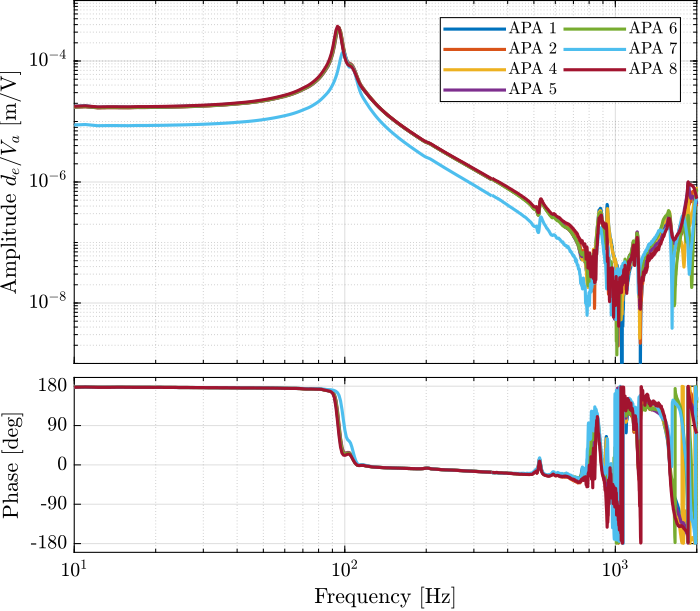
apa_frf_dvf_plant_tf.png

Figure 46: Estimated FRF for the DVF plant (transfer function from \(V_a\) to the encoder \(d_e\))

A zoom on the main resonance is shown in Figure 47. It is clear that expect for the APA 7, the response around the resonances are well matching for all the APA.

It is also clear that there is not a single resonance but two resonances, a first one at 95Hz and a second one at 105Hz.

Why is there a double resonance at around 94Hz?

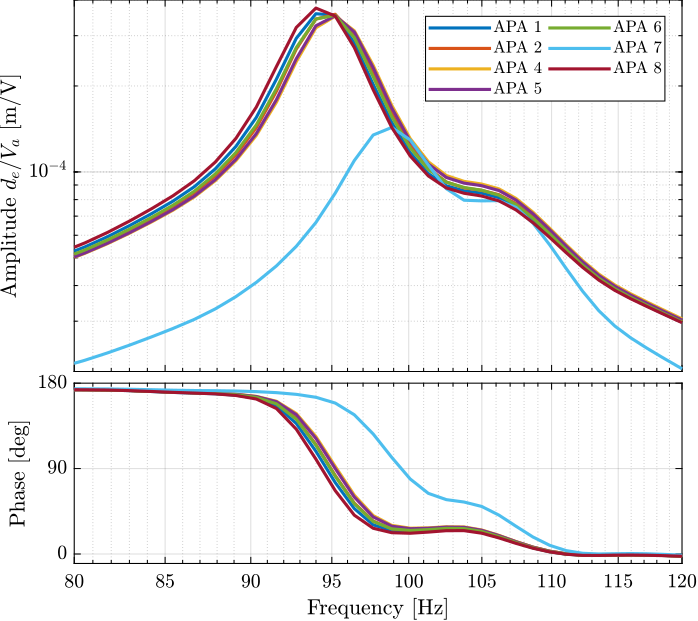
apa_frf_dvf_zoom_res_plant_tf.png

Figure 47: Estimated FRF for the DVF plant (transfer function from \(V_a\) to the encoder \(d_e\)) - Zoom on the main resonance

3.3.4 FRF Identification - IFF

In this section, the dynamics from \(V_a\) to \(V_s\) is identified.

First the coherence is computed and shown in Figure 48. The coherence is very nice from 10Hz to 2kHz. It is only dropping near a zeros at 40Hz, and near the resonance at 95Hz (the excitation amplitude being lowered). 

%% Coherence
coh_sweep = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
    [coh, ~] = mscohere(apa_sweep{i}.Va, apa_sweep{i}.Vs, win, [], [], 1/Ts);
    coh_sweep(:, i) = coh;
end

coh_noise_hf = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
    [coh, ~] = mscohere(apa_noise_hf{i}.Va, apa_noise_hf{i}.Vs, win, [], [], 1/Ts);
    coh_noise_hf(:, i) = coh;
end

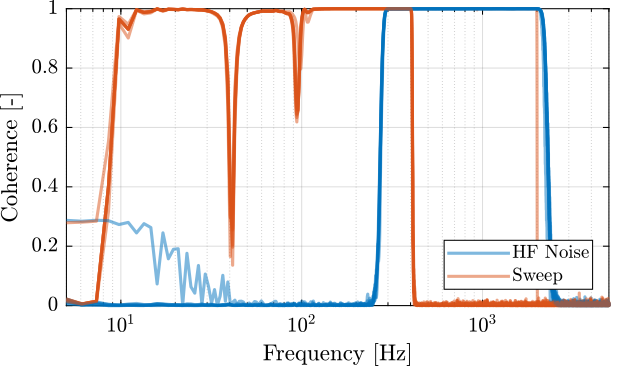
apa_frf_iff_plant_coh.png

Figure 48: Obtained coherence for the IFF plant

Then the FRF are estimated and shown in Figure 49 

%% FRF estimation of the transfer function from Va to Vs
iff_sweep = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
    [frf, ~] = tfestimate(apa_sweep{i}.Va, apa_sweep{i}.Vs, win, [], [], 1/Ts);
    iff_sweep(:, i) = frf;
end

iff_noise_hf = zeros(length(f), length(apa_nums));
for i = 1:length(apa_nums)
    [frf, ~] = tfestimate(apa_noise_hf{i}.Va, apa_noise_hf{i}.Vs, win, [], [], 1/Ts);
    iff_noise_hf(:, i) = frf;
end

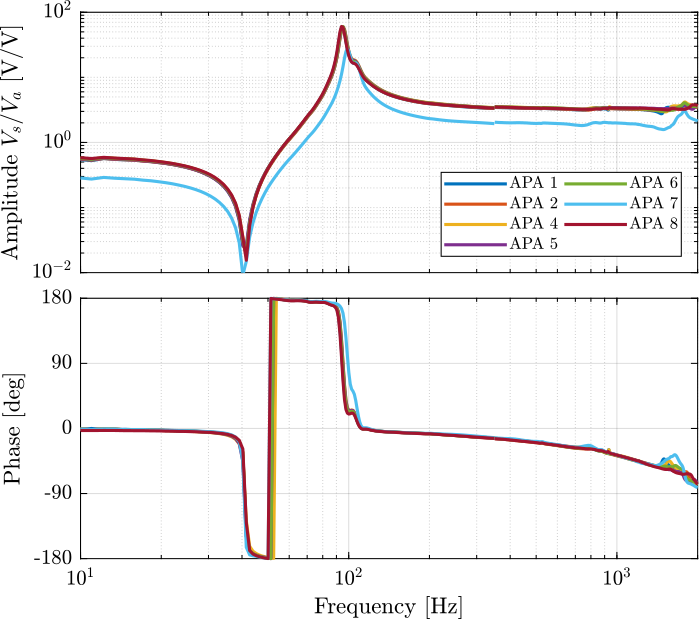
apa_frf_iff_plant_tf.png

Figure 49: Identified IFF Plant

4 Dynamical measurements - Struts

The same bench used in Section 3 is here used with the strut instead of only the APA.

The bench is shown in Figure 50. Measurements are performed either when no encoder is fixed to the strut (Figure 51) or when one encoder is fixed to the strut (Figure 50).

test_bench_leg_overview.png

Figure 50: Test Bench with Strut - Overview

test_bench_leg_front.png

Figure 51: Test Bench with Strut - Zoom on the strut

test_bench_leg_coder.png

Figure 52: Test Bench with Strut - Zoom on the strut with the encoder

4.1 Measurement on Strut 1

Measurements are first performed on the strut 1 that contains:

  • APA 1
  • flex 1 and flex 2

4.1.1 Without Encoder

4.1.1.1 FRF Identification - Setup

The identification is performed in three steps:

  1. White noise excitation with small amplitude. This is used to determine the main resonance of the system.
  2. Sweep sine excitation with the amplitude lowered around the resonance. The sweep sine is from 10Hz to 400Hz.
  3. High frequency noise. The noise is band-passed between 300Hz and 2kHz.

Then, the result of the second identification is used between 10Hz and 350Hz and the result of the third identification if used between 350Hz and 2kHz. 

leg_sweep    = load(sprintf('frf_data_leg_%i_sweep.mat',    1), 't', 'Va', 'Vs', 'de', 'da');
leg_noise_hf = load(sprintf('frf_data_leg_%i_noise_hf.mat', 1), 't', 'Va', 'Vs', 'de', 'da');

The time is the same for all measurements. 

%% Time vector
t = leg_sweep.t - leg_sweep.t(1) ; % Time vector [s]

%% Sampling
Ts = (t(end) - t(1))/(length(t)-1); % Sampling Time [s]
Fs = 1/Ts; % Sampling Frequency [Hz]

Then we defined a “Hanning” windows that will be used for the spectral analysis: 

win = hanning(ceil(0.5*Fs)); % Hannning Windows

We get the frequency vector that will be the same for all the frequency domain analysis. 

% Only used to have the frequency vector "f"
[~, f] = tfestimate(leg_sweep.Va, leg_sweep.de, win, [], [], 1/Ts);
4.1.1.2 FRF Identification - Displacement

In this section, the dynamics from the excitation voltage \(V_a\) to the interferometer \(d_a\) is identified.

We compute the coherence for 2nd and 3rd identification: 

[coh_sweep, ~]    = mscohere(leg_sweep.Va,    leg_sweep.da,    win, [], [], 1/Ts);
[coh_noise_hf, ~] = mscohere(leg_noise_hf.Va, leg_noise_hf.da, win, [], [], 1/Ts);

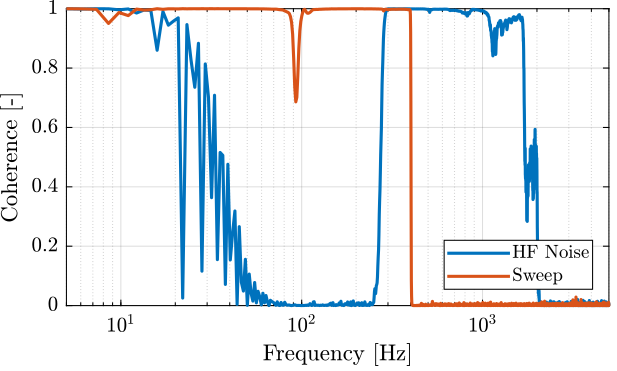
strut_1_frf_dvf_plant_coh.png

Figure 53: Obtained coherence for the plant from \(V_a\) to \(d_a\)

The transfer function from \(V_a\) to the interferometer measured displacement \(d_a\) is estimated and shown in Figure 54. 

[dvf_sweep, ~]    = tfestimate(leg_sweep.Va,    leg_sweep.da,    win, [], [], 1/Ts);
[dvf_noise_hf, ~] = tfestimate(leg_noise_hf.Va, leg_noise_hf.da, win, [], [], 1/Ts);

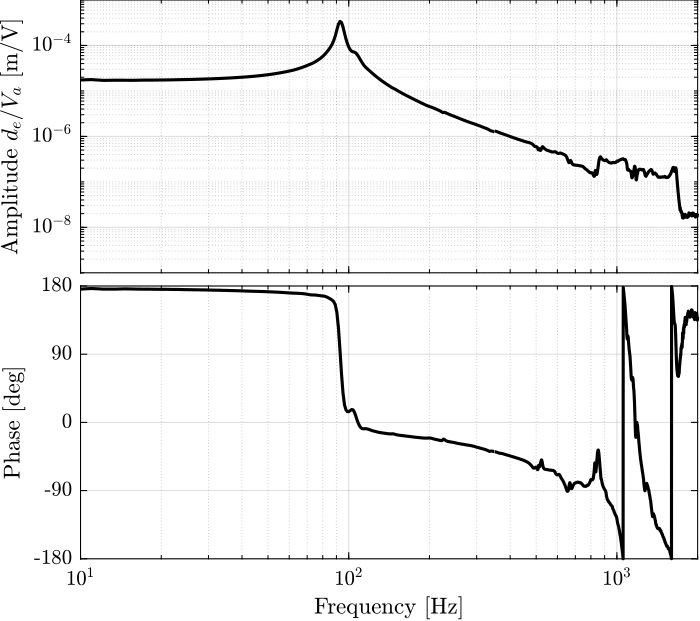
strut_1_frf_dvf_plant_tf.png

Figure 54: Estimated FRF for the DVF plant (transfer function from \(V_a\) to the interferometer \(d_a\))

4.1.1.3 FRF Identification - IFF

In this section, the dynamics from \(V_a\) to \(V_s\) is identified.

First the coherence is computed and shown in Figure 55. The coherence is very nice from 10Hz to 2kHz. It is only dropping near a zeros at 40Hz, and near the resonance at 95Hz (the excitation amplitude being lowered). 

[coh_sweep, ~] = mscohere(leg_sweep.Va, leg_sweep.Vs, win, [], [], 1/Ts);
[coh_noise_hf, ~] = mscohere(leg_noise_hf.Va, leg_noise_hf.Vs, win, [], [], 1/Ts);

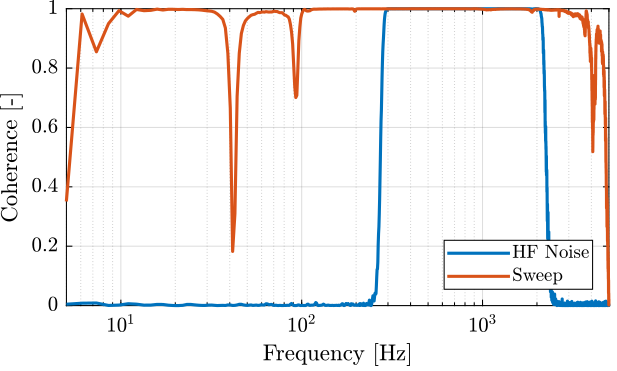
strut_1_frf_iff_plant_coh.png

Figure 55: Obtained coherence for the IFF plant

Then the FRF are estimated and shown in Figure 56 

[iff_sweep, ~] = tfestimate(leg_sweep.Va, leg_sweep.Vs, win, [], [], 1/Ts);
[iff_noise_hf, ~] = tfestimate(leg_noise_hf.Va, leg_noise_hf.Vs, win, [], [], 1/Ts);

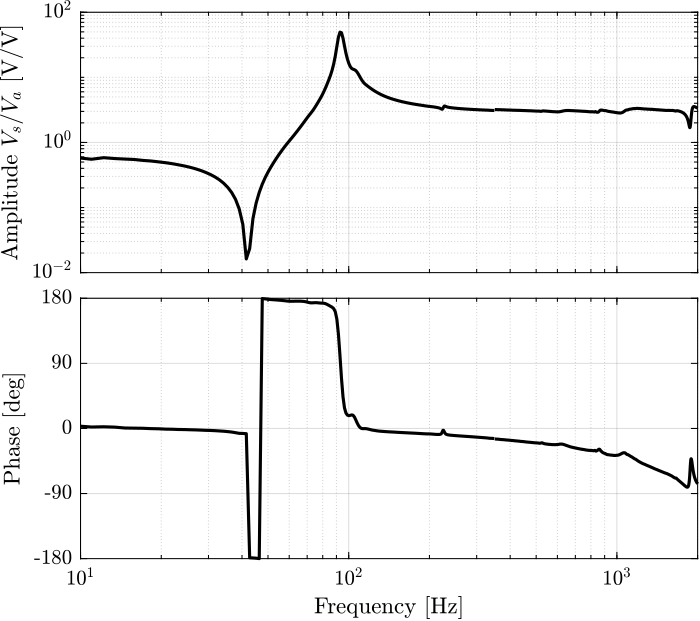
strut_1_frf_iff_plant_tf.png

Figure 56: Identified IFF Plant for the Strut 1

4.1.2 With Encoder

4.1.2.1 Measurement Data
leg_enc_sweep    = load(sprintf('frf_data_leg_coder_badly_align_%i_noise.mat',    1), 't', 'Va', 'Vs', 'de', 'da');
leg_enc_noise_hf = load(sprintf('frf_data_leg_coder_badly_align_%i_noise_hf.mat', 1), 't', 'Va', 'Vs', 'de', 'da');
4.1.2.2 FRF Identification - DVF

In this section, the dynamics from \(V_a\) to \(d_e\) is identified.

We compute the coherence for 2nd and 3rd identification: 

[coh_enc_sweep, ~]    = mscohere(leg_enc_sweep.Va,    leg_enc_sweep.de,    win, [], [], 1/Ts);
[coh_enc_noise_hf, ~] = mscohere(leg_enc_noise_hf.Va, leg_enc_noise_hf.de, win, [], [], 1/Ts);

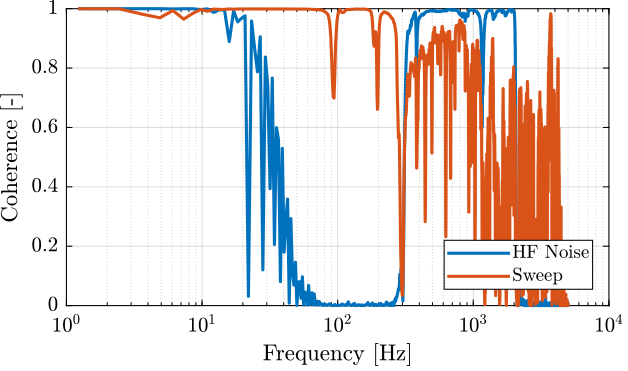
strut_1_enc_frf_dvf_plant_coh.png

Figure 57: Obtained coherence for the plant from \(V_a\) to \(d_e\)

[dvf_enc_sweep, ~]    = tfestimate(leg_enc_sweep.Va,    leg_enc_sweep.de,    win, [], [], 1/Ts);
[dvf_enc_noise_hf, ~] = tfestimate(leg_enc_noise_hf.Va, leg_enc_noise_hf.de, win, [], [], 1/Ts);

[dvf_int_sweep, ~]    = tfestimate(leg_enc_sweep.Va,    leg_enc_sweep.da,    win, [], [], 1/Ts);
[dvf_int_noise_hf, ~] = tfestimate(leg_enc_noise_hf.Va, leg_enc_noise_hf.da, win, [], [], 1/Ts);

The obtained transfer functions are shown in Figure 58.

They are all superimposed except for the APA7.

Why is the APA7 off? We could think that the APA7 is stiffer, but also the mass line is off.

It seems that there is a “gain” problem. The encoder seems fine (it measured the same as the Interferometer). Maybe it could be due to the amplifier?

Why is there a double resonance at around 94Hz?

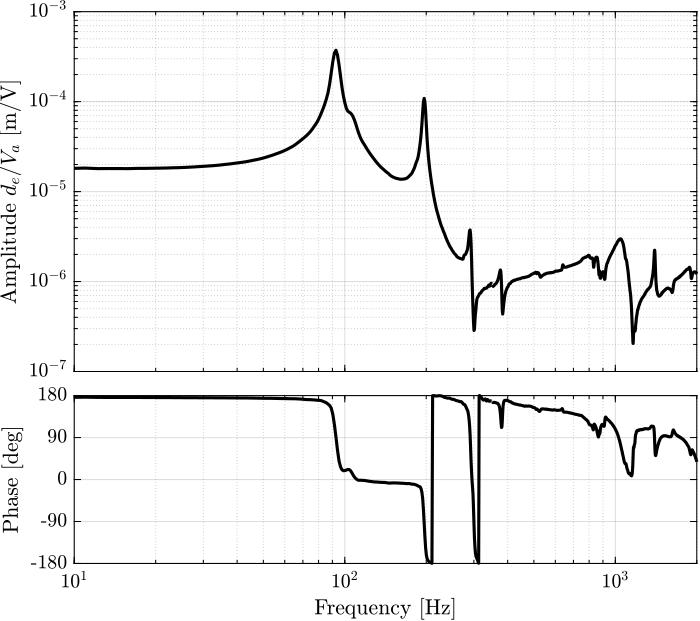
strut_1_enc_frf_dvf_plant_tf.png

Figure 58: Estimated FRF for the DVF plant (transfer function from \(V_a\) to the encoder \(d_e\))

4.1.2.3 Comparison of the Encoder and Interferometer

The interferometer could here represent the case where the encoders are fixed to the plates and not the APA.

The dynamics from \(V_a\) to \(d_e\) and from \(V_a\) to \(d_a\) are compared in Figure 59.

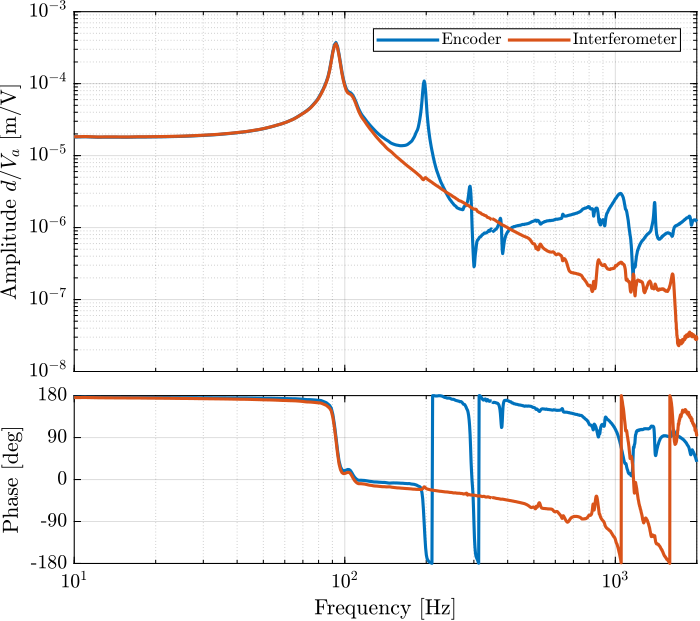
strut_1_comp_enc_int.png

Figure 59: Comparison of the transfer functions from excitation voltage \(V_a\) to either the encoder \(d_e\) or the interferometer \(d_a\)

It will clearly be difficult to do something (except some low frequency positioning) with the encoders fixed to the APA.

4.1.2.4 APA Resonances Frequency

As shown in Figure 60, we can clearly see three spurious resonances at 197Hz, 290Hz and 376Hz.

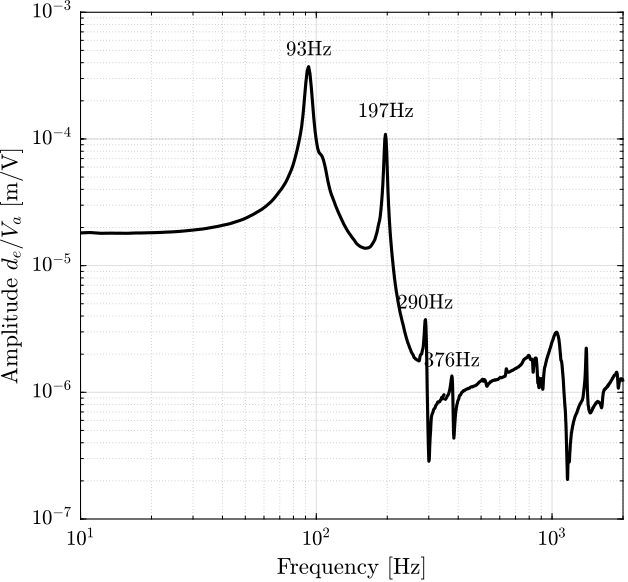
strut_1_spurious_resonances.png

Figure 60: Magnitude of the transfer function from excitation voltage \(V_a\) to encoder measurement \(d_e\). The frequency of the resonances are noted.

These resonances correspond to parasitic resonances of the APA itself. They are very close to what was estimated using the FEM:

  • X-bending mode at around 190Hz (Figure 61)
  • Y-bending mode at around 290Hz (Figure 62)
  • Z-torsion mode at around 400Hz (Figure 63)

mode_bending_x.gif

Figure 61: X-bending mode (189Hz)

mode_bending_y.gif

Figure 62: Y-bending mode (285Hz)

mode_torsion_z.gif

Figure 63: Z-torsion mode (400Hz)

The resonances are indeed due to limited stiffness of the APA.

4.1.2.5 Estimated Flexible Joint axial stiffness
load(sprintf('frf_data_leg_coder_%i_add_mass_closed_circuit.mat',    1), 't', 'Va', 'Vs', 'de', 'da');
de = de - de(1);
da = da - da(1);

figure;
hold on;
plot(t, de, 'DisplayName', 'Encoder')
plot(t, da, 'DisplayName', 'Interferometer')
hold off;
xlabel('Time [s]'); ylabel('Displacement [m]');
legend('location', 'northeast');

de_steps = [mean(de(t > 13 & t < 14));
            mean(de(t > 19 & t < 20));
            mean(de(t > 24 & t < 25));
            mean(de(t > 28.5 & t < 29.5));
            mean(de(t > 49 & t < 50))] - mean(de(t > 13 & t < 14));

da_steps = [mean(da(t > 13 & t < 14));
            mean(da(t > 19 & t < 20));
            mean(da(t > 24 & t < 25));
            mean(da(t > 28.5 & t < 29.5));
            mean(da(t > 49 & t < 50))] - mean(da(t > 13 & t < 14));

added_mass = [0; 1; 2; 3; 4];

lin_fit = (added_mass\abs(de_steps-da_steps) - abs(de_steps(1)-da_steps(1)));

figure;
hold on;
plot(added_mass, abs(de_steps-da_steps) - abs(de_steps(1)-da_steps(1)), 'ok')
plot(added_mass, added_mass*lin_fit, '-r')
hold off;

What is strange is that the encoder is measuring a larger displacement than the interferometer. That should be the opposite. Maybe is is caused by the fact that the APA is experiencing some bending and therefore a larger motion is measured on the encoder.

4.1.2.6 FRF Identification - IFF

In this section, the dynamics from \(V_a\) to \(V_s\) is identified.

First the coherence is computed and shown in Figure 55. The coherence is very nice from 10Hz to 2kHz. It is only dropping near a zeros at 40Hz, and near the resonance at 95Hz (the excitation amplitude being lowered). 

[coh_enc_sweep,    ~] = mscohere(leg_enc_sweep.Va,    leg_enc_sweep.Vs,    win, [], [], 1/Ts);
[coh_enc_noise_hf, ~] = mscohere(leg_enc_noise_hf.Va, leg_enc_noise_hf.Vs, win, [], [], 1/Ts);

strut_1_frf_iff_plant_coh.png

Figure 64: Obtained coherence for the IFF plant

Then the FRF are estimated and shown in Figure 65 

[iff_enc_sweep,    ~] = tfestimate(leg_enc_sweep.Va,    leg_enc_sweep.Vs,    win, [], [], 1/Ts);
[iff_enc_noise_hf, ~] = tfestimate(leg_enc_noise_hf.Va, leg_enc_noise_hf.Vs, win, [], [], 1/Ts);

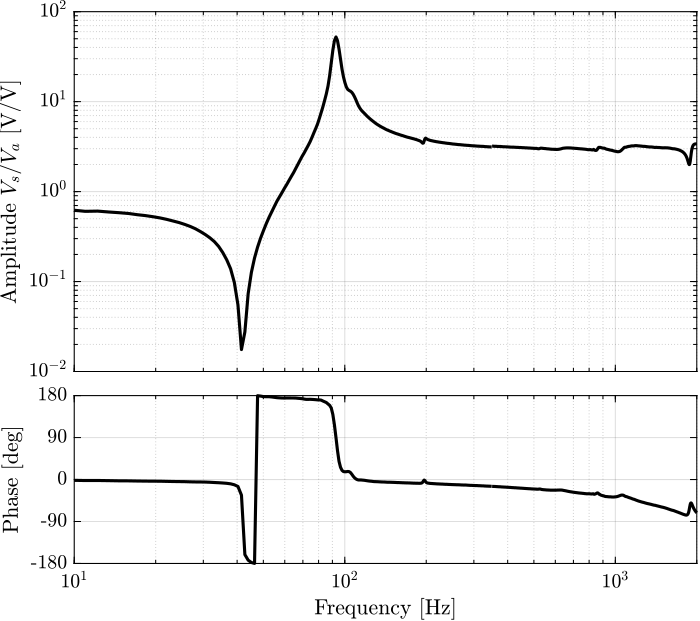
strut_1_enc_frf_iff_plant_tf.png

Figure 65: Identified IFF Plant

Let’s now compare the IFF plants whether the encoders are fixed to the APA or not (Figure 66).

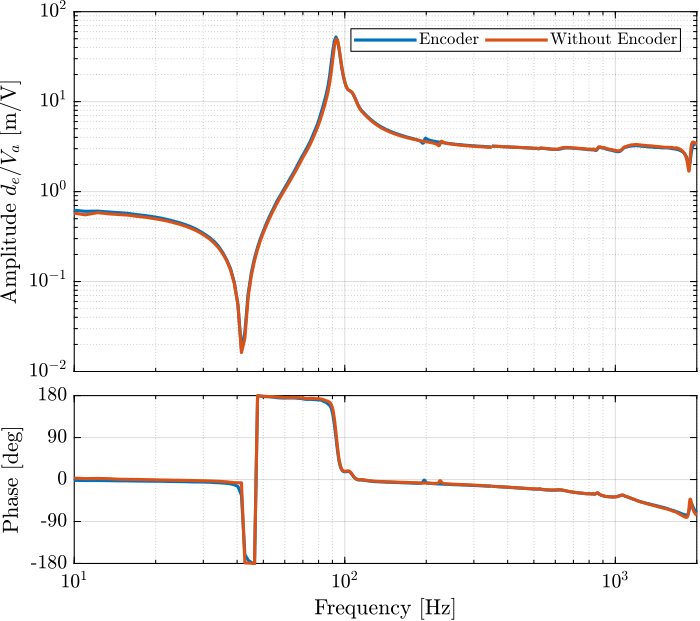
strut_1_frf_iff_effect_enc.png

Figure 66: Effect of the encoder on the IFF plant

We can see that the IFF does not change whether of not the encoder are fixed to the struts.

4.2 Comparison of all the Struts

Now all struts are measured using the same procedure and test bench.

4.2.1 FRF Identification - Setup

The identification is performed in two steps:

  1. White noise excitation with small amplitude. This is used to estimate the low frequency dynamics.
  2. High frequency noise. The noise is band-passed between 300Hz and 2kHz.

Then, the result of the first identification is used between 10Hz and 350Hz and the result of the second identification if used between 350Hz and 2kHz.

Here are the LEG numbers that have been measured. 

leg_nums = [1 2 3 4 5];

The data are loaded for both the first and second identification: 

%% Second identification
leg_noise = {};
for i = 1:length(leg_nums)
    leg_noise(i) = {load(sprintf('frf_data_leg_coder_%i_noise.mat', leg_nums(i)), 't', 'Va', 'Vs', 'de', 'da')};
end

%% Third identification
leg_noise_hf = {};
for i = 1:length(leg_nums)
    leg_noise_hf(i) = {load(sprintf('frf_data_leg_coder_%i_noise_hf.mat', leg_nums(i)), 't', 'Va', 'Vs', 'de', 'da')};
end

The time is the same for all measurements. 

%% Time vector
t = leg_noise{1}.t - leg_noise{1}.t(1) ; % Time vector [s]

%% Sampling
Ts = (t(end) - t(1))/(length(t)-1); % Sampling Time [s]
Fs = 1/Ts; % Sampling Frequency [Hz]

Then we defined a “Hanning” windows that will be used for the spectral analysis: 

win = hanning(ceil(0.5*Fs)); % Hannning Windows

We get the frequency vector that will be the same for all the frequency domain analysis. 

% Only used to have the frequency vector "f"
[~, f] = tfestimate(leg_noise{1}.Va, leg_noise{1}.de, win, [], [], 1/Ts);

4.2.2 FRF Identification - DVF

In this section, the dynamics from \(V_a\) to \(d_e\) is identified.

We compute the coherence for 2nd and 3rd identification: 

%% Coherence computation
coh_noise = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [coh, ~] = mscohere(leg_noise{i}.Va, leg_noise{i}.de, win, [], [], 1/Ts);
    coh_noise(:, i) = coh;
end

coh_noise_hf = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [coh, ~] = mscohere(leg_noise_hf{i}.Va, leg_noise_hf{i}.de, win, [], [], 1/Ts);
    coh_noise_hf(:, i) = coh;
end

The coherence is shown in Figure 67. It is clear that the Noise sine gives good coherence up to 400Hz and that the high frequency noise excitation signal helps increasing a little bit the coherence at high frequency.

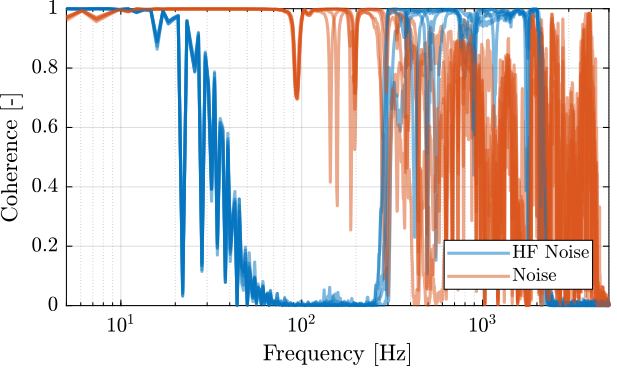
struts_frf_dvf_plant_coh.png

Figure 67: Obtained coherence for the plant from \(V_a\) to \(d_e\)

Then, the transfer function from the DAC output voltage \(V_a\) to the measured displacement by the encoders is computed: 

%% Transfer function estimation
dvf_noise = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [frf, ~] = tfestimate(leg_noise{i}.Va, leg_noise{i}.de, win, [], [], 1/Ts);
    dvf_noise(:, i) = frf;
end

dvf_noise_hf = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [frf, ~] = tfestimate(leg_noise_hf{i}.Va, leg_noise_hf{i}.de, win, [], [], 1/Ts);
    dvf_noise_hf(:, i) = frf;
end

The obtained transfer functions are shown in Figure 68.

They are all superimposed except for the LEG7.

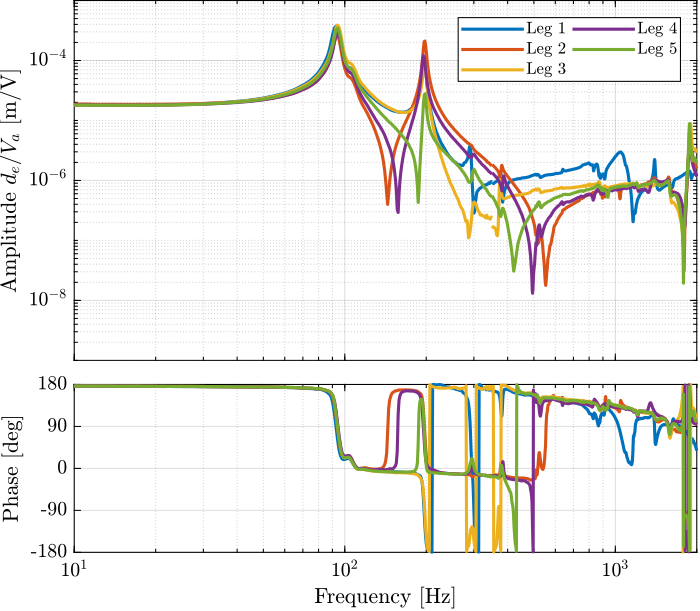
struts_frf_dvf_plant_tf.png

Figure 68: Estimated FRF for the DVF plant (transfer function from \(V_a\) to the encoder \(d_e\))

Depending on how the APA are mounted with the flexible joints, the dynamics can change a lot as shown in Figure 68. In the future, a “pin” will be used to better align the APA with the flexible joints. We can expect the amplitude of the spurious resonances to decrease.

4.2.3 FRF Identification - DVF with interferometer

In this section, the dynamics from \(V_a\) to \(d_a\) is identified.

We compute the coherence. 

%% Coherence computation
coh_noise = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [coh, ~] = mscohere(leg_noise{i}.Va, leg_noise{i}.da, win, [], [], 1/Ts);
    coh_noise(:, i) = coh;
end

coh_noise_hf = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [coh, ~] = mscohere(leg_noise_hf{i}.Va, leg_noise_hf{i}.da, win, [], [], 1/Ts);
    coh_noise_hf(:, i) = coh;
end

The coherence is shown in Figure 69. It is clear that the Noise sine gives good coherence up to 400Hz and that the high frequency noise excitation signal helps increasing a little bit the coherence at high frequency.

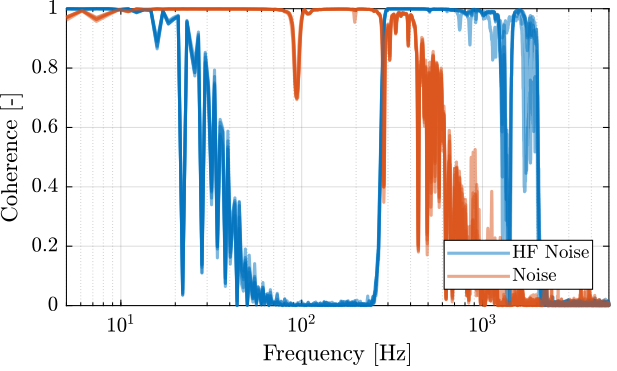
struts_frf_int_plant_coh.png

Figure 69: Obtained coherence for the plant from \(V_a\) to \(d_e\)

Then, the transfer function from the DAC output voltage \(V_a\) to the measured displacement by the Attocube is computed: 

%% Transfer function estimation
dvf_a_noise = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [frf, ~] = tfestimate(leg_noise{i}.Va, leg_noise{i}.da, win, [], [], 1/Ts);
    dvf_a_noise(:, i) = frf;
end

dvf_a_noise_hf = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [frf, ~] = tfestimate(leg_noise_hf{i}.Va, leg_noise_hf{i}.da, win, [], [], 1/Ts);
    dvf_a_noise_hf(:, i) = frf;
end

The obtained transfer functions are shown in Figure 70.

They are all superimposed except for the LEG7.

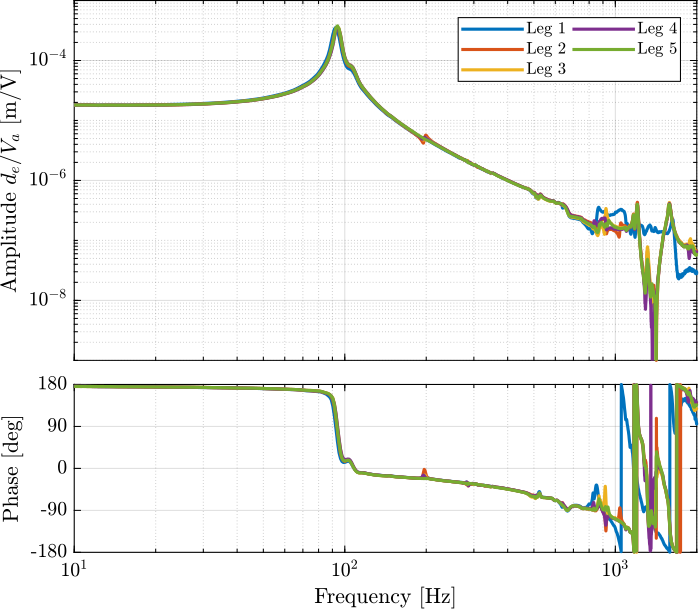
struts_frf_int_plant_tf.png

Figure 70: Estimated FRF for the DVF plant (transfer function from \(V_a\) to the encoder \(d_e\))

4.2.4 FRF Identification - IFF

In this section, the dynamics from \(V_a\) to \(V_s\) is identified.

First the coherence is computed and shown in Figure 71. The coherence is very nice from 10Hz to 2kHz. It is only dropping near a zeros at 40Hz, and near the resonance at 95Hz (the excitation amplitude being lowered). 

%% Coherence
coh_noise = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [coh, ~] = mscohere(leg_noise{i}.Va, leg_noise{i}.Vs, win, [], [], 1/Ts);
    coh_noise(:, i) = coh;
end

coh_noise_hf = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [coh, ~] = mscohere(leg_noise_hf{i}.Va, leg_noise_hf{i}.Vs, win, [], [], 1/Ts);
    coh_noise_hf(:, i) = coh;
end

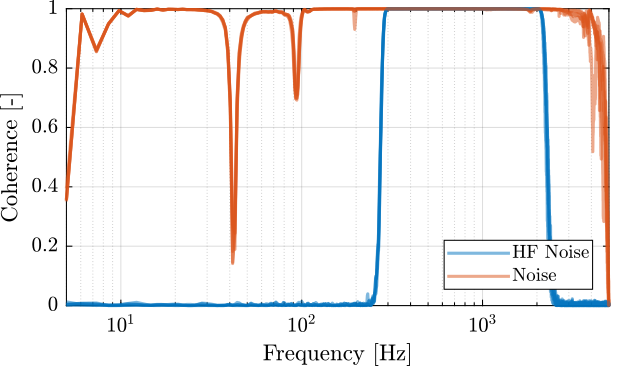
struts_frf_iff_plant_coh.png

Figure 71: Obtained coherence for the IFF plant

Then the FRF are estimated and shown in Figure 72 

%% FRF estimation of the transfer function from Va to Vs
iff_noise = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [frf, ~] = tfestimate(leg_noise{i}.Va, leg_noise{i}.Vs, win, [], [], 1/Ts);
    iff_noise(:, i) = frf;
end

iff_noise_hf = zeros(length(f), length(leg_nums));
for i = 1:length(leg_nums)
    [frf, ~] = tfestimate(leg_noise_hf{i}.Va, leg_noise_hf{i}.Vs, win, [], [], 1/Ts);
    iff_noise_hf(:, i) = frf;
end

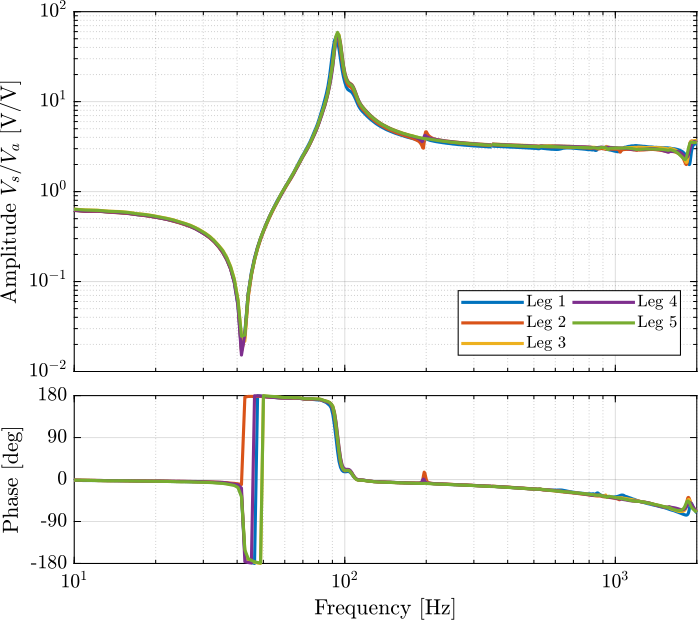
struts_frf_iff_plant_tf.png

Figure 72: Identified IFF Plant

5 Test Bench APA300ML - Simscape Model

5.1 Introduction

A simscape model (Figure 73) of the measurement bench is used.

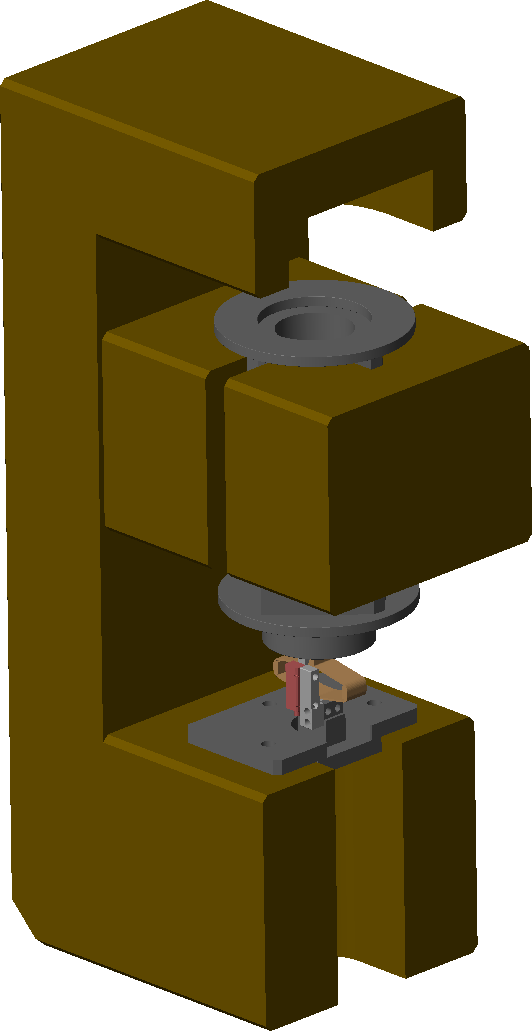
model_bench_apa.png

Figure 73: Screenshot of the Simscape model

5.2 First Identification

The APA is first initialized with default parameters and the transfer function from excitation voltage \(V_a\) (before the amplification of 20 due to the PD200 amplifier) to the sensor stack voltage \(V_s\), encoder \(d_L\) and interferometer \(z\) is identified. 

%% Initialize the structure containing the data used in the model
n_hexapod = struct();
n_hexapod.actuator = initializeAPA('type', '2dof');

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Va'],  1, 'openinput');  io_i = io_i + 1; % Actuator Voltage
io(io_i) = linio([mdl, '/Vs'],  1, 'openoutput'); io_i = io_i + 1; % Sensor Voltage
io(io_i) = linio([mdl, '/dL'],  1, 'openoutput'); io_i = io_i + 1; % Relative Motion Outputs
io(io_i) = linio([mdl, '/z'],   1, 'openoutput'); io_i = io_i + 1; % Vertical Motion

%% Run the linearization
Ga = linearize(mdl, io, 0.0, options);
Ga.InputName  = {'Va'};
Ga.OutputName = {'Vs', 'dL', 'z'};

The obtain dynamics are shown in Figure 74 and 75.

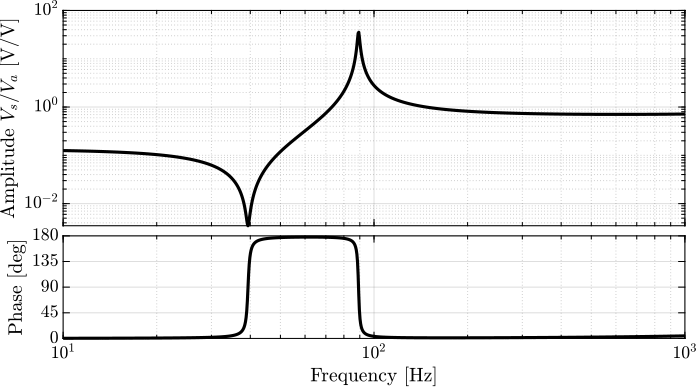
apa_model_bench_bode_vs.png

Figure 74: Bode plot of the transfer function from \(V_a\) to \(V_s\)

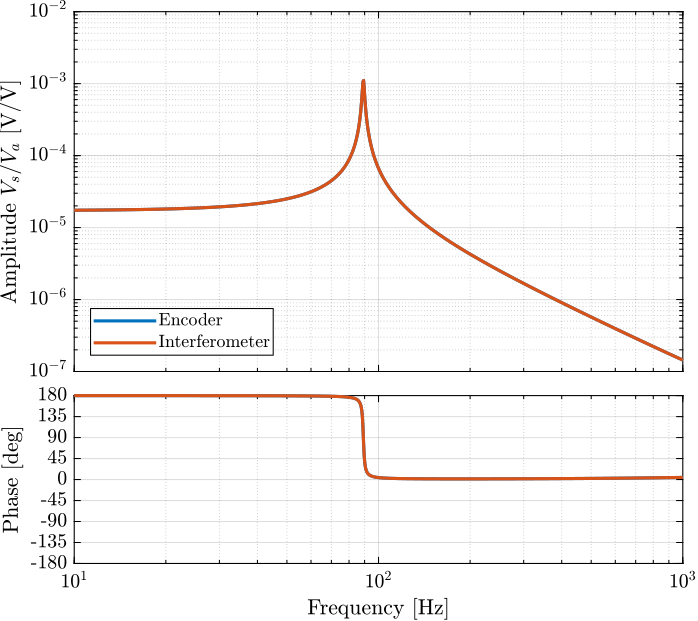
apa_model_bench_bode_dl_z.png

Figure 75: Bode plot of the transfer function from \(V_a\) to \(d_L\) and to \(z\)

5.3 Identify Sensor/Actuator constants and compare with measured FRF

5.3.1 How to identify these constants?

5.3.1.1 Piezoelectric Actuator Constant

Using the measurement test-bench, it is rather easy the determine the static gain between the applied voltage \(V_a\) to the induced displacement \(d\).

\begin{equation} d = g_{d/V_a} \cdot V_a \end{equation}

Using the Simscape model of the APA, it is possible to determine the static gain between the actuator force \(F_a\) to the induced displacement \(d\):

\begin{equation} d = g_{d/F_a} \cdot F_a \end{equation}

From the two gains, it is then easy to determine \(g_a\):

\begin{equation} g_a = \frac{F_a}{V_a} = \frac{F_a}{d} \cdot \frac{d}{V_a} = \frac{g_{d/V_a}}{g_{d/F_a}} \end{equation}
5.3.1.2 Piezoelectric Sensor Constant

Similarly, it is easy to determine the gain from the excitation voltage \(V_a\) to the voltage generated by the sensor stack \(V_s\):

\begin{equation} V_s = g_{V_s/V_a} V_a \end{equation}

Note here that there is an high pass filter formed by the piezo capacitor and parallel resistor.

The gain can be computed from the dynamical identification and taking the gain at the wanted frequency (above the first resonance).

Using the simscape model, compute the gain at the same frequency from the actuator force \(F_a\) to the strain of the sensor stack \(dl\):

\begin{equation} dl = g_{dl/F_a} F_a \end{equation}

Then, the “sensor” constant is:

\begin{equation} g_s = \frac{V_s}{dl} = \frac{V_s}{V_a} \cdot \frac{V_a}{F_a} \cdot \frac{F_a}{dl} = \frac{g_{V_s/V_a}}{g_a \cdot g_{dl/F_a}} \end{equation}

5.3.2 Identification Data

%% Load the identification Data
leg_sweep    = load(sprintf('frf_data_%i_sweep.mat',    1), 't', 'Va', 'Vs', 'de', 'da');
leg_noise_hf = load(sprintf('frf_data_%i_noise_hf.mat', 1), 't', 'Va', 'Vs', 'de', 'da');

The time is the same for all measurements. 

%% Time vector
t = leg_sweep.t - leg_sweep.t(1) ; % Time vector [s]

%% Sampling Time / Frequency
Ts = (t(end) - t(1))/(length(t)-1); % Sampling Time [s]
Fs = 1/Ts; % Sampling Frequency [Hz]

Then we defined a “Hanning” windows that will be used for the spectral analysis: 

%% Window used for spectral analysis
win = hanning(ceil(0.5*Fs)); % Hannning Windows

We get the frequency vector that will be the same for all the frequency domain analysis. 

%% Get the frequency vector "f" common to all further spectral data
[~, f] = tfestimate(leg_sweep.Va, leg_sweep.de, win, [], [], 1/Ts);

%% Estimate the transfer function from u to dLm
[dvf_sweep, ~]    = tfestimate(leg_sweep.Va,    leg_sweep.da,    win, [], [], 1/Ts);
[dvf_noise_hf, ~] = tfestimate(leg_noise_hf.Va, leg_noise_hf.da, win, [], [], 1/Ts);

%% Estimate the transfer function from u to taum
[iff_sweep, ~] = tfestimate(leg_sweep.Va, leg_sweep.Vs, win, [], [], 1/Ts);
[iff_noise_hf, ~] = tfestimate(leg_noise_hf.Va, leg_noise_hf.Vs, win, [], [], 1/Ts);

5.3.3 2DoF APA

5.3.3.1 2DoF APA
%% Initialize a 2DoF APA with Ga=Gs=1
n_hexapod.actuator = initializeAPA('type', '2dof', 'ga', 1, 'gs', 1);
5.3.3.2 Identification without actuator or sensor constants
%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Va'],  1, 'openinput');  io_i = io_i + 1; % Actuator Voltage
io(io_i) = linio([mdl, '/Vs'],  1, 'openoutput'); io_i = io_i + 1; % Sensor Voltage
io(io_i) = linio([mdl, '/dL'],  1, 'openoutput'); io_i = io_i + 1; % Relative Motion Outputs
io(io_i) = linio([mdl, '/z'],   1, 'openoutput'); io_i = io_i + 1; % Vertical Motion

%% Identification
Gs = linearize(mdl, io, 0.0, options);
Gs.InputName  = {'Va'};
Gs.OutputName = {'Vs', 'dL', 'z'};
5.3.3.3 Actuator Constant
%% Estimated Actuator Constant
ga = -mean(abs(dvf_sweep(f>10 & f<20)))./dcgain(Gs('dL', 'Va')); % [N/V]

ga = -32.1 [N/V]

n_hexapod.actuator.Ga = ones(6,1)*ga; % Actuator gain [N/V]
5.3.3.4 Sensor Constant
%% Estimated Sensor Constant
gs = -mean(abs(iff_sweep(f>400 & f<500)))./(ga*abs(squeeze(freqresp(Gs('Vs', 'Va'), 1e3, 'Hz')))); % [V/m]

gs = 0.085 [V/m]

n_hexapod.actuator.Gs = ones(6,1)*gs; % Sensor gain [V/m]
5.3.3.5 Comparison

Identify the dynamics with included constants. 

%% Identify again the dynamics with correct Ga,Gs
Gs = linearize(mdl, io, 0.0, options);
Gs = Gs*exp(-Ts*s);
Gs.InputName  = {'Va'};
Gs.OutputName = {'Vs', 'dL', 'z'};

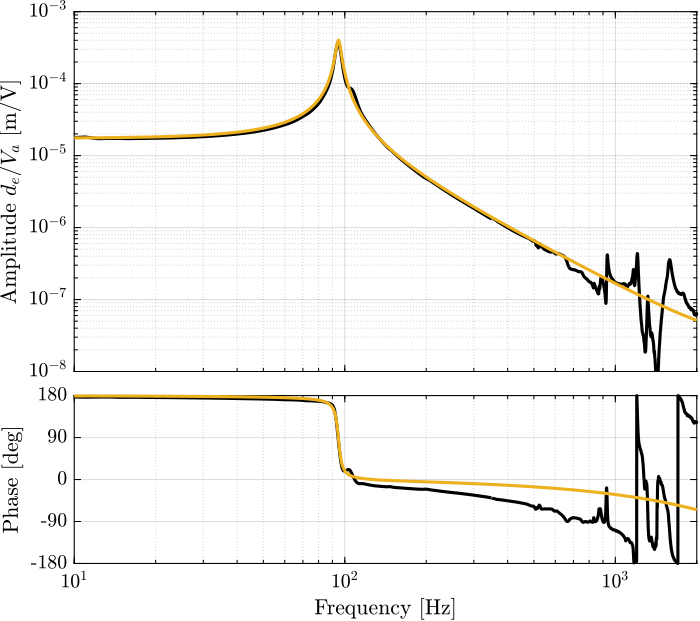
apa_act_constant_comp.png

Figure 76: Comparison of the experimental data and Simscape model (\(u\) to \(d\mathcal{L}_m\))

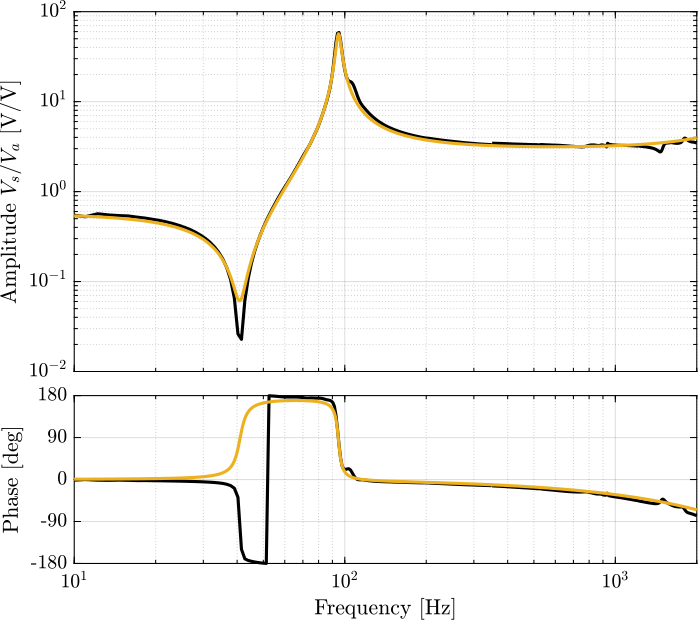
apa_sens_constant_comp.png

Figure 77: Comparison of the experimental data and Simscape model (\(V_a\) to \(V_s\))

5.3.4 Flexible APA

5.3.4.1 Flexible APA
%% Initialize the APA as a flexible body
n_hexapod.actuator = initializeAPA('type', 'flexible', 'ga', 1, 'gs', 1);
5.3.4.2 Identification without actuator or sensor constants
%% Identify the dynamics
Gs = linearize(mdl, io, 0.0, options);
Gs.InputName  = {'Va'};
Gs.OutputName = {'Vs', 'dL', 'z'};
5.3.4.3 Actuator Constant
%% Actuator Constant
ga = -mean(abs(dvf_sweep(f>10 & f<20)))./dcgain(Gs('dL', 'Va')); % [N/V]

ga = 23.4 [N/V]

n_hexapod.actuator.Ga = ones(6,1)*ga; % Actuator gain [N/V]
5.3.4.4 Sensor Constant
%% Sensor Constant
gs = -mean(abs(iff_sweep(f>400 & f<500)))./(ga*abs(squeeze(freqresp(Gs('Vs', 'Va'), 1e3, 'Hz')))); % [V/m]

gs = -4674826.805 [V/m]

n_hexapod.actuator.Gs = ones(6,1)*gs; % Sensor gain [V/m]
5.3.4.5 Comparison
%% Identify with updated constants
Gs = linearize(mdl, io, 0.0, options);
Gs = Gs*exp(-Ts*s);
Gs.InputName  = {'Va'};
Gs.OutputName = {'Vs', 'dL', 'z'};

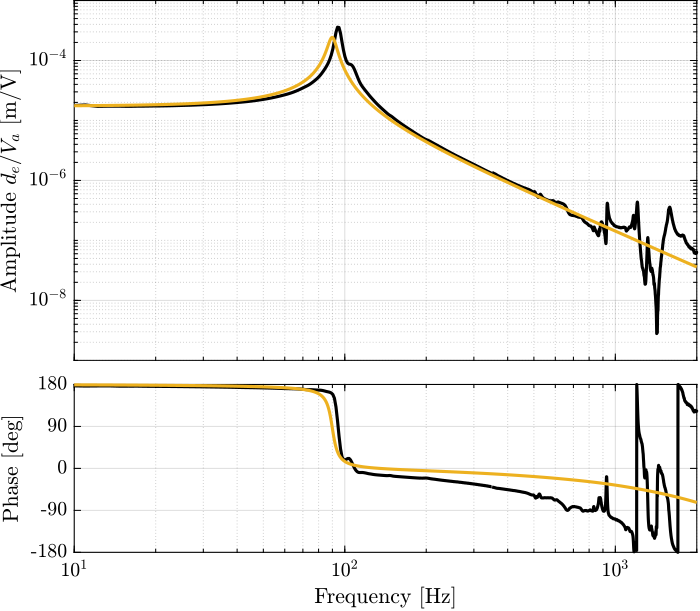
apa_act_constant_comp_flex.png

Figure 78: Comparison of the experimental data and Simscape model (\(u\) to \(d\mathcal{L}_m\))

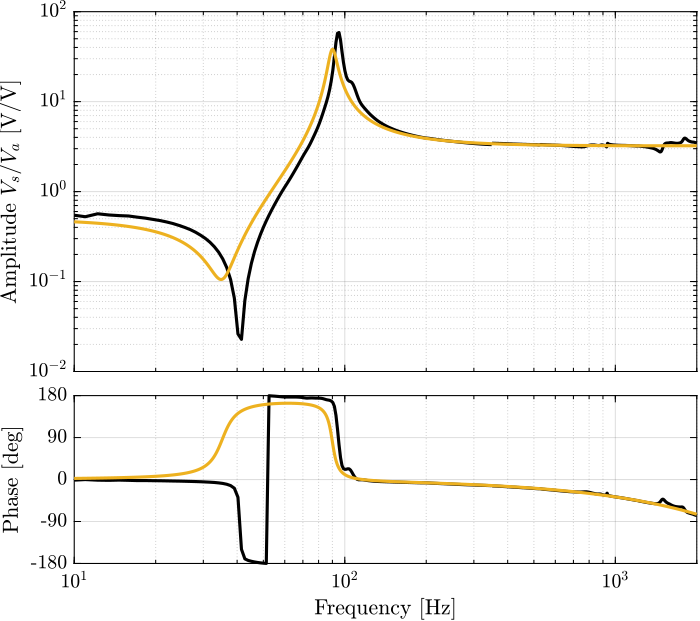
apa_sens_constant_comp_flex.png

Figure 79: Comparison of the experimental data and Simscape model (\(u\) to \(\tau_m\))

5.4 Optimize 2-DoF model to fit the experimental Data

%% Optimized parameters
n_hexapod.actuator = initializeAPA('type', '2dof', ...
                                   'Ga', -30.0, ...
                                   'Gs', 0.098, ...
                                   'k',  ones(6,1)*0.38e6, ...
                                   'ke', ones(6,1)*1.75e6, ...
                                   'ka', ones(6,1)*3e7, ...
                                   'c',  ones(6,1)*1.3e2, ...
                                   'ce', ones(6,1)*1e1, ...
                                   'ca', ones(6,1)*1e1 ...
                                   );

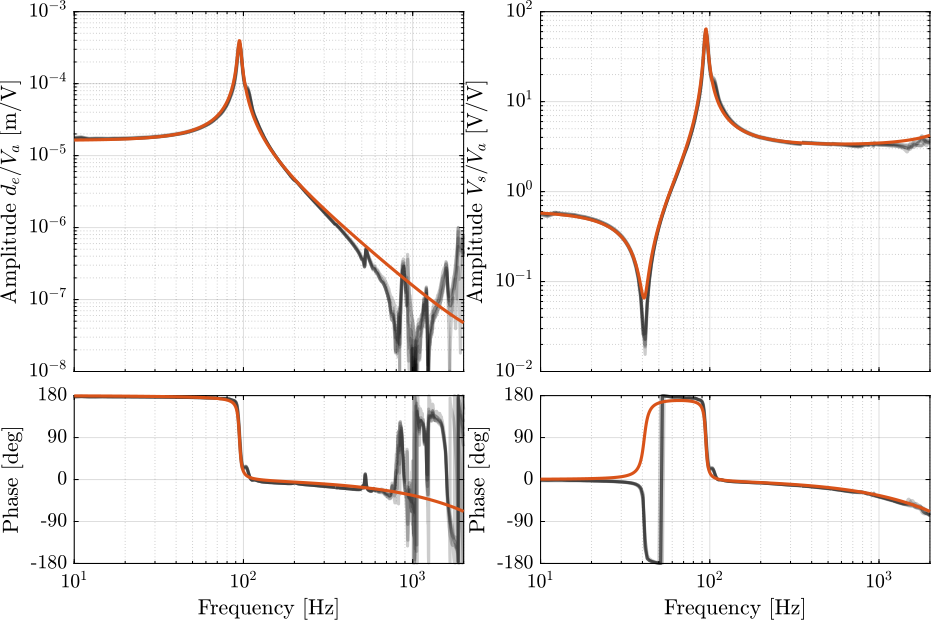
comp_apa_plant_after_opt.png

Figure 80: Comparison of the measured FRF and the optimized model

6 Test Bench Struts - Simscape Model

6.1 Introduction

6.2 First Identification

The object containing all the data is created. 

%% Initialize structure containing data for the Simscape model
n_hexapod = struct();
n_hexapod.flex_bot = initializeBotFlexibleJoint('type', '2dof');
n_hexapod.flex_top = initializeTopFlexibleJoint('type', '2dof');
n_hexapod.actuator = initializeAPA('type', '2dof');

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Va'],  1, 'openinput');  io_i = io_i + 1; % Actuator Voltage
io(io_i) = linio([mdl, '/Vs'],  1, 'openoutput'); io_i = io_i + 1; % Sensor Voltage
io(io_i) = linio([mdl, '/dL'],  1, 'openoutput'); io_i = io_i + 1; % Relative Motion Outputs
io(io_i) = linio([mdl, '/z'],   1, 'openoutput'); io_i = io_i + 1; % Vertical Motion

%% Run the linearization
Gs = linearize(mdl, io, 0.0, options);
Gs.InputName  = {'Va'};
Gs.OutputName = {'Vs', 'dL', 'z'};

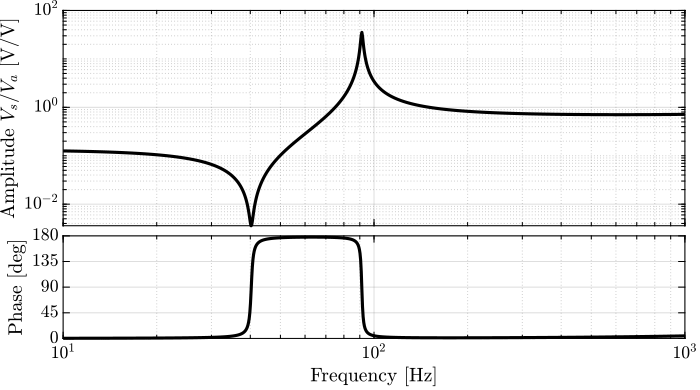
strut_bench_model_iff_bode.png

Figure 81: Identified transfer function from \(V_a\) to \(V_s\)

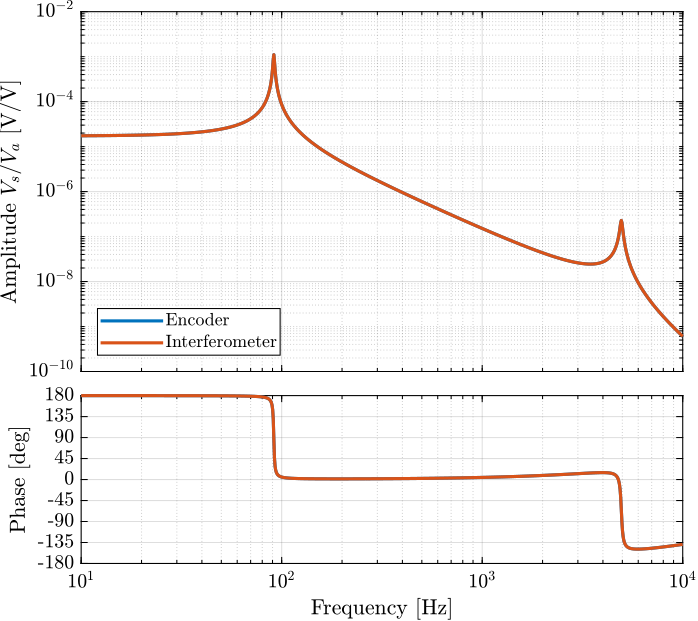
strut_bench_model_dvf_bode.png

Figure 82: Identified transfer function from \(V_a\) to \(d_L\)

6.3 Effect of flexible joints

Perfect 

%% Perfect Joints
n_hexapod.flex_bot = initializeBotFlexibleJoint('type', '2dof');
n_hexapod.flex_top = initializeTopFlexibleJoint('type', '3dof');

Gp = linearize(mdl, io, 0.0, options);
Gp.InputName  = {'Va'};
Gp.OutputName = {'Vs', 'dL', 'z'};

Top Flexible 

%% Top joint with Axial stiffness
n_hexapod.flex_bot = initializeBotFlexibleJoint('type', '2dof');
n_hexapod.flex_top = initializeTopFlexibleJoint('type', '4dof');

Gt = linearize(mdl, io, 0.0, options);
Gt.InputName  = {'Va'};
Gt.OutputName = {'Vs', 'dL', 'z'};

Bottom Flexible 

%% Bottom joint with Axial stiffness
n_hexapod.flex_bot = initializeBotFlexibleJoint('type', '4dof');
n_hexapod.flex_top = initializeTopFlexibleJoint('type', '3dof');

Gb = linearize(mdl, io, 0.0, options);
Gb.InputName  = {'Va'};
Gb.OutputName = {'Vs', 'dL', 'z'};

Both Flexible 

%% Both joints with Axial stiffness
n_hexapod.flex_bot = initializeBotFlexibleJoint('type', '4dof');
n_hexapod.flex_top = initializeTopFlexibleJoint('type', '4dof');

Gf = linearize(mdl, io, 0.0, options);
Gf.InputName  = {'Va'};
Gf.OutputName = {'Vs', 'dL', 'z'};

Comparison in Figures 83, 84 and 85.

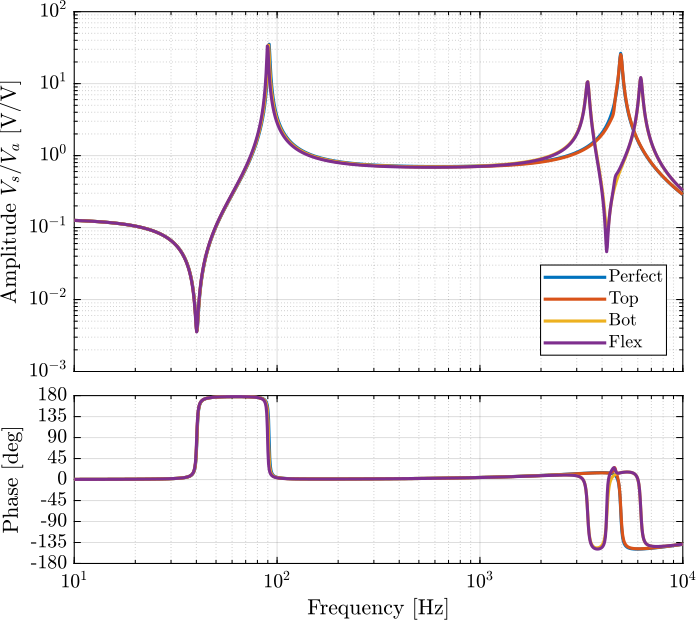
strut_effect_joint_comp_vs.png

Figure 83: Effect of the joint’s flexibility on the transfer function from \(V_a\) to \(V_s\)

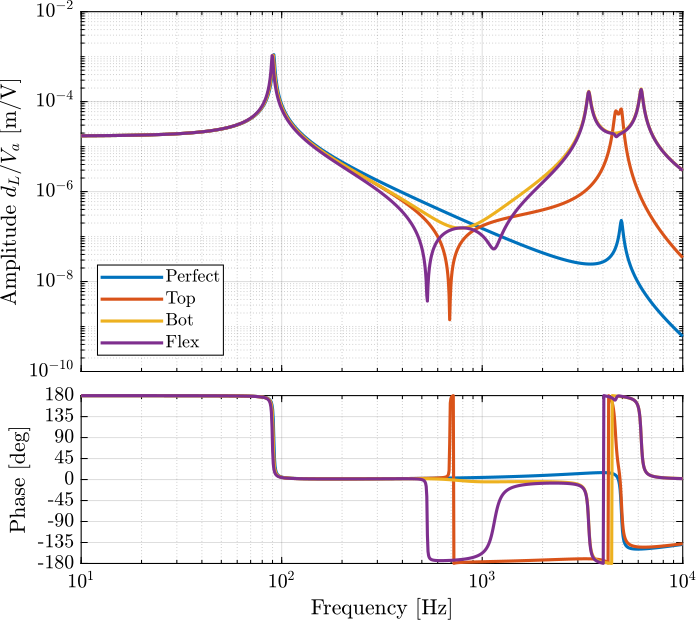
strut_effect_joint_comp_dl.png

Figure 84: Effect of the joint’s flexibility on the transfer function from \(V_a\) to \(d_L\) (encoder)

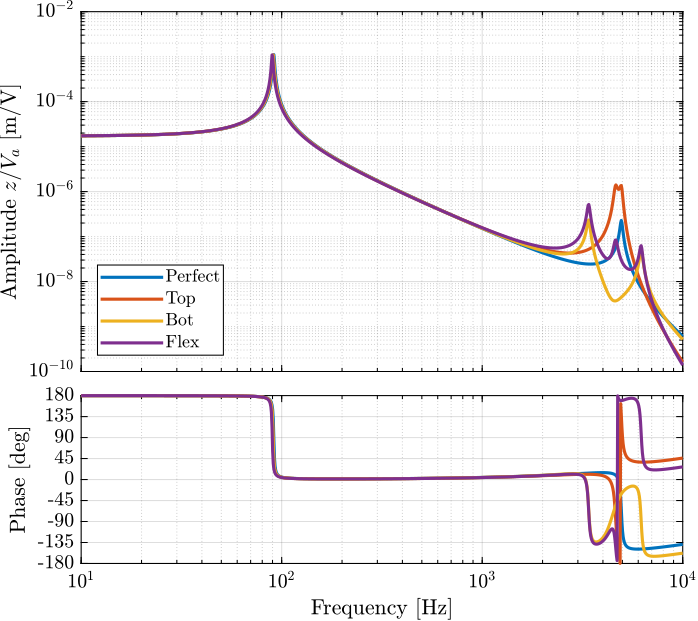
strut_effect_joint_comp_z.png

Figure 85: Effect of the joint’s flexibility on the transfer function from \(V_a\) to \(z\) (interferometer)

Imperfection of the flexible joints has the largest impact on the transfer function from \(V_a\) to \(d_L\). However, it has relatively small impact on the transfer functions from \(V_a\) to \(V_s\) and to \(z\).

6.4 Integral Force Feedback

6.4.1 Initialize the system

%% Initialize typical system
n_hexapod = struct();
n_hexapod.flex_bot = initializeBotFlexibleJoint('type', '2dof');
n_hexapod.flex_top = initializeTopFlexibleJoint('type', '3dof');
n_hexapod.actuator = initializeAPA('type', '2dof');

6.4.2 Plant Identification

%% Identify th edynamics
G = linearize(mdl, io, 0.0, options);
G.InputName  = {'Va'};
G.OutputName = {'Vs', 'dL', 'z'};

%% IFF Plant (transfer function from u to taum)
Giff = G('Vs', 'Va');

6.4.3 Root Locus

\begin{equation} K_{\text{IFF}} = \frac{g}{s + \omega_c} \end{equation} 
%% Cut-off frequency of the LPF
wc = 2*pi*20;

6.5 Comparison with the experimental Data

%% Initialize Simscape data
n_hexapod.flex_bot = initializeBotFlexibleJoint('type', '4dof');
n_hexapod.flex_top = initializeTopFlexibleJoint('type', '4dof');
n_hexapod.actuator = initializeAPA('type', '2dof');

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Va'],  1, 'openinput');  io_i = io_i + 1; % Actuator Voltage
io(io_i) = linio([mdl, '/Vs'],  1, 'openoutput'); io_i = io_i + 1; % Sensor Voltage
io(io_i) = linio([mdl, '/z'],   1, 'openoutput'); io_i = io_i + 1; % Relative Motion Outputs

%% Identification
Gs = exp(-s*Ts)*linearize(mdl, io, 0.0, options);
Gs.InputName  = {'Va'};
Gs.OutputName = {'Vs', 'z'};

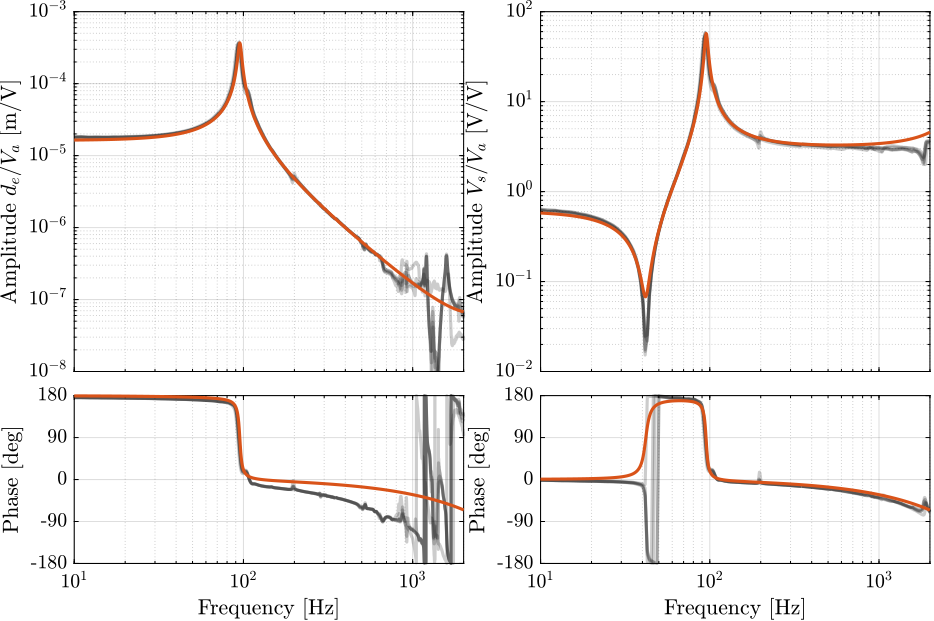
comp_strut_plant_after_opt.png

Figure 86: Comparison of the measured FRF and the optimized model

7 Function

7.1 initializeBotFlexibleJoint - Initialize Flexible Joint

Function description

function [flex_bot] = initializeBotFlexibleJoint(args)
% initializeBotFlexibleJoint -
%
% Syntax: [flex_bot] = initializeBotFlexibleJoint(args)
%
% Inputs:
%    - args -
%
% Outputs:
%    - flex_bot -

Optional Parameters

arguments
    args.type      char   {mustBeMember(args.type,{'2dof', '3dof', '4dof'})} = '2dof'

    args.kRx (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*5
    args.kRy (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*5
    args.kRz (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*260
    args.kz  (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*1e8

    args.cRx (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*0.1
    args.cRy (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*0.1
    args.cRz (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*0.1
    args.cz  (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*1e2
end

Initialize the structure

flex_bot = struct();

Set the Joint’s type

switch args.type
  case '2dof'
    flex_bot.type = 1;
  case '3dof'
    flex_bot.type = 2;
  case '4dof'
    flex_bot.type = 3;
end

Set parameters

flex_bot.kRx = args.kRx;
flex_bot.kRy = args.kRy;
flex_bot.kRz = args.kRz;
flex_bot.kz  = args.kz;

flex_bot.cRx = args.cRx;
flex_bot.cRy = args.cRy;
flex_bot.cRz = args.cRz;
flex_bot.cz  = args.cz;

7.2 initializeTopFlexibleJoint - Initialize Flexible Joint

Function description

function [flex_top] = initializeTopFlexibleJoint(args)
% initializeTopFlexibleJoint -
%
% Syntax: [flex_top] = initializeTopFlexibleJoint(args)
%
% Inputs:
%    - args -
%
% Outputs:
%    - flex_top -

Optional Parameters

arguments
    args.type      char   {mustBeMember(args.type,{'2dof', '3dof', '4dof'})} = '2dof'

    args.kRx (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*5
    args.kRy (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*5
    args.kRz (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*260
    args.kz  (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*1e8

    args.cRx (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*0.1
    args.cRy (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*0.1
    args.cRz (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*0.1
    args.cz  (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*1e2
end

Initialize the structure

flex_top = struct();

Set the Joint’s type

switch args.type
  case '2dof'
    flex_top.type = 1;
  case '3dof'
    flex_top.type = 2;
  case '4dof'
    flex_top.type = 3;
end

Set parameters

flex_top.kRx = args.kRx;
flex_top.kRy = args.kRy;
flex_top.kRz = args.kRz;
flex_top.kz  = args.kz;

flex_top.cRx = args.cRx;
flex_top.cRy = args.cRy;
flex_top.cRz = args.cRz;
flex_top.cz  = args.cz;

7.3 initializeAPA - Initialize APA

Function description

function [actuator] = initializeAPA(args)
% initializeAPA -
%
% Syntax: [actuator] = initializeAPA(args)
%
% Inputs:
%    - args -
%
% Outputs:
%    - actuator -

Optional Parameters

arguments
    args.type      char   {mustBeMember(args.type,{'2dof', 'flexible frame', 'flexible'})} = '2dof'

    args.Ga  (1,1) double {mustBeNumeric} = 0
    args.Gs  (1,1) double {mustBeNumeric} = 0

    % For 2DoF
    args.k   (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*0.38e6
    args.ke  (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*1.75e6
    args.ka  (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*3e7

    args.c   (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*3e1
    args.ce  (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*2e1
    args.ca  (6,1) double {mustBeNumeric, mustBePositive} = ones(6,1)*2e1

    args.Leq (6,1) double {mustBeNumeric} = ones(6,1)*0.056

    % Force Flexible APA
    args.xi (1,1) double {mustBeNumeric, mustBePositive} = 0.5

    % For Flexible Frame
    args.ks (1,1) double {mustBeNumeric, mustBePositive} = 235e6
    args.cs (1,1) double {mustBeNumeric, mustBePositive} = 1e1
end

Initialize Structure

actuator = struct();

Type

switch args.type
  case '2dof'
    actuator.type = 1;
  case 'flexible frame'
    actuator.type = 2;
  case 'flexible'
    actuator.type = 3;
end

Actuator/Sensor Constants

if args.Ga == 0
    switch args.type
      case '2dof'
        actuator.Ga = -30.0;
      case 'flexible frame'
        actuator.Ga = 1; % TODO
      case 'flexible'
        actuator.Ga = 23.4;
    end
else
    actuator.Ga = args.Ga; % Actuator gain [N/V]
end

if args.Gs == 0
    switch args.type
      case '2dof'
        actuator.Gs = 0.098;
      case 'flexible frame'
        actuator.Gs = 1; % TODO
      case 'flexible'
        actuator.Gs = -4674824;
    end
else
    actuator.Gs = args.Gs; % Sensor gain [V/m]
end

2DoF parameters

actuator.k  = args.k;  % [N/m]
actuator.ke = args.ke; % [N/m]
actuator.ka = args.ka; % [N/m]

actuator.c  = args.c;  % [N/(m/s)]
actuator.ce = args.ce; % [N/(m/s)]
actuator.ca = args.ca; % [N/(m/s)]

actuator.Leq = args.Leq; % [m]

Flexible frame and fully flexible

switch args.type
  case 'flexible frame'
    actuator.K = readmatrix('APA300ML_b_mat_K.CSV'); % Stiffness Matrix
    actuator.M = readmatrix('APA300ML_b_mat_M.CSV'); % Mass Matrix
    actuator.P = extractNodes('APA300ML_b_out_nodes_3D.txt'); % Node coordinates [m]
  case 'flexible'
    actuator.K = readmatrix('full_APA300ML_K.CSV'); % Stiffness Matrix
    actuator.M = readmatrix('full_APA300ML_M.CSV'); % Mass Matrix
    actuator.P = extractNodes('full_APA300ML_out_nodes_3D.txt'); % Node coordiantes [m]
end

actuator.xi = args.xi; % Damping ratio

actuator.ks = args.ks; % Stiffness of one stack [N/m]
actuator.cs = args.cs; % Damping of one stack [N/m]

7.4 generateSweepExc: Generate sweep sinus excitation

Function description

function [U_exc] = generateSweepExc(args)
% generateSweepExc - Generate a Sweep Sine excitation signal
%
% Syntax: [U_exc] = generateSweepExc(args)
%
% Inputs:
%    - args - Optinal arguments:
%        - Ts              - Sampling Time                                              - [s]
%        - f_start         - Start frequency of the sweep                               - [Hz]
%        - f_end           - End frequency of the sweep                                 - [Hz]
%        - V_mean          - Mean value of the excitation voltage                       - [V]
%        - V_exc           - Excitation Amplitude for the Sweep, could be numeric or TF - [V]
%        - t_start         - Time at which the sweep begins                             - [s]
%        - exc_duration    - Duration of the sweep                                      - [s]
%        - sweep_type      - 'logarithmic' or 'linear'                                  - [-]
%        - smooth_ends     - 'true' or 'false': smooth transition between 0 and V_mean  - [-]

Optional Parameters

arguments
    args.Ts              (1,1) double  {mustBeNumeric, mustBePositive} = 1e-4
    args.f_start         (1,1) double  {mustBeNumeric, mustBePositive} = 1
    args.f_end           (1,1) double  {mustBeNumeric, mustBePositive} = 1e3
    args.V_mean          (1,1) double  {mustBeNumeric} = 0
    args.V_exc                                         = 1
    args.t_start         (1,1) double  {mustBeNumeric, mustBeNonnegative} = 5
    args.exc_duration    (1,1) double  {mustBeNumeric, mustBePositive} = 10
    args.sweep_type            char    {mustBeMember(args.sweep_type,{'log', 'lin'})} = 'lin'
    args.smooth_ends           logical {mustBeNumericOrLogical} = true
end

Sweep Sine part

t_sweep = 0:args.Ts:args.exc_duration;

if strcmp(args.sweep_type, 'log')
    V_exc = sin(2*pi*args.f_start * args.exc_duration/log(args.f_end/args.f_start) * (exp(log(args.f_end/args.f_start)*t_sweep/args.exc_duration) - 1));
elseif strcmp(args.sweep_type, 'lin')
    V_exc = sin(2*pi*(args.f_start + (args.f_end - args.f_start)/2/args.exc_duration*t_sweep).*t_sweep);
else
    error('sweep_type should either be equal to "log" or to "lin"');
end

if isnumeric(args.V_exc)
    V_sweep = args.V_mean + args.V_exc*V_exc;
elseif isct(args.V_exc)
    if strcmp(args.sweep_type, 'log')
        V_sweep = args.V_mean + abs(squeeze(freqresp(args.V_exc, args.f_start*(args.f_end/args.f_start).^(t_sweep/args.exc_duration), 'Hz')))'.*V_exc;
    elseif strcmp(args.sweep_type, 'lin')
        V_sweep = args.V_mean + abs(squeeze(freqresp(args.V_exc, args.f_start+(args.f_end-args.f_start)/args.exc_duration*t_sweep, 'Hz')))'.*V_exc;
    end
end

Smooth Ends

if args.t_start > 0
    t_smooth_start = args.Ts:args.Ts:args.t_start;

    V_smooth_start = zeros(size(t_smooth_start));
    V_smooth_end   = zeros(size(t_smooth_start));

    if args.smooth_ends
        Vd_max = args.V_mean/(0.7*args.t_start);

        V_d = zeros(size(t_smooth_start));
        V_d(t_smooth_start < 0.2*args.t_start) = t_smooth_start(t_smooth_start < 0.2*args.t_start)*Vd_max/(0.2*args.t_start);
        V_d(t_smooth_start > 0.2*args.t_start & t_smooth_start < 0.7*args.t_start) = Vd_max;
        V_d(t_smooth_start > 0.7*args.t_start & t_smooth_start < 0.9*args.t_start) = Vd_max - (t_smooth_start(t_smooth_start > 0.7*args.t_start & t_smooth_start < 0.9*args.t_start) - 0.7*args.t_start)*Vd_max/(0.2*args.t_start);

        V_smooth_start = cumtrapz(V_d)*args.Ts;

        V_smooth_end = args.V_mean - V_smooth_start;
    end
else
    V_smooth_start = [];
    V_smooth_end = [];
end

Combine Excitation signals

V_exc = [V_smooth_start, V_sweep, V_smooth_end];
t_exc = args.Ts*[0:1:length(V_exc)-1];

U_exc = [t_exc; V_exc];

7.5 generateShapedNoise: Generate Shaped Noise excitation

Function description

function [U_exc] = generateShapedNoise(args)
% generateShapedNoise - Generate a Shaped Noise excitation signal
%
% Syntax: [U_exc] = generateShapedNoise(args)
%
% Inputs:
%    - args - Optinal arguments:
%        - Ts              - Sampling Time                                              - [s]
%        - V_mean          - Mean value of the excitation voltage                       - [V]
%        - V_exc           - Excitation Amplitude, could be numeric or TF               - [V rms]
%        - t_start         - Time at which the noise begins                             - [s]
%        - exc_duration    - Duration of the noise                                      - [s]
%        - smooth_ends     - 'true' or 'false': smooth transition between 0 and V_mean  - [-]

Optional Parameters

arguments
    args.Ts              (1,1) double  {mustBeNumeric, mustBePositive} = 1e-4
    args.V_mean          (1,1) double  {mustBeNumeric} = 0
    args.V_exc                                         = 1
    args.t_start         (1,1) double  {mustBeNumeric, mustBePositive} = 5
    args.exc_duration    (1,1) double  {mustBeNumeric, mustBePositive} = 10
    args.smooth_ends           logical {mustBeNumericOrLogical} = true
end

Shaped Noise

t_noise = 0:args.Ts:args.exc_duration;


if isnumeric(args.V_exc)
    V_noise = args.V_mean + args.V_exc*sqrt(1/args.Ts/2)*randn(length(t_noise), 1)';
elseif isct(args.V_exc)
    V_noise = args.V_mean + lsim(args.V_exc, sqrt(1/args.Ts/2)*randn(length(t_noise), 1), t_noise)';
end

Smooth Ends

t_smooth_start = args.Ts:args.Ts:args.t_start;

V_smooth_start = zeros(size(t_smooth_start));
V_smooth_end   = zeros(size(t_smooth_start));

if args.smooth_ends
    Vd_max = args.V_mean/(0.7*args.t_start);

    V_d = zeros(size(t_smooth_start));
    V_d(t_smooth_start < 0.2*args.t_start) = t_smooth_start(t_smooth_start < 0.2*args.t_start)*Vd_max/(0.2*args.t_start);
    V_d(t_smooth_start > 0.2*args.t_start & t_smooth_start < 0.7*args.t_start) = Vd_max;
    V_d(t_smooth_start > 0.7*args.t_start & t_smooth_start < 0.9*args.t_start) = Vd_max - (t_smooth_start(t_smooth_start > 0.7*args.t_start & t_smooth_start < 0.9*args.t_start) - 0.7*args.t_start)*Vd_max/(0.2*args.t_start);

    V_smooth_start = cumtrapz(V_d)*args.Ts;

    V_smooth_end = args.V_mean - V_smooth_start;
end

Combine Excitation signals

V_exc = [V_smooth_start, V_noise, V_smooth_end];
t_exc = args.Ts*[0:1:length(V_exc)-1];

U_exc = [t_exc; V_exc];

7.6 generateSinIncreasingAmpl: Generate Sinus with increasing amplitude

Function description

function [U_exc] = generateSinIncreasingAmpl(args)
% generateSinIncreasingAmpl - Generate Sinus with increasing amplitude
%
% Syntax: [U_exc] = generateSinIncreasingAmpl(args)
%
% Inputs:
%    - args - Optinal arguments:
%        - Ts              - Sampling Time                                              - [s]
%        - V_mean          - Mean value of the excitation voltage                       - [V]
%        - sin_ampls       - Excitation Amplitudes                                      - [V]
%        - sin_freq        - Excitation Frequency                                       - [Hz]
%        - sin_num         - Number of period for each amplitude                        - [-]
%        - t_start         - Time at which the excitation begins                        - [s]
%        - smooth_ends     - 'true' or 'false': smooth transition between 0 and V_mean  - [-]

Optional Parameters

arguments
    args.Ts              (1,1) double  {mustBeNumeric, mustBePositive} = 1e-4
    args.V_mean          (1,1) double  {mustBeNumeric} = 0
    args.sin_ampls             double  {mustBeNumeric, mustBePositive} = [0.1, 0.2, 0.3]
    args.sin_period      (1,1) double  {mustBeNumeric, mustBePositive} = 1
    args.sin_num         (1,1) double  {mustBeNumeric, mustBePositive, mustBeInteger} = 3
    args.t_start         (1,1) double  {mustBeNumeric, mustBePositive} = 5
    args.smooth_ends           logical {mustBeNumericOrLogical} = true
end

Sinus excitation

t_noise = 0:args.Ts:args.sin_period*args.sin_num;
sin_exc = [];

for sin_ampl = args.sin_ampls
    sin_exc = [sin_exc, args.V_mean + sin_ampl*sin(2*pi/args.sin_period*t_noise)];
end

Smooth Ends

t_smooth_start = args.Ts:args.Ts:args.t_start;

V_smooth_start = zeros(size(t_smooth_start));
V_smooth_end   = zeros(size(t_smooth_start));

if args.smooth_ends
    Vd_max = args.V_mean/(0.7*args.t_start);

    V_d = zeros(size(t_smooth_start));
    V_d(t_smooth_start < 0.2*args.t_start) = t_smooth_start(t_smooth_start < 0.2*args.t_start)*Vd_max/(0.2*args.t_start);
    V_d(t_smooth_start > 0.2*args.t_start & t_smooth_start < 0.7*args.t_start) = Vd_max;
    V_d(t_smooth_start > 0.7*args.t_start & t_smooth_start < 0.9*args.t_start) = Vd_max - (t_smooth_start(t_smooth_start > 0.7*args.t_start & t_smooth_start < 0.9*args.t_start) - 0.7*args.t_start)*Vd_max/(0.2*args.t_start);

    V_smooth_start = cumtrapz(V_d)*args.Ts;

    V_smooth_end = args.V_mean - V_smooth_start;
end

Combine Excitation signals

V_exc = [V_smooth_start, sin_exc, V_smooth_end];
t_exc = args.Ts*[0:1:length(V_exc)-1];

U_exc = [t_exc; V_exc];

Bibliography

Souleille, Adrien, Thibault Lampert, V Lafarga, Sylvain Hellegouarch, Alan Rondineau, Gonçalo Rodrigues, and Christophe Collette. 2018. “A Concept of Active Mount for Space Applications.” CEAS Space Journal 10 (2). Springer:157–65.

Author: Dehaeze Thomas

Created: 2021-06-09 mer. 19:01