Test Bench - Amplified Piezoelectric Actuator
Table of Contents
1 Experimental Setup
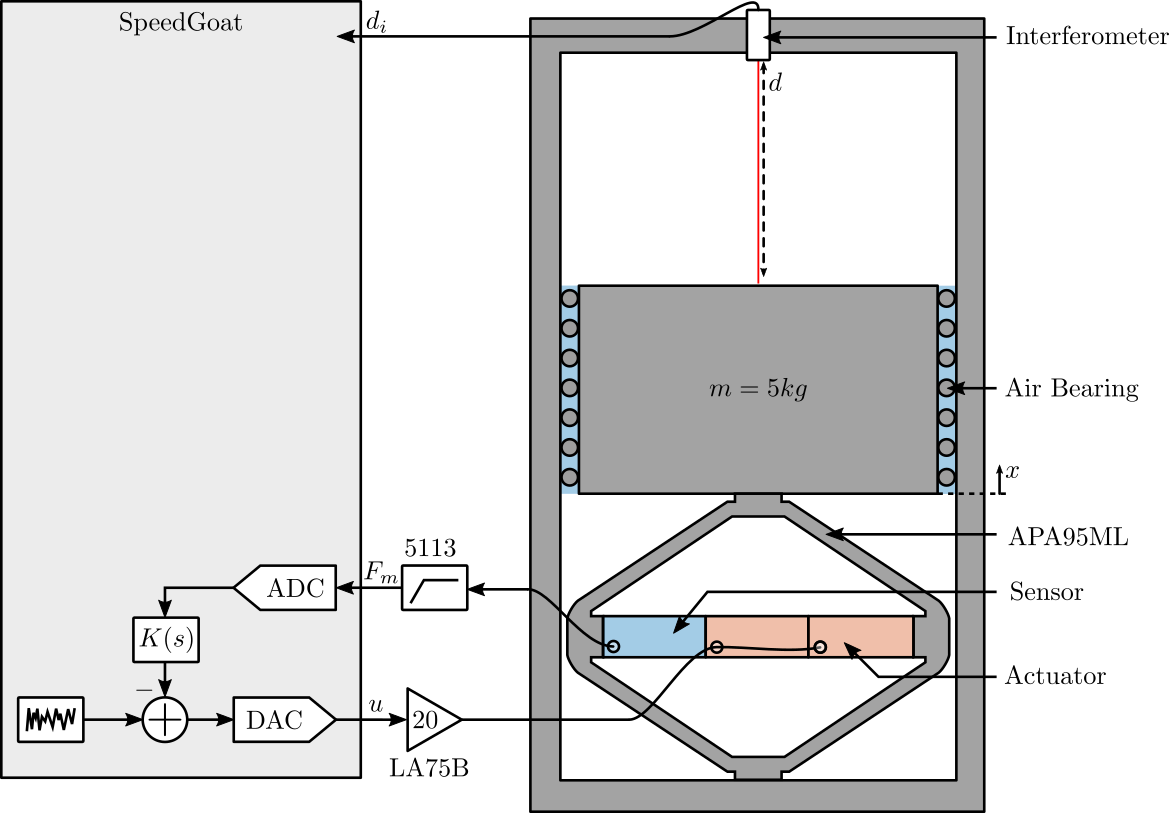
A schematic of the test-bench is shown in Figure 1.
A mass can be vertically moved using the amplified piezoelectric actuator (APA95ML). The displacement of the mass (relative to the mechanical frame) is measured by the interferometer.
The APA95ML has three stacks that can be used as actuator or as sensors.
Pictures of the test bench are shown in Figure 2 and 3.
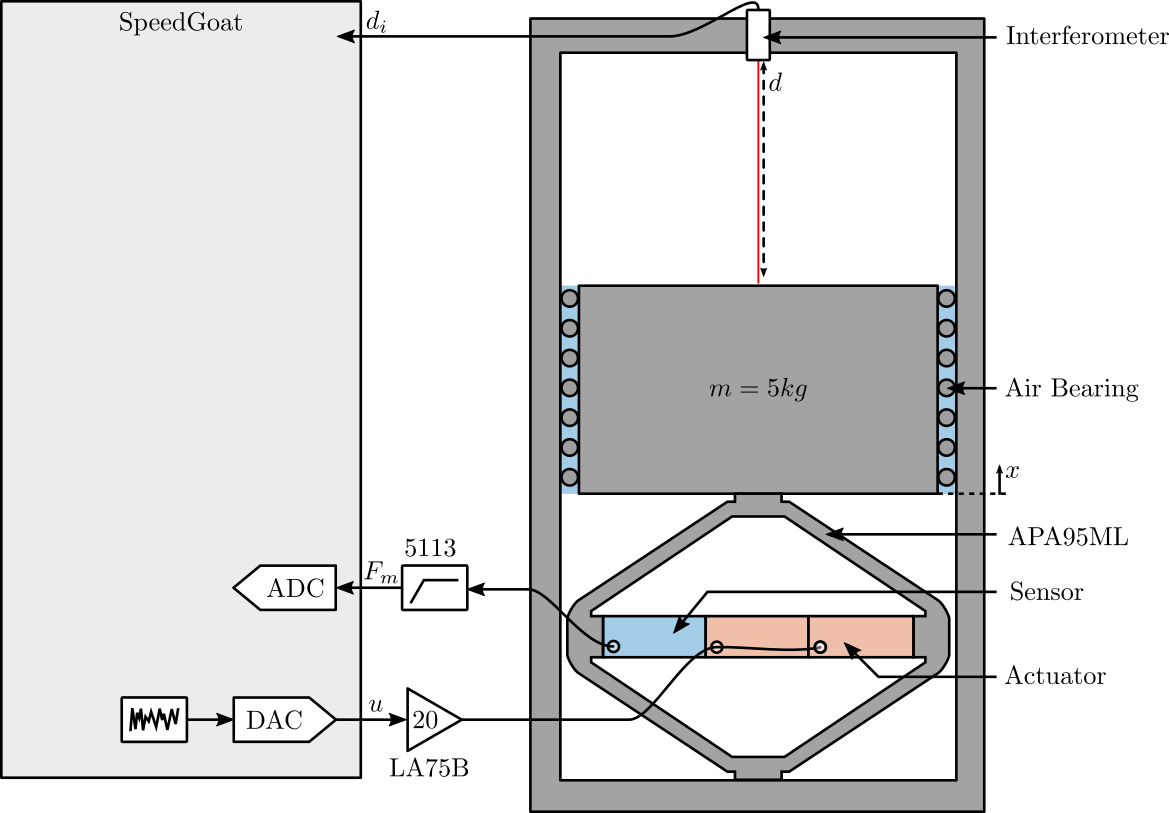
Figure 1: Schematic of the Setup

Figure 2: Picture of the Setup

Figure 3: Zoom on the APA
2 Estimation of electrical/mechanical relationships
In order to correctly model the piezoelectric actuator, we need to determine:
- \(g_a\): the ratio of the generated force \(F_a\) to the supply voltage \(V_a\) across the piezoelectric stack
- \(g_s\): the ratio of the generated voltage \(V_s\) across the piezoelectric stack when subject to a strain \(\Delta h\)
We estimate \(g_a\) and \(g_s\) using different approaches:
2.1 Estimation from Data-sheet
The stack parameters taken from the data-sheet are shown in Table 1.
| Parameter | Unit | Value |
|---|---|---|
| Nominal Stroke | \(\mu m\) | 20 |
| Blocked force | \(N\) | 4700 |
| Stiffness | \(N/\mu m\) | 235 |
| Voltage Range | \(V\) | -20..150 |
| Capacitance | \(\mu F\) | 4.4 |
| Length | \(mm\) | 20 |
| Stack Area | \(mm^2\) | 10x10 |
Let’s compute the generated force
The stroke is \(L_{\max} = 20\mu m\) for a voltage range of \(V_{\max} = 170 V\). Furthermore, the stiffness is \(k_a = 235 \cdot 10^6 N/m\).
The relation between the applied voltage and the generated force can be estimated as follows:
\begin{equation} g_a = k_a \frac{L_{\max}}{V_{\max}} \end{equation}ka = 235e6; % [N/m] Lmax = 20e-6; % [m] Vmax = 170; % [V]
ka*Lmax/Vmax % [N/V]
27.647
From the parameters of the stack, it seems not possible to estimate the relation between the strain and the generated voltage.
2.2 Estimation from Piezoelectric parameters
In order to make the conversion from applied voltage to generated force or from the strain to the generated voltage, we need to defined some parameters corresponding to the piezoelectric material:
d33 = 300e-12; % Strain constant [m/V] n = 80; % Number of layers per stack ka = 235e6; % Stack stiffness [N/m]
The ratio of the developed force to applied voltage is:
\begin{equation} \label{org8300de8} F_a = g_a V_a, \quad g_a = d_{33} n k_a \end{equation}where:
- \(F_a\): developed force in [N]
- \(n\): number of layers of the actuator stack
- \(d_{33}\): strain constant in [m/V]
- \(k_a\): actuator stack stiffness in [N/m]
- \(V_a\): applied voltage in [V]
If we take the numerical values, we obtain:
ga = d33*n*ka; % [N/V]
ga = 5.6 [N/V]
From (Fleming and Leang 2014) (page 123), the relation between relative displacement of the sensor stack and generated voltage is:
\begin{equation} \label{org312083f} V_s = \frac{d_{33}}{\epsilon^T s^D n} \Delta h \end{equation}where:
- \(V_s\): measured voltage in [V]
- \(d_{33}\): strain constant in [m/V]
- \(\epsilon^T\): permittivity under constant stress in [F/m]
- \(s^D\): elastic compliance under constant electric displacement in [m^2/N]
- \(n\): number of layers of the sensor stack
- \(\Delta h\): relative displacement in [m]
If we take the numerical values, we obtain:
d33 = 300e-12; % Strain constant [m/V] n = 80; % Number of layers per stack eT = 5.3e-9; % Permittivity under constant stress [F/m] sD = 2e-11; % Compliance under constant electric displacement [m2/N]
gs = d33/(eT*sD*n); % [V/m]
gs = 35.4 [V/um]
2.3 Estimation from Experiment
The idea here is to obtain the parameters \(g_a\) and \(g_s\) from the comparison of an experimental identification and the identification using Simscape.
Using the experimental identification, we can easily obtain the gain from the applied voltage to the generated displacement, but not to the generated force. However, from the Simscape model, we can easily have the link from the generated force to the displacement, them we can computed \(g_a\).
Similarly, it is fairly easy to experimentally obtain the gain from the stack displacement to the generated voltage across the stack. To link that to the strain of the sensor stack, the simscape model is used.
2.3.1 From actuator voltage \(V_a\) to actuator force \(F_a\)
The data from the identification test is loaded.
load('apa95ml_5kg_Amp_E505.mat', 't', 'um', 'y'); % Any offset value is removed: um = detrend(um, 0); % Amplifier Input Voltage [V] y = detrend(y , 0); % Mass displacement [m]
Now we add a factor 10 to take into account the gain of the voltage amplifier and thus obtain the voltage across the piezoelectric stack.
um = 10*um; % Stack Actuator Input Voltage [V]
Then, the transfer function from the stack voltage to the vertical displacement is computed.
Ts = t(end)/(length(t)-1); Fs = 1/Ts; win = hanning(ceil(1*Fs)); [tf_est, f] = tfestimate(um, y, win, [], [], 1/Ts);
The gain from input voltage of the stack to the vertical displacement is determined:
g_d_Va = 4e-7; % [m/V]
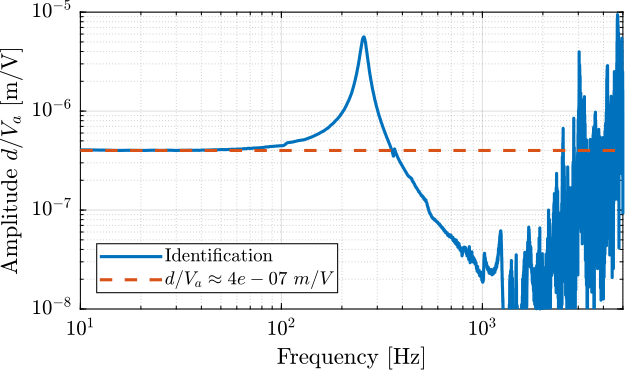
Figure 4: Transfer function from actuator stack voltage \(V_a\) to vertical displacement of the mass \(d\)
Then, the transfer function from forces applied by the stack actuator to the vertical displacement of the mass is identified from the Simscape model.
m = 5.5; %% Name of the Simulink File mdl = 'piezo_amplified_3d'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Fa'], 1, 'openinput'); io_i = io_i + 1; % Actuator Force [N] io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1; % Vertical Displacement [m] Gd = linearize(mdl, io);
The DC gain the the identified dynamics
g_d_Fa = abs(dcgain(Gd)); % [m/N]
G_d_Fa = 1.2e-08 [m/N]
And finally, the gain \(g_a\) from the the actuator voltage \(V_a\) to the generated force \(F_a\) can be computed:
\begin{equation} g_a = \frac{F_a}{V_a} = \frac{F_a}{d} \frac{d}{V_a} \end{equation}ga = g_d_Va/g_d_Fa;
ga = 33.7 [N/V]
The obtained comparison between the Simscape model and the identified dynamics is shown in Figure 5.
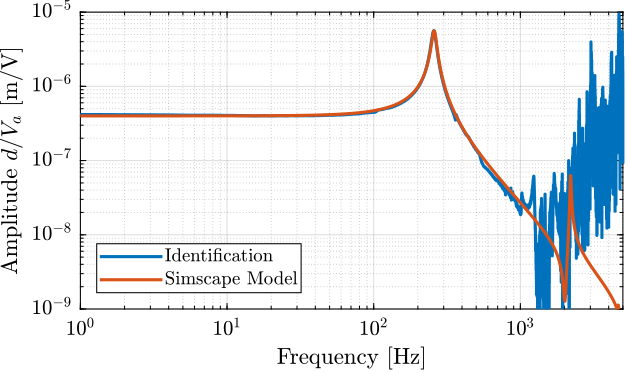
Figure 5: Comparison of the identified transfer function between actuator voltage \(V_a\) and vertical mass displacement \(d\)
2.3.2 From stack strain \(\Delta h\) to generated voltage \(V_s\)
Now, the gain from the stack strain \(\Delta h\) to the generated voltage \(V_s\) is estimated.
We can determine the gain from actuator voltage \(V_a\) to sensor voltage \(V_s\) thanks to the identification. Using the simscape model, we can have the transfer function from the actuator voltage \(V_a\) (using the previously estimated gain \(g_a\)) to the sensor stack strain \(\Delta h\).
Finally, using these two values, we can compute the gain \(g_s\) from the stack strain \(\Delta h\) to the generated Voltage \(V_s\).
Identification data is loaded.
load('apa95ml_5kg_2a_1s.mat', 't', 'u', 'v'); u = detrend(u, 0); % Input Voltage of the Amplifier [V] v = detrend(v, 0); % Voltage accross the stack sensor [V]
Here, an amplifier with a gain of 20 is used.
u = 20*u; % Input Voltage of the Amplifier [V]
Then, the transfer function from \(V_a\) to \(V_s\) is identified and its DC gain is estimated (Figure 6).
Ts = t(end)/(length(t)-1); Fs = 1/Ts; win = hann(ceil(10/Ts)); [tf_est, f] = tfestimate(u, v, win, [], [], 1/Ts);
g_Vs_Va = 0.022; % [V/V]
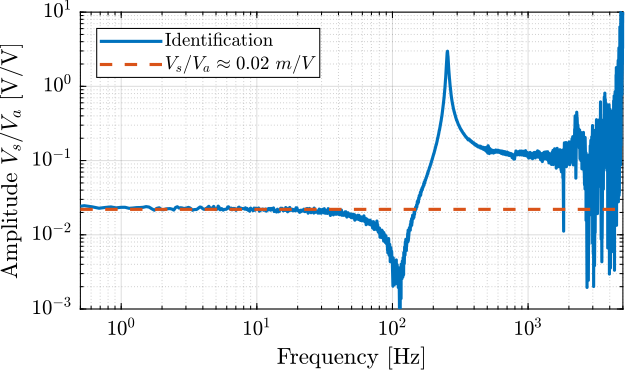
Figure 6: Transfer function from actuator stack voltage \(V_a\) to sensor stack voltage \(V_s\)
Now the transfer function from the actuator stack voltage to the sensor stack strain is estimated using the Simscape model.
m = 5.5; %% Name of the Simulink File mdl = 'piezo_amplified_3d'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Va'], 1, 'openinput'); io_i = io_i + 1; % Actuator Voltage [V] io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Sensor Stack displacement [m] Gf = linearize(mdl, io);
The gain from the actuator stack voltage to the sensor stack strain is estimated below.
G_dh_Va = abs(dcgain(Gf));
G_dh_Va = 6.2e-09 [m/V]
And finally, the gain \(g_s\) from the sensor stack strain to the generated voltage can be estimated:
\begin{equation} g_s = \frac{V_s}{\Delta h} = \frac{V_s}{V_a} \frac{V_a}{\Delta h} \end{equation}gs = g_Vs_Va/G_dh_Va; % [V/m]
gs = 3.5 [V/um]
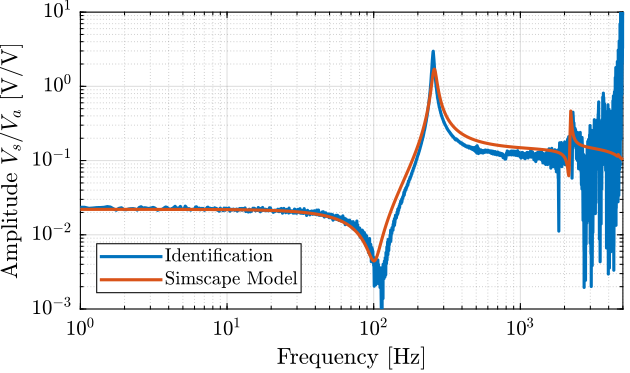
Figure 7: Comparison of the identified transfer function between actuator voltage \(V_a\) and sensor stack voltage
2.4 Conclusion
The obtained parameters \(g_a\) and \(g_s\) are not consistent between the different methods.
The one using the experimental data are saved and further used.
save('./matlab/mat/apa95ml_params.mat', 'ga', 'gs');
3 Simscape model of the test-bench
The idea here is to model the test-bench using Simscape.
Whereas the suspended mass and metrology frame can be considered as rigid bodies in the frequency range of interest, the Amplified Piezoelectric Actuator (APA) is flexible.
To model the APA, a Finite Element Model (FEM) is used (Figure 8) and imported into Simscape.

Figure 8: Finite Element Model of the APA95ML
3.1 Import Mass Matrix, Stiffness Matrix, and Interface Nodes Coordinates
We first extract the stiffness and mass matrices.
K = readmatrix('APA95ML_K.CSV'); M = readmatrix('APA95ML_M.CSV');
| 300000000.0 | -1000.0 | -30000.0 | -40.0 | 70000.0 | 300.0 | 20000000.0 | -30.0 | -5000.0 | 5 |
| -1000.0 | 50000000.0 | -7000.0 | 800000.0 | -20.0 | 300.0 | 3000.0 | 5000000.0 | 400.0 | -40000.0 |
| -30000.0 | -7000.0 | 100000000.0 | -200.0 | -60.0 | 70.0 | 3000.0 | 3000.0 | -8000000.0 | -30.0 |
| -40.0 | 800000.0 | -200.0 | 20000.0 | -0.4 | 4 | 30.0 | 40000.0 | 7 | -300.0 |
| 70000.0 | -20.0 | -60.0 | -0.4 | 3000.0 | 1 | -6000.0 | 10.0 | 8 | -0.1 |
| 300.0 | 300.0 | 70.0 | 4 | 1 | 40000.0 | -10.0 | -10.0 | 30.0 | 0.1 |
| 20000000.0 | 3000.0 | 3000.0 | 30.0 | -6000.0 | -10.0 | 300000000.0 | 2000.0 | 9000.0 | -100.0 |
| -30.0 | 5000000.0 | 3000.0 | 40000.0 | 10.0 | -10.0 | 2000.0 | 50000000.0 | -3000.0 | -800000.0 |
| -5000.0 | 400.0 | -8000000.0 | 7 | 8 | 30.0 | 9000.0 | -3000.0 | 100000000.0 | 100.0 |
| 5 | -40000.0 | -30.0 | -300.0 | -0.1 | 0.1 | -100.0 | -800000.0 | 100.0 | 20000.0 |
| 0.03 | 7e-08 | 2e-06 | -3e-09 | -0.0002 | -6e-08 | -0.001 | 8e-07 | 6e-07 | -8e-09 |
| 7e-08 | 0.02 | -1e-06 | 9e-05 | -3e-09 | -4e-09 | -1e-06 | -0.0006 | -4e-08 | 5e-06 |
| 2e-06 | -1e-06 | 0.02 | -3e-08 | -4e-08 | 1e-08 | 1e-07 | -2e-07 | 0.0003 | 1e-09 |
| -3e-09 | 9e-05 | -3e-08 | 1e-06 | -3e-11 | -3e-13 | -7e-09 | -5e-06 | -3e-10 | 3e-08 |
| -0.0002 | -3e-09 | -4e-08 | -3e-11 | 2e-06 | 6e-10 | 2e-06 | -7e-09 | -2e-09 | 7e-11 |
| -6e-08 | -4e-09 | 1e-08 | -3e-13 | 6e-10 | 1e-06 | 1e-08 | 3e-09 | -2e-09 | 2e-13 |
| -0.001 | -1e-06 | 1e-07 | -7e-09 | 2e-06 | 1e-08 | 0.03 | 4e-08 | -2e-06 | 8e-09 |
| 8e-07 | -0.0006 | -2e-07 | -5e-06 | -7e-09 | 3e-09 | 4e-08 | 0.02 | -9e-07 | -9e-05 |
| 6e-07 | -4e-08 | 0.0003 | -3e-10 | -2e-09 | -2e-09 | -2e-06 | -9e-07 | 0.02 | 2e-08 |
| -8e-09 | 5e-06 | 1e-09 | 3e-08 | 7e-11 | 2e-13 | 8e-09 | -9e-05 | 2e-08 | 1e-06 |
Then, we extract the coordinates of the interface nodes.
[int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('APA95ML_out_nodes_3D.txt');
The interface nodes are shown in Figure 9 and their coordinates are listed in Table 4.
| Total number of Nodes | 7 |
| Number of interface Nodes | 7 |
| Number of Modes | 6 |
| Size of M and K matrices | 48 |
| Node i | Node Number | x [m] | y [m] | z [m] |
|---|---|---|---|---|
| 1.0 | 40467.0 | 0.0 | 0.0 | 0.029997 |
| 2.0 | 40469.0 | 0.0 | 0.0 | -0.029997 |
| 3.0 | 40470.0 | -0.035 | 0.0 | 0.0 |
| 4.0 | 40475.0 | -0.015 | 0.0 | 0.0 |
| 5.0 | 40476.0 | -0.005 | 0.0 | 0.0 |
| 6.0 | 40477.0 | 0.015 | 0.0 | 0.0 |
| 7.0 | 40478.0 | 0.035 | 0.0 | 0.0 |
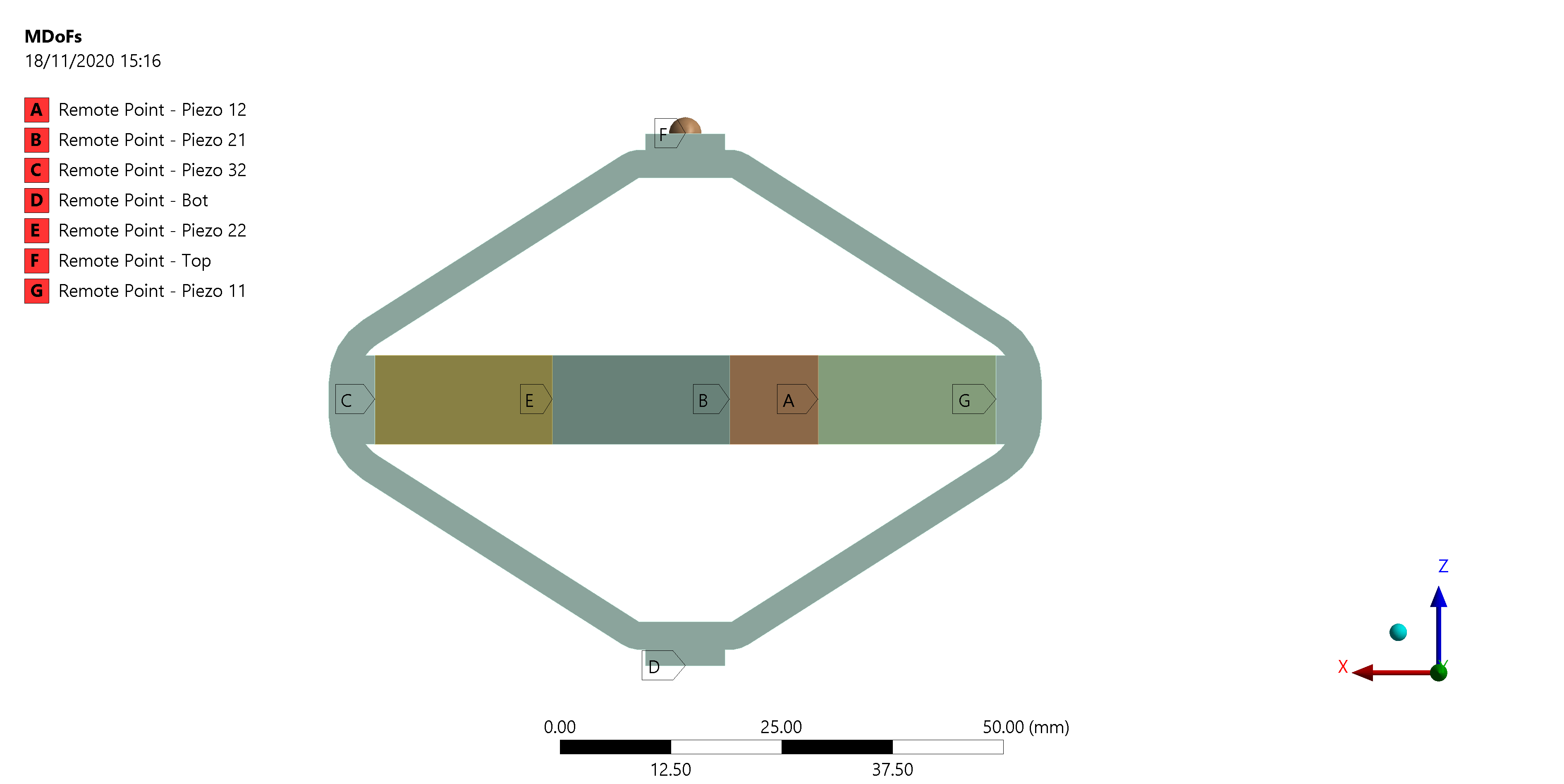
Figure 9: Interface Nodes chosen for the APA95ML
Using K, M and int_xyz, we can use the Reduced Order Flexible Solid simscape block.
3.2 Simscape Model
The flexible element is imported using the Reduced Order Flexible Solid Simscape block.
To model the actuator, an Internal Force block is added between the nodes 3 and 12.
A Relative Motion Sensor block is added between the nodes 1 and 2 to measure the displacement and the amplified piezo.
One mass is fixed at one end of the piezo-electric stack actuator, the other end is fixed to the world frame.
m = 5;
3.3 Dynamics from Actuator Voltage to Vertical Mass Displacement
The identified dynamics is shown in Figure 10.
%% Name of the Simulink File mdl = 'piezo_amplified_3d'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Va'], 1, 'openinput'); io_i = io_i + 1; % Actuator Voltage [V] io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1; % Vertical Displacement [m] Ghm = -linearize(mdl, io);
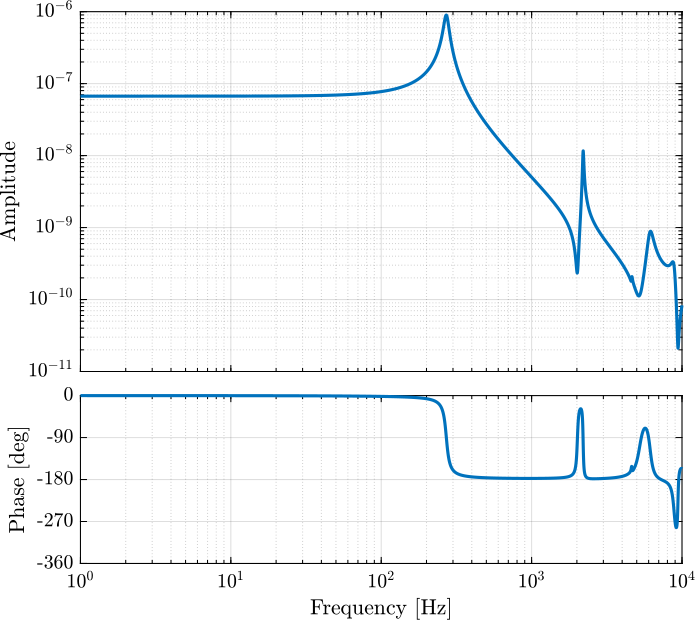
Figure 10: Dynamics from \(F\) to \(d\) without a payload and with a 5kg payload
3.4 Dynamics from Actuator Voltage to Force Sensor Voltage
The obtained dynamics is shown in Figure 11.
%% Name of the Simulink File mdl = 'piezo_amplified_3d'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Va'], 1, 'openinput'); io_i = io_i + 1; % Voltage Actuator [V] io(io_i) = linio([mdl, '/Vs'], 1, 'openoutput'); io_i = io_i + 1; % Sensor Voltage [V] Gfm = linearize(mdl, io);

Figure 11: Dynamics from \(F\) to \(F_m\) for \(m=0\) and \(m = 10kg\)
3.5 Save Data for further use
save('matlab/mat/fem_simscape_models.mat', 'Ghm', 'Gfm')
save('mat/fem_simscape_models.mat', 'Ghm', 'Gfm')
4 Huddle Test
4.1 Time Domain Data
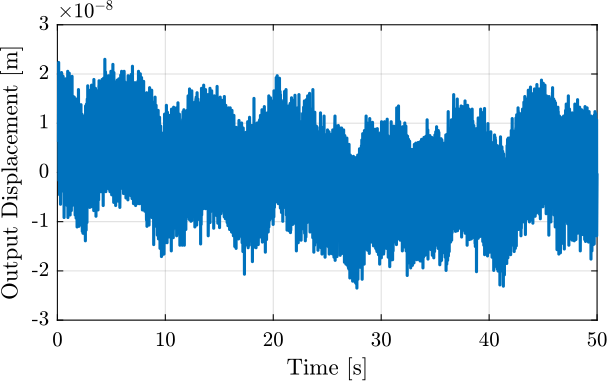
Figure 12: Measurement of the Mass displacement during Huddle Test
4.2 PSD of Measurement Noise
Ts = t(end)/(length(t)-1); Fs = 1/Ts; win = hanning(ceil(1*Fs));
[pxx, f] = pwelch(y(1000:end), win, [], [], Fs);
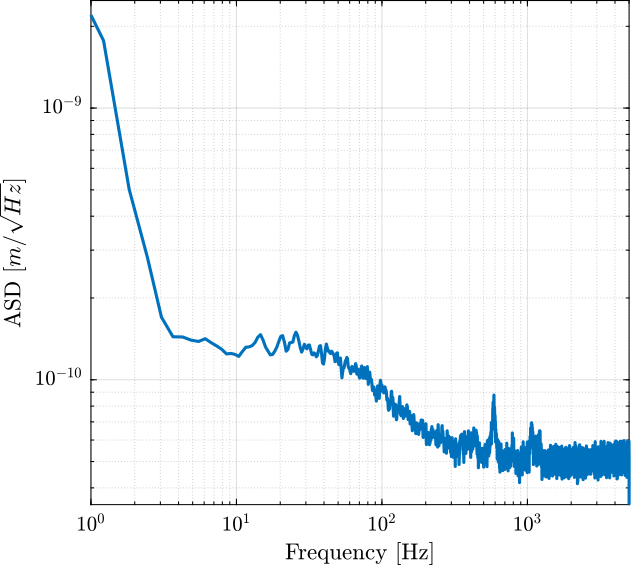
Figure 13: Amplitude Spectral Density of the Displacement during Huddle Test
5 Identification of the dynamics from actuator to displacement
[ ]List of equipment[ ]Schematic[ ]Problem of matching between the models? (there is a factor 10)
E505 with gain of 10.
5.1 Load Data
The data from the “noise test” and the identification test are loaded.
ht = load('huddle_test.mat', 't', 'u', 'y'); load('apa95ml_5kg_Amp_E505.mat', 't', 'um', 'y');
Any offset value is removed:
um = detrend(um, 0); % Input Voltage [V] y = detrend(y , 0); % Mass displacement [m] ht.u = detrend(ht.u, 0); ht.y = detrend(ht.y, 0);
Now we add a factor 10 to take into account the gain of the voltage amplifier.
um = 10*um; ht.u = 10*ht.u;
5.2 Comparison of the PSD with Huddle Test
Ts = t(end)/(length(t)-1); Fs = 1/Ts; win = hanning(ceil(1*Fs));
[pxx, f] = pwelch(y, win, [], [], Fs);
[pht, ~] = pwelch(ht.y, win, [], [], Fs);

Figure 14: Comparison of the ASD for the identification test and the huddle test
5.3 Compute TF estimate and Coherence
[tf_est, f] = tfestimate(um, -y, win, [], [], 1/Ts); [co_est, ~] = mscohere( um, -y, win, [], [], 1/Ts);
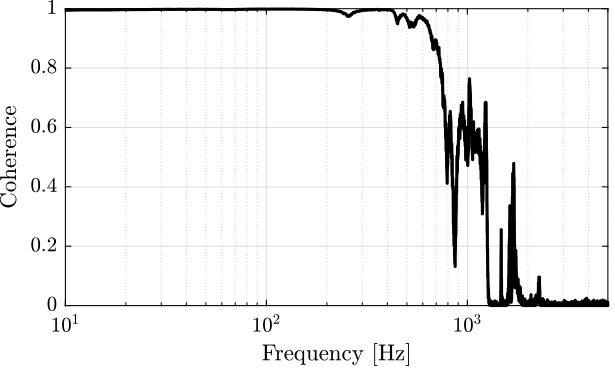
Figure 15: Coherence
Comparison with the FEM model
load('mat/fem_simscape_models.mat', 'Ghm');

Figure 16: Comparison of the identified transfer function and the one estimated from the FE model
6 Identification of the dynamics from actuator to force sensor
Two measurements are performed:
- Speedgoat DAC => Voltage Amplifier (x20) => 1 Piezo Stack => … => 2 Stacks as Force Sensor (parallel) => Speedgoat ADC
- Speedgoat DAC => Voltage Amplifier (x20) => 2 Piezo Stacks (parallel) => … => 1 Stack as Force Sensor => Speedgoat ADC
The obtained dynamics from force actuator to force sensor are compare with the FEM model.
The data are loaded:
load('apa95ml_5kg_2a_1s.mat', 't', 'u', 'v');
u = detrend(u, 0); v = detrend(v, 0);
u = 20*u;
Let’s use the amplifier gain to obtain the true voltage applied to the actuator stack(s)
The parameters of the piezoelectric stacks are defined below:
d33 = 3e-10; % Strain constant [m/V] n = 80; % Number of layers per stack eT = 1.6e-8; % Permittivity under constant stress [F/m] sD = 2e-11; % Elastic compliance under constant electric displacement [m2/N] ka = 235e6; % Stack stiffness [N/m]
From the FEM, we construct the transfer function from DAC voltage to ADC voltage.
Gfem_aa_s = exp(-s/1e4)*20*(2*d33*n*ka)*(G(3,1)+G(3,2))*d33/(eT*sD*n); Gfem_a_ss = exp(-s/1e4)*20*( d33*n*ka)*(G(3,1)+G(2,1))*d33/(eT*sD*n);
Gfem_aa_s = exp(-s/1e4)*20*(2*d33*n*ka)*Gfm*d33/(eT*sD*n); Gfem_a_ss = exp(-s/1e4)*20*( d33*n*ka)*Gfm*d33/(eT*sD*n);
The transfer function from input voltage to output voltage are computed and shown in Figure 17.
Ts = t(end)/(length(t)-1); Fs = 1/Ts; win = hann(ceil(10/Ts)); [tf_est, f] = tfestimate(u, v, win, [], [], 1/Ts); [coh, ~] = mscohere( u, v, win, [], [], 1/Ts);
load('mat/fem_simscape_models.mat', 'Gfm');
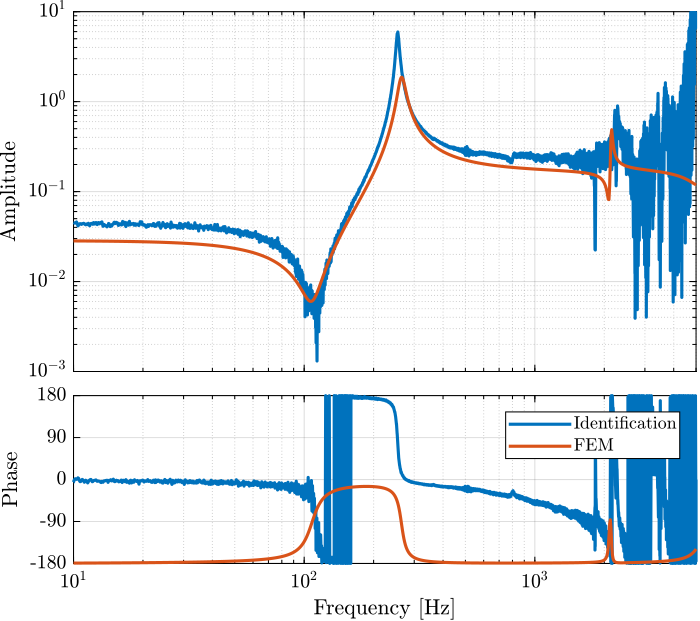
Figure 17: Comparison of the identified dynamics from voltage output to voltage input and the FEM
6.1 System Identification
w_z = 2*pi*111; % Zeros frequency [rad/s] w_p = 2*pi*255; % Pole frequency [rad/s] xi_z = 0.05; xi_p = 0.015; G_inf = 0.1; Gi = G_inf*(s^2 - 2*xi_z*w_z*s + w_z^2)/(s^2 + 2*xi_p*w_p*s + w_p^2);
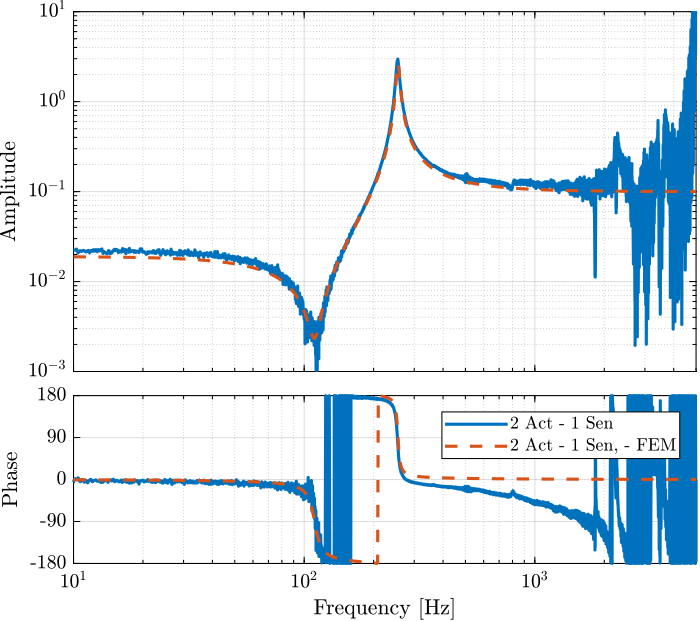
Figure 18: Identification of the IFF plant
6.2 Integral Force Feedback
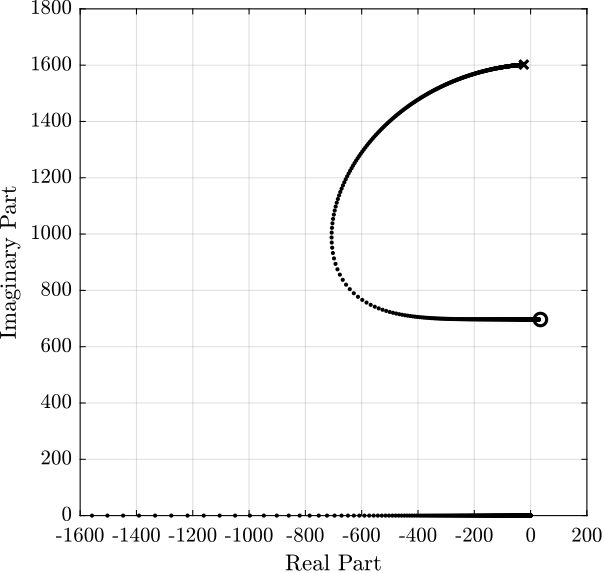
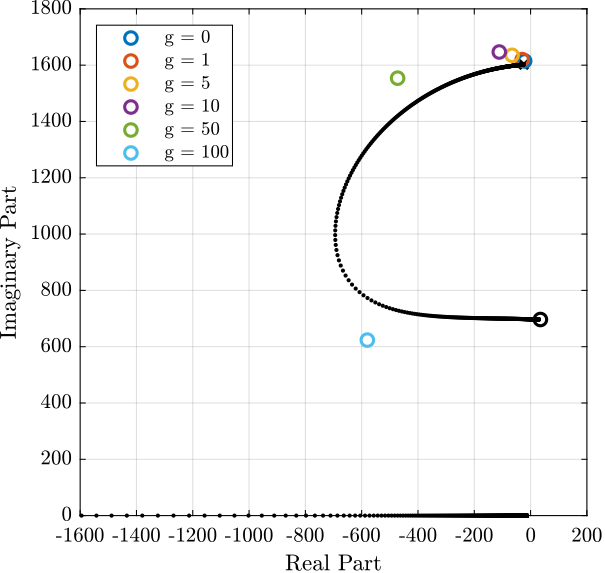
Figure 19: Root Locus for IFF
7 Integral Force Feedback
7.1 First tests with few gains
iff_g10 = load('apa95ml_iff_g10_res.mat', 'u', 't', 'y', 'v'); iff_g100 = load('apa95ml_iff_g100_res.mat', 'u', 't', 'y', 'v'); iff_of = load('apa95ml_iff_off_res.mat', 'u', 't', 'y', 'v');
Ts = 1e-4; win = hann(ceil(10/Ts)); [tf_iff_g10, f] = tfestimate(iff_g10.u, iff_g10.y, win, [], [], 1/Ts); [co_iff_g10, ~] = mscohere(iff_g10.u, iff_g10.y, win, [], [], 1/Ts); [tf_iff_g100, ~] = tfestimate(iff_g100.u, iff_g100.y, win, [], [], 1/Ts); [co_iff_g100, ~] = mscohere(iff_g100.u, iff_g100.y, win, [], [], 1/Ts); [tf_iff_of, ~] = tfestimate(iff_of.u, iff_of.y, win, [], [], 1/Ts); [co_iff_of, ~] = mscohere(iff_of.u, iff_of.y, win, [], [], 1/Ts);
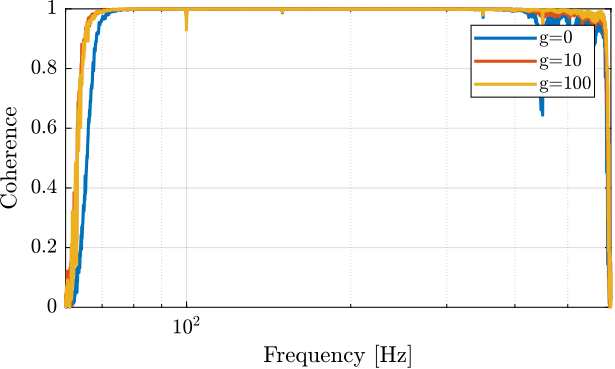
Figure 21: Coherence

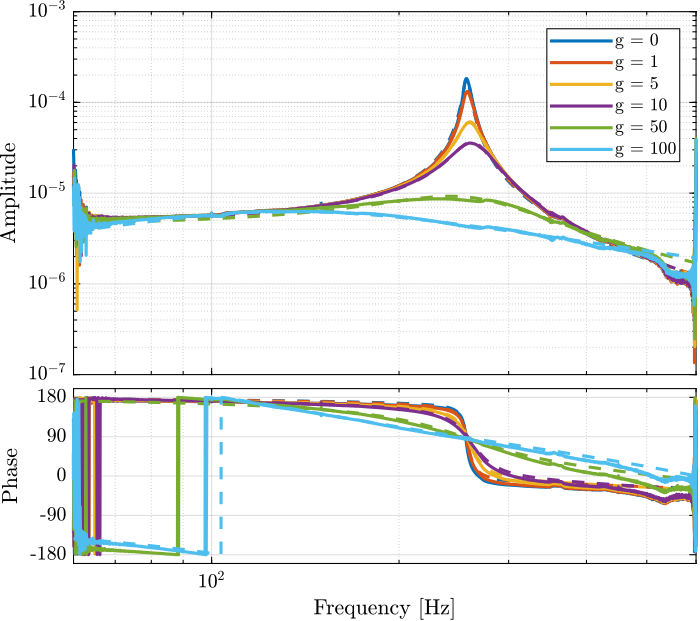
Figure 22: Bode plot for different values of IFF gain
7.2 Second test with many Gains
load('apa95ml_iff_test.mat', 'results');
Ts = 1e-4; win = hann(ceil(10/Ts));
tf_iff = {zeros(1, length(results))};
co_iff = {zeros(1, length(results))};
g_iff = [0, 1, 5, 10, 50, 100];
for i=1:length(results)
[tf_est, f] = tfestimate(results{i}.u, results{i}.y, win, [], [], 1/Ts);
[co_est, ~] = mscohere(results{i}.u, results{i}.y, win, [], [], 1/Ts);
tf_iff(i) = {tf_est};
co_iff(i) = {co_est};
end
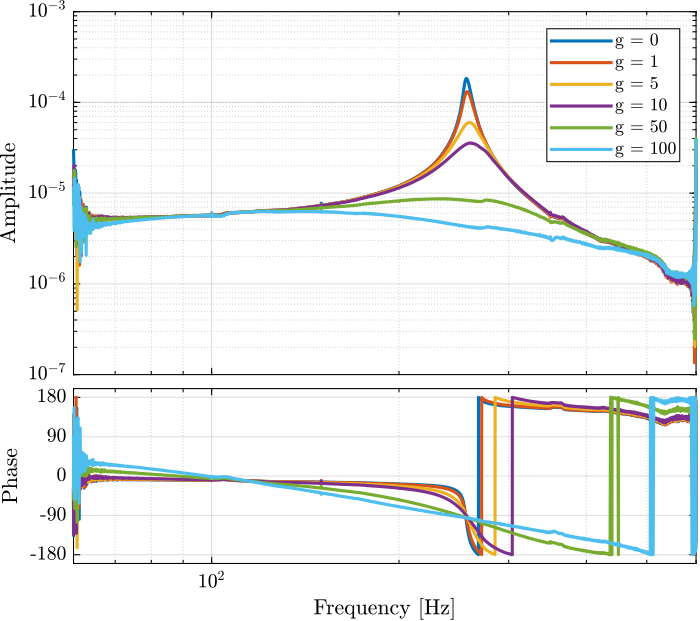
G_id = {zeros(1,length(results))};
f_start = 70; % [Hz]
f_end = 500; % [Hz]
for i = 1:length(results)
tf_id = tf_iff{i}(sum(f<f_start):length(f)-sum(f>f_end));
f_id = f(sum(f<f_start):length(f)-sum(f>f_end));
gfr = idfrd(tf_id, 2*pi*f_id, Ts);
G_id(i) = {procest(gfr,'P2UDZ')};
end