Test Bench - Amplified Piezoelectric Actuator
Table of Contents
1 Experimental Setup
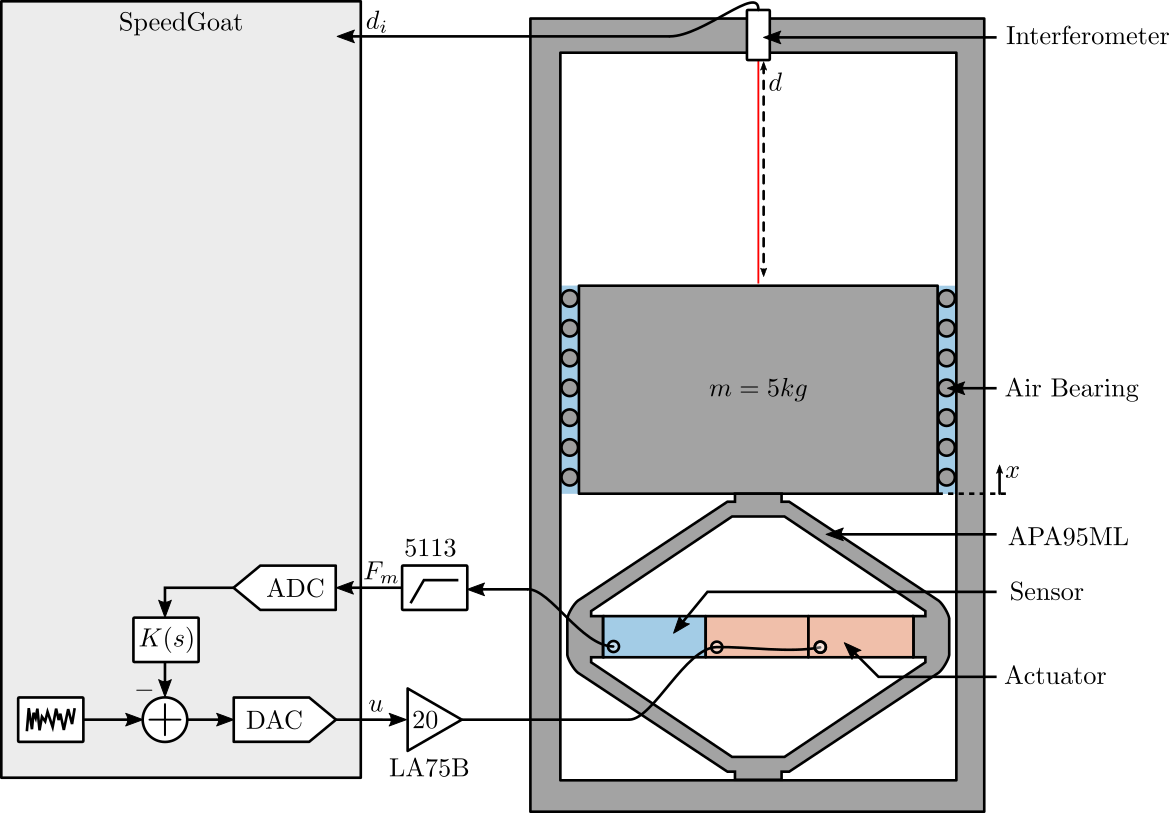
A schematic of the test-bench is shown in Figure 1.
A mass can be vertically moved using the amplified piezoelectric actuator (APA95ML). The displacement of the mass (relative to the mechanical frame) is measured by the interferometer.
The APA95ML has three stacks that can be used as actuator or as sensors.
Pictures of the test bench are shown in Figure 2 and 3.
Figure 1: Schematic of the Setup

Figure 2: Picture of the Setup

Figure 3: Zoom on the APA
2 Simscape model of the test-bench
The idea here is to model the test-bench using Simscape.
Whereas the suspended mass and metrology frame can be considered as rigid bodies in the frequency range of interest, the Amplified Piezoelectric Actuator (APA) is flexible.
To model the APA, a Finite Element Model (FEM) is used and imported into Simscape.
2.1 Import Mass Matrix, Stiffness Matrix, and Interface Nodes Coordinates
We first extract the stiffness and mass matrices.
K = extractMatrix('APA95ML_K.txt'); M = extractMatrix('APA95ML_M.txt');
| 300000000.0 | -30000.0 | 8000.0 | -200.0 | -30.0 | -60000.0 | 20000000.0 | -4000.0 | 500.0 | 8 |
| -30000.0 | 100000000.0 | 400.0 | 30.0 | 200.0 | -1 | 4000.0 | -8000000.0 | 800.0 | 7 |
| 8000.0 | 400.0 | 50000000.0 | -800000.0 | -300.0 | -40.0 | 300.0 | 100.0 | 5000000.0 | 40000.0 |
| -200.0 | 30.0 | -800000.0 | 20000.0 | 5 | 1 | -10.0 | -2 | -40000.0 | -300.0 |
| -30.0 | 200.0 | -300.0 | 5 | 40000.0 | 0.3 | -4 | -10.0 | 40.0 | 0.4 |
| -60000.0 | -1 | -40.0 | 1 | 0.3 | 3000.0 | 7000.0 | 0.8 | -1 | 0.0003 |
| 20000000.0 | 4000.0 | 300.0 | -10.0 | -4 | 7000.0 | 300000000.0 | 20000.0 | 3000.0 | 80.0 |
| -4000.0 | -8000000.0 | 100.0 | -2 | -10.0 | 0.8 | 20000.0 | 100000000.0 | -4000.0 | -100.0 |
| 500.0 | 800.0 | 5000000.0 | -40000.0 | 40.0 | -1 | 3000.0 | -4000.0 | 50000000.0 | 800000.0 |
| 8 | 7 | 40000.0 | -300.0 | 0.4 | 0.0003 | 80.0 | -100.0 | 800000.0 | 20000.0 |
| 0.03 | 2e-06 | -2e-07 | 1e-08 | 2e-08 | 0.0002 | -0.001 | 2e-07 | -8e-08 | -9e-10 |
| 2e-06 | 0.02 | -5e-07 | 7e-09 | 3e-08 | 2e-08 | -3e-07 | 0.0003 | -1e-08 | 1e-10 |
| -2e-07 | -5e-07 | 0.02 | -9e-05 | 4e-09 | -1e-08 | 2e-07 | -2e-08 | -0.0006 | -5e-06 |
| 1e-08 | 7e-09 | -9e-05 | 1e-06 | 6e-11 | 4e-10 | -1e-09 | 3e-11 | 5e-06 | 3e-08 |
| 2e-08 | 3e-08 | 4e-09 | 6e-11 | 1e-06 | 2e-10 | -2e-09 | 2e-10 | -7e-09 | -4e-11 |
| 0.0002 | 2e-08 | -1e-08 | 4e-10 | 2e-10 | 2e-06 | -2e-06 | -1e-09 | -7e-10 | -9e-12 |
| -0.001 | -3e-07 | 2e-07 | -1e-09 | -2e-09 | -2e-06 | 0.03 | -2e-06 | -1e-07 | -5e-09 |
| 2e-07 | 0.0003 | -2e-08 | 3e-11 | 2e-10 | -1e-09 | -2e-06 | 0.02 | -8e-07 | -1e-08 |
| -8e-08 | -1e-08 | -0.0006 | 5e-06 | -7e-09 | -7e-10 | -1e-07 | -8e-07 | 0.02 | 9e-05 |
| -9e-10 | 1e-10 | -5e-06 | 3e-08 | -4e-11 | -9e-12 | -5e-09 | -1e-08 | 9e-05 | 1e-06 |
Then, we extract the coordinates of the interface nodes.
[int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('APA95ML_out_nodes_3D.txt');
| Total number of Nodes | 168959 |
| Number of interface Nodes | 13 |
| Number of Modes | 30 |
| Size of M and K matrices | 108 |
| Node i | Node Number | x [m] | y [m] | z [m] |
|---|---|---|---|---|
| 1.0 | 168947.0 | 0.0 | 0.03 | 0.0 |
| 2.0 | 168949.0 | 0.0 | -0.03 | 0.0 |
| 3.0 | 168950.0 | -0.035 | 0.0 | 0.0 |
| 4.0 | 168951.0 | -0.028 | 0.0 | 0.0 |
| 5.0 | 168952.0 | -0.021 | 0.0 | 0.0 |
| 6.0 | 168953.0 | -0.014 | 0.0 | 0.0 |
| 7.0 | 168954.0 | -0.007 | 0.0 | 0.0 |
| 8.0 | 168955.0 | 0.0 | 0.0 | 0.0 |
| 9.0 | 168956.0 | 0.007 | 0.0 | 0.0 |
| 10.0 | 168957.0 | 0.014 | 0.0 | 0.0 |
| 11.0 | 168958.0 | 0.021 | 0.0 | 0.0 |
| 12.0 | 168959.0 | 0.035 | 0.0 | 0.0 |
| 13.0 | 168960.0 | 0.028 | 0.0 | 0.0 |
Using K, M and int_xyz, we can use the Reduced Order Flexible Solid simscape block.
2.2 Piezoelectric parameters
In order to make the conversion from applied voltage to generated force or from the strain to the generated voltage, we need to defined some parameters corresponding to the piezoelectric material:
d33 = 300e-12; % Strain constant [m/V] n = 80; % Number of layers per stack eT = 1.6e-8; % Permittivity under constant stress [F/m] sD = 1e-11; % Compliance under constant electric displacement [m2/N] ka = 235e6; % Stack stiffness [N/m] C = 5e-6; % Stack capactiance [F]
The ratio of the developed force to applied voltage is:
\begin{equation} \label{org1eea105} F_a = g_a V_a, \quad g_a = d_{33} n k_a \end{equation}where:
- \(F_a\): developed force in [N]
- \(n\): number of layers of the actuator stack
- \(d_{33}\): strain constant in [m/V]
- \(k_a\): actuator stack stiffness in [N/m]
- \(V_a\): applied voltage in [V]
If we take the numerical values, we obtain:
d33*n*ka % [N/V]
5.64
From (Fleming and Leang 2014) (page 123), the relation between relative displacement of the sensor stack and generated voltage is:
\begin{equation} \label{org7e93246} V_s = \frac{d_{33}}{\epsilon^T s^D n} \Delta h \end{equation}where:
- \(V_s\): measured voltage in [V]
- \(d_{33}\): strain constant in [m/V]
- \(\epsilon^T\): permittivity under constant stress in [F/m]
- \(s^D\): elastic compliance under constant electric displacement in [m^2/N]
- \(n\): number of layers of the sensor stack
- \(\Delta h\): relative displacement in [m]
If we take the numerical values, we obtain:
1e-6*d33/(eT*sD*n) % [V/um]
23.438
2.3 Simscape Model
The flexible element is imported using the Reduced Order Flexible Solid Simscape block.
To model the actuator, an Internal Force block is added between the nodes 3 and 12.
A Relative Motion Sensor block is added between the nodes 1 and 2 to measure the displacement and the amplified piezo.
[ ]Add schematic of the model with interface nodes
One mass is fixed at one end of the piezo-electric stack actuator, the other end is fixed to the world frame.
m = 5;
2.4 Dynamics from Actuator Voltage to Vertical Mass Displacement
The identified dynamics is shown in Figure 4.
%% Name of the Simulink File mdl = 'piezo_amplified_3d'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Va'], 1, 'openinput'); io_i = io_i + 1; % Actuator Voltage [V] io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1; % Vertical Displacement [m] Ghm = -linearize(mdl, io);
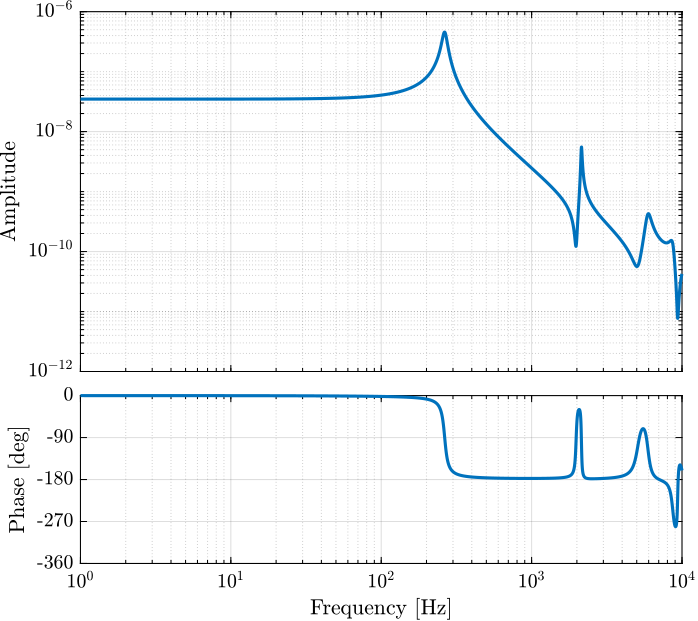
Figure 4: Dynamics from \(F\) to \(d\) without a payload and with a 5kg payload
2.5 Dynamics from Actuator Voltage to Force Sensor Voltage
The obtained dynamics is shown in Figure 5.
%% Name of the Simulink File mdl = 'piezo_amplified_3d'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Va'], 1, 'openinput'); io_i = io_i + 1; % Voltage Actuator [V] io(io_i) = linio([mdl, '/Vs'], 1, 'openoutput'); io_i = io_i + 1; % Sensor Voltage [V] Gfm = linearize(mdl, io);

Figure 5: Dynamics from \(F\) to \(F_m\) for \(m=0\) and \(m = 10kg\)
2.6 Save Data for further use
save('matlab/mat/fem_simscape_models.mat', 'Ghm', 'Gfm')
save('mat/fem_simscape_models.mat', 'Ghm', 'Gfm')
3 Estimation of piezoelectric parameters
3.1 From actuator voltage to vertical displacement
The data from the “noise test” and the identification test are loaded.
load('apa95ml_5kg_Amp_E505.mat', 't', 'um', 'y');
Any offset value is removed:
um = detrend(um, 0); % Amplifier Input Voltage [V] y = detrend(y , 0); % Mass displacement [m]
Now we add a factor 10 to take into account the gain of the voltage amplifier.
um = 10*um; % Stack Actuator Input Voltage [V]
Ts = t(end)/(length(t)-1); Fs = 1/Ts; win = hanning(ceil(1*Fs));
[tf_est, f] = tfestimate(um, y, win, [], [], 1/Ts);
The gain from input voltage of the stack to the vertical displacement is determined:
gD = 4e-7; % [m/V]
K = extractMatrix('APA95ML_K.txt'); M = extractMatrix('APA95ML_M.txt'); [int_xyz, int_i, n_xyz, n_i, nodes] = extractNodes('APA95ML_out_nodes_3D.txt');
Define parameters just for the simulation. Should not change any results
d33 = 1; % Strain constant [m/V] n = 1; % Number of layers per stack eT = 1; % Permittivity under constant stress [F/m] sD = 1; % Compliance under constant electric displacement [m2/N] ka = 1; % Stack stiffness [N/m] C = 1; % Stack capactiance [F]
m = 5; %% Name of the Simulink File mdl = 'piezo_amplified_3d'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Fa'], 1, 'openinput'); io_i = io_i + 1; % Actuator Force [N] io(io_i) = linio([mdl, '/y'], 1, 'openoutput'); io_i = io_i + 1; % Vertical Displacement [m] Gd = linearize(mdl, io);
gF = abs(dcgain(Gd)); % [m/N] ans = gF
6.1695e-09
\[ g_a = g_D/g_F \] in [N/V]
ga = gD/gF ans = ga
64.835
na = 2; ns = 1; d33 = 300e-12; n = 80; ka = 235e6; gL = 1.7; na/(na+ns)*gL*d33*n*ka
6.392
[ ]Why is there a factor 10 with the “theoretical estimation?”
3.2 From actuator voltage to sensor Voltage
load('apa95ml_5kg_2a_1s.mat', 't', 'u', 'v');
u = detrend(u, 0); % Input Voltage of the Amplifier [V] v = detrend(v, 0); % Voltage accross the stack sensor [V]
u = 20*u; % Input Voltage of the Amplifier [V]
Ts = t(end)/(length(t)-1); Fs = 1/Ts; win = hann(ceil(10/Ts)); [tf_est, f] = tfestimate(u, v, win, [], [], 1/Ts);
gV = 0.022; % [V/V]
m = 5; %% Name of the Simulink File mdl = 'piezo_amplified_3d'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Fa'], 1, 'openinput'); io_i = io_i + 1; % Actuator Force [N] io(io_i) = linio([mdl, '/dL'], 1, 'openoutput'); io_i = io_i + 1; % Sensor Stack displacement [m] Gf = linearize(mdl, io);
\(g_F\) in [m/N]
gF = abs(dcgain(Gf));
ans = gF
2.1546e-10
Finally, we compute the gain from strain of the sensor stack to its generated voltage: \[ g_S = \frac{g_V}{g_F g_a} \] Gs in [V/m]
gS = gV/gF/ga; ans = gS
15749000.0
d33 = 300e-12; eT = 5.3e-9; sD = 2e-11; n = 80; d33/(eT*sD*n)
35377000.0
4 Huddle Test
4.1 Time Domain Data

Figure 6: Measurement of the Mass displacement during Huddle Test
4.2 PSD of Measurement Noise
Ts = t(end)/(length(t)-1); Fs = 1/Ts; win = hanning(ceil(1*Fs));
[pxx, f] = pwelch(y(1000:end), win, [], [], Fs);

Figure 7: Amplitude Spectral Density of the Displacement during Huddle Test
5 Identification of the dynamics from actuator to displacement
[ ]List of equipment[ ]Schematic[ ]Problem of matching between the models? (there is a factor 10)
E505 with gain of 10.
5.1 Load Data
The data from the “noise test” and the identification test are loaded.
ht = load('huddle_test.mat', 't', 'u', 'y'); load('apa95ml_5kg_Amp_E505.mat', 't', 'um', 'y');
Any offset value is removed:
um = detrend(um, 0); % Input Voltage [V] y = detrend(y , 0); % Mass displacement [m] ht.u = detrend(ht.u, 0); ht.y = detrend(ht.y, 0);
Now we add a factor 10 to take into account the gain of the voltage amplifier.
um = 10*um; ht.u = 10*ht.u;
5.2 Comparison of the PSD with Huddle Test
Ts = t(end)/(length(t)-1); Fs = 1/Ts; win = hanning(ceil(1*Fs));
[pxx, f] = pwelch(y, win, [], [], Fs);
[pht, ~] = pwelch(ht.y, win, [], [], Fs);

Figure 8: Comparison of the ASD for the identification test and the huddle test
5.3 Compute TF estimate and Coherence
[tf_est, f] = tfestimate(um, -y, win, [], [], 1/Ts); [co_est, ~] = mscohere( um, -y, win, [], [], 1/Ts);

Figure 9: Coherence
Comparison with the FEM model
load('mat/fem_simscape_models.mat', 'Ghm');
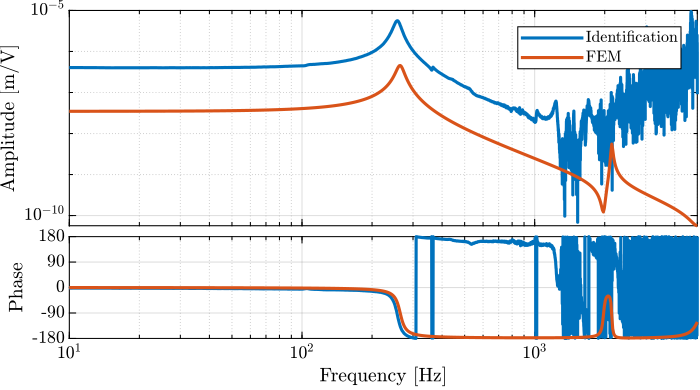
Figure 10: Comparison of the identified transfer function and the one estimated from the FE model
6 Identification of the dynamics from actuator to force sensor
Two measurements are performed:
- Speedgoat DAC => Voltage Amplifier (x20) => 1 Piezo Stack => … => 2 Stacks as Force Sensor (parallel) => Speedgoat ADC
- Speedgoat DAC => Voltage Amplifier (x20) => 2 Piezo Stacks (parallel) => … => 1 Stack as Force Sensor => Speedgoat ADC
The obtained dynamics from force actuator to force sensor are compare with the FEM model.
The data are loaded:
load('apa95ml_5kg_2a_1s.mat', 't', 'u', 'v');
u = detrend(u, 0); v = detrend(v, 0);
u = 20*u;
Let’s use the amplifier gain to obtain the true voltage applied to the actuator stack(s)
The parameters of the piezoelectric stacks are defined below:
d33 = 3e-10; % Strain constant [m/V] n = 80; % Number of layers per stack eT = 1.6e-8; % Permittivity under constant stress [F/m] sD = 2e-11; % Elastic compliance under constant electric displacement [m2/N] ka = 235e6; % Stack stiffness [N/m]
From the FEM, we construct the transfer function from DAC voltage to ADC voltage.
Gfem_aa_s = exp(-s/1e4)*20*(2*d33*n*ka)*(G(3,1)+G(3,2))*d33/(eT*sD*n); Gfem_a_ss = exp(-s/1e4)*20*( d33*n*ka)*(G(3,1)+G(2,1))*d33/(eT*sD*n);
Gfem_aa_s = exp(-s/1e4)*20*(2*d33*n*ka)*Gfm*d33/(eT*sD*n); Gfem_a_ss = exp(-s/1e4)*20*( d33*n*ka)*Gfm*d33/(eT*sD*n);
The transfer function from input voltage to output voltage are computed and shown in Figure 11.
Ts = t(end)/(length(t)-1); Fs = 1/Ts; win = hann(ceil(10/Ts)); [tf_est, f] = tfestimate(u, v, win, [], [], 1/Ts); [coh, ~] = mscohere( u, v, win, [], [], 1/Ts);
load('mat/fem_simscape_models.mat', 'Gfm');
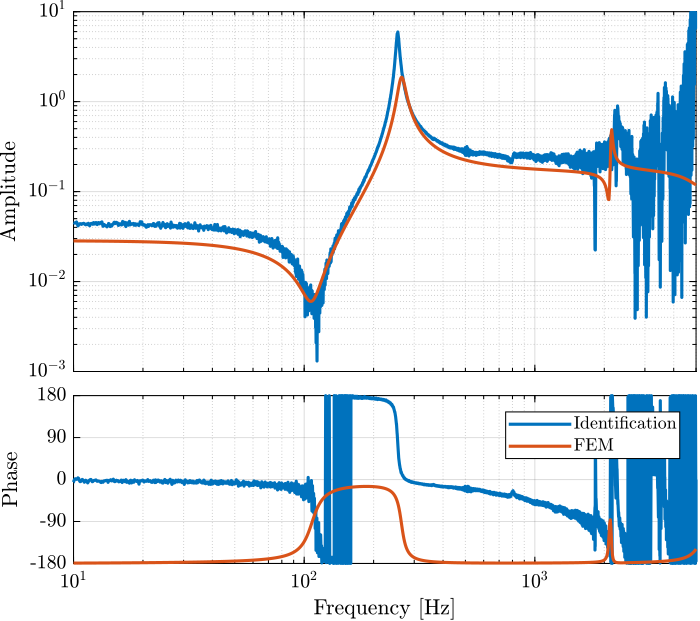
Figure 11: Comparison of the identified dynamics from voltage output to voltage input and the FEM
6.1 System Identification
w_z = 2*pi*111; % Zeros frequency [rad/s] w_p = 2*pi*255; % Pole frequency [rad/s] xi_z = 0.05; xi_p = 0.015; G_inf = 0.1; Gi = G_inf*(s^2 - 2*xi_z*w_z*s + w_z^2)/(s^2 + 2*xi_p*w_p*s + w_p^2);

Figure 12: Identification of the IFF plant
6.2 Integral Force Feedback

Figure 13: Root Locus for IFF
7 Integral Force Feedback
7.1 First tests with few gains
iff_g10 = load('apa95ml_iff_g10_res.mat', 'u', 't', 'y', 'v'); iff_g100 = load('apa95ml_iff_g100_res.mat', 'u', 't', 'y', 'v'); iff_of = load('apa95ml_iff_off_res.mat', 'u', 't', 'y', 'v');
Ts = 1e-4; win = hann(ceil(10/Ts)); [tf_iff_g10, f] = tfestimate(iff_g10.u, iff_g10.y, win, [], [], 1/Ts); [co_iff_g10, ~] = mscohere(iff_g10.u, iff_g10.y, win, [], [], 1/Ts); [tf_iff_g100, ~] = tfestimate(iff_g100.u, iff_g100.y, win, [], [], 1/Ts); [co_iff_g100, ~] = mscohere(iff_g100.u, iff_g100.y, win, [], [], 1/Ts); [tf_iff_of, ~] = tfestimate(iff_of.u, iff_of.y, win, [], [], 1/Ts); [co_iff_of, ~] = mscohere(iff_of.u, iff_of.y, win, [], [], 1/Ts);
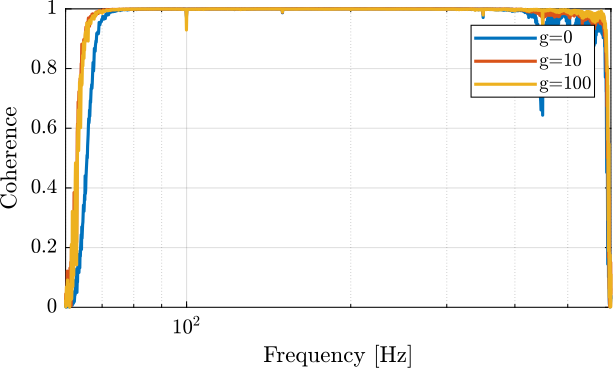
Figure 15: Coherence
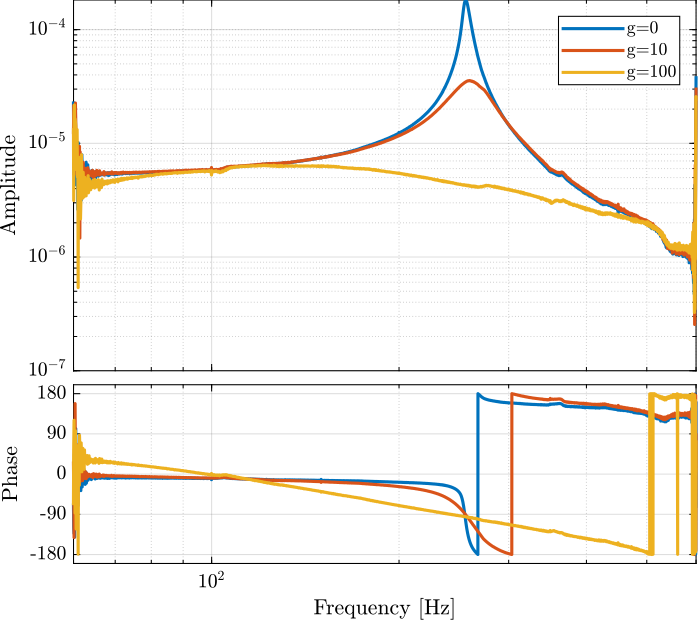
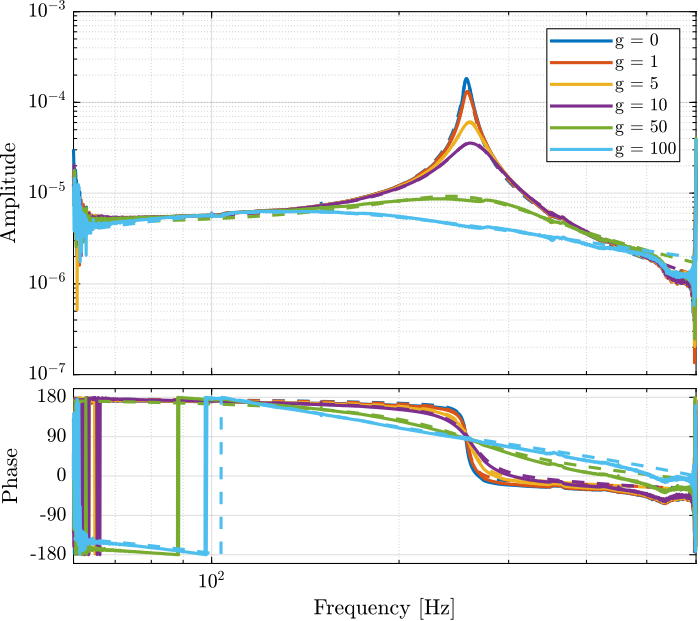
Figure 16: Bode plot for different values of IFF gain
7.2 Second test with many Gains
load('apa95ml_iff_test.mat', 'results');
Ts = 1e-4; win = hann(ceil(10/Ts));
tf_iff = {zeros(1, length(results))};
co_iff = {zeros(1, length(results))};
g_iff = [0, 1, 5, 10, 50, 100];
for i=1:length(results)
[tf_est, f] = tfestimate(results{i}.u, results{i}.y, win, [], [], 1/Ts);
[co_est, ~] = mscohere(results{i}.u, results{i}.y, win, [], [], 1/Ts);
tf_iff(i) = {tf_est};
co_iff(i) = {co_est};
end
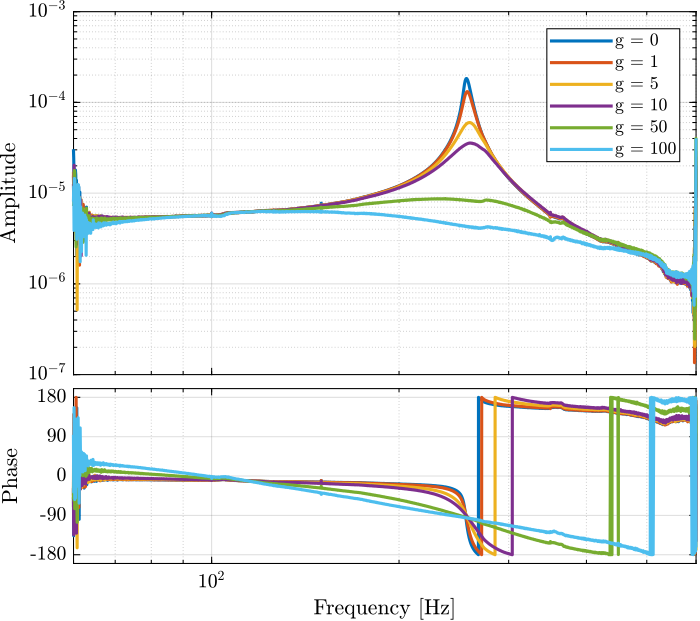
G_id = {zeros(1,length(results))};
f_start = 70; % [Hz]
f_end = 500; % [Hz]
for i = 1:length(results)
tf_id = tf_iff{i}(sum(f<f_start):length(f)-sum(f>f_end));
f_id = f(sum(f<f_start):length(f)-sum(f>f_end));
gfr = idfrd(tf_id, 2*pi*f_id, Ts);
G_id(i) = {procest(gfr,'P2UDZ')};
end