SVD Control
Table of Contents
1 Gravimeter - Simscape Model
1.1 Introduction

Figure 1: Model of the gravimeter
1.2 Simscape Model - Parameters
open('gravimeter.slx')
Parameters
l = 1.0; % Length of the mass [m] la = 0.5; % Position of Act. [m] h = 3.4; % Height of the mass [m] ha = 1.7; % Position of Act. [m] m = 400; % Mass [kg] I = 115; % Inertia [kg m^2] k = 15e3; % Actuator Stiffness [N/m] c = 0.03; % Actuator Damping [N/(m/s)] deq = 0.2; % Length of the actuators [m] g = 0; % Gravity [m/s2]
1.3 System Identification - Without Gravity
%% Name of the Simulink File mdl = 'gravimeter'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/F1'], 1, 'openinput'); io_i = io_i + 1; io(io_i) = linio([mdl, '/F2'], 1, 'openinput'); io_i = io_i + 1; io(io_i) = linio([mdl, '/F3'], 1, 'openinput'); io_i = io_i + 1; io(io_i) = linio([mdl, '/Acc_side'], 1, 'openoutput'); io_i = io_i + 1; io(io_i) = linio([mdl, '/Acc_side'], 2, 'openoutput'); io_i = io_i + 1; io(io_i) = linio([mdl, '/Acc_top'], 1, 'openoutput'); io_i = io_i + 1; io(io_i) = linio([mdl, '/Acc_top'], 2, 'openoutput'); io_i = io_i + 1; G = linearize(mdl, io); G.InputName = {'F1', 'F2', 'F3'}; G.OutputName = {'Ax1', 'Az1', 'Ax2', 'Az2'};
pole(G)
ans =
-0.000473481142385795 + 21.7596190728632i
-0.000473481142385795 - 21.7596190728632i
-7.49842879459172e-05 + 8.6593576906982i
-7.49842879459172e-05 - 8.6593576906982i
-5.1538686792578e-06 + 2.27025295182756i
-5.1538686792578e-06 - 2.27025295182756i
The plant as 6 states as expected (2 translations + 1 rotation)
size(G)
State-space model with 4 outputs, 3 inputs, and 6 states.
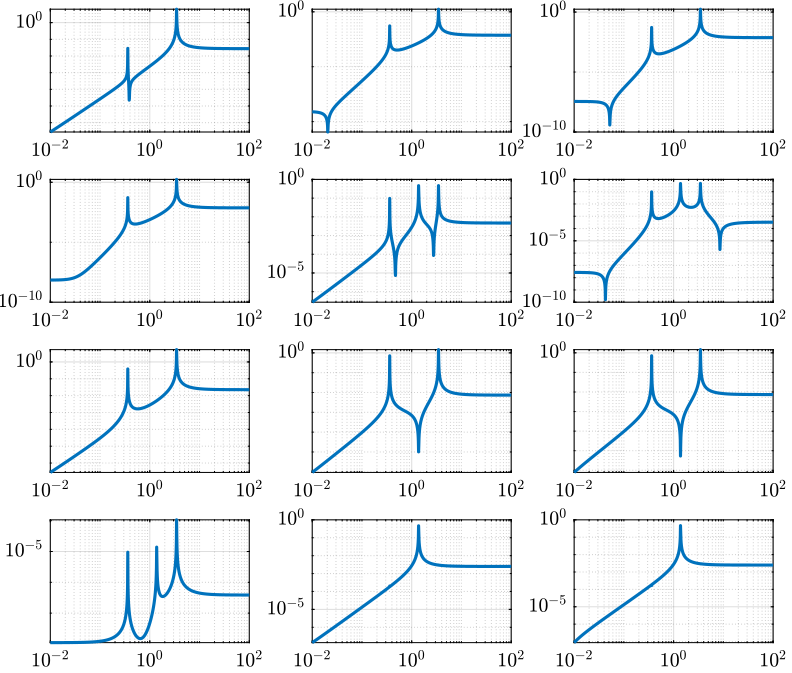
Figure 2: Open Loop Transfer Function from 3 Actuators to 4 Accelerometers
1.4 System Identification - With Gravity
g = 9.80665; % Gravity [m/s2]
Gg = linearize(mdl, io);
Gg.InputName = {'F1', 'F2', 'F3'};
Gg.OutputName = {'Ax1', 'Az1', 'Ax2', 'Az2'};
We can now see that the system is unstable due to gravity.
pole(Gg)
ans =
-10.9848275341252 + 0i
10.9838836405201 + 0i
-7.49855379478109e-05 + 8.65962885770051i
-7.49855379478109e-05 - 8.65962885770051i
-6.68819548733559e-06 + 0.832960422243848i
-6.68819548733559e-06 - 0.832960422243848i
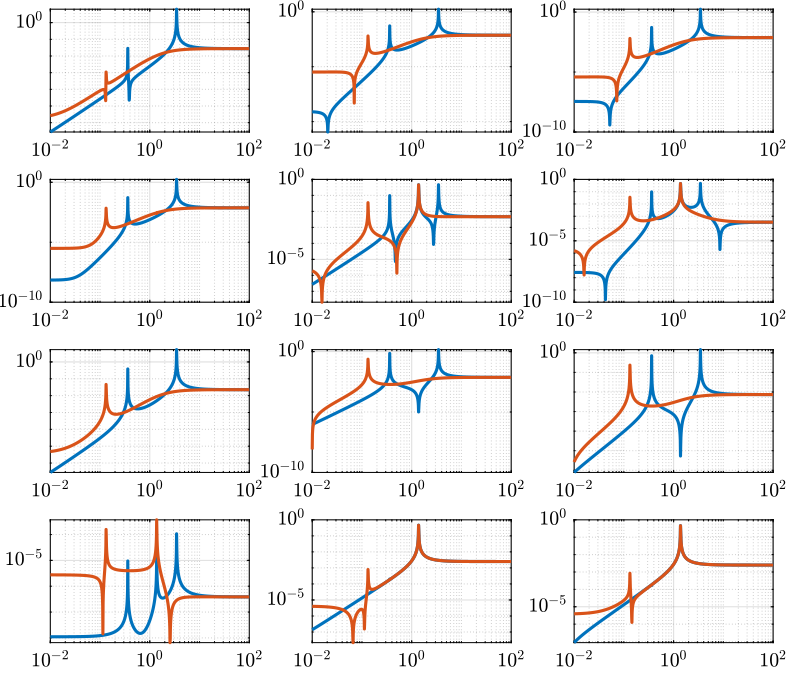
Figure 3: Open Loop Transfer Function from 3 Actuators to 4 Accelerometers with an without gravity
1.5 Analytical Model
1.5.1 Parameters
Bode options.
P = bodeoptions; P.FreqUnits = 'Hz'; P.MagUnits = 'abs'; P.MagScale = 'log'; P.Grid = 'on'; P.PhaseWrapping = 'on'; P.Title.FontSize = 14; P.XLabel.FontSize = 14; P.YLabel.FontSize = 14; P.TickLabel.FontSize = 12; P.Xlim = [1e-1,1e2]; P.MagLowerLimMode = 'manual'; P.MagLowerLim= 1e-3;
Frequency vector.
w = 2*pi*logspace(-1,2,1000); % [rad/s]
1.5.2 Generation of the State Space Model
Mass matrix
M = [m 0 0
0 m 0
0 0 I];
Jacobian of the bottom sensor
Js1 = [1 0 h/2 0 1 -l/2];
Jacobian of the top sensor
Js2 = [1 0 -h/2 0 1 0];
Jacobian of the actuators
Ja = [1 0 ha % Left horizontal actuator 0 1 -la % Left vertical actuator 0 1 la]; % Right vertical actuator Jta = Ja';
Stiffness and Damping matrices
K = k*Jta*Ja; C = c*Jta*Ja;
State Space Matrices
E = [1 0 0
0 1 0
0 0 1]; %projecting ground motion in the directions of the legs
AA = [zeros(3) eye(3)
-M\K -M\C];
BB = [zeros(3,6)
M\Jta M\(k*Jta*E)];
CC = [[Js1;Js2] zeros(4,3);
zeros(2,6)
(Js1+Js2)./2 zeros(2,3)
(Js1-Js2)./2 zeros(2,3)
(Js1-Js2)./(2*h) zeros(2,3)];
DD = [zeros(4,6)
zeros(2,3) eye(2,3)
zeros(6,6)];
State Space model:
- Input = three actuators and three ground motions
- Output = the bottom sensor; the top sensor; the ground motion; the half sum; the half difference; the rotation
system_dec = ss(AA,BB,CC,DD);
size(system_dec)
State-space model with 12 outputs, 6 inputs, and 6 states.
1.5.3 Comparison with the Simscape Model

Figure 4: Comparison of the analytical and the Simscape models
1.5.4 Analysis
% figure % bode(system_dec,P); % return
%% svd decomposition % system_dec_freq = freqresp(system_dec,w); % S = zeros(3,length(w)); % for m = 1:length(w) % S(:,m) = svd(system_dec_freq(1:4,1:3,m)); % end % figure % loglog(w./(2*pi), S);hold on; % % loglog(w./(2*pi), abs(Val(1,:)),w./(2*pi), abs(Val(2,:)),w./(2*pi), abs(Val(3,:))); % xlabel('Frequency [Hz]');ylabel('Singular Value [-]'); % legend('\sigma_1','\sigma_2','\sigma_3');%,'\sigma_4','\sigma_5','\sigma_6'); % ylim([1e-8 1e-2]); % % %condition number % figure % loglog(w./(2*pi), S(1,:)./S(3,:));hold on; % % loglog(w./(2*pi), abs(Val(1,:)),w./(2*pi), abs(Val(2,:)),w./(2*pi), abs(Val(3,:))); % xlabel('Frequency [Hz]');ylabel('Condition number [-]'); % % legend('\sigma_1','\sigma_2','\sigma_3');%,'\sigma_4','\sigma_5','\sigma_6'); % % %performance indicator % system_dec_svd = freqresp(system_dec(1:4,1:3),2*pi*10); % [U,S,V] = svd(system_dec_svd); % H_svd_OL = -eye(3,4);%-[zpk(-2*pi*10,-2*pi*40,40/10) 0 0 0; 0 10*zpk(-2*pi*40,-2*pi*200,40/200) 0 0; 0 0 zpk(-2*pi*2,-2*pi*10,10/2) 0];% - eye(3,4);% % H_svd = pinv(V')*H_svd_OL*pinv(U); % % system_dec_control_svd_ = feedback(system_dec,g*pinv(V')*H*pinv(U)); % % OL_dec = g_svd*H_svd*system_dec(1:4,1:3); % OL_freq = freqresp(OL_dec,w); % OL = G*H % CL_system = feedback(eye(3),-g_svd*H_svd*system_dec(1:4,1:3)); % CL_freq = freqresp(CL_system,w); % CL = (1+G*H)^-1 % % CL_system_2 = feedback(system_dec,H); % % CL_freq_2 = freqresp(CL_system_2,w); % CL = G/(1+G*H) % for i = 1:size(w,2) % OL(:,i) = svd(OL_freq(:,:,i)); % CL (:,i) = svd(CL_freq(:,:,i)); % %CL2 (:,i) = svd(CL_freq_2(:,:,i)); % end % % un = ones(1,length(w)); % figure % loglog(w./(2*pi),OL(3,:)+1,'k',w./(2*pi),OL(3,:)-1,'b',w./(2*pi),1./CL(1,:),'r--',w./(2*pi),un,'k:');hold on;% % % loglog(w./(2*pi), 1./(CL(2,:)),w./(2*pi), 1./(CL(3,:))); % % semilogx(w./(2*pi), 1./(CL2(1,:)),w./(2*pi), 1./(CL2(2,:)),w./(2*pi), 1./(CL2(3,:))); % xlabel('Frequency [Hz]');ylabel('Singular Value [-]'); % legend('GH \sigma_{inf} +1 ','GH \sigma_{inf} -1','S 1/\sigma_{sup}');%,'\lambda_1','\lambda_2','\lambda_3'); % % figure % loglog(w./(2*pi),OL(1,:)+1,'k',w./(2*pi),OL(1,:)-1,'b',w./(2*pi),1./CL(3,:),'r--',w./(2*pi),un,'k:');hold on;% % % loglog(w./(2*pi), 1./(CL(2,:)),w./(2*pi), 1./(CL(3,:))); % % semilogx(w./(2*pi), 1./(CL2(1,:)),w./(2*pi), 1./(CL2(2,:)),w./(2*pi), 1./(CL2(3,:))); % xlabel('Frequency [Hz]');ylabel('Singular Value [-]'); % legend('GH \sigma_{sup} +1 ','GH \sigma_{sup} -1','S 1/\sigma_{inf}');%,'\lambda_1','\lambda_2','\lambda_3');
1.5.5 Control Section
system_dec_10Hz = freqresp(system_dec,2*pi*10); system_dec_0Hz = freqresp(system_dec,0); system_decReal_10Hz = pinv(align(system_dec_10Hz)); [Ureal,Sreal,Vreal] = svd(system_decReal_10Hz(1:4,1:3)); normalizationMatrixReal = abs(pinv(Ureal)*system_dec_0Hz(1:4,1:3)*pinv(Vreal')); [U,S,V] = svd(system_dec_10Hz(1:4,1:3)); normalizationMatrix = abs(pinv(U)*system_dec_0Hz(1:4,1:3)*pinv(V')); H_dec = ([zpk(-2*pi*5,-2*pi*30,30/5) 0 0 0 0 zpk(-2*pi*4,-2*pi*20,20/4) 0 0 0 0 0 zpk(-2*pi,-2*pi*10,10)]); H_cen_OL = [zpk(-2*pi,-2*pi*10,10) 0 0; 0 zpk(-2*pi,-2*pi*10,10) 0; 0 0 zpk(-2*pi*5,-2*pi*30,30/5)]; H_cen = pinv(Jta)*H_cen_OL*pinv([Js1; Js2]); % H_svd_OL = -[1/normalizationMatrix(1,1) 0 0 0 % 0 1/normalizationMatrix(2,2) 0 0 % 0 0 1/normalizationMatrix(3,3) 0]; % H_svd_OL_real = -[1/normalizationMatrixReal(1,1) 0 0 0 % 0 1/normalizationMatrixReal(2,2) 0 0 % 0 0 1/normalizationMatrixReal(3,3) 0]; H_svd_OL = -[1/normalizationMatrix(1,1)*zpk(-2*pi*10,-2*pi*60,60/10) 0 0 0 0 1/normalizationMatrix(2,2)*zpk(-2*pi*5,-2*pi*30,30/5) 0 0 0 0 1/normalizationMatrix(3,3)*zpk(-2*pi*2,-2*pi*10,10/2) 0]; H_svd_OL_real = -[1/normalizationMatrixReal(1,1)*zpk(-2*pi*10,-2*pi*60,60/10) 0 0 0 0 1/normalizationMatrixReal(2,2)*zpk(-2*pi*5,-2*pi*30,30/5) 0 0 0 0 1/normalizationMatrixReal(3,3)*zpk(-2*pi*2,-2*pi*10,10/2) 0]; % H_svd_OL_real = -[zpk(-2*pi*10,-2*pi*40,40/10) 0 0 0; 0 10*zpk(-2*pi*10,-2*pi*100,100/10) 0 0; 0 0 zpk(-2*pi*2,-2*pi*10,10/2) 0];%-eye(3,4); % H_svd_OL = -[zpk(-2*pi*10,-2*pi*40,40/10) 0 0 0; 0 zpk(-2*pi*4,-2*pi*20,4/20) 0 0; 0 0 zpk(-2*pi*2,-2*pi*10,10/2) 0];% - eye(3,4);% H_svd = pinv(V')*H_svd_OL*pinv(U); H_svd_real = pinv(Vreal')*H_svd_OL_real*pinv(Ureal); OL_dec = g*H_dec*system_dec(1:4,1:3); OL_cen = g*H_cen_OL*pinv([Js1; Js2])*system_dec(1:4,1:3)*pinv(Jta); OL_svd = 100*H_svd_OL*pinv(U)*system_dec(1:4,1:3)*pinv(V'); OL_svd_real = 100*H_svd_OL_real*pinv(Ureal)*system_dec(1:4,1:3)*pinv(Vreal');
% figure % bode(OL_dec,w,P);title('OL Decentralized'); % figure % bode(OL_cen,w,P);title('OL Centralized');
figure bode(g*system_dec(1:4,1:3),w,P); title('gain * Plant');
figure bode(OL_svd,OL_svd_real,w,P); title('OL SVD'); legend('SVD of Complex plant','SVD of real approximation of the complex plant')
figure bode(system_dec(1:4,1:3),pinv(U)*system_dec(1:4,1:3)*pinv(V'),P);
CL_dec = feedback(system_dec,g*H_dec,[1 2 3],[1 2 3 4]); CL_cen = feedback(system_dec,g*H_cen,[1 2 3],[1 2 3 4]); CL_svd = feedback(system_dec,100*H_svd,[1 2 3],[1 2 3 4]); CL_svd_real = feedback(system_dec,100*H_svd_real,[1 2 3],[1 2 3 4]);
pzmap_testCL(system_dec,H_dec,g,[1 2 3],[1 2 3 4])
title('Decentralized control');
pzmap_testCL(system_dec,H_cen,g,[1 2 3],[1 2 3 4])
title('Centralized control');
pzmap_testCL(system_dec,H_svd,100,[1 2 3],[1 2 3 4])
title('SVD control');
pzmap_testCL(system_dec,H_svd_real,100,[1 2 3],[1 2 3 4])
title('Real approximation SVD control');
P.Ylim = [1e-8 1e-3]; figure bodemag(system_dec(1:4,1:3),CL_dec(1:4,1:3),CL_cen(1:4,1:3),CL_svd(1:4,1:3),CL_svd_real(1:4,1:3),P); title('Motion/actuator') legend('Control OFF','Decentralized control','Centralized control','SVD control','SVD control real appr.');
P.Ylim = [1e-5 1e1]; figure bodemag(system_dec(1:4,4:6),CL_dec(1:4,4:6),CL_cen(1:4,4:6),CL_svd(1:4,4:6),CL_svd_real(1:4,4:6),P); title('Transmissibility'); legend('Control OFF','Decentralized control','Centralized control','SVD control','SVD control real appr.');
figure bodemag(system_dec([7 9],4:6),CL_dec([7 9],4:6),CL_cen([7 9],4:6),CL_svd([7 9],4:6),CL_svd_real([7 9],4:6),P); title('Transmissibility from half sum and half difference in the X direction'); legend('Control OFF','Decentralized control','Centralized control','SVD control','SVD control real appr.');
figure bodemag(system_dec([8 10],4:6),CL_dec([8 10],4:6),CL_cen([8 10],4:6),CL_svd([8 10],4:6),CL_svd_real([8 10],4:6),P); title('Transmissibility from half sum and half difference in the Z direction'); legend('Control OFF','Decentralized control','Centralized control','SVD control','SVD control real appr.');
1.5.6 Greshgorin radius
system_dec_freq = freqresp(system_dec,w); x1 = zeros(1,length(w)); z1 = zeros(1,length(w)); x2 = zeros(1,length(w)); S1 = zeros(1,length(w)); S2 = zeros(1,length(w)); S3 = zeros(1,length(w)); for t = 1:length(w) x1(t) = (abs(system_dec_freq(1,2,t))+abs(system_dec_freq(1,3,t)))/abs(system_dec_freq(1,1,t)); z1(t) = (abs(system_dec_freq(2,1,t))+abs(system_dec_freq(2,3,t)))/abs(system_dec_freq(2,2,t)); x2(t) = (abs(system_dec_freq(3,1,t))+abs(system_dec_freq(3,2,t)))/abs(system_dec_freq(3,3,t)); system_svd = pinv(Ureal)*system_dec_freq(1:4,1:3,t)*pinv(Vreal'); S1(t) = (abs(system_svd(1,2))+abs(system_svd(1,3)))/abs(system_svd(1,1)); S2(t) = (abs(system_svd(2,1))+abs(system_svd(2,3)))/abs(system_svd(2,2)); S2(t) = (abs(system_svd(3,1))+abs(system_svd(3,2)))/abs(system_svd(3,3)); end limit = 0.5*ones(1,length(w));
figure loglog(w./(2*pi),x1,w./(2*pi),z1,w./(2*pi),x2,w./(2*pi),limit,'--'); legend('x_1','z_1','x_2','Limit'); xlabel('Frequency [Hz]'); ylabel('Greshgorin radius [-]');
figure loglog(w./(2*pi),S1,w./(2*pi),S2,w./(2*pi),S3,w./(2*pi),limit,'--'); legend('S1','S2','S3','Limit'); xlabel('Frequency [Hz]'); ylabel('Greshgorin radius [-]'); % set(gcf,'color','w')
1.5.7 Injecting ground motion in the system to have the output
Fr = logspace(-2,3,1e3); w=2*pi*Fr*1i; %fit of the ground motion data in m/s^2/rtHz Fr_ground_x = [0.07 0.1 0.15 0.3 0.7 0.8 0.9 1.2 5 10]; n_ground_x1 = [4e-7 4e-7 2e-6 1e-6 5e-7 5e-7 5e-7 1e-6 1e-5 3.5e-5]; Fr_ground_v = [0.07 0.08 0.1 0.11 0.12 0.15 0.25 0.6 0.8 1 1.2 1.6 2 6 10]; n_ground_v1 = [7e-7 7e-7 7e-7 1e-6 1.2e-6 1.5e-6 1e-6 9e-7 7e-7 7e-7 7e-7 1e-6 2e-6 1e-5 3e-5]; n_ground_x = interp1(Fr_ground_x,n_ground_x1,Fr,'linear'); n_ground_v = interp1(Fr_ground_v,n_ground_v1,Fr,'linear'); % figure % loglog(Fr,abs(n_ground_v),Fr_ground_v,n_ground_v1,'*'); % xlabel('Frequency [Hz]');ylabel('ASD [m/s^2 /rtHz]'); % return %converting into PSD n_ground_x = (n_ground_x).^2; n_ground_v = (n_ground_v).^2; %Injecting ground motion in the system and getting the outputs system_dec_f = (freqresp(system_dec,abs(w))); PHI = zeros(size(Fr,2),12,12); for p = 1:size(Fr,2) Sw=zeros(6,6); Iact = zeros(3,3); Sw(4,4) = n_ground_x(p); Sw(5,5) = n_ground_v(p); Sw(6,6) = n_ground_v(p); Sw(1:3,1:3) = Iact; PHI(p,:,:) = (system_dec_f(:,:,p))*Sw(:,:)*(system_dec_f(:,:,p))'; end x1 = PHI(:,1,1); z1 = PHI(:,2,2); x2 = PHI(:,3,3); z2 = PHI(:,4,4); wx = PHI(:,5,5); wz = PHI(:,6,6); x12 = PHI(:,1,3); z12 = PHI(:,2,4); PHIwx = PHI(:,1,5); PHIwz = PHI(:,2,6); xsum = PHI(:,7,7); zsum = PHI(:,8,8); xdelta = PHI(:,9,9); zdelta = PHI(:,10,10); rot = PHI(:,11,11);
2 Gravimeter - Functions
2.1 align
This Matlab function is accessible here.
function [A] = align(V) %A!ALIGN(V) returns a constat matrix A which is the real alignment of the %INVERSE of the complex input matrix V %from Mohit slides if (nargin ==0) || (nargin > 1) disp('usage: mat_inv_real = align(mat)') return end D = pinv(real(V'*V)); A = D*real(V'*diag(exp(1i * angle(diag(V*D*V.'))/2))); end
2.2 pzmap_testCL
This Matlab function is accessible here.
function [] = pzmap_testCL(system,H,gain,feedin,feedout) % evaluate and plot the pole-zero map for the closed loop system for % different values of the gain [~, n] = size(gain); [m1, n1, ~] = size(H); [~,n2] = size(feedin); figure for i = 1:n % if n1 == n2 system_CL = feedback(system,gain(i)*H,feedin,feedout); [P,Z] = pzmap(system_CL); plot(real(P(:)),imag(P(:)),'x',real(Z(:)),imag(Z(:)),'o');hold on xlabel('Real axis (s^{-1})');ylabel('Imaginary Axis (s^{-1})'); % clear P Z % else % system_CL = feedback(system,gain(i)*H(:,1+(i-1)*m1:m1+(i-1)*m1),feedin,feedout); % % [P,Z] = pzmap(system_CL); % plot(real(P(:)),imag(P(:)),'x',real(Z(:)),imag(Z(:)),'o');hold on % xlabel('Real axis (s^{-1})');ylabel('Imaginary Axis (s^{-1})'); % clear P Z % end end str = {strcat('gain = ' , num2str(gain(1)))}; % at the end of first loop, z being loop output str = [str , strcat('gain = ' , num2str(gain(1)))]; % after 2nd loop for i = 2:n str = [str , strcat('gain = ' , num2str(gain(i)))]; % after 2nd loop str = [str , strcat('gain = ' , num2str(gain(i)))]; % after 2nd loop end legend(str{:}) end
3 Stewart Platform - Simscape Model
In this analysis, we wish to applied SVD control to the Stewart Platform shown in Figure 5.
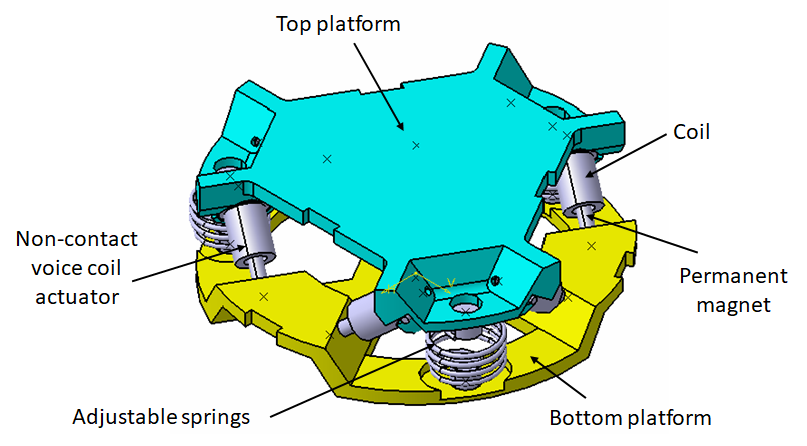
Figure 5: Stewart Platform CAD View
The analysis of the SVD control applied to the Stewart platform is performed in the following sections:
- Section 3.1: The parameters of the Simscape model of the Stewart platform are defined
- Section 3.2: The plant is identified from the Simscape model and the centralized plant is computed thanks to the Jacobian
- Section 3.3: The identified Dynamics is shown
- Section 3.4: A real approximation of the plant is computed for further decoupling using the Singular Value Decomposition (SVD)
- Section 3.5: The decoupling is performed thanks to the SVD. The effectiveness of the decoupling is verified using the Gershorin Radii
- Section 3.6: The dynamics of the decoupled plant is shown
- Section 3.7: A diagonal controller is defined to control the decoupled plant
- Section 3.8: Finally, the closed loop system properties are studied
3.1 Simscape Model - Parameters
3.2 Identification of the plant
The dynamics is identified from forces applied by each legs to the measured acceleration of the top platform.
%% Name of the Simulink File mdl = 'drone_platform'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Dw'], 1, 'openinput'); io_i = io_i + 1; io(io_i) = linio([mdl, '/u'], 1, 'openinput'); io_i = io_i + 1; io(io_i) = linio([mdl, '/Inertial Sensor'], 1, 'openoutput'); io_i = io_i + 1; G = linearize(mdl, io); G.InputName = {'Dwx', 'Dwy', 'Dwz', 'Rwx', 'Rwy', 'Rwz', ... 'F1', 'F2', 'F3', 'F4', 'F5', 'F6'}; G.OutputName = {'Ax', 'Ay', 'Az', 'Arx', 'Ary', 'Arz'};
There are 24 states (6dof for the bottom platform + 6dof for the top platform).
size(G)
State-space model with 6 outputs, 12 inputs, and 24 states.
The “centralized” plant \(\bm{G}_x\) is now computed (Figure 6).
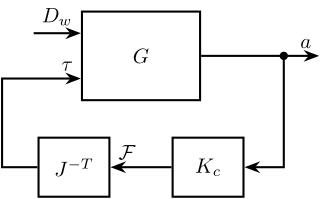
Figure 6: Centralized control architecture
Thanks to the Jacobian, we compute the transfer functions in the inertial frame (transfer function from forces and torques applied to the top platform to the absolute acceleration of the top platform).
Gx = G*blkdiag(eye(6), inv(J')); Gx.InputName = {'Dwx', 'Dwy', 'Dwz', 'Rwx', 'Rwy', 'Rwz', ... 'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz'};
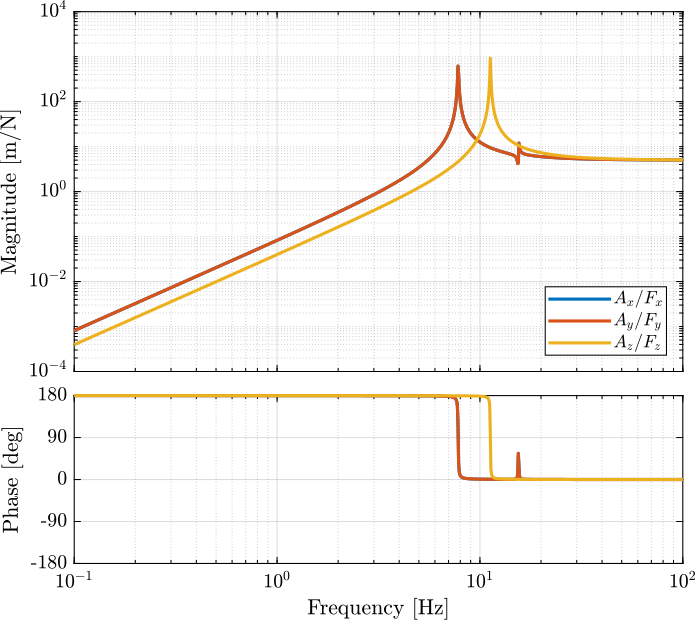
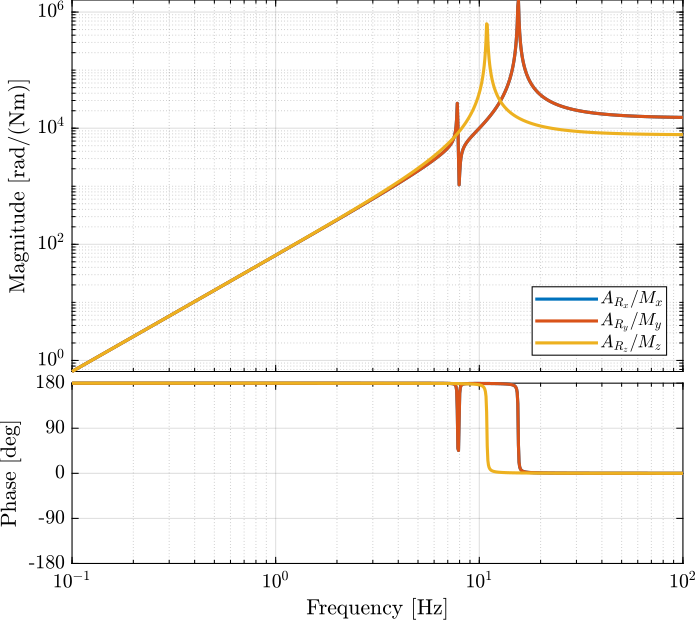
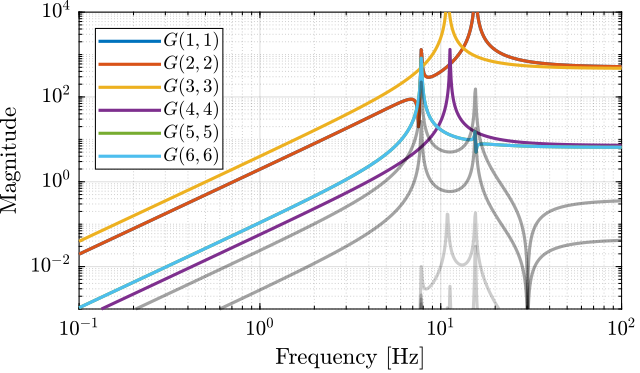
3.3 Obtained Dynamics
3.4 Real Approximation of \(G\) at the decoupling frequency
Let’s compute a real approximation of the complex matrix \(H_1\) which corresponds to the the transfer function \(G_c(j\omega_c)\) from forces applied by the actuators to the measured acceleration of the top platform evaluated at the frequency \(\omega_c\).
wc = 2*pi*30; % Decoupling frequency [rad/s] Gc = G({'Ax', 'Ay', 'Az', 'Arx', 'Ary', 'Arz'}, ... {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'}); % Transfer function to find a real approximation H1 = evalfr(Gc, j*wc);
The real approximation is computed as follows:
D = pinv(real(H1'*H1)); H1 = inv(D*real(H1'*diag(exp(j*angle(diag(H1*D*H1.'))/2))));
| 4.4 | -2.1 | -2.1 | 4.4 | -2.4 | -2.4 |
| -0.2 | -3.9 | 3.9 | 0.2 | -3.8 | 3.8 |
| 3.4 | 3.4 | 3.4 | 3.4 | 3.4 | 3.4 |
| -367.1 | -323.8 | 323.8 | 367.1 | 43.3 | -43.3 |
| -162.0 | -237.0 | -237.0 | -162.0 | 398.9 | 398.9 |
| 220.6 | -220.6 | 220.6 | -220.6 | 220.6 | -220.6 |
Note that the plant \(G\) at \(\omega_c\) is already an almost real matrix. This can be seen on the Bode plots where the phase is close to 1. This can be verified below where only the real value of \(G(\omega_c)\) is shown
| 4.4 | -2.1 | -2.1 | 4.4 | -2.4 | -2.4 |
| -0.2 | -3.9 | 3.9 | 0.2 | -3.8 | 3.8 |
| 3.4 | 3.4 | 3.4 | 3.4 | 3.4 | 3.4 |
| -367.1 | -323.8 | 323.8 | 367.1 | 43.3 | -43.3 |
| -162.0 | -237.0 | -237.0 | -162.0 | 398.9 | 398.9 |
| 220.6 | -220.6 | 220.6 | -220.6 | 220.6 | -220.6 |
3.5 Verification of the decoupling using the “Gershgorin Radii”
First, the Singular Value Decomposition of \(H_1\) is performed: \[ H_1 = U \Sigma V^H \]
[U,S,V] = svd(H1);
Then, the “Gershgorin Radii” is computed for the plant \(G_c(s)\) and the “SVD Decoupled Plant” \(G_d(s)\): \[ G_d(s) = U^T G_c(s) V \]
This is computed over the following frequencies.
freqs = logspace(-2, 2, 1000); % [Hz]
Gershgorin Radii for the coupled plant:
Gr_coupled = zeros(length(freqs), size(Gc,2)); H = abs(squeeze(freqresp(Gc, freqs, 'Hz'))); for out_i = 1:size(Gc,2) Gr_coupled(:, out_i) = squeeze((sum(H(out_i,:,:)) - H(out_i,out_i,:))./H(out_i, out_i, :)); end
Gershgorin Radii for the decoupled plant using SVD:
Gd = U'*Gc*V; Gr_decoupled = zeros(length(freqs), size(Gd,2)); H = abs(squeeze(freqresp(Gd, freqs, 'Hz'))); for out_i = 1:size(Gd,2) Gr_decoupled(:, out_i) = squeeze((sum(H(out_i,:,:)) - H(out_i,out_i,:))./H(out_i, out_i, :)); end
Gershgorin Radii for the decoupled plant using the Jacobian:
Gj = Gc*inv(J'); Gr_jacobian = zeros(length(freqs), size(Gj,2)); H = abs(squeeze(freqresp(Gj, freqs, 'Hz'))); for out_i = 1:size(Gj,2) Gr_jacobian(:, out_i) = squeeze((sum(H(out_i,:,:)) - H(out_i,out_i,:))./H(out_i, out_i, :)); end

Figure 9: Gershgorin Radii of the Coupled and Decoupled plants
3.6 Decoupled Plant
3.7 Diagonal Controller
The controller \(K\) is a diagonal controller consisting a low pass filters with a crossover frequency \(\omega_c\) and a DC gain \(C_g\).
wc = 2*pi*0.1; % Crossover Frequency [rad/s] C_g = 50; % DC Gain K = eye(6)*C_g/(s+wc);
The control diagram for the centralized control is shown in Figure 6.
The controller \(K_c\) is “working” in an cartesian frame. The Jacobian is used to convert forces in the cartesian frame to forces applied by the actuators.

Figure 12: Control Diagram for the Centralized control
The feedback system is computed as shown below.
G_cen = feedback(G, inv(J')*K, [7:12], [1:6]);
The SVD control architecture is shown in Figure 13. The matrices \(U\) and \(V\) are used to decoupled the plant \(G\).
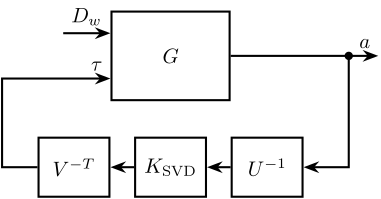
Figure 13: Control Diagram for the SVD control
The feedback system is computed as shown below.
G_svd = feedback(G, pinv(V')*K*pinv(U), [7:12], [1:6]);
3.8 Closed-Loop system Performances
Let’s first verify the stability of the closed-loop systems:
isstable(G_cen)
ans = logical 1
isstable(G_svd)
ans = logical 0
The obtained transmissibility in Open-loop, for the centralized control as well as for the SVD control are shown in Figure 14.

Figure 14: Obtained Transmissibility