SVD Control

1. Simscape Model - Gravimeter
- 1.1. Simulink
2. Simscape Model - Stewart Platform
- 2.1. Jacobian
- 2.2. Simulink

1 Simscape Model - Gravimeter

1.1 Simulink

open('gravimeter.slx')

%% Name of the Simulink File
mdl = 'gravimeter';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F1'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/F2'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/F3'], 1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/Acc_side'], 1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Acc_side'], 2, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Acc_top'], 1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Acc_top'], 2, 'openoutput'); io_i = io_i + 1;

G = linearize(mdl, io);
G.InputName  = {'F1', 'F2', 'F3'};
G.OutputName = {'Ax1', 'Az1', 'Ax2', 'Az2'};

The plant as 6 states as expected (2 translations + 1 rotation)

size(G)

State-space model with 4 outputs, 3 inputs, and 6 states.

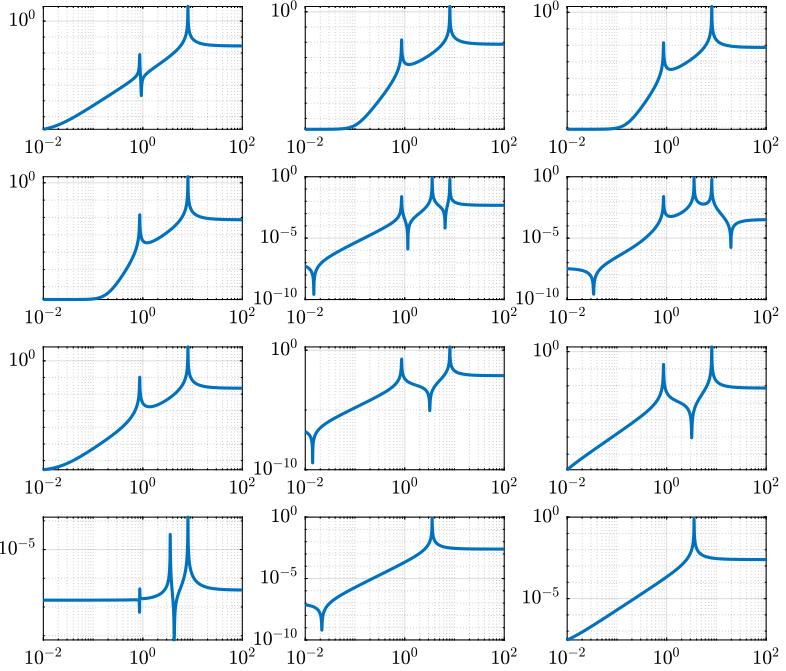
Figure 1: Open Loop Transfer Function from 3 Actuators to 4 Accelerometers

2 Simscape Model - Stewart Platform

2.1 Jacobian

First, the position of the “joints” (points of force application) are estimated and the Jacobian computed.

open('stewart_platform/drone_platform_jacobian.slx');

sim('drone_platform_jacobian');

Aa = [a1.Data(1,:);
      a2.Data(1,:);
      a3.Data(1,:);
      a4.Data(1,:);
      a5.Data(1,:);
      a6.Data(1,:)]';

Ab = [b1.Data(1,:);
      b2.Data(1,:);
      b3.Data(1,:);
      b4.Data(1,:);
      b5.Data(1,:);
      b6.Data(1,:)]';

As = (Ab - Aa)./vecnorm(Ab - Aa);

l = vecnorm(Ab - Aa)';

J = [As' , cross(Ab, As)'];

save('./jacobian.mat', 'Aa', 'Ab', 'As', 'l', 'J');

2.2 Simulink

open('stewart_platform/drone_platform.slx');

Definition of spring parameters

kx = 50; % [N/m]
ky = 50;
kz = 50;

cx = 0.025; % [Nm/rad]
cy = 0.025;
cz = 0.025;

We load the Jacobian.

load('./jacobian.mat', 'Aa', 'Ab', 'As', 'l', 'J');

The dynamics is identified from forces applied by each legs to the measured acceleration of the top platform.

%% Name of the Simulink File
mdl = 'drone_platform';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/u'],               1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/Inertial Sensor'], 1, 'openoutput'); io_i = io_i + 1;

G = linearize(mdl, io);
G.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
G.OutputName = {'Ax', 'Ay', 'Az', 'Arx', 'Ary', 'Arz'};

Thanks to the Jacobian, we compute the transfer functions in the frame of the legs and in an inertial frame.

Gx = -G*inv(J');
Gx.InputName  = {'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz'};

Gl = -J*G;
Gl.OutputName  = {'A1', 'A2', 'A3', 'A4', 'A5', 'A6'};

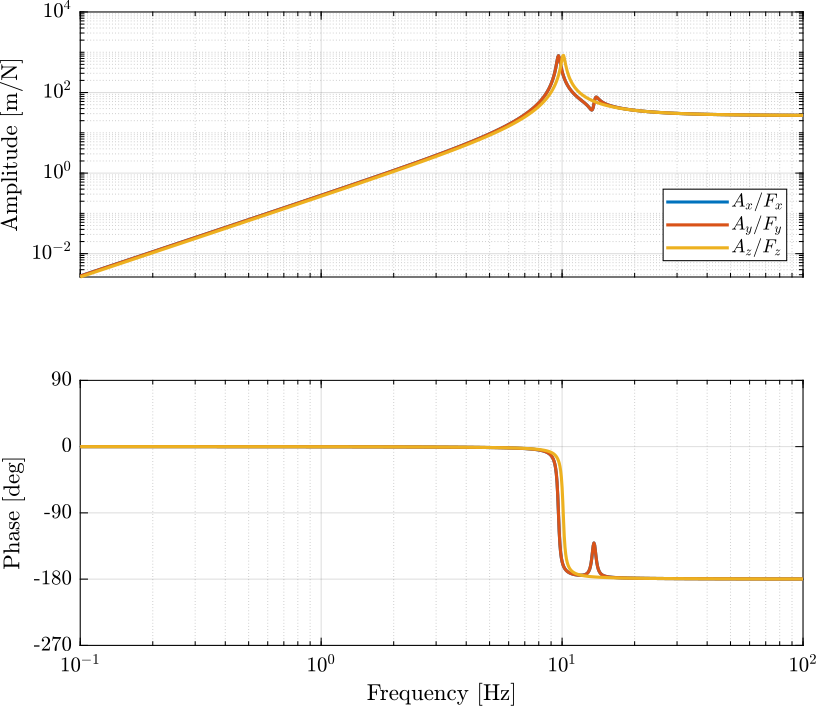
Figure 2: Stewart Platform Plant from forces applied by the legs to the acceleration of the platform

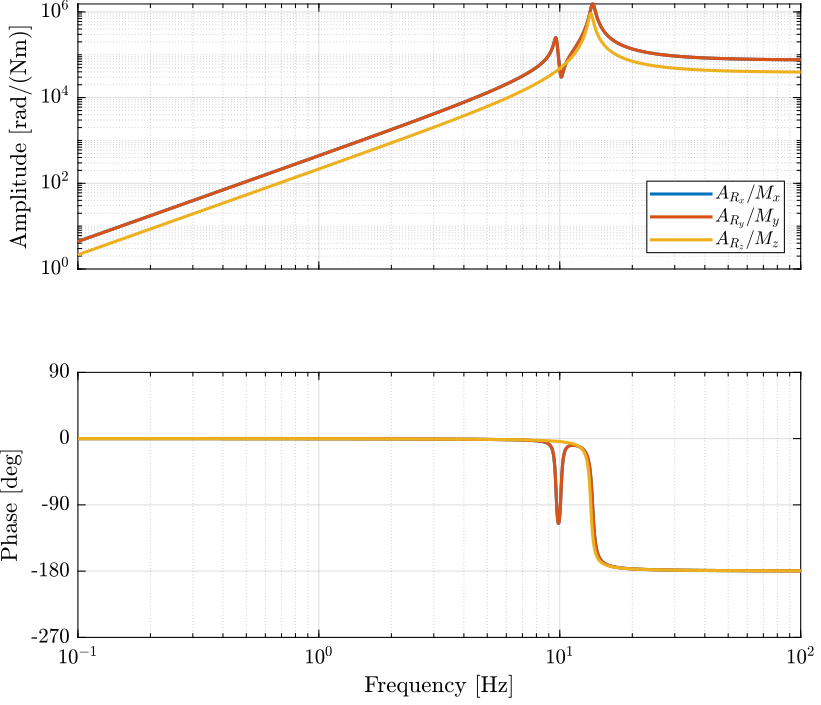
Figure 3: Stewart Platform Plant from torques applied by the legs to the angular acceleration of the platform

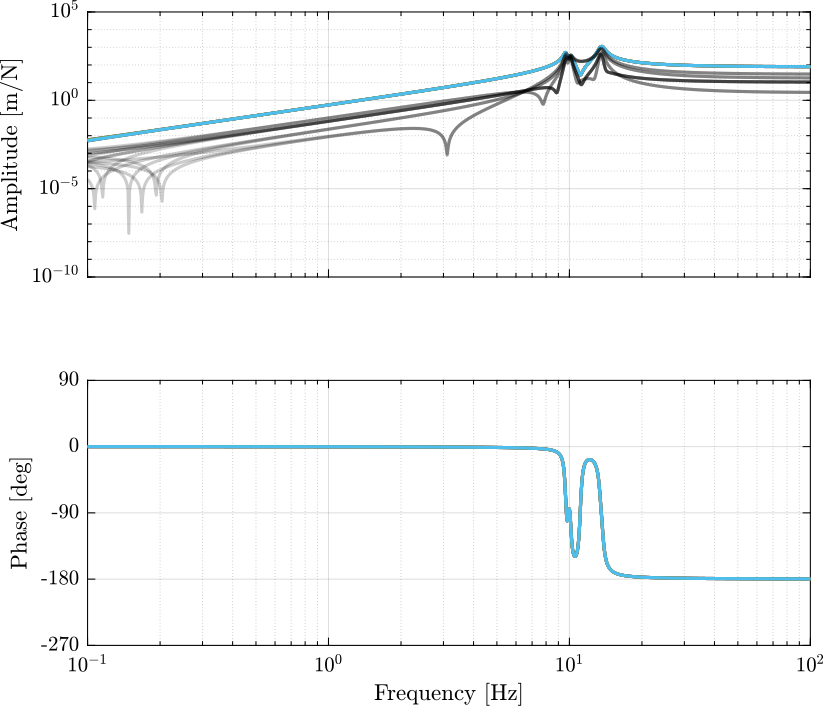
Figure 4: Stewart Platform Plant from forces applied by the legs to displacement of the legs