Cubic configuration for the Stewart Platform

1. TODO Configuration Analysis - Stiffness Matrix
2. TODO Cubic size analysis
3. Functions
- 3.1. generateCubicConfiguration: Generate a Cubic Configuration

The discovery of the Cubic configuration is done in geng94_six_degree_of_freed_activ. Further analysis is conducted in

The specificity of the Cubic configuration is that each actuator is orthogonal with the others.

The cubic (or orthogonal) configuration of the Stewart platform is now widely used (preumont07_six_axis_singl_stage_activ,jafari03_orthog_gough_stewar_platf_microm).

According to preumont07_six_axis_singl_stage_activ, the cubic configuration provides a uniform stiffness in all directions and minimizes the crosscoupling from actuator to sensor of different legs (being orthogonal to each other).

To generate and study the Cubic configuration, generateCubicConfiguration is used (description in section 3.1). The goal is to study the benefits of using a cubic configuration:

Equal stiffness in all the degrees of freedom?
No coupling between the actuators?
Is the center of the cube an important point?

1 TODO Configuration Analysis - Stiffness Matrix

1.1 Cubic Stewart platform centered with the cube center - Jacobian estimated at the cube center

We create a cubic Stewart platform (figure 1) in such a way that the center of the cube (black dot) is located at the center of the Stewart platform (blue dot). The Jacobian matrix is estimated at the location of the center of the cube.

Figure 1: Centered cubic configuration

opts = struct(...
    'H_tot', 100, ... % Total height of the Hexapod [mm]
    'L',     200/sqrt(3), ... % Size of the Cube [mm]
    'H',     60, ... % Height between base joints and platform joints [mm]
    'H0',    200/2-60/2 ... % Height between the corner of the cube and the plane containing the base joints [mm]
    );
stewart = initializeCubicConfiguration(opts);
opts = struct(...
    'Jd_pos', [0, 0, -50], ... % Position of the Jacobian for displacement estimation from the top of the mobile platform [mm]
    'Jf_pos', [0, 0, -50]  ... % Position of the Jacobian for force location from the top of the mobile platform [mm]
    );
stewart = computeGeometricalProperties(stewart, opts);

save('./mat/stewart.mat', 'stewart');

K = stewart.Jf'*stewart.Jf;

2	1.9e-18	-2.3e-17	1.8e-18	5.5e-17	-1.5e-17
1.9e-18	2	6.8e-18	-6.1e-17	-1.6e-18	4.8e-18
-2.3e-17	6.8e-18	2	-6.7e-18	4.9e-18	5.3e-19
1.8e-18	-6.1e-17	-6.7e-18	0.0067	-2.3e-20	-6.1e-20
5.5e-17	-1.6e-18	4.9e-18	-2.3e-20	0.0067	1e-18
-1.5e-17	4.8e-18	5.3e-19	-6.1e-20	1e-18	0.027

1.2 Cubic Stewart platform centered with the cube center - Jacobian not estimated at the cube center

We create a cubic Stewart platform with center of the cube located at the center of the Stewart platform (figure 1). The Jacobian matrix is not estimated at the location of the center of the cube.

opts = struct(...
    'H_tot', 100, ... % Total height of the Hexapod [mm]
    'L',     200/sqrt(3), ... % Size of the Cube [mm]
    'H',     60, ... % Height between base joints and platform joints [mm]
    'H0',    200/2-60/2 ... % Height between the corner of the cube and the plane containing the base joints [mm]
    );
stewart = initializeCubicConfiguration(opts);
opts = struct(...
    'Jd_pos', [0, 0, 0], ... % Position of the Jacobian for displacement estimation from the top of the mobile platform [mm]
    'Jf_pos', [0, 0, 0]  ... % Position of the Jacobian for force location from the top of the mobile platform [mm]
    );
stewart = computeGeometricalProperties(stewart, opts);

K = stewart.Jf'*stewart.Jf;

2	1.9e-18	-2.3e-17	1.5e-18	-0.1	-1.5e-17
1.9e-18	2	6.8e-18	0.1	-1.6e-18	4.8e-18
-2.3e-17	6.8e-18	2	-5.1e-19	-5.5e-18	5.3e-19
1.5e-18	0.1	-5.1e-19	0.012	-3e-19	3.1e-19
-0.1	-1.6e-18	-5.5e-18	-3e-19	0.012	1.9e-18
-1.5e-17	4.8e-18	5.3e-19	3.1e-19	1.9e-18	0.027

1.3 Cubic Stewart platform not centered with the cube center - Jacobian estimated at the cube center

Here, the “center” of the Stewart platform is not at the cube center (figure 2). The Jacobian is estimated at the cube center.

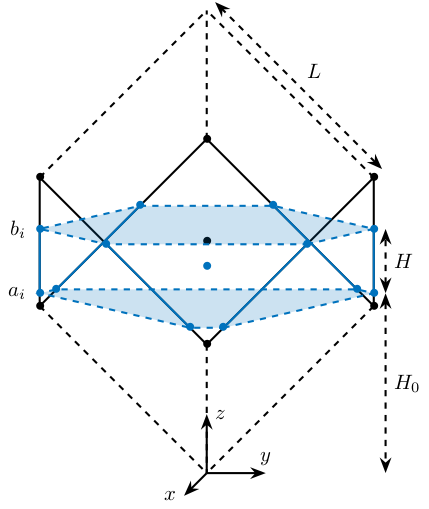
Figure 2: Not centered cubic configuration

The center of the cube is at \(z = 110\). The Stewart platform is from \(z = H_0 = 75\) to \(z = H_0 + H_{tot} = 175\). The center height of the Stewart platform is then at \(z = \frac{175-75}{2} = 50\). The center of the cube from the top platform is at \(z = 110 - 175 = -65\).

opts = struct(...
    'H_tot', 100,         ... % Total height of the Hexapod [mm]
    'L',     220/sqrt(3), ... % Size of the Cube [mm]
    'H',     60,          ... % Height between base joints and platform joints [mm]
    'H0',    75           ... % Height between the corner of the cube and the plane containing the base joints [mm]
    );
stewart = initializeCubicConfiguration(opts);
opts = struct(...
    'Jd_pos', [0, 0, -65], ... % Position of the Jacobian for displacement estimation from the top of the mobile platform [mm]
    'Jf_pos', [0, 0, -65]  ... % Position of the Jacobian for force location from the top of the mobile platform [mm]
    );
stewart = computeGeometricalProperties(stewart, opts);

K = stewart.Jf'*stewart.Jf;

2	-1.8e-17	2.6e-17	3.3e-18	0.04	1.7e-19
-1.8e-17	2	1.9e-16	-0.04	2.2e-19	-5.3e-19
2.6e-17	1.9e-16	2	-8.9e-18	6.5e-19	-5.8e-19
3.3e-18	-0.04	-8.9e-18	0.0089	-9.3e-20	9.8e-20
0.04	2.2e-19	6.5e-19	-9.3e-20	0.0089	-2.4e-18
1.7e-19	-5.3e-19	-5.8e-19	9.8e-20	-2.4e-18	0.032

We obtain \(k_x = k_y = k_z\) and \(k_{\theta_x} = k_{\theta_y}\), but the Stiffness matrix is not diagonal.

1.4 Cubic Stewart platform not centered with the cube center - Jacobian estimated at the Stewart platform center

Here, the “center” of the Stewart platform is not at the cube center. The Jacobian is estimated at the center of the Stewart platform.

opts = struct(...
    'H_tot', 100, ... % Total height of the Hexapod [mm]
    'L',     220/sqrt(3), ... % Size of the Cube [mm]
    'H',     60, ... % Height between base joints and platform joints [mm]
    'H0',    75 ... % Height between the corner of the cube and the plane containing the base joints [mm]
    );
stewart = initializeCubicConfiguration(opts);
opts = struct(...
    'Jd_pos', [0, 0, -60], ... % Position of the Jacobian for displacement estimation from the top of the mobile platform [mm]
    'Jf_pos', [0, 0, -60]  ... % Position of the Jacobian for force location from the top of the mobile platform [mm]
    );
stewart = computeGeometricalProperties(stewart, opts);

K = stewart.Jf'*stewart.Jf;

2	-1.8e-17	2.6e-17	-5.7e-19	0.03	1.7e-19
-1.8e-17	2	1.9e-16	-0.03	2.2e-19	-5.3e-19
2.6e-17	1.9e-16	2	-1.5e-17	6.5e-19	-5.8e-19
-5.7e-19	-0.03	-1.5e-17	0.0085	4.9e-20	1.7e-19
0.03	2.2e-19	6.5e-19	4.9e-20	0.0085	-1.1e-18
1.7e-19	-5.3e-19	-5.8e-19	1.7e-19	-1.1e-18	0.032

We obtain \(k_x = k_y = k_z\) and \(k_{\theta_x} = k_{\theta_y}\), but the Stiffness matrix is not diagonal.

1.5 Conclusion

The cubic configuration permits to have \(k_x = k_y = k_z\) and \(k_{\theta\x} = k_{\theta_y}\)
The stiffness matrix \(K\) is diagonal for the cubic configuration if the Stewart platform and the cube are centered and the Jacobian is estimated at the cube center

2 TODO Cubic size analysis

We here study the effect of the size of the cube used for the Stewart configuration.

We fix the height of the Stewart platform, the center of the cube is at the center of the Stewart platform.

We only vary the size of the cube.

H_cubes = 250:20:350;
stewarts = {zeros(length(H_cubes), 1)};

for i = 1:length(H_cubes)
  H_cube = H_cubes(i);
  H_tot = 100;
  H = 80;

  opts = struct(...
      'H_tot', H_tot, ... % Total height of the Hexapod [mm]
      'L',     H_cube/sqrt(3), ... % Size of the Cube [mm]
      'H',     H, ... % Height between base joints and platform joints [mm]
      'H0',    H_cube/2-H/2 ... % Height between the corner of the cube and the plane containing the base joints [mm]
      );
  stewart = initializeCubicConfiguration(opts);

  opts = struct(...
      'Jd_pos', [0, 0, H_cube/2-opts.H0-opts.H_tot], ... % Position of the Jacobian for displacement estimation from the top of the mobile platform [mm]
      'Jf_pos', [0, 0, H_cube/2-opts.H0-opts.H_tot]  ... % Position of the Jacobian for force location from the top of the mobile platform [mm]
      );
  stewart = computeGeometricalProperties(stewart, opts);
  stewarts(i) = {stewart};
end

The Stiffness matrix is computed for all generated Stewart platforms.

Ks = zeros(6, 6, length(H_cube));
for i = 1:length(H_cubes)
  Ks(:, :, i) = stewarts{i}.Jd'*stewarts{i}.Jd;
end

The only elements of \(K\) that vary are \(k_{\theta_x} = k_{\theta_y}\) and \(k_{\theta_z}\).

Finally, we plot \(k_{\theta_x} = k_{\theta_y}\) and \(k_{\theta_z}\)

figure;
hold on;
plot(H_cubes, squeeze(Ks(4, 4, :)), 'DisplayName', '$k_{\theta_x}$');
plot(H_cubes, squeeze(Ks(6, 6, :)), 'DisplayName', '$k_{\theta_z}$');
hold off;
legend('location', 'northwest');
xlabel('Cube Size [mm]'); ylabel('Rotational stiffnes [normalized]');

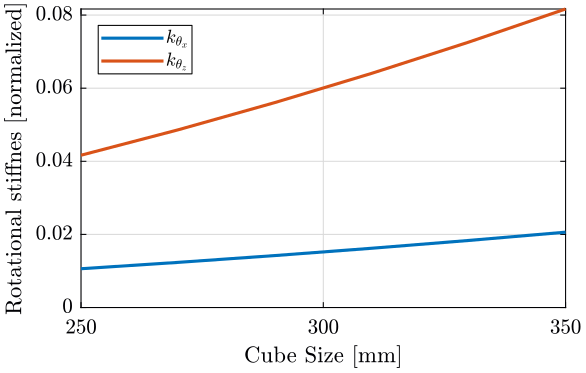
Figure 3: \(k_{\theta_x} = k_{\theta_y}\) and \(k_{\theta_z}\) function of the size of the cube

We observe that \(k_{\theta_x} = k_{\theta_y}\) and \(k_{\theta_z}\) increase linearly with the cube size.

In order to maximize the rotational stiffness of the Stewart platform, the size of the cube should be the highest possible. In that case, the legs will the further separated. Size of the cube is then limited by allowed space.

3 Functions

3.1 `generateCubicConfiguration`: Generate a Cubic Configuration

This Matlab function is accessible here.

Function description

function [stewart] = generateCubicConfiguration(stewart, args)
% generateCubicConfiguration - Generate a Cubic Configuration
%
% Syntax: [stewart] = generateCubicConfiguration(stewart, args)
%
% Inputs:
%    - stewart - A structure with the following fields
%        - H   [1x1] - Total height of the platform [m]
%    - args - Can have the following fields:
%        - Hc  [1x1] - Height of the "useful" part of the cube [m]
%        - FOc [1x1] - Height of the center of the cube with respect to {F} [m]
%        - FHa [1x1] - Height of the plane joining the points ai with respect to the frame {F} [m]
%        - MHb [1x1] - Height of the plane joining the points bi with respect to the frame {M} [m]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%        - Fa  [3x6] - Its i'th column is the position vector of joint ai with respect to {F}
%        - Mb  [3x6] - Its i'th column is the position vector of joint bi with respect to {M}

Documentation

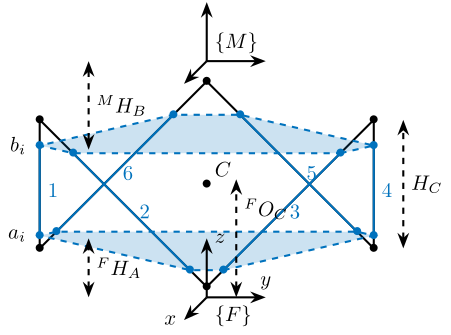
Figure 4: Cubic Configuration

Optional Parameters

arguments
    stewart
    args.Hc  (1,1) double {mustBeNumeric, mustBePositive} = 60e-3
    args.FOc (1,1) double {mustBeNumeric} = 50e-3
    args.FHa (1,1) double {mustBeNumeric, mustBePositive} = 15e-3
    args.MHb (1,1) double {mustBeNumeric, mustBePositive} = 15e-3
end

Position of the Cube

We define the useful points of the cube with respect to the Cube’s center. \({}^{C}C\) are the 6 vertices of the cubes expressed in a frame {C} which is located at the center of the cube and aligned with {F} and {M}.

sx = [ 2; -1; -1];
sy = [ 0;  1; -1];
sz = [ 1;  1;  1];

R = [sx, sy, sz]./vecnorm([sx, sy, sz]);

L = args.Hc*sqrt(3);

Cc = R'*[[0;0;L],[L;0;L],[L;0;0],[L;L;0],[0;L;0],[0;L;L]] - [0;0;1.5*args.Hc];

CCf = [Cc(:,1), Cc(:,3), Cc(:,3), Cc(:,5), Cc(:,5), Cc(:,1)]; % CCf(:,i) corresponds to the bottom cube's vertice corresponding to the i'th leg
CCm = [Cc(:,2), Cc(:,2), Cc(:,4), Cc(:,4), Cc(:,6), Cc(:,6)]; % CCm(:,i) corresponds to the top cube's vertice corresponding to the i'th leg

Compute the pose

We can compute the vector of each leg \({}^{C}\hat{\bm{s}}_{i}\) (unit vector from \({}^{C}C_{f}\) to \({}^{C}C_{m}\)).

CSi = (CCm - CCf)./vecnorm(CCm - CCf);

We now which to compute the position of the joints \(a_{i}\) and \(b_{i}\).

stewart.Fa = CCf + [0; 0; args.FOc] + ((args.FHa-(args.FOc-args.Hc/2))./CSi(3,:)).*CSi;
stewart.Mb = CCf + [0; 0; args.FOc-stewart.H] + ((stewart.H-args.MHb-(args.FOc-args.Hc/2))./CSi(3,:)).*CSi;

Bibliography

[geng94_six_degree_of_freed_activ] Geng & Haynes, Six Degree-Of-Freedom Active Vibration Control Using the Stewart Platforms, IEEE Transactions on Control Systems Technology, 2(1), 45-53 (1994). link. doi.
[preumont07_six_axis_singl_stage_activ] Preumont, Horodinca, Romanescu, de Marneffe, Avraam, Deraemaeker, Bossens & Abu Hanieh, A Six-Axis Single-Stage Active Vibration Isolator Based on Stewart Platform, Journal of Sound and Vibration, 300(3-5), 644-661 (2007). link. doi.
[jafari03_orthog_gough_stewar_platf_microm] Jafari & McInroy, Orthogonal Gough-Stewart Platforms for Micromanipulation, IEEE Transactions on Robotics and Automation, 19(4), 595-603 (2003). link. doi.