Stewart Platform - Simscape Model

1. Procedure
2. Matlab Code
- 2.1. Simscape Model
- 2.2. Test the functions
3. initializeFramesPositions: Initialize the positions of frames {A}, {B}, {F} and {M}
4. generateCubicConfiguration: Generate a Cubic Configuration
5. computeJointsPose: Compute the Pose of the Joints
6. initializeStrutDynamics: Add Stiffness and Damping properties of each strut
7. computeJacobian: Compute the Jacobian Matrix
8. inverseKinematics: Compute Inverse Kinematics
9. forwardKinematicsApprox: Compute the Forward Kinematics

Stewart platforms are generated in multiple steps.

We define 4 important frames:

\(\{F\}\): Frame fixed to the Fixed base and located at the center of its bottom surface. This is used to fix the Stewart platform to some support.
\(\{M\}\): Frame fixed to the Moving platform and located at the center of its top surface. This is used to place things on top of the Stewart platform.
\(\{A\}\): Frame fixed to the fixed base. It defined the center of rotation of the moving platform.
\(\{B\}\): Frame fixed to the moving platform. The motion of the moving platforms and forces applied to it are defined with respect to this frame \(\{B\}\).

Then, we define the location of the spherical joints:

\(\bm{a}_{i}\) are the position of the spherical joints fixed to the fixed base
\(\bm{b}_{i}\) are the position of the spherical joints fixed to the moving platform

We define the rest position of the Stewart platform:

For simplicity, we suppose that the fixed base and the moving platform are parallel and aligned with the vertical axis at their rest position.
Thus, to define the rest position of the Stewart platform, we just have to defined its total height \(H\). \(H\) corresponds to the distance from the bottom of the fixed base to the top of the moving platform.

From \(\bm{a}_{i}\) and \(\bm{b}_{i}\), we can determine the length and orientation of each strut:

\(l_{i}\) is the length of the strut
\({}^{A}\hat{\bm{s}}_{i}\) is the unit vector align with the strut

The position of the Spherical joints can be computed using various methods:

Cubic configuration
Circular configuration
Arbitrary position
These methods should be easily scriptable and corresponds to specific functions that returns \({}^{F}\bm{a}_{i}\) and \({}^{M}\bm{b}_{i}\). The input of these functions are the parameters corresponding to the wanted geometry.

For Simscape, we need:

The position and orientation of each spherical joint fixed to the fixed base: \({}^{F}\bm{a}_{i}\) and \({}^{F}\bm{R}_{a_{i}}\)
The position and orientation of each spherical joint fixed to the moving platform: \({}^{M}\bm{b}_{i}\) and \({}^{M}\bm{R}_{b_{i}}\)
The rest length of each strut: \(l_{i}\)
The stiffness and damping of each actuator: \(k_{i}\) and \(c_{i}\)
The position of the frame \(\{A\}\) with respect to the frame \(\{F\}\): \({}^{F}\bm{O}_{A}\)
The position of the frame \(\{B\}\) with respect to the frame \(\{M\}\): \({}^{M}\bm{O}_{B}\)

1 Procedure

The procedure to define the Stewart platform is the following:

Define the initial position of frames {A}, {B}, {F} and {M}. We do that using the initializeFramesPositions function. We have to specify the total height of the Stewart platform \(H\) and the position \({}^{M}O_{B}\) of {B} with respect to {M}.
Compute the positions of joints \({}^{F}a_{i}\) and \({}^{M}b_{i}\). We can do that using various methods depending on the wanted architecture:
- generateCubicConfiguration permits to generate a cubic configuration
Compute the position and orientation of the joints with respect to the fixed base and the moving platform. This is done with the computeJointsPose function.
Define the dynamical properties of the Stewart platform. The output are the stiffness and damping of each strut \(k_{i}\) and \(c_{i}\). This can be done we simply choosing directly the stiffness and damping of each strut. The stiffness and damping of each actuator can also be determine from the wanted stiffness of the Stewart platform for instance.
Define the mass and inertia of each element of the Stewart platform.

By following this procedure, we obtain a Matlab structure stewart that contains all the information for the Simscape model and for further analysis.

2 Matlab Code

2.1 Simscape Model

open('stewart_platform.slx')

2.2 Test the functions

stewart = initializeFramesPositions('H', 90e-3, 'MO_B', 45e-3);
stewart = generateCubicConfiguration(stewart, 'Hc', 60e-3, 'FOc', 45e-3, 'FHa', 5e-3, 'MHb', 5e-3);
stewart = computeJointsPose(stewart);
stewart = initializeStrutDynamics(stewart, 'Ki', 1e6*ones(6,1), 'Ci', 1e2*ones(6,1));
stewart = computeJacobian(stewart);
[Li, dLi] = inverseKinematics(stewart, 'AP', [0;0;0.00001], 'ARB', eye(3));
[P, R] = forwardKinematicsApprox(stewart, 'dL', dLi)

3 `initializeFramesPositions`: Initialize the positions of frames {A}, {B}, {F} and {M}

This Matlab function is accessible here.

3.1 Function description

function [stewart] = initializeFramesPositions(args)
% initializeFramesPositions - Initialize the positions of frames {A}, {B}, {F} and {M}
%
% Syntax: [stewart] = initializeFramesPositions(args)
%
% Inputs:
%    - args - Can have the following fields:
%        - H    [1x1] - Total Height of the Stewart Platform (height from {F} to {M}) [m]
%        - MO_B [1x1] - Height of the frame {B} with respect to {M} [m]
%
% Outputs:
%    - stewart - A structure with the following fields:
%        - H    [1x1] - Total Height of the Stewart Platform [m]
%        - FO_M [3x1] - Position of {M} with respect to {F} [m]
%        - MO_B [3x1] - Position of {B} with respect to {M} [m]
%        - FO_A [3x1] - Position of {A} with respect to {F} [m]

3.2 Documentation

Figure 1: Definition of the position of the frames

3.3 Optional Parameters

arguments
    args.H    (1,1) double {mustBeNumeric, mustBePositive} = 90e-3
    args.MO_B (1,1) double {mustBeNumeric} = 50e-3
end

3.4 Initialize the Stewart structure

stewart = struct();

3.5 Compute the position of each frame

stewart.H = args.H; % Total Height of the Stewart Platform [m]

stewart.FO_M = [0; 0; stewart.H]; % Position of {M} with respect to {F} [m]

stewart.MO_B = [0; 0; args.MO_B]; % Position of {B} with respect to {M} [m]

stewart.FO_A = stewart.MO_B + stewart.FO_M; % Position of {A} with respect to {F} [m]

4 `generateCubicConfiguration`: Generate a Cubic Configuration

This Matlab function is accessible here.

4.1 Function description

function [stewart] = generateCubicConfiguration(stewart, args)
% generateCubicConfiguration - Generate a Cubic Configuration
%
% Syntax: [stewart] = generateCubicConfiguration(stewart, args)
%
% Inputs:
%    - stewart - A structure with the following fields
%        - H   [1x1] - Total height of the platform [m]
%    - args - Can have the following fields:
%        - Hc  [1x1] - Height of the "useful" part of the cube [m]
%        - FOc [1x1] - Height of the center of the cube with respect to {F} [m]
%        - FHa [1x1] - Height of the plane joining the points ai with respect to the frame {F} [m]
%        - MHb [1x1] - Height of the plane joining the points bi with respect to the frame {M} [m]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%        - Fa  [3x6] - Its i'th column is the position vector of joint ai with respect to {F}
%        - Mb  [3x6] - Its i'th column is the position vector of joint bi with respect to {M}

4.2 Documentation

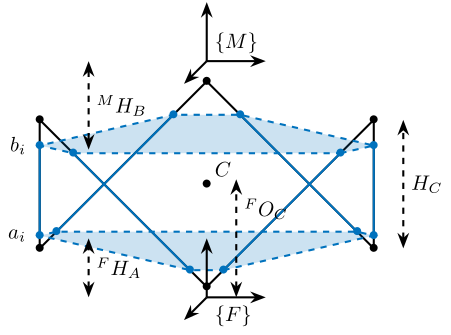
Figure 2: Cubic Configuration

4.3 Optional Parameters

arguments
    stewart
    args.Hc  (1,1) double {mustBeNumeric, mustBePositive} = 60e-3
    args.FOc (1,1) double {mustBeNumeric} = 50e-3
    args.FHa (1,1) double {mustBeNumeric, mustBePositive} = 15e-3
    args.MHb (1,1) double {mustBeNumeric, mustBePositive} = 15e-3
end

4.4 Position of the Cube

We define the useful points of the cube with respect to the Cube’s center. \({}^{C}C\) are the 6 vertices of the cubes expressed in a frame {C} which is located at the center of the cube and aligned with {F} and {M}.

sx = [ 2; -1; -1];
sy = [ 0;  1; -1];
sz = [ 1;  1;  1];

R = [sx, sy, sz]./vecnorm([sx, sy, sz]);

L = args.Hc*sqrt(3);

Cc = R'*[[0;0;L],[L;0;L],[L;0;0],[L;L;0],[0;L;0],[0;L;L]] - [0;0;1.5*args.Hc];

CCf = [Cc(:,1), Cc(:,3), Cc(:,3), Cc(:,5), Cc(:,5), Cc(:,1)]; % CCf(:,i) corresponds to the bottom cube's vertice corresponding to the i'th leg
CCm = [Cc(:,2), Cc(:,2), Cc(:,4), Cc(:,4), Cc(:,6), Cc(:,6)]; % CCm(:,i) corresponds to the top cube's vertice corresponding to the i'th leg

4.5 Compute the pose

We can compute the vector of each leg \({}^{C}\hat{\bm{s}}_{i}\) (unit vector from \({}^{C}C_{f}\) to \({}^{C}C_{m}\)).

CSi = (CCm - CCf)./vecnorm(CCm - CCf);

We now which to compute the position of the joints \(a_{i}\) and \(b_{i}\).

stewart.Fa = CCf + [0; 0; args.FOc] + ((args.FHa-(args.FOc-args.Hc/2))./CSi(3,:)).*CSi;
stewart.Mb = CCf + [0; 0; args.FOc-stewart.H] + ((stewart.H-args.MHb-(args.FOc-args.Hc/2))./CSi(3,:)).*CSi;

5 `computeJointsPose`: Compute the Pose of the Joints

This Matlab function is accessible here.

5.1 Function description

function [stewart] = computeJointsPose(stewart)
% computeJointsPose -
%
% Syntax: [stewart] = computeJointsPose(stewart)
%
% Inputs:
%    - stewart - A structure with the following fields
%        - Fa   [3x6] - Its i'th column is the position vector of joint ai with respect to {F}
%        - Mb   [3x6] - Its i'th column is the position vector of joint bi with respect to {M}
%        - FO_A [3x1] - Position of {A} with respect to {F}
%        - MO_B [3x1] - Position of {B} with respect to {M}
%        - FO_M [3x1] - Position of {M} with respect to {F}
%
% Outputs:
%    - stewart - A structure with the following added fields
%        - Aa  [3x6]   - The i'th column is the position of ai with respect to {A}
%        - Ab  [3x6]   - The i'th column is the position of bi with respect to {A}
%        - Ba  [3x6]   - The i'th column is the position of ai with respect to {B}
%        - Bb  [3x6]   - The i'th column is the position of bi with respect to {B}
%        - l   [6x1]   - The i'th element is the initial length of strut i
%        - As  [3x6]   - The i'th column is the unit vector of strut i expressed in {A}
%        - Bs  [3x6]   - The i'th column is the unit vector of strut i expressed in {B}
%        - FRa [3x3x6] - The i'th 3x3 array is the rotation matrix to orientate the bottom of the i'th strut from {F}
%        - MRb [3x3x6] - The i'th 3x3 array is the rotation matrix to orientate the top of the i'th strut from {M}

5.2 Documentation

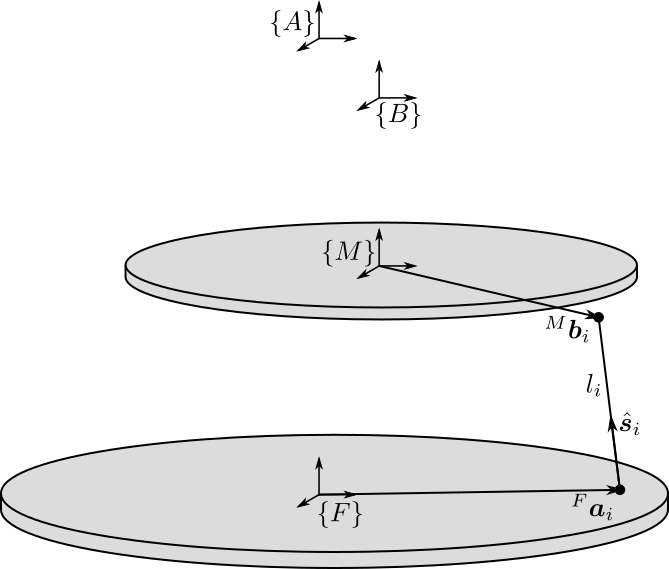
Figure 3: Position and orientation of the struts

5.3 Compute the position of the Joints

stewart.Aa = stewart.Fa - repmat(stewart.FO_A, [1, 6]);
stewart.Bb = stewart.Mb - repmat(stewart.MO_B, [1, 6]);

stewart.Ab = stewart.Bb - repmat(-stewart.MO_B-stewart.FO_M+stewart.FO_A, [1, 6]);
stewart.Ba = stewart.Aa - repmat( stewart.MO_B+stewart.FO_M-stewart.FO_A, [1, 6]);

5.4 Compute the strut length and orientation

stewart.As = (stewart.Ab - stewart.Aa)./vecnorm(stewart.Ab - stewart.Aa); % As_i is the i'th vector of As

stewart.l = vecnorm(stewart.Ab - stewart.Aa)';

stewart.Bs = (stewart.Bb - stewart.Ba)./vecnorm(stewart.Bb - stewart.Ba);

5.5 Compute the orientation of the Joints

stewart.FRa = zeros(3,3,6);
stewart.MRb = zeros(3,3,6);

for i = 1:6
  stewart.FRa(:,:,i) = [cross([0;1;0], stewart.As(:,i)) , cross(stewart.As(:,i), cross([0;1;0], stewart.As(:,i))) , stewart.As(:,i)];
  stewart.FRa(:,:,i) = stewart.FRa(:,:,i)./vecnorm(stewart.FRa(:,:,i));

  stewart.MRb(:,:,i) = [cross([0;1;0], stewart.Bs(:,i)) , cross(stewart.Bs(:,i), cross([0;1;0], stewart.Bs(:,i))) , stewart.Bs(:,i)];
  stewart.MRb(:,:,i) = stewart.MRb(:,:,i)./vecnorm(stewart.MRb(:,:,i));
end

6 `initializeStrutDynamics`: Add Stiffness and Damping properties of each strut

This Matlab function is accessible here.

6.1 Function description

function [stewart] = initializeStrutDynamics(stewart, args)
% initializeStrutDynamics - Add Stiffness and Damping properties of each strut
%
% Syntax: [stewart] = initializeStrutDynamics(args)
%
% Inputs:
%    - args - Structure with the following fields:
%        - Ki [6x1] - Stiffness of each strut [N/m]
%        - Ci [6x1] - Damping of each strut [N/(m/s)]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%        - Ki [6x1] - Stiffness of each strut [N/m]
%        - Ci [6x1] - Damping of each strut [N/(m/s)]

6.2 Optional Parameters

arguments
    stewart
    args.Ki (6,1) double {mustBeNumeric, mustBePositive} = 1e6*ones(6,1)
    args.Ci (6,1) double {mustBeNumeric, mustBePositive} = 1e2*ones(6,1)
end

6.3 Add Stiffness and Damping properties of each strut

stewart.Ki = args.Ki;
stewart.Ci = args.Ci;

7 `computeJacobian`: Compute the Jacobian Matrix

This Matlab function is accessible here.

7.1 Function description

function [stewart] = computeJacobian(stewart)
% computeJacobian -
%
% Syntax: [stewart] = computeJacobian(stewart)
%
% Inputs:
%    - stewart - With at least the following fields:
%        - As [3x6] - The 6 unit vectors for each strut expressed in {A}
%        - Ab [3x6] - The 6 position of the joints bi expressed in {A}
%
% Outputs:
%    - stewart - With the 3 added field:
%        - J [6x6] - The Jacobian Matrix
%        - K [6x6] - The Stiffness Matrix
%        - C [6x6] - The Compliance Matrix

7.2 Compute Jacobian Matrix

stewart.J = [stewart.As' , cross(stewart.Ab, stewart.As)'];

7.3 Compute Stiffness Matrix

stewart.K = stewart.J'*diag(stewart.Ki)*stewart.J;

7.4 Compute Compliance Matrix

stewart.C = inv(stewart.K);

8 `inverseKinematics`: Compute Inverse Kinematics

This Matlab function is accessible here.

8.1 Function description

function [Li, dLi] = inverseKinematics(stewart, args)
% inverseKinematics - Compute the needed length of each strut to have the wanted position and orientation of {B} with respect to {A}
%
% Syntax: [stewart] = inverseKinematics(stewart)
%
% Inputs:
%    - stewart - A structure with the following fields
%        - Aa   [3x6] - The positions ai expressed in {A}
%        - Bb   [3x6] - The positions bi expressed in {B}
%    - args - Can have the following fields:
%        - AP   [3x1] - The wanted position of {B} with respect to {A}
%        - ARB  [3x3] - The rotation matrix that gives the wanted orientation of {B} with respect to {A}
%
% Outputs:
%    - Li   [6x1] - The 6 needed length of the struts in [m] to have the wanted pose of {B} w.r.t. {A}
%    - dLi  [6x1] - The 6 needed displacement of the struts from the initial position in [m] to have the wanted pose of {B} w.r.t. {A}

8.2 Optional Parameters

arguments
    stewart
    args.AP  (3,1) double {mustBeNumeric} = zeros(3,1)
    args.ARB (3,3) double {mustBeNumeric} = eye(3)
end

8.3 Theory

For inverse kinematic analysis, it is assumed that the position \({}^A\bm{P}\) and orientation of the moving platform \({}^A\bm{R}_B\) are given and the problem is to obtain the joint variables, namely, \(\bm{L} = [l_1, l_2, \dots, l_6]^T\).

From the geometry of the manipulator, the loop closure for each limb, \(i = 1, 2, \dots, 6\) can be written as

\begin{align*} l_i {}^A\hat{\bm{s}}_i &= {}^A\bm{A} + {}^A\bm{b}_i - {}^A\bm{a}_i \\ &= {}^A\bm{A} + {}^A\bm{R}_b {}^B\bm{b}_i - {}^A\bm{a}_i \end{align*}

To obtain the length of each actuator and eliminate \(\hat{\bm{s}}_i\), it is sufficient to dot multiply each side by itself:

\begin{equation} l_i^2 \left[ {}^A\hat{\bm{s}}_i^T {}^A\hat{\bm{s}}_i \right] = \left[ {}^A\bm{P} + {}^A\bm{R}_B {}^B\bm{b}_i - {}^A\bm{a}_i \right]^T \left[ {}^A\bm{P} + {}^A\bm{R}_B {}^B\bm{b}_i - {}^A\bm{a}_i \right] \end{equation}

Hence, for \(i = 1, 2, \dots, 6\), each limb length can be uniquely determined by:

\begin{equation} l_i = \sqrt{{}^A\bm{P}^T {}^A\bm{P} + {}^B\bm{b}_i^T {}^B\bm{b}_i + {}^A\bm{a}_i^T {}^A\bm{a}_i - 2 {}^A\bm{P}^T {}^A\bm{a}_i + 2 {}^A\bm{P}^T \left[{}^A\bm{R}_B {}^B\bm{b}_i\right] - 2 \left[{}^A\bm{R}_B {}^B\bm{b}_i\right]^T {}^A\bm{a}_i} \end{equation}

If the position and orientation of the moving platform lie in the feasible workspace of the manipulator, one unique solution to the limb length is determined by the above equation. Otherwise, when the limbs’ lengths derived yield complex numbers, then the position or orientation of the moving platform is not reachable.

8.4 Compute

Li = sqrt(args.AP'*args.AP + diag(stewart.Bb'*stewart.Bb) + diag(stewart.Aa'*stewart.Aa) - (2*args.AP'*stewart.Aa)' + (2*args.AP'*(args.ARB*stewart.Bb))' - diag(2*(args.ARB*stewart.Bb)'*stewart.Aa));

dLi = Li-stewart.l;

9 `forwardKinematicsApprox`: Compute the Forward Kinematics

This Matlab function is accessible here.

9.1 Function description

function [P, R] = forwardKinematicsApprox(stewart, args)
% forwardKinematicsApprox - Computed the approximate pose of {B} with respect to {A} from the length of each strut and using
%                           the Jacobian Matrix
%
% Syntax: [P, R] = forwardKinematicsApprox(stewart, args)
%
% Inputs:
%    - stewart - A structure with the following fields
%        - J  [6x6] - The Jacobian Matrix
%    - args - Can have the following fields:
%        - dL [6x1] - Displacement of each strut [m]
%
% Outputs:
%    - P  [3x1] - The estimated position of {B} with respect to {A}
%    - R  [3x3] - The estimated rotation matrix that gives the orientation of {B} with respect to {A}

9.2 Optional Parameters

arguments
    stewart
    args.dL (6,1) double {mustBeNumeric} = zeros(6,1)
end

9.3 Computation

From a small displacement of each strut \(d\bm{\mathcal{L}}\), we can compute the position and orientation of {B} with respect to {A} using the following formula: \[ d \bm{\mathcal{X}} = \bm{J}^{-1} d\bm{\mathcal{L}} \]

X = stewart.J\args.dL;

The position vector corresponds to the first 3 elements.

P = X(1:3);

The next 3 elements are the orientation of {B} with respect to {A} expressed using the screw axis.

theta = norm(X(4:6));
s = X(4:6)/theta;

We then compute the corresponding rotation matrix.

R = [s(1)^2*(1-cos(theta)) + cos(theta) ,        s(1)*s(2)*(1-cos(theta)) - s(3)*sin(theta), s(1)*s(3)*(1-cos(theta)) + s(2)*sin(theta);
     s(2)*s(1)*(1-cos(theta)) + s(3)*sin(theta), s(2)^2*(1-cos(theta)) + cos(theta),         s(2)*s(3)*(1-cos(theta)) - s(1)*sin(theta);
     s(3)*s(1)*(1-cos(theta)) - s(2)*sin(theta), s(3)*s(2)*(1-cos(theta)) + s(1)*sin(theta), s(3)^2*(1-cos(theta)) + cos(theta)];

Stewart Platform - Simscape Model

Table of Contents

1 Procedure

2 Matlab Code

2.1 Simscape Model

2.2 Test the functions

3 initializeFramesPositions: Initialize the positions of frames {A}, {B}, {F} and {M}

3.1 Function description

3.2 Documentation

3.3 Optional Parameters

3.4 Initialize the Stewart structure

3.5 Compute the position of each frame

4 generateCubicConfiguration: Generate a Cubic Configuration

4.1 Function description

4.2 Documentation

4.3 Optional Parameters

4.4 Position of the Cube

4.5 Compute the pose

5 computeJointsPose: Compute the Pose of the Joints

5.1 Function description

5.2 Documentation

5.3 Compute the position of the Joints

5.4 Compute the strut length and orientation

5.5 Compute the orientation of the Joints

6 initializeStrutDynamics: Add Stiffness and Damping properties of each strut

6.1 Function description

6.2 Optional Parameters

6.3 Add Stiffness and Damping properties of each strut

7 computeJacobian: Compute the Jacobian Matrix

7.1 Function description

7.2 Compute Jacobian Matrix

7.3 Compute Stiffness Matrix

7.4 Compute Compliance Matrix

8 inverseKinematics: Compute Inverse Kinematics

8.1 Function description

8.2 Optional Parameters

8.3 Theory

8.4 Compute

9 forwardKinematicsApprox: Compute the Forward Kinematics

9.1 Function description

9.2 Optional Parameters

9.3 Computation

3 `initializeFramesPositions`: Initialize the positions of frames {A}, {B}, {F} and {M}

4 `generateCubicConfiguration`: Generate a Cubic Configuration

5 `computeJointsPose`: Compute the Pose of the Joints

6 `initializeStrutDynamics`: Add Stiffness and Damping properties of each strut

7 `computeJacobian`: Compute the Jacobian Matrix

8 `inverseKinematics`: Compute Inverse Kinematics

9 `forwardKinematicsApprox`: Compute the Forward Kinematics