<?xml version="1.0" encoding="utf-8"?>
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN"
"http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<!-- 2019-08-26 lun. 11:56 -->
<meta http-equiv="Content-Type" content="text/html;charset=utf-8" />
<meta name="viewport" content="width=device-width, initial-scale=1" />
<title>Stewart Platform - Simscape Model</title>
<meta name="generator" content="Org mode" />
<meta name="author" content="Thomas Dehaeze" />
<style type="text/css">
<!--/*--><![CDATA[/*><!--*/
.title { text-align: center;
margin-bottom: .2em; }
.subtitle { text-align: center;
font-size: medium;
font-weight: bold;
margin-top:0; }
.todo { font-family: monospace; color: red; }
.done { font-family: monospace; color: green; }
.priority { font-family: monospace; color: orange; }
.tag { background-color: #eee; font-family: monospace;
padding: 2px; font-size: 80%; font-weight: normal; }
.timestamp { color: #bebebe; }
.timestamp-kwd { color: #5f9ea0; }
.org-right { margin-left: auto; margin-right: 0px; text-align: right; }
.org-left { margin-left: 0px; margin-right: auto; text-align: left; }
.org-center { margin-left: auto; margin-right: auto; text-align: center; }
.underline { text-decoration: underline; }
#postamble p, #preamble p { font-size: 90%; margin: .2em; }
p.verse { margin-left: 3%; }
pre {
border: 1px solid #ccc;
box-shadow: 3px 3px 3px #eee;
padding: 8pt;
font-family: monospace;
overflow: auto;
margin: 1.2em;
}
pre.src {
position: relative;
overflow: visible;
padding-top: 1.2em;
}
pre.src:before {
display: none;
position: absolute;
background-color: white;
top: -10px;
right: 10px;
padding: 3px;
border: 1px solid black;
}
pre.src:hover:before { display: inline;}
/* Languages per Org manual */
pre.src-asymptote:before { content: 'Asymptote'; }
pre.src-awk:before { content: 'Awk'; }
pre.src-C:before { content: 'C'; }
/* pre.src-C++ doesn't work in CSS */
pre.src-clojure:before { content: 'Clojure'; }
pre.src-css:before { content: 'CSS'; }
pre.src-D:before { content: 'D'; }
pre.src-ditaa:before { content: 'ditaa'; }
pre.src-dot:before { content: 'Graphviz'; }
pre.src-calc:before { content: 'Emacs Calc'; }
pre.src-emacs-lisp:before { content: 'Emacs Lisp'; }
pre.src-fortran:before { content: 'Fortran'; }
pre.src-gnuplot:before { content: 'gnuplot'; }
pre.src-haskell:before { content: 'Haskell'; }
pre.src-hledger:before { content: 'hledger'; }
pre.src-java:before { content: 'Java'; }
pre.src-js:before { content: 'Javascript'; }
pre.src-latex:before { content: 'LaTeX'; }
pre.src-ledger:before { content: 'Ledger'; }
pre.src-lisp:before { content: 'Lisp'; }
pre.src-lilypond:before { content: 'Lilypond'; }
pre.src-lua:before { content: 'Lua'; }
pre.src-matlab:before { content: 'MATLAB'; }
pre.src-mscgen:before { content: 'Mscgen'; }
pre.src-ocaml:before { content: 'Objective Caml'; }
pre.src-octave:before { content: 'Octave'; }
pre.src-org:before { content: 'Org mode'; }
pre.src-oz:before { content: 'OZ'; }
pre.src-plantuml:before { content: 'Plantuml'; }
pre.src-processing:before { content: 'Processing.js'; }
pre.src-python:before { content: 'Python'; }
pre.src-R:before { content: 'R'; }
pre.src-ruby:before { content: 'Ruby'; }
pre.src-sass:before { content: 'Sass'; }
pre.src-scheme:before { content: 'Scheme'; }
pre.src-screen:before { content: 'Gnu Screen'; }
pre.src-sed:before { content: 'Sed'; }
pre.src-sh:before { content: 'shell'; }
pre.src-sql:before { content: 'SQL'; }
pre.src-sqlite:before { content: 'SQLite'; }
/* additional languages in org.el's org-babel-load-languages alist */
pre.src-forth:before { content: 'Forth'; }
pre.src-io:before { content: 'IO'; }
pre.src-J:before { content: 'J'; }
pre.src-makefile:before { content: 'Makefile'; }
pre.src-maxima:before { content: 'Maxima'; }
pre.src-perl:before { content: 'Perl'; }
pre.src-picolisp:before { content: 'Pico Lisp'; }
pre.src-scala:before { content: 'Scala'; }
pre.src-shell:before { content: 'Shell Script'; }
pre.src-ebnf2ps:before { content: 'ebfn2ps'; }
/* additional language identifiers per "defun org-babel-execute"
in ob-*.el */
pre.src-cpp:before { content: 'C++'; }
pre.src-abc:before { content: 'ABC'; }
pre.src-coq:before { content: 'Coq'; }
pre.src-groovy:before { content: 'Groovy'; }
/* additional language identifiers from org-babel-shell-names in
ob-shell.el: ob-shell is the only babel language using a lambda to put
the execution function name together. */
pre.src-bash:before { content: 'bash'; }
pre.src-csh:before { content: 'csh'; }
pre.src-ash:before { content: 'ash'; }
pre.src-dash:before { content: 'dash'; }
pre.src-ksh:before { content: 'ksh'; }
pre.src-mksh:before { content: 'mksh'; }
pre.src-posh:before { content: 'posh'; }
/* Additional Emacs modes also supported by the LaTeX listings package */
pre.src-ada:before { content: 'Ada'; }
pre.src-asm:before { content: 'Assembler'; }
pre.src-caml:before { content: 'Caml'; }
pre.src-delphi:before { content: 'Delphi'; }
pre.src-html:before { content: 'HTML'; }
pre.src-idl:before { content: 'IDL'; }
pre.src-mercury:before { content: 'Mercury'; }
pre.src-metapost:before { content: 'MetaPost'; }
pre.src-modula-2:before { content: 'Modula-2'; }
pre.src-pascal:before { content: 'Pascal'; }
pre.src-ps:before { content: 'PostScript'; }
pre.src-prolog:before { content: 'Prolog'; }
pre.src-simula:before { content: 'Simula'; }
pre.src-tcl:before { content: 'tcl'; }
pre.src-tex:before { content: 'TeX'; }
pre.src-plain-tex:before { content: 'Plain TeX'; }
pre.src-verilog:before { content: 'Verilog'; }
pre.src-vhdl:before { content: 'VHDL'; }
pre.src-xml:before { content: 'XML'; }
pre.src-nxml:before { content: 'XML'; }
/* add a generic configuration mode; LaTeX export needs an additional
(add-to-list 'org-latex-listings-langs '(conf " ")) in .emacs */
pre.src-conf:before { content: 'Configuration File'; }
table { border-collapse:collapse; }
caption.t-above { caption-side: top; }
caption.t-bottom { caption-side: bottom; }
td, th { vertical-align:top; }
th.org-right { text-align: center; }
th.org-left { text-align: center; }
th.org-center { text-align: center; }
td.org-right { text-align: right; }
td.org-left { text-align: left; }
td.org-center { text-align: center; }
dt { font-weight: bold; }
.footpara { display: inline; }
.footdef { margin-bottom: 1em; }
.figure { padding: 1em; }
.figure p { text-align: center; }
.equation-container {
display: table;
text-align: center;
width: 100%;
}
.equation {
vertical-align: middle;
}
.equation-label {
display: table-cell;
text-align: right;
vertical-align: middle;
}
.inlinetask {
padding: 10px;
border: 2px solid gray;
margin: 10px;
background: #ffffcc;
}
#org-div-home-and-up
{ text-align: right; font-size: 70%; white-space: nowrap; }
textarea { overflow-x: auto; }
.linenr { font-size: smaller }
.code-highlighted { background-color: #ffff00; }
.org-info-js_info-navigation { border-style: none; }
#org-info-js_console-label
{ font-size: 10px; font-weight: bold; white-space: nowrap; }
.org-info-js_search-highlight
{ background-color: #ffff00; color: #000000; font-weight: bold; }
.org-svg { width: 90%; }
/*]]>*/-->
</style>
<link rel="stylesheet" type="text/css" href="./css/htmlize.css"/>
<link rel="stylesheet" type="text/css" href="./css/readtheorg.css"/>
<script src="./js/jquery.min.js"></script>
<script src="./js/bootstrap.min.js"></script>
<script src="./js/jquery.stickytableheaders.min.js"></script>
<script src="./js/readtheorg.js"></script>
<script type="text/javascript">
/*
@licstart The following is the entire license notice for the
JavaScript code in this tag.
Copyright (C) 2012-2019 Free Software Foundation, Inc.
The JavaScript code in this tag is free software: you can
redistribute it and/or modify it under the terms of the GNU
General Public License (GNU GPL) as published by the Free Software
Foundation, either version 3 of the License, or (at your option)
any later version. The code is distributed WITHOUT ANY WARRANTY;
without even the implied warranty of MERCHANTABILITY or FITNESS
FOR A PARTICULAR PURPOSE. See the GNU GPL for more details.
As additional permission under GNU GPL version 3 section 7, you
may distribute non-source (e.g., minimized or compacted) forms of
that code without the copy of the GNU GPL normally required by
section 4, provided you include this license notice and a URL
through which recipients can access the Corresponding Source.
@licend The above is the entire license notice
for the JavaScript code in this tag.
*/
<!--/*--><![CDATA[/*><!--*/
function CodeHighlightOn(elem, id)
{
var target = document.getElementById(id);
if(null != target) {
elem.cacheClassElem = elem.className;
elem.cacheClassTarget = target.className;
target.className = "code-highlighted";
elem.className = "code-highlighted";
}
}
function CodeHighlightOff(elem, id)
{
var target = document.getElementById(id);
if(elem.cacheClassElem)
elem.className = elem.cacheClassElem;
if(elem.cacheClassTarget)
target.className = elem.cacheClassTarget;
}
/*]]>*///-->
</script>
<script type="text/x-mathjax-config">
MathJax.Hub.Config({
displayAlign: "center",
displayIndent: "0em",
"HTML-CSS": { scale: 100,
linebreaks: { automatic: "false" },
webFont: "TeX"
},
SVG: {scale: 100,
linebreaks: { automatic: "false" },
font: "TeX"},
NativeMML: {scale: 100},
TeX: { equationNumbers: {autoNumber: "AMS"},
MultLineWidth: "85%",
TagSide: "right",
TagIndent: ".8em"
}
});
</script>
<script type="text/javascript"
src="https://cdnjs.cloudflare.com/ajax/libs/mathjax/2.7.0/MathJax.js?config=TeX-AMS_HTML"></script>
</head>
<body>
<div id="org-div-home-and-up">
<a accesskey="h" href="./index.html"> UP </a>
|
<a accesskey="H" href="./index.html"> HOME </a>
</div><div id="content">
<h1 class="title">Stewart Platform - Simscape Model</h1>
<div id="table-of-contents">
<h2>Table of Contents</h2>
<div id="text-table-of-contents">
<ul>
<li><a href="#orge1bdaa4">1. initializeGeneralConfiguration</a>
<ul>
<li><a href="#orgb189499">1.1. Function description</a></li>
<li><a href="#org26f683d">1.2. Optional Parameters</a></li>
<li><a href="#org22df53a">1.3. Geometry Description</a></li>
<li><a href="#orgcf32e31">1.4. Compute Aa and Ab</a></li>
<li><a href="#org4931162">1.5. Returns Stewart Structure</a></li>
</ul>
</li>
<li><a href="#orgc4f14da">2. computeGeometricalProperties</a>
<ul>
<li><a href="#org7550562">2.1. Function description</a></li>
<li><a href="#org0ec8d5e">2.2. Optional Parameters</a></li>
<li><a href="#orgdc858fe">2.3. Rotation matrices</a></li>
<li><a href="#orgc0b0116">2.4. Jacobian matrices</a></li>
</ul>
</li>
<li><a href="#org35cb27a">3. initializeMechanicalElements</a>
<ul>
<li><a href="#orgeeb3d2f">3.1. Function description</a></li>
<li><a href="#org02f8d24">3.2. Optional Parameters</a></li>
<li><a href="#orga56f635">3.3. Bottom Plate</a></li>
<li><a href="#orge8a195c">3.4. Top Plate</a></li>
<li><a href="#org8725a51">3.5. Legs</a></li>
<li><a href="#org722b78f">3.6. Ball Joints</a></li>
</ul>
</li>
<li><a href="#org5ba95d3">4. initializeSample</a>
<ul>
<li><a href="#org2dd34bb">4.1. Function description</a></li>
<li><a href="#org2aa1dac">4.2. Optional Parameters</a></li>
<li><a href="#orgea68e95">4.3. Save the Sample structure</a></li>
</ul>
</li>
</ul>
</div>
</div>
<p>
Stewart platforms are generated in multiple steps.
</p>
<p>
First, geometrical parameters are defined:
</p>
<ul class="org-ul">
<li>\({}^Aa_i\) - Position of the joints fixed to the fixed base w.r.t \(\{A\}\)</li>
<li>\({}^Ab_i\) - Position of the joints fixed to the mobile platform w.r.t \(\{A\}\)</li>
<li>\({}^Bb_i\) - Position of the joints fixed to the mobile platform w.r.t \(\{B\}\)</li>
<li>\(H\) - Total height of the mobile platform</li>
</ul>
<p>
These parameter are enough to determine all the kinematic properties of the platform like the Jacobian, stroke, stiffness, …
These geometrical parameters can be generated using different functions: <code>initializeCubicConfiguration</code> for cubic configuration or <code>initializeGeneralConfiguration</code> for more general configuration.
</p>
<p>
A function <code>computeGeometricalProperties</code> is then used to compute:
</p>
<ul class="org-ul">
<li>\(J_f\) - Jacobian matrix for the force location</li>
<li>\(J_d\) - Jacobian matrix for displacement estimation</li>
<li>\(R_m\) - Rotation matrices to position the leg vectors</li>
</ul>
<p>
Then, geometrical parameters are computed for all the mechanical elements with the function <code>initializeMechanicalElements</code>:
</p>
<ul class="org-ul">
<li>Shape of the platforms
<ul class="org-ul">
<li>External Radius</li>
<li>Internal Radius</li>
<li>Density</li>
<li>Thickness</li>
</ul></li>
<li>Shape of the Legs
<ul class="org-ul">
<li>Radius</li>
<li>Size of ball joint</li>
<li>Density</li>
</ul></li>
</ul>
<p>
Other Parameters are defined for the Simscape simulation:
</p>
<ul class="org-ul">
<li>Sample mass, volume and position (<code>initializeSample</code> function)</li>
<li>Location of the inertial sensor</li>
<li>Location of the point for the differential measurements</li>
<li>Location of the Jacobian point for velocity/displacement computation</li>
</ul>
<div id="outline-container-orge1bdaa4" class="outline-2">
<h2 id="orge1bdaa4"><span class="section-number-2">1</span> initializeGeneralConfiguration</h2>
<div class="outline-text-2" id="text-1">
</div>
<div id="outline-container-orgb189499" class="outline-3">
<h3 id="orgb189499"><span class="section-number-3">1.1</span> Function description</h3>
<div class="outline-text-3" id="text-1-1">
<p>
The <code>initializeGeneralConfiguration</code> function takes one structure that contains configurations for the hexapod and returns one structure representing the Hexapod.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">function</span> <span class="org-variable-name"><span class="org-rainbow-delimiters-depth-1">[</span></span><span class="org-variable-name">stewart</span><span class="org-variable-name"><span class="org-rainbow-delimiters-depth-1">]</span></span> = <span class="org-function-name">initializeGeneralConfiguration</span><span class="org-rainbow-delimiters-depth-1">(</span><span class="org-variable-name">opts_param</span><span class="org-rainbow-delimiters-depth-1">)</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-org26f683d" class="outline-3">
<h3 id="org26f683d"><span class="section-number-3">1.2</span> Optional Parameters</h3>
<div class="outline-text-3" id="text-1-2">
<p>
Default values for opts.
</p>
<div class="org-src-container">
<pre class="src src-matlab">opts = struct<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-underline">...</span>
<span class="org-string">'H_tot'</span>, <span class="org-highlight-numbers-number">90</span>, <span class="org-underline">...</span> <span class="org-comment">% Height of the platform [mm]</span>
<span class="org-string">'H_joint'</span>, <span class="org-highlight-numbers-number">15</span>, <span class="org-underline">...</span> <span class="org-comment">% Height of the joints [mm]</span>
<span class="org-string">'H_plate'</span>, <span class="org-highlight-numbers-number">10</span>, <span class="org-underline">...</span> <span class="org-comment">% Thickness of the fixed and mobile platforms [mm]</span>
<span class="org-string">'R_bot'</span>, <span class="org-highlight-numbers-number">100</span>, <span class="org-underline">...</span> <span class="org-comment">% Radius where the legs articulations are positionned [mm]</span>
<span class="org-string">'R_top'</span>, <span class="org-highlight-numbers-number">80</span>, <span class="org-underline">...</span> <span class="org-comment">% Radius where the legs articulations are positionned [mm]</span>
<span class="org-string">'a_bot'</span>, <span class="org-highlight-numbers-number">10</span>, <span class="org-underline">...</span> <span class="org-comment">% Angle Offset [deg]</span>
<span class="org-string">'a_top'</span>, <span class="org-highlight-numbers-number">40</span>, <span class="org-underline">...</span> <span class="org-comment">% Angle Offset [deg]</span>
<span class="org-string">'da_top'</span>, <span class="org-highlight-numbers-number">0</span> <span class="org-underline">...</span> % Angle Offset from <span class="org-highlight-numbers-number">0</span> position [deg]
<span class="org-rainbow-delimiters-depth-1">)</span>;
</pre>
</div>
<p>
Populate opts with input parameters
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">if</span> exist<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-string">'opts_param','var'</span><span class="org-rainbow-delimiters-depth-1">)</span>
<span class="org-keyword">for</span> <span class="org-variable-name">opt</span> = <span class="org-constant">fieldnames</span><span class="org-constant"><span class="org-rainbow-delimiters-depth-1">(</span></span><span class="org-constant">opts_param</span><span class="org-constant"><span class="org-rainbow-delimiters-depth-1">)</span></span><span class="org-constant">'</span>
opts.<span class="org-rainbow-delimiters-depth-1">(</span>opt<span class="org-rainbow-delimiters-depth-2">{</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-2">}</span><span class="org-rainbow-delimiters-depth-1">)</span> = opts_param.<span class="org-rainbow-delimiters-depth-1">(</span>opt<span class="org-rainbow-delimiters-depth-2">{</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-2">}</span><span class="org-rainbow-delimiters-depth-1">)</span>;
<span class="org-keyword">end</span>
<span class="org-keyword">end</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-org22df53a" class="outline-3">
<h3 id="org22df53a"><span class="section-number-3">1.3</span> Geometry Description</h3>
<div class="outline-text-3" id="text-1-3">
<div id="orgeb6375e" class="figure">
<p><img src="./figs/stewart_bottom_plate.png" alt="stewart_bottom_plate.png" />
</p>
<p><span class="figure-number">Figure 1: </span>Schematic of the bottom plates with all the parameters</p>
</div>
</div>
</div>
<div id="outline-container-orgcf32e31" class="outline-3">
<h3 id="orgcf32e31"><span class="section-number-3">1.4</span> Compute Aa and Ab</h3>
<div class="outline-text-3" id="text-1-4">
<p>
We compute \([a_1, a_2, a_3, a_4, a_5, a_6]^T\) and \([b_1, b_2, b_3, b_4, b_5, b_6]^T\).
</p>
<div class="org-src-container">
<pre class="src src-matlab">Aa = zeros<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">6</span>, <span class="org-highlight-numbers-number">3</span><span class="org-rainbow-delimiters-depth-1">)</span>; <span class="org-comment">% [mm]</span>
Ab = zeros<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">6</span>, <span class="org-highlight-numbers-number">3</span><span class="org-rainbow-delimiters-depth-1">)</span>; <span class="org-comment">% [mm]</span>
Bb = zeros<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">6</span>, <span class="org-highlight-numbers-number">3</span><span class="org-rainbow-delimiters-depth-1">)</span>; <span class="org-comment">% [mm]</span>
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">for</span> <span class="org-variable-name">i</span> = <span class="org-constant"><span class="org-highlight-numbers-number">1</span></span><span class="org-constant">:</span><span class="org-constant"><span class="org-highlight-numbers-number">3</span></span>
Aa<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">2</span><span class="org-type">*</span><span class="org-constant">i</span><span class="org-type">-</span><span class="org-highlight-numbers-number">1</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-1">)</span> = <span class="org-rainbow-delimiters-depth-1">[</span>opts.R_bot<span class="org-type">*</span>cos<span class="org-rainbow-delimiters-depth-2">(</span> <span class="org-constant">pi</span><span class="org-type">/</span><span class="org-highlight-numbers-number">180</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-3">(</span><span class="org-highlight-numbers-number">120</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-4">(</span><span class="org-constant">i</span><span class="org-type">-</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-4">)</span> <span class="org-type">-</span> opts.a_bot<span class="org-rainbow-delimiters-depth-3">)</span> <span class="org-rainbow-delimiters-depth-2">)</span>, <span class="org-underline">...</span>
opts.R_bot<span class="org-type">*</span>sin<span class="org-rainbow-delimiters-depth-2">(</span> <span class="org-constant">pi</span><span class="org-type">/</span><span class="org-highlight-numbers-number">180</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-3">(</span><span class="org-highlight-numbers-number">120</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-4">(</span><span class="org-constant">i</span><span class="org-type">-</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-4">)</span> <span class="org-type">-</span> opts.a_bot<span class="org-rainbow-delimiters-depth-3">)</span> <span class="org-rainbow-delimiters-depth-2">)</span>, <span class="org-underline">...</span>
opts.H_plate<span class="org-type">+</span>opts.H_joint<span class="org-rainbow-delimiters-depth-1">]</span>;
Aa<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">2</span><span class="org-type">*</span><span class="org-constant">i</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-1">)</span> = <span class="org-rainbow-delimiters-depth-1">[</span>opts.R_bot<span class="org-type">*</span>cos<span class="org-rainbow-delimiters-depth-2">(</span> <span class="org-constant">pi</span><span class="org-type">/</span><span class="org-highlight-numbers-number">180</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-3">(</span><span class="org-highlight-numbers-number">120</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-4">(</span><span class="org-constant">i</span><span class="org-type">-</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-4">)</span> <span class="org-type">+</span> opts.a_bot<span class="org-rainbow-delimiters-depth-3">)</span> <span class="org-rainbow-delimiters-depth-2">)</span>, <span class="org-underline">...</span>
opts.R_bot<span class="org-type">*</span>sin<span class="org-rainbow-delimiters-depth-2">(</span> <span class="org-constant">pi</span><span class="org-type">/</span><span class="org-highlight-numbers-number">180</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-3">(</span><span class="org-highlight-numbers-number">120</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-4">(</span><span class="org-constant">i</span><span class="org-type">-</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-4">)</span> <span class="org-type">+</span> opts.a_bot<span class="org-rainbow-delimiters-depth-3">)</span> <span class="org-rainbow-delimiters-depth-2">)</span>, <span class="org-underline">...</span>
opts.H_plate<span class="org-type">+</span>opts.H_joint<span class="org-rainbow-delimiters-depth-1">]</span>;
Ab<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">2</span><span class="org-type">*</span><span class="org-constant">i</span><span class="org-type">-</span><span class="org-highlight-numbers-number">1</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-1">)</span> = <span class="org-rainbow-delimiters-depth-1">[</span>opts.R_top<span class="org-type">*</span>cos<span class="org-rainbow-delimiters-depth-2">(</span> <span class="org-constant">pi</span><span class="org-type">/</span><span class="org-highlight-numbers-number">180</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-3">(</span><span class="org-highlight-numbers-number">120</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-4">(</span><span class="org-constant">i</span><span class="org-type">-</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-4">)</span> <span class="org-type">+</span> opts.da_top <span class="org-type">-</span> opts.a_top<span class="org-rainbow-delimiters-depth-3">)</span> <span class="org-rainbow-delimiters-depth-2">)</span>, <span class="org-underline">...</span>
opts.R_top<span class="org-type">*</span>sin<span class="org-rainbow-delimiters-depth-2">(</span> <span class="org-constant">pi</span><span class="org-type">/</span><span class="org-highlight-numbers-number">180</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-3">(</span><span class="org-highlight-numbers-number">120</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-4">(</span><span class="org-constant">i</span><span class="org-type">-</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-4">)</span> <span class="org-type">+</span> opts.da_top <span class="org-type">-</span> opts.a_top<span class="org-rainbow-delimiters-depth-3">)</span> <span class="org-rainbow-delimiters-depth-2">)</span>, <span class="org-underline">...</span>
opts.H_tot <span class="org-type">-</span> opts.H_plate <span class="org-type">-</span> opts.H_joint<span class="org-rainbow-delimiters-depth-1">]</span>;
Ab<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">2</span><span class="org-type">*</span><span class="org-constant">i</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-1">)</span> = <span class="org-rainbow-delimiters-depth-1">[</span>opts.R_top<span class="org-type">*</span>cos<span class="org-rainbow-delimiters-depth-2">(</span> <span class="org-constant">pi</span><span class="org-type">/</span><span class="org-highlight-numbers-number">180</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-3">(</span><span class="org-highlight-numbers-number">120</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-4">(</span><span class="org-constant">i</span><span class="org-type">-</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-4">)</span> <span class="org-type">+</span> opts.da_top <span class="org-type">+</span> opts.a_top<span class="org-rainbow-delimiters-depth-3">)</span> <span class="org-rainbow-delimiters-depth-2">)</span>, <span class="org-underline">...</span>
opts.R_top<span class="org-type">*</span>sin<span class="org-rainbow-delimiters-depth-2">(</span> <span class="org-constant">pi</span><span class="org-type">/</span><span class="org-highlight-numbers-number">180</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-3">(</span><span class="org-highlight-numbers-number">120</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-4">(</span><span class="org-constant">i</span><span class="org-type">-</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-4">)</span> <span class="org-type">+</span> opts.da_top <span class="org-type">+</span> opts.a_top<span class="org-rainbow-delimiters-depth-3">)</span> <span class="org-rainbow-delimiters-depth-2">)</span>, <span class="org-underline">...</span>
opts.H_tot <span class="org-type">-</span> opts.H_plate <span class="org-type">-</span> opts.H_joint<span class="org-rainbow-delimiters-depth-1">]</span>;
<span class="org-keyword">end</span>
Bb = Ab <span class="org-type">-</span> opts.H_tot<span class="org-type">*</span><span class="org-rainbow-delimiters-depth-1">[</span><span class="org-highlight-numbers-number">0</span>,<span class="org-highlight-numbers-number">0</span>,<span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-1">]</span>;
</pre>
</div>
</div>
</div>
<div id="outline-container-org4931162" class="outline-3">
<h3 id="org4931162"><span class="section-number-3">1.5</span> Returns Stewart Structure</h3>
<div class="outline-text-3" id="text-1-5">
<div class="org-src-container">
<pre class="src src-matlab"> stewart = struct<span class="org-rainbow-delimiters-depth-1">()</span>;
stewart.Aa = Aa;
stewart.Ab = Ab;
stewart.Bb = Bb;
stewart.H_tot = opts.H_tot;
<span class="org-keyword">end</span>
</pre>
</div>
</div>
</div>
</div>
<div id="outline-container-orgc4f14da" class="outline-2">
<h2 id="orgc4f14da"><span class="section-number-2">2</span> computeGeometricalProperties</h2>
<div class="outline-text-2" id="text-2">
</div>
<div id="outline-container-org7550562" class="outline-3">
<h3 id="org7550562"><span class="section-number-3">2.1</span> Function description</h3>
<div class="outline-text-3" id="text-2-1">
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">function</span> <span class="org-variable-name"><span class="org-rainbow-delimiters-depth-1">[</span></span><span class="org-variable-name">stewart</span><span class="org-variable-name"><span class="org-rainbow-delimiters-depth-1">]</span></span> = <span class="org-function-name">computeGeometricalProperties</span><span class="org-rainbow-delimiters-depth-1">(</span><span class="org-variable-name">stewart</span>, <span class="org-variable-name">opts_param</span><span class="org-rainbow-delimiters-depth-1">)</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-org0ec8d5e" class="outline-3">
<h3 id="org0ec8d5e"><span class="section-number-3">2.2</span> Optional Parameters</h3>
<div class="outline-text-3" id="text-2-2">
<p>
Default values for opts.
</p>
<div class="org-src-container">
<pre class="src src-matlab">opts = struct<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-underline">...</span>
<span class="org-string">'Jd_pos'</span>, <span class="org-rainbow-delimiters-depth-2">[</span><span class="org-highlight-numbers-number">0</span>, <span class="org-highlight-numbers-number">0</span>, <span class="org-highlight-numbers-number">30</span><span class="org-rainbow-delimiters-depth-2">]</span>, <span class="org-underline">...</span> <span class="org-comment">% Position of the Jacobian for displacement estimation from the top of the mobile platform [mm]</span>
<span class="org-string">'Jf_pos'</span>, <span class="org-rainbow-delimiters-depth-2">[</span><span class="org-highlight-numbers-number">0</span>, <span class="org-highlight-numbers-number">0</span>, <span class="org-highlight-numbers-number">30</span><span class="org-rainbow-delimiters-depth-2">]</span> <span class="org-underline">...</span> <span class="org-comment">% Position of the Jacobian for force location from the top of the mobile platform [mm]</span>
<span class="org-rainbow-delimiters-depth-1">)</span>;
</pre>
</div>
<p>
Populate opts with input parameters
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">if</span> exist<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-string">'opts_param','var'</span><span class="org-rainbow-delimiters-depth-1">)</span>
<span class="org-keyword">for</span> <span class="org-variable-name">opt</span> = <span class="org-constant">fieldnames</span><span class="org-constant"><span class="org-rainbow-delimiters-depth-1">(</span></span><span class="org-constant">opts_param</span><span class="org-constant"><span class="org-rainbow-delimiters-depth-1">)</span></span><span class="org-constant">'</span>
opts.<span class="org-rainbow-delimiters-depth-1">(</span>opt<span class="org-rainbow-delimiters-depth-2">{</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-2">}</span><span class="org-rainbow-delimiters-depth-1">)</span> = opts_param.<span class="org-rainbow-delimiters-depth-1">(</span>opt<span class="org-rainbow-delimiters-depth-2">{</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-2">}</span><span class="org-rainbow-delimiters-depth-1">)</span>;
<span class="org-keyword">end</span>
<span class="org-keyword">end</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-orgdc858fe" class="outline-3">
<h3 id="orgdc858fe"><span class="section-number-3">2.3</span> Rotation matrices</h3>
<div class="outline-text-3" id="text-2-3">
<p>
We initialize \(l_i\) and \(\hat{s}_i\)
</p>
<div class="org-src-container">
<pre class="src src-matlab">leg_length = zeros<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">6</span>, <span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-1">)</span>; <span class="org-comment">% [mm]</span>
leg_vectors = zeros<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">6</span>, <span class="org-highlight-numbers-number">3</span><span class="org-rainbow-delimiters-depth-1">)</span>;
</pre>
</div>
<p>
We compute \(b_i - a_i\), and then:
</p>
\begin{align*}
l_i &= \left|b_i - a_i\right| \\
\hat{s}_i &= \frac{b_i - a_i}{l_i}
\end{align*}
<div class="org-src-container">
<pre class="src src-matlab">legs = stewart.Ab <span class="org-type">-</span> stewart.Aa;
<span class="org-keyword">for</span> <span class="org-variable-name">i</span> = <span class="org-constant"><span class="org-highlight-numbers-number">1</span></span><span class="org-constant">:</span><span class="org-constant"><span class="org-highlight-numbers-number">6</span></span>
leg_length<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span><span class="org-rainbow-delimiters-depth-1">)</span> = norm<span class="org-rainbow-delimiters-depth-1">(</span>legs<span class="org-rainbow-delimiters-depth-2">(</span><span class="org-constant">i</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-2">)</span><span class="org-rainbow-delimiters-depth-1">)</span>;
leg_vectors<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-1">)</span> = legs<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-1">)</span> <span class="org-type">/</span> leg_length<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span><span class="org-rainbow-delimiters-depth-1">)</span>;
<span class="org-keyword">end</span>
</pre>
</div>
<p>
We compute rotation matrices to have the orientation of the legs.
The rotation matrix transforms the \(z\) axis to the axis of the leg. The other axis are not important here.
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart.Rm = struct<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-string">'R'</span>, eye<span class="org-rainbow-delimiters-depth-2">(</span><span class="org-highlight-numbers-number">3</span><span class="org-rainbow-delimiters-depth-2">)</span><span class="org-rainbow-delimiters-depth-1">)</span>;
<span class="org-keyword">for</span> <span class="org-variable-name">i</span> = <span class="org-constant"><span class="org-highlight-numbers-number">1</span></span><span class="org-constant">:</span><span class="org-constant"><span class="org-highlight-numbers-number">6</span></span>
sx = cross<span class="org-rainbow-delimiters-depth-1">(</span>leg_vectors<span class="org-rainbow-delimiters-depth-2">(</span><span class="org-constant">i</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-2">)</span>, <span class="org-rainbow-delimiters-depth-2">[</span><span class="org-highlight-numbers-number">1</span> <span class="org-highlight-numbers-number">0</span> <span class="org-highlight-numbers-number">0</span><span class="org-rainbow-delimiters-depth-2">]</span><span class="org-rainbow-delimiters-depth-1">)</span>;
sx = sx<span class="org-type">/</span>norm<span class="org-rainbow-delimiters-depth-1">(</span>sx<span class="org-rainbow-delimiters-depth-1">)</span>;
sy = <span class="org-type">-</span>cross<span class="org-rainbow-delimiters-depth-1">(</span>sx, leg_vectors<span class="org-rainbow-delimiters-depth-2">(</span><span class="org-constant">i</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-2">)</span><span class="org-rainbow-delimiters-depth-1">)</span>;
sy = sy<span class="org-type">/</span>norm<span class="org-rainbow-delimiters-depth-1">(</span>sy<span class="org-rainbow-delimiters-depth-1">)</span>;
sz = leg_vectors<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-1">)</span>;
sz = sz<span class="org-type">/</span>norm<span class="org-rainbow-delimiters-depth-1">(</span>sz<span class="org-rainbow-delimiters-depth-1">)</span>;
stewart.Rm<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span><span class="org-rainbow-delimiters-depth-1">)</span>.R = <span class="org-rainbow-delimiters-depth-1">[</span>sx', sy', sz'<span class="org-rainbow-delimiters-depth-1">]</span>;
<span class="org-keyword">end</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-orgc0b0116" class="outline-3">
<h3 id="orgc0b0116"><span class="section-number-3">2.4</span> Jacobian matrices</h3>
<div class="outline-text-3" id="text-2-4">
<p>
Compute Jacobian Matrix
</p>
<div class="org-src-container">
<pre class="src src-matlab">Jd = zeros<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">6</span><span class="org-rainbow-delimiters-depth-1">)</span>;
<span class="org-keyword">for</span> <span class="org-variable-name">i</span> = <span class="org-constant"><span class="org-highlight-numbers-number">1</span></span><span class="org-constant">:</span><span class="org-constant"><span class="org-highlight-numbers-number">6</span></span>
Jd<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span>, <span class="org-highlight-numbers-number">1</span><span class="org-type">:</span><span class="org-highlight-numbers-number">3</span><span class="org-rainbow-delimiters-depth-1">)</span> = leg_vectors<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span>, <span class="org-type">:</span><span class="org-rainbow-delimiters-depth-1">)</span>;
Jd<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span>, <span class="org-highlight-numbers-number">4</span><span class="org-type">:</span><span class="org-highlight-numbers-number">6</span><span class="org-rainbow-delimiters-depth-1">)</span> = cross<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">001</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-2">(</span>stewart.Bb<span class="org-rainbow-delimiters-depth-3">(</span><span class="org-constant">i</span>, <span class="org-type">:</span><span class="org-rainbow-delimiters-depth-3">)</span> <span class="org-type">-</span> opts.Jd_pos<span class="org-rainbow-delimiters-depth-2">)</span>, leg_vectors<span class="org-rainbow-delimiters-depth-2">(</span><span class="org-constant">i</span>, <span class="org-type">:</span><span class="org-rainbow-delimiters-depth-2">)</span><span class="org-rainbow-delimiters-depth-1">)</span>;
<span class="org-keyword">end</span>
stewart.Jd = Jd;
stewart.Jd_inv = inv<span class="org-rainbow-delimiters-depth-1">(</span>Jd<span class="org-rainbow-delimiters-depth-1">)</span>;
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">Jf = zeros<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">6</span><span class="org-rainbow-delimiters-depth-1">)</span>;
<span class="org-keyword">for</span> <span class="org-variable-name">i</span> = <span class="org-constant"><span class="org-highlight-numbers-number">1</span></span><span class="org-constant">:</span><span class="org-constant"><span class="org-highlight-numbers-number">6</span></span>
Jf<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span>, <span class="org-highlight-numbers-number">1</span><span class="org-type">:</span><span class="org-highlight-numbers-number">3</span><span class="org-rainbow-delimiters-depth-1">)</span> = leg_vectors<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span>, <span class="org-type">:</span><span class="org-rainbow-delimiters-depth-1">)</span>;
Jf<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-constant">i</span>, <span class="org-highlight-numbers-number">4</span><span class="org-type">:</span><span class="org-highlight-numbers-number">6</span><span class="org-rainbow-delimiters-depth-1">)</span> = cross<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">001</span><span class="org-type">*</span><span class="org-rainbow-delimiters-depth-2">(</span>stewart.Bb<span class="org-rainbow-delimiters-depth-3">(</span><span class="org-constant">i</span>, <span class="org-type">:</span><span class="org-rainbow-delimiters-depth-3">)</span> <span class="org-type">-</span> opts.Jf_pos<span class="org-rainbow-delimiters-depth-2">)</span>, leg_vectors<span class="org-rainbow-delimiters-depth-2">(</span><span class="org-constant">i</span>, <span class="org-type">:</span><span class="org-rainbow-delimiters-depth-2">)</span><span class="org-rainbow-delimiters-depth-1">)</span>;
<span class="org-keyword">end</span>
stewart.Jf = Jf;
stewart.Jf_inv = inv<span class="org-rainbow-delimiters-depth-1">(</span>Jf<span class="org-rainbow-delimiters-depth-1">)</span>;
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">end</span>
</pre>
</div>
</div>
</div>
</div>
<div id="outline-container-org35cb27a" class="outline-2">
<h2 id="org35cb27a"><span class="section-number-2">3</span> initializeMechanicalElements</h2>
<div class="outline-text-2" id="text-3">
</div>
<div id="outline-container-orgeeb3d2f" class="outline-3">
<h3 id="orgeeb3d2f"><span class="section-number-3">3.1</span> Function description</h3>
<div class="outline-text-3" id="text-3-1">
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">function</span> <span class="org-variable-name"><span class="org-rainbow-delimiters-depth-1">[</span></span><span class="org-variable-name">stewart</span><span class="org-variable-name"><span class="org-rainbow-delimiters-depth-1">]</span></span> = <span class="org-function-name">initializeMechanicalElements</span><span class="org-rainbow-delimiters-depth-1">(</span><span class="org-variable-name">stewart</span>, <span class="org-variable-name">opts_param</span><span class="org-rainbow-delimiters-depth-1">)</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-org02f8d24" class="outline-3">
<h3 id="org02f8d24"><span class="section-number-3">3.2</span> Optional Parameters</h3>
<div class="outline-text-3" id="text-3-2">
<p>
Default values for opts.
</p>
<div class="org-src-container">
<pre class="src src-matlab">opts = struct<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-underline">...</span>
<span class="org-string">'thickness'</span>, <span class="org-highlight-numbers-number">10</span>, <span class="org-underline">...</span> <span class="org-comment">% Thickness of the base and platform [mm]</span>
<span class="org-string">'density'</span>, <span class="org-highlight-numbers-number">1000</span>, <span class="org-underline">...</span> <span class="org-comment">% Density of the material used for the hexapod [kg/m3]</span>
<span class="org-string">'k_ax'</span>, <span class="org-highlight-numbers-number">1e8</span>, <span class="org-underline">...</span> <span class="org-comment">% Stiffness of each actuator [N/m]</span>
<span class="org-string">'c_ax'</span>, <span class="org-highlight-numbers-number">1000</span>, <span class="org-underline">...</span> <span class="org-comment">% Damping of each actuator [N/(m/s)]</span>
<span class="org-string">'stroke'</span>, <span class="org-highlight-numbers-number">50e</span><span class="org-type">-</span><span class="org-highlight-numbers-number">6</span> <span class="org-underline">...</span> <span class="org-comment">% Maximum stroke of each actuator [m]</span>
<span class="org-rainbow-delimiters-depth-1">)</span>;
</pre>
</div>
<p>
Populate opts with input parameters
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">if</span> exist<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-string">'opts_param','var'</span><span class="org-rainbow-delimiters-depth-1">)</span>
<span class="org-keyword">for</span> <span class="org-variable-name">opt</span> = <span class="org-constant">fieldnames</span><span class="org-constant"><span class="org-rainbow-delimiters-depth-1">(</span></span><span class="org-constant">opts_param</span><span class="org-constant"><span class="org-rainbow-delimiters-depth-1">)</span></span><span class="org-constant">'</span>
opts.<span class="org-rainbow-delimiters-depth-1">(</span>opt<span class="org-rainbow-delimiters-depth-2">{</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-2">}</span><span class="org-rainbow-delimiters-depth-1">)</span> = opts_param.<span class="org-rainbow-delimiters-depth-1">(</span>opt<span class="org-rainbow-delimiters-depth-2">{</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-2">}</span><span class="org-rainbow-delimiters-depth-1">)</span>;
<span class="org-keyword">end</span>
<span class="org-keyword">end</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-orga56f635" class="outline-3">
<h3 id="orga56f635"><span class="section-number-3">3.3</span> Bottom Plate</h3>
<div class="outline-text-3" id="text-3-3">
<div id="org61c842c" class="figure">
<p><img src="./figs/stewart_bottom_plate.png" alt="stewart_bottom_plate.png" />
</p>
<p><span class="figure-number">Figure 2: </span>Schematic of the bottom plates with all the parameters</p>
</div>
<p>
The bottom plate structure is initialized.
</p>
<div class="org-src-container">
<pre class="src src-matlab">BP = struct<span class="org-rainbow-delimiters-depth-1">()</span>;
</pre>
</div>
<p>
We defined its internal radius (if there is a hole in the bottom plate) and its outer radius.
</p>
<div class="org-src-container">
<pre class="src src-matlab">BP.Rint = <span class="org-highlight-numbers-number">0</span>; <span class="org-comment">% Internal Radius [mm]</span>
BP.Rext = <span class="org-highlight-numbers-number">150</span>; <span class="org-comment">% External Radius [mm]</span>
</pre>
</div>
<p>
We define its thickness.
</p>
<div class="org-src-container">
<pre class="src src-matlab">BP.H = opts.thickness; <span class="org-comment">% Thickness of the Bottom Plate [mm]</span>
</pre>
</div>
<p>
We defined the density of the material of the bottom plate.
</p>
<div class="org-src-container">
<pre class="src src-matlab">BP.density = opts.density; <span class="org-comment">% Density of the material [kg/m3]</span>
</pre>
</div>
<p>
And its color.
</p>
<div class="org-src-container">
<pre class="src src-matlab">BP.color = <span class="org-rainbow-delimiters-depth-1">[</span><span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">7</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">7</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">7</span><span class="org-rainbow-delimiters-depth-1">]</span>; <span class="org-comment">% Color [RGB]</span>
</pre>
</div>
<p>
Then the profile of the bottom plate is computed and will be used by Simscape
</p>
<div class="org-src-container">
<pre class="src src-matlab">BP.shape = <span class="org-rainbow-delimiters-depth-1">[</span>BP.Rint BP.H; BP.Rint <span class="org-highlight-numbers-number">0</span>; BP.Rext <span class="org-highlight-numbers-number">0</span>; BP.Rext BP.H<span class="org-rainbow-delimiters-depth-1">]</span>; <span class="org-comment">% [mm]</span>
</pre>
</div>
<p>
The structure is added to the stewart structure
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart.BP = BP;
</pre>
</div>
</div>
</div>
<div id="outline-container-orge8a195c" class="outline-3">
<h3 id="orge8a195c"><span class="section-number-3">3.4</span> Top Plate</h3>
<div class="outline-text-3" id="text-3-4">
<p>
The top plate structure is initialized.
</p>
<div class="org-src-container">
<pre class="src src-matlab">TP = struct<span class="org-rainbow-delimiters-depth-1">()</span>;
</pre>
</div>
<p>
We defined the internal and external radius of the top plate.
</p>
<div class="org-src-container">
<pre class="src src-matlab">TP.Rint = <span class="org-highlight-numbers-number">0</span>; <span class="org-comment">% [mm]</span>
TP.Rext = <span class="org-highlight-numbers-number">100</span>; <span class="org-comment">% [mm]</span>
</pre>
</div>
<p>
The thickness of the top plate.
</p>
<div class="org-src-container">
<pre class="src src-matlab">TP.H = <span class="org-highlight-numbers-number">10</span>; <span class="org-comment">% [mm]</span>
</pre>
</div>
<p>
The density of its material.
</p>
<div class="org-src-container">
<pre class="src src-matlab">TP.density = opts.density; <span class="org-comment">% Density of the material [kg/m3]</span>
</pre>
</div>
<p>
Its color.
</p>
<div class="org-src-container">
<pre class="src src-matlab">TP.color = <span class="org-rainbow-delimiters-depth-1">[</span><span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">7</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">7</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">7</span><span class="org-rainbow-delimiters-depth-1">]</span>; <span class="org-comment">% Color [RGB]</span>
</pre>
</div>
<p>
Then the shape of the top plate is computed
</p>
<div class="org-src-container">
<pre class="src src-matlab">TP.shape = <span class="org-rainbow-delimiters-depth-1">[</span>TP.Rint TP.H; TP.Rint <span class="org-highlight-numbers-number">0</span>; TP.Rext <span class="org-highlight-numbers-number">0</span>; TP.Rext TP.H<span class="org-rainbow-delimiters-depth-1">]</span>;
</pre>
</div>
<p>
The structure is added to the stewart structure
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart.TP = TP;
</pre>
</div>
</div>
</div>
<div id="outline-container-org8725a51" class="outline-3">
<h3 id="org8725a51"><span class="section-number-3">3.5</span> Legs</h3>
<div class="outline-text-3" id="text-3-5">
<div id="org50ef74c" class="figure">
<p><img src="./figs/stewart_legs.png" alt="stewart_legs.png" />
</p>
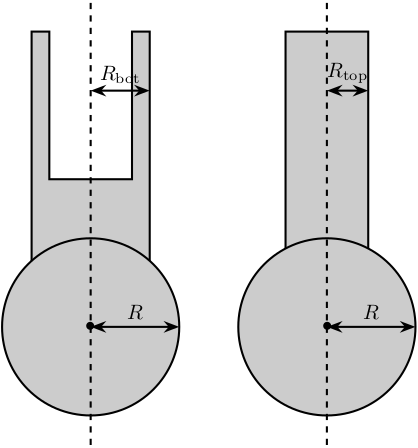
<p><span class="figure-number">Figure 3: </span>Schematic for the legs of the Stewart platform</p>
</div>
<p>
The leg structure is initialized.
</p>
<div class="org-src-container">
<pre class="src src-matlab">Leg = struct<span class="org-rainbow-delimiters-depth-1">()</span>;
</pre>
</div>
<p>
The maximum Stroke of each leg is defined.
</p>
<div class="org-src-container">
<pre class="src src-matlab">Leg.stroke = opts.stroke; <span class="org-comment">% [m]</span>
</pre>
</div>
<p>
The stiffness and damping of each leg are defined
</p>
<div class="org-src-container">
<pre class="src src-matlab">Leg.k_ax = opts.k_ax; <span class="org-comment">% Stiffness of each leg [N/m]</span>
Leg.c_ax = opts.c_ax; <span class="org-comment">% Damping of each leg [N/(m/s)]</span>
</pre>
</div>
<p>
The radius of the legs are defined
</p>
<div class="org-src-container">
<pre class="src src-matlab">Leg.Rtop = <span class="org-highlight-numbers-number">10</span>; <span class="org-comment">% Radius of the cylinder of the top part of the leg[mm]</span>
Leg.Rbot = <span class="org-highlight-numbers-number">12</span>; <span class="org-comment">% Radius of the cylinder of the bottom part of the leg [mm]</span>
</pre>
</div>
<p>
The density of its material.
</p>
<div class="org-src-container">
<pre class="src src-matlab">Leg.density = opts.density; <span class="org-comment">% Density of the material used for the legs [kg/m3]</span>
</pre>
</div>
<p>
Its color.
</p>
<div class="org-src-container">
<pre class="src src-matlab">Leg.color = <span class="org-rainbow-delimiters-depth-1">[</span><span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">5</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">5</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">5</span><span class="org-rainbow-delimiters-depth-1">]</span>; <span class="org-comment">% Color of the top part of the leg [RGB]</span>
</pre>
</div>
<p>
The radius of spheres representing the ball joints are defined.
</p>
<div class="org-src-container">
<pre class="src src-matlab">Leg.R = <span class="org-highlight-numbers-number">1</span>.<span class="org-highlight-numbers-number">3</span><span class="org-type">*</span>Leg.Rbot; <span class="org-comment">% Size of the sphere at the extremity of the leg [mm]</span>
</pre>
</div>
<p>
We estimate the length of the legs.
</p>
<div class="org-src-container">
<pre class="src src-matlab">legs = stewart.Ab <span class="org-type">-</span> stewart.Aa;
Leg.lenght = norm<span class="org-rainbow-delimiters-depth-1">(</span>legs<span class="org-rainbow-delimiters-depth-2">(</span><span class="org-highlight-numbers-number">1</span>,<span class="org-type">:</span><span class="org-rainbow-delimiters-depth-2">)</span><span class="org-rainbow-delimiters-depth-1">)</span><span class="org-type">/</span><span class="org-highlight-numbers-number">1</span>.<span class="org-highlight-numbers-number">5</span>;
</pre>
</div>
<p>
Then the shape of the bottom leg is estimated
</p>
<div class="org-src-container">
<pre class="src src-matlab">Leg.shape.bot = <span class="org-underline">...</span>
<span class="org-rainbow-delimiters-depth-1">[</span><span class="org-highlight-numbers-number">0</span> <span class="org-highlight-numbers-number">0</span>; <span class="org-underline">...</span>
Leg.Rbot <span class="org-highlight-numbers-number">0</span>; <span class="org-underline">...</span>
Leg.Rbot Leg.lenght; <span class="org-underline">...</span>
Leg.Rtop Leg.lenght; <span class="org-underline">...</span>
Leg.Rtop <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">2</span><span class="org-type">*</span>Leg.lenght; <span class="org-underline">...</span>
<span class="org-highlight-numbers-number">0</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">2</span><span class="org-type">*</span>Leg.lenght<span class="org-rainbow-delimiters-depth-1">]</span>;
</pre>
</div>
<p>
The structure is added to the stewart structure
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart.Leg = Leg;
</pre>
</div>
</div>
</div>
<div id="outline-container-org722b78f" class="outline-3">
<h3 id="org722b78f"><span class="section-number-3">3.6</span> Ball Joints</h3>
<div class="outline-text-3" id="text-3-6">
<div id="org38b2e38" class="figure">
<p><img src="./figs/stewart_ball_joints.png" alt="stewart_ball_joints.png" />
</p>
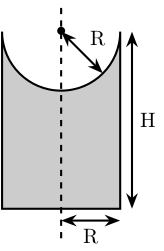
<p><span class="figure-number">Figure 4: </span>Schematic of the support for the ball joints</p>
</div>
<p>
<code>SP</code> is the structure representing the support for the ball joints at the extremity of each leg.
</p>
<p>
The <code>SP</code> structure is initialized.
</p>
<div class="org-src-container">
<pre class="src src-matlab">SP = struct<span class="org-rainbow-delimiters-depth-1">()</span>;
</pre>
</div>
<p>
We can define its rotational stiffness and damping. For now, we use perfect joints.
</p>
<div class="org-src-container">
<pre class="src src-matlab">SP.k = <span class="org-highlight-numbers-number">0</span>; <span class="org-comment">% [N*m/deg]</span>
SP.c = <span class="org-highlight-numbers-number">0</span>; <span class="org-comment">% [N*m/deg]</span>
</pre>
</div>
<p>
Its height is defined
</p>
<div class="org-src-container">
<pre class="src src-matlab">SP.H = stewart.Aa<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-highlight-numbers-number">1</span>, <span class="org-highlight-numbers-number">3</span><span class="org-rainbow-delimiters-depth-1">)</span> <span class="org-type">-</span> BP.H; <span class="org-comment">% [mm]</span>
</pre>
</div>
<p>
Its radius is based on the radius on the sphere at the end of the legs.
</p>
<div class="org-src-container">
<pre class="src src-matlab">SP.R = Leg.R; <span class="org-comment">% [mm]</span>
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">SP.section = <span class="org-rainbow-delimiters-depth-1">[</span><span class="org-highlight-numbers-number">0</span> SP.H<span class="org-type">-</span>SP.R;
<span class="org-highlight-numbers-number">0</span> <span class="org-highlight-numbers-number">0</span>;
SP.R <span class="org-highlight-numbers-number">0</span>;
SP.R SP.H<span class="org-rainbow-delimiters-depth-1">]</span>;
</pre>
</div>
<p>
The density of its material is defined.
</p>
<div class="org-src-container">
<pre class="src src-matlab">SP.density = opts.density; % [kg<span class="org-type">/</span>m<span class="org-type">^</span><span class="org-highlight-numbers-number">3</span>]
</pre>
</div>
<p>
Its color is defined.
</p>
<div class="org-src-container">
<pre class="src src-matlab">SP.color = <span class="org-rainbow-delimiters-depth-1">[</span><span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">7</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">7</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">7</span><span class="org-rainbow-delimiters-depth-1">]</span>; <span class="org-comment">% [RGB]</span>
</pre>
</div>
<p>
The structure is added to the Hexapod structure
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart.SP = SP;
</pre>
</div>
</div>
</div>
</div>
<div id="outline-container-org5ba95d3" class="outline-2">
<h2 id="org5ba95d3"><span class="section-number-2">4</span> initializeSample</h2>
<div class="outline-text-2" id="text-4">
</div>
<div id="outline-container-org2dd34bb" class="outline-3">
<h3 id="org2dd34bb"><span class="section-number-3">4.1</span> Function description</h3>
<div class="outline-text-3" id="text-4-1">
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">function</span> <span class="org-variable-name"><span class="org-rainbow-delimiters-depth-1">[]</span></span> = <span class="org-function-name">initializeSample</span><span class="org-rainbow-delimiters-depth-1">(</span><span class="org-variable-name">opts_param</span><span class="org-rainbow-delimiters-depth-1">)</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-org2aa1dac" class="outline-3">
<h3 id="org2aa1dac"><span class="section-number-3">4.2</span> Optional Parameters</h3>
<div class="outline-text-3" id="text-4-2">
<p>
Default values for opts.
</p>
<div class="org-src-container">
<pre class="src src-matlab">sample = struct<span class="org-rainbow-delimiters-depth-1">(</span> <span class="org-underline">...</span>
<span class="org-string">'radius'</span>, <span class="org-highlight-numbers-number">100</span>, <span class="org-underline">...</span> <span class="org-comment">% radius of the cylinder [mm]</span>
<span class="org-string">'height'</span>, <span class="org-highlight-numbers-number">100</span>, <span class="org-underline">...</span> <span class="org-comment">% height of the cylinder [mm]</span>
<span class="org-string">'mass'</span>, <span class="org-highlight-numbers-number">10</span>, <span class="org-underline">...</span> <span class="org-comment">% mass of the cylinder [kg]</span>
<span class="org-string">'measheight'</span>, <span class="org-highlight-numbers-number">50</span>, <span class="org-underline">...</span> <span class="org-comment">% measurement point z-offset [mm]</span>
<span class="org-string">'offset'</span>, <span class="org-rainbow-delimiters-depth-2">[</span><span class="org-highlight-numbers-number">0</span>, <span class="org-highlight-numbers-number">0</span>, <span class="org-highlight-numbers-number">0</span><span class="org-rainbow-delimiters-depth-2">]</span>, <span class="org-underline">...</span> <span class="org-comment">% offset position of the sample [mm]</span>
<span class="org-string">'color'</span>, <span class="org-rainbow-delimiters-depth-2">[</span><span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">9</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">1</span> <span class="org-highlight-numbers-number">0</span>.<span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-2">]</span> <span class="org-underline">...</span>
<span class="org-rainbow-delimiters-depth-1">)</span>;
</pre>
</div>
<p>
Populate opts with input parameters
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">if</span> exist<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-string">'opts_param','var'</span><span class="org-rainbow-delimiters-depth-1">)</span>
<span class="org-keyword">for</span> <span class="org-variable-name">opt</span> = <span class="org-constant">fieldnames</span><span class="org-constant"><span class="org-rainbow-delimiters-depth-1">(</span></span><span class="org-constant">opts_param</span><span class="org-constant"><span class="org-rainbow-delimiters-depth-1">)</span></span><span class="org-constant">'</span>
sample.<span class="org-rainbow-delimiters-depth-1">(</span>opt<span class="org-rainbow-delimiters-depth-2">{</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-2">}</span><span class="org-rainbow-delimiters-depth-1">)</span> = opts_param.<span class="org-rainbow-delimiters-depth-1">(</span>opt<span class="org-rainbow-delimiters-depth-2">{</span><span class="org-highlight-numbers-number">1</span><span class="org-rainbow-delimiters-depth-2">}</span><span class="org-rainbow-delimiters-depth-1">)</span>;
<span class="org-keyword">end</span>
<span class="org-keyword">end</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-orgea68e95" class="outline-3">
<h3 id="orgea68e95"><span class="section-number-3">4.3</span> Save the Sample structure</h3>
<div class="outline-text-3" id="text-4-3">
<div class="org-src-container">
<pre class="src src-matlab">save<span class="org-rainbow-delimiters-depth-1">(</span><span class="org-string">'./mat/sample.mat', 'sample'</span><span class="org-rainbow-delimiters-depth-1">)</span>;
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">end</span>
</pre>
</div>
</div>
</div>
</div>
</div>
<div id="postamble" class="status">
<p class="author">Author: Thomas Dehaeze</p>
<p class="date">Created: 2019-08-26 lun. 11:56</p>
<p class="validation"><a href="http://validator.w3.org/check?uri=referer">Validate</a></p>
</div>
</body>
</html>