<?xml version="1.0" encoding="utf-8"?>
<?xml version="1.0" encoding="utf-8"?>
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN"
"http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<!-- 2020-03-02 lun. 17:57 -->
<meta http-equiv="Content-Type" content="text/html;charset=utf-8" />
<meta name="viewport" content="width=device-width, initial-scale=1" />
<title>Stewart Platform - Decentralized Active Damping</title>
<meta name="generator" content="Org mode" />
<meta name="author" content="Dehaeze Thomas" />
<style type="text/css">
<!--/*--><![CDATA[/*><!--*/
.title { text-align: center;
margin-bottom: .2em; }
.subtitle { text-align: center;
font-size: medium;
font-weight: bold;
margin-top:0; }
.todo { font-family: monospace; color: red; }
.done { font-family: monospace; color: green; }
.priority { font-family: monospace; color: orange; }
.tag { background-color: #eee; font-family: monospace;
padding: 2px; font-size: 80%; font-weight: normal; }
.timestamp { color: #bebebe; }
.timestamp-kwd { color: #5f9ea0; }
.org-right { margin-left: auto; margin-right: 0px; text-align: right; }
.org-left { margin-left: 0px; margin-right: auto; text-align: left; }
.org-center { margin-left: auto; margin-right: auto; text-align: center; }
.underline { text-decoration: underline; }
#postamble p, #preamble p { font-size: 90%; margin: .2em; }
p.verse { margin-left: 3%; }
pre {
border: 1px solid #ccc;
box-shadow: 3px 3px 3px #eee;
padding: 8pt;
font-family: monospace;
overflow: auto;
margin: 1.2em;
}
pre.src {
position: relative;
overflow: visible;
padding-top: 1.2em;
}
pre.src:before {
display: none;
position: absolute;
background-color: white;
top: -10px;
right: 10px;
padding: 3px;
border: 1px solid black;
}
pre.src:hover:before { display: inline;}
/* Languages per Org manual */
pre.src-asymptote:before { content: 'Asymptote'; }
pre.src-awk:before { content: 'Awk'; }
pre.src-C:before { content: 'C'; }
/* pre.src-C++ doesn't work in CSS */
pre.src-clojure:before { content: 'Clojure'; }
pre.src-css:before { content: 'CSS'; }
pre.src-D:before { content: 'D'; }
pre.src-ditaa:before { content: 'ditaa'; }
pre.src-dot:before { content: 'Graphviz'; }
pre.src-calc:before { content: 'Emacs Calc'; }
pre.src-emacs-lisp:before { content: 'Emacs Lisp'; }
pre.src-fortran:before { content: 'Fortran'; }
pre.src-gnuplot:before { content: 'gnuplot'; }
pre.src-haskell:before { content: 'Haskell'; }
pre.src-hledger:before { content: 'hledger'; }
pre.src-java:before { content: 'Java'; }
pre.src-js:before { content: 'Javascript'; }
pre.src-latex:before { content: 'LaTeX'; }
pre.src-ledger:before { content: 'Ledger'; }
pre.src-lisp:before { content: 'Lisp'; }
pre.src-lilypond:before { content: 'Lilypond'; }
pre.src-lua:before { content: 'Lua'; }
pre.src-matlab:before { content: 'MATLAB'; }
pre.src-mscgen:before { content: 'Mscgen'; }
pre.src-ocaml:before { content: 'Objective Caml'; }
pre.src-octave:before { content: 'Octave'; }
pre.src-org:before { content: 'Org mode'; }
pre.src-oz:before { content: 'OZ'; }
pre.src-plantuml:before { content: 'Plantuml'; }
pre.src-processing:before { content: 'Processing.js'; }
pre.src-python:before { content: 'Python'; }
pre.src-R:before { content: 'R'; }
pre.src-ruby:before { content: 'Ruby'; }
pre.src-sass:before { content: 'Sass'; }
pre.src-scheme:before { content: 'Scheme'; }
pre.src-screen:before { content: 'Gnu Screen'; }
pre.src-sed:before { content: 'Sed'; }
pre.src-sh:before { content: 'shell'; }
pre.src-sql:before { content: 'SQL'; }
pre.src-sqlite:before { content: 'SQLite'; }
/* additional languages in org.el's org-babel-load-languages alist */
pre.src-forth:before { content: 'Forth'; }
pre.src-io:before { content: 'IO'; }
pre.src-J:before { content: 'J'; }
pre.src-makefile:before { content: 'Makefile'; }
pre.src-maxima:before { content: 'Maxima'; }
pre.src-perl:before { content: 'Perl'; }
pre.src-picolisp:before { content: 'Pico Lisp'; }
pre.src-scala:before { content: 'Scala'; }
pre.src-shell:before { content: 'Shell Script'; }
pre.src-ebnf2ps:before { content: 'ebfn2ps'; }
/* additional language identifiers per "defun org-babel-execute"
in ob-*.el */
pre.src-cpp:before { content: 'C++'; }
pre.src-abc:before { content: 'ABC'; }
pre.src-coq:before { content: 'Coq'; }
pre.src-groovy:before { content: 'Groovy'; }
/* additional language identifiers from org-babel-shell-names in
ob-shell.el: ob-shell is the only babel language using a lambda to put
the execution function name together. */
pre.src-bash:before { content: 'bash'; }
pre.src-csh:before { content: 'csh'; }
pre.src-ash:before { content: 'ash'; }
pre.src-dash:before { content: 'dash'; }
pre.src-ksh:before { content: 'ksh'; }
pre.src-mksh:before { content: 'mksh'; }
pre.src-posh:before { content: 'posh'; }
/* Additional Emacs modes also supported by the LaTeX listings package */
pre.src-ada:before { content: 'Ada'; }
pre.src-asm:before { content: 'Assembler'; }
pre.src-caml:before { content: 'Caml'; }
pre.src-delphi:before { content: 'Delphi'; }
pre.src-html:before { content: 'HTML'; }
pre.src-idl:before { content: 'IDL'; }
pre.src-mercury:before { content: 'Mercury'; }
pre.src-metapost:before { content: 'MetaPost'; }
pre.src-modula-2:before { content: 'Modula-2'; }
pre.src-pascal:before { content: 'Pascal'; }
pre.src-ps:before { content: 'PostScript'; }
pre.src-prolog:before { content: 'Prolog'; }
pre.src-simula:before { content: 'Simula'; }
pre.src-tcl:before { content: 'tcl'; }
pre.src-tex:before { content: 'TeX'; }
pre.src-plain-tex:before { content: 'Plain TeX'; }
pre.src-verilog:before { content: 'Verilog'; }
pre.src-vhdl:before { content: 'VHDL'; }
pre.src-xml:before { content: 'XML'; }
pre.src-nxml:before { content: 'XML'; }
/* add a generic configuration mode; LaTeX export needs an additional
(add-to-list 'org-latex-listings-langs '(conf " ")) in .emacs */
pre.src-conf:before { content: 'Configuration File'; }
table { border-collapse:collapse; }
caption.t-above { caption-side: top; }
caption.t-bottom { caption-side: bottom; }
td, th { vertical-align:top; }
th.org-right { text-align: center; }
th.org-left { text-align: center; }
th.org-center { text-align: center; }
td.org-right { text-align: right; }
td.org-left { text-align: left; }
td.org-center { text-align: center; }
dt { font-weight: bold; }
.footpara { display: inline; }
.footdef { margin-bottom: 1em; }
.figure { padding: 1em; }
.figure p { text-align: center; }
.equation-container {
display: table;
text-align: center;
width: 100%;
}
.equation {
vertical-align: middle;
}
.equation-label {
display: table-cell;
text-align: right;
vertical-align: middle;
}
.inlinetask {
padding: 10px;
border: 2px solid gray;
margin: 10px;
background: #ffffcc;
}
#org-div-home-and-up
{ text-align: right; font-size: 70%; white-space: nowrap; }
textarea { overflow-x: auto; }
.linenr { font-size: smaller }
.code-highlighted { background-color: #ffff00; }
.org-info-js_info-navigation { border-style: none; }
#org-info-js_console-label
{ font-size: 10px; font-weight: bold; white-space: nowrap; }
.org-info-js_search-highlight
{ background-color: #ffff00; color: #000000; font-weight: bold; }
.org-svg { width: 90%; }
/*]]>*/-->
</style>
<link rel="stylesheet" type="text/css" href="./css/htmlize.css"/>
<link rel="stylesheet" type="text/css" href="./css/readtheorg.css"/>
<script src="./js/jquery.min.js"></script>
<script src="./js/bootstrap.min.js"></script>
<script src="./js/jquery.stickytableheaders.min.js"></script>
<script src="./js/readtheorg.js"></script>
<script type="text/javascript">
// @license magnet:?xt=urn:btih:1f739d935676111cfff4b4693e3816e664797050&dn=gpl-3.0.txt GPL-v3-or-Later
<!--/*--><![CDATA[/*><!--*/
function CodeHighlightOn(elem, id)
{
var target = document.getElementById(id);
if(null != target) {
elem.cacheClassElem = elem.className;
elem.cacheClassTarget = target.className;
target.className = "code-highlighted";
elem.className = "code-highlighted";
}
}
function CodeHighlightOff(elem, id)
{
var target = document.getElementById(id);
if(elem.cacheClassElem)
elem.className = elem.cacheClassElem;
if(elem.cacheClassTarget)
target.className = elem.cacheClassTarget;
}
/*]]>*///-->
// @license-end
</script>
<script>
MathJax = {
tex: { macros: {
bm: ["\\boldsymbol{#1}",1],
}
}
};
</script>
<script type="text/javascript"
src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js"></script>
</head>
<body>
<div id="org-div-home-and-up">
<a accesskey="h" href="./index.html"> UP </a>
|
<a accesskey="H" href="./index.html"> HOME </a>
</div><div id="content">
<h1 class="title">Stewart Platform - Decentralized Active Damping</h1>
<div id="table-of-contents">
<h2>Table of Contents</h2>
<div id="text-table-of-contents">
<ul>
<li><a href="#orgd59c804">1. Inertial Control</a>
<ul>
<li><a href="#org5f749c8">1.1. Identification of the Dynamics</a></li>
<li><a href="#orgd0f78f7">1.2. Effect of the Flexible Joint stiffness and Actuator amplification on the Dynamics</a></li>
<li><a href="#org3f64d96">1.3. Obtained Damping</a></li>
<li><a href="#org8e1ece7">1.4. Conclusion</a></li>
</ul>
</li>
<li><a href="#org74c7eb4">2. Integral Force Feedback</a>
<ul>
<li><a href="#orgcd99b62">2.1. Identification of the Dynamics with perfect Joints</a></li>
<li><a href="#org1b7a953">2.2. Effect of the Flexible Joint stiffness and Actuator amplification on the Dynamics</a></li>
<li><a href="#org1d362f0">2.3. Obtained Damping</a></li>
<li><a href="#org63f9110">2.4. Conclusion</a></li>
</ul>
</li>
<li><a href="#org08917d6">3. Direct Velocity Feedback</a>
<ul>
<li><a href="#org5364f58">3.1. Identification of the Dynamics with perfect Joints</a></li>
<li><a href="#org81b6713">3.2. Effect of the Flexible Joint stiffness and Actuator amplification on the Dynamics</a></li>
<li><a href="#orge328103">3.3. Obtained Damping</a></li>
<li><a href="#org48c963f">3.4. Conclusion</a></li>
</ul>
</li>
<li><a href="#org183f3f2">4. Compliance and Transmissibility Comparison</a>
<ul>
<li><a href="#org0ed1499">4.1. Initialization</a></li>
<li><a href="#orgcd64c04">4.2. Identification</a></li>
<li><a href="#orgd30c62d">4.3. Results</a></li>
</ul>
</li>
</ul>
</div>
</div>
<p>
The following decentralized active damping techniques are briefly studied:
</p>
<ul class="org-ul">
<li>Inertial Control (proportional feedback of the absolute velocity): Section <a href="#orgeb37c7d">1</a></li>
<li>Integral Force Feedback: Section <a href="#orgab5e6b5">2</a></li>
<li>Direct feedback of the relative velocity of each strut: Section <a href="#org0aa816a">3</a></li>
</ul>
<div id="outline-container-orgd59c804" class="outline-2">
<h2 id="orgd59c804"><span class="section-number-2">1</span> Inertial Control</h2>
<div class="outline-text-2" id="text-1">
<p>
<a id="orgeb37c7d"></a>
</p>
<div class="note">
<p>
The Matlab script corresponding to this section is accessible <a href="../matlab/active_damping_inertial.m">here</a>.
</p>
<p>
To run the script, open the Simulink Project, and type <code>run active_damping_inertial.m</code>.
</p>
</div>
</div>
<div id="outline-container-org5f749c8" class="outline-3">
<h3 id="org5f749c8"><span class="section-number-3">1.1</span> Identification of the Dynamics</h3>
<div class="outline-text-3" id="text-1-1">
<div class="org-src-container">
<pre class="src src-matlab">stewart = initializeStewartPlatform();
stewart = initializeFramesPositions(stewart, <span class="org-string">'H'</span>, 90e<span class="org-type">-</span>3, <span class="org-string">'MO_B'</span>, 45e<span class="org-type">-</span>3);
stewart = generateGeneralConfiguration(stewart);
stewart = computeJointsPose(stewart);
stewart = initializeStrutDynamics(stewart);
stewart = initializeJointDynamics(stewart, <span class="org-string">'type_F'</span>, <span class="org-string">'universal_p'</span>, <span class="org-string">'type_M'</span>, <span class="org-string">'spherical_p'</span>);
stewart = initializeCylindricalPlatforms(stewart);
stewart = initializeCylindricalStruts(stewart);
stewart = computeJacobian(stewart);
stewart = initializeStewartPose(stewart);
stewart = initializeInertialSensor(stewart, <span class="org-string">'type'</span>, <span class="org-string">'accelerometer'</span>, <span class="org-string">'freq'</span>, 5e3);
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">ground = initializeGround(<span class="org-string">'type'</span>, <span class="org-string">'rigid'</span>, <span class="org-string">'rot_point'</span>, stewart.platform_F.FO_A);
payload = initializePayload(<span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
controller = initializeController(<span class="org-string">'type'</span>, <span class="org-string">'open-loop'</span>);
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak"><span class="org-comment">%% Options for Linearized</span></span>
options = linearizeOptions;
options.SampleTime = 0;
<span class="org-matlab-cellbreak"><span class="org-comment">%% Name of the Simulink File</span></span>
mdl = <span class="org-string">'stewart_platform_model'</span>;
<span class="org-matlab-cellbreak"><span class="org-comment">%% Input/Output definition</span></span>
clear io; io_i = 1;
io(io_i) = linio([mdl, <span class="org-string">'/Controller'</span>], 1, <span class="org-string">'openinput'</span>); io_i = io_i <span class="org-type">+</span> 1; <span class="org-comment">% Actuator Force Inputs [N]</span>
io(io_i) = linio([mdl, <span class="org-string">'/Stewart Platform'</span>], 1, <span class="org-string">'openoutput'</span>, [], <span class="org-string">'Vm'</span>); io_i = io_i <span class="org-type">+</span> 1; <span class="org-comment">% Absolute velocity of each leg [m/s]</span>
<span class="org-matlab-cellbreak"><span class="org-comment">%% Run the linearization</span></span>
G = linearize(mdl, io, options);
G.InputName = {<span class="org-string">'F1'</span>, <span class="org-string">'F2'</span>, <span class="org-string">'F3'</span>, <span class="org-string">'F4'</span>, <span class="org-string">'F5'</span>, <span class="org-string">'F6'</span>};
G.OutputName = {<span class="org-string">'Vm1'</span>, <span class="org-string">'Vm2'</span>, <span class="org-string">'Vm3'</span>, <span class="org-string">'Vm4'</span>, <span class="org-string">'Vm5'</span>, <span class="org-string">'Vm6'</span>};
</pre>
</div>
<p>
The transfer function from actuator forces to force sensors is shown in Figure <a href="#org834d990">1</a>.
</p>
<div id="org834d990" class="figure">
<p><img src="figs/inertial_plant_coupling.png" alt="inertial_plant_coupling.png" />
</p>
<p><span class="figure-number">Figure 1: </span>Transfer function from the Actuator force \(F_{i}\) to the absolute velocity of the same leg \(v_{m,i}\) and to the absolute velocity of the other legs \(v_{m,j}\) with \(i \neq j\) in grey (<a href="./figs/inertial_plant_coupling.png">png</a>, <a href="./figs/inertial_plant_coupling.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-orgd0f78f7" class="outline-3">
<h3 id="orgd0f78f7"><span class="section-number-3">1.2</span> Effect of the Flexible Joint stiffness and Actuator amplification on the Dynamics</h3>
<div class="outline-text-3" id="text-1-2">
<p>
We add some stiffness and damping in the flexible joints and we re-identify the dynamics.
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart = initializeJointDynamics(stewart, <span class="org-string">'type_F'</span>, <span class="org-string">'universal'</span>, <span class="org-string">'type_M'</span>, <span class="org-string">'spherical'</span>);
Gf = linearize(mdl, io, options);
Gf.InputName = {<span class="org-string">'F1'</span>, <span class="org-string">'F2'</span>, <span class="org-string">'F3'</span>, <span class="org-string">'F4'</span>, <span class="org-string">'F5'</span>, <span class="org-string">'F6'</span>};
Gf.OutputName = {<span class="org-string">'Vm1'</span>, <span class="org-string">'Vm2'</span>, <span class="org-string">'Vm3'</span>, <span class="org-string">'Vm4'</span>, <span class="org-string">'Vm5'</span>, <span class="org-string">'Vm6'</span>};
</pre>
</div>
<p>
We now use the amplified actuators and re-identify the dynamics
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart = initializeAmplifiedStrutDynamics(stewart);
Ga = linearize(mdl, io, options);
Ga.InputName = {<span class="org-string">'F1'</span>, <span class="org-string">'F2'</span>, <span class="org-string">'F3'</span>, <span class="org-string">'F4'</span>, <span class="org-string">'F5'</span>, <span class="org-string">'F6'</span>};
Ga.OutputName = {<span class="org-string">'Vm1'</span>, <span class="org-string">'Vm2'</span>, <span class="org-string">'Vm3'</span>, <span class="org-string">'Vm4'</span>, <span class="org-string">'Vm5'</span>, <span class="org-string">'Vm6'</span>};
</pre>
</div>
<p>
The new dynamics from force actuator to force sensor is shown in Figure <a href="#org683c779">2</a>.
</p>
<div id="org683c779" class="figure">
<p><img src="figs/inertial_plant_flexible_joint_decentralized.png" alt="inertial_plant_flexible_joint_decentralized.png" />
</p>
<p><span class="figure-number">Figure 2: </span>Transfer function from the Actuator force \(F_{i}\) to the absolute velocity sensor \(v_{m,i}\) (<a href="./figs/inertial_plant_flexible_joint_decentralized.png">png</a>, <a href="./figs/inertial_plant_flexible_joint_decentralized.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-org3f64d96" class="outline-3">
<h3 id="org3f64d96"><span class="section-number-3">1.3</span> Obtained Damping</h3>
<div class="outline-text-3" id="text-1-3">
<p>
The control is a performed in a decentralized manner.
The \(6 \times 6\) control is a diagonal matrix with pure proportional action on the diagonal:
\[ K(s) = g
\begin{bmatrix}
1 & & 0 \\
& \ddots & \\
0 & & 1
\end{bmatrix} \]
</p>
<p>
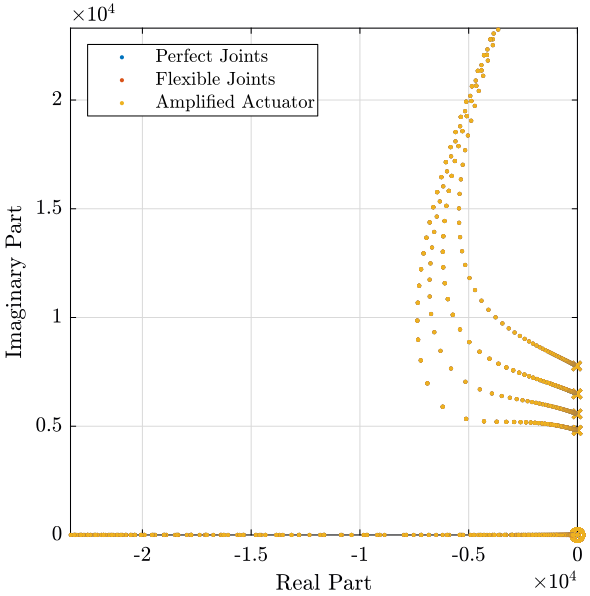
The root locus is shown in figure <a href="#org9af9e33">3</a>.
</p>
<div id="org9af9e33" class="figure">
<p><img src="figs/root_locus_inertial_rot_stiffness.png" alt="root_locus_inertial_rot_stiffness.png" />
</p>
<p><span class="figure-number">Figure 3: </span>Root Locus plot with Decentralized Inertial Control when considering the stiffness of flexible joints (<a href="./figs/root_locus_inertial_rot_stiffness.png">png</a>, <a href="./figs/root_locus_inertial_rot_stiffness.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-org8e1ece7" class="outline-3">
<h3 id="org8e1ece7"><span class="section-number-3">1.4</span> Conclusion</h3>
<div class="outline-text-3" id="text-1-4">
<div class="important">
<p>
We do not have guaranteed stability with Inertial control. This is because of the flexibility inside the internal sensor.
</p>
</div>
</div>
</div>
</div>
<div id="outline-container-org74c7eb4" class="outline-2">
<h2 id="org74c7eb4"><span class="section-number-2">2</span> Integral Force Feedback</h2>
<div class="outline-text-2" id="text-2">
<p>
<a id="orgab5e6b5"></a>
</p>
<div class="note">
<p>
The Matlab script corresponding to this section is accessible <a href="../matlab/active_damping_iff.m">here</a>.
</p>
<p>
To run the script, open the Simulink Project, and type <code>run active_damping_iff.m</code>.
</p>
</div>
</div>
<div id="outline-container-orgcd99b62" class="outline-3">
<h3 id="orgcd99b62"><span class="section-number-3">2.1</span> Identification of the Dynamics with perfect Joints</h3>
<div class="outline-text-3" id="text-2-1">
<p>
We first initialize the Stewart platform without joint stiffness.
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart = initializeStewartPlatform();
stewart = initializeFramesPositions(stewart, <span class="org-string">'H'</span>, 90e<span class="org-type">-</span>3, <span class="org-string">'MO_B'</span>, 45e<span class="org-type">-</span>3);
stewart = generateGeneralConfiguration(stewart);
stewart = computeJointsPose(stewart);
stewart = initializeStrutDynamics(stewart);
stewart = initializeJointDynamics(stewart, <span class="org-string">'type_F'</span>, <span class="org-string">'universal_p'</span>, <span class="org-string">'type_M'</span>, <span class="org-string">'spherical_p'</span>);
stewart = initializeCylindricalPlatforms(stewart);
stewart = initializeCylindricalStruts(stewart);
stewart = computeJacobian(stewart);
stewart = initializeStewartPose(stewart);
stewart = initializeInertialSensor(stewart, <span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">ground = initializeGround(<span class="org-string">'type'</span>, <span class="org-string">'rigid'</span>, <span class="org-string">'rot_point'</span>, stewart.platform_F.FO_A);
payload = initializePayload(<span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
controller = initializeController(<span class="org-string">'type'</span>, <span class="org-string">'open-loop'</span>);
</pre>
</div>
<p>
And we identify the dynamics from force actuators to force sensors.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak"><span class="org-comment">%% Name of the Simulink File</span></span>
mdl = <span class="org-string">'stewart_platform_model'</span>;
<span class="org-matlab-cellbreak"><span class="org-comment">%% Input/Output definition</span></span>
clear io; io_i = 1;
io(io_i) = linio([mdl, <span class="org-string">'/Controller'</span>], 1, <span class="org-string">'openinput'</span>); io_i = io_i <span class="org-type">+</span> 1; <span class="org-comment">% Actuator Force Inputs [N]</span>
io(io_i) = linio([mdl, <span class="org-string">'/Stewart Platform'</span>], 1, <span class="org-string">'openoutput'</span>, [], <span class="org-string">'Taum'</span>); io_i = io_i <span class="org-type">+</span> 1; <span class="org-comment">% Force Sensor Outputs [N]</span>
<span class="org-matlab-cellbreak"><span class="org-comment">%% Run the linearization</span></span>
G = linearize(mdl, io);
G.InputName = {<span class="org-string">'F1'</span>, <span class="org-string">'F2'</span>, <span class="org-string">'F3'</span>, <span class="org-string">'F4'</span>, <span class="org-string">'F5'</span>, <span class="org-string">'F6'</span>};
G.OutputName = {<span class="org-string">'Fm1'</span>, <span class="org-string">'Fm2'</span>, <span class="org-string">'Fm3'</span>, <span class="org-string">'Fm4'</span>, <span class="org-string">'Fm5'</span>, <span class="org-string">'Fm6'</span>};
</pre>
</div>
<p>
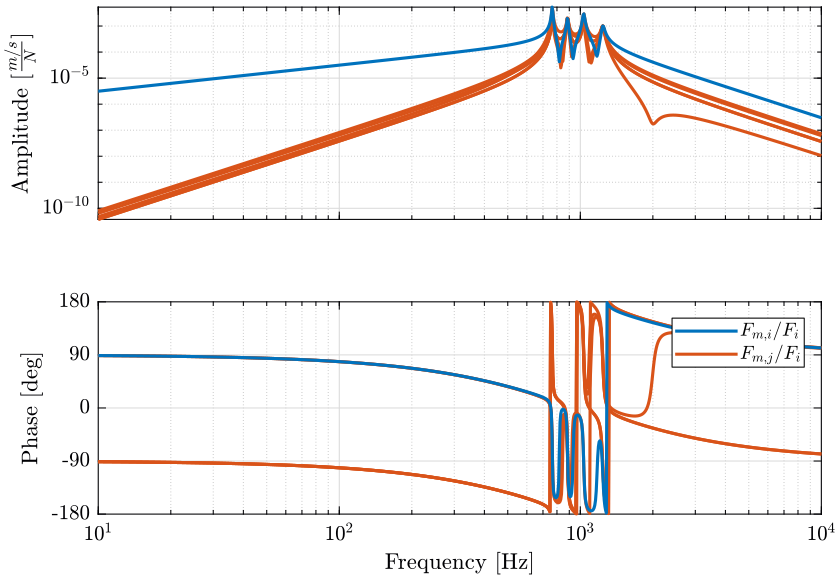
The transfer function from actuator forces to force sensors is shown in Figure <a href="#org3fca9dd">4</a>.
</p>
<div id="org3fca9dd" class="figure">
<p><img src="figs/iff_plant_coupling.png" alt="iff_plant_coupling.png" />
</p>
<p><span class="figure-number">Figure 4: </span>Transfer function from the Actuator force \(F_{i}\) to the Force sensor of the same leg \(F_{m,i}\) and to the force sensor of the other legs \(F_{m,j}\) with \(i \neq j\) in grey (<a href="./figs/iff_plant_coupling.png">png</a>, <a href="./figs/iff_plant_coupling.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-org1b7a953" class="outline-3">
<h3 id="org1b7a953"><span class="section-number-3">2.2</span> Effect of the Flexible Joint stiffness and Actuator amplification on the Dynamics</h3>
<div class="outline-text-3" id="text-2-2">
<p>
We add some stiffness and damping in the flexible joints and we re-identify the dynamics.
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart = initializeJointDynamics(stewart, <span class="org-string">'type_F'</span>, <span class="org-string">'universal'</span>, <span class="org-string">'type_M'</span>, <span class="org-string">'spherical'</span>);
Gf = linearize(mdl, io);
Gf.InputName = {<span class="org-string">'F1'</span>, <span class="org-string">'F2'</span>, <span class="org-string">'F3'</span>, <span class="org-string">'F4'</span>, <span class="org-string">'F5'</span>, <span class="org-string">'F6'</span>};
Gf.OutputName = {<span class="org-string">'Fm1'</span>, <span class="org-string">'Fm2'</span>, <span class="org-string">'Fm3'</span>, <span class="org-string">'Fm4'</span>, <span class="org-string">'Fm5'</span>, <span class="org-string">'Fm6'</span>};
</pre>
</div>
<p>
We now use the amplified actuators and re-identify the dynamics
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart = initializeAmplifiedStrutDynamics(stewart);
Ga = linearize(mdl, io);
Ga.InputName = {<span class="org-string">'F1'</span>, <span class="org-string">'F2'</span>, <span class="org-string">'F3'</span>, <span class="org-string">'F4'</span>, <span class="org-string">'F5'</span>, <span class="org-string">'F6'</span>};
Ga.OutputName = {<span class="org-string">'Fm1'</span>, <span class="org-string">'Fm2'</span>, <span class="org-string">'Fm3'</span>, <span class="org-string">'Fm4'</span>, <span class="org-string">'Fm5'</span>, <span class="org-string">'Fm6'</span>};
</pre>
</div>
<p>
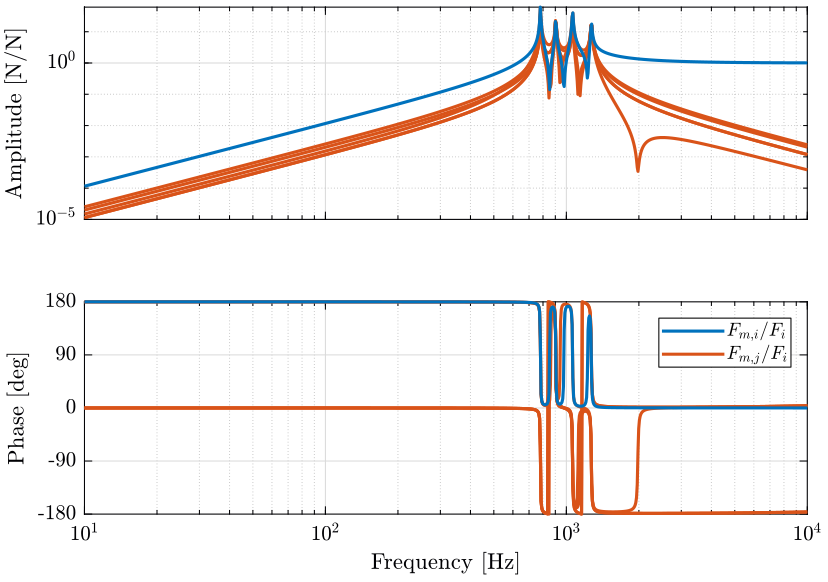
The new dynamics from force actuator to force sensor is shown in Figure <a href="#org090868b">5</a>.
</p>
<div id="org090868b" class="figure">
<p><img src="figs/iff_plant_flexible_joint_decentralized.png" alt="iff_plant_flexible_joint_decentralized.png" />
</p>
<p><span class="figure-number">Figure 5: </span>Transfer function from the Actuator force \(F_{i}\) to the force sensor \(F_{m,i}\) (<a href="./figs/iff_plant_flexible_joint_decentralized.png">png</a>, <a href="./figs/iff_plant_flexible_joint_decentralized.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-org1d362f0" class="outline-3">
<h3 id="org1d362f0"><span class="section-number-3">2.3</span> Obtained Damping</h3>
<div class="outline-text-3" id="text-2-3">
<p>
The control is a performed in a decentralized manner.
The \(6 \times 6\) control is a diagonal matrix with pure integration action on the diagonal:
\[ K(s) = g
\begin{bmatrix}
\frac{1}{s} & & 0 \\
& \ddots & \\
0 & & \frac{1}{s}
\end{bmatrix} \]
</p>
<p>
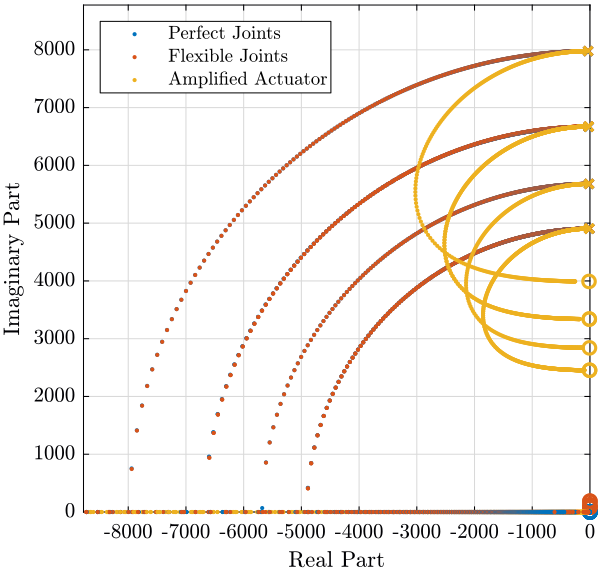
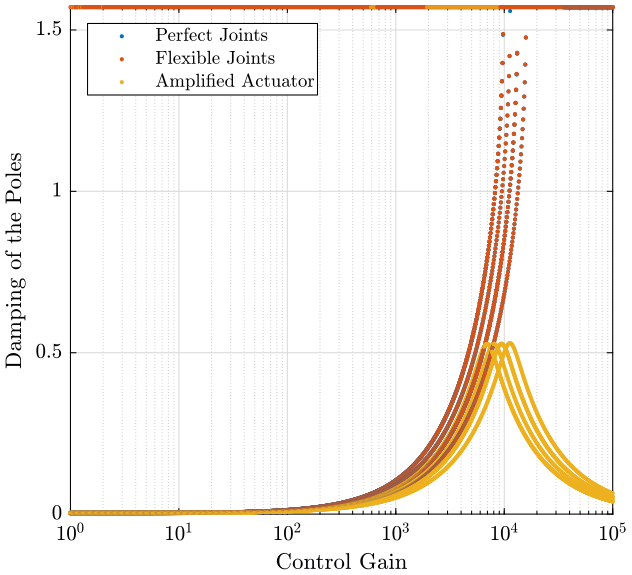
The root locus is shown in figure <a href="#orge21bbea">6</a> and the obtained pole damping function of the control gain is shown in figure <a href="#org94d6943">7</a>.
</p>
<div id="orge21bbea" class="figure">
<p><img src="figs/root_locus_iff_rot_stiffness.png" alt="root_locus_iff_rot_stiffness.png" />
</p>
<p><span class="figure-number">Figure 6: </span>Root Locus plot with Decentralized Integral Force Feedback when considering the stiffness of flexible joints (<a href="./figs/root_locus_iff_rot_stiffness.png">png</a>, <a href="./figs/root_locus_iff_rot_stiffness.pdf">pdf</a>)</p>
</div>
<div id="org94d6943" class="figure">
<p><img src="figs/pole_damping_gain_iff_rot_stiffness.png" alt="pole_damping_gain_iff_rot_stiffness.png" />
</p>
<p><span class="figure-number">Figure 7: </span>Damping of the poles with respect to the gain of the Decentralized Integral Force Feedback when considering the stiffness of flexible joints (<a href="./figs/pole_damping_gain_iff_rot_stiffness.png">png</a>, <a href="./figs/pole_damping_gain_iff_rot_stiffness.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-org63f9110" class="outline-3">
<h3 id="org63f9110"><span class="section-number-3">2.4</span> Conclusion</h3>
<div class="outline-text-3" id="text-2-4">
<div class="important">
<p>
The joint stiffness has a huge impact on the attainable active damping performance when using force sensors.
Thus, if Integral Force Feedback is to be used in a Stewart platform with flexible joints, the rotational stiffness of the joints should be minimized.
</p>
</div>
</div>
</div>
</div>
<div id="outline-container-org08917d6" class="outline-2">
<h2 id="org08917d6"><span class="section-number-2">3</span> Direct Velocity Feedback</h2>
<div class="outline-text-2" id="text-3">
<p>
<a id="org0aa816a"></a>
</p>
<div class="note">
<p>
The Matlab script corresponding to this section is accessible <a href="../matlab/active_damping_dvf.m">here</a>.
</p>
<p>
To run the script, open the Simulink Project, and type <code>run active_damping_dvf.m</code>.
</p>
</div>
</div>
<div id="outline-container-org5364f58" class="outline-3">
<h3 id="org5364f58"><span class="section-number-3">3.1</span> Identification of the Dynamics with perfect Joints</h3>
<div class="outline-text-3" id="text-3-1">
<p>
We first initialize the Stewart platform without joint stiffness.
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart = initializeStewartPlatform();
stewart = initializeFramesPositions(stewart, <span class="org-string">'H'</span>, 90e<span class="org-type">-</span>3, <span class="org-string">'MO_B'</span>, 45e<span class="org-type">-</span>3);
stewart = generateGeneralConfiguration(stewart);
stewart = computeJointsPose(stewart);
stewart = initializeStrutDynamics(stewart);
stewart = initializeJointDynamics(stewart, <span class="org-string">'type_F'</span>, <span class="org-string">'universal_p'</span>, <span class="org-string">'type_M'</span>, <span class="org-string">'spherical_p'</span>);
stewart = initializeCylindricalPlatforms(stewart);
stewart = initializeCylindricalStruts(stewart);
stewart = computeJacobian(stewart);
stewart = initializeStewartPose(stewart);
stewart = initializeInertialSensor(stewart, <span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">ground = initializeGround(<span class="org-string">'type'</span>, <span class="org-string">'rigid'</span>, <span class="org-string">'rot_point'</span>, stewart.platform_F.FO_A);
payload = initializePayload(<span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
controller = initializeController(<span class="org-string">'type'</span>, <span class="org-string">'open-loop'</span>);
</pre>
</div>
<p>
And we identify the dynamics from force actuators to force sensors.
</p>
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-matlab-cellbreak"><span class="org-comment">%% Options for Linearized</span></span>
options = linearizeOptions;
options.SampleTime = 0;
<span class="org-matlab-cellbreak"><span class="org-comment">%% Name of the Simulink File</span></span>
mdl = <span class="org-string">'stewart_platform_model'</span>;
<span class="org-matlab-cellbreak"><span class="org-comment">%% Input/Output definition</span></span>
clear io; io_i = 1;
io(io_i) = linio([mdl, <span class="org-string">'/Controller'</span>], 1, <span class="org-string">'openinput'</span>); io_i = io_i <span class="org-type">+</span> 1; <span class="org-comment">% Actuator Force Inputs [N]</span>
io(io_i) = linio([mdl, <span class="org-string">'/Stewart Platform'</span>], 1, <span class="org-string">'openoutput'</span>, [], <span class="org-string">'dLm'</span>); io_i = io_i <span class="org-type">+</span> 1; <span class="org-comment">% Relative Displacement Outputs [m]</span>
<span class="org-matlab-cellbreak"><span class="org-comment">%% Run the linearization</span></span>
G = linearize(mdl, io, options);
G.InputName = {<span class="org-string">'F1'</span>, <span class="org-string">'F2'</span>, <span class="org-string">'F3'</span>, <span class="org-string">'F4'</span>, <span class="org-string">'F5'</span>, <span class="org-string">'F6'</span>};
G.OutputName = {<span class="org-string">'Dm1'</span>, <span class="org-string">'Dm2'</span>, <span class="org-string">'Dm3'</span>, <span class="org-string">'Dm4'</span>, <span class="org-string">'Dm5'</span>, <span class="org-string">'Dm6'</span>};
</pre>
</div>
<p>
The transfer function from actuator forces to relative motion sensors is shown in Figure <a href="#orgcc86228">8</a>.
</p>
<div id="orgcc86228" class="figure">
<p><img src="figs/dvf_plant_coupling.png" alt="dvf_plant_coupling.png" />
</p>
<p><span class="figure-number">Figure 8: </span>Transfer function from the Actuator force \(F_{i}\) to the Relative Motion Sensor \(D_{m,j}\) with \(i \neq j\) (<a href="./figs/dvf_plant_coupling.png">png</a>, <a href="./figs/dvf_plant_coupling.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-org81b6713" class="outline-3">
<h3 id="org81b6713"><span class="section-number-3">3.2</span> Effect of the Flexible Joint stiffness and Actuator amplification on the Dynamics</h3>
<div class="outline-text-3" id="text-3-2">
<p>
We add some stiffness and damping in the flexible joints and we re-identify the dynamics.
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart = initializeJointDynamics(stewart, <span class="org-string">'type_F'</span>, <span class="org-string">'universal'</span>, <span class="org-string">'type_M'</span>, <span class="org-string">'spherical'</span>);
Gf = linearize(mdl, io, options);
Gf.InputName = {<span class="org-string">'F1'</span>, <span class="org-string">'F2'</span>, <span class="org-string">'F3'</span>, <span class="org-string">'F4'</span>, <span class="org-string">'F5'</span>, <span class="org-string">'F6'</span>};
Gf.OutputName = {<span class="org-string">'Dm1'</span>, <span class="org-string">'Dm2'</span>, <span class="org-string">'Dm3'</span>, <span class="org-string">'Dm4'</span>, <span class="org-string">'Dm5'</span>, <span class="org-string">'Dm6'</span>};
</pre>
</div>
<p>
We now use the amplified actuators and re-identify the dynamics
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart = initializeAmplifiedStrutDynamics(stewart);
Ga = linearize(mdl, io, options);
Ga.InputName = {<span class="org-string">'F1'</span>, <span class="org-string">'F2'</span>, <span class="org-string">'F3'</span>, <span class="org-string">'F4'</span>, <span class="org-string">'F5'</span>, <span class="org-string">'F6'</span>};
Ga.OutputName = {<span class="org-string">'Dm1'</span>, <span class="org-string">'Dm2'</span>, <span class="org-string">'Dm3'</span>, <span class="org-string">'Dm4'</span>, <span class="org-string">'Dm5'</span>, <span class="org-string">'Dm6'</span>};
</pre>
</div>
<p>
The new dynamics from force actuator to relative motion sensor is shown in Figure <a href="#org5a86447">9</a>.
</p>
<div id="org5a86447" class="figure">
<p><img src="figs/dvf_plant_flexible_joint_decentralized.png" alt="dvf_plant_flexible_joint_decentralized.png" />
</p>
<p><span class="figure-number">Figure 9: </span>Transfer function from the Actuator force \(F_{i}\) to the relative displacement sensor \(D_{m,i}\) (<a href="./figs/dvf_plant_flexible_joint_decentralized.png">png</a>, <a href="./figs/dvf_plant_flexible_joint_decentralized.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-orge328103" class="outline-3">
<h3 id="orge328103"><span class="section-number-3">3.3</span> Obtained Damping</h3>
<div class="outline-text-3" id="text-3-3">
<p>
The control is a performed in a decentralized manner.
The \(6 \times 6\) control is a diagonal matrix with pure derivative action on the diagonal:
\[ K(s) = g
\begin{bmatrix}
s & & \\
& \ddots & \\
& & s
\end{bmatrix} \]
</p>
<p>
The root locus is shown in figure <a href="#org277d60d">10</a>.
</p>
<div id="org277d60d" class="figure">
<p><img src="figs/root_locus_dvf_rot_stiffness.png" alt="root_locus_dvf_rot_stiffness.png" />
</p>
<p><span class="figure-number">Figure 10: </span>Root Locus plot with Direct Velocity Feedback when considering the Stiffness of flexible joints (<a href="./figs/root_locus_dvf_rot_stiffness.png">png</a>, <a href="./figs/root_locus_dvf_rot_stiffness.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-org48c963f" class="outline-3">
<h3 id="org48c963f"><span class="section-number-3">3.4</span> Conclusion</h3>
<div class="outline-text-3" id="text-3-4">
<div class="important">
<p>
Joint stiffness does increase the resonance frequencies of the system but does not change the attainable damping when using relative motion sensors.
</p>
</div>
</div>
</div>
</div>
<div id="outline-container-org183f3f2" class="outline-2">
<h2 id="org183f3f2"><span class="section-number-2">4</span> Compliance and Transmissibility Comparison</h2>
<div class="outline-text-2" id="text-4">
</div>
<div id="outline-container-org0ed1499" class="outline-3">
<h3 id="org0ed1499"><span class="section-number-3">4.1</span> Initialization</h3>
<div class="outline-text-3" id="text-4-1">
<p>
We first initialize the Stewart platform without joint stiffness.
</p>
<div class="org-src-container">
<pre class="src src-matlab">stewart = initializeStewartPlatform();
stewart = initializeFramesPositions(stewart, <span class="org-string">'H'</span>, 90e<span class="org-type">-</span>3, <span class="org-string">'MO_B'</span>, 45e<span class="org-type">-</span>3);
stewart = generateGeneralConfiguration(stewart);
stewart = computeJointsPose(stewart);
stewart = initializeStrutDynamics(stewart);
stewart = initializeJointDynamics(stewart, <span class="org-string">'type_F'</span>, <span class="org-string">'universal_p'</span>, <span class="org-string">'type_M'</span>, <span class="org-string">'spherical_p'</span>);
stewart = initializeCylindricalPlatforms(stewart);
stewart = initializeCylindricalStruts(stewart);
stewart = computeJacobian(stewart);
stewart = initializeStewartPose(stewart);
stewart = initializeInertialSensor(stewart, <span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
</pre>
</div>
<p>
The rotation point of the ground is located at the origin of frame \(\{A\}\).
</p>
<div class="org-src-container">
<pre class="src src-matlab">ground = initializeGround(<span class="org-string">'type'</span>, <span class="org-string">'rigid'</span>, <span class="org-string">'rot_point'</span>, stewart.platform_F.FO_A);
payload = initializePayload(<span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
controller = initializeController(<span class="org-string">'type'</span>, <span class="org-string">'open-loop'</span>);
</pre>
</div>
</div>
</div>
<div id="outline-container-orgcd64c04" class="outline-3">
<h3 id="orgcd64c04"><span class="section-number-3">4.2</span> Identification</h3>
<div class="outline-text-3" id="text-4-2">
<p>
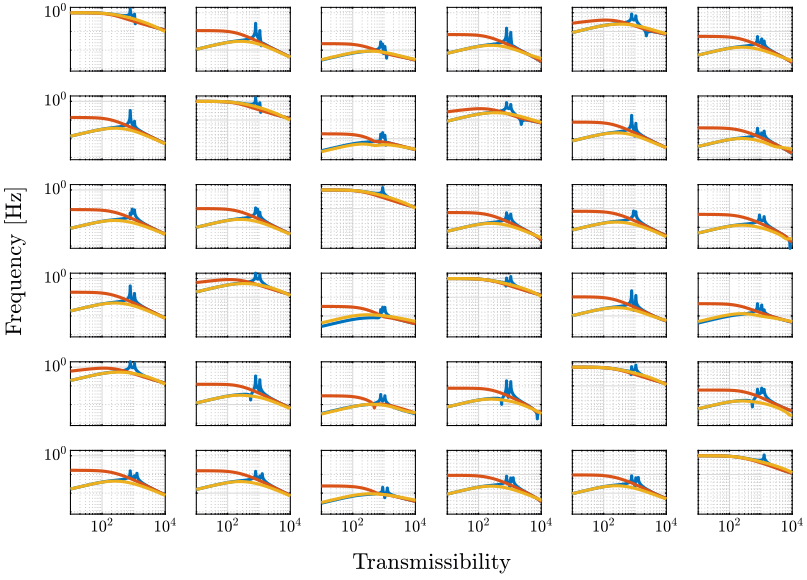
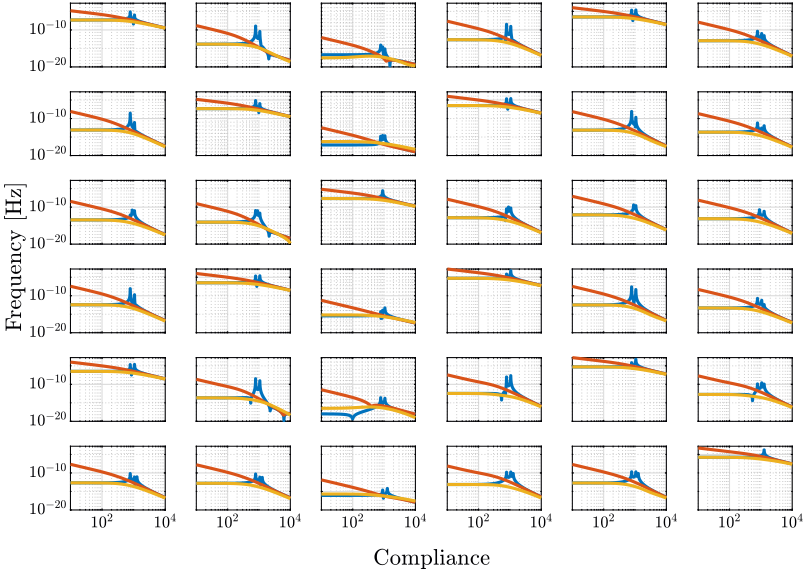
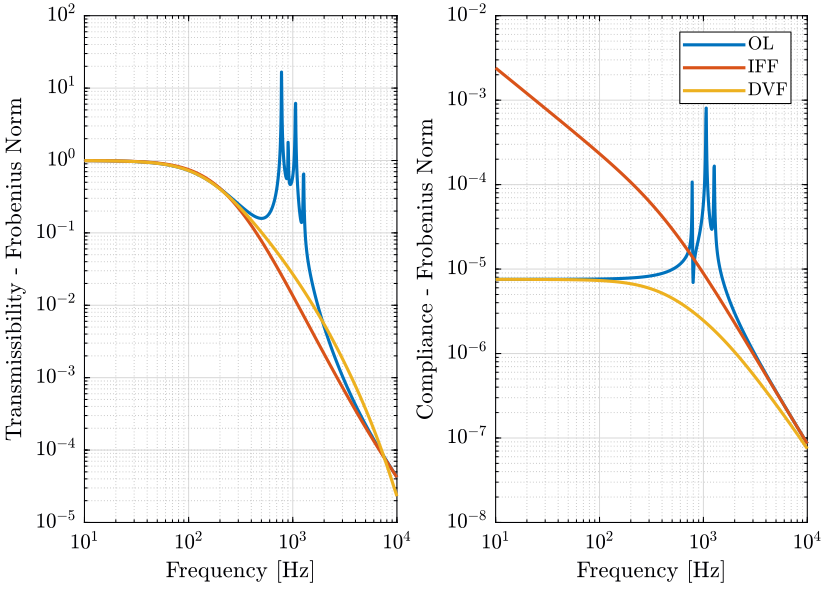
Let’s first identify the transmissibility and compliance in the open-loop case.
</p>
<div class="org-src-container">
<pre class="src src-matlab">controller = initializeController(<span class="org-string">'type'</span>, <span class="org-string">'open-loop'</span>);
[T_ol, T_norm_ol, freqs] = computeTransmissibility();
[C_ol, C_norm_ol, freqs] = computeCompliance();
</pre>
</div>
<p>
Now, let’s identify the transmissibility and compliance for the Integral Force Feedback architecture.
</p>
<div class="org-src-container">
<pre class="src src-matlab">controller = initializeController(<span class="org-string">'type'</span>, <span class="org-string">'iff'</span>);
K_iff = (1e4<span class="org-type">/</span>s)<span class="org-type">*</span>eye(6);
[T_iff, T_norm_iff, <span class="org-type">~</span>] = computeTransmissibility();
[C_iff, C_norm_iff, <span class="org-type">~</span>] = computeCompliance();
</pre>
</div>
<p>
And for the Direct Velocity Feedback.
</p>
<div class="org-src-container">
<pre class="src src-matlab">controller = initializeController(<span class="org-string">'type'</span>, <span class="org-string">'dvf'</span>);
K_dvf = 1e4<span class="org-type">*</span>s<span class="org-type">/</span>(1<span class="org-type">+</span>s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>5000)<span class="org-type">*</span>eye(6);
[T_dvf, T_norm_dvf, <span class="org-type">~</span>] = computeTransmissibility();
[C_dvf, C_norm_dvf, <span class="org-type">~</span>] = computeCompliance();
</pre>
</div>
</div>
</div>
<div id="outline-container-orgd30c62d" class="outline-3">
<h3 id="orgd30c62d"><span class="section-number-3">4.3</span> Results</h3>
<div class="outline-text-3" id="text-4-3">
<div id="org6691389" class="figure">
<p><img src="figs/transmissibility_iff_dvf.png" alt="transmissibility_iff_dvf.png" />
</p>
<p><span class="figure-number">Figure 11: </span>Obtained transmissibility for Open-Loop Control (Blue), Integral Force Feedback (Red) and Direct Velocity Feedback (Yellow) (<a href="./figs/transmissibility_iff_dvf.png">png</a>, <a href="./figs/transmissibility_iff_dvf.pdf">pdf</a>)</p>
</div>
<div id="orgd29218a" class="figure">
<p><img src="figs/compliance_iff_dvf.png" alt="compliance_iff_dvf.png" />
</p>
<p><span class="figure-number">Figure 12: </span>Obtained compliance for Open-Loop Control (Blue), Integral Force Feedback (Red) and Direct Velocity Feedback (Yellow) (<a href="./figs/compliance_iff_dvf.png">png</a>, <a href="./figs/compliance_iff_dvf.pdf">pdf</a>)</p>
</div>
<div id="org2ee9711" class="figure">
<p><img src="figs/frobenius_norm_T_C_iff_dvf.png" alt="frobenius_norm_T_C_iff_dvf.png" />
</p>
<p><span class="figure-number">Figure 13: </span>Frobenius norm of the Transmissibility and Compliance Matrices (<a href="./figs/frobenius_norm_T_C_iff_dvf.png">png</a>, <a href="./figs/frobenius_norm_T_C_iff_dvf.pdf">pdf</a>)</p>
</div>
</div>
</div>
</div>
</div>
<div id="postamble" class="status">
<p class="author">Author: Dehaeze Thomas</p>
<p class="date">Created: 2020-03-02 lun. 17:57</p>
</div>
</body>
</html>