Kinematic Study of the Stewart Platform
Table of Contents
- 1. Jacobian Analysis
- 2. Stiffness Analysis
- 3. Forward and Inverse Kinematics
- 4. Estimated required actuator stroke from specified platform mobility
- 5. Estimated platform mobility from specified actuator stroke
- 6. Functions
The kinematic analysis of a parallel manipulator is well described in taghirad13_paral:
Kinematic analysis refers to the study of the geometry of motion of a robot, without considering the forces an torques that cause the motion. In this analysis, the relation between the geometrical parameters of the manipulator with the final motion of the moving platform is derived and analyzed.
The current document is divided in the following sections:
- Section 1: The Jacobian matrix is derived from the geometry of the Stewart platform. Then it is shown that the Jacobian can link velocities and forces present in the system, and thus this matrix can be very useful for both analysis and control of the Stewart platform.
- Section 2: The stiffness and compliance matrices are derived from the Jacobian matrix and the stiffness of each strut.
- Section 3: The Forward and Inverse kinematic problems are presented.
1 Jacobian Analysis
From taghirad13_paral:
The Jacobian matrix not only reveals the relation between the joint variable velocities of a parallel manipulator to the moving platform linear and angular velocities, it also constructs the transformation needed to find the actuator forces from the forces and moments acting on the moving platform.
1.1 Jacobian Computation
If we note:
- \({}^A\hat{\bm{s}}_i\) the unit vector representing the direction of the i’th strut and expressed in frame \(\{A\}\)
- \({}^A\bm{b}_i\) the position vector of the i’th joint fixed to the mobile platform and expressed in frame \(\{A\}\)
Then, we can compute the Jacobian with the following equation (the superscript \(A\) is ignored):
\begin{equation*} \bm{J} = \begin{bmatrix} {\hat{\bm{s}}_1}^T & (\bm{b}_1 \times \hat{\bm{s}}_1)^T \\ {\hat{\bm{s}}_2}^T & (\bm{b}_2 \times \hat{\bm{s}}_2)^T \\ {\hat{\bm{s}}_3}^T & (\bm{b}_3 \times \hat{\bm{s}}_3)^T \\ {\hat{\bm{s}}_4}^T & (\bm{b}_4 \times \hat{\bm{s}}_4)^T \\ {\hat{\bm{s}}_5}^T & (\bm{b}_5 \times \hat{\bm{s}}_5)^T \\ {\hat{\bm{s}}_6}^T & (\bm{b}_6 \times \hat{\bm{s}}_6)^T \end{bmatrix} \end{equation*}
The Jacobian matrix \(\bm{J}\) can be computed using the computeJacobian function (accessible here).
For instance:
stewart = computeJacobian(stewart);
This will add three new matrix to the stewart structure:
Jthe Jacobian matrixKthe stiffness matrixCthe compliance matrix
1.2 Jacobian - Velocity loop closure
The Jacobian matrix links the input joint rate \(\dot{\bm{\mathcal{L}}} = [ \dot{l}_1, \dot{l}_2, \dot{l}_3, \dot{l}_4, \dot{l}_5, \dot{l}_6 ]^T\) of each strut to the output twist vector of the mobile platform is denoted by \(\dot{\bm{X}} = [^A\bm{v}_p, {}^A\bm{\omega}]^T\):
\begin{equation*} \dot{\bm{\mathcal{L}}} = \bm{J} \dot{\bm{\mathcal{X}}} \end{equation*}The input joint rate \(\dot{\bm{\mathcal{L}}}\) can be measured by taking the derivative of the relative motion sensor in each strut. The output twist vector can be measured with a “Transform Sensor” block measuring the relative velocity and relative angular velocity of frame \(\{B\}\) with respect to frame \(\{A\}\).
If the Jacobian matrix is inversible, we can also compute \(\dot{\bm{\mathcal{X}}}\) from \(\dot{\bm{\mathcal{L}}}\).
\begin{equation*} \dot{\bm{\mathcal{X}}} = \bm{J}^{-1} \dot{\bm{\mathcal{L}}} \end{equation*}The Jacobian matrix can also be used to approximate forward and inverse kinematics for small displacements. This is explained in section 3.3.
1.3 Jacobian - Static Force Transformation
If we note:
- \(\bm{\tau} = [\tau_1, \tau_2, \cdots, \tau_6]^T\): vector of actuator forces applied in each strut
- \(\bm{\mathcal{F}} = [\bm{f}, \bm{n}]^T\): external force/torque action on the mobile platform at \(\bm{O}_B\)
We find that the transpose of the Jacobian matrix links the two by the following equation:
\begin{equation*} \bm{\mathcal{F}} = \bm{J}^T \bm{\tau} \end{equation*}If the Jacobian matrix is inversible, we also have the following relation:
\begin{equation*} \bm{\tau} = \bm{J}^{-T} \bm{\mathcal{F}} \end{equation*}2 Stiffness Analysis
Here, we focus on the deflections of the manipulator moving platform that are the result of the external applied wrench to the mobile platform. The amount of these deflections are a function of the applied wrench as well as the manipulator structural stiffness.
2.1 Computation of the Stiffness and Compliance Matrix
As explain in this document, each Actuator is modeled by 3 elements in parallel:
- A spring with a stiffness \(k_{i}\)
- A dashpot with a damping \(c_{i}\)
The stiffness of the actuator \(k_i\) links the applied actuator force \(\delta \tau_i\) and the corresponding small deflection \(\delta l_i\):
\begin{equation*} \tau_i = k_i \delta l_i, \quad i = 1,\ \dots,\ 6 \end{equation*}If we combine these 6 relations:
\begin{equation*} \bm{\tau} = \mathcal{K} \delta \bm{\mathcal{L}} \quad \mathcal{K} = \text{diag}\left[ k_1,\ \dots,\ k_6 \right] \end{equation*}Substituting \(\bm{\tau} = \bm{J}^{-T} \bm{\mathcal{F}}\) and \(\delta \bm{\mathcal{L}} = \bm{J} \cdot \delta \bm{\mathcal{X}}\) gives
\begin{equation*} \bm{\mathcal{F}} = \bm{J}^T \mathcal{K} \bm{J} \cdot \delta \bm{\mathcal{X}} \end{equation*}And then we identify the stiffness matrix \(\bm{K}\):
\begin{equation*} \bm{K} = \bm{J}^T \mathcal{K} \bm{J} \end{equation*}If the stiffness matrix \(\bm{K}\) is inversible, the compliance matrix of the manipulator is defined as
\begin{equation*} \bm{C} = \bm{K}^{-1} = (\bm{J}^T \mathcal{K} \bm{J})^{-1} \end{equation*}The compliance matrix of a manipulator shows the mapping of the moving platform wrench applied at \(\bm{O}_B\) to its small deflection by
\begin{equation*} \delta \bm{\mathcal{X}} = \bm{C} \cdot \bm{\mathcal{F}} \end{equation*}
The stiffness and compliance matrices are computed using the computeJacobian function (accessible here).
3 Forward and Inverse Kinematics
3.1 Inverse Kinematics
For inverse kinematic analysis, it is assumed that the position \({}^A\bm{P}\) and orientation of the moving platform \({}^A\bm{R}_B\) are given and the problem is to obtain the joint variables \(\bm{\mathcal{L}} = \left[ l_1, l_2, l_3, l_4, l_5, l_6 \right]^T\).
This problem can be easily solved using the loop closures.
The obtain joint variables are:
\begin{equation*} \begin{aligned} l_i = &\Big[ {}^A\bm{P}^T {}^A\bm{P} + {}^B\bm{b}_i^T {}^B\bm{b}_i + {}^A\bm{a}_i^T {}^A\bm{a}_i - 2 {}^A\bm{P}^T {}^A\bm{a}_i + \dots\\ &2 {}^A\bm{P}^T \left[{}^A\bm{R}_B {}^B\bm{b}_i\right] - 2 \left[{}^A\bm{R}_B {}^B\bm{b}_i\right]^T {}^A\bm{a}_i \Big]^{1/2} \end{aligned} \end{equation*}If the position and orientation of the platform lie in the feasible workspace, the solution is unique. Otherwise, the solution gives complex numbers.
This inverse kinematic solution can be obtained using the function inverseKinematics (described here).
3.2 Forward Kinematics
In forward kinematic analysis, it is assumed that the vector of limb lengths \(\bm{L}\) is given and the problem is to find the position \({}^A\bm{P}\) and the orientation \({}^A\bm{R}_B\).
This is a difficult problem that requires to solve nonlinear equations.
In a next section, an approximate solution of the forward kinematics problem is proposed for small displacements.
3.3 Approximate solution of the Forward and Inverse Kinematic problem for small displacement using the Jacobian matrix
For small displacements mobile platform displacement \(\delta \bm{\mathcal{X}} = [\delta x, \delta y, \delta z, \delta \theta_x, \delta \theta_y, \delta \theta_z ]^T\) around \(\bm{\mathcal{X}}_0\), the associated joint displacement can be computed using the Jacobian:
\begin{equation*} \delta\bm{\mathcal{L}} = \bm{J} \delta\bm{\mathcal{X}} \end{equation*}Similarly, for small joint displacements \(\delta\bm{\mathcal{L}} = [ \delta l_1,\ \dots,\ \delta l_6 ]^T\) around \(\bm{\mathcal{L}}_0\), it is possible to find the induced small displacement of the mobile platform:
\begin{equation*} \delta\bm{\mathcal{X}} = \bm{J}^{-1} \delta\bm{\mathcal{L}} \end{equation*}These two relations solve the forward and inverse kinematic problems for small displacement in a approximate way. As the inverse kinematic can be easily solved exactly this is not much useful, however, as the forward kinematic problem is difficult to solve, this approximation can be very useful for small displacements.
The function forwardKinematicsApprox (described here) can be used to solve the forward kinematic problem using the Jacobian matrix.
3.4 Estimation of the range validity of the approximate inverse kinematics
As we know how to exactly solve the Inverse kinematic problem, we can compare the exact solution with the approximate solution using the Jacobian matrix. For small displacements, the approximate solution is expected to work well. We would like here to determine up to what displacement this approximation can be considered as correct.
Then, we can determine the range for which the approximate inverse kinematic is valid. This will also gives us the range for which the approximate forward kinematic is valid.
3.4.1 Stewart architecture definition
We first define some general Stewart architecture.
stewart = initializeFramesPositions('H', 90e-3, 'MO_B', 45e-3); stewart = generateGeneralConfiguration(stewart); stewart = computeJointsPose(stewart); stewart = initializeStewartPose(stewart); stewart = initializeCylindricalPlatforms(stewart); stewart = initializeCylindricalStruts(stewart); stewart = initializeStrutDynamics(stewart); stewart = initializeJointDynamics(stewart); stewart = computeJacobian(stewart);
3.4.2 Comparison for “pure” translations
Let’s first compare the perfect and approximate solution of the inverse for pure \(x\) translations.
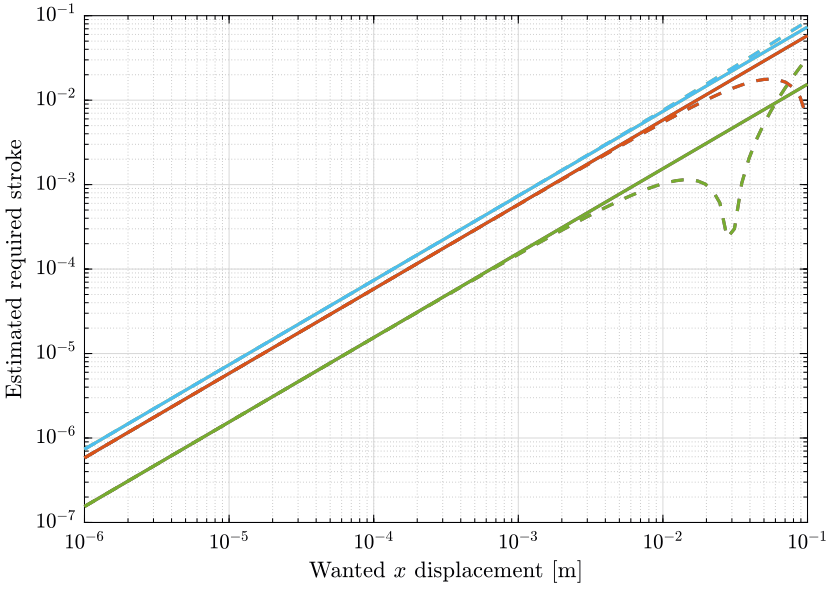
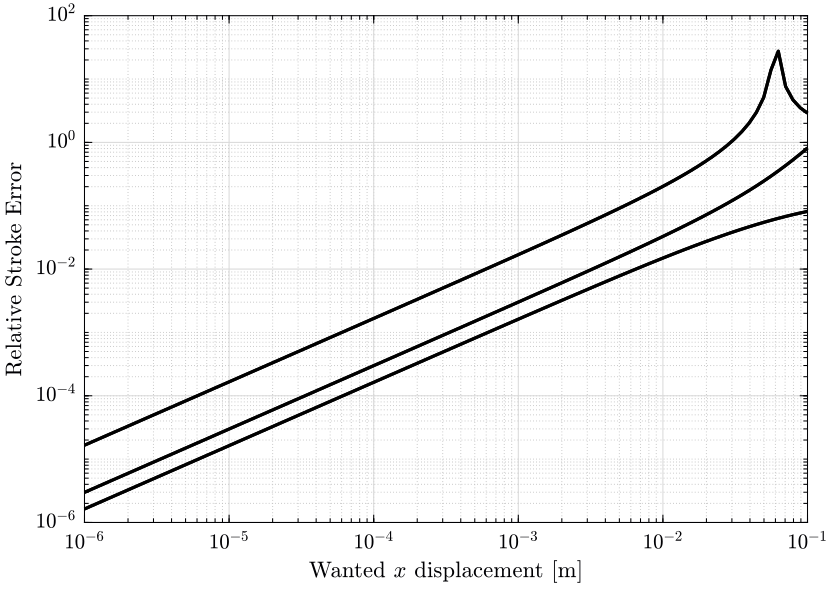
We compute the approximate and exact required strut stroke to have the wanted mobile platform \(x\) displacement. The estimate required strut stroke for both the approximate and exact solutions are shown in Figure 1. The relative strut length displacement is shown in Figure 2.
Xrs = logspace(-6, -1, 100); % Wanted X translation of the mobile platform [m] Ls_approx = zeros(6, length(Xrs)); Ls_exact = zeros(6, length(Xrs)); for i = 1:length(Xrs) Xr = Xrs(i); L_approx(:, i) = stewart.J*[Xr; 0; 0; 0; 0; 0;]; [~, L_exact(:, i)] = inverseKinematics(stewart, 'AP', [Xr; 0; 0]); end
3.4.3 Conclusion
For small wanted displacements (up to \(\approx 1\%\) of the size of the Hexapod), the approximate inverse kinematic solution using the Jacobian matrix is quite correct.
4 Estimated required actuator stroke from specified platform mobility
Let’s say one want to design a Stewart platform with some specified mobility (position and orientation). One may want to determine the required actuator stroke required to obtain the specified mobility. This is what is analyzed in this section.
4.1 Stewart architecture definition
Let’s first define the Stewart platform architecture that we want to study.
stewart = initializeFramesPositions('H', 90e-3, 'MO_B', 45e-3); stewart = generateGeneralConfiguration(stewart); stewart = computeJointsPose(stewart); stewart = initializeStewartPose(stewart); stewart = initializeCylindricalPlatforms(stewart); stewart = initializeCylindricalStruts(stewart); stewart = initializeStrutDynamics(stewart, 'Ki', 1e6*ones(6,1), 'Ci', 1e2*ones(6,1)); stewart = initializeJointDynamics(stewart); stewart = computeJacobian(stewart);
4.2 Wanted translations and rotations
Let’s now define the wanted extreme translations and rotations.
Tx_max = 50e-6; % Translation [m] Ty_max = 50e-6; % Translation [m] Tz_max = 50e-6; % Translation [m] Rx_max = 30e-6; % Rotation [rad] Ry_max = 30e-6; % Rotation [rad] Rz_max = 0; % Rotation [rad]
4.3 Needed stroke for “pure” rotations or translations
As a first estimation, we estimate the needed actuator stroke for “pure” rotations and translation. We do that using either the Inverse Kinematic solution or the Jacobian matrix as an approximation.
LTx = stewart.J*[Tx_max 0 0 0 0 0]'; LTy = stewart.J*[0 Ty_max 0 0 0 0]'; LTz = stewart.J*[0 0 Tz_max 0 0 0]'; LRx = stewart.J*[0 0 0 Rx_max 0 0]'; LRy = stewart.J*[0 0 0 0 Ry_max 0]'; LRz = stewart.J*[0 0 0 0 0 Rz_max]';
The obtain required stroke is:
From -3.8e-05[m] to 3.8e-05[m]: Total stroke = 76.1[um]
This is surely a low estimation of the required stroke.
4.4 Needed stroke for “combined” rotations or translations
We know would like to have a more precise estimation.
To do so, we may estimate the required actuator stroke for all possible combination of translation and rotation.
Let’s first generate all the possible combination of maximum translation and rotations.
Ps = [2*(dec2bin(0:5^2-1,5)-'0')-1, zeros(5^2, 1)].*[Tx_max Ty_max Tz_max Rx_max Ry_max Rz_max];
| Tx [m] | Ty [m] | Tz [m] | Rx [rad] | Ry [rad] | Rz [rad] |
|---|---|---|---|---|---|
| -5.0e-05 | -5.0e-05 | -5.0e-05 | -3.0e-05 | -3.0e-05 | 0.0e+00 |
| -5.0e-05 | -5.0e-05 | -5.0e-05 | -3.0e-05 | 3.0e-05 | 0.0e+00 |
| -5.0e-05 | -5.0e-05 | -5.0e-05 | 3.0e-05 | -3.0e-05 | 0.0e+00 |
| -5.0e-05 | -5.0e-05 | -5.0e-05 | 3.0e-05 | 3.0e-05 | 0.0e+00 |
| -5.0e-05 | -5.0e-05 | 5.0e-05 | -3.0e-05 | -3.0e-05 | 0.0e+00 |
| -5.0e-05 | -5.0e-05 | 5.0e-05 | -3.0e-05 | 3.0e-05 | 0.0e+00 |
| -5.0e-05 | -5.0e-05 | 5.0e-05 | 3.0e-05 | -3.0e-05 | 0.0e+00 |
| -5.0e-05 | -5.0e-05 | 5.0e-05 | 3.0e-05 | 3.0e-05 | 0.0e+00 |
| -5.0e-05 | 5.0e-05 | -5.0e-05 | -3.0e-05 | -3.0e-05 | 0.0e+00 |
| -5.0e-05 | 5.0e-05 | -5.0e-05 | -3.0e-05 | 3.0e-05 | 0.0e+00 |
| -5.0e-05 | 5.0e-05 | -5.0e-05 | 3.0e-05 | -3.0e-05 | 0.0e+00 |
| -5.0e-05 | 5.0e-05 | -5.0e-05 | 3.0e-05 | 3.0e-05 | 0.0e+00 |
| -5.0e-05 | 5.0e-05 | 5.0e-05 | -3.0e-05 | -3.0e-05 | 0.0e+00 |
| -5.0e-05 | 5.0e-05 | 5.0e-05 | -3.0e-05 | 3.0e-05 | 0.0e+00 |
| -5.0e-05 | 5.0e-05 | 5.0e-05 | 3.0e-05 | -3.0e-05 | 0.0e+00 |
| -5.0e-05 | 5.0e-05 | 5.0e-05 | 3.0e-05 | 3.0e-05 | 0.0e+00 |
| 5.0e-05 | -5.0e-05 | -5.0e-05 | -3.0e-05 | -3.0e-05 | 0.0e+00 |
| 5.0e-05 | -5.0e-05 | -5.0e-05 | -3.0e-05 | 3.0e-05 | 0.0e+00 |
| 5.0e-05 | -5.0e-05 | -5.0e-05 | 3.0e-05 | -3.0e-05 | 0.0e+00 |
| 5.0e-05 | -5.0e-05 | -5.0e-05 | 3.0e-05 | 3.0e-05 | 0.0e+00 |
| 5.0e-05 | -5.0e-05 | 5.0e-05 | -3.0e-05 | -3.0e-05 | 0.0e+00 |
| 5.0e-05 | -5.0e-05 | 5.0e-05 | -3.0e-05 | 3.0e-05 | 0.0e+00 |
| 5.0e-05 | -5.0e-05 | 5.0e-05 | 3.0e-05 | -3.0e-05 | 0.0e+00 |
| 5.0e-05 | -5.0e-05 | 5.0e-05 | 3.0e-05 | 3.0e-05 | 0.0e+00 |
| 5.0e-05 | 5.0e-05 | -5.0e-05 | -3.0e-05 | -3.0e-05 | 0.0e+00 |
For all possible combination, we compute the required actuator stroke using the inverse kinematic solution.
L_min = 0; L_max = 0; for i = 1:size(Ps,1) Rx = [1 0 0; 0 cos(Ps(i, 4)) -sin(Ps(i, 4)); 0 sin(Ps(i, 4)) cos(Ps(i, 4))]; Ry = [ cos(Ps(i, 5)) 0 sin(Ps(i, 5)); 0 1 0; -sin(Ps(i, 5)) 0 cos(Ps(i, 5))]; Rz = [cos(Ps(i, 6)) -sin(Ps(i, 6)) 0; sin(Ps(i, 6)) cos(Ps(i, 6)) 0; 0 0 1]; ARB = Rz*Ry*Rx; [~, Ls] = inverseKinematics(stewart, 'AP', Ps(i, 1:3)', 'ARB', ARB); if min(Ls) < L_min L_min = min(Ls) end if max(Ls) > L_max L_max = max(Ls) end end
We obtain the required actuator stroke:
From -8.9e-05[m] to 8.9e-05[m]: Total stroke = 177.2[um]
This is probably a much realistic estimation of the required actuator stroke.
5 Estimated platform mobility from specified actuator stroke
Here, from some value of the actuator stroke, we would like to estimate the mobility of the Stewart platform.
As explained in section 3, the forward kinematic problem of the Stewart platform is quite difficult to solve. However, for small displacements, we can use the Jacobian as an approximate solution.
5.1 Stewart architecture definition
Let’s first define the Stewart platform architecture that we want to study.
stewart = initializeFramesPositions('H', 90e-3, 'MO_B', 45e-3); stewart = generateGeneralConfiguration(stewart); stewart = computeJointsPose(stewart); stewart = initializeStewartPose(stewart); stewart = initializeCylindricalPlatforms(stewart); stewart = initializeCylindricalStruts(stewart); stewart = initializeStrutDynamics(stewart, 'Ki', 1e6*ones(6,1), 'Ci', 1e2*ones(6,1)); stewart = initializeJointDynamics(stewart); stewart = computeJacobian(stewart);
Let’s now define the actuator stroke.
L_min = -50e-6; % [m] L_max = 50e-6; % [m]
5.2 TODO Approximate Forward Dynamics
6 Functions
6.1 computeJacobian: Compute the Jacobian Matrix
This Matlab function is accessible here.
Function description
function [stewart] = computeJacobian(stewart) % computeJacobian - % % Syntax: [stewart] = computeJacobian(stewart) % % Inputs: % - stewart - With at least the following fields: % - As [3x6] - The 6 unit vectors for each strut expressed in {A} % - Ab [3x6] - The 6 position of the joints bi expressed in {A} % % Outputs: % - stewart - With the 3 added field: % - J [6x6] - The Jacobian Matrix % - K [6x6] - The Stiffness Matrix % - C [6x6] - The Compliance Matrix
Compute Jacobian Matrix
stewart.J = [stewart.As' , cross(stewart.Ab, stewart.As)'];
Compute Stiffness Matrix
stewart.K = stewart.J'*diag(stewart.Ki)*stewart.J;
Compute Compliance Matrix
stewart.C = inv(stewart.K);
6.2 inverseKinematics: Compute Inverse Kinematics
This Matlab function is accessible here.
Function description
function [Li, dLi] = inverseKinematics(stewart, args) % inverseKinematics - Compute the needed length of each strut to have the wanted position and orientation of {B} with respect to {A} % % Syntax: [stewart] = inverseKinematics(stewart) % % Inputs: % - stewart - A structure with the following fields % - Aa [3x6] - The positions ai expressed in {A} % - Bb [3x6] - The positions bi expressed in {B} % - args - Can have the following fields: % - AP [3x1] - The wanted position of {B} with respect to {A} % - ARB [3x3] - The rotation matrix that gives the wanted orientation of {B} with respect to {A} % % Outputs: % - Li [6x1] - The 6 needed length of the struts in [m] to have the wanted pose of {B} w.r.t. {A} % - dLi [6x1] - The 6 needed displacement of the struts from the initial position in [m] to have the wanted pose of {B} w.r.t. {A}
Optional Parameters
arguments
stewart
args.AP (3,1) double {mustBeNumeric} = zeros(3,1)
args.ARB (3,3) double {mustBeNumeric} = eye(3)
end
Theory
For inverse kinematic analysis, it is assumed that the position \({}^A\bm{P}\) and orientation of the moving platform \({}^A\bm{R}_B\) are given and the problem is to obtain the joint variables, namely, \(\bm{L} = [l_1, l_2, \dots, l_6]^T\).
From the geometry of the manipulator, the loop closure for each limb, \(i = 1, 2, \dots, 6\) can be written as
\begin{align*} l_i {}^A\hat{\bm{s}}_i &= {}^A\bm{A} + {}^A\bm{b}_i - {}^A\bm{a}_i \\ &= {}^A\bm{A} + {}^A\bm{R}_b {}^B\bm{b}_i - {}^A\bm{a}_i \end{align*}To obtain the length of each actuator and eliminate \(\hat{\bm{s}}_i\), it is sufficient to dot multiply each side by itself:
\begin{equation} l_i^2 \left[ {}^A\hat{\bm{s}}_i^T {}^A\hat{\bm{s}}_i \right] = \left[ {}^A\bm{P} + {}^A\bm{R}_B {}^B\bm{b}_i - {}^A\bm{a}_i \right]^T \left[ {}^A\bm{P} + {}^A\bm{R}_B {}^B\bm{b}_i - {}^A\bm{a}_i \right] \end{equation}Hence, for \(i = 1, 2, \dots, 6\), each limb length can be uniquely determined by:
\begin{equation} l_i = \sqrt{{}^A\bm{P}^T {}^A\bm{P} + {}^B\bm{b}_i^T {}^B\bm{b}_i + {}^A\bm{a}_i^T {}^A\bm{a}_i - 2 {}^A\bm{P}^T {}^A\bm{a}_i + 2 {}^A\bm{P}^T \left[{}^A\bm{R}_B {}^B\bm{b}_i\right] - 2 \left[{}^A\bm{R}_B {}^B\bm{b}_i\right]^T {}^A\bm{a}_i} \end{equation}If the position and orientation of the moving platform lie in the feasible workspace of the manipulator, one unique solution to the limb length is determined by the above equation. Otherwise, when the limbs’ lengths derived yield complex numbers, then the position or orientation of the moving platform is not reachable.
Compute
Li = sqrt(args.AP'*args.AP + diag(stewart.Bb'*stewart.Bb) + diag(stewart.Aa'*stewart.Aa) - (2*args.AP'*stewart.Aa)' + (2*args.AP'*(args.ARB*stewart.Bb))' - diag(2*(args.ARB*stewart.Bb)'*stewart.Aa));
dLi = Li-stewart.l;
6.3 forwardKinematicsApprox: Compute the Approximate Forward Kinematics
This Matlab function is accessible here.
Function description
function [P, R] = forwardKinematicsApprox(stewart, args) % forwardKinematicsApprox - Computed the approximate pose of {B} with respect to {A} from the length of each strut and using % the Jacobian Matrix % % Syntax: [P, R] = forwardKinematicsApprox(stewart, args) % % Inputs: % - stewart - A structure with the following fields % - J [6x6] - The Jacobian Matrix % - args - Can have the following fields: % - dL [6x1] - Displacement of each strut [m] % % Outputs: % - P [3x1] - The estimated position of {B} with respect to {A} % - R [3x3] - The estimated rotation matrix that gives the orientation of {B} with respect to {A}
Optional Parameters
arguments
stewart
args.dL (6,1) double {mustBeNumeric} = zeros(6,1)
end
Computation
From a small displacement of each strut \(d\bm{\mathcal{L}}\), we can compute the position and orientation of {B} with respect to {A} using the following formula: \[ d \bm{\mathcal{X}} = \bm{J}^{-1} d\bm{\mathcal{L}} \]
X = stewart.J\args.dL;
The position vector corresponds to the first 3 elements.
P = X(1:3);
The next 3 elements are the orientation of {B} with respect to {A} expressed using the screw axis.
theta = norm(X(4:6)); s = X(4:6)/theta;
We then compute the corresponding rotation matrix.
R = [s(1)^2*(1-cos(theta)) + cos(theta) , s(1)*s(2)*(1-cos(theta)) - s(3)*sin(theta), s(1)*s(3)*(1-cos(theta)) + s(2)*sin(theta); s(2)*s(1)*(1-cos(theta)) + s(3)*sin(theta), s(2)^2*(1-cos(theta)) + cos(theta), s(2)*s(3)*(1-cos(theta)) - s(1)*sin(theta); s(3)*s(1)*(1-cos(theta)) - s(2)*sin(theta), s(3)*s(2)*(1-cos(theta)) + s(1)*sin(theta), s(3)^2*(1-cos(theta)) + cos(theta)];
Bibliography
- [taghirad13_paral] Taghirad, Parallel robots : mechanics and control, CRC Press (2013).