Stewart Platform with Flexible Elements

1. Simscape Model

1 Simscape Model

1.1 Flexible APA

apa = load('./mat/APA300ML.mat', 'int_xyz', 'int_i', 'n_xyz', 'n_i', 'nodes', 'M', 'K');

Total number of Nodes	7
Number of interface Nodes	7
Number of Modes	6
Size of M and K matrices	48

Table 1: Coordinates of the interface nodes
Node i	Node Number	x [m]	y [m]
1.0	53917.0	0.0	-0.015
2.0	53918.0	0.0	0.015
3.0	53919.0	-0.0325	0.0
4.0	53920.0	-0.0125	0.0
5.0	53921.0	-0.0075	0.0
6.0	53922.0	0.0125	0.0
7.0	53923.0	0.0325	0.0

1.2 Flexible Joint

flex_joint = load('./mat/flexor_ID16.mat', 'int_xyz', 'int_i', 'n_xyz', 'n_i', 'nodes', 'M', 'K');

Total number of Nodes	2
Number of interface Nodes	2
Number of Modes	6
Size of M and K matrices	18

Table 2: Coordinates of the interface nodes
Node i	Node Number	x [m]	y [m]	z [m]
1.0	181278.0	0.0	0.0	0.0
2.0	181279.0	0.0	0.0	-0.0

Caracteristic	Value
Axial Stiffness [N/um]	119
Bending Stiffness [Nm/rad]	33
Bending Stiffness [Nm/rad]	33
Torsion Stiffness [Nm/rad]	236

1.3 Identification

And we identify the dynamics from force actuators to force sensors.

%% Options for Linearized
options = linearizeOptions;
options.SampleTime = 0;

%% Name of the Simulink File
mdl = 'stewart_platform_model';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Controller'],        1, 'openinput');  io_i = io_i + 1; % Actuator Force Inputs [N]
io(io_i) = linio([mdl, '/Stewart Platform'],  1, 'openoutput', [], 'dLm'); io_i = io_i + 1; % Relative Displacement Outputs [m]
io(io_i) = linio([mdl, '/Stewart Platform'],  1, 'openoutput', [], 'Taum'); io_i = io_i + 1; % Force Sensors [N]

ground = initializeGround('type', 'none');
payload = initializePayload('type', 'rigid', 'm', 50);
controller = initializeController('type', 'open-loop');

disturbances = initializeDisturbances();

1.4 No Flexible Elements

stewart = initializeStewartPlatform();
stewart = initializeFramesPositions(stewart);
stewart = generateGeneralConfiguration(stewart);
stewart = computeJointsPose(stewart);
% stewart = initializeStrutDynamics(stewart, 'K', 1.8e6*ones(6,1));
stewart = initializeAmplifiedStrutDynamics(stewart, 'Kr', 0.9e6*ones(6,1), 'Ka', 0.9e6*ones(6,1));
stewart = initializeJointDynamics(stewart, 'Kf_M', 33*ones(6,1), 'Kt_M', 235*ones(6,1), 'Kf_F', 33*ones(6,1), 'Kt_F', 235*ones(6,1));
stewart = initializeCylindricalPlatforms(stewart);
stewart = initializeCylindricalStruts(stewart);
stewart = computeJacobian(stewart);
stewart = initializeStewartPose(stewart);
stewart = initializeInertialSensor(stewart);

references = initializeReferences(stewart);

%% Run the linearization
G = linearize(mdl, io, options);
G.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
G.OutputName = {'Dm1', 'Dm2', 'Dm3', 'Dm4', 'Dm5', 'Dm6', 'Fm1', 'Fm2', 'Fm3', 'Fm4', 'Fm5', 'Fm6'};

1.5 Flexible joints

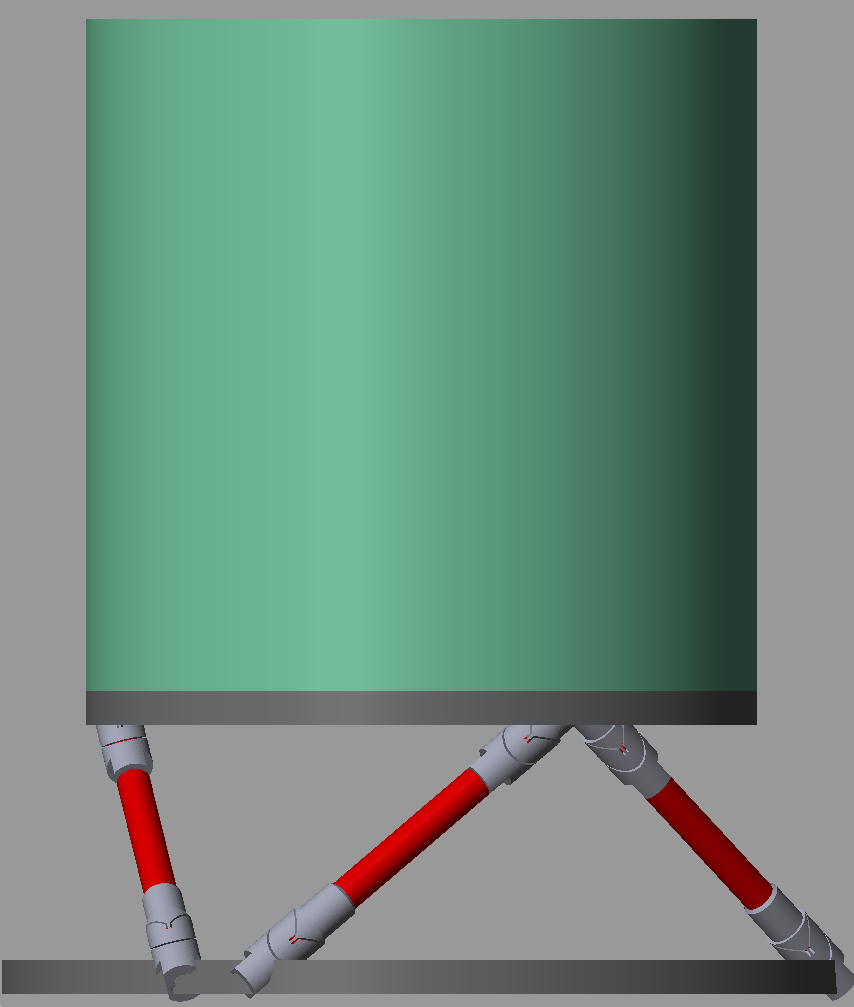
Figure 1: Figure caption

stewart = initializeStewartPlatform();
stewart = initializeFramesPositions(stewart);
stewart = generateGeneralConfiguration(stewart);
stewart = computeJointsPose(stewart);
stewart = initializeAmplifiedStrutDynamics(stewart, 'Kr', 0.9e6*ones(6,1), 'Ka', 0.9e6*ones(6,1));
stewart = initializeJointDynamics(stewart, 'type_F', 'flexible', 'K_F', flex_joint.K, 'M_F', flex_joint.M, 'n_xyz_F', flex_joint.n_xyz, 'xi_F', 0.1, 'step_file_F', 'mat/flexor_ID16.STEP', 'type_M', 'flexible', 'K_M', flex_joint.K, 'M_M', flex_joint.M, 'n_xyz_M', flex_joint.n_xyz, 'xi_M', 0.1, 'step_file_M', 'mat/flexor_ID16.STEP');
stewart = initializeCylindricalPlatforms(stewart);
stewart = initializeCylindricalStruts(stewart);
stewart = computeJacobian(stewart);
stewart = initializeStewartPose(stewart);
stewart = initializeInertialSensor(stewart);

%% Run the linearization
Gj = linearize(mdl, io, options);
Gj.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
Gj.OutputName = {'Dm1', 'Dm2', 'Dm3', 'Dm4', 'Dm5', 'Dm6', 'Fm1', 'Fm2', 'Fm3', 'Fm4', 'Fm5', 'Fm6'};

1.6 Flexible APA

Figure 2: Figure caption

stewart = initializeStewartPlatform();
stewart = initializeFramesPositions(stewart);
stewart = generateGeneralConfiguration(stewart);
stewart = computeJointsPose(stewart);
stewart = initializeFlexibleStrutDynamics(stewart, 'H', 0.03, 'K', apa.K, 'M', apa.M, 'n_xyz', apa.n_xyz, 'xi', 0.1, 'step_file', 'mat/APA300ML.STEP');
stewart = initializeJointDynamics(stewart, 'Kf_M', 33*ones(6,1), 'Kt_M', 235, 'Kf_F', 33*ones(6,1), 'Kt_F', 235);
stewart = initializeCylindricalPlatforms(stewart);
stewart = initializeCylindricalStruts(stewart, 'type_F', 'none', 'type_M', 'none');
stewart = computeJacobian(stewart);
stewart = initializeStewartPose(stewart);
stewart = initializeInertialSensor(stewart);

%% Run the linearization
Ga = -linearize(mdl, io, options);
Ga.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
Ga.OutputName = {'Dm1', 'Dm2', 'Dm3', 'Dm4', 'Dm5', 'Dm6', 'Fm1', 'Fm2', 'Fm3', 'Fm4', 'Fm5', 'Fm6'};

1.7 Flexible Joints and APA

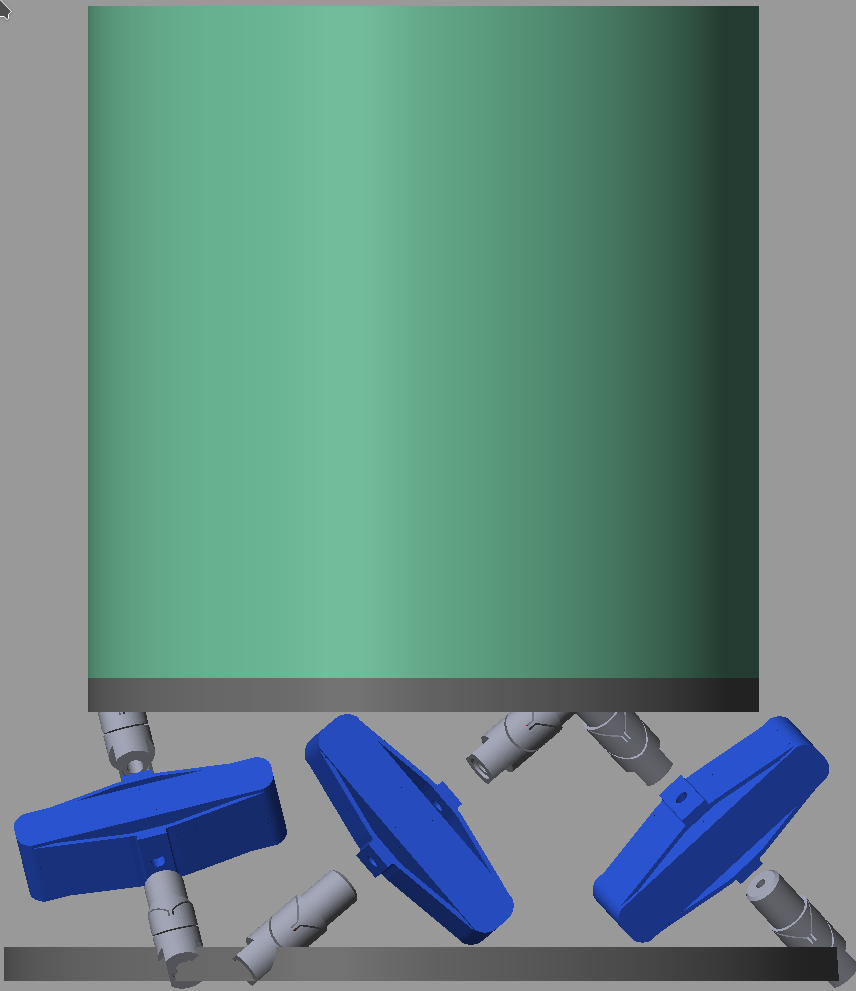
Figure 3: Figure caption

stewart = initializeStewartPlatform();
stewart = initializeFramesPositions(stewart);
stewart = generateGeneralConfiguration(stewart);
stewart = computeJointsPose(stewart);
stewart = initializeFlexibleStrutDynamics(stewart, 'H', 0.03, 'K', apa.K, 'M', apa.M, 'n_xyz', apa.n_xyz, 'xi', 0.1, 'step_file', 'mat/APA300ML.STEP');
stewart = initializeJointDynamics(stewart, 'type_F', 'flexible', 'K_F', flex_joint.K, 'M_F', flex_joint.M, 'n_xyz_F', flex_joint.n_xyz, 'xi_F', 0.1, 'step_file_F', 'mat/flexor_ID16.STEP', 'type_M', 'flexible', 'K_M', flex_joint.K, 'M_M', flex_joint.M, 'n_xyz_M', flex_joint.n_xyz, 'xi_M', 0.1, 'step_file_M', 'mat/flexor_ID16.STEP');
stewart = initializeCylindricalPlatforms(stewart);
stewart = initializeCylindricalStruts(stewart, 'type_F', 'none', 'type_M', 'none');
stewart = computeJacobian(stewart);
stewart = initializeStewartPose(stewart);
stewart = initializeInertialSensor(stewart);

Gf = -linearize(mdl, io, options);
Gf.InputName  = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'};
Gf.OutputName = {'Dm1', 'Dm2', 'Dm3', 'Dm4', 'Dm5', 'Dm6', 'Fm1', 'Fm2', 'Fm3', 'Fm4', 'Fm5', 'Fm6'};

1.8 Direct Velocity Feedback

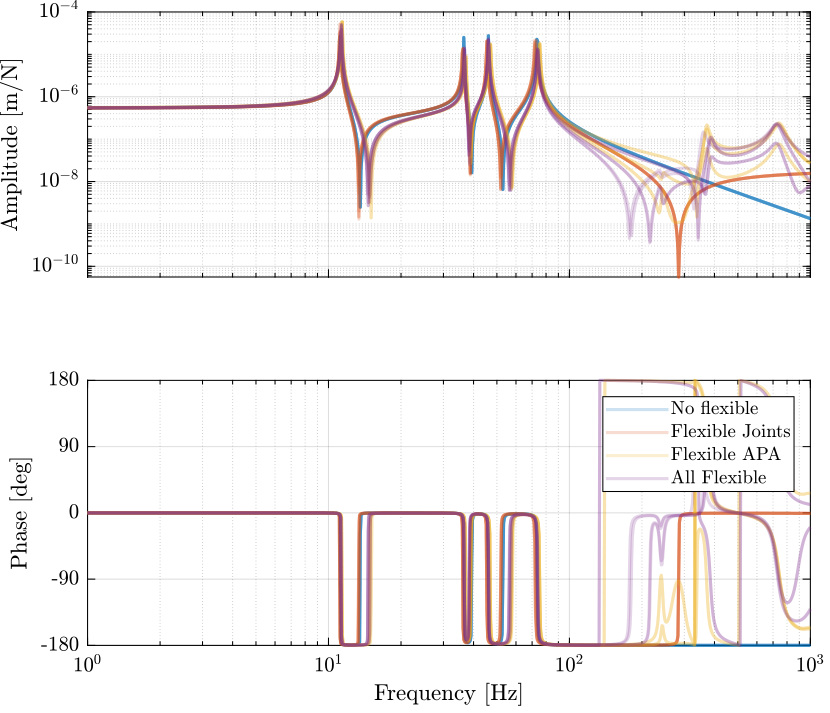
Figure 4: Change of the DVF plant dynamics with the added flexible elements

1.9 Integral Force Feedback

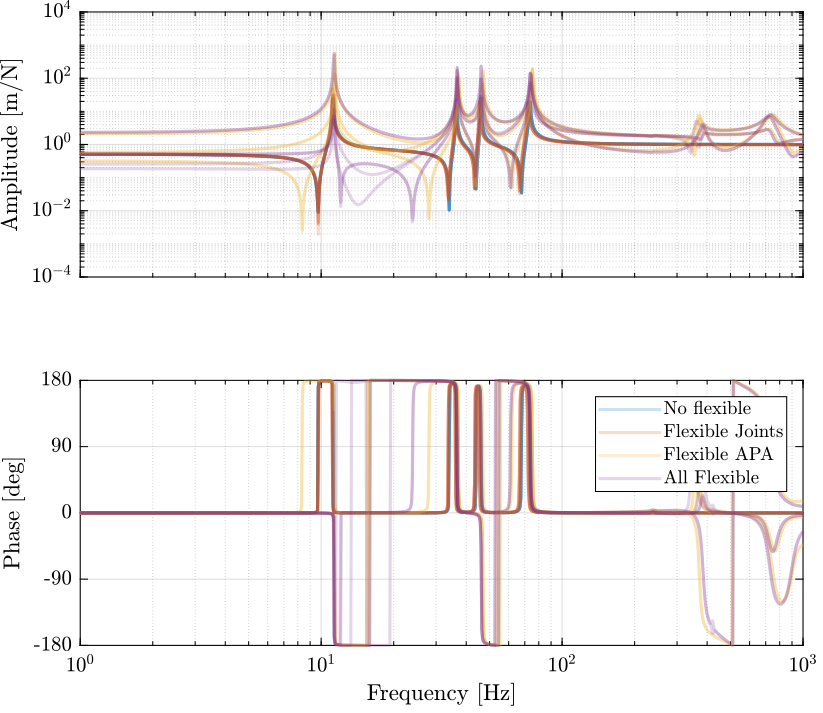
Figure 5: Change of the IFF plant dynamics with the added flexible elements