Compute Spectral Densities of signals with Matlab

1. Spectral Analysis - Basics
2. Technique 1 : Approximation with a transfer function
3. Technique 2 : IFFT
4. TODO Compute the Noise level and Signal level from PSD
- 4.1. Computation

This document presents the mathematics as well as the matlab scripts to do various spectral analysis on a measured signal.

Some matlab documentation about Spectral Analysis can be found here.

First, in section 1, some basics of spectral analysis are presented.

In some cases, we want to generate a time domain signal with defined Power Spectral Density. Two methods are presented in sections 2 and 3.

Finally, some notes are done on how to compute the noise level and signal level from a given Power Spectral Density in section 4.

1 Spectral Analysis - Basics

Typically this signal is coming from an inertial sensor, a force sensor or any other sensor.

We here take the example of a signal coming from a Geophone measurement the vertical velocity of the floor at the ESRF.

1.1 PSD of ADC quantization noise

This is taken from here.

Let's note:

\(q\) is the corresponding value in [V] of the least significant bit (LSB)
\(\Delta V\) is the full range of the ADC in [V]
\(n\) is the number of ADC's bits
\(f_s\) is the sample frequency in [Hz]

Let's suppose that the ADC is ideal. The only noise comes from the quantization error. Interestingly, the noise amplitude is uniformly distributed.

The quantization noise can take a value between \(\pm q/2\), and the probability density function is constant in this range (i.e., it’s a uniform distribution). Since the integral of the probability density function is equal to one, its value will be \(1/q\) for \(-q/2 < e < q/2\) (Fig. 1).

Figure 1: Probability density function \(p(e)\) of the ADC error \(e\)

Now, we can calculate the time average power of the quantization noise as

\begin{equation} P_q = \int_{-q/2}^{q/2} e^2 p(e) de = \frac{q^2}{12} \end{equation}

The other important parameter of a noise source is the power spectral density (PSD), which indicates how the noise power spreads in different frequency bands. To find the power spectral density, we need to calculate the Fourier transform of the autocorrelation function of the noise.

Assuming that the noise samples are not correlated with one another, we can approximate the autocorrelation function with a delta function in the time domain. Since the Fourier transform of a delta function is equal to one, the power spectral density will be frequency independent. Therefore, the quantization noise is white noise with total power equal to \(P_q = \frac{q^2}{12}\).

Thus, the two-sided PSD (from \(\frac{-f_s}{2}\) to \(\frac{f_s}{2}\)), we should divide the noise power \(P_q\) by \(f_s\):

\begin{equation} \int_{-f_s/2}^{f_s/2} \Gamma(f) d f = f_s \Gamma = \frac{q^2}{12} \end{equation}

Finally:

\begin{equation} \begin{align} \Gamma &= \frac{q^2}{12 f_s} \\ &= \frac{\left(\frac{\Delta V}{2^n}\right)^2}{12 f_s} \text{ in } \left[ \frac{V^2}{Hz} \right] \end{align} \end{equation}

1.2 Sensitivity of the instrumentation

The measured signal \(x\) by the ADC is in Volts. The corresponding real velocity \(v\) in m/s.

To obtain the real quantity as measured by the sensor, one have to know the sensitivity of the sensors and electronics used.

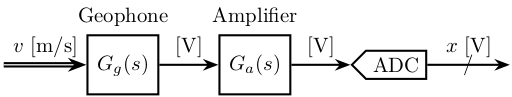
Figure 2: Schematic of the instrumentation used for the measurement

1.3 Convert the time domain from volts to velocity

Let's say, we know that the sensitivity of the geophone used is \[ G_g(s) = G_0 \frac{\frac{s}{2\pi f_0}}{1 + \frac{s}{2\pi f_0}} \quad \left[\frac{V}{m/s}\right] \]

G0 = 88; % Sensitivity [V/(m/s)]
f0 = 2; % Cut-off frequency [Hz]

Gg = G0*(s/2/pi/f0)/(1+s/2/pi/f0);

And the gain of the amplifier is 1000: \(G_m(s) = 1000\).

Gm = 1000;

If \({G_m(s)}^{-1} {G_g(s)}^{-1}\) is proper, we can simulate this dynamical system to go from the voltage to the velocity units (figure 3).

data = load('mat/data_028.mat', 'data'); data = data.data;

t = data(:, 3); % [s]
x = data(:, 1)-mean(data(:, 1)); % The offset if removed (coming from the voltage amplifier) [v]

dt = t(2)-t(1); Fs = 1/dt;

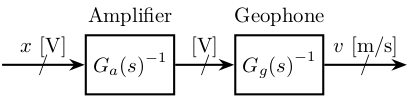
Figure 3: Schematic of the instrumentation used for the measurement

We simulate this system with matlab:

v = lsim(inv(Gg*Gm), x, t);

And we plot the obtained velocity

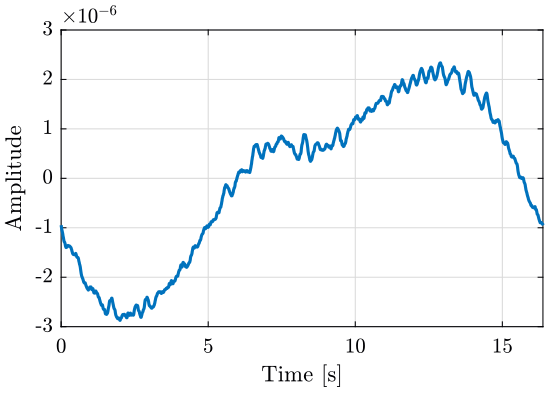
figure;
plot(t, v);
xlabel("Time [s]"); ylabel("Velocity [m/s]");

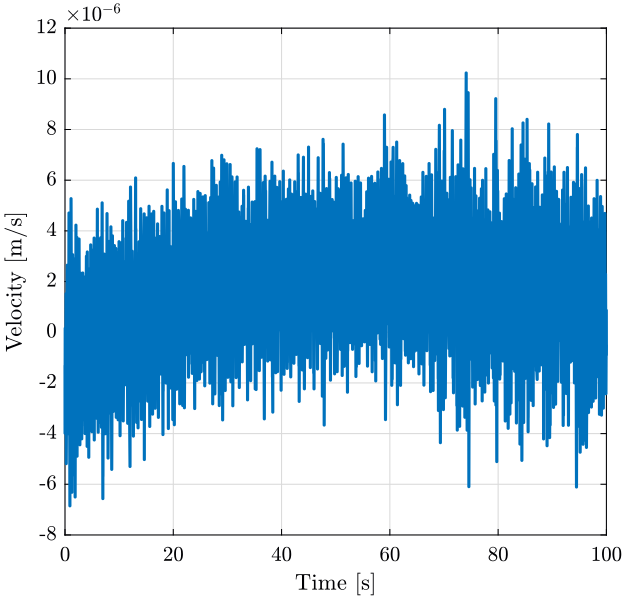
Figure 4: Measured Velocity

1.4 Power Spectral Density and Amplitude Spectral Density

We now have the velocity in the time domain: \[ v(t)\ [m/s] \]

To compute the Power Spectral Density (PSD): \[ S_v(f)\ \left[\frac{(m/s)^2}{Hz}\right] \]

To compute that with matlab, we use the pwelch function.

We first have to defined a window:

win = hanning(ceil(10*Fs)); % 10s window

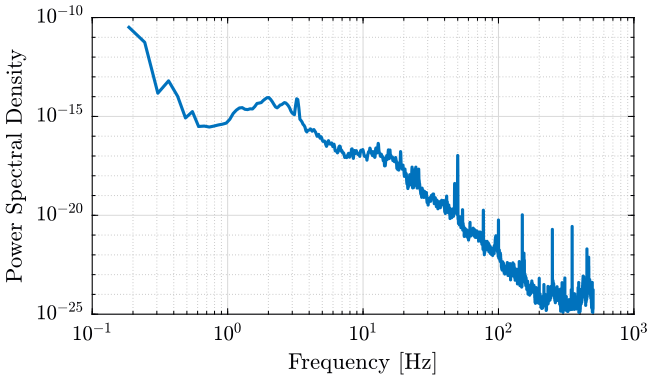
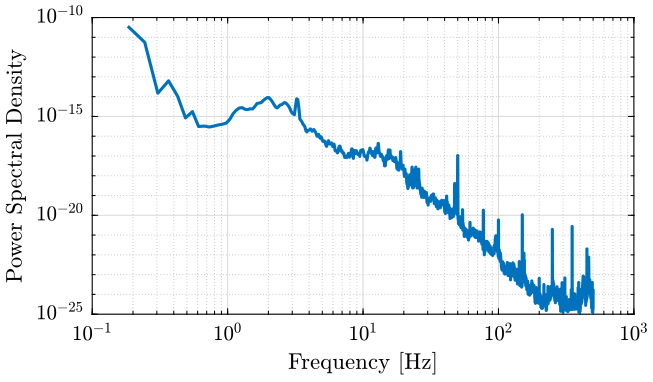
[Sv, f] = pwelch(v, win, [], [], Fs);

figure;
loglog(f, Sv);
xlabel('Frequency [Hz]');
ylabel('Power Spectral Density $\left[\frac{(m/s)^2}{Hz}\right]$')

The Amplitude Spectral Density (ASD) is the square root of the Power Spectral Density:

\begin{equation} \Gamma_{vv}(f) = \sqrt{S_{vv}(f)} \quad \left[ \frac{m/s}{\sqrt{Hz}} \right] \end{equation}

figure;
loglog(f, sqrt(Sv));
xlabel('Frequency [Hz]');
ylabel('Amplitude Spectral Density $\left[\frac{m/s}{\sqrt{Hz}}\right]$')

1.5 Modification of a signal's Power Spectral Density when going through an LTI system

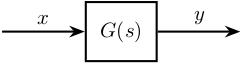
Figure 5: Schematic of the instrumentation used for the measurement

We can show that:

\begin{equation} S_{yy}(\omega) = \left|G(j\omega)\right|^2 S_{xx}(\omega) \end{equation}

And we also have:

\begin{equation} \Gamma_{yy}(\omega) = \left|G(j\omega)\right| \Gamma_{xx}(\omega) \end{equation}

1.6 From PSD of the velocity to the PSD of the displacement

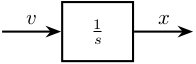
Figure 6: Schematic of the instrumentation used for the measurement

The displacement is the integral of the velocity.

We then have that

\begin{equation} S_{xx}(\omega) = \left|\frac{1}{j \omega}\right|^2 S_{vv}(\omega) \end{equation}

Using a frequency variable in Hz:

\begin{equation} S_{xx}(f) = \left| \frac{1}{j 2\pi f} \right|^2 S_{vv}(f) \end{equation}

For the Amplitude Spectral Density:

\begin{equation} \Gamma_{xx}(f) = \frac{1}{2\pi f} \Gamma_{vv}(f) \end{equation}

\begin{equation} S_{xx}(\omega = 1) = S_{vv}(\omega = 1) \end{equation}

Now if we want to obtain the Power Spectral Density of the Position or Acceleration: For each frequency: \[ \left| \frac{d sin(2 \pi f t)}{dt} \right| = | 2 \pi f | \times | \cos(2\pi f t) | \]

\[ \left| \int_0^t sin(2 \pi f \tau) d\tau \right| = \left| \frac{1}{2 \pi f} \right| \times | \cos(2\pi f t) | \]

\[ ASD_x(f) = \frac{1}{2\pi f} ASD_v(f) \ \left[\frac{m}{\sqrt{Hz}}\right] \]

\[ ASD_a(f) = 2\pi f ASD_v(f) \ \left[\frac{m/s^2}{\sqrt{Hz}}\right] \] And we have \[ PSD_x(f) = {ASD_x(f)}^2 = \frac{1}{(2 \pi f)^2} {ASD_v(f)}^2 = \frac{1}{(2 \pi f)^2} PSD_v(f) \]

Note here that we always have \[ PSD_x \left(f = \frac{1}{2\pi}\right) = PSD_v \left(f = \frac{1}{2\pi}\right) = PSD_a \left(f = \frac{1}{2\pi}\right), \quad \frac{1}{2\pi} \approx 0.16 [Hz] \]

1.7 Cumulative Power/Amplitude Spectrum

If we want to compute the Cumulative Power Spectrum: \[ CPS_v(f) = \int_0^f PSD_v(\nu) d\nu \quad [(m/s)^2] \]

We can also want to integrate from high frequency to low frequency: \[ CPS_v(f) = \int_f^\infty PSD_v(\nu) d\nu \quad [(m/s)^2] \]

The Cumulative Amplitude Spectrum is then the square root of the Cumulative Power Spectrum: \[ CAS_v(f) = \sqrt{CPS_v(f)} = \sqrt{\int_f^\infty PSD_v(\nu) d\nu} \quad [m/s] \]

Then, we can obtain the Root Mean Square value of the velocity: \[ v_{\text{rms}} = CAS_v(0) \quad [m/s \ \text{rms}] \]

figure;
hold on;
plot(f, cumtrapz(f, Sv));
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('Cumulative Power Spectrum [$(m/s)^2$]')

In order to integrate from high frequency to low frequency:

figure;
hold on;
plot(f, flip(-cumtrapz(flip(f), flip(Sv))));
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('Cumulative Power Spectrum [$(m/s)^2$]')

1.8 TODO Add best practices from the Article and simple snippet that works

2 Technique 1 : Approximation with a transfer function

2.1 Signal's PSD

We load the PSD of the signal we wish to replicate.

load('./mat/dist_psd.mat', 'dist_f');

We remove the first value with very high PSD.

dist_f.f = dist_f.f(3:end);
dist_f.psd_gm = dist_f.psd_gm(3:end);

The PSD of the signal is shown on figure fig:psd_ground_motion.

Figure 7: PSD of the signal (png, pdf)

2.2 Transfer Function that approximate the ASD

G_gm = 0.002*(s^2 + 3.169*s + 27.74)/(s*(s+32.73)*(s+8.829)*(s+7.983)^2);

2.3 Generated Time domain signal

Fs = 2*dist_f.f(end);
Ts = 1/Fs;

t = 0:Ts:500;
u = sqrt(Fs/2)*randn(length(t), 1);

u_o = lsim(G_gm, u, t);

figure;
plot(t, u_o);

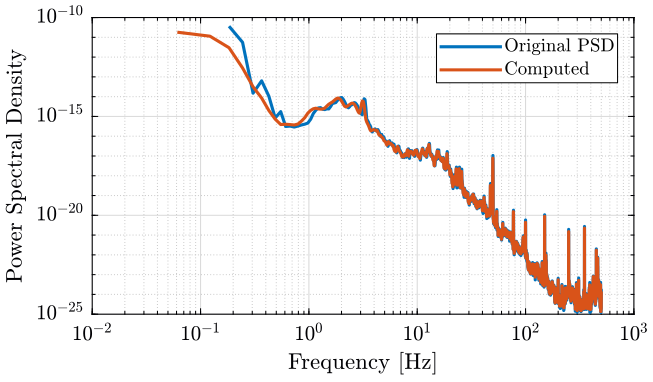
2.4 Comparison of the Power Spectral Densities

nx = length(u_o);
na = 16;
win = hanning(floor(nx/na));

[pxx, f] = pwelch(u_o, win, 0, [], Fs);

Finally, we compare the PSD of the original signal and the obtained signal on figure fig:psd_comparison.

2.5 Simulink

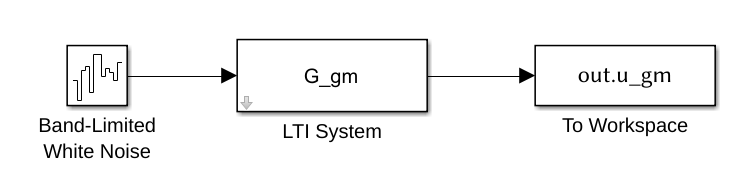
Figure 8: Simulink Schematic

The parameters for the Band-Limited White Noise are:

Noise Power: 1

nx = length(out.u_gm.Data);
na = 8;
win = hanning(floor(nx/na));

[pxx, f] = pwelch(out.u_gm.Data, win, 0, [], 1e3);

3 Technique 2 : IFFT

The technique comes from preumont94_random_vibrat_spect_analy (section 12.11).

3.1 Signal's PSD

We load the PSD of the signal we wish to replicate.

load('./mat/dist_psd.mat', 'dist_f');

We remove the first value with very high PSD.

dist_f.f = dist_f.f(3:end);
dist_f.psd_gm = dist_f.psd_gm(3:end);

The PSD of the signal is shown on figure fig:psd_original.

Figure 9: PSD of the original signal (png, pdf)

3.2 Algorithm

We define some parameters.

Fs = 2*dist_f.f(end);   % Sampling Frequency of data is twice the maximum frequency of the PSD vector [Hz]
N = 2*length(dist_f.f); % Number of Samples match the one of the wanted PSD
T0 = N/Fs;              % Signal Duration [s]
df = 1/T0;              % Frequency resolution of the DFT [Hz]
                        % Also equal to (dist_f.f(2)-dist_f.f(1))

We then specify the wanted PSD.

phi = dist_f.psd_gm;

Create amplitudes corresponding to wanted PSD.

C = zeros(N/2,1);
for i = 1:N/2
  C(i) = sqrt(phi(i)*df);
end

Add random phase to C.

theta = 2*pi*rand(N/2,1); % Generate random phase [rad]

Cx = [0 ; C.*complex(cos(theta),sin(theta))];
Cx = [Cx; flipud(conj(Cx(2:end)))];;

3.3 Obtained Time Domain Signal

The time domain data is generated by an inverse FFT. We normalize the ifft Matlab command.

u = 1/(sqrt(2)*df*1/Fs)*ifft(Cx); % Normalisation of the IFFT
t = linspace(0, T0, N+1); % Time Vector [s]

Figure 10: Obtained signal in the time domain (png, pdf)

3.4 PSD Comparison

We duplicate the time domain signal to have a longer signal and thus a more precise PSD result.

u_rep = repmat(u, 10, 1);

We compute the PSD of the obtained signal with the following commands.

nx = length(u_rep);
na = 16;
win = hanning(floor(nx/na));

[pxx, f] = pwelch(u_rep, win, 0, [], Fs);