phd-test-bench-nano-hexapod/test-bench-nano-hexapod.org

Nano-Hexapod - Test Bench

• Introduction
• Nano-Hexapod Assembly Procedure
• Suspended Table
  • Introduction
  • Experimental Setup
  • Modal analysis of the suspended table
  • Multi-body Model of the suspended table
• Nano-Hexapod Measured Dynamics
  • Introduction
  • Modal analysis
  • Identification of the dynamics
  • Effect of payload mass on the dynamics
• Nano-Hexapod Model Dynamics
  • Introduction
  • Nano-Hexapod model dynamics
  • Dynamical coupling
  • Effect of payload mass
• Conclusion
• Bibliography
• Glossary
• Footnotes

---

This report is also available as a pdf.

---

Introduction   ignore

Prior to the nano-hexapod assembly, all the struts were mounted and individually characterized. In Section ref:sec:test_nhexa_mounting, the assembly procedure of the nano-hexapod is presented.

To identify the dynamics of the nano-hexapod, a special suspended table was developed, which consisted of a stiff "optical breadboard" suspended on top of four soft springs. The Nano-Hexapod was then mounted on top of the suspended table such that its dynamics is not affected by complex dynamics except from the suspension modes of the table that can be well characterized and modeled (Section ref:sec:test_nhexa_table).

The obtained nano-hexapod dynamics is analyzed in Section ref:sec:test_nhexa_dynamics, and compared with the multi-body model in Section ref:sec:test_nhexa_model.

Nano-Hexapod Assembly Procedure

<<sec:test_nhexa_mounting>> The assembly of the nano-hexapod is critical for both avoiding additional stress in the flexible joints (that would result in a loss of stroke) and for precisely determining the Jacobian matrix. The goal was to fix the six struts to the two nano-hexapod plates (shown in Figure ref:fig:test_nhexa_nano_hexapod_plates) while the two plates were parallel and aligned vertically so that all the flexible joints did not experience any stress. To do so, a precisely machined mounting tool (Figure ref:fig:test_nhexa_center_part_hexapod_mounting) is used to position the two nano-hexapod plates during the assembly procedure.

The mechanical tolerances of the received plates were checked using a FARO arm¹ (Figure ref:fig:test_nhexa_plates_tolerances) and were found to comply with the requirements². The same was done for the mounting tool³. The two plates were then fixed to the mounting tool, as shown in Figure ref:fig:test_nhexa_mounting_tool_hexapod_top_view. The main goal of this "mounting tool" is to position the flexible joint interfaces (the "V" shapes) of both plates so that a cylinder can rest on the 4 flat interfaces at the same time.

The quality of the positioning can be estimated by measuring the "straightness" of the top and bottom "V" interfaces. This corresponds to the diameter of the smallest cylinder which contains all points along the measured axis. This was again done using the FARO arm, and the results for all six struts are summarized in Table ref:tab:measured_straightness. The straightness was found to be better than $15\,\mu m$ for all struts⁴, which is sufficiently good to not induce significant stress of the flexible joint during assembly.

Strut	Meas 1	Meas 2
1	$7\,\mu m$	$3\, \mu m$
2	$11\, \mu m$	$11\, \mu m$
3	$15\, \mu m$	$14\, \mu m$
4	$6\, \mu m$	$6\, \mu m$
5	$7\, \mu m$	$5\, \mu m$
6	$6\, \mu m$	$7\, \mu m$

The encoder rulers and heads were then fixed to the top and bottom plates, respectively (Figure ref:fig:test_nhexa_mount_encoder), and the encoder heads were aligned to maximize the received contrast.

The six struts were then fixed to the bottom and top plates one by one. First, the top flexible joint is fixed so that its flat reference surface is in contact with the top plate. This step precisely determines the position of the flexible joint with respect to the top plate. The bottom flexible joint is then fixed. After mounting all six struts, the mounting tool (Figure ref:fig:test_nhexa_center_part_hexapod_mounting) can be disassembled, and the nano-hexapod as shown in Figure ref:fig:test_nhexa_nano_hexapod_mounted is fully assembled.

Suspended Table

<<sec:test_nhexa_table>>

Introduction

When a dynamical system is fixed to a support (such as a granite or an optical table), its dynamics will couple to the support dynamics. This may results in additional modes appearing in the system dynamics, which are difficult to predict and model. To prevent this issue, the strategy adopted here is to mount the nano-hexapod on top a suspended table with low frequency suspension modes.

In this case, the modes of the suspended table were chosen to be at much lower frequency than those of the nano-hexapod such that good decoupling is obtained. Another key advantage is that the suspension modes of the table can be easily represented using a multi-body model. Therefore, the measured dynamics of the nano-hexapod on top of the suspended table can be compared to a multi-body model representing the same experimental conditions. The model of the Nano-Hexapod can thus be precisely tuned to match the measured dynamics.

The developed suspended table is described in Section ref:ssec:test_nhexa_table_setup. The modal analysis of the table is done in ref:ssec:test_nhexa_table_identification. Finally, the multi-body model representing the suspended table was tuned to match the measured modes (Section ref:ssec:test_nhexa_table_model).

Experimental Setup

<<ssec:test_nhexa_table_setup>>

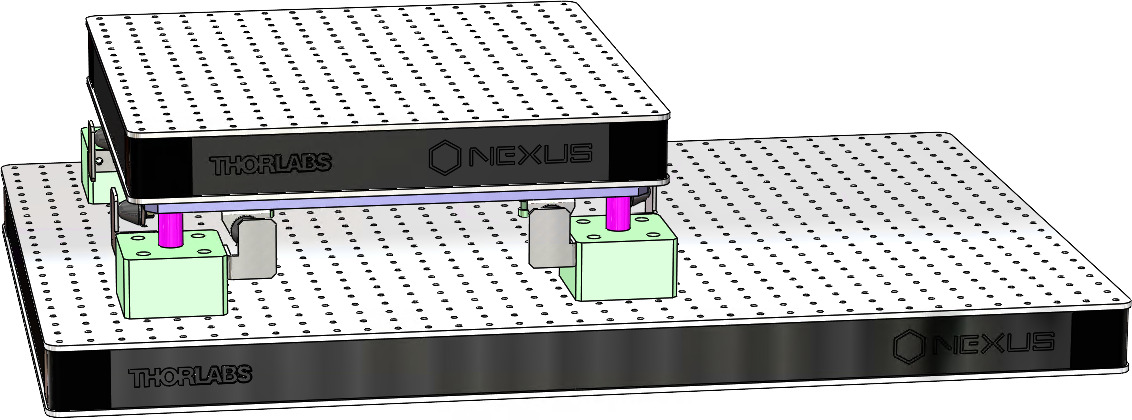
The design of the suspended table is quite straightforward. First, an optical table with high frequency flexible mode was selected⁵. Then, four springs⁶ were selected with low spring rate such that the suspension modes are below 10Hz. Finally, some interface elements were designed, and mechanical lateral mechanical stops were added (Figure ref:fig:test_nhexa_suspended_table_cad).

Modal analysis of the suspended table

<<ssec:test_nhexa_table_identification>>

In order to perform a modal analysis of the suspended table, a total of 15 3-axis accelerometers⁷ were fixed to the breadboard. Using an instrumented hammer, the first 9 modes could be identified and are summarized in Table ref:tab:test_nhexa_suspended_table_modes. The first 6 modes are suspension modes (i.e. rigid body mode of the breadboard) and are located below 10Hz. The next modes are the flexible modes of the breadboard as shown in Figure ref:fig:test_nhexa_table_flexible_modes, and are located above 700Hz.

\hfill

Modes	Frequency	Description
1,2	1.3 Hz	X-Y translations
3	2.0 Hz	Z rotation
4	6.9 Hz	Z translation
5,6	9.5 Hz	X-Y rotations
7	701 Hz	"Membrane" Mode
8	989 Hz	Complex mode
9	1025 Hz	Complex mode

Multi-body Model of the suspended table

<<ssec:test_nhexa_table_model>>

The multi-body model of the suspended table consists simply of two solid bodies connected by 4 springs. The 4 springs are here modeled with "bushing joints" that have stiffness and damping properties in x, y, and z directions.

The model order is 12, which corresponds to the 6 suspension modes. The inertia properties of the parts were determined from the geometry and material densities. The stiffness of the springs was initially set from the datasheet nominal value of $17.8\,N/mm$ and then reduced down to $14\,N/mm$ to better match the measured suspension modes. The stiffness of the springs in the horizontal plane is set at $0.5\,N/mm$. The obtained suspension modes of the multi-body model are compared with the measured modes in Table ref:tab:test_nhexa_suspended_table_simscape_modes.

%% Configure Simscape Model
table_type = 'Suspended'; % On top of vibration table
device_type = 'None'; % No device on the vibration table
payload_num = 0; % No Payload

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/F'],      1, 'openinput');  io_i = io_i + 1;
io(io_i) = linio([mdl, '/F_v'],  1, 'openoutput'); io_i = io_i + 1;

%% Run the linearization
G = linearize(mdl, io);
G.InputName  = {'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz'};
G.OutputName  = {'Vdx', 'Vdy', 'Vdz', 'Vrx', 'Vry', 'Vrz'};

%% Compute the resonance frequencies
ws = eig(G.A);
ws = ws(imag(ws) > 0);

Directions	$D_x$, $D_y$	$R_z$	$D_z$	$R_x$, $R_y$
Multi-body	1.3 Hz	1.8 Hz	6.8 Hz	9.5 Hz
Experimental	1.3 Hz	2.0 Hz	6.9 Hz	9.5 Hz

Nano-Hexapod Measured Dynamics

<<sec:test_nhexa_dynamics>>

Introduction   ignore

The Nano-Hexapod was then mounted on top of the suspended table, as shown in Figure ref:fig:test_nhexa_hexa_suspended_table. All instrumentation (Speedgoat with ADC, DAC, piezoelectric voltage amplifiers and digital interfaces for the encoder) were configured and connected to the nano-hexapod using many cables.

A modal analysis of the nano-hexapod is first performed in Section ref:ssec:test_nhexa_enc_struts_modal_analysis. The results of the modal analysis will be useful to better understand the measured dynamics from actuators to sensors.

A block diagram of the (open-loop) system is shown in Figure ref:fig:test_nhexa_nano_hexapod_signals. The frequency response functions from controlled signals $\mathbf{u}$ to the force sensors voltages $\mathbf{V}_s$ and to the encoders measured displacements $\mathbf{d}_e$ are experimentally identified in Section ref:ssec:test_nhexa_identification. The effect of the payload mass on the dynamics is discussed in Section ref:ssec:test_nhexa_added_mass.

\definecolor{instrumentation}{rgb}{0, 0.447, 0.741}
\definecolor{mechanics}{rgb}{0.8500, 0.325, 0.098}

\begin{tikzpicture}
  % Blocs
  \node[block={4.0cm}{3.0cm}, fill=mechanics!20!white] (nano_hexapod) {Mechanics};
  \coordinate[] (inputF)  at (nano_hexapod.west);
  \coordinate[] (outputL) at ($(nano_hexapod.south east)!0.8!(nano_hexapod.north east)$);
  \coordinate[] (outputF) at ($(nano_hexapod.south east)!0.2!(nano_hexapod.north east)$);

  \node[block, left= 0.8 of inputF,  fill=instrumentation!20!white, align=center] (F_stack) {\tiny Actuator \\ \tiny stacks};
  \node[block, left= 0.8 of F_stack, fill=instrumentation!20!white] (PD200)   {PD200};
  \node[DAC,   left= 0.8 of PD200,   fill=instrumentation!20!white] (F_DAC)   {DAC};
  \node[block, right=0.8 of outputF, fill=instrumentation!20!white, align=center] (Fm_stack){\tiny Sensor \\ \tiny stack};
  \node[ADC,   right=0.8 of Fm_stack,fill=instrumentation!20!white] (Fm_ADC)  {ADC};
  \node[block, right=0.8 of outputL, fill=instrumentation!20!white] (encoder) {\tiny Encoder};

  % Connections and labels
  \draw[->] ($(F_DAC.west)+(-0.8,0)$) node[above right]{$\mathbf{u}$} node[below right]{$[V]$} -- node[sloped]{$/$} (F_DAC.west);
  \draw[->] (F_DAC.east)   -- node[midway, above]{$\tilde{\mathbf{u}}$}node[midway, below]{$[V]$} (PD200.west);
  \draw[->] (PD200.east)   -- node[midway, above]{$\mathbf{V}_a$}node[midway, below]{$[V]$} (F_stack.west);
  \draw[->] (F_stack.east) -- (inputF) node[above left]{$\mathbf{\tau}$}node[below left]{$[N]$};

  \draw[->] (outputF)       -- (Fm_stack.west) node[above left]{$\mathbf{\epsilon}$} node[below left]{$[m]$};
  \draw[->] (Fm_stack.east) -- node[midway, above]{$\tilde{\mathbf{V}}_s$}node[midway, below]{$[V]$} (Fm_ADC.west);
  \draw[->] (Fm_ADC.east)   -- node[sloped]{$/$} ++(0.8, 0)coordinate(end) node[above left]{$\mathbf{V}_s$}node[below left]{$[V]$};

  \draw[->] (outputL)      -- (encoder.west) node[above left]{$\mathbf{d}_e$} node[below left]{$[m]$};
  \draw[->] (encoder.east) -- node[sloped]{$/$} (encoder-|end) node[above left]{$\mathbf{d}_{e}$}node[below left]{$[m]$};

  % Nano-Hexapod
  \begin{scope}[on background layer]
    \node[fit={(F_stack.west|-nano_hexapod.south) (Fm_stack.east|-nano_hexapod.north)}, fill=black!20!white, draw, inner sep=2pt] (system) {};
    \node[above] at (system.north) {Nano-Hexapod};
  \end{scope}
\end{tikzpicture}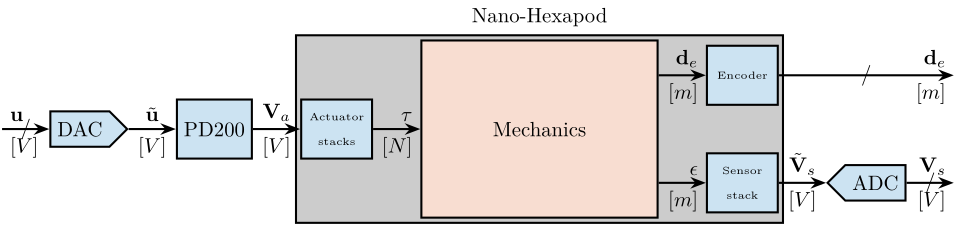

Modal analysis

<<ssec:test_nhexa_enc_struts_modal_analysis>>

To facilitate the future analysis of the measured plant dynamics, a basic modal analysis of the nano-hexapod is performed. Five 3-axis accelerometers were fixed on the top platform of the nano-hexapod (Figure ref:fig:test_nhexa_modal_analysis) and the top platform was excited using an instrumented hammer.

Between 100Hz and 200Hz, 6 suspension modes (i.e. rigid body modes of the top platform) were identified. At around 700Hz, two flexible modes of the top plate were observed (see Figure ref:fig:test_nhexa_hexa_flexible_modes). These modes are summarized in Table ref:tab:test_nhexa_hexa_modal_modes_list.

Mode	Frequency	Description
1	120 Hz	Suspension Mode: Y-translation
2	120 Hz	Suspension Mode: X-translation
3	145 Hz	Suspension Mode: Z-translation
4	165 Hz	Suspension Mode: Y-rotation
5	165 Hz	Suspension Mode: X-rotation
6	190 Hz	Suspension Mode: Z-rotation
7	692 Hz	(flexible) Membrane mode of the top platform
8	709 Hz	Second flexible mode of the top platform

Identification of the dynamics

<<ssec:test_nhexa_identification>>

The dynamics of the nano-hexapod from the six command signals ($u_1$ to $u_6$) to the six measured displacement by the encoders ($d_{e1}$ to $d_{e6}$) and to the six force sensors ($V_{s1}$ to $V_{s6}$) were identified by generating low-pass filtered white noise for each command signal, one by one.

The $6 \times 6$ FRF matrix from $\mathbf{u}$ ot $\mathbf{d}_e$ is shown in Figure ref:fig:test_nhexa_identified_frf_de. The diagonal terms are displayed using colored lines, and all the 30 off-diagonal terms are displayed by gray lines.

All six diagonal terms are well superimposed up to at least $1\,kHz$, indicating good manufacturing and mounting uniformity. Below the first suspension mode, good decoupling can be observed (the amplitude of all off-diagonal terms are $\approx 20$ times smaller than the diagonal terms), indicating the correct assembly of all parts.

From 10Hz up to 1kHz, around 10 resonance frequencies can be observed. The first 4 are suspension modes (at 122Hz, 143Hz, 165Hz and 191Hz) which correlate the modes measured during the modal analysis in Section ref:ssec:test_nhexa_enc_struts_modal_analysis. Three modes at 237Hz, 349Hz and 395Hz are attributed to the internal strut resonances (this will be checked in Section ref:ssec:test_nhexa_comp_model_coupling). Except for the mode at 237Hz, their impact on the dynamics is small. The two modes at 665Hz and 695Hz are attributed to the flexible modes of the top platform. Other modes can be observed above 1kHz, which can be attributed to flexible modes of the encoder supports or to flexible modes of the top platform.

Up to at least 1kHz, an alternating pole/zero pattern is observed, which makes the control easier to tune. This would not have occurred if the encoders were fixed to the struts.

%% Identification of the transfer function from u to de and from u to Vs without payload
% Load identification data
load('test_nhexa_identification_data_mass_0.mat', 'data');

% Setup useful variables
Ts = 1e-4; % Sampling Time [s]
Nfft = floor(1/Ts); % Number of points for the FFT computation
win = hanning(Nfft); % Hanning window
Noverlap = floor(Nfft/2); % Overlap between frequency analysis

% And we get the frequency vector
[~, f] = tfestimate(data{1}.u, data{1}.de, win, Noverlap, Nfft, 1/Ts);

% Transfer function from u to de
G_de = zeros(length(f), 6, 6);

for i = 1:6
    G_de(:,:,i) = tfestimate(data{i}.u, data{i}.de, win, Noverlap, Nfft, 1/Ts);
end

% Transfer function from u to Vs
G_Vs = zeros(length(f), 6, 6);

for i = 1:6
    G_Vs(:,:,i) = tfestimate(data{i}.u, data{i}.Vs, win, Noverlap, Nfft, 1/Ts);
end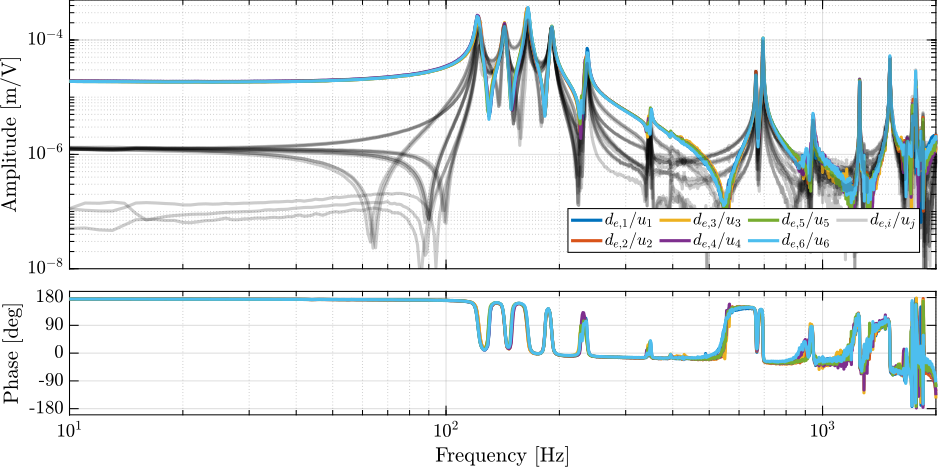

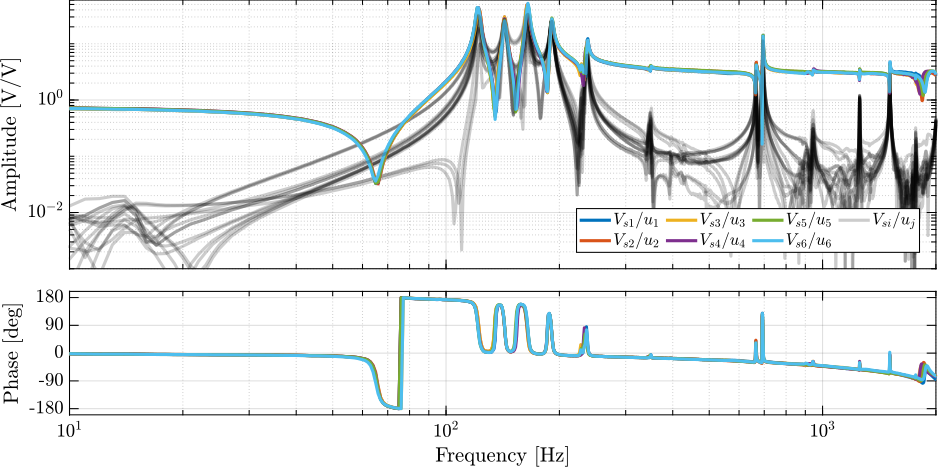
Similarly, the $6 \times 6$ FRF matrix from $\mathbf{u}$ to $\mathbf{V}_s$ is shown in Figure ref:fig:test_nhexa_identified_frf_Vs. Alternating poles and zeros can be observed up to at least 2kHz, which is a necessary characteristics for applying decentralized IFF. Similar to what was observed for the encoder outputs, all the "diagonal" terms are well superimposed, indicating that the same controller can be applied to all the struts. The first flexible mode of the struts as 235Hz has large amplitude, and therefore, it should be possible to add some damping to this mode using IFF.

Effect of payload mass on the dynamics

<<ssec:test_nhexa_added_mass>>

One major challenge for controlling the NASS is the wanted robustness to a variation of payload mass; therefore, it is necessary to understand how the dynamics of the nano-hexapod changes with a change in payload mass.

To study how the dynamics changes with the payload mass, up to three "cylindrical masses" of $13\,kg$ each can be added for a total of $\approx 40\,kg$. These three cylindrical masses on top of the nano-hexapod are shown in Figure ref:fig:test_nhexa_table_mass_3.

%% Set to true only if all the FRF matrices should again computed
% from the experimental data
compute_frf = false;
if compute_frf

    %% Identification of the FRF matrices from u to de and to Vs
    % Load identification Data
    meas_added_mass = {...
        load('test_nhexa_identification_data_mass_0.mat', 'data'), ....
        load('test_nhexa_identification_data_mass_1.mat', 'data'), ....
        load('test_nhexa_identification_data_mass_2.mat', 'data'), ....
        load('test_nhexa_identification_data_mass_3.mat', 'data')};

    % Setup useful variables
    Ts = 1e-4; % Sampling Time [s]
    Nfft = floor(1/Ts); % Number of points for the FFT computation
    win = hanning(Nfft); % Hanning window
    Noverlap = floor(Nfft/2); % Overlap between frequency analysis

    % And we get the frequency vector
    [~, f] = tfestimate(meas_added_mass{1}.data{1}.u, meas_added_mass{1}.data{1}.de, win, Noverlap, Nfft, 1/Ts);

    % FRF from u to de
    G_de = {};

    for i_mass = [0:3]
        G_de(i_mass+1) = {zeros(length(f), 6, 6)};
        for i_strut = 1:6
            G_de{i_mass+1}(:,:,i_strut) = tfestimate(meas_added_mass{i_mass+1}.data{i_strut}.u, meas_added_mass{i_mass+1}.data{i_strut}.de, win, Noverlap, Nfft, 1/Ts);
        end
    end

    % FRF from u to Vs
    G_Vs = {};

    for i_mass = [0:3]
        G_Vs(i_mass+1) = {zeros(length(f), 6, 6)};
        for i_strut = 1:6
            G_Vs{i_mass+1}(:,:,i_strut) = tfestimate(meas_added_mass{i_mass+1}.data{i_strut}.u, meas_added_mass{i_mass+1}.data{i_strut}.Vs, win, Noverlap, Nfft, 1/Ts);
        end
    end

    % The identified dynamics are then saved for further use.
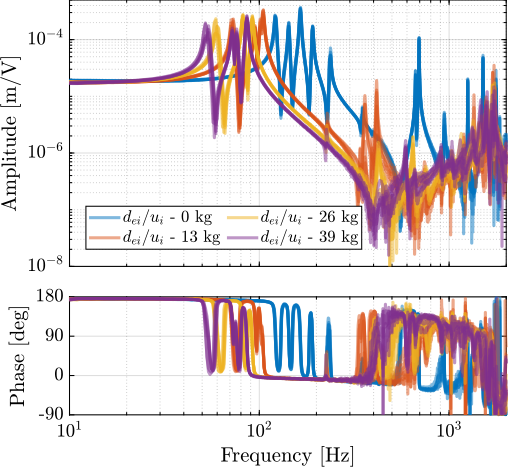
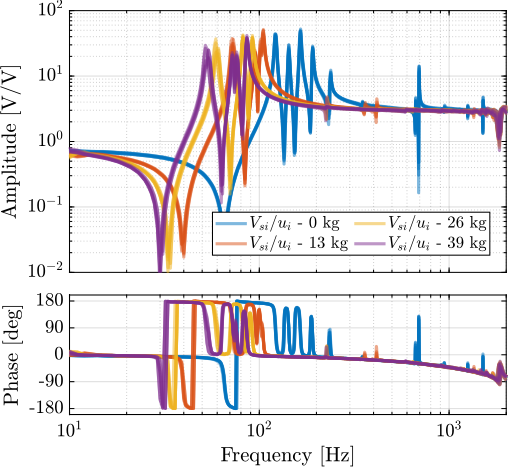
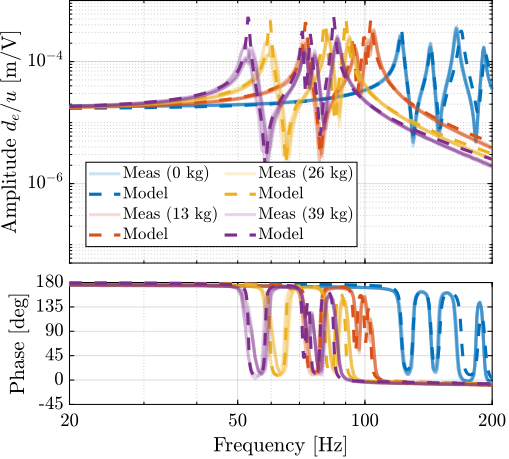
    save('./mat/test_nhexa_identified_frf_masses.mat', 'f', 'G_Vs', 'G_de')

end

The obtained frequency response functions from actuator signal $u_i$ to the associated encoder $d_{ei}$ for the four payload conditions (no mass, 13kg, 26kg and 39kg) are shown in Figure ref:fig:test_nhexa_identified_frf_de_masses. As expected, the frequency of the suspension modes decreased with increasing payload mass. The low frequency gain does not change because it is linked to the stiffness property of the nano-hexapod and not to its mass property.

The frequencies of the two flexible modes of the top plate first decreased significantly when the first mass was added (from $\approx 700\,Hz$ to $\approx 400\,Hz$). This is because the added mass is composed of two half cylinders that are not fixed together. Therefore, it adds a lot of mass to the top plate without increasing stiffness in one direction. When more than one "mass layer" is added, the half cylinders are added at some angles such that rigidity is added in all directions (see how the three mass "layers" are positioned in Figure ref:fig:test_nhexa_table_mass_3). In this case, the frequency of these flexible modes is increased. In practice, the payload should be one solid body, and no decrease in the frequency of this flexible mode should be observed. The apparent amplitude of the flexible mode of the strut at 237Hz becomes smaller as the payload mass increased.

The measured FRFs from $u_i$ to $V_{si}$ are shown in Figure ref:fig:test_nhexa_identified_frf_Vs_masses. For all tested payloads, the measured FRF always have alternating poles and zeros, indicating that IFF can be applied in a robust manner.

Nano-Hexapod Model Dynamics

<<sec:test_nhexa_model>>

Introduction   ignore

In this section, the dynamics measured in Section ref:sec:test_nhexa_dynamics is compared with those estimated from the multi-body model. The nano-hexapod multi-body model was therefore added on top of the vibration table multi-body model, as shown in Figure ref:fig:test_nhexa_hexa_simscape.

The model should exhibit certain characteristics that are verified in this section. First, it should match the measured system dynamics from actuators to sensors presented in Section ref:sec:test_nhexa_dynamics. Both the "direct" terms (Section ref:ssec:test_nhexa_comp_model) and "coupling" terms (Section ref:ssec:test_nhexa_comp_model_coupling) of the multi-body model are compared with the measured dynamics. Second, it should also represents how the system dynamics changes when a payload is fixed to the top platform. This is checked in Section ref:ssec:test_nhexa_comp_model_masses.

Nano-Hexapod model dynamics

<<ssec:test_nhexa_comp_model>>

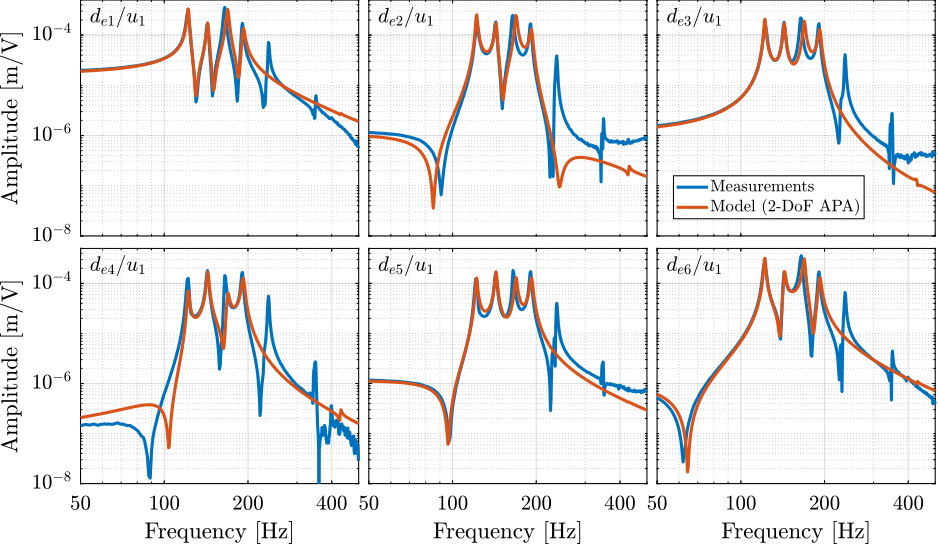
The multi-body model of the nano-hexapod was first configured with 4-DoF flexible joints, 2-DoF APA, and rigid top and bottom plates. The stiffness values of the flexible joints were chosen based on the values estimated using the test bench and on the FEM. The parameters of the APA model were determined from the test bench of the APA. The $6 \times 6$ transfer function matrices from $\mathbf{u}$ to $\mathbf{d}_e$ and from $\mathbf{u}$ to $\mathbf{V}_s$ are then extracted from the multi-body model.

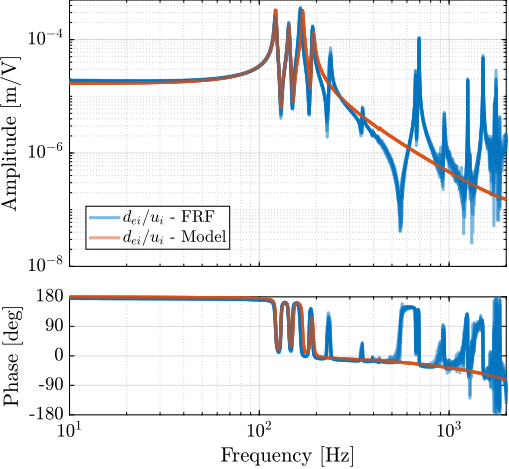
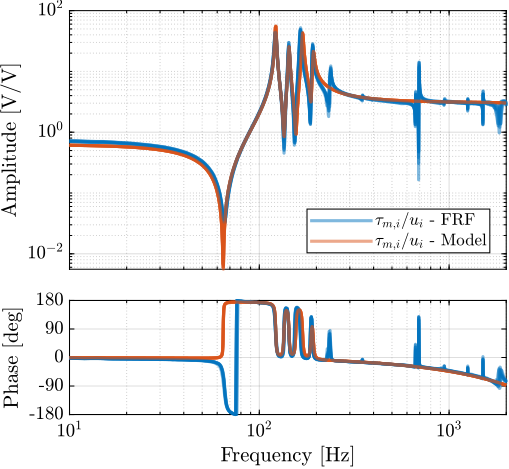
First, is it evaluated how well the models matches the "direct" terms of the measured FRF matrix. To do so, the diagonal terms of the extracted transfer function matrices are compared with the measured FRF in Figure ref:fig:test_nhexa_comp_simscape_diag. It can be seen that the 4 suspension modes of the nano-hexapod (at 122Hz, 143Hz, 165Hz and 191Hz) are well modeled. The three resonances that were attributed to "internal" flexible modes of the struts (at 237Hz, 349Hz and 395Hz) cannot be seen in the model, which is reasonable because the APAs are here modeled as a simple uniaxial 2-DoF system. At higher frequencies, no resonances can be observed in the model, as the top plate and the encoder supports are modeled as rigid bodies.

Dynamical coupling

<<ssec:test_nhexa_comp_model_coupling>>

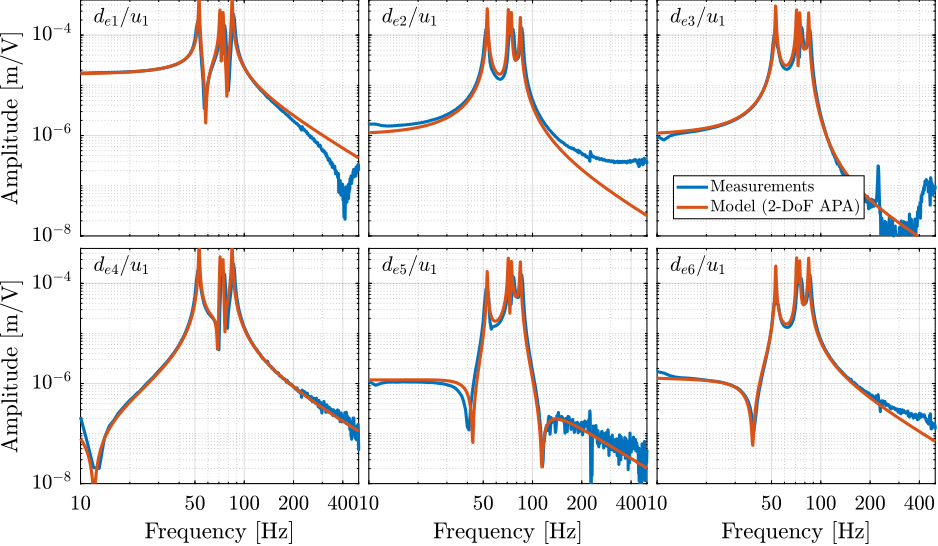
Another desired feature of the model is that it effectively represents coupling in the system, as this is often the limiting factor for the control of MIMO systems. Instead of comparing the full 36 elements of the $6 \times 6$ FFR matrix from $\mathbf{u}$ to $\mathbf{d}_e$, only the first "column" is compared (Figure ref:fig:test_nhexa_comp_simscape_de_all), which corresponds to the transfer function from the command $u_1$ to the six measured encoder displacements $d_{e1}$ to $d_{e6}$. It can be seen that the coupling in the model matches the measurements well up to the first un-modeled flexible mode at 237Hz. Similar results are observed for all other coupling terms and for the transfer function from $\mathbf{u}$ to $\mathbf{V}_s$.

Comparison of the measured (in blue) and modeled (in red) frequency transfer functions from the first control signal $u_1$ to the six encoders $d_{e1}$ to $d_{e6}$. The APA are here modeled with a 2-DoF mass-spring-damper system.

The APA300ML was then modeled with a super-element extracted from a FE-software. The obtained transfer functions from $u_1$ to the six measured encoder displacements $d_{e1}$ to $d_{e6}$ are compared with the measured FRF in Figure ref:fig:test_nhexa_comp_simscape_de_all_flex. While the damping of the suspension modes for the super-element is underestimated (which could be solved by properly tuning the proportional damping coefficients), the flexible modes of the struts at 237Hz and 349Hz are well modeled. Even the mode 395Hz can be observed in the model. Therefore, if the modes of the struts are to be modeled, the super-element of the APA300ML can be used at the cost of obtaining a much higher order model.

%% Load the plant model with Flexible APA
flex_ol = load('test_nhexa_simscape_flexible_masses.mat', 'G_Vs', 'G_de');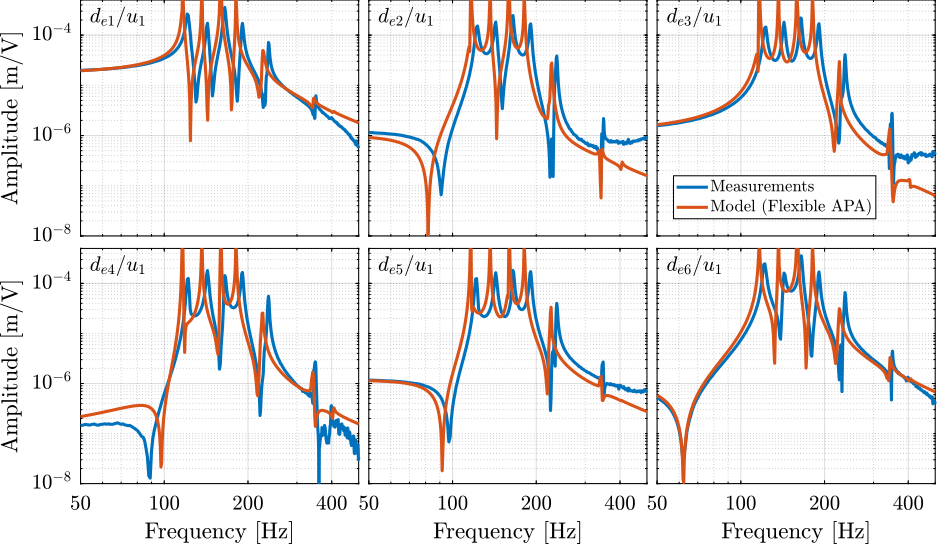

Comparison of the measured (in blue) and modeled (in red) frequency transfer functions from the first control signal $u_1$ to the six encoders $d_{e1}$ to $d_{e6}$. The APA are here modeled with a "super-element".

Effect of payload mass

<<ssec:test_nhexa_comp_model_masses>>

Another important characteristic of the model is that it should represents the dynamics of the system well for all considered payloads. The model dynamics is therefore compared with the measured dynamics for 4 payloads (no payload, 13kg, 26kg and 39kg) in Figure ref:fig:test_nhexa_comp_simscape_diag_masses. The observed shift of the suspension modes to lower frequencies with increased payload mass is well represented by the multi-body model. The complex conjugate zeros also well match the experiments both for the encoder outputs (Figure ref:fig:test_nhexa_comp_simscape_de_diag_masses) and the force sensor outputs (Figure ref:fig:test_nhexa_comp_simscape_Vs_diag_masses).

Note that the model displays smaller damping than that observed experimentally for high values of the payload mass. One option could be to tune the damping as a function of the mass (similar to what is done with the Rayleigh damping). However, as decentralized IFF will be applied, the damping is actively brought, and the open-loop damping value should have very little impact on the obtained plant dynamics.

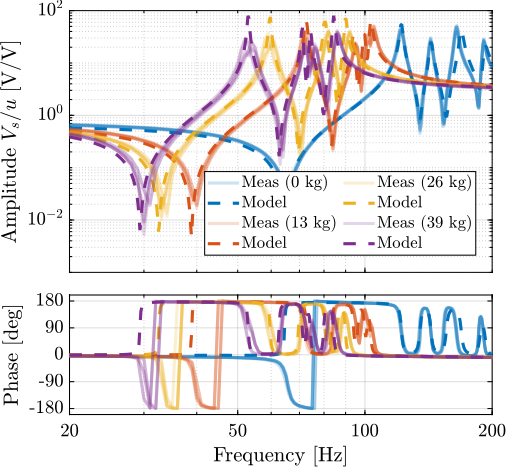
In order to also check if the model well represents the coupling when high payload masses are used, the transfer functions from $u_1$ to $d_{e1}$ to $d_{e6}$ are compared in the case of the 39kg payload in Figure ref:fig:test_nhexa_comp_simscape_de_all_high_mass. Excellent match between experimental and model coupling is observed. Therefore, the model effectively represents the system coupling for different payloads.

Comparison of the measured (in blue) and modeled (in red) frequency transfer functions from the first control signal $u_1$ to the six encoders $d_{e1}$ to $d_{e6}$

Conclusion

The goal of this test bench was to obtain an accurate model of the nano-hexapod that could then be included on top of the micro-station model. The adopted strategy was to identify the nano-hexapod dynamics under conditions in which all factors that could have affected the nano-hexapod dynamics were considered. This was achieved by developing a suspended table with low frequency suspension modes that can be accurately modeled (Section ref:sec:test_nhexa_table). Although the dynamics of the nano-hexapod was indeed impacted by the dynamics of the suspended platform, this impact was also considered in the multi-body model.

The dynamics of the nano-hexapod was then identified in Section ref:sec:test_nhexa_dynamics. Below the first suspension mode, good decoupling could be observed for the transfer function from $\bm{u}$ to $\bm{d}_e$, which enables the design of a decentralized positioning controller based on the encoders for relative positioning purposes. Many other modes were present above 700Hz, which will inevitably limit the achievable bandwidth. The observed effect of the payload's mass on the dynamics was quite large, which also represents a complex control challenge.

The frequency response functions from the six DAC voltages $\bm{u}$ to the six force sensors voltages $\bm{V}_s$ all have alternating complex conjugate poles and complex conjugate zeros for all the tested payloads (Figure ref:fig:test_nhexa_comp_simscape_Vs_diag_masses). This indicates that it is possible to implement decentralized Integral Force Feedback in a robust manner.

The developed multi-body model of the nano-hexapod was found to accurately represents the suspension modes of the Nano-Hexapod (Section ref:sec:test_nhexa_model). Both FRF matrices from $\mathbf{u}$ to $\mathbf{V}_s$ and from $\mathbf{u}$ to $\mathbf{d}_e$ are well matching with the measurements, even when considering coupling (i.e. off-diagonal) terms, which are very important from a control perspective. At frequencies above the suspension modes, the Nano-Hexapod model became inaccurate because the flexible modes were not modeled. It was found that modeling the APA300ML using a super-element allows to model the internal resonances of the struts. The same can be done with the top platform and the encoder supports; however, the model order would be higher and may become unpractical for simulation.

Obtaining a model that accurately represents the complex dynamics of the Nano-Hexapod was made possible by the modeling approach used in this study. This approach involved tuning and validating models of individual components (such as the APA and flexible joints) using dedicated test benches. The different models could then be combined to form the Nano-Hexapod dynamical model. If a model of the nano-hexapod was developed in one time, it would be difficult to tune all the model parameters to match the measured dynamics, or even to know if the model "structure" would be adequate to represent the system dynamics.

Bibliography   ignore

Glossary   ignore

printglossaries:

Footnotes

⁷PCB 356B18. Sensitivity is $1\,V/g$, measurement range is $\pm 5\,g$ and bandwidth is $0.5$ to $5\,\text{kHz}$. ⁶"SZ8005 20 x 044" from Steinel. The spring rate is specified at $17.8\,N/mm$ ⁵The 450 mm x 450 mm x 60 mm Nexus B4545A from Thorlabs. ⁴As the accuracy of the FARO arm is $\pm 13\,\mu m$, the true straightness is probably better than the values indicated. The limitation of the instrument is here reached. ³The height dimension is better than $40\,\mu m$. The diameter fitting of 182g6 and 24g6 with the two plates is verified. ²Location of all the interface surfaces with the flexible joints were checked. The fittings (182H7 and 24H8) with the interface element were also checked. ¹FARO Arm Platinum 4ft, specified accuracy of $\pm 13\mu m$

---