Control in a rotating frame

Table of Contents

The objective of this note it to highlight some control problems that arises when controlling the position of an object using actuators that are rotating with respect to a fixed reference frame.

In section 1, a simple system composed of a spindle and a translation stage is defined and the equations of motion are written. The rotation induces some coupling between the actuators and their displacement, and modifies the dynamics of the system. This is studied using the equations, and some numerical computations are used to compare the use of voice coil and piezoelectric actuators.

Then, in section 2, two different control approach are compared where:

In section 3, the analytical study will be validated using a multi body model of the studied system.

Finally, in section 4, the control strategies are implemented using Simulink and Simscape and compared.

1 System Description and Analysis

1.1 System description

The system consists of one 2 degree of freedom translation stage on top of a spindle (figure 1).

The control inputs are the forces applied by the actuators of the translation stage (\(F_u\) and \(F_v\)). As the translation stage is rotating around the Z axis due to the spindle, the forces are applied along \(u\) and \(v\).

The measurement is either the \(x-y\) displacement of the object located on top of the translation stage or the \(u-v\) displacement of the sample with respect to a fixed reference frame.

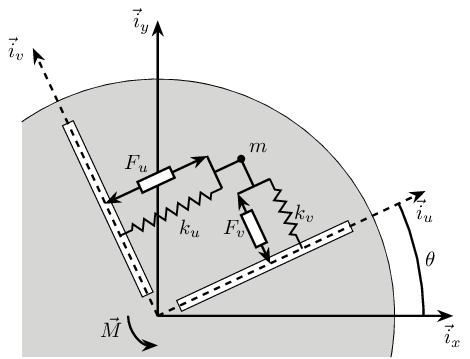
rotating_frame_2dof.png

Figure 1: Schematic of the mecanical system

In the following block diagram:

  • \(G\) is the transfer function from the forces applied in the actuators to the measurement
  • \(K\) is the controller to design
  • \(J\) is a Jacobian matrix usually used to change the reference frame

Indices \(x\) and \(y\) corresponds to signals in the fixed reference frame (along \(\vec{i}_x\) and \(\vec{i}_y\)):

  • \(D_x\) is the measured position of the sample
  • \(r_x\) is the reference signal which corresponds to the wanted \(D_x\)
  • \(\epsilon_x\) is the position error

Indices \(u\) and \(v\) corresponds to signals in the rotating reference frame (\(\vec{i}_u\) and \(\vec{i}_v\)):

  • \(F_u\) and \(F_v\) are forces applied by the actuators
  • \(\epsilon_u\) and \(\epsilon_v\) are position error of the sample along \(\vec{i}_u\) and \(\vec{i}_v\)

1.2 Equations

Based on the figure 1, we can write the equations of motion of the system.

Let's express the kinetic energy \(T\) and the potential energy \(V\) of the mass \(m\):

\begin{align} \label{orgea74efb} T & = \frac{1}{2} m \left( \dot{x}^2 + \dot{y}^2 \right) \\ V & = \frac{1}{2} k \left( x^2 + y^2 \right) \end{align}

The Lagrangian is the kinetic energy minus the potential energy.

\begin{equation} \label{org31791c4} L = T-V = \frac{1}{2} m \left( \dot{x}^2 + \dot{y}^2 \right) - \frac{1}{2} k \left( x^2 + y^2 \right) \end{equation}

The partial derivatives of the Lagrangian with respect to the variables \((x, y)\) are:

\begin{align*} \label{org8251906} \frac{\partial L}{\partial x} & = -kx \\ \frac{\partial L}{\partial y} & = -ky \\ \frac{d}{dt}\frac{\partial L}{\partial \dot{x}} & = m\ddot{x} \\ \frac{d}{dt}\frac{\partial L}{\partial \dot{y}} & = m\ddot{y} \end{align*}

The external forces applied to the mass are:

\begin{align*} F_{\text{ext}, x} &= F_u \cos{\theta} - F_v \sin{\theta}\\ F_{\text{ext}, y} &= F_u \sin{\theta} + F_v \cos{\theta} \end{align*}

By appling the Lagrangian equations, we obtain:

\begin{align} m\ddot{x} + kx = F_u \cos{\theta} - F_v \sin{\theta}\\ m\ddot{y} + ky = F_u \sin{\theta} + F_v \cos{\theta} \end{align}

We then change coordinates from \((x, y)\) to \((d_x, d_y, \theta)\).

\begin{align*} x & = d_u \cos{\theta} - d_v \sin{\theta}\\ y & = d_u \sin{\theta} + d_v \cos{\theta} \end{align*}

We obtain:

\begin{align*} \ddot{x} & = \ddot{d_u} \cos{\theta} - 2\dot{d_u}\dot{\theta}\sin{\theta} - d_u\ddot{\theta}\sin{\theta} - d_u\dot{\theta}^2 \cos{\theta} - \ddot{d_v} \sin{\theta} - 2\dot{d_v}\dot{\theta}\cos{\theta} - d_v\ddot{\theta}\cos{\theta} + d_v\dot{\theta}^2 \sin{\theta} \\ \ddot{y} & = \ddot{d_u} \sin{\theta} + 2\dot{d_u}\dot{\theta}\cos{\theta} + d_u\ddot{\theta}\cos{\theta} - d_u\dot{\theta}^2 \sin{\theta} + \ddot{d_v} \cos{\theta} - 2\dot{d_v}\dot{\theta}\sin{\theta} - d_v\ddot{\theta}\sin{\theta} - d_v\dot{\theta}^2 \cos{\theta} \\ \end{align*}

By injecting the previous result into the Lagrangian equation, we obtain:

\begin{align*} m \ddot{d_u} \cos{\theta} - 2m\dot{d_u}\dot{\theta}\sin{\theta} - m d_u\ddot{\theta}\sin{\theta} - m d_u\dot{\theta}^2 \cos{\theta} -m \ddot{d_v} \sin{\theta} - 2m\dot{d_v}\dot{\theta}\cos{\theta} - m d_v\ddot{\theta}\cos{\theta} + m d_v\dot{\theta}^2 \sin{\theta} + k d_u \cos{\theta} - k d_v \sin{\theta} = F_u \cos{\theta} - F_v \sin{\theta} \\ m \ddot{d_u} \sin{\theta} + 2m\dot{d_u}\dot{\theta}\cos{\theta} + m d_u\ddot{\theta}\cos{\theta} - m d_u\dot{\theta}^2 \sin{\theta} + m \ddot{d_v} \cos{\theta} - 2m\dot{d_v}\dot{\theta}\sin{\theta} - m d_v\ddot{\theta}\sin{\theta} - m d_v\dot{\theta}^2 \cos{\theta} + k d_u \sin{\theta} + k d_v \cos{\theta} = F_u \sin{\theta} + F_v \cos{\theta} \end{align*}

Which is equivalent to:

\begin{align*} m \ddot{d_u} - 2m\dot{d_u}\dot{\theta}\frac{\sin{\theta}}{\cos{\theta}} - m d_u\ddot{\theta}\frac{\sin{\theta}}{\cos{\theta}} - m d_u\dot{\theta}^2 -m \ddot{d_v} \frac{\sin{\theta}}{\cos{\theta}} - 2m\dot{d_v}\dot{\theta} - m d_v\ddot{\theta} + m d_v\dot{\theta}^2 \frac{\sin{\theta}}{\cos{\theta}} + k d_u - k d_v \frac{\sin{\theta}}{\cos{\theta}} = F_u - F_v \frac{\sin{\theta}}{\cos{\theta}} \\ m \ddot{d_u} + 2m\dot{d_u}\dot{\theta}\frac{\cos{\theta}}{\sin{\theta}} + m d_u\ddot{\theta}\frac{\cos{\theta}}{\sin{\theta}} - m d_u\dot{\theta}^2 + m \ddot{d_v} \frac{\cos{\theta}}{\sin{\theta}} - 2m\dot{d_v}\dot{\theta} - m d_v\ddot{\theta} - m d_v\dot{\theta}^2 \frac{\cos{\theta}}{\sin{\theta}} + k d_u + k d_v \frac{\cos{\theta}}{\sin{\theta}} = F_u + F_v \frac{\cos{\theta}}{\sin{\theta}} \end{align*}

We can then subtract and add the previous equations to obtain the following equations:

\begin{equation} \label{org953c633} m \ddot{d_u} + (k - m\dot{\theta}^2) d_u = F_u + 2 m\dot{d_v}\dot{\theta} + m d_v\ddot{\theta} \end{equation} \begin{equation} \label{org84282f4} m \ddot{d_v} + (k - m\dot{\theta}^2) d_v = F_v - 2 m\dot{d_u}\dot{\theta} - m d_u\ddot{\theta} \end{equation}

We obtain two differential equations that are coupled through:

  • Euler forces: \(m d_v \ddot{\theta}\)
  • Coriolis forces: \(2 m \dot{d_v} \dot{\theta}\)

Without the coupling terms, each equation is the equation of a one degree of freedom mass-spring system with mass \(m\) and stiffness \(k- m\dot{\theta}^2\). Thus, the term \(- m\dot{\theta}^2\) acts like a negative stiffness (due to centrifugal forces).

The forces induced by the rotating reference frame are independent of the stiffness of the actuator. The resulting effect of those forces should then be higher when using softer actuators.

1.3 Numerical Values for the NASS

Let's define the parameters for the NASS.

Light sample mass [kg] 3.5e+01
Heavy sample mass [kg] 8.5e+01
Max rot. speed - light [rpm] 6.0e+01
Max rot. speed - heavy [rpm] 1.0e+00
Voice Coil Stiffness [N/m] 1.0e+03
Piezo Stiffness [N/m] 1.0e+08
Max rot. acceleration [rad/s2] 1.0e+00
Max mass excentricity [m] 1.0e-02
Max Horizontal speed [m/s] 2.0e-01

1.4 Euler and Coriolis forces - Numerical Result

First we will determine the value for Euler and Coriolis forces during regular experiment.

  • Euler forces: \(m d_v \ddot{\theta}\)
  • Coriolis forces: \(2 m \dot{d_v} \dot{\theta}\)

The obtained values are displayed in table 1.

Table 1: Euler and Coriolis forces for the NASS
  Light Heavy
Coriolis 88.0N 3.6N
Euler 0.4N 0.8N

1.5 Negative Spring Effect - Numerical Result

The negative stiffness due to the rotation is equal to \(-m{\omega_0}^2\).

The values for the negative spring effect are displayed in table 2.

This is definitely negligible when using piezoelectric actuators. It may not be the case when using voice coil actuators.

Table 2: Negative Spring effect
  Light Heavy
Neg. Spring 1381.7[N/m] 0.9[N/m]

1.6 Limitations due to coupling

To simplify, we consider a constant rotating speed \(\dot{\theta} = \omega_0\) and thus \(\ddot{\theta} = 0\).

From equations \eqref{org953c633} and \eqref{org84282f4}, we obtain:

\begin{align*} (m s^2 + (k - m{\omega_0}^2)) d_u &= F_u + 2 m {\omega_0} s d_v \\ (m s^2 + (k - m{\omega_0}^2)) d_v &= F_v - 2 m {\omega_0} s d_u \\ \end{align*}

From second equation: \[ d_v = \frac{1}{m s^2 + (k - m{\omega_0}^2)} F_v - \frac{2 m {\omega_0} s}{m s^2 + (k - m{\omega_0}^2)} d_u \]

And we re-inject \(d_v\) into the first equation:

\begin{equation*} (m s^2 + (k - m{\omega_0}^2)) d_u = F_u + \frac{2 m {\omega_0} s}{m s^2 + (k - m{\omega_0}^2)} F_v - \frac{(2 m {\omega_0} s)^2}{m s^2 + (k - m{\omega_0}^2)} d_u \end{equation*} \begin{equation*} \frac{(m s^2 + (k - m{\omega_0}^2))^2 + (2 m {\omega_0} s)^2}{m s^2 + (k - m{\omega_0}^2)} d_u = F_u + \frac{2 m {\omega_0} s}{m s^2 + (k - m{\omega_0}^2)} F_v \end{equation*}

Finally we obtain \(d_u\) function of \(F_u\) and \(F_v\). \[ d_u = \frac{m s^2 + (k - m{\omega_0}^2)}{(m s^2 + (k - m{\omega_0}^2))^2 + (2 m {\omega_0} s)^2} F_u + \frac{2 m {\omega_0} s}{(m s^2 + (k - m{\omega_0}^2))^2 + (2 m {\omega_0} s)^2} F_v \]

Similarly we can obtain \(d_v\) function of \(F_u\) and \(F_v\): \[ d_v = \frac{m s^2 + (k - m{\omega_0}^2)}{(m s^2 + (k - m{\omega_0}^2))^2 + (2 m {\omega_0} s)^2} F_v - \frac{2 m {\omega_0} s}{(m s^2 + (k - m{\omega_0}^2))^2 + (2 m {\omega_0} s)^2} F_u \]

The two previous equations can be written in a matrix form:

\begin{equation} \label{orgb104ecd} \begin{bmatrix} d_u \\ d_v \end{bmatrix} = \frac{1}{(m s^2 + (k - m{\omega_0}^2))^2 + (2 m {\omega_0} s)^2} \begin{bmatrix} ms^2 + (k-m{\omega_0}^2) & 2 m \omega_0 s \\ -2 m \omega_0 s & ms^2 + (k-m{\omega_0}^2) \\ \end{bmatrix} \begin{bmatrix} F_u \\ F_v \end{bmatrix} \end{equation}

Then, coupling is negligible if \(|-m \omega^2 + (k - m{\omega_0}^2)| \gg |2 m {\omega_0} \omega|\).

1.6.1 Numerical Analysis

We plot on the same graph \(\frac{|-m \omega^2 + (k - m {\omega_0}^2)|}{|2 m \omega_0 \omega|}\) for the voice coil and the piezo:

  • with the light sample (figure 2).
  • with the heavy sample (figure 3).

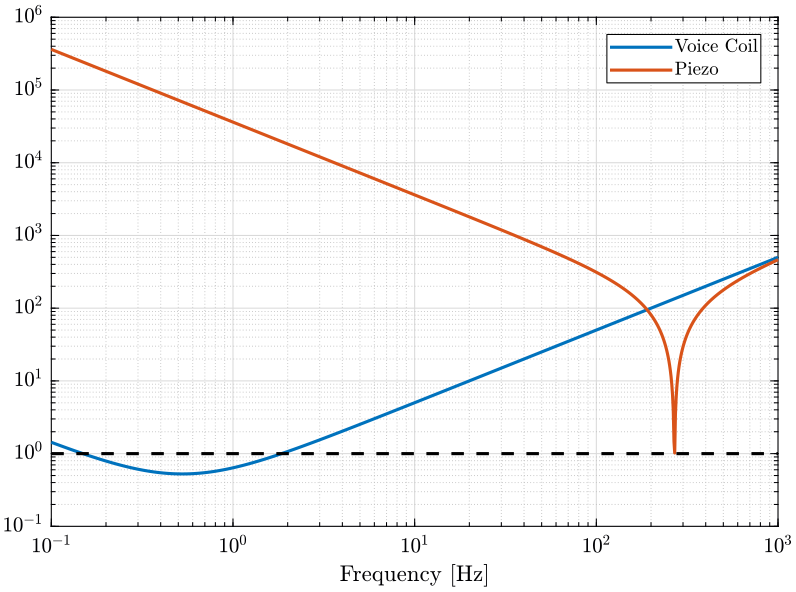
coupling_light.png

Figure 2: Relative Coupling for light mass and high rotation speed

coupling_heavy.png

Figure 3: Relative Coupling for heavy mass and low rotation speed

Coupling is higher for actuators with small stiffness.

1.7 Limitations due to negative stiffness effect

If \(\max{\dot{\theta}} \ll \sqrt{\frac{k}{m}}\), then the negative spring effect is negligible and \(k - m\dot{\theta}^2 \approx k\).

Let's estimate what is the maximum rotation speed for which the negative stiffness effect is still negligible (\(\omega_\text{max} = 0.1 \sqrt{\frac{k}{m}}\)). Results are shown table 3.

Table 3: Maximum rotation speed at which negative stiffness is negligible (\(0.1\sqrt{\frac{k}{m}}\))
  Voice Coil Piezo
Light 5[rpm] 1614[rpm]
Heavy 3[rpm] 1036[rpm]

The negative spring effect is proportional to the rotational speed \(\omega\). The system dynamics will be much more affected when using soft actuator.

Negative stiffness effect has very important effect when using soft actuators.

The system can even goes unstable when \(m \omega^2 > k\), that is when the centrifugal forces are higher than the forces due to stiffness.

From this analysis, we can determine the lowest practical stiffness that is possible to use: \(k_\text{min} = 10 m \omega^2\) (table sec:tab:mink)

Table 4: Minimum possible stiffness
  Light Heavy
k min [N/m] 2199 89

1.8 Effect of rotation speed on the plant

As shown in equation \eqref{orgb104ecd}, the plant changes with the rotation speed \(\omega_0\).

Then, we compute the bode plot of the direct term and coupling term for multiple rotating speed.

Then we compare the result between voice coil and piezoelectric actuators.

1.8.1 Voice coil actuator

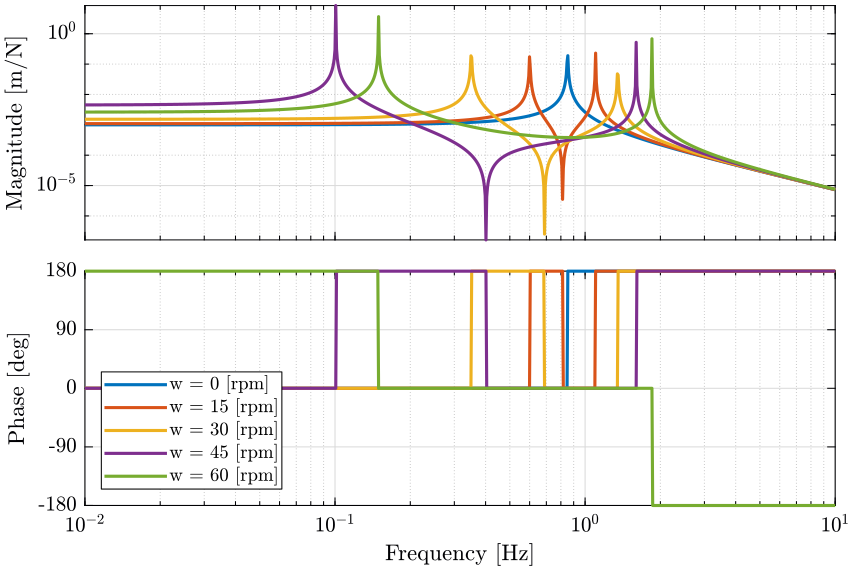
G_ws_vc.png

Figure 4: Bode plot of the direct transfer function term (from \(F_u\) to \(D_u\)) for multiple rotation speed - Voice coil

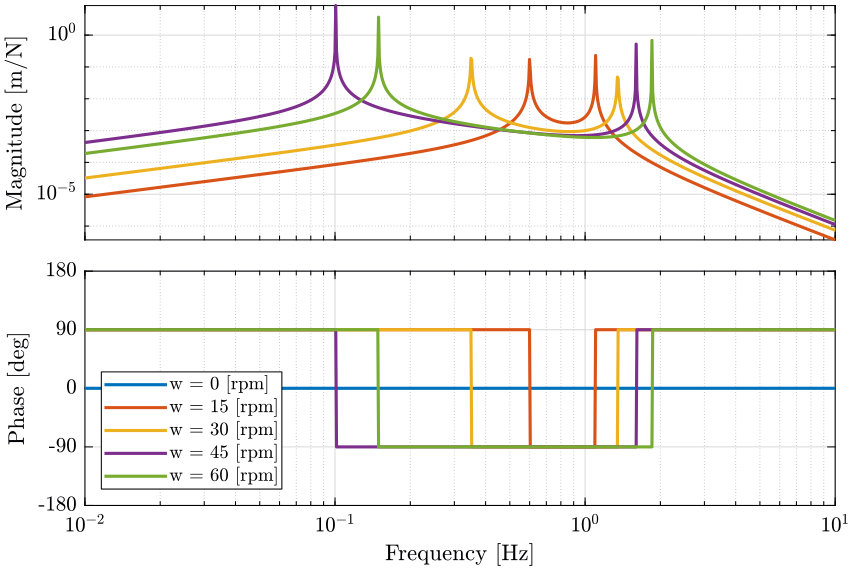
Gc_ws_vc.png

Figure 5: caption

1.8.2 Piezoelectric actuator

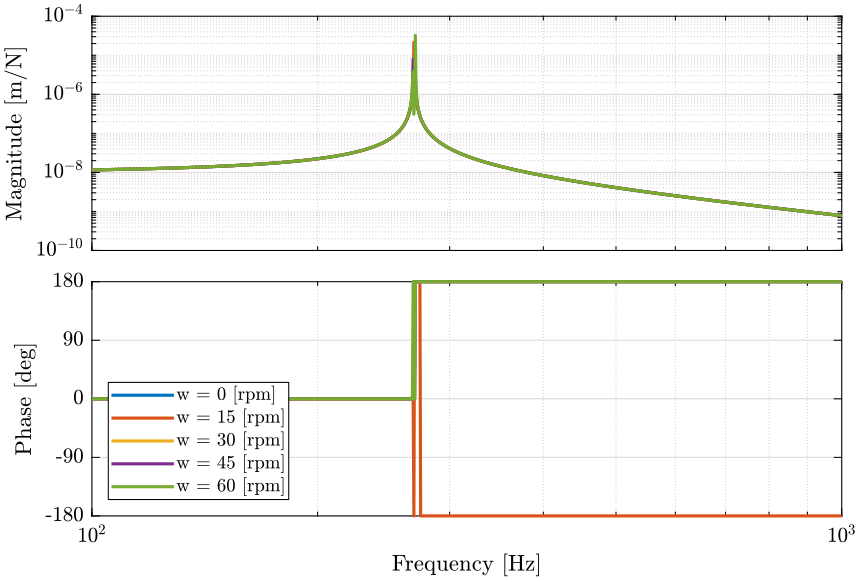
G_ws_pz.png

Figure 6: Bode plot of the direct transfer function term (from \(F_u\) to \(D_u\)) for multiple rotation speed - Piezoelectric actuator

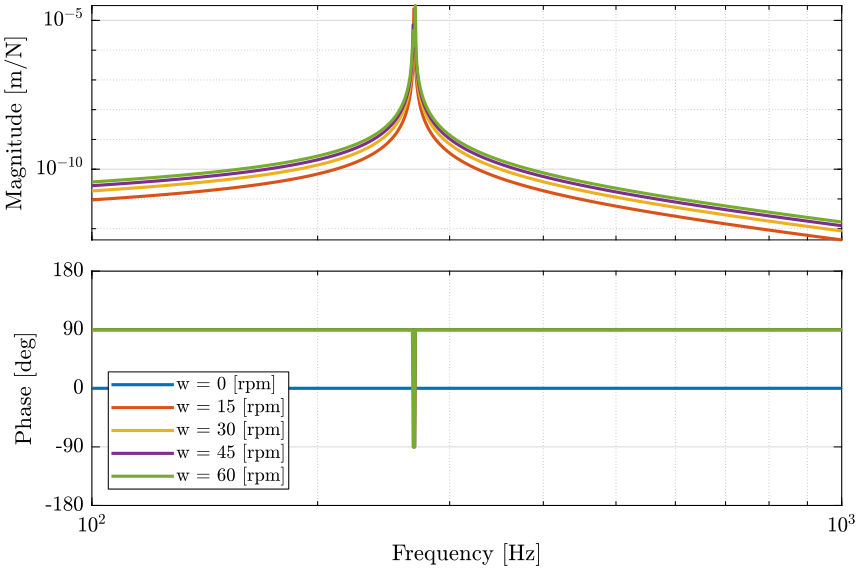
Gc_ws_pz.png

Figure 7: Bode plot of the coupling transfer function term (from \(F_u\) to \(D_v\)) for multiple rotation speed - Piezoelectric actuator

1.8.3 Analysis

When the rotation speed is null, the coupling terms are equal to zero and the diagonal terms corresponds to one degree of freedom mass spring system.

When the rotation speed in not null, the resonance frequency is duplicated into two pairs of complex conjugate poles.

As the rotation speed increases, one of the two resonant frequency goes to lower frequencies as the other one goes to higher frequencies.

The poles of the coupling terms are the same as the poles of the diagonal terms. The magnitude of the coupling terms are increasing with the rotation speed.

As shown in the previous figures, the system with voice coil is much more sensitive to rotation speed.

1.8.4 Campbell diagram

The poles of the system are computed for multiple values of the rotation frequency. To simplify the computation of the poles, we add some damping to the system. 

m = mlight;
k = kvc;
c = 0.1*sqrt(k*m);

wsvc = linspace(0, 10, 100); % [rad/s]

polesvc = zeros(2, length(wsvc));

for i = 1:length(wsvc)
  polei = pole(1/((m*s^2 + c*s + (k - m*wsvc(i)^2))^2 + (2*m*wsvc(i)*s)^2));
  polesvc(:, i) = sort(polei(imag(polei) > 0));
end

m = mlight;
k = kpz;
c = 0.1*sqrt(k*m);

wspz = linspace(0, 1000, 100); % [rad/s]

polespz = zeros(2, length(wspz));

for i = 1:length(wspz)
  polei = pole(1/((m*s^2 + c*s + (k - m*wspz(i)^2))^2 + (2*m*wspz(i)*s)^2));
  polespz(:, i) = sort(polei(imag(polei) > 0));
end

We then plot the real and imaginary part of the poles as a function of the rotation frequency (figures 8 and 9).

When the real part of one pole becomes positive, the system goes unstable.

For the voice coil (figure 8), the system is unstable when the rotation speed is above 5 rad/s. The real and imaginary part of the poles of the system with piezoelectric actuators are changing much less (figure 9).

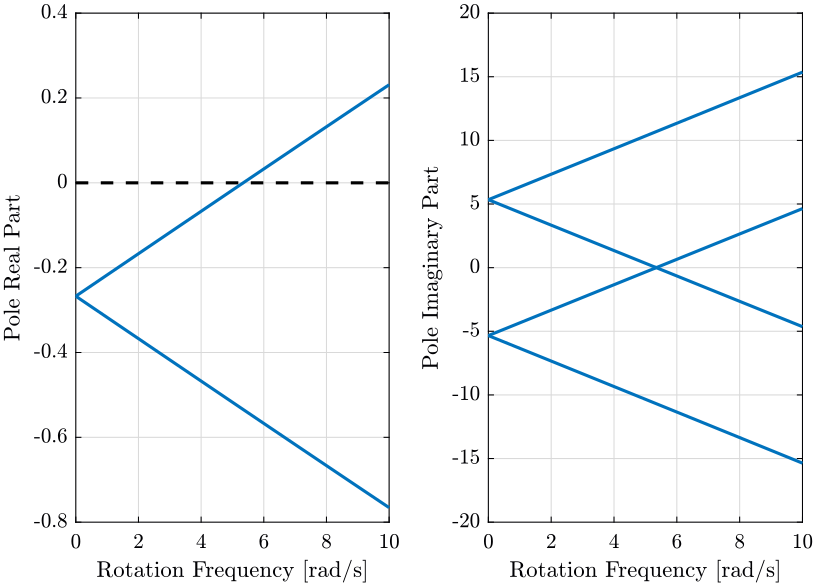
poles_w_vc.png

Figure 8: Real and Imaginary part of the poles of the system as a function of the rotation speed - Voice Coil and light sample

poles_w_pz.png

Figure 9: Real and Imaginary part of the poles of the system as a function of the rotation speed - Piezoelectric actuator and light sample

2 Control Strategies

2.1 Measurement in the fixed reference frame

First, let's consider a measurement in the fixed referenced frame.

The transfer function from actuator \([F_u, F_v]\) to sensor \([D_x, D_y]\) is then \(G(\theta)\).

Then the measurement is subtracted to the reference signal \([r_x, r_y]\) to obtain the position error in the fixed reference frame \([\epsilon_x, \epsilon_y]\).

The position error \([\epsilon_x, \epsilon_y]\) is then express in the rotating frame corresponding to the actuators \([\epsilon_u, \epsilon_v]\).

Finally, the control low \(K\) links the position errors \([\epsilon_u, \epsilon_v]\) to the actuator forces \([F_u, F_v]\).

The block diagram is shown on figure 10.

control_measure_fixed_2dof.png

Figure 10: Control with a measure from fixed frame

The loop gain is then \(L = G(\theta) K J(\theta)\).

One question we wish to answer is: is \(G(\theta) J(\theta) = G(\theta_0) J(\theta_0)\)?

2.2 Measurement in the rotating frame

Let's consider that the measurement is made in the rotating reference frame.

The corresponding block diagram is shown figure 11.

control_measure_rotating_2dof.png

Figure 11: Control with a measure from rotating frame

The loop gain is \(L = G K\).

3 Multi Body Model - Simscape

3.1 Initialization

Let's load the previously defined parameters for the model. 

bode_opts = bodeoptions;
bode_opts.FreqUnits = 'Hz';
bode_opts.MagUnits  = 'abs';
bode_opts.MagScale  = 'log';
bode_opts.Grid      = 'on';
bode_opts.PhaseVisible = 'off';
bode_opts.Title.FontSize     = 10;
bode_opts.XLabel.FontSize    = 10;
bode_opts.YLabel.FontSize    = 10;
bode_opts.TickLabel.FontSize = 10;

First we define the parameters that must be defined in order to run the Simscape simulation. 

w = 2*pi; % Rotation speed [rad/s]

theta_e = 0; % Static measurement error on the angle theta [rad]

m = 5; % mass of the sample [kg]

mTuv = 30;% Mass of the moving part of the Tuv stage [kg]
kTuv = 1e8; % Stiffness of the Tuv stage [N/m]
cTuv = 0; % Damping of the Tuv stage [N/(m/s)]

Then, we defined parameters that will be used in the following analysis. 

mlight = 5; % Mass for light sample [kg]
mheavy = 55; % Mass for heavy sample [kg]

wlight = 2*pi; % Max rot. speed for light sample [rad/s]
wheavy = 2*pi/60; % Max rot. speed for heavy sample [rad/s]

kvc = 1e3; % Voice Coil Stiffness [N/m]
kpz = 1e8; % Piezo Stiffness [N/m]

d = 0.01; % Maximum excentricity from rotational axis [m]

freqs = logspace(-2, 3, 1000); % Frequency vector for analysis [Hz]

3.2 Identification in the rotating referenced frame

We initialize the inputs and outputs of the system to identify:

  • Inputs: \(f_u\) and \(f_v\)
  • Outputs: \(d_u\) and \(d_v\)
%% Options for Linearized
options = linearizeOptions;
options.SampleTime = 0;

%% Name of the Simulink File
mdl = 'rotating_frame';

%% Input/Output definition
io(1) = linio([mdl, '/fu'], 1, 'input');
io(2) = linio([mdl, '/fv'], 1, 'input');

io(3) = linio([mdl, '/du'], 1, 'output');
io(4) = linio([mdl, '/dv'], 1, 'output');

We start we identify the transfer functions at high speed with the light sample. 

w = wlight; % Rotation speed [rad/s]
m = mlight; % mass of the sample [kg]

kTuv = kpz;
Gpz_light = linearize(mdl, io, 0.1);
Gpz_light.InputName  = {'Fu', 'Fv'};
Gpz_light.OutputName = {'Du', 'Dv'};

kTuv = kvc;
Gvc_light = linearize(mdl, io, 0.1);
Gvc_light.InputName  = {'Fu', 'Fv'};
Gvc_light.OutputName = {'Du', 'Dv'};

Then we identify the system with an heavy mass and low speed. 

w = wheavy; % Rotation speed [rad/s]
m = mheavy; % mass of the sample [kg]

kTuv = kpz;
Gpz_heavy = linearize(mdl, io, 0.1);
Gpz_heavy.InputName  = {'Fu', 'Fv'};
Gpz_heavy.OutputName = {'Du', 'Dv'};

kTuv = kvc;
Gvc_heavy = linearize(mdl, io, 0.1);
Gvc_heavy.InputName  = {'Fu', 'Fv'};
Gvc_heavy.OutputName = {'Du', 'Dv'};

3.3 Coupling ratio between \(f_{uv}\) and \(d_{uv}\)

In order to validate the equations written, we can compute the coupling ratio using the simscape model and compare with the equations.

From the previous identification, we plot the coupling ratio in both case (figure 12).

We obtain the same result than the analytical case (figures 2 and 3).

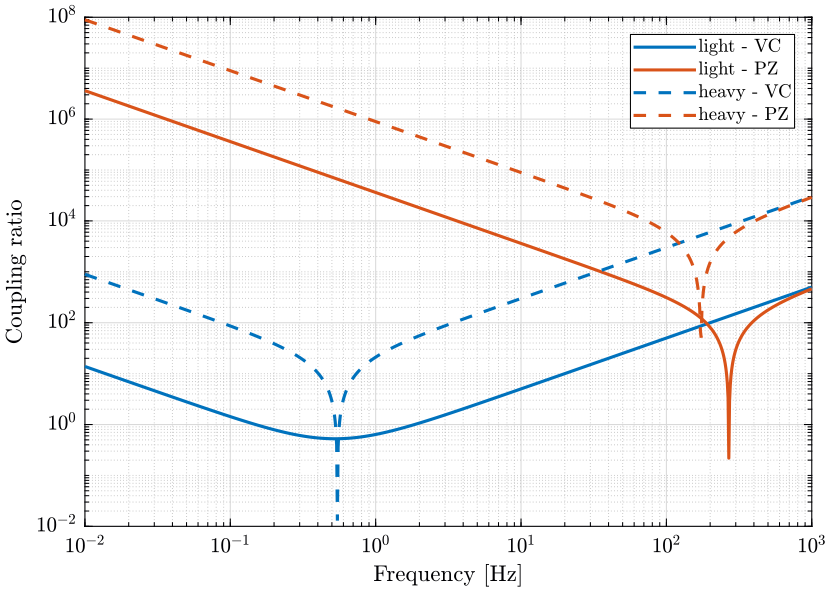
coupling_ratio_light_heavy.png

Figure 12: Coupling ratio obtained with the Simscape model

3.4 Plant Control - SISO approach

3.4.1 Plant identification

The goal is to study the control problems due to the coupling that appears because of the rotation.

First, we identify the system when the rotation speed is null and then when the rotation speed is equal to 60rpm.

The actuators are voice coil with some damping added.

The bode plot of the system not rotating and rotating at 60rpm is shown figure 13.

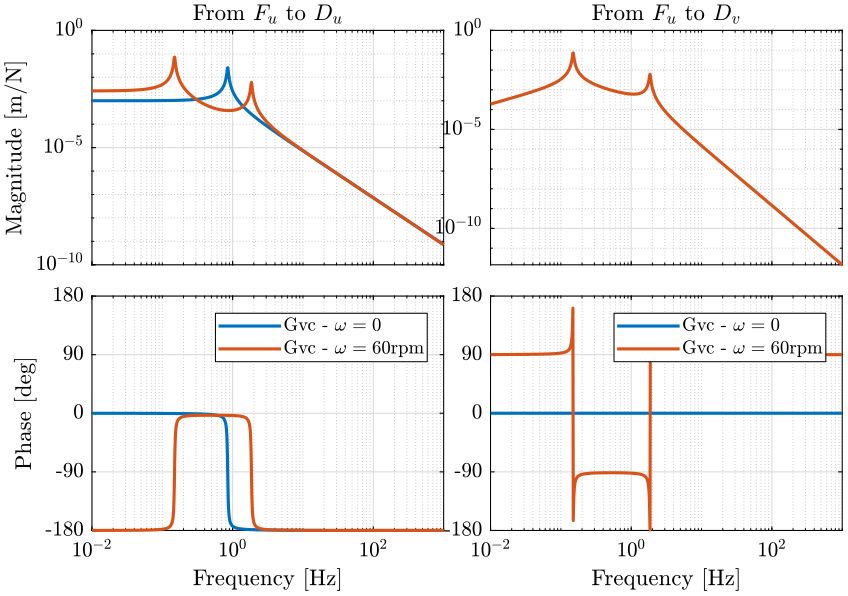
Gvc_speed.png

Figure 13: Change of transfer functions due to rotating speed

3.4.2 Effect of rotation speed

We first identify the system (voice coil and light mass) for multiple rotation speed. Then we compute the bode plot of the system (figure 14).

As the rotation frequency increases:

  • one pole goes to lower frequencies while the other goes to higher frequencies
  • one zero appears between the two poles
  • the zero disappears when \(\omega > \sqrt{\frac{k}{m}}\) and the low frequency pole becomes unstable (positive real part)

To stabilize the unstable pole, we need a control bandwidth of at least twice of frequency of the unstable pole.

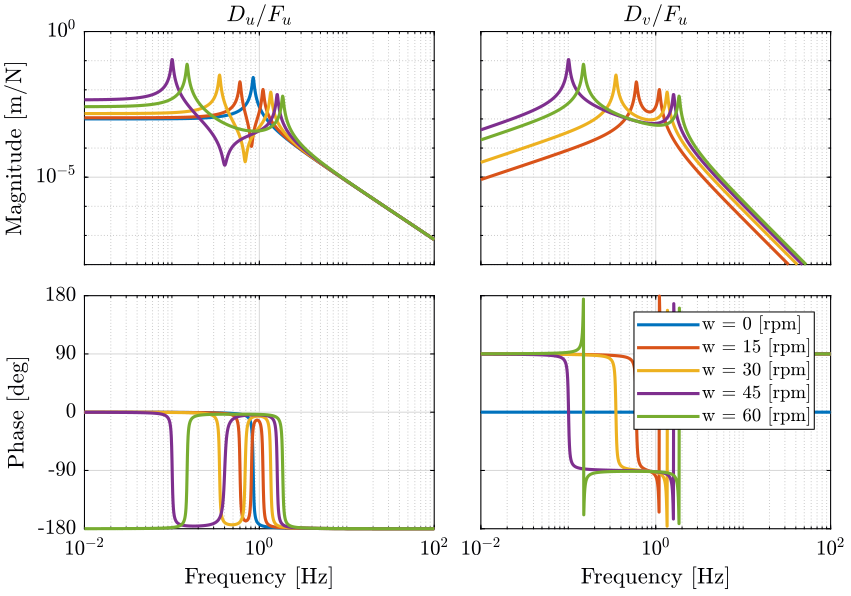
Guu_uv_ws.png

Figure 14: Diagonal term as a function of the rotation frequency

Then, we can look at the same plots for the piezoelectric actuator (figure 15). The effect of the rotation frequency has very little effect on the dynamics of the system to control.

Guu_ws_pz.png

Figure 15: Diagonal term as a function of the rotation frequency

3.4.3 Controller design

We design a controller based on the identification when the system is not rotating.

The obtained controller is a lead-lag controller with the following transfer function. 

Kll = 2.0698e09*(s+40.45)*(s+1.181)/((s+0.01)*(s+198.4)*(s+2790));
K = [Kll 0;
     0   Kll];

K.InputName  = {'Du', 'Dv'};
K.OutputName = {'Fu', 'Fv'};

The loop gain is displayed figure 16.

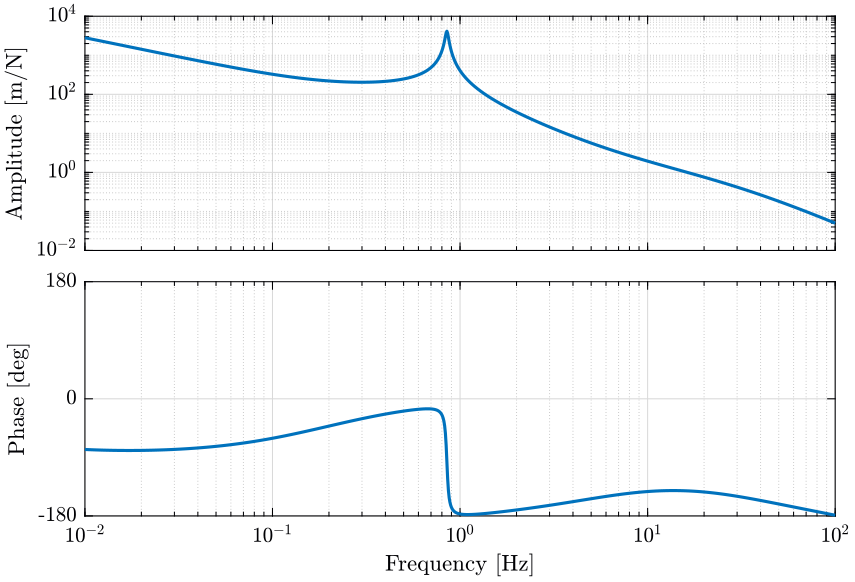
Gvc_loop_gain.png

Figure 16: Loop gain obtained for a lead-lag controller on the system with a voice coil

3.4.4 Controlling the rotating system

We here want to see if the system is robust with respect to the rotation speed. We use the controller that was designed based on the dynamics of the non-rotating system.

Let's first plot the SISO loop gain.

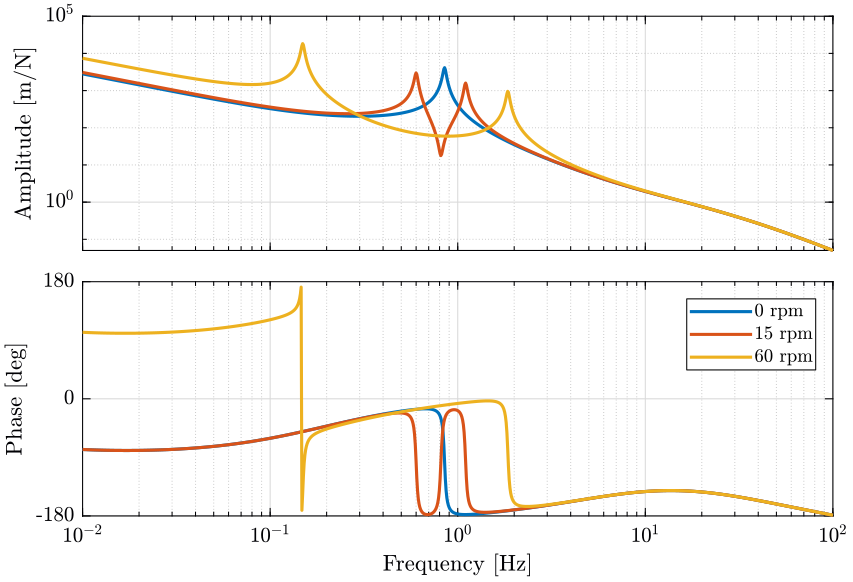
loop_gain_turning.png

Figure 17: Loop Gain \(G_u * K\)

We can now compute the close-loop systems. 

Gvc_cl = {zeros(1, length(ws))};
for i = 1:length(ws)
  Gvc_cl{i} = feedback(Gs_vc{i}, K, 'name');
end

Let's now look on figure 18 at the evolution of the poles of the system when closing only one loop (controlling only one direction). We see that two complex conjugate poles are approaching the real axis and then they separate: one goes to positive real part and the other goes to negative real part. The system then goes unstable at some point (here for \(\omega=60rpm\)). 

figure;
hold on;
for i = 1:length(ws)
  sys = feedback(Gs_vc{i}(1, 1), K(1, 1), 'name');
  plot(real(pole(sys)), imag(pole(sys)), 'o', 'DisplayName', sprintf('$\\omega = %.0f rpm$', ws(i)/(2*pi)*60));
end
hold off;
xlim([-80, 10]);
xlabel('Real Axis'); ylabel('Imaginary Axis');
legend('Location', 'northeast');

evolution_poles_u.png

Figure 18: Evolution of the poles of the closed-loop system when closing just one loop

If we look at the poles of the closed loop-system for multiple rotating speed (figure 19) when closing the two loops (MIMO system), we see that they all have a negative real part (stable system), and their evolution on the complex plane is rather small compare to the open loop evolution. 

figure;
hold on;
for i = 1:length(ws)
  plot(real(pole(Gvc_cl{i})), imag(pole(Gvc_cl{i})), 'o', 'DisplayName', sprintf('$\\omega = %.0f rpm$', ws(i)/(2*pi)*60));
end
hold off;
xlim([-80, 0]);
xlabel('Real Axis'); ylabel('Imaginary Axis');
legend('Location', 'northeast');

poles_cl_system.png

Figure 19: Evolution of the poles of the closed-loop system

3.4.5 Close loop performance

First, we create the closed loop systems. Then, we plot the transfer function from the reference signals \([r_u, r_v]\) to the output \([d_u, d_v]\) (figure 20). 

freqs = logspace(-2, 3, 1000);

figure;
ax1 = subplot(1,2,1);
title('$G_{r_u \to d_u}$')
hold on;
for i = 1:length(ws)
  sys = Gvc_cl{i}*K;
  plot(freqs, abs(squeeze(freqresp(sys(1, 1), freqs, 'Hz'))));
end
hold off;
xlim([freqs(1), freqs(end)]);
ylim([1e-4, 10]);
set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log');
xlabel('Frequency [Hz]'); ylabel('Magnitude [m/N]');

ax2 = subplot(1,2,2);
title('$G_{r_u \to d_v}$')
hold on;
for i = 1:length(ws)
  sys = Gvc_cl{i}*K;
  plot(freqs, abs(squeeze(freqresp(sys(1, 2), freqs, 'Hz'))), 'DisplayName', sprintf('$\\omega = %.0f rpm$', ws(i)/(2*pi)*60));
end
hold off;
xlim([freqs(1), freqs(end)]);
ylim([1e-4, 10]);
set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log');
xlabel('Frequency [Hz]');
legend('Location', 'northeast')

linkaxes([ax1,ax2],'x');

perfcomp.png

Figure 20: Close loop performance for \(\omega = 0\) and \(\omega = 60 rpm\)

3.4.6 Conclusion

Even though considering one input and output at a time would results in an unstable system (figure 18), when using the diagonal MIMO controller, the system stays stable (figure 19). This could be understood by saying that when controlling both directions at the same time, the coupling effect should be much lower than when controlling only one direction.

The close-loop performance does not vary a lot with the rotating speed (figure 20) even tough the open loop system is varying quite a lot (figure 14).

3.5 BKMK Plant Control - MIMO approach

3.5.1 Analysis - SVD

The singular value decomposition of a MIMO system \(G\) is defined as follow: \[ G = U \Sigma V^H \]

With:

  • \(\Sigma\) is an \(2 \times 2\) matrix with 2 non-negative singular values \(\sigma_i\), arranged in descending order along its main diagonal
  • \(U\) is an \(2 \times 2\) unitary matrix. The columns vectors of \(U\), denoted \(u_i\), represent the output directions of the plant. They are orthonomal
  • \(V\) is an \(2 \times 2\) unitary matrix. The columns vectors of \(V\), denoted \(v_i\), represent the input directions of the plant. They are orthonomal

We first look at the evolution of the singular values as a function of frequency (figure 21).

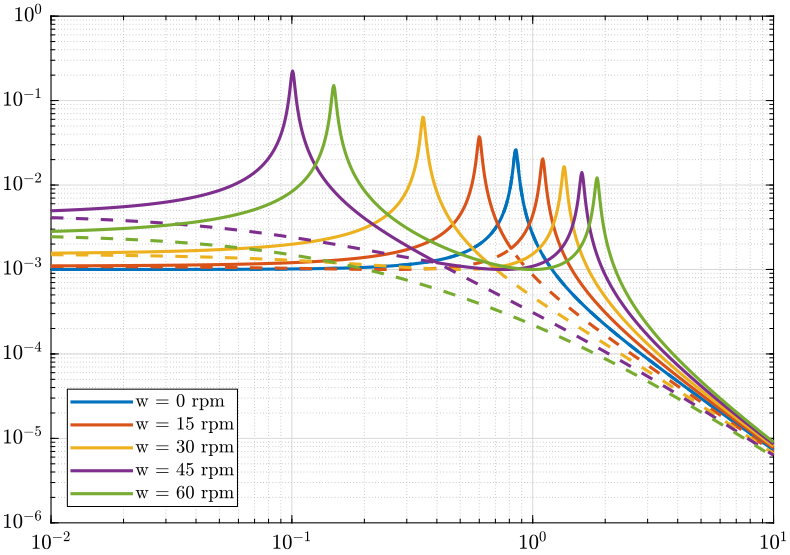
G_sigma.png

Figure 21: Evolution of the singular values with frequency

4 Control Implementation

Author: Dehaeze Thomas

Created: 2019-06-04 mar. 10:16

Validate