NASS - Effect of rotation
Table of Contents
- 1. System Description and Analysis
- 2. Integral Force Feedback
- 3. Integral Force Feedback with an High Pass Filter
- 4. IFF with a stiffness in parallel with the force sensor
- 5. Relative Damping Control
- 6. Comparison of Active Damping Techniques
- 7. Rotating Nano-Hexapod
- 8. Nano-Active-Stabilization-System with rotation
- 9. Conclusion
This report is also available as a pdf.
An important aspect of the Nano Active Stabilization System (NASS) is that the nano-hexapod is continuously rotating around a vertical axis while the external metrology is not. Such rotation induces gyroscopic effects that may impact the system dynamics and obtained performances.
In this report, this rotating aspect of the NASS is studied. It is structured in several sections:
- Section sec:rotating_system_description: a simple model of a rotating suspended platform that will be used throughout this study is presented. The effect of the rotation velocity on the system dynamics is shown.
- Section sec:rotating_iff_pure_int: Integral Force Feedback (IFF) is applied to the rotating platform, and it is shown that the unconditional stability of IFF is lost due to Gyroscopic effects induced by the rotation.
- Section sec:rotating_iff_pseudo_int: A first modification of the IFF control law is proposed such that damping can be added to the suspension modes in a robust way. This modification consists of adding an high pass filter to the IFF controller. Optimal high pass filter cut-off frequency is computed.
- Section sec:rotating_iff_parallel_stiffness: A second modification is proposed to regain the unconditional stability of IFF. This modification consists of adding stiffness in parallel to the force sensors. Optimal parallel stiffness is computed.
- Section sec:rotating_relative_damp_control: Relative damping control is applied to the rotating system.
- Section sec:rotating_comp_act_damp: Once the optimal control parameters for the three tested active damping techniques are obtained, they are compared in terms of achievable damping, obtained damped plant and closed-loop compliance and transmissibility.
- Section sec:rotating_nano_hexapod: the previous analysis is applied on three nano-hexapod stiffnesses and optimal active damping controller are obtained.
- Section sec:rotating_nass: up until this section, the study was performed on a very simplistic model that just captures the rotation aspect and the model parameters were not tuned to corresponds to the NASS. In this last section, a model of the micro-station is added below the suspended platform (i.e. the nano-hexapod) with a rotating spindle and parameters tuned to match the NASS dynamics. The goal is to determine if the rotation imposes performance limitation for the NASS.
To run the Matlab code, go in the matlab directory and run the Matlab files corresponding to each section (see Table tab:section_matlab_code).
| Sections | Matlab File |
|---|---|
| Section sec:rotating_system_description | rotating_1_system_description.m |
| Section sec:rotating_iff_pure_int | rotating_2_iff_pure_int.m |
| Section sec:rotating_iff_pseudo_int | rotating_3_iff_hpf.m |
| Section sec:rotating_iff_parallel_stiffness | rotating_4_iff_kp.m |
| Section sec:rotating_relative_damp_control | rotating_5_rdc.m |
| Section sec:rotating_comp_act_damp | rotating_5_act_damp_comparison.m |
| Section sec:rotating_nano_hexapod | rotating_6_nano_hexapod.m |
| Section sec:rotating_nass | rotating_6_nass.m |
1. System Description and Analysis
The studied system consists of a 2 degree of freedom translation stage on top of a rotating stage (Figure fig:rotating_3dof_model_schematic).
The rotating stage is supposed to be ideal, meaning it induces a perfect rotation \(\theta(t) = \Omega t\) where \(\Omega\) is the rotational speed in \(\si{\radian\per\s}\).
The suspended platform consists of two orthogonal actuators each represented by three elements in parallel: a spring with a stiffness \(k\) in \(\si{\newton\per\meter}\), a dashpot with a damping coefficient \(c\) in \(\si{\newton\per(\meter\per\second)}\) and an ideal force source \(F_u, F_v\). A payload with a mass \(m\) in \(\si{\kilo\gram}\), is mounted on the (rotating) suspended platform.
Two reference frames are used: an inertial frame \((\vec{i}_x, \vec{i}_y, \vec{i}_z)\) and a uniform rotating frame \((\vec{i}_u, \vec{i}_v, \vec{i}_w)\) rigidly fixed on top of the rotating stage with \(\vec{i}_w\) aligned with the rotation axis. The position of the payload is represented by \((d_u, d_v, 0)\) expressed in the rotating frame.
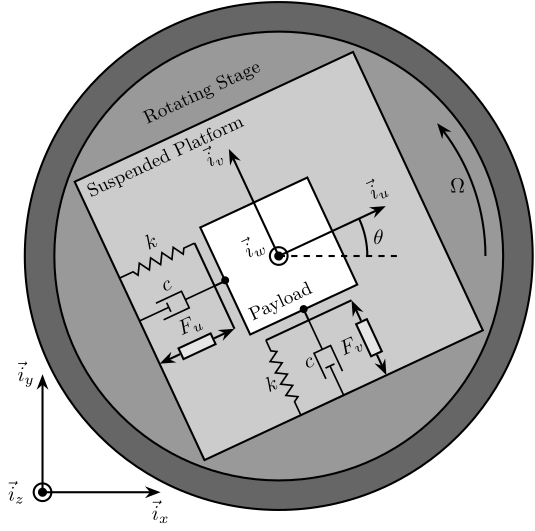
Figure 1: Schematic of the studied system
1.1. Equations of motion
To obtain the equations of motion for the system represented in Figure fig:rotating_3dof_model_schematic, the Lagrangian equations are used:
\begin{equation} \label{org5f12e94} \frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_i} \right) + \frac{\partial D}{\partial \dot{q}_i} - \frac{\partial L}{\partial q_i} = Q_i \end{equation}with \(L = T - V\) the Lagrangian, \(T\) the kinetic coenergy, \(V\) the potential energy, \(D\) the dissipation function, and \(Q_i\) the generalized force associated with the generalized variable \(\begin{bmatrix}q_1 & q_2\end{bmatrix} = \begin{bmatrix}d_u & d_v\end{bmatrix}\). The equation of motion corresponding to the constant rotation along \(\vec{i}_w\) is disregarded as this motion is considered to be imposed by the rotation stage.
\begin{equation} \label{orgdc4e5f6} \begin{aligned} T &= \frac{1}{2} m \left( ( \dot{d}_u - \Omega d_v )^2 + ( \dot{d}_v + \Omega d_u )^2 \right), \\ V &= \frac{1}{2} k \big( {d_u}^2 + {d_v}^2 \big), \ Q_1 = F_u, \\ D &= \frac{1}{2} c \big( \dot{d}_u{}^2 + \dot{d}_v{}^2 \big), \ Q_2 = F_v \end{aligned} \end{equation}Substituting equations eq:energy_functions_lagrange into equation eq:lagrangian_equations for both generalized coordinates gives two coupled differential equations eq:eom_coupled_1 and eq:eom_coupled_2.
\begin{subequations} \label{orgf489dbd} \begin{align} m \ddot{d}_u + c \dot{d}_u + ( k - m \Omega^2 ) d_u &= F_u + 2 m \Omega \dot{d}_v \label{eq:eom_coupled_1} \\ m \ddot{d}_v + c \dot{d}_v + ( k \underbrace{-\,m \Omega^2}_{\text{Centrif.}} ) d_v &= F_v \underbrace{-\,2 m \Omega \dot{d}_u}_{\text{Coriolis}} \label{eq:eom_coupled_2} \end{align} \end{subequations}The uniform rotation of the system induces two gyroscopic effects as shown in equation eq:eom_coupled:
- Centrifugal forces: that can been seen as an added negative stiffness \(- m \Omega^2\) along \(\vec{i}_u\) and \(\vec{i}_v\)
- Coriolis Forces: that adds coupling between the two orthogonal directions.
One can verify that without rotation (\(\Omega = 0\)) the system becomes equivalent to two uncoupled one degree of freedom mass-spring-damper systems.
1.2. Transfer Functions in the Laplace domain
To study the dynamics of the system, the differential equations of motions eq:eom_coupled are converted into the Laplace domain and the \(2 \times 2\) transfer function matrix \(\mathbf{G}_d\) from \(\begin{bmatrix}F_u & F_v\end{bmatrix}\) to \(\begin{bmatrix}d_u & d_v\end{bmatrix}\) in equation eq:Gd_mimo_tf is obtained. Its elements are shown in equation eq:Gd_indiv_el.
\begin{equation} \label{org835660b} \begin{bmatrix} d_u \\ d_v \end{bmatrix} = \mathbf{G}_d \begin{bmatrix} F_u \\ F_v \end{bmatrix} \end{equation} \begin{subequations} \label{org64bb6d3} \begin{align} \mathbf{G}_{d}(1,1) &= \mathbf{G}_{d}(2,2) = \frac{ms^2 + cs + k - m \Omega^2}{\left( m s^2 + cs + k - m \Omega^2 \right)^2 + \left( 2 m \Omega s \right)^2} \\ \mathbf{G}_{d}(1,2) &= -\mathbf{G}_{d}(2,1) = \frac{2 m \Omega s}{\left( m s^2 + cs + k - m \Omega^2 \right)^2 + \left( 2 m \Omega s \right)^2} \end{align} \end{subequations}To simplify the analysis, the undamped natural frequency \(\omega_0\) and the damping ratio \(\xi\) are used as in equation eq:xi_and_omega.
\begin{equation} \label{org6fb81ba} \omega_0 = \sqrt{\frac{k}{m}} \text{ in } \si{\radian\per\second}, \quad \xi = \frac{c}{2 \sqrt{k m}} \end{equation}The elements of transfer function matrix \(\mathbf{G}_d\) are now described by equation eq:Gd_w0_xi_k.
\begin{subequations} \label{orgf71f00f} \begin{align} \mathbf{G}_{d}(1,1) &= \frac{\frac{1}{k} \left( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right)}{\left( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right)^2 + \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)^2} \\ \mathbf{G}_{d}(1,2) &= \frac{\frac{1}{k} \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)}{\left( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right)^2 + \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)^2} \end{align} \end{subequations}1.3. System Poles: Campbell Diagram
The poles of \(\mathbf{G}_d\) are the complex solutions \(p\) of equation eq:poles.
\begin{equation} \label{orgbd9d5cd} \left( \frac{p^2}{{\omega_0}^2} + 2 \xi \frac{p}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right)^2 + \left( 2 \frac{\Omega}{\omega_0} \frac{p}{\omega_0} \right)^2 = 0 \end{equation}Supposing small damping (\(\xi \ll 1\)), two pairs of complex conjugate poles are obtained as shown in equation eq:pole_values.
\begin{subequations} \label{org4ae8a0c} \begin{align} p_{+} &= - \xi \omega_0 \left( 1 + \frac{\Omega}{\omega_0} \right) \pm j \omega_0 \left( 1 + \frac{\Omega}{\omega_0} \right) \\ p_{-} &= - \xi \omega_0 \left( 1 - \frac{\Omega}{\omega_0} \right) \pm j \omega_0 \left( 1 - \frac{\Omega}{\omega_0} \right) \end{align} \end{subequations}The real and complex parts of these two pairs of complex conjugate poles are represented in Figure fig:rotating_campbell_diagram as a function of the rotational speed \(\Omega\). As the rotational speed increases, \(p_{+}\) goes to higher frequencies and \(p_{-}\) goes to lower frequencies. The system becomes unstable for \(\Omega > \omega_0\) as the real part of \(p_{-}\) is positive. Physically, the negative stiffness term \(-m\Omega^2\) induced by centrifugal forces exceeds the spring stiffness \(k\).
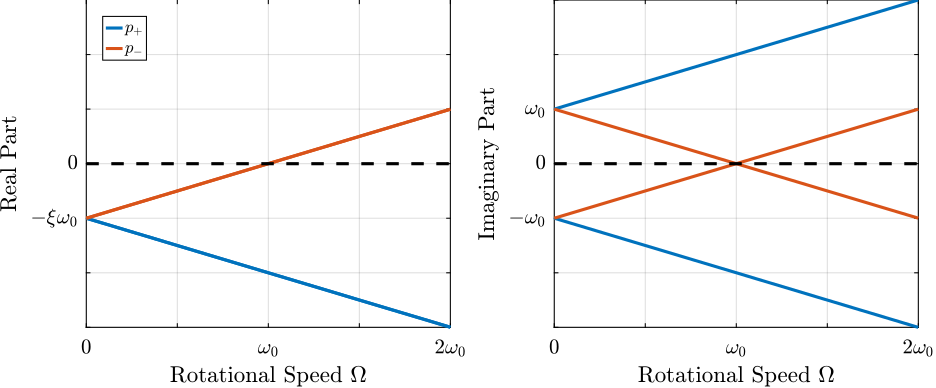
Figure 2: Campbell diagram - Real and Imaginary parts of the poles as a function of the rotating velocity
1.4. System Dynamics: Effect of rotation
The system dynamics from actuator forces \([F_u, F_v]\) to the relative motion \([d_u, d_v]\) is identified for several rotating velocities.
Looking at the transfer function matrix \(\mathbf{G}_d\) in equation eq:Gd_w0_xi_k, one can see that the two diagonal (direct) terms are equal and that the two off-diagonal (coupling) terms are opposite. The bode plot of these two terms are shown in Figure fig:rotating_direct_coupling_bode_plot for several rotational speeds \(\Omega\). These plots confirm the expected behavior: the frequency of the two pairs of complex conjugate poles are further separated as \(\Omega\) increases. For \(\Omega > \omega_0\), the low frequency pair of complex conjugate poles \(p_{-}\) becomes unstable.
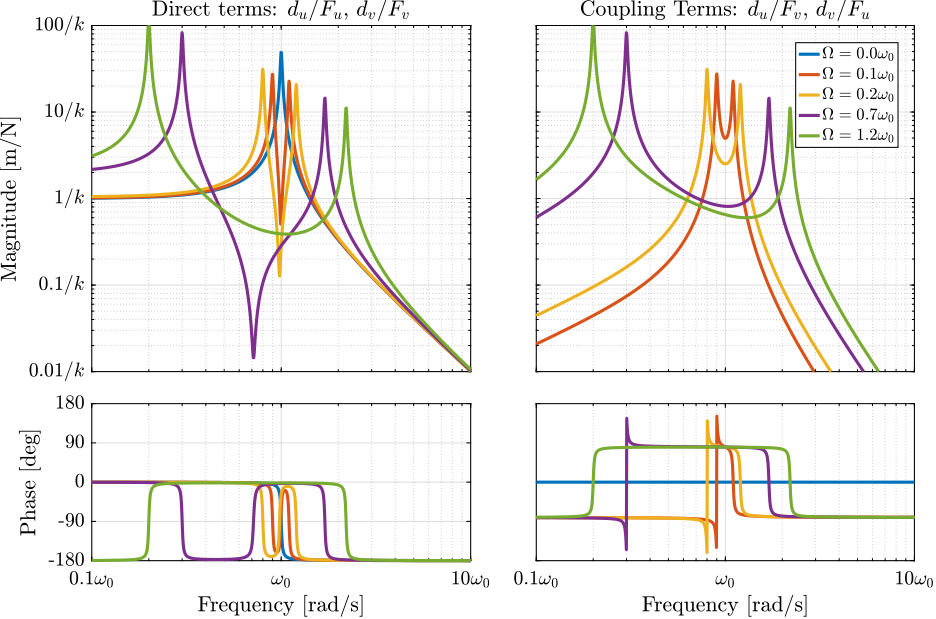
Figure 3: Bode plot of the direct and coupling terms for several rotating velocities
2. Integral Force Feedback
In order to further decrease the residual vibrations, active damping can be used for reducing the magnification of the response in the vicinity of the resonances (Collette, Janssens, and Artoos 2011).
Many active damping techniques have been developed over the years such as Positive Position Feedback (PPF) (Lin and McInroy 2006; Fanson and Caughey 1990), Integral Force Feedback (IFF) (Preumont, Dufour, and Malekian 1991) and Direct Velocity Feedback (DVF) (Karnopp, Crosby, and Harwood 1974; Serrand and Elliott 2000; Preumont et al. 2002). \par
In (Preumont, Dufour, and Malekian 1992), the IFF control scheme has been proposed, where a force sensor, a force actuator and an integral controller are used to directly augment the damping of a mechanical system. When the force sensor is collocated with the actuator, the open-loop transfer function has alternating poles and zeros which facilitate to guarantee the stability of the closed loop system (Preumont et al. 2002). It was latter shown that this property holds for multiple collated actuator/sensor pairs (Preumont, De Marneffe, and Krenk 2008). \par
The main advantages of IFF over other active damping techniques are the guaranteed stability even in presence of flexible dynamics, good performances and robustness properties (Preumont et al. 2002). \par
Several improvements of the classical IFF have been proposed, such as adding a feed-through term to increase the achievable damping (Teo and Fleming 2015) or adding an high pass filter to recover the loss of compliance at low frequency (Chesné, Milhomem, and Collette 2016). Recently, an \(\mathcal{H}_\infty\) optimization criterion has been used to derive optimal gains for the IFF controller (Zhao et al. 2019). \par
However, none of these study have been applied to a rotating system. In this section, Integral Force Feedback strategy is applied on the rotating suspended platform, and it is shown that gyroscopic effects alters the system dynamics and that IFF cannot be applied as is.
2.1. System and Equations of motion
In order to apply Integral Force Feedback, two force sensors are added in series with the actuators (Figure fig:rotating_3dof_model_schematic_iff). Two identical controllers \(K_F\) are then used to feedback each of the sensed force to its associated actuator:
\begin{equation} K_{F}(s) = g \cdot \frac{1}{s} \end{equation}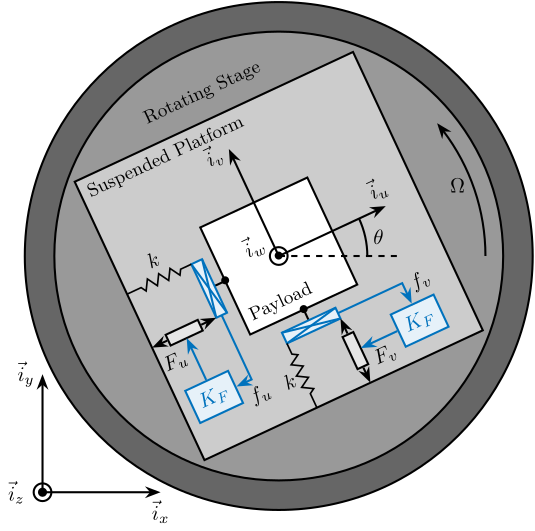
Figure 4: System with added Force Sensor in series with the actuators (shown in blue with the associated controllers)
The forces \(\begin{bmatrix}f_u & f_v\end{bmatrix}\) measured by the two force sensors represented in Figure fig:rotating_3dof_model_schematic_iff are described by equation eq:measured_force.
\begin{equation} \label{org1d5ff63} \begin{bmatrix} f_{u} \\ f_{v} \end{bmatrix} = \begin{bmatrix} F_u \\ F_v \end{bmatrix} - (c s + k) \begin{bmatrix} d_u \\ d_v \end{bmatrix} \end{equation}The transfer function matrix \(\mathbf{G}_{f}\) from actuator forces to measured forces in equation eq:Gf_mimo_tf can be obtained by inserting equation eq:Gd_w0_xi_k into equation eq:measured_force. Its elements are shown in equation eq:Gf_indiv_el.
\begin{equation} \label{orgf7c3d88} \begin{bmatrix} f_{u} \\ f_{v} \end{bmatrix} = \mathbf{G}_{f} \begin{bmatrix} F_u \\ F_v \end{bmatrix} \end{equation} \begin{subequations} \label{org37772f3} \label{eq:Gf} \begin{align} \mathbf{G}_{f}(1,1) &= \mathbf{G}_{f}(2,2) = \frac{\left( \frac{s^2}{{\omega_0}^2} - \frac{\Omega^2}{{\omega_0}^2} \right) \left( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right) + \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)^2}{\left( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right)^2 + \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)^2} \label{eq:Gf_diag_tf} \\ \mathbf{G}_{f}(1,2) &= -\mathbf{G}_{f}(2,1) = \frac{- \left( 2 \xi \frac{s}{\omega_0} + 1 \right) \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)}{\left( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right)^2 + \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)^2} \label{eq:Gf_off_diag_tf} \end{align} \end{subequations}The zeros of the diagonal terms of \(\mathbf{G}_f\) in equation eq:Gf_diag_tf are computed, and neglecting the damping for simplicity, two complex conjugated zeros \(z_{c}\) are obtained in equation eq:iff_zero_cc, and two real zeros \(z_{r}\) in equation eq:iff_zero_real.
\begin{subequations} \begin{align} z_c &= \pm j \omega_0 \sqrt{\frac{1}{2} \sqrt{8 \frac{\Omega^2}{{\omega_0}^2} + 1} + \frac{\Omega^2}{{\omega_0}^2} + \frac{1}{2} } \label{eq:iff_zero_cc} \\ z_r &= \pm \omega_0 \sqrt{\frac{1}{2} \sqrt{8 \frac{\Omega^2}{{\omega_0}^2} + 1} - \frac{\Omega^2}{{\omega_0}^2} - \frac{1}{2} } \label{eq:iff_zero_real} \end{align} \end{subequations}It is interesting to see that the frequency of the pair of complex conjugate zeros \(z_c\) in equation eq:iff_zero_cc always lies between the frequency of the two pairs of complex conjugate poles \(p_{-}\) and \(p_{+}\) in equation eq:pole_values. This is what usually gives the unconditional stability of IFF when collocated force sensors are used.
However, for non-null rotational speeds, the two real zeros \(z_r\) in equation eq:iff_zero_real are inducing a non-minimum phase behavior. This can be seen in the Bode plot of the diagonal terms (Figure fig:rotating_iff_bode_plot_effect_rot) where the low frequency gain is no longer zero while the phase stays at \(\SI{180}{\degree}\).
The low frequency gain of \(\mathbf{G}_f\) increases with the rotational speed \(\Omega\) as shown in equation eq:low_freq_gain_iff_plan.
\begin{equation} \label{orgde800d4} \lim_{\omega \to 0} \left| \mathbf{G}_f (j\omega) \right| = \begin{bmatrix} \frac{\Omega^2}{{\omega_0}^2 - \Omega^2} & 0 \\ 0 & \frac{\Omega^2}{{\omega_0}^2 - \Omega^2} \end{bmatrix} \end{equation}This can be explained as follows: a constant actuator force \(F_u\) induces a small displacement of the mass \(d_u = \frac{F_u}{k - m\Omega^2}\) (Hooke’s law taking into account the negative stiffness induced by the rotation). This small displacement then increases the centrifugal force \(m\Omega^2d_u = \frac{\Omega^2}{{\omega_0}^2 - \Omega^2} F_u\) which is then measured by the force sensors.
2.2. Effect of the rotation speed on the IFF plant dynamics
The transfer functions from actuator forces \([F_u,\ F_v]\) to the measured force sensors \([f_u,\ f_v]\) are identified for several rotating velocities and shown in Figure fig:rotating_iff_bode_plot_effect_rot.
As was expected from the derived equations of motion:
- when \(0 < \Omega < \omega_0\): the low frequency gain is no longer zero and two (non-minimum phase) real zero appears at low frequency. The low frequency gain increases with \(\Omega\). A pair of (minimum phase) complex conjugate zeros appears between the two complex conjugate poles that are split further apart as \(\Omega\) increases.
- when \(\omega_0 < \Omega\): the low frequency pole becomes unstable.
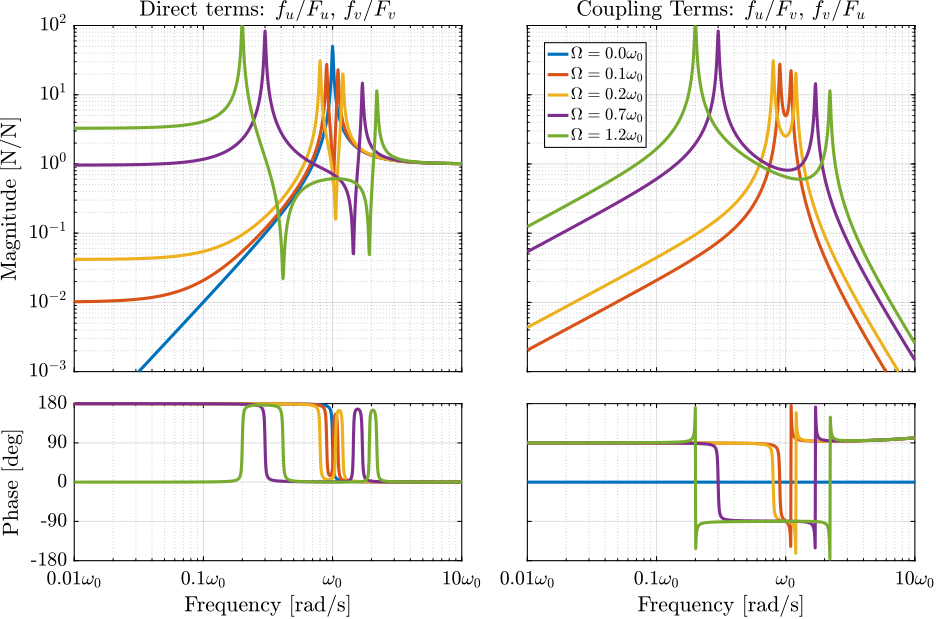
Figure 5: Bode plot of the direct and coupling term for Integral Force Feedback - Effect of rotation
2.3. Decentralized Integral Force Feedback
The control diagram for decentralized Integral Force Feedback is shown in Figure fig:rotating_iff_diagram.
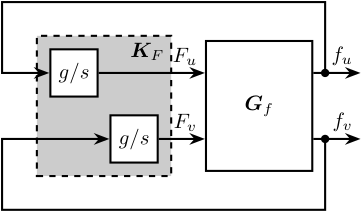
Figure 6: Control diagram for decentralized Integral Force Feedback
The decentralized IFF controller \(\bm{K}_F\) corresponds to a diagonal controller with integrators:
\begin{equation} \label{orgf9e884d} \begin{aligned} \mathbf{K}_{F}(s) &= \begin{bmatrix} K_{F}(s) & 0 \\ 0 & K_{F}(s) \end{bmatrix} \\ K_{F}(s) &= g \cdot \frac{1}{s} \end{aligned} \end{equation}In order to see how the IFF controller affects the poles of the closed loop system, a Root Locus plot (Figure fig:rotating_root_locus_iff_pure_int) is constructed as follows: the poles of the closed-loop system are drawn in the complex plane as the controller gain \(g\) varies from \(0\) to \(\infty\) for the two controllers \(K_{F}\) simultaneously. As explained in (Preumont, De Marneffe, and Krenk 2008; Skogestad and Postlethwaite 2007), the closed-loop poles start at the open-loop poles (shown by \(\tikz[baseline=-0.6ex] \node[cross out, draw=black, minimum size=1ex, line width=2pt, inner sep=0pt, outer sep=0pt] at (0, 0){};\)) for \(g = 0\) and coincide with the transmission zeros (shown by \(\tikz[baseline=-0.6ex] \draw[line width=2pt, inner sep=0pt, outer sep=0pt] (0,0) circle[radius=3pt];\)) as \(g \to \infty\).
Whereas collocated IFF is usually associated with unconditional stability (Preumont, Dufour, and Malekian 1991), this property is lost due to gyroscopic effects as soon as the rotation velocity in non-null. This can be seen in the Root Locus plot (Figure fig:rotating_root_locus_iff_pure_int) where poles corresponding to the controller are bound to the right half plane implying closed-loop system instability.
Physically, this can be explained like so: at low frequency, the loop gain is very large due to the pure integrator in \(K_{F}\) and the finite gain of the plant (Figure fig:rotating_iff_bode_plot_effect_rot). The control system is thus canceling the spring forces which makes the suspended platform no able to hold the payload against centrifugal forces, hence the instability.
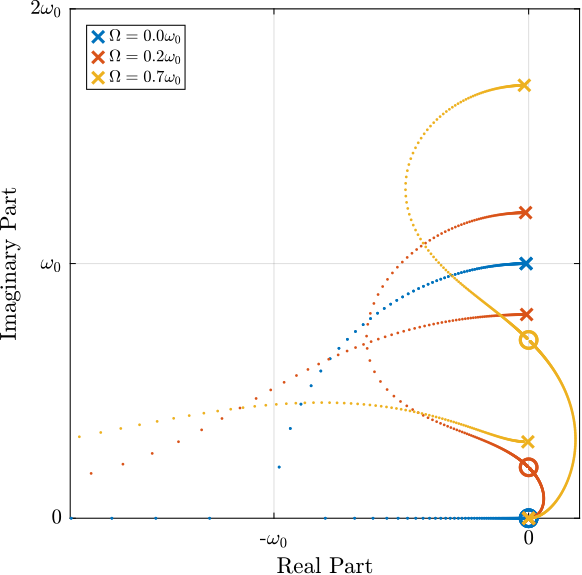
Figure 7: Root Locus for the Decentralized Integral Force Feedback controller. Several rotating speed are shown.
3. Integral Force Feedback with an High Pass Filter
As was explained in the previous section, the instability of the IFF controller applied on the rotating system comes in part from the high gain at low frequency caused by the pure integrators.
In order to limit the low frequency controller gain, an High Pass Filter (HPF) can be added to the controller as shown in equation eq:iff_lhf.
\begin{equation} \label{org519caa4} \boxed{K_{F}(s) = g \cdot \frac{1}{s} \cdot \underbrace{\frac{s/\omega_i}{1 + s/\omega_i}}_{\text{HPF}} = g \cdot \frac{1}{s + \omega_i}} \end{equation}This is equivalent as to slightly shifting the controller pole to the left along the real axis.
This modification of the IFF controller is typically done to avoid saturation associated with the pure integrator (Preumont, Dufour, and Malekian 1991; de Marneffe 2007). This is however not why this high pass filter is added here.
3.1. Modified Integral Force Feedback Controller
The Integral Force Feedback Controller is modified such that instead of using pure integrators, pseudo integrators (i.e. low pass filters) are used:
\begin{equation} K_{\text{IFF}}(s) = g\frac{1}{\omega_i + s} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \end{equation}where \(\omega_i\) characterize down to which frequency the signal is integrated.
Let’s arbitrary choose the following control parameters:
%% Modified IFF - parameters g = 2; % Controller gain wi = 0.1; % HPF Cut-Off frequency [rad/s] Kiff = (g/s)*eye(2); % Pure IFF Kiff_hpf = (g/(wi+s))*eye(2); % IFF with added HPF
The loop gains (\(K_F(s)\) times the direct dynamics \(f_u/F_u\)) with and without the added HPF are shown in Figure fig:rotating_iff_modified_loop_gain. The effect of the added HPF limits the low frequency gain to finite values as expected.

Figure 8: Loop gain for the IFF with pure integrator and modified IFF with added high pass filter (\(\Omega = 0.1\omega_0\))
The Root Locus plots for the decentralized IFF with and without the HPF are displayed in Figure fig:rotating_iff_root_locus_hpf. With the added HPF, the poles of the closed loop system are shown to be stable up to some value of the gain \(g_\text{max}\) given by equation eq:gmax_iff_hpf.
\begin{equation} \label{orga755fa2} \boxed{g_{\text{max}} = \omega_i \left( \frac{{\omega_0}^2}{\Omega^2} - 1 \right)} \end{equation}It is interesting to note that \(g_{\text{max}}\) also corresponds to the controller gain at which the low frequency loop gain (Figure fig:rotating_iff_modified_loop_gain) reaches one.
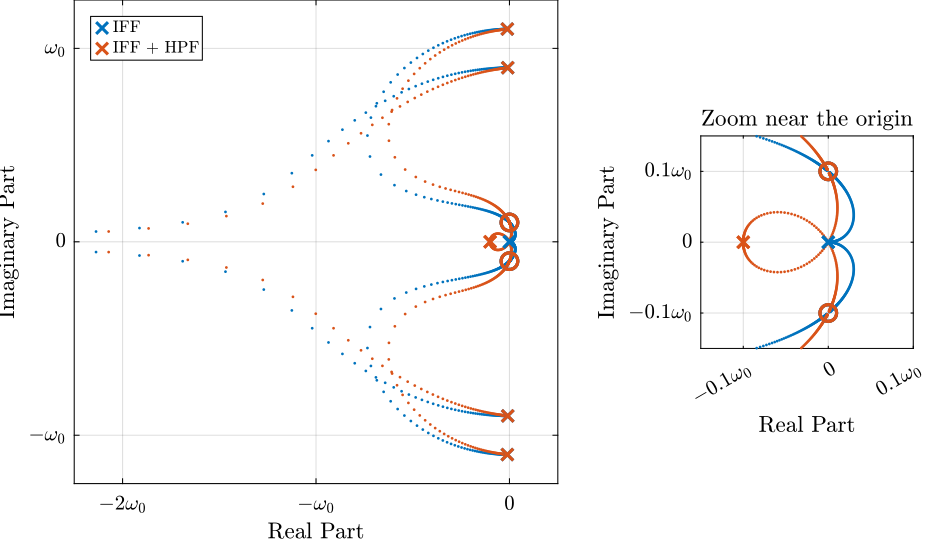
Figure 9: Root Locus for the initial IFF and the modified IFF
3.2. Optimal IFF with HPF parameters \(\omega_i\) and \(g\)
Two parameters can be tuned for the modified controller in equation eq:iff_lhf: the gain \(g\) and the pole’s location \(\omega_i\). The optimal values of \(\omega_i\) and \(g\) are here considered as the values for which the damping of all the closed-loop poles are simultaneously maximized.
In order to visualize how \(\omega_i\) does affect the attainable damping, the Root Locus plots for several \(\omega_i\) are displayed in Figure fig:rotating_root_locus_iff_modified_effect_wi. It is shown that even though small \(\omega_i\) seem to allow more damping to be added to the suspension modes, the control gain \(g\) may be limited to small values due to equation eq:gmax_iff_hpf.
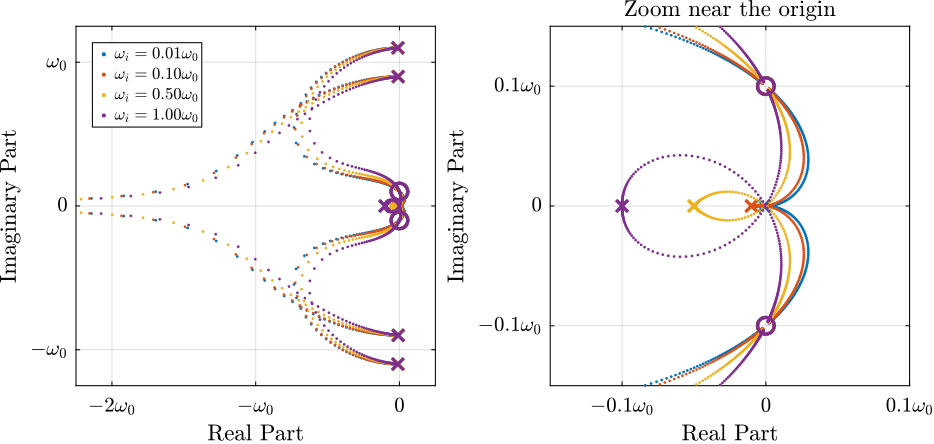
Figure 10: Root Locus for several high pass filter cut-off frequency
In order to study this trade off, the attainable closed-loop damping ratio \(\xi_{\text{cl}}\) is computed as a function of \(\omega_i/\omega_0\). The gain \(g_{\text{opt}}\) at which this maximum damping is obtained is also displayed and compared with the gain \(g_{\text{max}}\) at which the system becomes unstable (Figure fig:rotating_iff_hpf_optimal_gain).
Three regions can be observed:
- \(\omega_i/\omega_0 < 0.02\): the added damping is limited by the maximum allowed control gain \(g_{\text{max}}\)
- \(0.02 < \omega_i/\omega_0 < 0.2\): the attainable damping ratio is maximized and is reached for \(g \approx 2\)
- \(0.2 < \omega_i/\omega_0\): the added damping decreases as \(\omega_i/\omega_0\) increases.
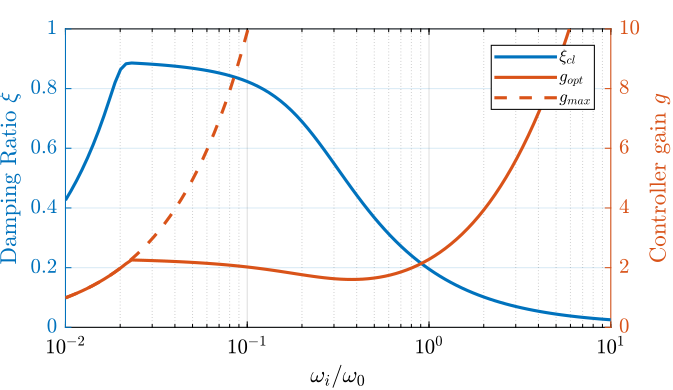
Figure 11: Attainable damping ratio \(\xi_\text{cl}\) as a function of \(\omega_i/\omega_0\). Corresponding control gain \(g_\text{opt}\) and \(g_\text{max}\) are also shown
3.3. Obtained Damped Plant
Let’s choose \(\omega_i = 0.1 \cdot \omega_0\) and compute the damped plant. The undamped and damped plants are compared in Figure fig:rotating_iff_hpf_damped_plant in blue and red respectively. A well damped plant is indeed obtained.
However, the magnitude of the coupling term (\(d_v/F_u\)) is larger then IFF is applied.
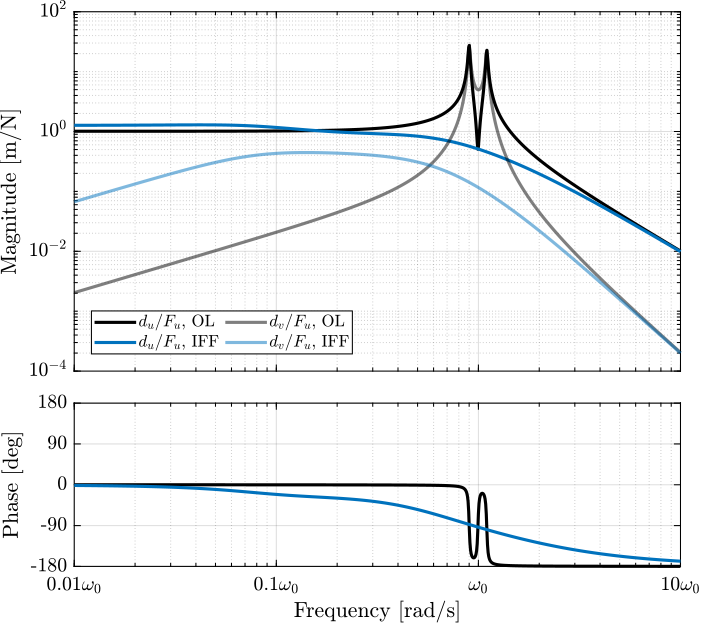
Figure 12: Damped plant with IFF and added HPF - Transfer function from \(F_u\) to \(d_u\), \(\omega_i = 0.1 \cdot \omega_0\), \(\Omega = 0.1 \cdot \omega_0\)
In order to study how \(\omega_i\) affects the coupling of the damped plant, the closed-loop plant is identified for several \(\omega_i\). The direct and coupling terms of the plants are shown in Figure fig:rotating_iff_hpf_damped_plant_effect_wi_coupling (left) and the ratio between the two (i.e. the coupling ratio) is shown in Figure fig:rotating_iff_hpf_damped_plant_effect_wi_coupling (right).
The coupling ratio is decreasing as \(\omega_i\) increases. There is therefore a trade-off between achievable damping and coupling ratio for the choice of \(\omega_i\). The same trade-off can be seen between achievable damping and loss of compliance at low frequency (see Figure fig:rotating_iff_hpf_effect_wi_compliance).

Figure 13: Effect of \(\omega_i\) on the damped plant coupling
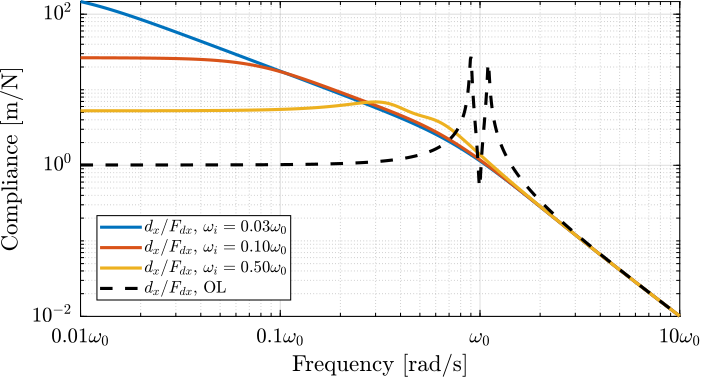
Figure 14: Effect of \(\omega_i\) on the obtained compliance
4. IFF with a stiffness in parallel with the force sensor
In this section it is proposed to add springs in parallel with the force sensors to counteract the negative stiffness induced by the gyroscopic effects.
Such springs are schematically shown in Figure fig:rotating_3dof_model_schematic_iff_parallel_springs where \(k_a\) is the stiffness of the actuator and \(k_p\) the added stiffness in parallel with the actuator and force sensor.
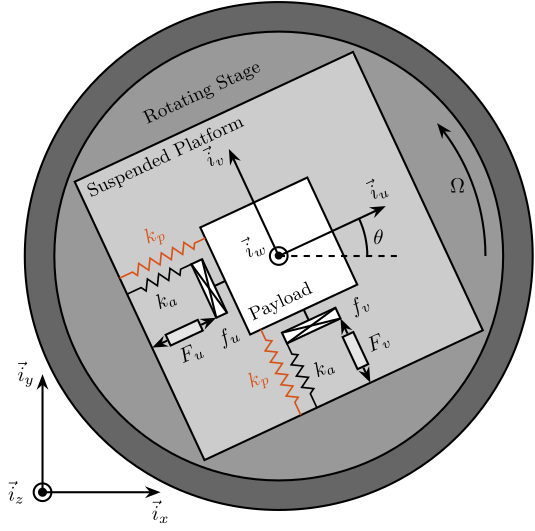
Figure 15: Studied system with additional springs in parallel with the actuators and force sensors (shown in red)
4.1. Equations
The forces measured by the two force sensors represented in Figure fig:rotating_3dof_model_schematic_iff_parallel_springs are described by Eq. eq:measured_force_kp.
\begin{equation} \label{org045d174} \begin{bmatrix} f_{u} \\ f_{v} \end{bmatrix} = \begin{bmatrix} F_u \\ F_v \end{bmatrix} - (c s + k_a) \begin{bmatrix} d_u \\ d_v \end{bmatrix} \end{equation}In order to keep the overall stiffness \(k = k_a + k_p\) constant, thus not modifying the open-loop poles as \(k_p\) is changed, a scalar parameter \(\alpha\) (\(0 \le \alpha < 1\)) is defined to describe the fraction of the total stiffness in parallel with the actuator and force sensor as in Eq. eq:kp_alpha.
\begin{equation} \label{org35866b1} k_p = \alpha k, \quad k_a = (1 - \alpha) k \end{equation}After the equations of motion derived and transformed in the Laplace domain, the transfer function matrix \(\mathbf{G}_k\) in Eq. eq:Gk_mimo_tf is computed. Its elements are shown in Eq. eq:Gk_diag and eq:Gk_off_diag.
\begin{equation} \label{org34e38f3} \begin{bmatrix} f_u \\ f_v \end{bmatrix} = \mathbf{G}_k \begin{bmatrix} F_u \\ F_v \end{bmatrix} \end{equation} \begin{subequations} \label{org6952558} \begin{align} \mathbf{G}_{k}(1,1) &= \mathbf{G}_{k}(2,2) = \frac{\big( \frac{s^2}{{\omega_0}^2} - \frac{\Omega^2}{{\omega_0}^2} + \alpha \big) \big( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \big) + \big( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \big)^2}{\big( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \big)^2 + \big( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \big)^2} \label{eq:Gk_diag} \\ \mathbf{G}_{k}(1,2) &= -\mathbf{G}_{k}(2,1) = \frac{- \left( 2 \xi \frac{s}{\omega_0} + 1 - \alpha \right) \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)}{\left( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right)^2 + \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)^2} \label{eq:Gk_off_diag} \end{align} \end{subequations}Comparing \(\mathbf{G}_k\) in Eq. eq:Gk with \(\mathbf{G}_f\) in Eq. eq:Gf shows that while the poles of the system are kept the same, the zeros of the diagonal terms have changed. The two real zeros \(z_r\) in Eq. eq:iff_zero_real that were inducing a non-minimum phase behavior are transformed into two complex conjugate zeros if the condition in Eq. eq:kp_cond_cc_zeros holds.
\begin{equation} \label{org21fe602} \boxed{\alpha > \frac{\Omega^2}{{\omega_0}^2} \quad \Leftrightarrow \quad k_p > m \Omega^2} \end{equation}Thus, if the added parallel stiffness \(k_p\) is higher than the negative stiffness induced by centrifugal forces \(m \Omega^2\), the dynamics from actuator to its collocated force sensor will show minimum phase behavior.
4.2. Effect of the parallel stiffness on the IFF plant
The IFF plant (transfer function from \([F_u, F_v]\) to \([f_u, f_v]\)) is identified in three different cases:
- without parallel stiffness \(k_p = 0\)
- with a small parallel stiffness \(k_p < m \Omega^2\)
- with a large parallel stiffness \(k_p > m \Omega^2\)
The Bode plots of the obtained dynamics are shown in Figure fig:rotating_iff_effect_kp. One can see that for \(k_p > m \Omega^2\), the two real zeros with \(k_p < m \Omega^2\) are transformed into two complex conjugate zeros and the systems shows alternating complex conjugate poles and zeros.
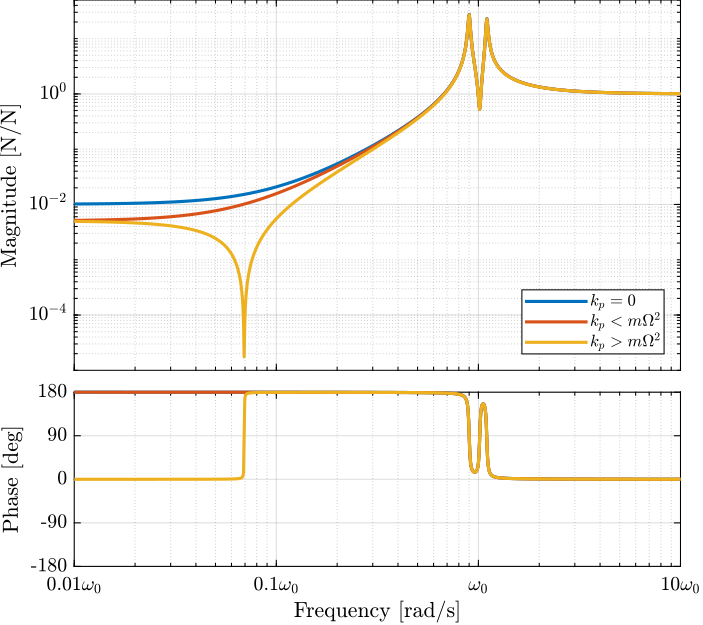
Figure 16: Effect of the parallel stiffness on the IFF plant: Bode plot of \(G_{k}(1,1) = f_u/F_u\) without parallel spring, with parallel spring stiffness \(k_p < m \Omega^2\) and \(k_p > m \Omega^2\), \(\Omega = 0.1 \omega_0\)
Figure fig:rotating_iff_kp_root_locus shows the Root Locus plots for \(k_p = 0\), \(k_p < m \Omega^2\) and \(k_p > m \Omega^2\) when \(K_F\) is a pure integrator as in Eq. eq:Kf_pure_int. It is shown that if the added stiffness is higher than the maximum negative stiffness, the poles of the closed-loop system are bounded on the (stable) left half-plane, and hence the unconditional stability of IFF is recovered.
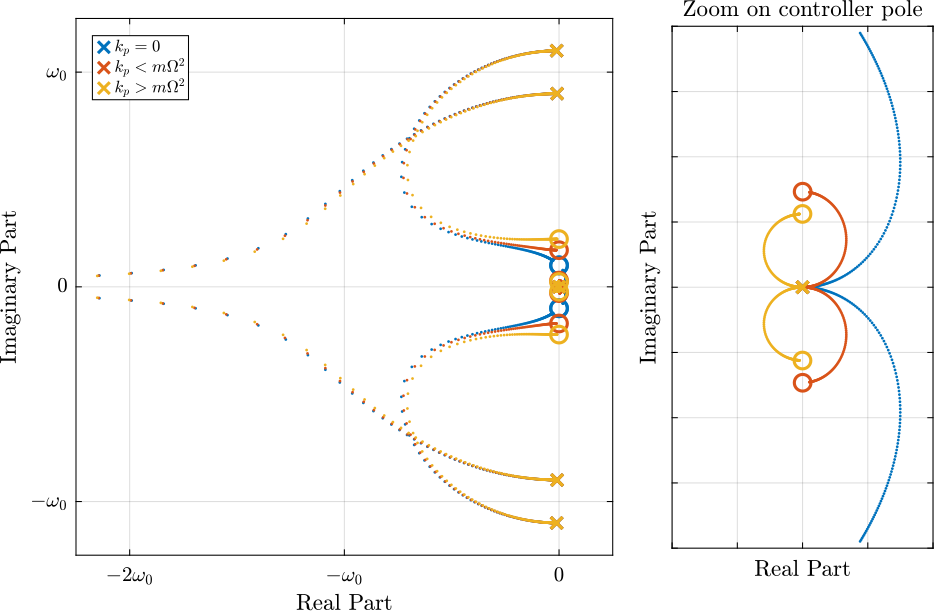
Figure 17: Root Locus for IFF without parallel spring, with small parallel spring and with large parallel spring
4.3. Effect of \(k_p\) on the attainable damping
Even though the parallel stiffness \(k_p\) has no impact on the open-loop poles (as the overall stiffness \(k\) is kept constant), it has a large impact on the transmission zeros. Moreover, as the attainable damping is generally proportional to the distance between poles and zeros (Preumont 2018), the parallel stiffness \(k_p\) is foreseen to have some impact on the attainable damping.
To study this effect, Root Locus plots for several parallel stiffnesses \(k_p > m \Omega^2\) are shown in Figure fig:rotating_iff_kp_root_locus_effect_kp. The frequencies of the transmission zeros of the system are increasing with an increase of the parallel stiffness \(k_p\) (thus getting closer to the poles) and the associated attainable damping is reduced.
Therefore, even though the parallel stiffness \(k_p\) should be larger than \(m \Omega^2\) for stability reasons, it should not be taken too large as this would limit the attainable damping.

Figure 18: Root Locus: Effect of the parallel stiffness on the attainable damping, \(\Omega = 0.1 \omega_0\)
This is confirmed by the Figure fig:rotating_iff_kp_optimal_gain where the attainable closed-loop damping ratio \(\xi_{\text{cl}}\) and the associated optimal control gain \(g_\text{opt}\) are computed as a function of the parallel stiffness.

Figure 19: Attainable damping ratio \(\xi_\text{cl}\) as a function of the parallel stiffness \(k_p\). Corresponding control gain \(g_\text{opt}\) is also shown. Values for \(k_p < m\Omega^2\) are not shown as the system is unstable.
4.4. Damped plant
Let’s choose a parallel stiffness equal to \(k_p = 2 m \Omega^2\) and compute the damped plant. The damped and undamped transfer functions from \(F_u\) to \(d_u\) are compared in Figure fig:rotating_iff_kp_damped_plant.
Even though the two resonances are well damped, the IFF changes the low frequency behavior of the plant which is usually not wanted. This is due to the fact that “pure” integrators are used, and that the low frequency loop gains becomes large below some frequency.

Figure 20: Damped plant with IFF - Transfer function from \(F_u\) to \(d_u\)
In order to lower the low frequency gain, an high pass filter is added to the IFF controller (which is equivalent as shifting the controller pole to the left in the complex plane):
\begin{equation} K_{\text{IFF}}(s) = g\frac{1}{\omega_i + s} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \end{equation}Let’s see how the high pass filter impacts the attainable damping. The controller gain \(g\) is kept constant while \(\omega_i\) is changed, and the minimum damping ratio of the damped plant is computed. The obtained damping ratio as a function of \(\omega_i/\omega_0\) (where \(\omega_0\) is the resonance of the system without rotation) is shown in Figure fig:rotating_iff_kp_added_hpf_effect_damping.
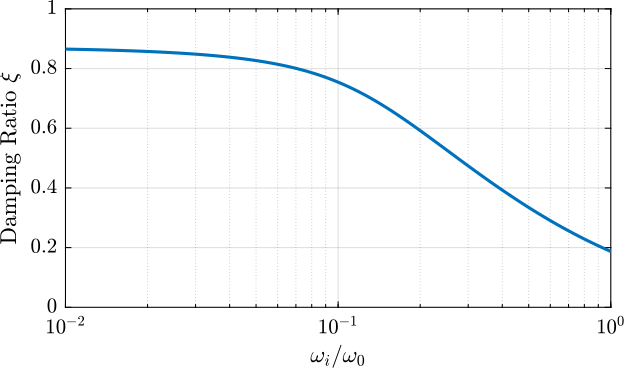
Figure 21: Effect of the high pass filter cut-off frequency on the obtained damping
Let’s choose \(\omega_i = 0.1 \cdot \omega_0\) and compute the damped plant again. The Bode plots of the undamped, damped with “pure” IFF, and with added high pass filters are shown in Figure fig:rotating_iff_kp_added_hpf_damped_plant. The added high pass filter gives almost the same damping properties while giving acceptable low frequency behavior.
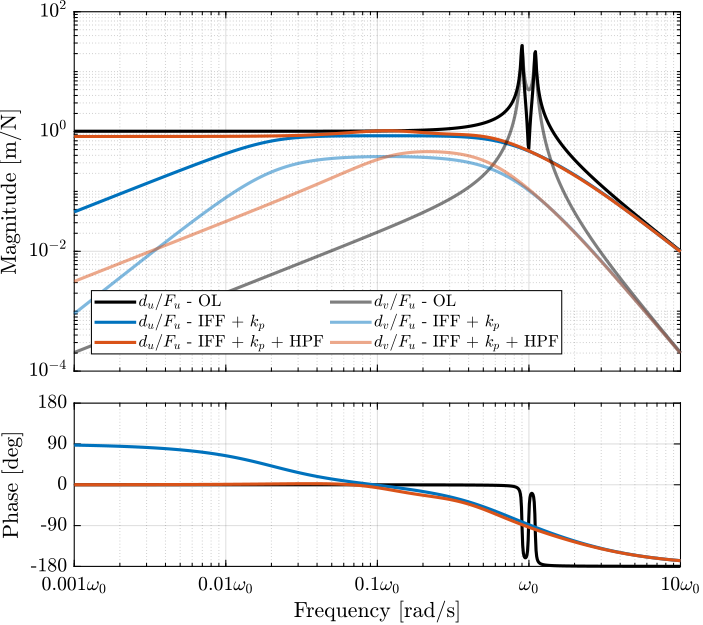
Figure 22: Damped plant with IFF - Transfer function from \(F_u\) to \(d_u\)
5. Relative Damping Control
In order to apply a “relative damping control strategy”, relative motion sensors are added in parallel with the actuators as shown in Figure fig:rotating_3dof_model_schematic_rdc.
Two controllers \(K_d\) are used to fed back the relative motion to the actuator. \(K_d\) is a derivator:
\begin{equation} K_d(s) = s \end{equation}To be implemented in practice, it is usually replaced by a an high pass filter:
\begin{equation} K_d(s) = \frac{s}{s + \omega_d} \end{equation}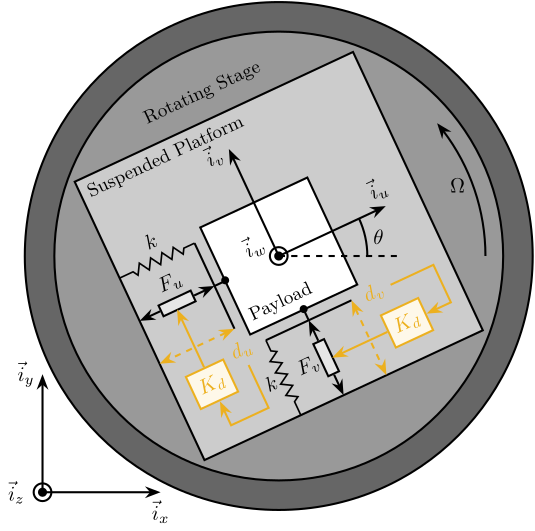
Figure 23: System with relative motion sensor and decentralized “relative damping control” applied.
5.1. Equations of motion
Let’s note \(\bm{G}_d\) the transfer function between actuator forces and measured relative motion in parallel with the actuators:
\begin{equation} \begin{bmatrix} d_u \\ d_v \end{bmatrix} = \mathbf{G}_d \begin{bmatrix} F_u \\ F_v \end{bmatrix} \end{equation}With:
\begin{subequations} \begin{align} \mathbf{G}_{d}(1,1) &= \mathbf{G}_{d}(2,2) = \frac{\frac{1}{k} \left( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right)}{\left( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right)^2 + \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)^2} \\ \mathbf{G}_{d}(1,2) &= -\mathbf{G}_{d}(2,1) = \frac{\frac{1}{k} \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)}{\left( \frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1 - \frac{{\Omega}^2}{{\omega_0}^2} \right)^2 + \left( 2 \frac{\Omega}{\omega_0} \frac{s}{\omega_0} \right)^2} \end{align} \end{subequations}Neglecting the damping for simplicity (\(\xi \ll 1\)), the direct terms have two complex conjugate zeros:
\begin{equation} z = \pm j \sqrt{\omega_0^2 - \omega^2} \end{equation}Which are between the two pairs of complex conjugate poles at:
\begin{align} p_1 &= \pm j (\omega_0 - \omega) \\ p_2 &= \pm j (\omega_0 + \omega) \end{align}Therefore, for \(\Omega < \sqrt{k/m}\) (i.e. stable system), the transfer functions for Relative Damping Control have alternating complex conjugate poles and zeros.
5.2. Decentralized Relative Damping Control
The transfer functions from \([F_u,\ F_v]\) to \([d_u,\ d_v]\) is identified and shown in Figure fig:rotating_rdc_plant_effect_rot for several rotating velocities.
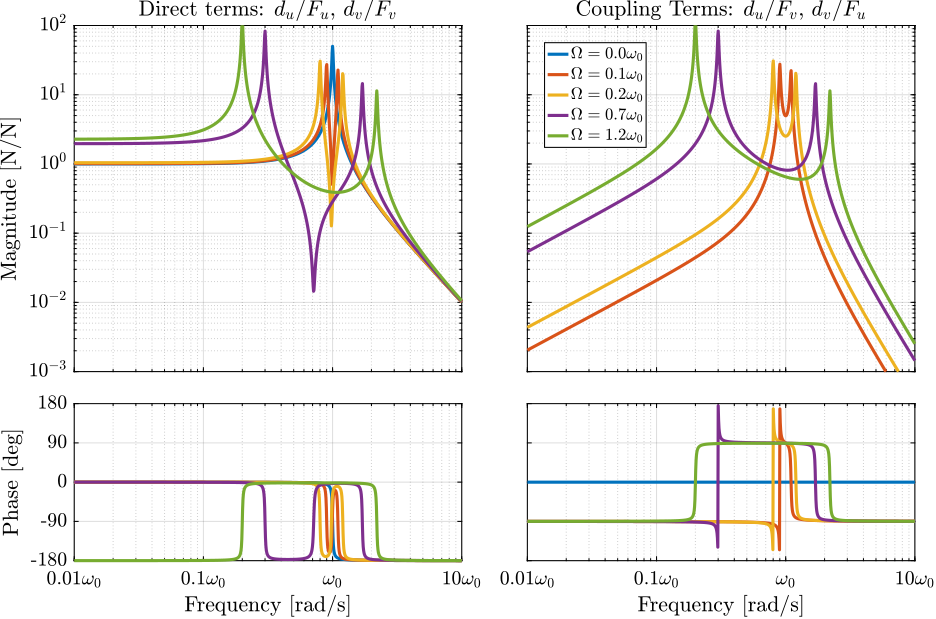
Figure 24: Bode plot of the direct and coupling term for the “relative damping control” plant - Effect of rotation
In order to see if large damping can be added with Relative Damping Control, the root locus is computed (Figure fig:rotating_rdc_root_locus). The closed-loop system is unconditionally stable and the poles can be damped as much as wanted.

Figure 25: Root Locus for Relative Damping Control
5.3. Damped Plant
Let’s select a reasonable “Relative Damping Control” gain, and compute the closed-loop damped system. The open-loop and damped plants are compared in Figure fig:rotating_rdc_damped_plant.
The rotating aspect does not add any complexity for the use of Relative Damping Control. It does not increase the low frequency coupling as compared to Integral Force Feedback.
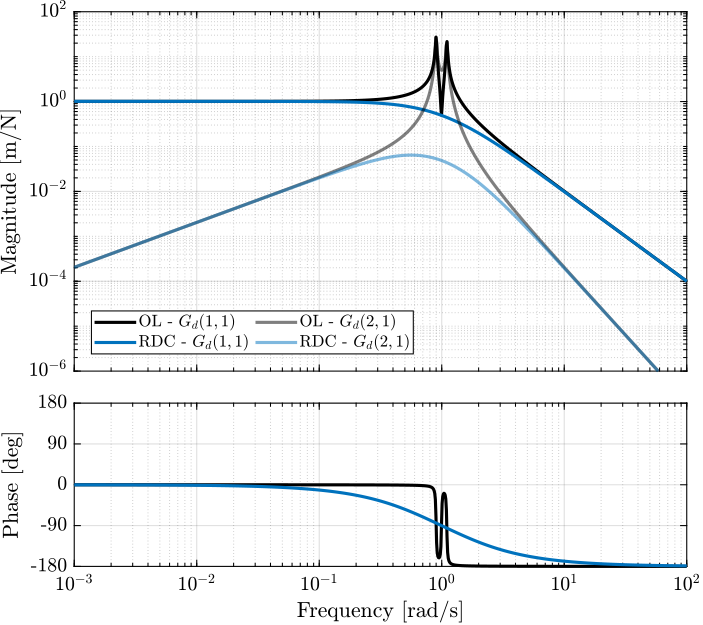
Figure 26: Damped plant using Relative Damping Control
6. Comparison of Active Damping Techniques
These two proposed IFF modifications as well as relative damping control are now compared in terms of added damping and closed-loop behavior.
For the following comparisons, the cut-off frequency for the added HPF is set to \(\omega_i = 0.1 \omega_0\) and the stiffness of the parallel springs is set to \(k_p = 5 m \Omega^2\) (corresponding to \(\alpha = 0.05\)). These values are chosen based on previous discussion about optimal parameters.
6.1. Root Locus
Figure fig:rotating_comp_techniques_root_locus shows the Root Locus plots for the two proposed IFF modifications as well as for relative damping control. While the two pairs of complex conjugate open-loop poles are identical for both IFF modifications, the transmission zeros are not. This means that the closed-loop behavior of both systems will differ when large control gains are used.
One can observe that the closed loop poles corresponding to the system with added springs (in red) are bounded to the left half plane implying unconditional stability. This is not the case for the system where the controller is augmented with an HPF (in blue).
It is interesting to note that the maximum added damping is very similar for both techniques.
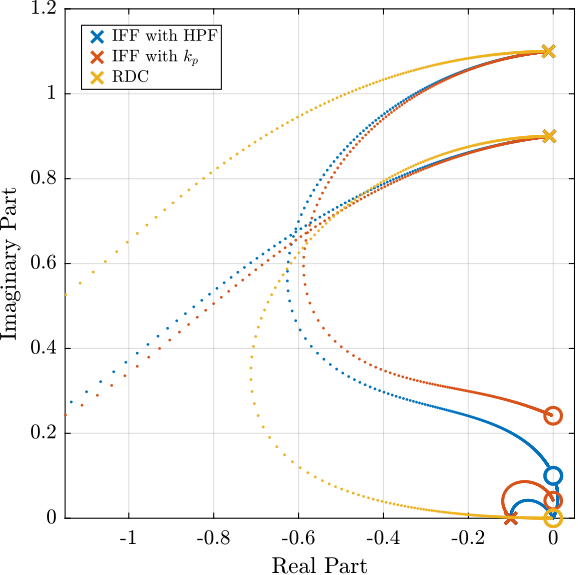
Figure 27: Comparison of active damping techniques for rotating platform - Root Locus
6.2. Obtained Damped Plant
The actively damped plants are computed for the three techniques and compared in Figure fig:rotating_comp_techniques_dampled_plants.
It is shown that while the diagonal (direct) terms of the damped plants are similar for the three active damping techniques, of off-diagonal (coupling) terms are not. Integral Force Feedback strategy is adding some coupling at low frequency which may negatively impact the positioning performances.

Figure 28: Comparison of the damped plants obtained with the three active damping techniques
6.3. Transmissibility And Compliance
The proposed active damping techniques are now compared in terms of closed-loop transmissibility and compliance.
The transmissibility is here defined as the transfer function from a displacement of the rotating stage along \(\vec{i}_x\) to the displacement of the payload along the same direction. It is used to characterize how much vibration is transmitted through the suspended platform to the payload.
The compliance describes the displacement response of the payload to external forces applied to it. This is a useful metric when disturbances are directly applied to the payload. It is here defined as the transfer function from external forces applied on the payload along \(\vec{i}_x\) to the displacement of the payload along the same direction.
Very similar results are obtained for the two proposed IFF modifications in terms of transmissibility and compliance (Figure fig:rotating_comp_techniques_transmissibility_compliance).
Using IFF degrades the compliance at low frequency while using relative damping control degrades the transmissibility at high frequency. This is very well known characteristics of these common active damping techniques that holds when applied to rotating platforms.

Figure 29: Comparison of the obtained transmissibilty and compliance for the three tested active damping techniques
7. Rotating Nano-Hexapod
The current analysis is now applied on a model representing the rotating nano-hexapod.
Three nano-hexapod stiffnesses are tested: \(k_n = \SI{0.01}{\N\per\mu\m}\), \(k_n = \SI{1}{\N\per\mu\m}\) and \(k_n = \SI{100}{\N\per\mu\m}\).
Only the maximum rotating velocity is considered (\(\Omega = \SI{60}{rpm}\)) with the light sample (\(m_s = \SI{1}{kg}\)) as this is the worst identified case scenario.
7.1. Nano-Active-Stabilization-System - Plant Dynamics
For the NASS, the maximum rotating velocity is \(\Omega = \SI[parse-numbers=false]{2\pi}{\radian\per\s}\) for a suspended mass on top of the nano-hexapod’s actuators equal to \(m_n + m_s = \SI{16}{\kilo\gram}\). The parallel stiffness corresponding to the centrifugal forces is \(m \Omega^2 \approx \SI{0.6}{\newton\per\mm}\).
The transfer functions from nano-hexapod actuator force \(F_u\) to the displacement of the nano-hexapod in the same direction \(d_u\) as well as in the orthogonal direction \(d_v\) (coupling) are shown in Figure fig:rotating_nano_hexapod_dynamics for all three considered nano-hexapod stiffnesses.
It is shown that the rotation has the largest effect on the soft nano-hexapod:
- larger coupling (the ratio of the coupling term to the direct term is larger for the sort nano-hexapod)
- larger shift of poles as a function of the rotating velocity
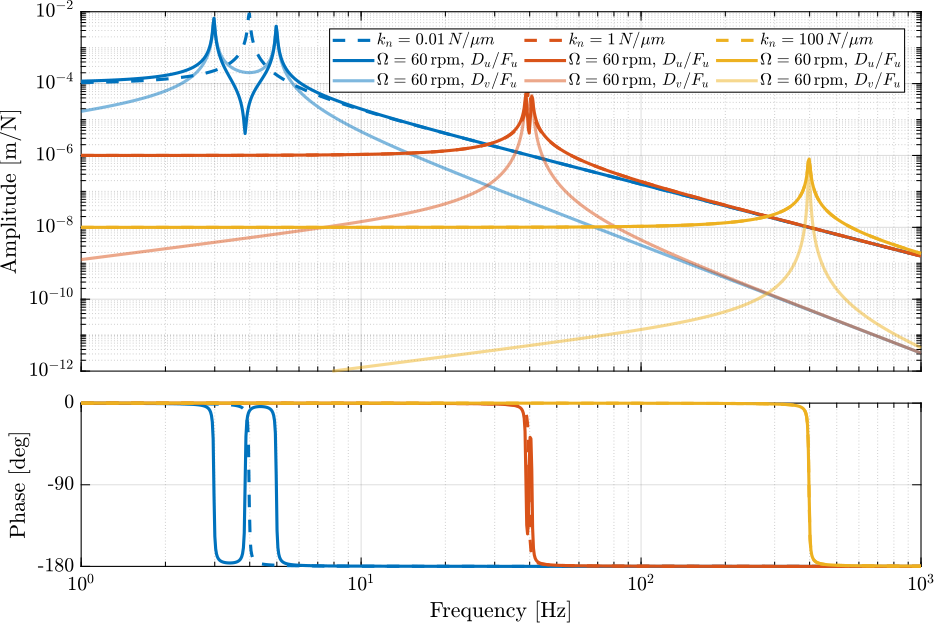
Figure 30: Effect of rotation on the nano-hexapod dynamics - Dashed lines are the plants without rotation, solid lines are plants at maximum rotating velocity, and shaded lines are coupling terms at maximum rotating velocity
7.2. Optimal IFF with High Pass Filter
Let’s apply Integral Force Feedback with an added High Pass Filter to the three nano-hexapods.
First, let’s find the parameters of the IFF controller that yield best simultaneous damping. The results are shown in Figure fig:rotating_iff_hpf_nass_optimal_gain. The added damping for the soft nano-hexapod is quite low and is limited by the maximum usable gain.
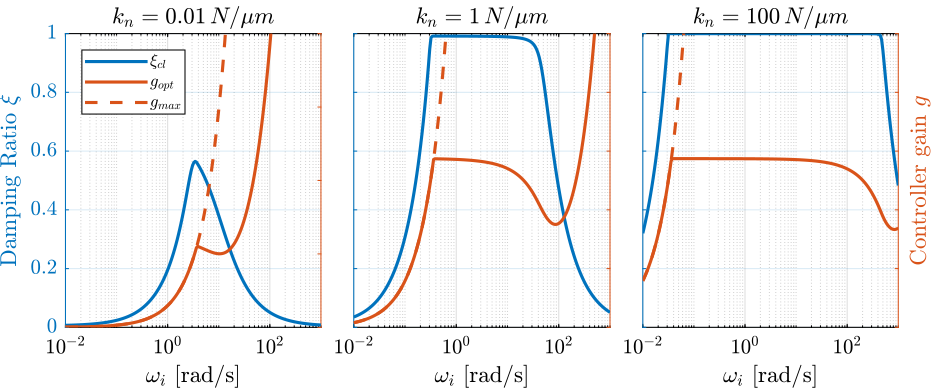
Figure 31: Optimal high pass filter cut-off frequency \(\omega_i\) that yields maximum simultaneous damping
The IFF parameters are chosen as follow:
- for \(k_n = \SI{0.01}{\N\per\mu\m}\): \(\omega_i\) is chosen such that the maximum damping is achieved while the gain is less than half of the maximum gain at which the system is unstable. This is done to have some control robustness.
- for \(k_n = \SI{1}{\N\per\mu\m}\) and \(k_n = \SI{100}{\N\per\mu\m}\): the largest \(\omega_i\) is chosen such that obtained damping is \(\SI{95}{\percent}\) of the maximum achievable damping. Large \(\omega_i\) is chosen here to limit the loss of compliance and the increase of coupling at low frequency as was shown in Section sec:rotating_iff_pseudo_int.
The obtained IFF parameters and the achievable damping are summarized in Table tab:iff_hpf_opt_iff_hpf_params_nass.
| \(\omega_i\) | \(g\) | \(\xi\) | |
|---|---|---|---|
| \(k_n = 0.01\,N/\mu m\) | 7.32 | 51.13 | 0.45 |
| \(k_n = 1\,N/\mu m\) | 39.17 | 426.95 | 0.93 |
| \(k_n = 100\,N/\mu m\) | 499.45 | 3774.63 | 0.94 |
The Root Locus for all three nano-hexapods are shown in Figure fig:rotating_root_locus_iff_hpf_nass with included optimal chosen gains.
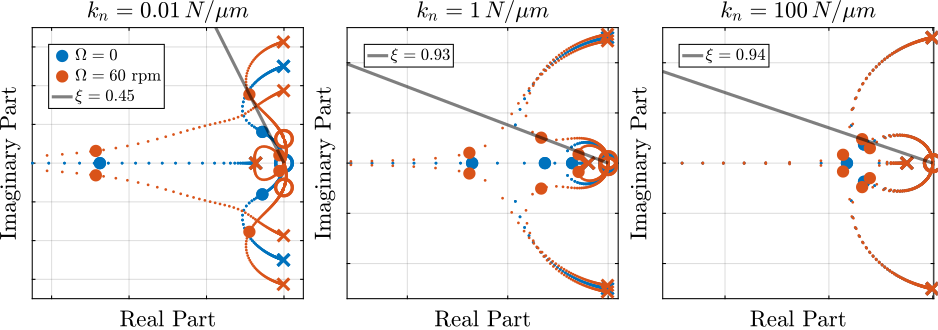
Figure 32: Root Locus for modified IFF with high pass filter. Optimal \(\omega_i\) is used. The three nano-hexapod stiffnesses are compared. The grey line indicates the minimum damping obtained with the optimal chosen control parameters.
7.3. Optimal IFF with Parallel Stiffness
For each considered nano-hexapod stiffness, the parallel stiffness \(k_p\) is varied from \(k_{p,\text{min}} = m\Omega^2\) (the minimum stiffness to have unconditional stability) to \(k_{p,\text{max}} = k_n\) (the total nano-hexapod stiffness). In order to keep the overall stiffness constant, the actuator stiffness \(k_a\) is decreased when \(k_p\) is increased:
\begin{equation} k_a = k_n - k_p \end{equation}With \(k_n\) the total nano-hexapod stiffness.
An high pass filter is also added to limit the low frequency gain. The cut-off frequency \(\omega_i\) is chosen to be one tenth of the system resonance:
\begin{equation} \omega_i = \omega_0/10 \end{equation}The achievable maximum simultaneous damping of all the modes is computed as a function of the parallel stiffnesses. The comparison for the nano-hexapod stiffnesses is done in Figure fig:rotating_iff_kp_nass_optimal_gain. It is shown that the soft nano-hexapod cannot yield good damping. For the two stiff options, the achievable damping starts to significantly decrease when the parallel stiffness is one tenth of the total stiffness \(k_p = k_n/10\).
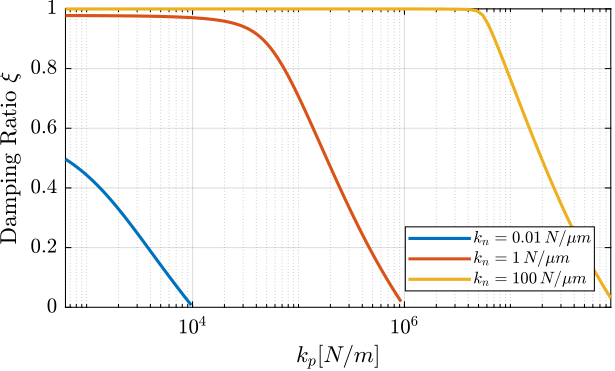
Figure 33: Maximum achievable simultaneous damping with IFF as a function of the parallel stiffness for all three nano-hexapod stiffnesses
Let’s choose \(k_p = \SI{e3}{\newton\per\m}\), \(k_p = \SI{e4}{\newton\per\m}\) and \(k_p = \SI{e6}{\newton\per\m}\) for the three considered nano-hexapods respectively based on Figure fig:rotating_iff_kp_nass_optimal_gain.
The corresponding optimal controller gains are shown in Table tab:iff_kp_opt_iff_kp_params_nass.
| \(g\) | \(\xi_{\text{opt}}\) | |
|---|---|---|
| \(k_n = 0.01\,N/\mu m\) | 47.9 | 0.44 |
| \(k_n = 1\,N/\mu m\) | 465.57 | 0.97 |
| \(k_n = 100\,N/\mu m\) | 4624.25 | 1.0 |
The root locus for the three nano-hexapod with parallel stiffnesses are shown in Figure fig:rotating_root_locus_iff_kp_nass.
Similarly to what was found with the IFF and added High Pass Filter:
- the stiff nano-hexapod is less affected by the rotation than the soft one
- the achievable damping is much larger with the stiff nano-hexapods
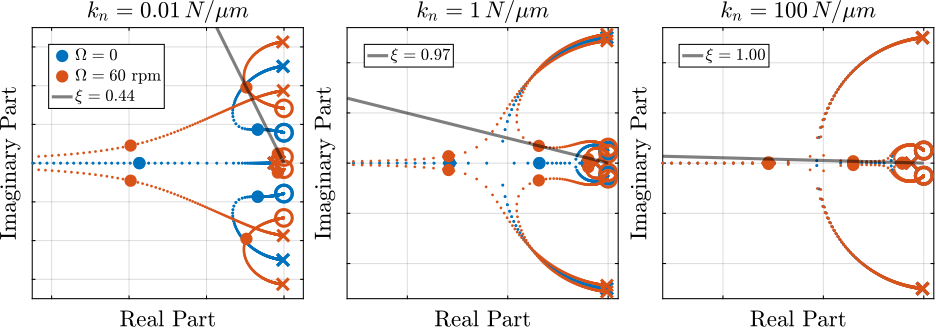
Figure 34: Root Locus for optimal parameters (IFF + \(k_p\) strategy) - Comparison of attainable damping with the three nano-hexapod stiffnesses
7.4. Optimal Relative Motion Control
For each considered nano-hexapod stiffness, relative damping control is applied and the achievable damping ratio as a function of the controller gain is shown in Figure fig:rotating_rdc_optimal_gain.

Figure 35: Achievable simultaneous damping with “Relative Damping Control” as a function of the controller gain for all three nano-hexapod stiffnesses
The gain is chosen is chosen such that 99% of modal damping is obtained. The root locus for all three nano-hexapod stiffnesses are shown in Figure fig:rotating_root_locus_rdc_nass.
Relative damping control is much less impacted by gyroscopic effects. It can be easily applied on the nano-hexapod with and without rotation without much differences.
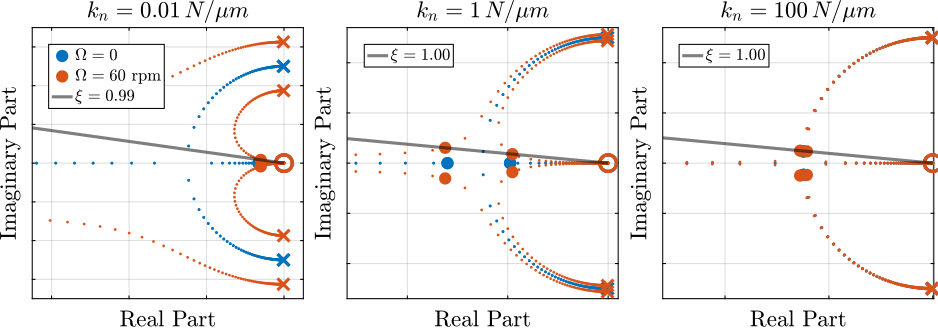
Figure 36: Root Locus for optimal parameters - Comparison of attainable damping with the soft and moderately stiff nano-hexapods
7.5. Comparison of the obtained damped plants
Let’s now compare the obtained damped plants for the three active damping techniques applied on the three nano-hexapod stiffnesses (Figure fig:rotating_nass_damped_plant_comp).
Similarly to what was concluded in previous analysis:
- IFF adds coupling below the resonance frequency as compared to the open-loop and RDC cases
- Add three methods are yielding good damping, except for IFF applied on the soft nano-hexapod where things are more complicated
- Coupling is smaller for stiff nano-hexapods
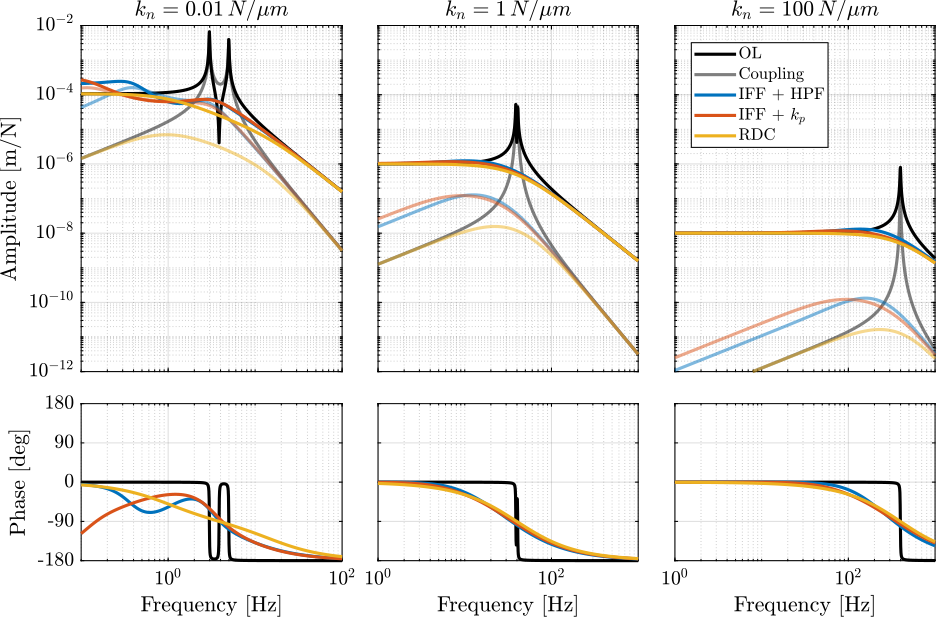
Figure 37: Comparison of the damped plants (direct and coupling terms) for the three proposed active damping techniques (IFF with HPF, IFF with \(k_p\) and RDC) applied on the three nano-hexapod stiffnesses. \(\Omega = 60\,\text{rmp}\) and \(m_n + m_s = \SI{16}{\kg}\).
8. Nano-Active-Stabilization-System with rotation
Up until now, the model used consisted of an infinitely stiff vertical rotating stage with a X-Y suspended stage.
While quite simplistic, this allowed to study the effects of rotation and the associated limitations when active damping is to be applied.
In this section, the limited compliance of the micro-station is taken into account as well as the rotation of the spindle.
8.1. NASS model
In order to be a bit closer to the NASS application, the 2DoF nano-hexapod (modelled as shown in Figure fig:rotating_3dof_model_schematic) is now located on top of a model of the micro-station including (see Figure fig:rotating_nass_model for a 3D view):
- the floor whose motion is imposed
- a 2DoF granite (\(k_{g,x} = k_{g,y} = \SI{950}{\N\per\mu\m}\), \(m_g = \SI{2500}{\kg}\))
- a 2DoF \(T_y\) stage (\(k_{t,x} = k_{t,y} = \SI{520}{\N\per\mu\m}\), \(m_g = \SI{600}{\kg}\))
- a spindle (vertical rotation) stage whose rotation is imposed (\(m_s = \SI{600}{\kg}\))
- a 2DoF micro-hexapod (\(k_{h,x} = k_{h,y} = \SI{61}{\N\per\mu\m}\), \(m_g = \SI{15}{\kg}\))
A payload is rigidly fixed to the nano-hexapod and the \(x,y\) motion of the payload is measured with respect to the granite.
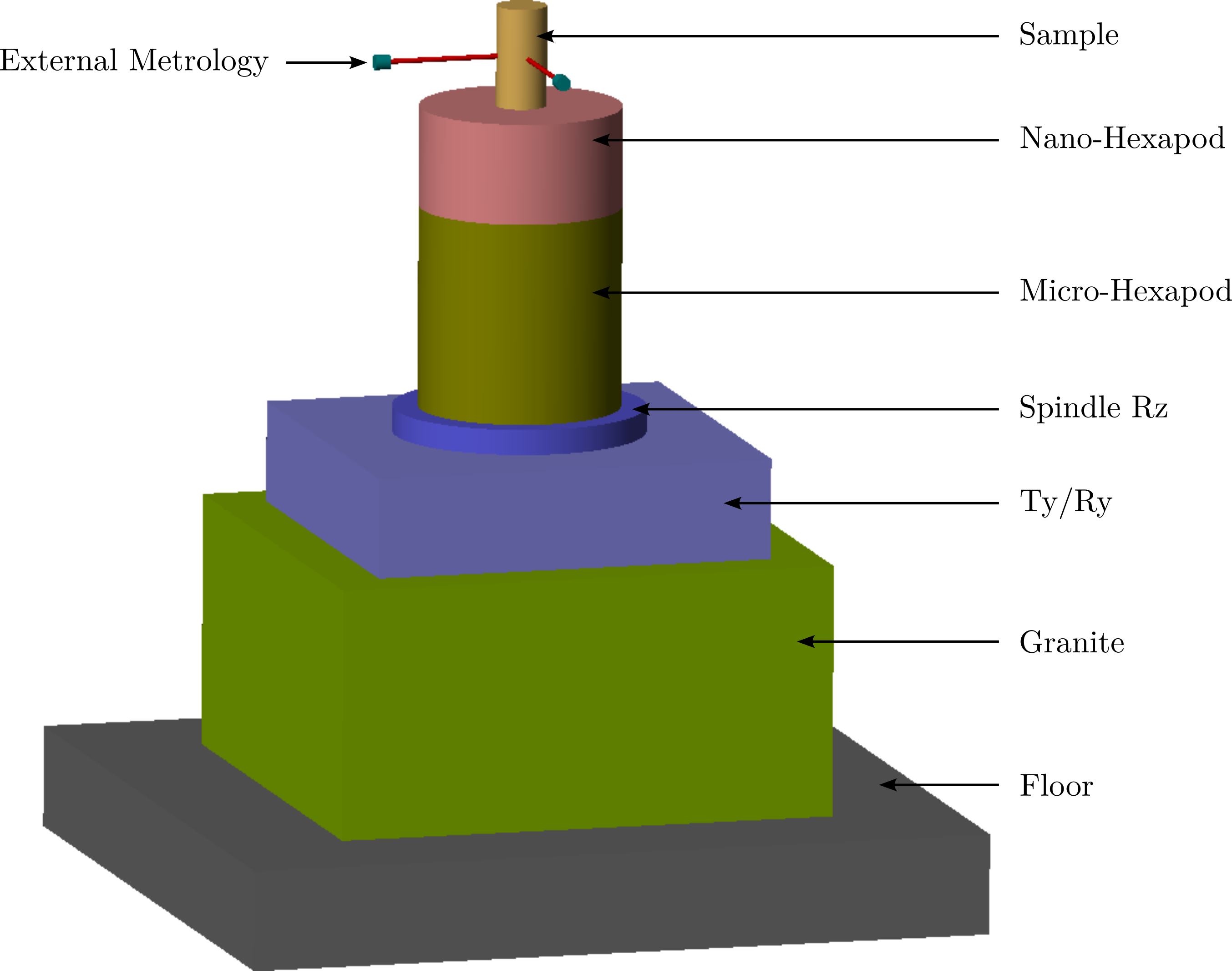
Figure 38: 3D view of the Nano-Active-Stabilization-System model.
8.2. System dynamics
The dynamics of the undamped and damped plants are identified. The active damping parameters used are the optimal ones previously identified (i.e. for the rotating nano-hexapod fixed on a rigid platform).
The undamped and damped plants are shown in Figure fig:rotating_nass_plant_comp_stiffness. Three nano-hexapod velocities are shown (from left to right): \(k_n = \SI{0.01}{\N\per\mu\m}\), \(k_n = \SI{1}{\N\per\mu\m}\) and \(k_n = \SI{100}{\N\per\mu\m}\). The direct terms are shown by the solid curves while the coupling terms are shown by the shaded ones.
It can be observed on Figure fig:rotating_nass_plant_comp_stiffness that:
- Coupling (ratio between the off-diagonal and direct terms) is larger for the soft nano-hexapod
- Damping added by the three proposed techniques is quite high and the obtained plant is rather easy to control
- There is some coupling between nano-hexapod and micro-station dynamics for the stiff nano-hexapod (mode at 200Hz)
- The two proposed IFF modification yields similar results
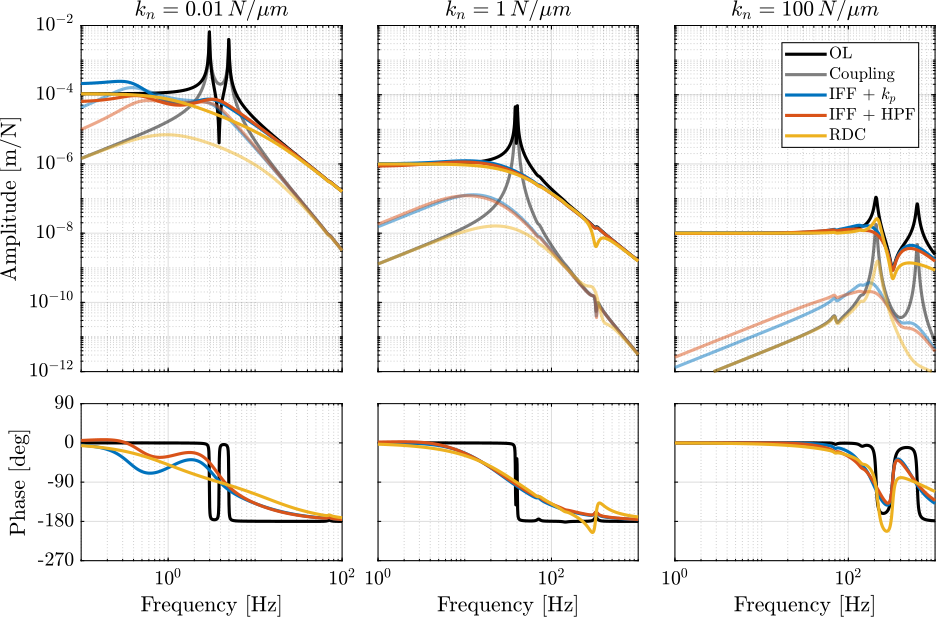
Figure 39: Bode plot of the transfer function from nano-hexapod actuator to measured motion by the external metrology
To confirm that the coupling is smaller when the stiffness of the nano-hexapod is increase, the coupling ratio for the three nano-hexapod stiffnesses are shown in Figure fig:rotating_nass_plant_coupling_comp.
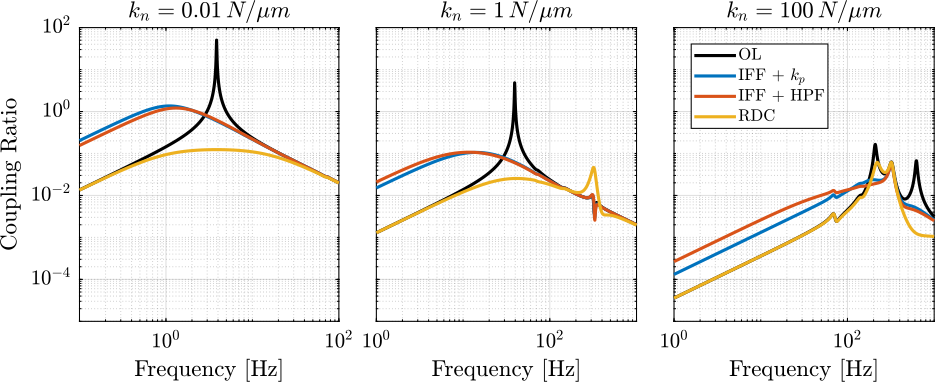
Figure 40: Coupling ratio for the proposed active damping techniques evaluated for the three nano-hexapod stiffnesses
8.3. Effect of disturbances
The effect of three disturbances are considered:
- Floor motion (Figure fig:rotating_nass_effect_floor_motion)
- Micro-Station vibrations (Figure fig:rotating_nass_effect_stage_vibration)
- Direct force applied on the payload (Figure fig:rotating_nass_effect_direct_forces)
Conclusions are similar than with the uniaxial (non-rotating) model:
- Regarding the effect of floor motion and forces applied on the payload:
- The stiffer, the better (magnitudes are lower for the right curves, Figures fig:rotating_nass_effect_floor_motion and fig:rotating_nass_effect_direct_forces)
- Integral Force Feedback degrades the performances at low frequency compared to relative damping control
- Regarding the effect of micro-station vibrations:
- Having a soft nano-hexapod allows to filter these vibrations between the suspensions modes of the nano-hexapod and some flexible modes of the micro-station. Using relative damping control reduce this filtering (Figure fig:rotating_nass_effect_stage_vibration, left).
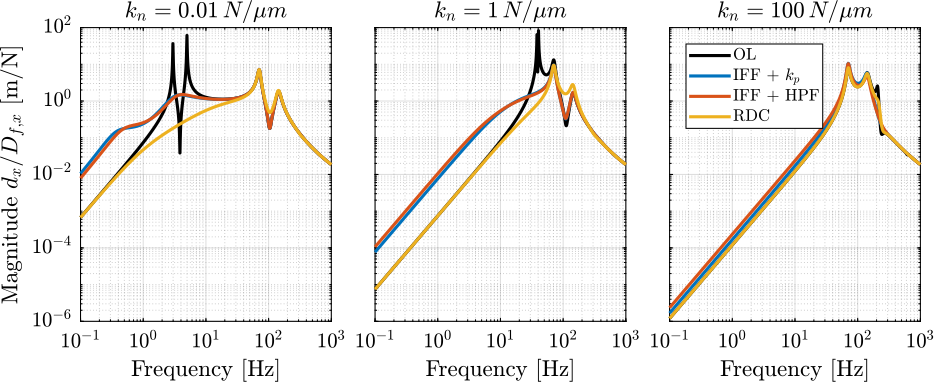
Figure 41: Effect of Floor motion on the position error - Comparison of active damping techniques for the three nano-hexapod stiffnesses
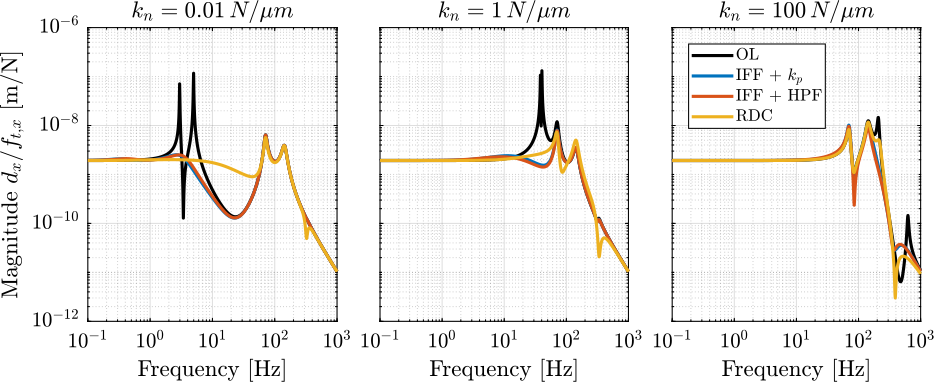
Figure 42: Effect of micro-station vibrations on the position error - Comparison of active damping techniques for the three nano-hexapod stiffnesses
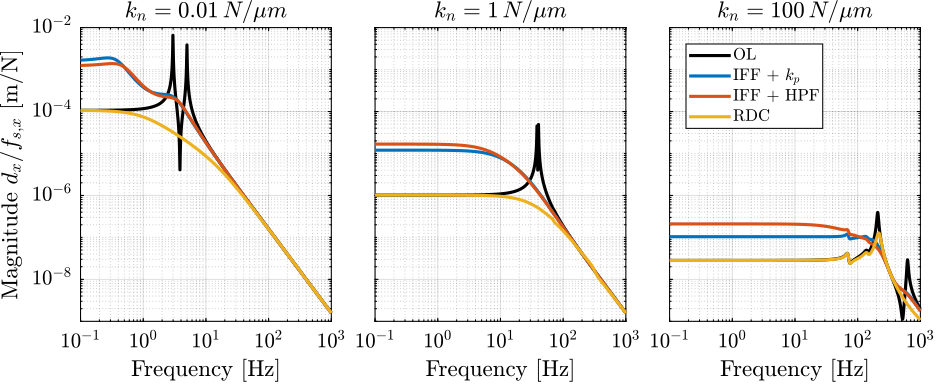
Figure 43: Effect of sample forces on the position error - Comparison of active damping techniques for the three nano-hexapod stiffnesses
9. Conclusion
In this study, the gyroscopic effects induced by the spindle’s rotation have been studied using a spindle model (Section sec:rotating_system_description). Decentralized IFF with pure integrators was shown to be unstable when applied to rotating platforms (Section sec:rotating_iff_pure_int). Two modifications of the classical IFF control have been proposed to overcome this issue.
The first modification concerns the controller and consists of adding an high pass filter to the pure integrators. This is equivalent as to moving the controller pole to the left along the real axis. This allows the closed loop system to be stable up to some value of the controller gain (Section sec:rotating_iff_pseudo_int).
The second proposed modification concerns the mechanical system. Additional springs are added in parallel with the actuators and force sensors. It was shown that if the stiffness \(k_p\) of the additional springs is larger than the negative stiffness \(m \Omega^2\) induced by centrifugal forces, the classical decentralized IFF regains its unconditional stability property (Section sec:rotating_iff_parallel_stiffness).
These two modifications were compared with relative damping control in Section sec:rotating_comp_act_damp. While having very different implementations, both proposed modifications were found to be very similar when it comes to the attainable damping and the obtained closed loop system behavior.
Then, this study has been applied to a rotating system that corresponds to the nano-hexapod parameters (Section sec:rotating_nano_hexapod). To be closer to the real system dynamics, the limited compliance of the micro-station has been taken into account. Results show that the two proposed IFF modifications can be applied for the NASS even in the presence of spindle rotation.