Identification of the disturbances

1. Simscape Model
2. Identification
3. Sensitivity to Disturbances
4. Power Spectral Density of the effect of the disturbances
5. Compute the Power Spectral Density of the disturbance force
6. Noise Budget
7. Save
8. Error motion of the Sample without Control

The goal here is to extract the Power Spectral Density of the sources of perturbation.

The sources of perturbations are (schematically shown in figure 1):

\(D_w\): Ground Motion
Parasitic forces applied in the system when scanning with the Translation Stage and the Spindle (\(F_{rz}\) and \(F_{ty}\)). These forces can be due to imperfect guiding for instance.

Because we cannot measure directly the perturbation forces, we have the measure the effect of those perturbations on the system (in terms of velocity for instance using geophones, \(D\) on figure 1) and then, using a model, compute the forces that induced such velocity.

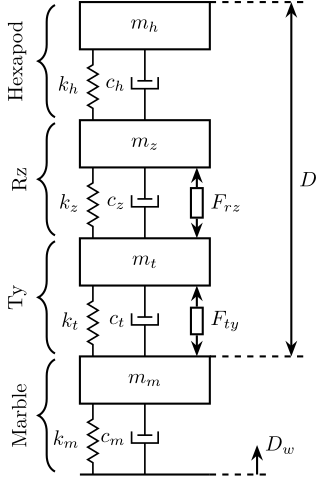
Figure 1: Schematic of the Micro Station and the sources of disturbance

This file is divided in the following sections:

Section 1: the simscape model used here is presented
Section 2: transfer functions from the disturbance forces to the relative velocity of the hexapod with respect to the granite are computed using the Simscape Model representing the experimental setup
Section 3: the bode plot of those transfer functions are shown
Section 4: the measured PSD of the effect of the disturbances are shown
Section 5: from the model and the measured PSD, the PSD of the disturbance forces are computed
Section 6: with the computed PSD, the noise budget of the system is done

1 Simscape Model

The following Simscape model of the micro-station is the same model used for the dynamical analysis. However, we here constrain all the stage to only move in the vertical direction.

We add disturbances forces in the vertical direction for the Translation Stage and the Spindle. Also, we measure the absolute displacement of the granite and of the top platform of the Hexapod.

We load the configuration and we set a small StopTime.

load('mat/conf_simulink.mat');
set_param(conf_simulink, 'StopTime', '0.5');

We initialize all the stages.

initializeGround();
initializeGranite('type', 'modal-analysis');
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod('type', 'modal-analysis');
initializeAxisc('type', 'none');
initializeMirror('type', 'none');
initializeNanoHexapod('type', 'none');
initializeSample('type', 'none');

2 Identification

The transfer functions from the disturbance forces to the relative velocity of the hexapod with respect to the granite are computed using the Simscape Model representing the experimental setup with the code below.

%% Options for Linearized
options = linearizeOptions;
options.SampleTime = 0;

%% Name of the Simulink File
mdl = 'nass_model';

%% Micro-Hexapod
  clear io; io_i = 1;
  io(io_i) = linio([mdl, '/Disturbances'], 1, 'openinput', [], 'Dwz'); io_i = io_i + 1; % Vertical Ground Motion
  io(io_i) = linio([mdl, '/Disturbances'], 1, 'openinput', [], 'Fty_z'); io_i = io_i + 1; % Parasitic force Ty
  io(io_i) = linio([mdl, '/Disturbances'], 1, 'openinput', [], 'Frz_z'); io_i = io_i + 1; % Parasitic force Rz
  io(io_i) = linio([mdl, '/Micro-Station/Granite/Modal Analysis/accelerometer'], 1, 'openoutput'); io_i = io_i + 1; % Absolute motion - Granite
  io(io_i) = linio([mdl, '/Micro-Station/Micro Hexapod/Modal Analysis/accelerometer'],  1, 'openoutput'); io_i = io_i + 1; % Absolute Motion - Hexapod
  % io(io_i) = linio([mdl, '/Vm'],   1, 'openoutput'); io_i = io_i + 1; % Relative Velocity hexapod/granite

% Run the linearization
G = linearize(mdl, io, 0);

% We Take only the outputs corresponding to the vertical acceleration
G = G([3,9], :);

% Input/Output names
G.InputName  = {'Dw', 'Fty', 'Frz'};
G.OutputName = {'Agm', 'Ahm'};

% We integrate 1 time the output to have the velocity and we
% substract the absolute velocities to have the relative velocity
G = (1/s)*tf([-1, 1])*G;

% Input/Output names
G.InputName  = {'Dw', 'Fty', 'Frz'};
G.OutputName = {'Vm'};

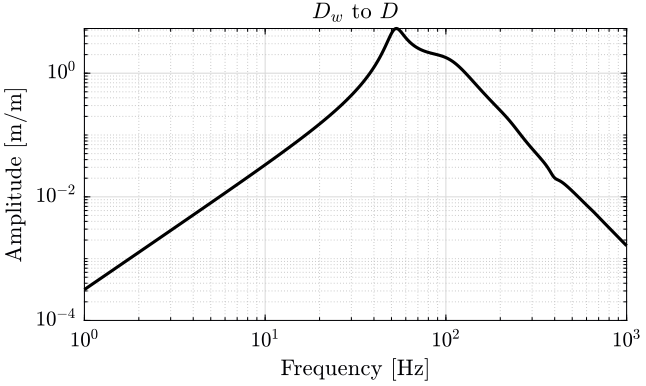
3 Sensitivity to Disturbances

Figure 2: Sensitivity to Ground Motion (png, pdf)

Figure 3: Sensitivity to vertical forces applied by the Ty stage (png, pdf)

Figure 4: Sensitivity to vertical forces applied by the Rz stage (png, pdf)

4 Power Spectral Density of the effect of the disturbances

The PSD of the relative velocity between the hexapod and the marble in \([(m/s)^2/Hz]\) are loaded for the following sources of disturbance:

Slip Ring Rotation
Scan of the translation stage (effect in the vertical direction and in the horizontal direction)

Also, the Ground Motion is measured.

gm  = load('./mat/psd_gm.mat', 'f', 'psd_gm');
rz  = load('./mat/pxsp_r.mat', 'f', 'pxsp_r');
tyz = load('./mat/pxz_ty_r.mat', 'f', 'pxz_ty_r');
tyx = load('./mat/pxe_ty_r.mat', 'f', 'pxe_ty_r');

We now compute the relative velocity between the hexapod and the granite due to ground motion.

gm.psd_rv = gm.psd_gm.*abs(squeeze(freqresp(G('Vm', 'Dw'), gm.f, 'Hz'))).^2;

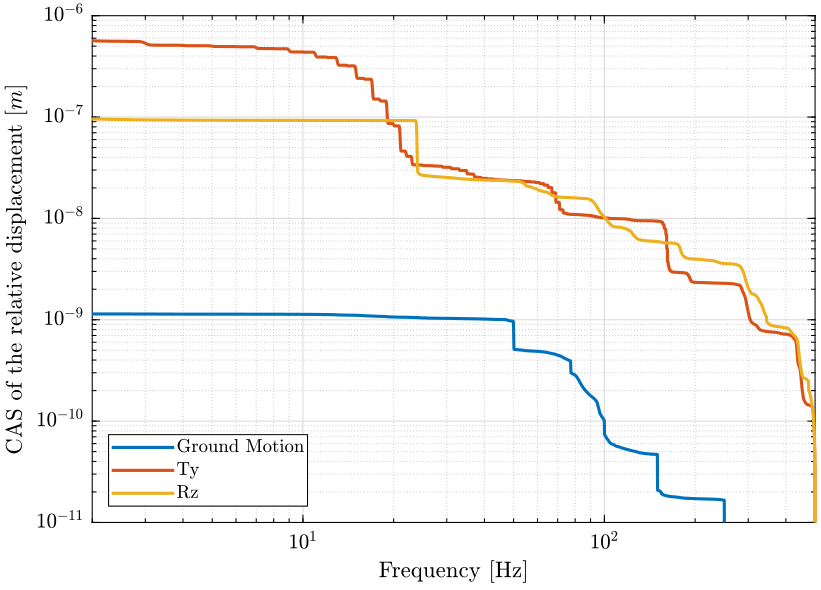
The Power Spectral Density of the relative motion/velocity of the hexapod with respect to the granite are shown in figures 5 and 6.

The Cumulative Amplitude Spectrum of the relative motion is shown in figure 7.

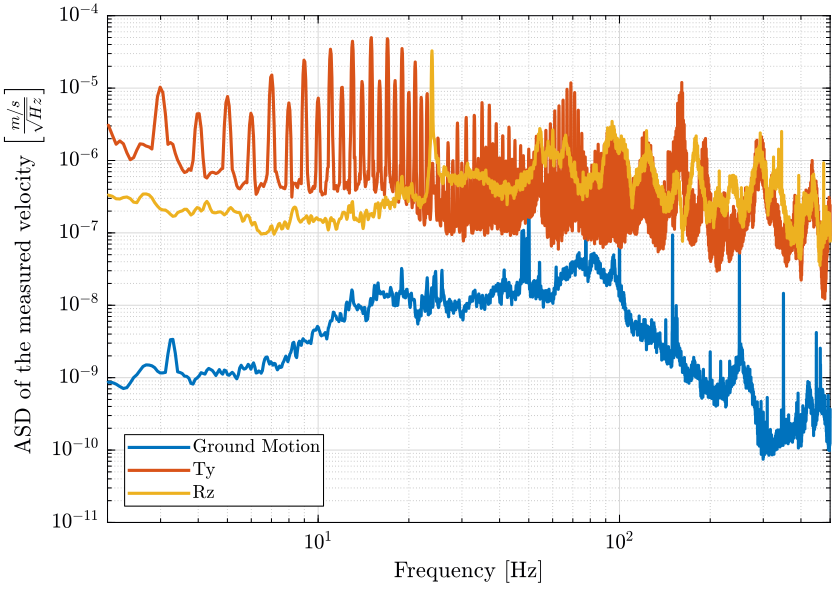
Figure 5: Amplitude Spectral Density of the relative velocity of the hexapod with respect to the granite due to different sources of perturbation (png, pdf)

Figure 6: Amplitude Spectral Density of the relative displacement of the hexapod with respect to the granite due to different sources of perturbation (png, pdf)

Figure 7: Cumulative Amplitude Spectrum of the relative motion due to different sources of perturbation (png, pdf)

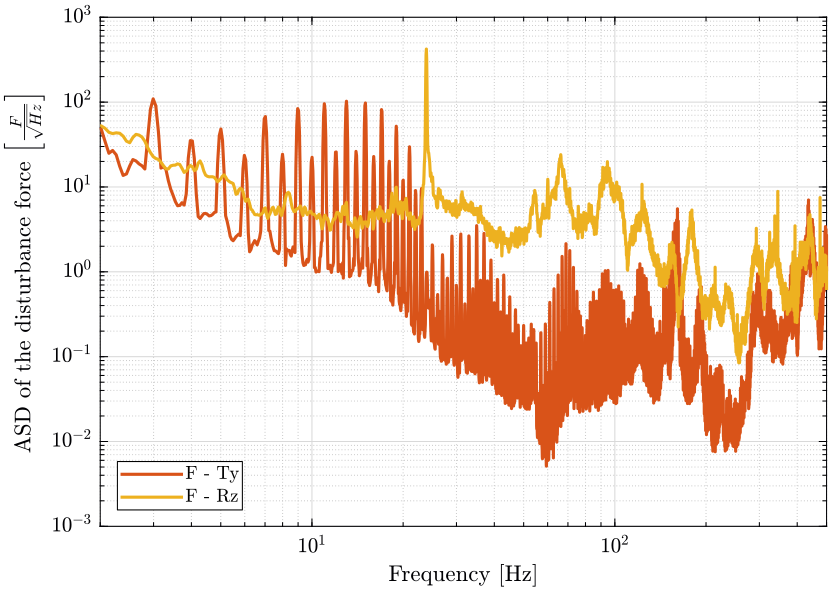
5 Compute the Power Spectral Density of the disturbance force

Now, from the extracted transfer functions from the disturbance force to the relative motion of the hexapod with respect to the granite (section 3) and from the measured PSD of the relative motion (section 4), we can compute the PSD of the disturbance force.

rz.psd_f  = rz.pxsp_r./abs(squeeze(freqresp(G('Vm', 'Frz'), rz.f, 'Hz'))).^2;
tyz.psd_f = tyz.pxz_ty_r./abs(squeeze(freqresp(G('Vm', 'Fty'), tyz.f, 'Hz'))).^2;

Figure 8: Amplitude Spectral Density of the disturbance force (png, pdf)

6 Noise Budget

Now, from the compute spectral density of the disturbance sources, we can compute the resulting relative motion of the Hexapod with respect to the granite using the model. We should verify that this is coherent with the measurements.

Figure 9: Computed Effect of the disturbances on the relative displacement hexapod/granite (png, pdf)

Figure 10: CAS of the total Relative Displacement due to all considered sources of perturbation (png, pdf)

7 Save

The PSD of the disturbance force are now saved for further analysis.

dist_f = struct();

dist_f.f = gm.f; % Frequency Vector [Hz]

dist_f.psd_gm = gm.psd_gm; % Power Spectral Density of the Ground Motion [m^2/Hz]
dist_f.psd_ty = tyz.psd_f; % Power Spectral Density of the force induced by the Ty stage in the Z direction [N^2/Hz]
dist_f.psd_rz = rz.psd_f; % Power Spectral Density of the force induced by the Rz stage in the Z direction [N^2/Hz]

save('./mat/dist_psd.mat', 'dist_f');

8 Error motion of the Sample without Control

initializeGround();
initializeGranite('Foffset', false);
initializeTy('Foffset', false);
initializeRy('Foffset', false);
initializeRz('Foffset', false);
initializeMicroHexapod('Foffset', false);
initializeAxisc('type', 'rigid');
initializeMirror('type', 'rigid');

The nano-hexapod is a piezoelectric hexapod and the sample has a mass of 50kg.

initializeNanoHexapod('type', 'rigid');
initializeSample('type', 'rigid', 'mass', 50);

We set the references and disturbances to zero.

initializeReferences();
initializeDisturbances();

We set the controller type to Open-Loop.

initializeController('type', 'open-loop');

And we put some gravity.

initializeSimscapeConfiguration('gravity', false);

We do not need to log any signal.

initializeLoggingConfiguration('log', 'all');

initializePosError('error', false);

load('mat/conf_simulink.mat');
set_param(conf_simulink, 'StopTime', '1');

We simulate the model.

sim('nass_model');

figure;
subplot(1, 2, 1);
hold on;
plot(simout.Em.Eg.Time, simout.Em.Eg.Data(:, 1), 'DisplayName', 'X');
plot(simout.Em.Eg.Time, simout.Em.Eg.Data(:, 2), 'DisplayName', 'Y');
plot(simout.Em.Eg.Time, simout.Em.Eg.Data(:, 3), 'DisplayName', 'Z');
hold off;
xlabel('Time [s]');
ylabel('Position error [m]');
legend();

subplot(1, 2, 2);
hold on;
plot(simout.Em.Eg.Time, simout.Em.Eg.Data(:, 4));
plot(simout.Em.Eg.Time, simout.Em.Eg.Data(:, 5));
plot(simout.Em.Eg.Time, simout.Em.Eg.Data(:, 6));
hold off;
xlabel('Time [s]');
ylabel('Orientation error [rad]');

Eg = simout.Em.Eg;
save('./mat/motion_error_ol.mat', 'Eg');