UP | HOME

Active Damping with an uni-axial model

Table of Contents

First, in section 1, we will looked at the undamped system.

Then, we will compare three active damping techniques:

For each of the active damping technique, we will:

The disturbances are:

1 Undamped System

All the files (data and Matlab scripts) are accessible here.

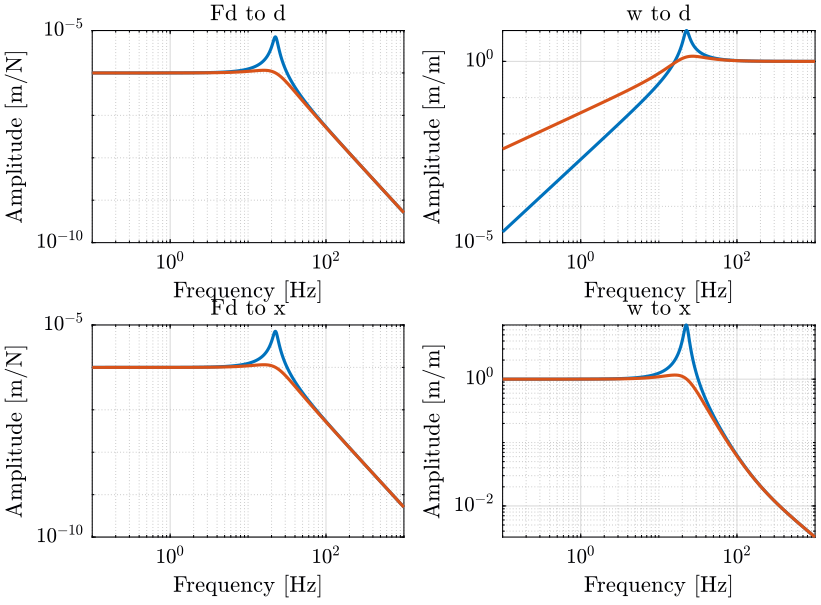
We first look at the undamped system. The performance of this undamped system will be compared with the damped system using various techniques.

1.1 Init

We initialize all the stages with the default parameters. The nano-hexapod is a piezoelectric hexapod and the sample has a mass of 50kg. 

  initializeReferences();
  initializeGround();
  initializeGranite();
  initializeTy();
  initializeRy();
  initializeRz();
  initializeMicroHexapod();
  initializeAxisc();
  initializeMirror();
  initializeNanoHexapod('actuator', 'piezo');
  initializeSample('mass', 50);

All the controllers are set to 0. 

  K = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K', '-append');
  K_iff = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K_iff', '-append');
  K_rmc = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K_rmc', '-append');
  K_dvf = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K_dvf', '-append');

1.2 Identification

We identify the various transfer functions of the system 

  G = identifyPlant();

And we save it for further analysis. 

  save('./mat/active_damping_uniaxial_plants.mat', 'G', '-append');

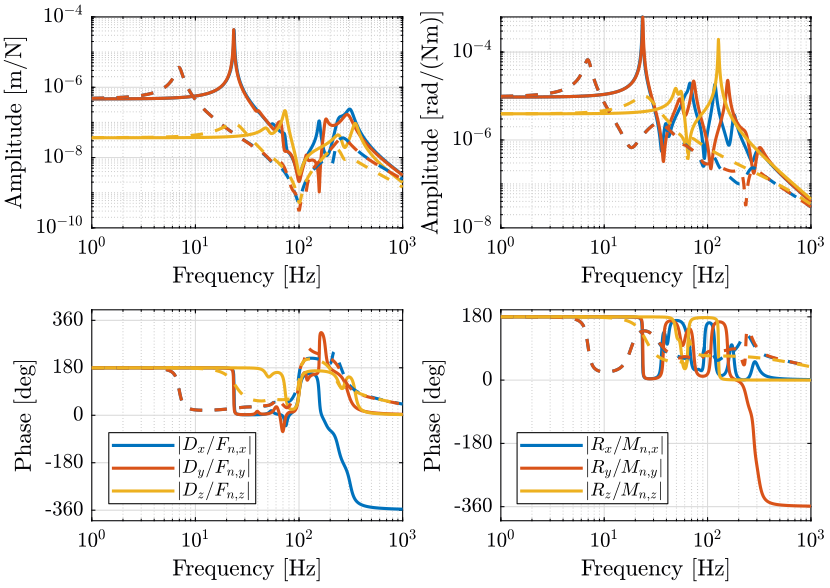
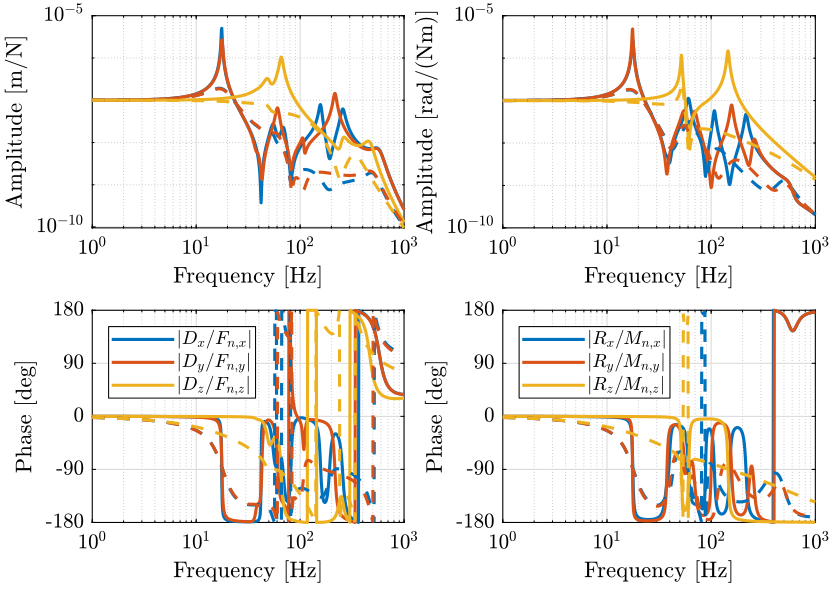
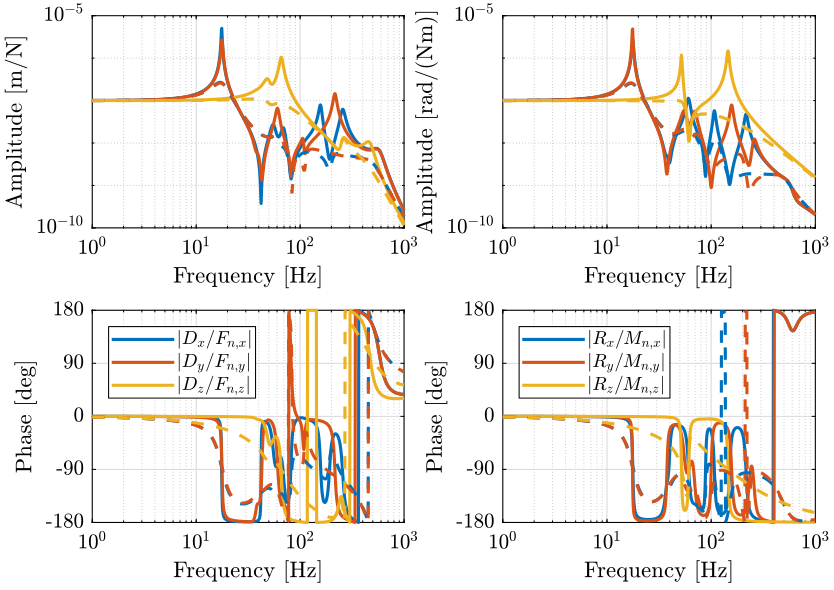
1.3 Sensitivity to disturbances

The sensitivity to disturbances are shown on figure 1.

sensitivity_dist_undamped.png

Figure 1: Undamped sensitivity to disturbances (png, pdf)

sensitivity_dist_stages.png

Figure 2: Sensitivity to force disturbances in various stages (png, pdf)

1.4 Undamped Plant

The “plant” (transfer function from forces applied by the nano-hexapod to the measured displacement of the sample with respect to the granite) bode plot is shown on figure 1.

plant_undamped.png

Figure 3: Transfer Function from cartesian forces to displacement for the undamped plant (png, pdf)

2 Integral Force Feedback

All the files (data and Matlab scripts) are accessible here.

Integral Force Feedback is applied. In section 2.1, IFF is applied on a uni-axial system to understand its behavior. Then, it is applied on the simscape model.

2.1 One degree-of-freedom example

2.1.1 Equations

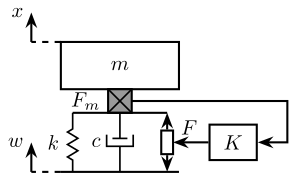
iff_1dof.png

Figure 4: Integral Force Feedback applied to a 1dof system

The dynamic of the system is described by the following equation:

\begin{equation} ms^2x = F_d - kx - csx + kw + csw + F \end{equation}

The measured force \(F_m\) is:

\begin{align} F_m &= F - kx - csx + kw + csw \\ &= ms^2 x - F_d \end{align}

The Integral Force Feedback controller is \(K = -\frac{g}{s}\), and thus the applied force by this controller is:

\begin{equation} F_{\text{IFF}} = -\frac{g}{s} F_m = -\frac{g}{s} (ms^2 x - F_d) \end{equation}

Once the IFF is applied, the new dynamics of the system is:

\begin{equation} ms^2x = F_d + F - kx - csx + kw + csw - \frac{g}{s} (ms^2x - F_d) \end{equation}

And finally:

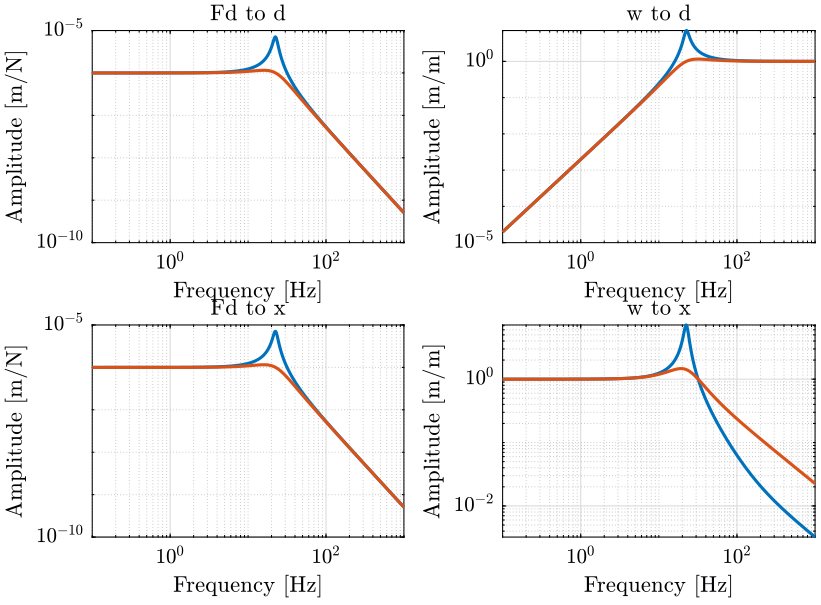
\begin{equation} x = F_d \frac{1 + \frac{g}{s}}{ms^2 + (mg + c)s + k} + F \frac{1}{ms^2 + (mg + c)s + k} + w \frac{k + cs}{ms^2 + (mg + c)s + k} \end{equation}

We can see that this:

  • adds damping to the system by a value \(mg\)
  • lower the compliance as low frequency by a factor: \(1 + g/s\)

If we want critical damping:

\begin{equation} \xi = \frac{1}{2} \frac{c + gm}{\sqrt{km}} = \frac{1}{2} \end{equation}

This is attainable if we have:

\begin{equation} g = \frac{\sqrt{km} - c}{m} \end{equation}

2.1.2 Matlab Example

Let define the system parameters. 

  m = 50; % [kg]
  k = 1e6; % [N/m]
  c = 1e3; % [N/(m/s)]

The state space model of the system is defined below. 

  A = [-c/m -k/m;
       1     0];

  B = [1/m 1/m -1;
       0   0    0];

  C = [ 0  1;
       -c -k];

  D = [0 0 0;
       1 0 0];

  sys = ss(A, B, C, D);
  sys.InputName = {'F', 'Fd', 'wddot'};
  sys.OutputName = {'d', 'Fm'};
  sys.StateName = {'ddot', 'd'};

The controller \(K_\text{IFF}\) is: 

  Kiff = -((sqrt(k*m)-c)/m)/s;
  Kiff.InputName = {'Fm'};
  Kiff.OutputName = {'F'};

And the closed loop system is computed below. 

  sys_iff = feedback(sys, Kiff, 'name', +1);

iff_1dof_sensitivitiy.png

Figure 5: Sensitivity to disturbance when IFF is applied on the 1dof system (png, pdf)

2.2 Control Design

Let’s load the undamped plant: 

  load('./mat/active_damping_uniaxial_plants.mat', 'G');

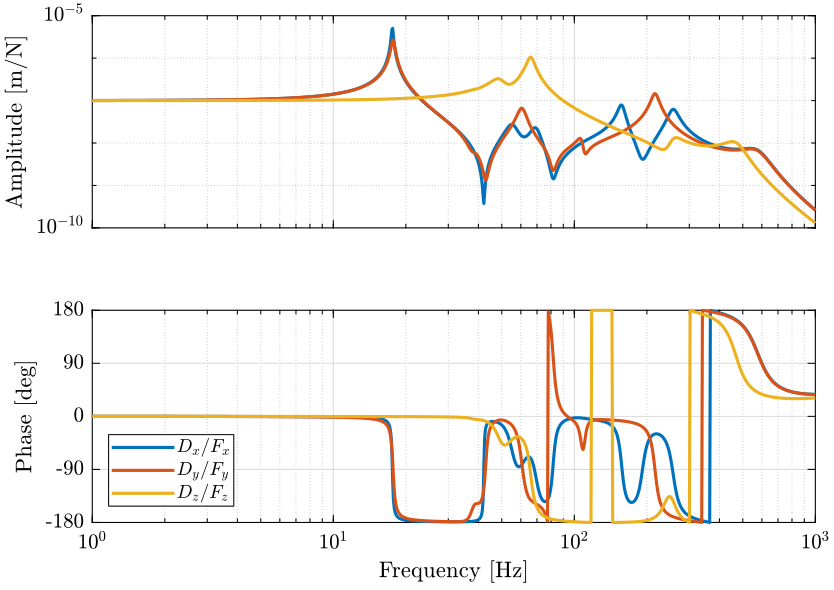
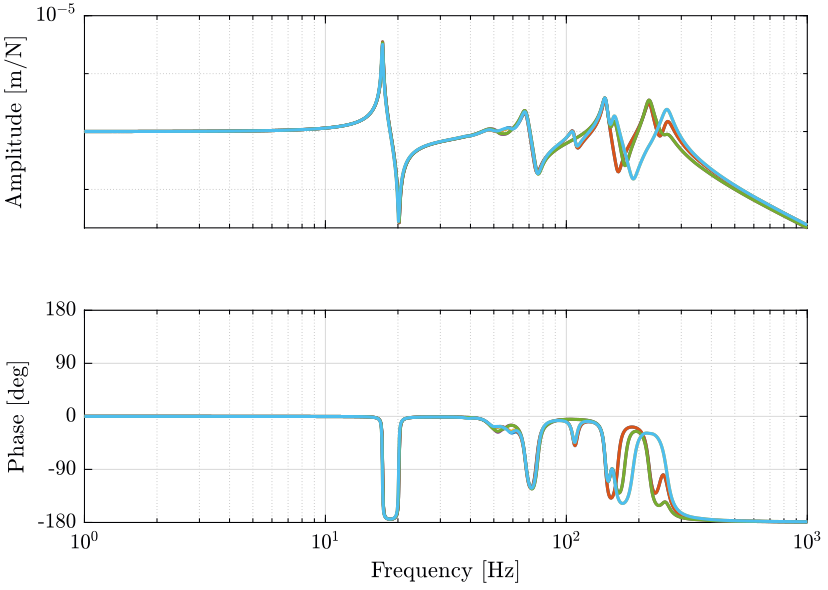
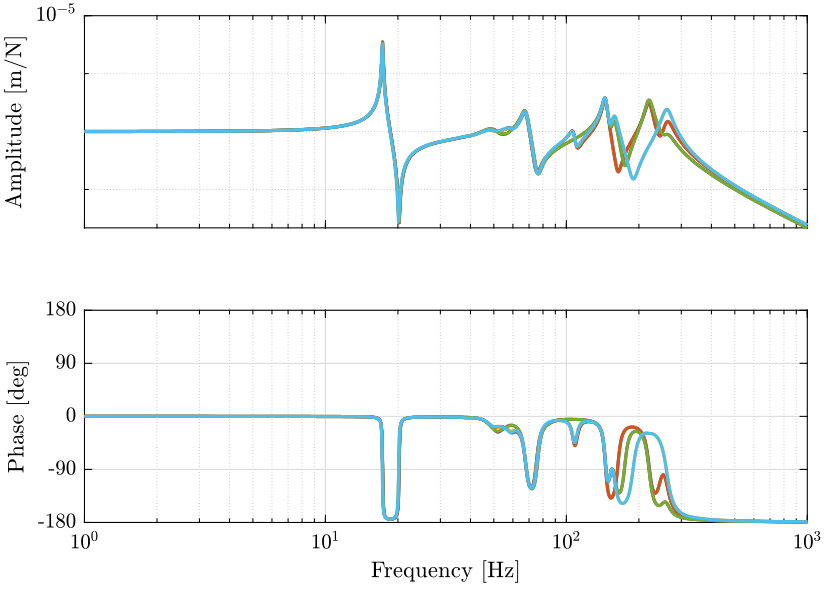
Let’s look at the transfer function from actuator forces in the nano-hexapod to the force sensor in the nano-hexapod legs for all 6 pairs of actuator/sensor (figure 6).

iff_plant.png

Figure 6: Transfer function from forces applied in the legs to force sensor (png, pdf)

The controller for each pair of actuator/sensor is: 

  K_iff = -1000/s;

The corresponding loop gains are shown in figure 7.

iff_open_loop.png

Figure 7: Loop Gain for the Integral Force Feedback (png, pdf)

2.3 Identification of the damped plant

Let’s initialize the system prior to identification. 

  initializeReferences();
  initializeGround();
  initializeGranite();
  initializeTy();
  initializeRy();
  initializeRz();
  initializeMicroHexapod();
  initializeAxisc();
  initializeMirror();
  initializeNanoHexapod('actuator', 'piezo');
  initializeSample('mass', 50);

All the controllers are set to 0. 

  K = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K', '-append');
  K_iff = -K_iff*eye(6);
  save('./mat/controllers_uniaxial.mat', 'K_iff', '-append');
  K_rmc = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K_rmc', '-append');
  K_dvf = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K_dvf', '-append');

We identify the system dynamics now that the IFF controller is ON. 

  G_iff = identifyPlant();

And we save the damped plant for further analysis 

  save('./mat/active_damping_uniaxial_plants.mat', 'G_iff', '-append');

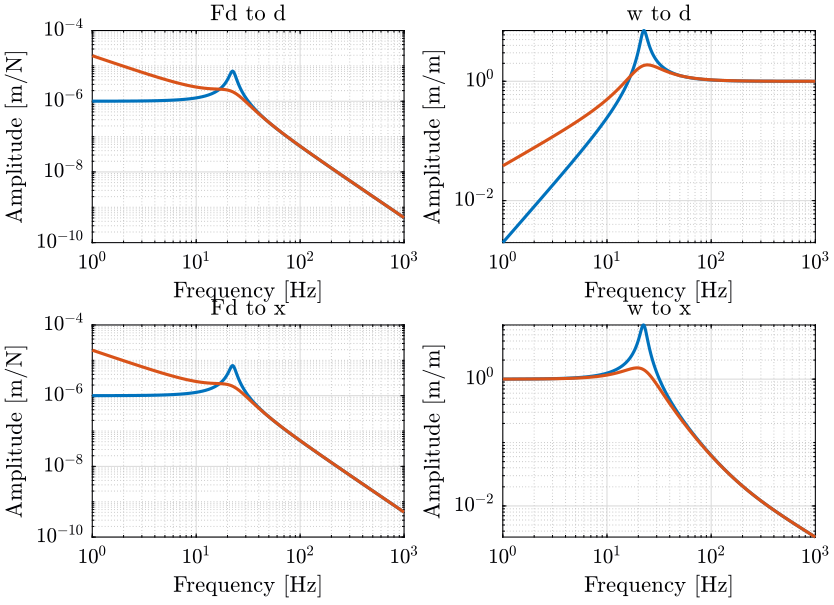
2.4 Sensitivity to disturbances

As shown on figure 8:

  • The top platform of the nano-hexapod how behaves as a “free-mass”.
  • The transfer function from direct forces \(F_s\) to the relative displacement \(D\) is equivalent to the one of an isolated mass.
  • The transfer function from ground motion \(D_g\) to the relative displacement \(D\) tends to the transfer function from \(D_g\) to the displacement of the granite (the sample is being isolated thanks to IFF). However, as the goal is to make the relative displacement \(D\) as small as possible (e.g. to make the sample motion follows the granite motion), this is not a good thing.

sensitivity_dist_iff.png

Figure 8: Sensitivity to disturbance once the IFF controller is applied to the system (png, pdf)

The order of the models are very high and thus the plots may be wrong. For instance, the plots are not the same when using minreal.

sensitivity_dist_stages_iff.png

Figure 9: Sensitivity to force disturbances in various stages when IFF is applied (png, pdf)

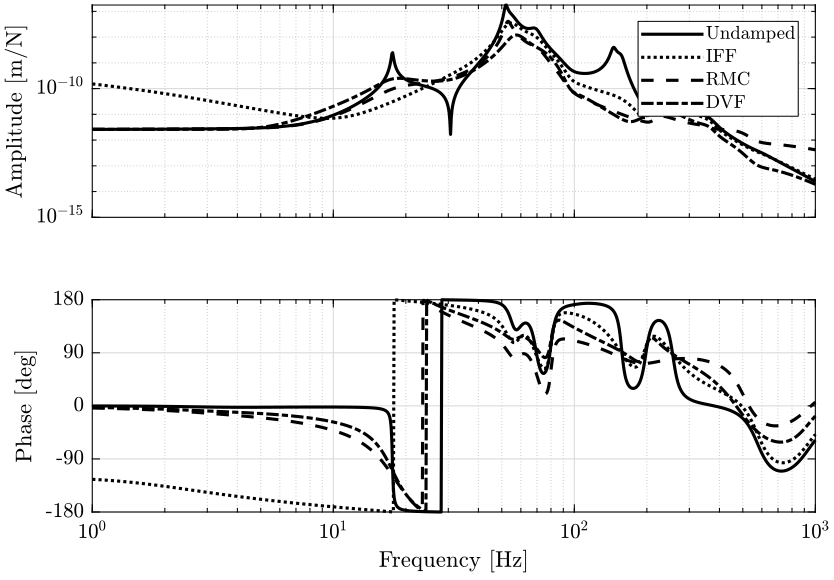
2.5 Damped Plant

Now, look at the new damped plant to control.

It damps the plant (resonance of the nano hexapod as well as other resonances) as shown in figure 10.

plant_iff_damped.png

Figure 10: Damped Plant after IFF is applied (png, pdf)

However, it increases coupling at low frequency (figure 11).

plant_iff_coupling.png

Figure 11: Coupling induced by IFF (png, pdf)

2.6 Conclusion

Integral Force Feedback:

  • Robust (guaranteed stability)
  • Acceptable Damping
  • Increase the sensitivity to disturbances at low frequencies

3 Relative Motion Control

All the files (data and Matlab scripts) are accessible here.

In the Relative Motion Control (RMC), a derivative feedback is applied between the measured actuator displacement to the actuator force input.

3.1 One degree-of-freedom example

3.1.1 Equations

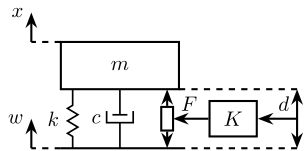
rmc_1dof.png

Figure 12: Relative Motion Control applied to a 1dof system

The dynamic of the system is:

\begin{equation} ms^2x = F_d - kx - csx + kw + csw + F \end{equation}

In terms of the stage deformation \(d = x - w\):

\begin{equation} (ms^2 + cs + k) d = -ms^2 w + F_d + F \end{equation}

The relative motion control law is:

\begin{equation} K = -g s \end{equation}

Thus, the applied force is:

\begin{equation} F = -g s d \end{equation}

And the new dynamics will be:

\begin{equation} d = w \frac{-ms^2}{ms^2 + (c + g)s + k} + F_d \frac{1}{ms^2 + (c + g)s + k} + F \frac{1}{ms^2 + (c + g)s + k} \end{equation}

And thus damping is added.

If critical damping is wanted:

\begin{equation} \xi = \frac{1}{2}\frac{c + g}{\sqrt{km}} = \frac{1}{2} \end{equation}

This corresponds to a gain:

\begin{equation} g = \sqrt{km} - c \end{equation}

3.1.2 Matlab Example

Let define the system parameters. 

  m = 50; % [kg]
  k = 1e6; % [N/m]
  c = 1e3; % [N/(m/s)]

The state space model of the system is defined below. 

  A = [-c/m -k/m;
       1     0];

  B = [1/m 1/m -1;
       0   0    0];

  C = [ 0  1;
       -c -k];

  D = [0 0 0;
       1 0 0];

  sys = ss(A, B, C, D);
  sys.InputName = {'F', 'Fd', 'wddot'};
  sys.OutputName = {'d', 'Fm'};
  sys.StateName = {'ddot', 'd'};

The controller \(K_\text{RMC}\) is: 

  Krmc = -(sqrt(k*m)-c)*s;
  Krmc.InputName = {'d'};
  Krmc.OutputName = {'F'};

And the closed loop system is computed below. 

  sys_rmc = feedback(sys, Krmc, 'name', +1);

rmc_1dof_sensitivitiy.png

Figure 13: Sensitivity to disturbance when RMC is applied on the 1dof system (png, pdf)

3.2 Control Design

Let’s load the undamped plant: 

  load('./mat/active_damping_uniaxial_plants.mat', 'G');

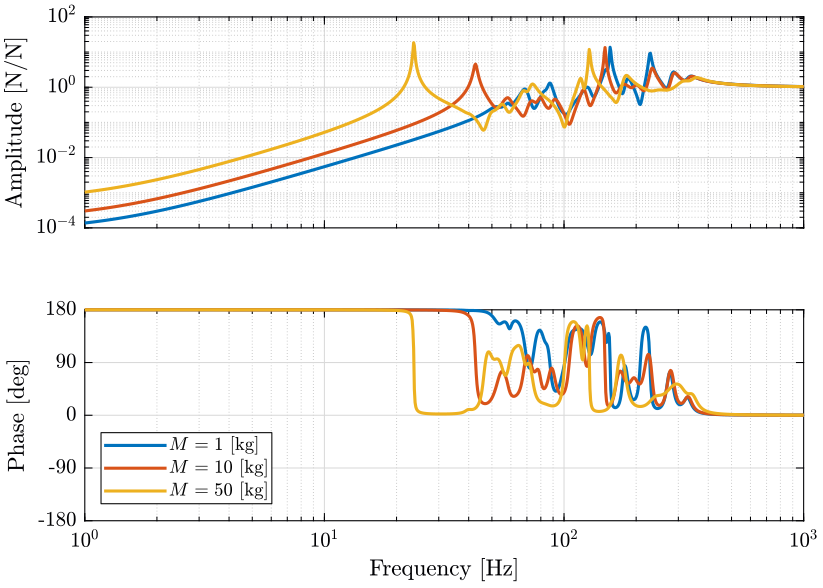
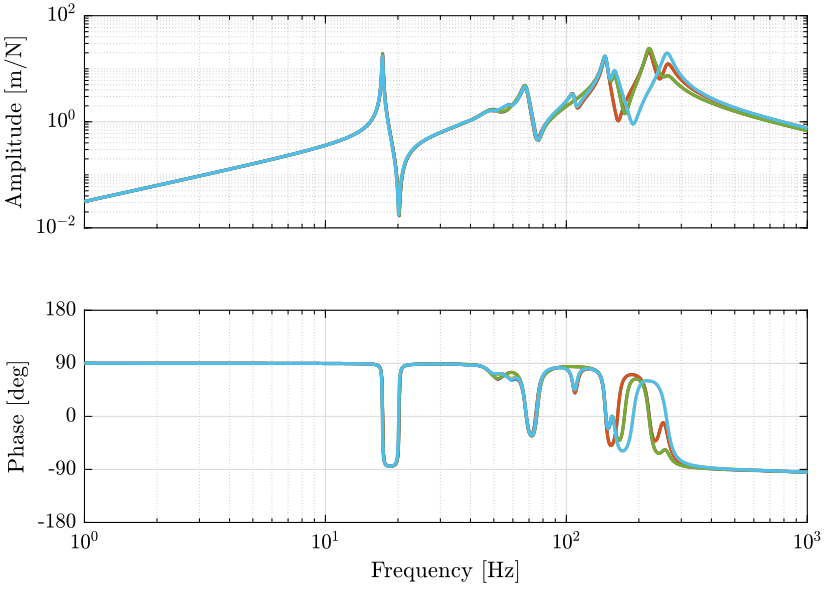
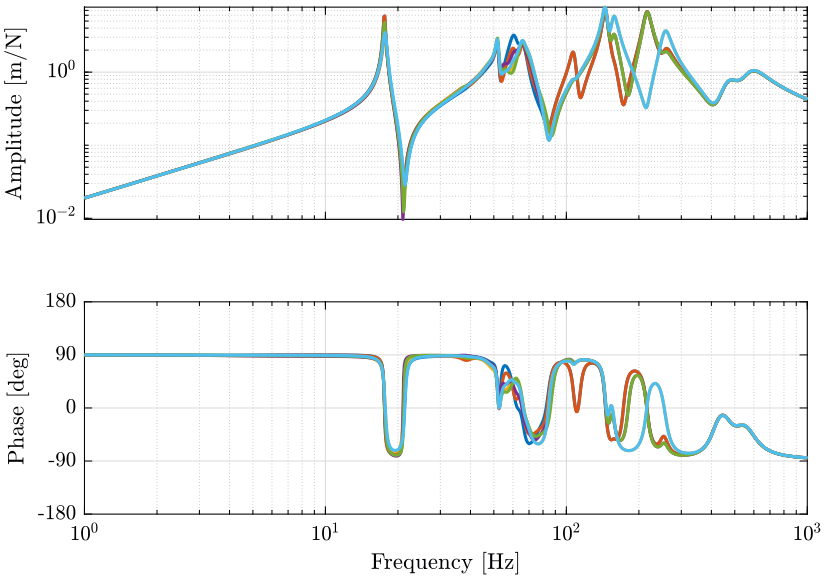
Let’s look at the transfer function from actuator forces in the nano-hexapod to the measured displacement of the actuator for all 6 pairs of actuator/sensor (figure 14).

rmc_plant.png

Figure 14: Transfer function from forces applied in the legs to leg displacement sensor (png, pdf)

The Relative Motion Controller is defined below. A Low pass Filter is added to make the controller transfer function proper. 

  K_rmc = s*50000/(1 + s/2/pi/10000);

The obtained loop gains are shown in figure 15.

rmc_open_loop.png

Figure 15: Loop Gain for the Integral Force Feedback (png, pdf)

3.3 Identification of the damped plant

Let’s initialize the system prior to identification. 

  initializeReferences();
  initializeGround();
  initializeGranite();
  initializeTy();
  initializeRy();
  initializeRz();
  initializeMicroHexapod();
  initializeAxisc();
  initializeMirror();
  initializeNanoHexapod('actuator', 'piezo');
  initializeSample('mass', 50);

And initialize the controllers. 

  K = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K', '-append');
  K_iff = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K_iff', '-append');
  K_rmc = -K_rmc*eye(6);
  save('./mat/controllers_uniaxial.mat', 'K_rmc', '-append');
  K_dvf = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K_dvf', '-append');

We identify the system dynamics now that the RMC controller is ON. 

  G_rmc = identifyPlant();

And we save the damped plant for further analysis. 

  save('./mat/active_damping_uniaxial_plants.mat', 'G_rmc', '-append');

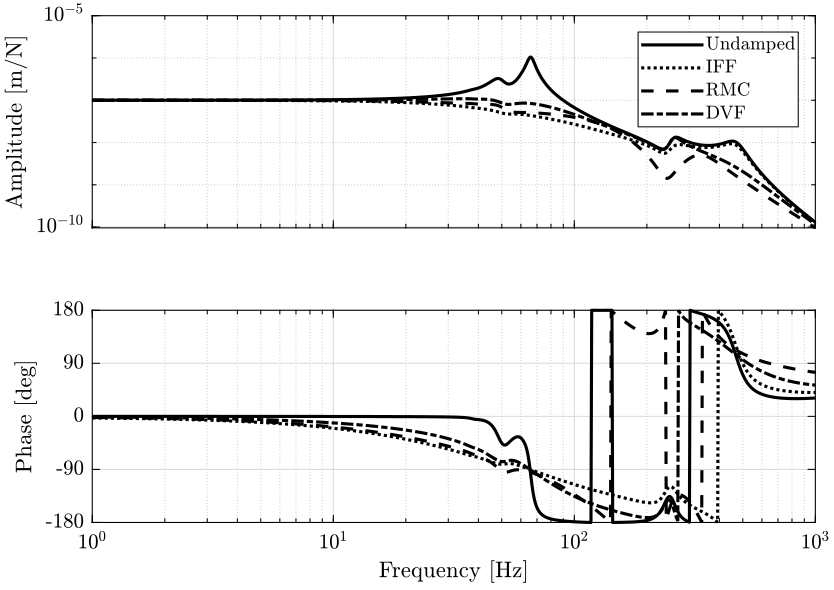
3.4 Sensitivity to disturbances

As shown in figure 16, RMC control succeed in lowering the sensitivity to disturbances near resonance of the system.

sensitivity_dist_rmc.png

Figure 16: Sensitivity to disturbance once the RMC controller is applied to the system (png, pdf)

sensitivity_dist_stages_rmc.png

Figure 17: Sensitivity to force disturbances in various stages when RMC is applied (png, pdf)

3.5 Damped Plant

plant_rmc_damped.png

Figure 18: Damped Plant after RMC is applied (png, pdf)

3.6 Conclusion

Relative Motion Control:

4 Direct Velocity Feedback

All the files (data and Matlab scripts) are accessible here.

In the Relative Motion Control (RMC), a feedback is applied between the measured velocity of the platform to the actuator force input.

4.1 One degree-of-freedom example

4.1.1 Equations

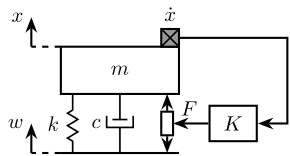
dvf_1dof.png

Figure 19: Direct Velocity Feedback applied to a 1dof system

The dynamic of the system is:

\begin{equation} ms^2x = F_d - kx - csx + kw + csw + F \end{equation}

In terms of the stage deformation \(d = x - w\):

\begin{equation} (ms^2 + cs + k) d = -ms^2 w + F_d + F \end{equation}

The direct velocity feedback law shown in figure 19 is:

\begin{equation} K = -g \end{equation}

Thus, the applied force is:

\begin{equation} F = -g \dot{x} \end{equation}

And the new dynamics will be:

\begin{equation} d = w \frac{-ms^2 - gs}{ms^2 + (c + g)s + k} + F_d \frac{1}{ms^2 + (c + g)s + k} + F \frac{1}{ms^2 + (c + g)s + k} \end{equation}

And thus damping is added.

If critical damping is wanted:

\begin{equation} \xi = \frac{1}{2}\frac{c + g}{\sqrt{km}} = \frac{1}{2} \end{equation}

This corresponds to a gain:

\begin{equation} g = \sqrt{km} - c \end{equation}

4.1.2 Matlab Example

Let define the system parameters. 

  m = 50; % [kg]
  k = 1e6; % [N/m]
  c = 1e3; % [N/(m/s)]

The state space model of the system is defined below. 

  A = [-c/m -k/m;
       1     0];

  B = [1/m 1/m -1;
       0   0    0];

  C = [1 0;
       0 1;
       0 0];

  D = [0 0 0;
       0 0 0;
       0 0 1];

  sys = ss(A, B, C, D);
  sys.InputName = {'F', 'Fd', 'wddot'};
  sys.OutputName = {'ddot', 'd', 'wddot'};
  sys.StateName = {'ddot', 'd'};

Because we need \(\dot{x}\) for feedback, we compute it from the outputs 

  G_xdot = [1, 0, 1/s;
            0, 1, 0];
  G_xdot.InputName = {'ddot', 'd', 'wddot'};
  G_xdot.OutputName = {'xdot', 'd'};

Finally, the system is described by sys as defined below. 

  sys = series(sys, G_xdot, [1 2 3], [1 2 3]);

The controller \(K_\text{DVF}\) is: 

  Kdvf = tf(-(sqrt(k*m)-c));
  Kdvf.InputName = {'xdot'};
  Kdvf.OutputName = {'F'};

And the closed loop system is computed below. 

  sys_dvf = feedback(sys, Kdvf, 'name', +1);

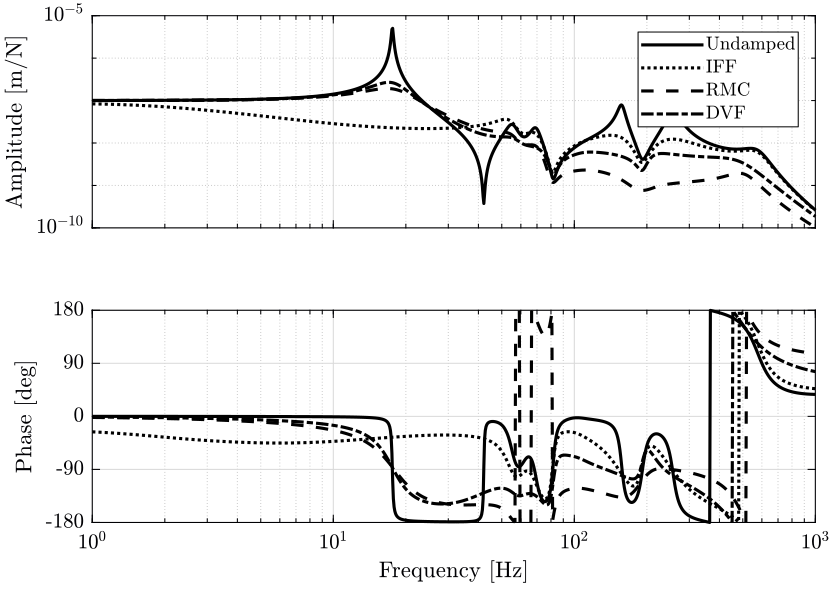
The obtained sensitivity to disturbances is shown in figure 20.

dvf_1dof_sensitivitiy.png

Figure 20: Sensitivity to disturbance when DVF is applied on the 1dof system (png, pdf)

4.2 Control Design

Let’s load the undamped plant: 

  load('./mat/active_damping_uniaxial_plants.mat', 'G');

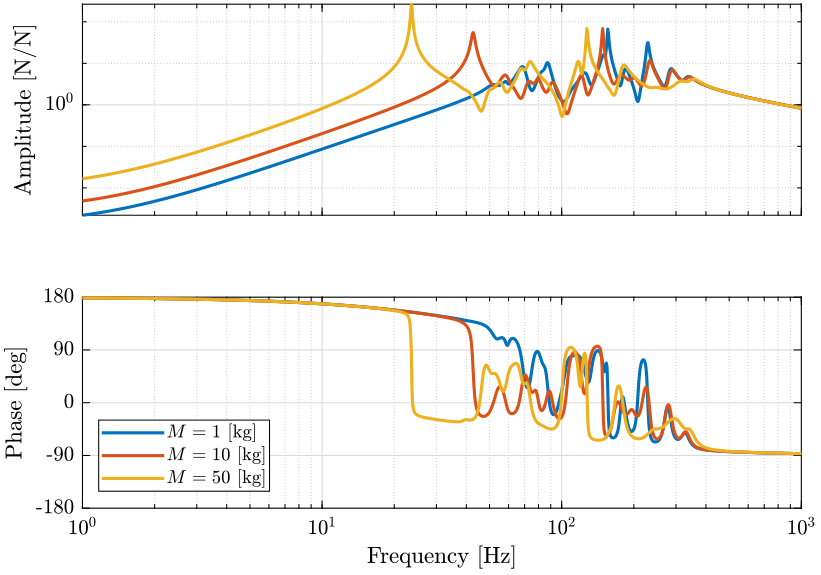
Let’s look at the transfer function from actuator forces in the nano-hexapod to the measured velocity of the nano-hexapod platform in the direction of the corresponding actuator for all 6 pairs of actuator/sensor (figure 21).

dvf_plant.png

Figure 21: Transfer function from forces applied in the legs to leg velocity sensor (png, pdf)

The controller is defined below and the obtained loop gain is shown in figure 22. 

  K_dvf = tf(3e4);

dvf_open_loop_gain.png

Figure 22: Loop Gain for DVF (png, pdf)

4.3 Identification of the damped plant

Let’s initialize the system prior to identification. 

  initializeReferences();
  initializeGround();
  initializeGranite();
  initializeTy();
  initializeRy();
  initializeRz();
  initializeMicroHexapod();
  initializeAxisc();
  initializeMirror();
  initializeNanoHexapod('actuator', 'piezo');
  initializeSample('mass', 50);

And initialize the controllers. 

  K = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K', '-append');
  K_iff = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K_iff', '-append');
  K_rmc = tf(zeros(6));
  save('./mat/controllers_uniaxial.mat', 'K_rmc', '-append');
  K_dvf = -K_dvf*eye(6);
  save('./mat/controllers_uniaxial.mat', 'K_dvf', '-append');

We identify the system dynamics now that the RMC controller is ON. 

  G_dvf = identifyPlant();

And we save the damped plant for further analysis. 

  save('./mat/active_damping_uniaxial_plants.mat', 'G_dvf', '-append');

4.4 Sensitivity to disturbances

sensitivity_dist_dvf.png

Figure 23: Sensitivity to disturbance once the DVF controller is applied to the system (png, pdf)

sensitivity_dist_stages_dvf.png

Figure 24: Sensitivity to force disturbances in various stages when DVF is applied (png, pdf)

4.5 Damped Plant

plant_dvf_damped.png

Figure 25: Damped Plant after DVF is applied (png, pdf)

4.6 Conclusion

Direct Velocity Feedback:

5 Comparison

5.1 Load the plants

  load('./mat/active_damping_uniaxial_plants.mat', 'G', 'G_iff', 'G_rmc', 'G_dvf');

5.2 Sensitivity to Disturbance

sensitivity_comp_ground_motion_z.png

Figure 26: caption (png, pdf)

sensitivity_comp_direct_forces_z.png

Figure 27: caption (png, pdf)

sensitivity_comp_spindle_z.png

Figure 28: caption (png, pdf)

sensitivity_comp_ty_z.png

Figure 29: caption (png, pdf)

sensitivity_comp_ty_x.png

Figure 30: caption (png, pdf)

5.3 Damped Plant

plant_comp_damping_z.png

Figure 31: Plant for the \(z\) direction for different active damping technique used (png, pdf)

plant_comp_damping_x.png

Figure 32: Plant for the \(x\) direction for different active damping technique used (png, pdf)

plant_comp_damping_coupling.png

Figure 33: Comparison of one off-diagonal plant for different damping technique applied (png, pdf)

6 Conclusion

Author: Dehaeze Thomas

Created: 2021-02-20 sam. 23:08