<?xml version="1.0" encoding="utf-8"?>
<?xml version="1.0" encoding="utf-8"?>
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN"
"http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<!-- 2020-04-17 ven. 14:10 -->
<meta http-equiv="Content-Type" content="text/html;charset=utf-8" />
<title>Control of the NASS with optimal stiffness</title>
<meta name="generator" content="Org mode" />
<meta name="author" content="Dehaeze Thomas" />
<link rel="stylesheet" type="text/css" href="./css/htmlize.css"/>
<link rel="stylesheet" type="text/css" href="./css/readtheorg.css"/>
<script src="./js/jquery.min.js"></script>
<script src="./js/bootstrap.min.js"></script>
<script src="./js/jquery.stickytableheaders.min.js"></script>
<script src="./js/readtheorg.js"></script>
<script>MathJax = {
tex: {
tags: 'ams',
macros: {bm: ["\\boldsymbol{#1}",1],}
}
};
</script>
<script type="text/javascript" src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js"></script>
</head>
<body>
<div id="org-div-home-and-up">
<a accesskey="h" href="./index.html"> UP </a>
|
<a accesskey="H" href="./index.html"> HOME </a>
</div><div id="content">
<h1 class="title">Control of the NASS with optimal stiffness</h1>
<div id="table-of-contents">
<h2>Table of Contents</h2>
<div id="text-table-of-contents">
<ul>
<li><a href="#org99c5b6d">1. Low Authority Control - Decentralized Direct Velocity Feedback</a>
<ul>
<li><a href="#orgf3f8aed">1.1. Initialization</a></li>
<li><a href="#orgc5a1e81">1.2. Identification</a></li>
<li><a href="#orgfef1a3f">1.3. Controller Design</a></li>
<li><a href="#org3c73014">1.4. Effect of the Low Authority Control on the Primary Plant</a></li>
<li><a href="#orgee5dbee">1.5. Effect of the Low Authority Control on the Sensibility to Disturbances</a></li>
<li><a href="#org882e1ac">1.6. Conclusion</a></li>
</ul>
</li>
<li><a href="#org81dc0a8">2. Primary Control in the leg space</a>
<ul>
<li><a href="#org1e7a412">2.1. Plant in the leg space</a></li>
<li><a href="#orgf39520c">2.2. Control in the leg space</a></li>
<li><a href="#org16d192f">2.3. Sensibility to Disturbances and Noise Budget</a></li>
<li><a href="#org84f68cc">2.4. Simulations</a></li>
<li><a href="#orgbeadec8">2.5. Results</a></li>
<li><a href="#orgd61852c">2.6. Conclusion</a></li>
</ul>
</li>
<li><a href="#org9bd2bf8">3. Primary Control in the task space</a>
<ul>
<li><a href="#org07b4a9d">3.1. Plant in the task space</a></li>
<li><a href="#org7d888f9">3.2. Control in the task space</a>
<ul>
<li><a href="#orgb28634b">3.2.1. Stability</a></li>
</ul>
</li>
<li><a href="#org57e2cfd">3.3. Simulation</a></li>
<li><a href="#org8c0882d">3.4. Conclusion</a></li>
</ul>
</li>
</ul>
</div>
</div>
<div id="outline-container-org99c5b6d" class="outline-2">
<h2 id="org99c5b6d"><span class="section-number-2">1</span> Low Authority Control - Decentralized Direct Velocity Feedback</h2>
<div class="outline-text-2" id="text-1">
<p>
<a id="orgfec42cb"></a>
</p>
<div id="org7f11a74" class="figure">
<p><img src="figs/control_architecture_dvf.png" alt="control_architecture_dvf.png" />
</p>
<p><span class="figure-number">Figure 1: </span>Low Authority Control: Decentralized Direct Velocity Feedback</p>
</div>
</div>
<div id="outline-container-orgf3f8aed" class="outline-3">
<h3 id="orgf3f8aed"><span class="section-number-3">1.1</span> Initialization</h3>
<div class="outline-text-3" id="text-1-1">
<div class="org-src-container">
<pre class="src src-matlab">initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();
initializeAxisc();
initializeMirror();
initializeSimscapeConfiguration();
initializeDisturbances(<span class="org-string">'enable'</span>, <span class="org-constant">false</span>);
initializeLoggingConfiguration(<span class="org-string">'log'</span>, <span class="org-string">'none'</span>);
initializeController(<span class="org-string">'type'</span>, <span class="org-string">'hac-dvf'</span>);
</pre>
</div>
<p>
We set the stiffness of the payload fixation:
</p>
<div class="org-src-container">
<pre class="src src-matlab">Kp = 1e8; <span class="org-comment">% [N/m]</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-orgc5a1e81" class="outline-3">
<h3 id="orgc5a1e81"><span class="section-number-3">1.2</span> Identification</h3>
<div class="outline-text-3" id="text-1-2">
<div class="org-src-container">
<pre class="src src-matlab">K = tf(zeros(6));
Kdvf = tf(zeros(6));
</pre>
</div>
<p>
We identify the system for the following payload masses:
</p>
<div class="org-src-container">
<pre class="src src-matlab">Ms = [1, 10, 50];
</pre>
</div>
<p>
The nano-hexapod has the following leg’s stiffness and damping.
</p>
<div class="org-src-container">
<pre class="src src-matlab">initializeNanoHexapod(<span class="org-string">'k'</span>, 1e5, <span class="org-string">'c'</span>, 2e2);
</pre>
</div>
</div>
</div>
<div id="outline-container-orgfef1a3f" class="outline-3">
<h3 id="orgfef1a3f"><span class="section-number-3">1.3</span> Controller Design</h3>
<div class="outline-text-3" id="text-1-3">
<p>
The obtain dynamics from actuators forces \(\tau_i\) to the relative motion of the legs \(d\mathcal{L}_i\) is shown in Figure <a href="#orgdb7af3b">2</a> for the three considered payload masses.
</p>
<p>
The Root Locus is shown in Figure <a href="#org5814b4f">3</a> and wee see that we have unconditional stability.
</p>
<p>
In order to choose the gain such that we obtain good damping for all the three payload masses, we plot the damping ration of the modes as a function of the gain for all three payload masses in Figure <a href="#orgb16b2c3">4</a>.
</p>
<div id="orgdb7af3b" class="figure">
<p><img src="figs/opt_stiff_dvf_plant.png" alt="opt_stiff_dvf_plant.png" />
</p>
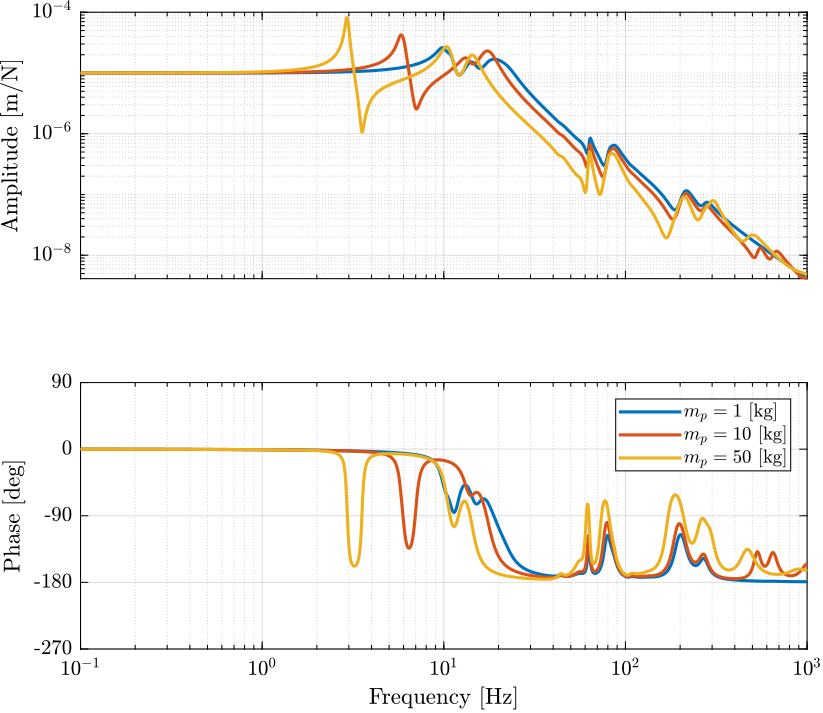
<p><span class="figure-number">Figure 2: </span>Dynamics for the Direct Velocity Feedback active damping for three payload masses</p>
</div>
<div id="org5814b4f" class="figure">
<p><img src="figs/opt_stiff_dvf_root_locus.png" alt="opt_stiff_dvf_root_locus.png" />
</p>
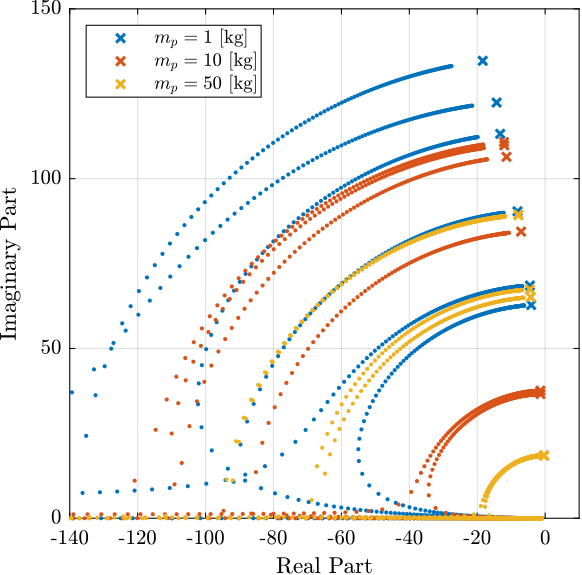
<p><span class="figure-number">Figure 3: </span>Root Locus for the DVF controll for three payload masses</p>
</div>
<p>
Damping as function of the gain
</p>
<div id="orgb16b2c3" class="figure">
<p><img src="figs/opt_stiff_dvf_damping_gain.png" alt="opt_stiff_dvf_damping_gain.png" />
</p>
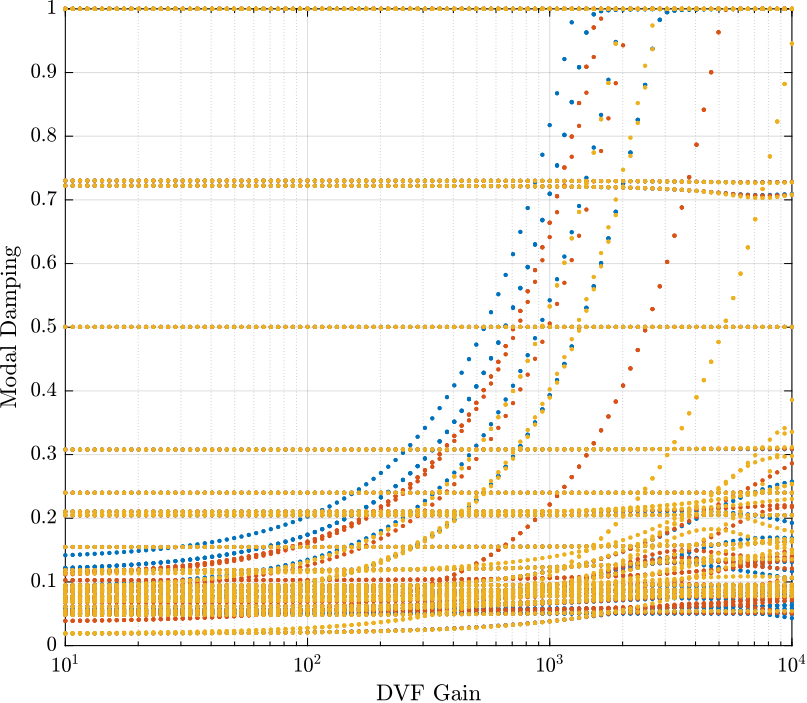
<p><span class="figure-number">Figure 4: </span>Damping ratio of the poles as a function of the DVF gain</p>
</div>
<p>
Finally, we use the following controller for the Decentralized Direct Velocity Feedback:
</p>
<div class="org-src-container">
<pre class="src src-matlab">Kdvf = 5e3<span class="org-type">*</span>s<span class="org-type">/</span>(1<span class="org-type">+</span>s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>1e3)<span class="org-type">*</span>eye(6);
</pre>
</div>
</div>
</div>
<div id="outline-container-org3c73014" class="outline-3">
<h3 id="org3c73014"><span class="section-number-3">1.4</span> Effect of the Low Authority Control on the Primary Plant</h3>
<div class="outline-text-3" id="text-1-4">
<p>
Let’s identify the dynamics from actuator forces \(\bm{\tau}\) to displacement as measured by the metrology \(\bm{\mathcal{X}}\):
\[ \bm{G}(s) = \frac{\bm{\mathcal{X}}}{\bm{\tau}} \]
We do so both when the DVF is applied and when it is not applied.
</p>
<p>
Then, we compute the transfer function from forces applied by the actuators \(\bm{\mathcal{F}}\) to the measured position error in the frame of the nano-hexapod \(\bm{\epsilon}_{\mathcal{X}_n}\):
\[ \bm{G}_\mathcal{X}(s) = \frac{\bm{\epsilon}_{\mathcal{X}_n}}{\bm{\mathcal{F}}} = \bm{G}(s) \bm{J}^{-T} \]
The obtained dynamics is shown in Figure <a href="#org45c1265">5</a>.
</p>
<div class="important">
<p>
A zero with a positive real part is introduced in the transfer function from \(\mathcal{F}_y\) to \(\mathcal{X}_y\) after Decentralized Direct Velocity Feedback is applied.
</p>
</div>
<p>
And we compute the transfer function from actuator forces \(\bm{\tau}\) to position error of each leg \(\bm{\epsilon}_\mathcal{L}\):
\[ \bm{G}_\mathcal{L} = \frac{\bm{\epsilon}_\mathcal{L}}{\bm{\tau}} = \bm{J} \bm{G}(s) \]
The obtained dynamics is shown in Figure <a href="#org069e296">6</a>.
</p>
<div id="org45c1265" class="figure">
<p><img src="figs/opt_stiff_primary_plant_damped_X.png" alt="opt_stiff_primary_plant_damped_X.png" />
</p>
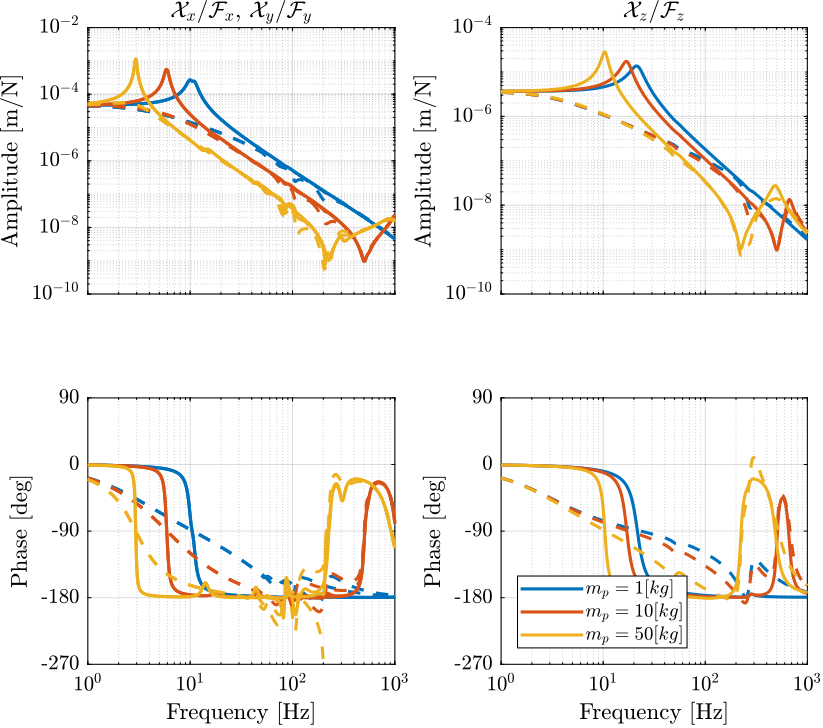
<p><span class="figure-number">Figure 5: </span>Primary plant in the task space with (dashed) and without (solid) Direct Velocity Feedback</p>
</div>
<div id="org069e296" class="figure">
<p><img src="figs/opt_stiff_primary_plant_damped_L.png" alt="opt_stiff_primary_plant_damped_L.png" />
</p>
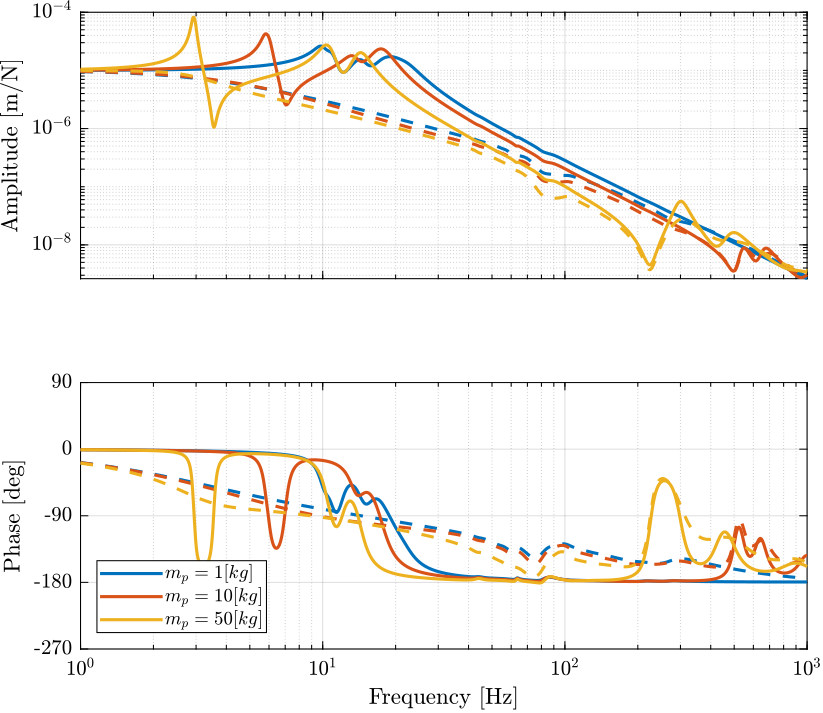
<p><span class="figure-number">Figure 6: </span>Primary plant in the space of the legs with (dashed) and without (solid) Direct Velocity Feedback</p>
</div>
<p>
The coupling (off diagonal elements) of \(\bm{G}_\mathcal{X}\) are shown in Figure <a href="#orgbb4e497">7</a> both when DVF is applied and when it is not.
</p>
<p>
The coupling does not change a lot with DVF.
</p>
<p>
The coupling in the space of the legs \(\bm{G}_\mathcal{L}\) are shown in Figure <a href="#orgc43d759">8</a>.
</p>
<div class="important">
<p>
The magnitude of the coupling between \(\tau_i\) and \(d\mathcal{L}_j\) (Figure <a href="#orgc43d759">8</a>) around the resonance of the nano-hexapod (where the coupling is the highest) is considerably reduced when DVF is applied.
</p>
</div>
<div id="orgbb4e497" class="figure">
<p><img src="figs/opt_stiff_primary_plant_damped_coupling_X.png" alt="opt_stiff_primary_plant_damped_coupling_X.png" />
</p>
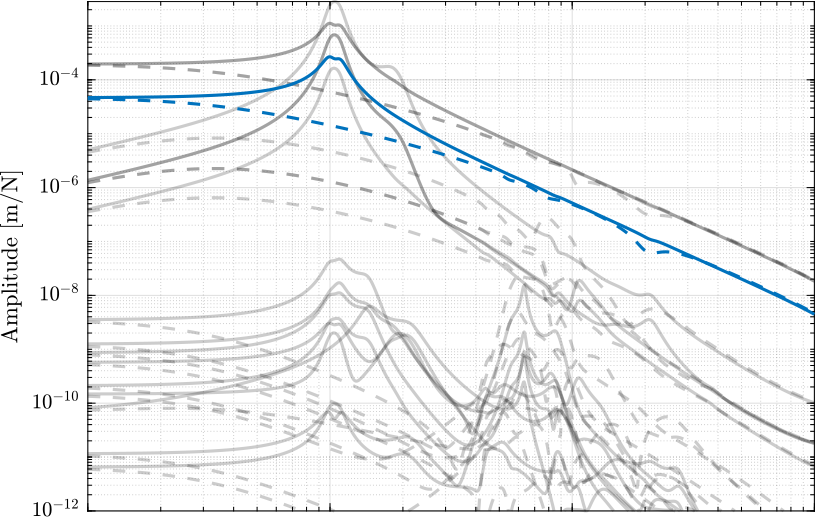
<p><span class="figure-number">Figure 7: </span>Coupling in the primary plant in the task with (dashed) and without (solid) Direct Velocity Feedback</p>
</div>
<div id="orgc43d759" class="figure">
<p><img src="figs/opt_stiff_primary_plant_damped_coupling_L.png" alt="opt_stiff_primary_plant_damped_coupling_L.png" />
</p>
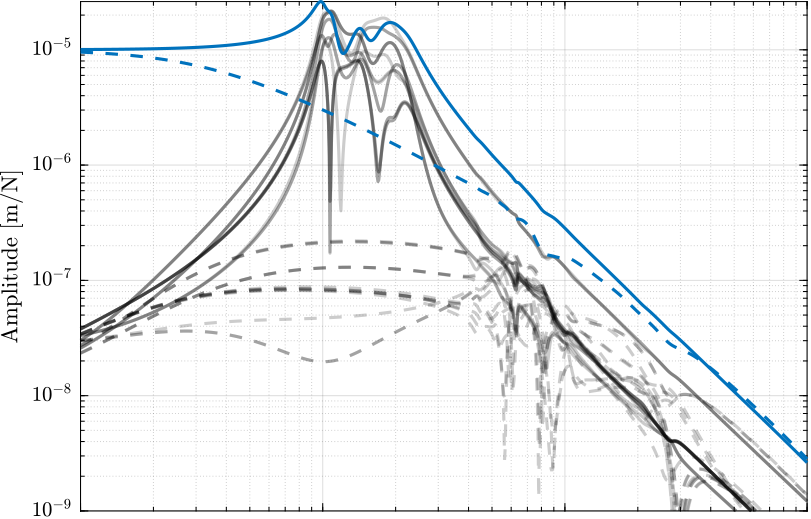
<p><span class="figure-number">Figure 8: </span>Coupling in the primary plant in the space of the legs with (dashed) and without (solid) Direct Velocity Feedback</p>
</div>
</div>
</div>
<div id="outline-container-orgee5dbee" class="outline-3">
<h3 id="orgee5dbee"><span class="section-number-3">1.5</span> Effect of the Low Authority Control on the Sensibility to Disturbances</h3>
<div class="outline-text-3" id="text-1-5">
<p>
We may now see how Decentralized Direct Velocity Feedback changes the sensibility to disturbances, namely:
</p>
<ul class="org-ul">
<li>Ground motion</li>
<li>Spindle and Translation stage vibrations</li>
<li>Direct forces applied to the sample</li>
</ul>
<p>
To simplify the analysis, we here only consider the vertical direction, thus, we will look at the transfer functions:
</p>
<ul class="org-ul">
<li>from vertical ground motion \(D_{w,z}\) to the vertical position error of the sample \(E_z\)</li>
<li>from vertical vibration forces of the spindle \(F_{R_z,z}\) to \(E_z\)</li>
<li>from vertical vibration forces of the translation stage \(F_{T_y,z}\) to \(E_z\)</li>
<li>from vertical direct forces (such as cable forces) \(F_{d,z}\) to \(E_z\)</li>
</ul>
<p>
The norm of these transfer functions are shown in Figure <a href="#org199898b">9</a>.
</p>
<div id="org199898b" class="figure">
<p><img src="figs/opt_stiff_sensibility_dist_dvf.png" alt="opt_stiff_sensibility_dist_dvf.png" />
</p>
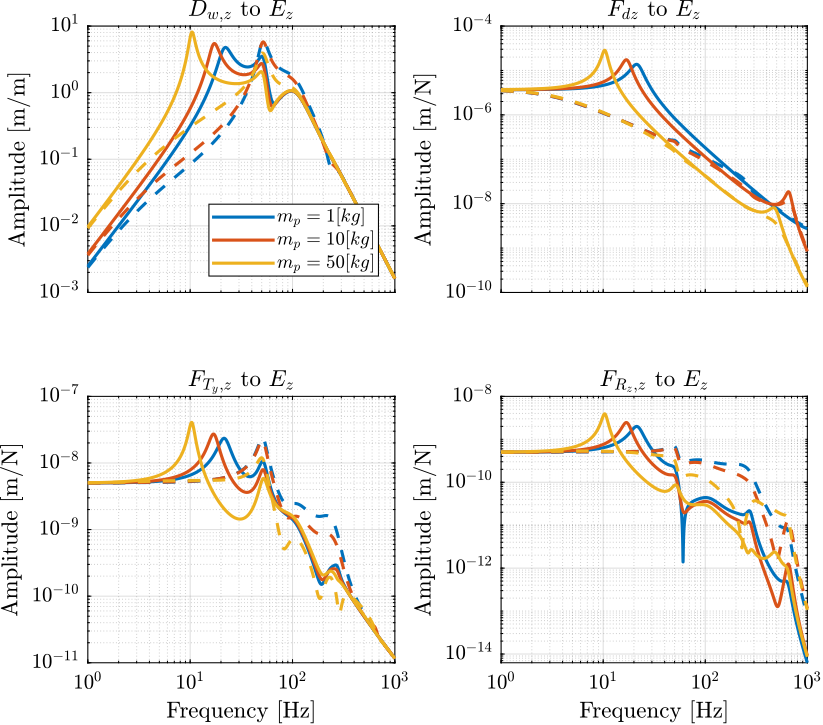
<p><span class="figure-number">Figure 9: </span>Norm of the transfer function from vertical disturbances to vertical position error with (dashed) and without (solid) Direct Velocity Feedback applied</p>
</div>
<div class="important">
<p>
Decentralized Direct Velocity Feedback is shown to increase the effect of stages vibrations at high frequency and to reduce the effect of ground motion and direct forces at low frequency.
</p>
</div>
</div>
</div>
<div id="outline-container-org882e1ac" class="outline-3">
<h3 id="org882e1ac"><span class="section-number-3">1.6</span> Conclusion</h3>
<div class="outline-text-3" id="text-1-6">
<div class="important">
<p>
</p>
</div>
</div>
</div>
</div>
<div id="outline-container-org81dc0a8" class="outline-2">
<h2 id="org81dc0a8"><span class="section-number-2">2</span> Primary Control in the leg space</h2>
<div class="outline-text-2" id="text-2">
<p>
<a id="orgd0beb6a"></a>
</p>
<p>
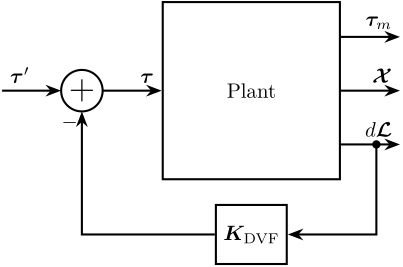
In this section we implement the control architecture shown in Figure <a href="#org7d5c8bc">10</a> consisting of:
</p>
<ul class="org-ul">
<li>an inner loop with a decentralized direct velocity feedback control</li>
<li>an outer loop where the controller \(\bm{K}_\mathcal{L}\) is designed in the frame of the legs</li>
</ul>
<div id="org7d5c8bc" class="figure">
<p><img src="figs/control_architecture_hac_dvf_pos_L.png" alt="control_architecture_hac_dvf_pos_L.png" />
</p>
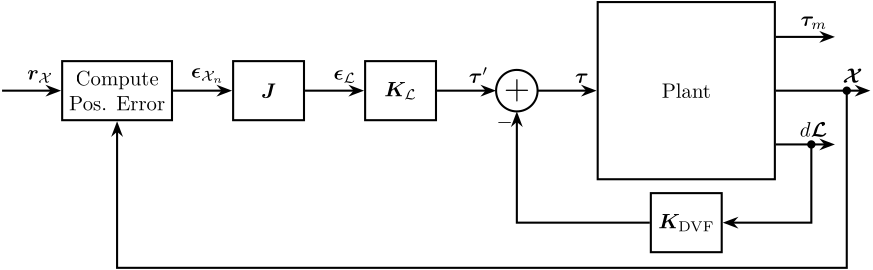
<p><span class="figure-number">Figure 10: </span>Cascade Control Architecture. The inner loop consist of a decentralized Direct Velocity Feedback. The outer loop consist of position control in the leg’s space</p>
</div>
<p>
The controller for decentralized direct velocity feedback is the one designed in Section <a href="#orgfec42cb">1</a>.
</p>
</div>
<div id="outline-container-org1e7a412" class="outline-3">
<h3 id="org1e7a412"><span class="section-number-3">2.1</span> Plant in the leg space</h3>
<div class="outline-text-3" id="text-2-1">
<p>
We now look at the transfer function matrix from \(\bm{\tau}^\prime\) to \(\bm{\epsilon}_{\mathcal{X}_n}\) for the design of \(\bm{K}_\mathcal{L}\).
</p>
<p>
The diagonal elements of the transfer function matrix from \(\bm{\tau}^\prime\) to \(\bm{\epsilon}_{\mathcal{X}_n}\) for the three considered masses are shown in Figure <a href="#org23d23ae">11</a>.
</p>
<p>
The plant dynamics below \(100\ [Hz]\) is only slightly dependent on the payload mass.
</p>
<div id="org23d23ae" class="figure">
<p><img src="figs/opt_stiff_primary_plant_L.png" alt="opt_stiff_primary_plant_L.png" />
</p>
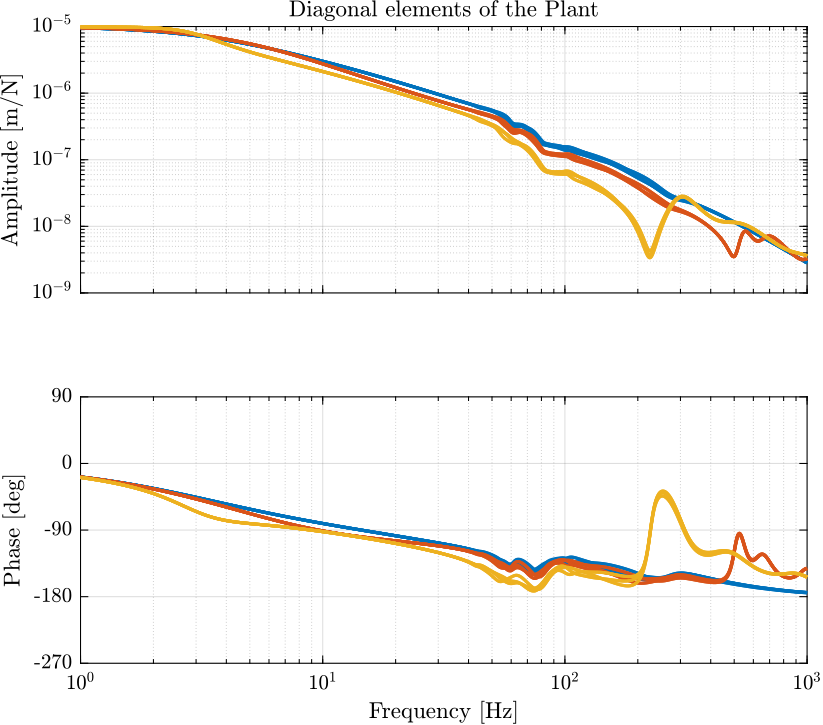
<p><span class="figure-number">Figure 11: </span>Diagonal elements of the transfer function matrix from \(\bm{\tau}^\prime\) to \(\bm{\epsilon}_{\mathcal{X}_n}\) for the three considered masses</p>
</div>
</div>
</div>
<div id="outline-container-orgf39520c" class="outline-3">
<h3 id="orgf39520c"><span class="section-number-3">2.2</span> Control in the leg space</h3>
<div class="outline-text-3" id="text-2-2">
<p>
We design a diagonal controller with all the same diagonal elements.
</p>
<p>
The requirements for the controller are:
</p>
<ul class="org-ul">
<li>Crossover frequency of around 100Hz</li>
<li>Stable for all the considered payload masses</li>
<li>Sufficient phase and gain margin</li>
<li>Integral action at low frequency</li>
</ul>
<p>
The design controller is as follows:
</p>
<ul class="org-ul">
<li>Lead centered around the crossover</li>
<li>An integrator below 10Hz</li>
<li>A low pass filter at 250Hz</li>
</ul>
<p>
The loop gain is shown in Figure <a href="#orgbcc0acb">12</a>.
</p>
<div class="org-src-container">
<pre class="src src-matlab">h = 2.0;
Kl = 2e7 <span class="org-type">*</span> eye(6) <span class="org-type">*</span> ...
1<span class="org-type">/</span>h<span class="org-type">*</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>100<span class="org-type">/</span>h) <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>100<span class="org-type">*</span>h) <span class="org-type">+</span> 1) <span class="org-type">*</span> ...
1<span class="org-type">/</span>h<span class="org-type">*</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>200<span class="org-type">/</span>h) <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>200<span class="org-type">*</span>h) <span class="org-type">+</span> 1) <span class="org-type">*</span> ...
(s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>10 <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>10) <span class="org-type">*</span> ...
1<span class="org-type">/</span>(1 <span class="org-type">+</span> s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>300);
</pre>
</div>
<div id="orgbcc0acb" class="figure">
<p><img src="figs/opt_stiff_primary_loop_gain_L.png" alt="opt_stiff_primary_loop_gain_L.png" />
</p>
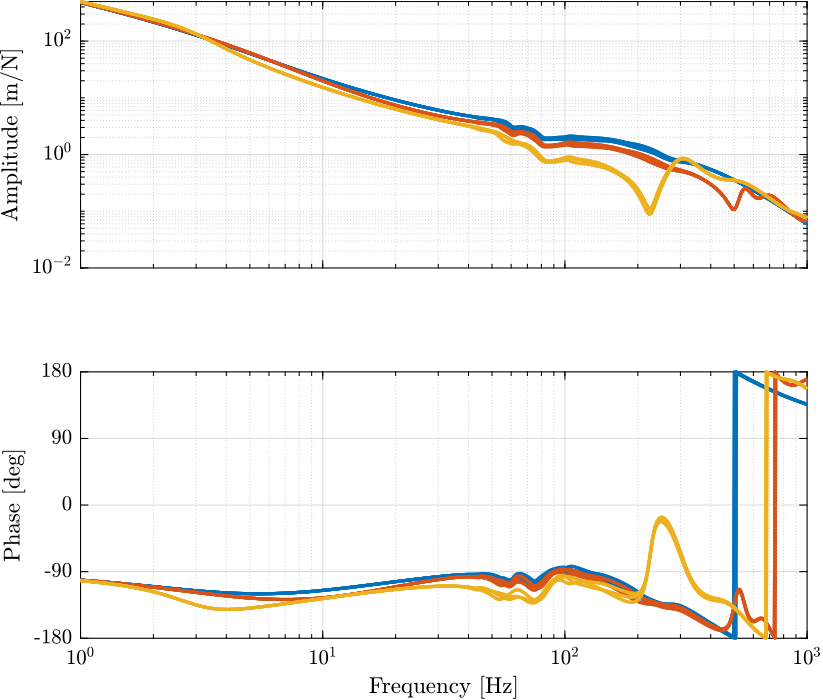
<p><span class="figure-number">Figure 12: </span>Loop gain for the primary plant</p>
</div>
<p>
Finally, we include the Jacobian in the control and we ignore the measurement of the vertical rotation as for the real system.
</p>
<div class="org-src-container">
<pre class="src src-matlab">load(<span class="org-string">'mat/stages.mat'</span>, <span class="org-string">'nano_hexapod'</span>);
K = Kl<span class="org-type">*</span>nano_hexapod.J<span class="org-type">*</span>diag([1, 1, 1, 1, 1, 0]);
</pre>
</div>
</div>
</div>
<div id="outline-container-org16d192f" class="outline-3">
<h3 id="org16d192f"><span class="section-number-3">2.3</span> Sensibility to Disturbances and Noise Budget</h3>
<div class="outline-text-3" id="text-2-3">
<p>
We identify the transfer function from disturbances to the position error of the sample when the HAC-LAC control is applied.
</p>
<p>
We compare the norm of these transfer function for the vertical direction when no control is applied and when HAC-LAC control is applied: Figure <a href="#org9650e03">13</a>.
</p>
<div id="org9650e03" class="figure">
<p><img src="figs/opt_stiff_primary_control_L_senbility_dist.png" alt="opt_stiff_primary_control_L_senbility_dist.png" />
</p>
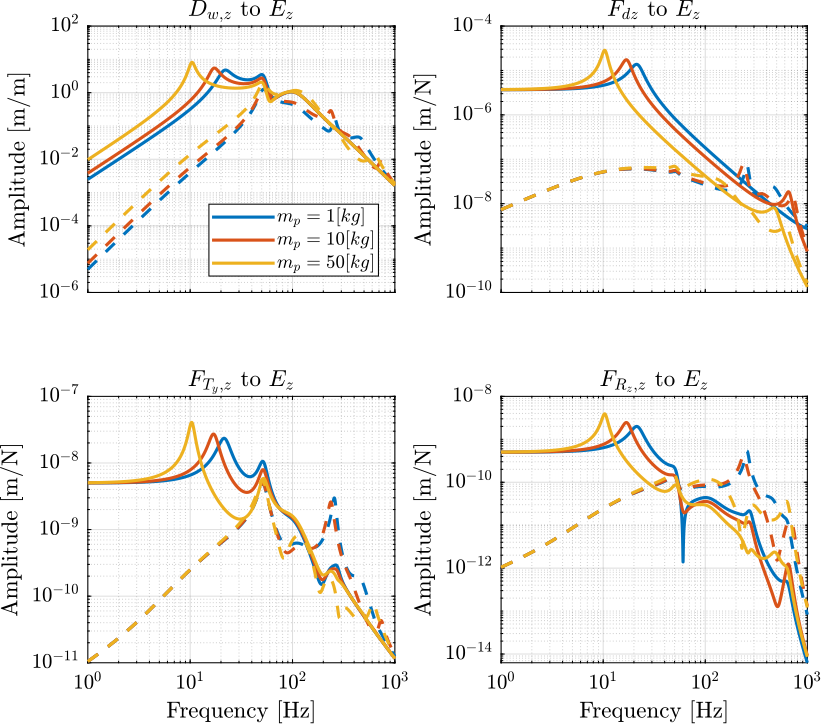
<p><span class="figure-number">Figure 13: </span>Sensibility to disturbances when the HAC-LAC control is applied</p>
</div>
<p>
Then, we load the Power Spectral Density of the perturbations and we look at the obtained PSD of the displacement error in the vertical direction due to the disturbances:
</p>
<ul class="org-ul">
<li>Figure <a href="#org32928e0">14</a>: Amplitude Spectral Density of the vertical position error due to both the vertical ground motion and the vertical vibrations of the spindle</li>
<li>Figure <a href="#org7fda8f7">15</a>: Comparison of the Amplitude Spectral Density of the vertical position error in Open Loop and with the HAC-DVF Control</li>
<li>Figure <a href="#org073608b">16</a>: Comparison of the Cumulative Amplitude Spectrum of the vertical position error in Open Loop and with the HAC-DVF Control</li>
</ul>
<div id="org32928e0" class="figure">
<p><img src="figs/opt_stiff_primary_control_L_psd_dist.png" alt="opt_stiff_primary_control_L_psd_dist.png" />
</p>
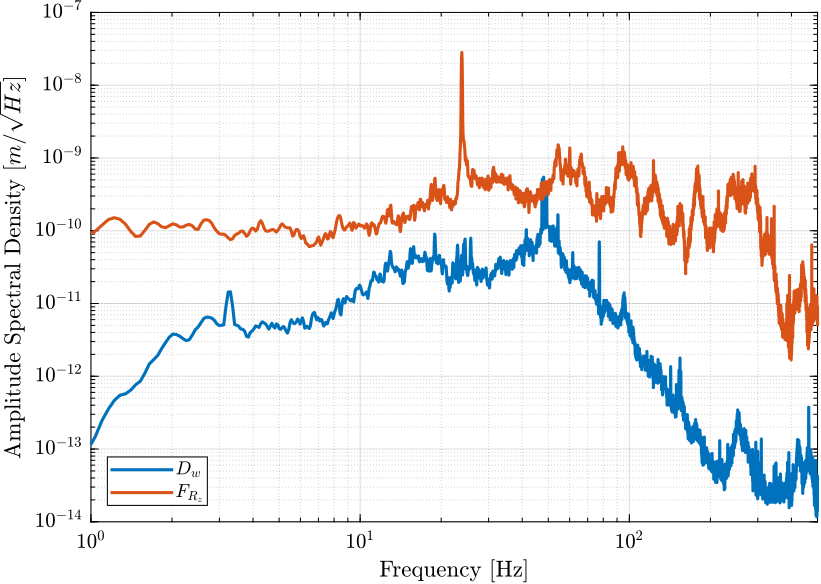
<p><span class="figure-number">Figure 14: </span>Amplitude Spectral Density of the vertical position error of the sample when the HAC-DVF control is applied due to both the ground motion and spindle vibrations</p>
</div>
<div id="org7fda8f7" class="figure">
<p><img src="figs/opt_stiff_primary_control_L_psd_tot.png" alt="opt_stiff_primary_control_L_psd_tot.png" />
</p>
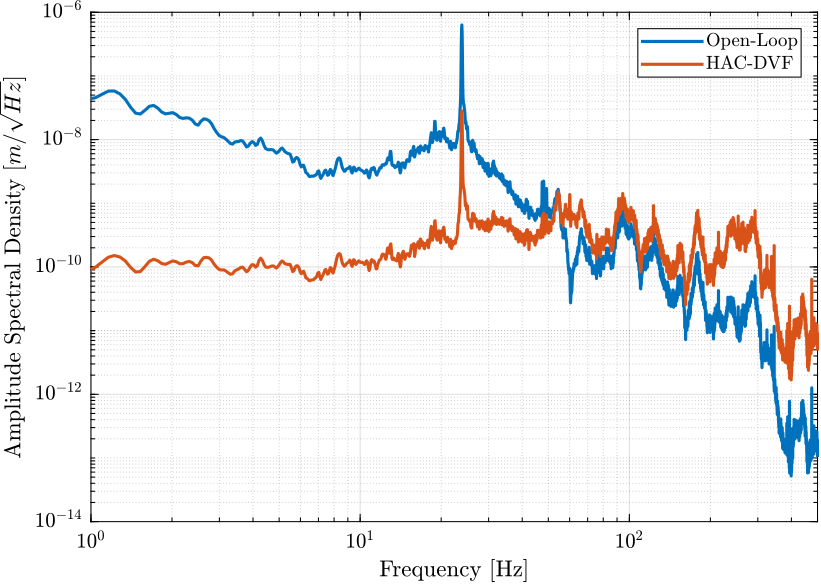
<p><span class="figure-number">Figure 15: </span>Amplitude Spectral Density of the vertical position error of the sample in Open-Loop and when the HAC-DVF control is applied</p>
</div>
<div id="org073608b" class="figure">
<p><img src="figs/opt_stiff_primary_control_L_cas_tot.png" alt="opt_stiff_primary_control_L_cas_tot.png" />
</p>
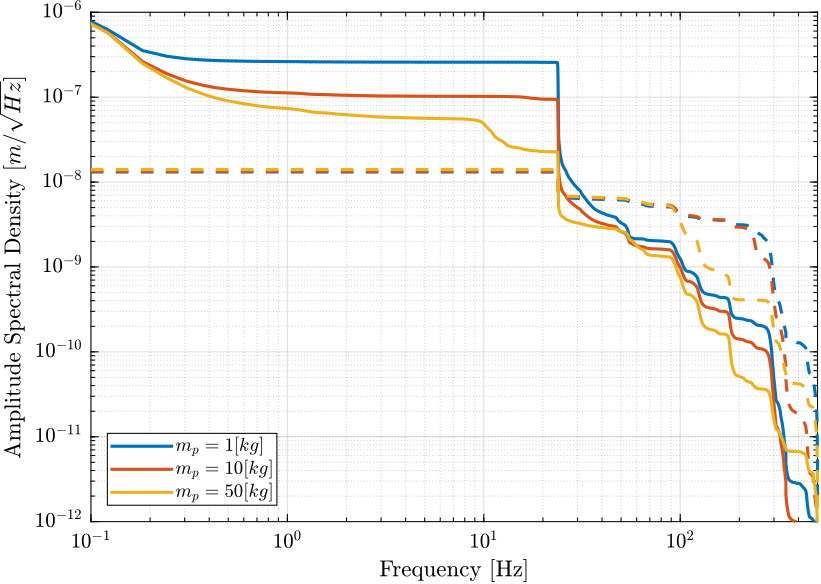
<p><span class="figure-number">Figure 16: </span>Cumulative Amplitude Spectrum of the vertical position error of the sample in Open-Loop and when the HAC-DVF control is applied</p>
</div>
</div>
</div>
<div id="outline-container-org84f68cc" class="outline-3">
<h3 id="org84f68cc"><span class="section-number-3">2.4</span> Simulations</h3>
<div class="outline-text-3" id="text-2-4">
<p>
Let’s now simulate a tomography experiment.
To do so, we include all disturbances except vibrations of the translation stage.
</p>
<div class="org-src-container">
<pre class="src src-matlab">initializeDisturbances();
initializeSimscapeConfiguration(<span class="org-string">'gravity'</span>, <span class="org-constant">false</span>);
initializeLoggingConfiguration(<span class="org-string">'log'</span>, <span class="org-string">'all'</span>);
</pre>
</div>
<p>
And we run the simulation for all three payload Masses.
</p>
</div>
</div>
<div id="outline-container-orgbeadec8" class="outline-3">
<h3 id="orgbeadec8"><span class="section-number-3">2.5</span> Results</h3>
<div class="outline-text-3" id="text-2-5">
<p>
Let’s now see how this controller performs.
</p>
<p>
First, we compute the Power Spectral Density of the sample’s position error and we compare it with the open loop case in Figure <a href="#org6cab6ef">17</a>.
</p>
<p>
Similarly, the Cumulative Amplitude Spectrum is shown in Figure <a href="#org33e9f1a">18</a>.
</p>
<p>
Finally, the time domain position error signals are shown in Figure <a href="#orgf0f1950">19</a>.
</p>
<div id="org6cab6ef" class="figure">
<p><img src="figs/opt_stiff_hac_dvf_L_psd_disp_error.png" alt="opt_stiff_hac_dvf_L_psd_disp_error.png" />
</p>
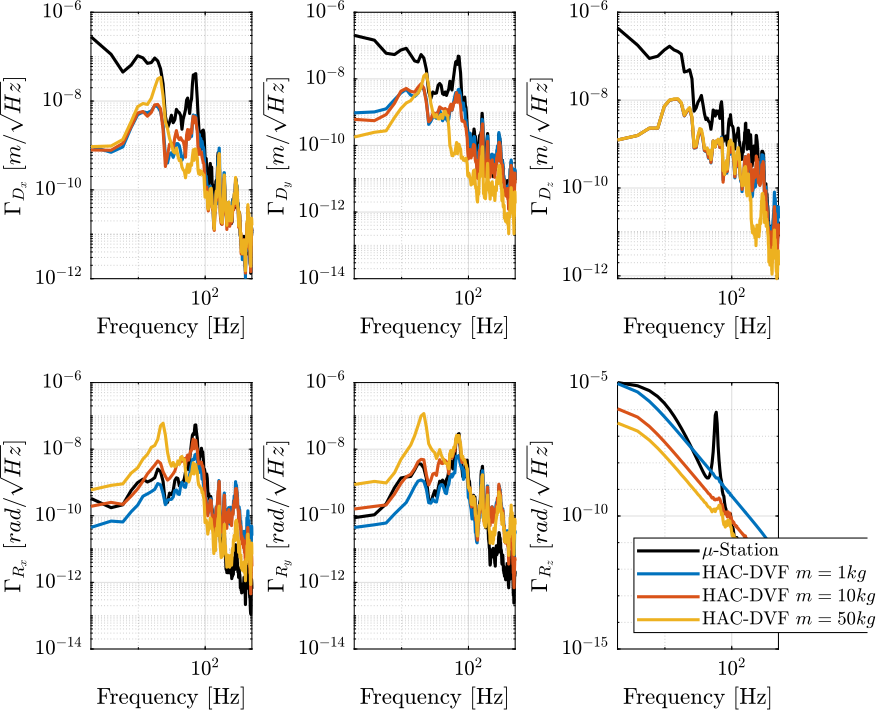
<p><span class="figure-number">Figure 17: </span>Amplitude Spectral Density of the position error in Open Loop and with the HAC-LAC controller</p>
</div>
<div id="org33e9f1a" class="figure">
<p><img src="figs/opt_stiff_hac_dvf_L_cas_disp_error.png" alt="opt_stiff_hac_dvf_L_cas_disp_error.png" />
</p>
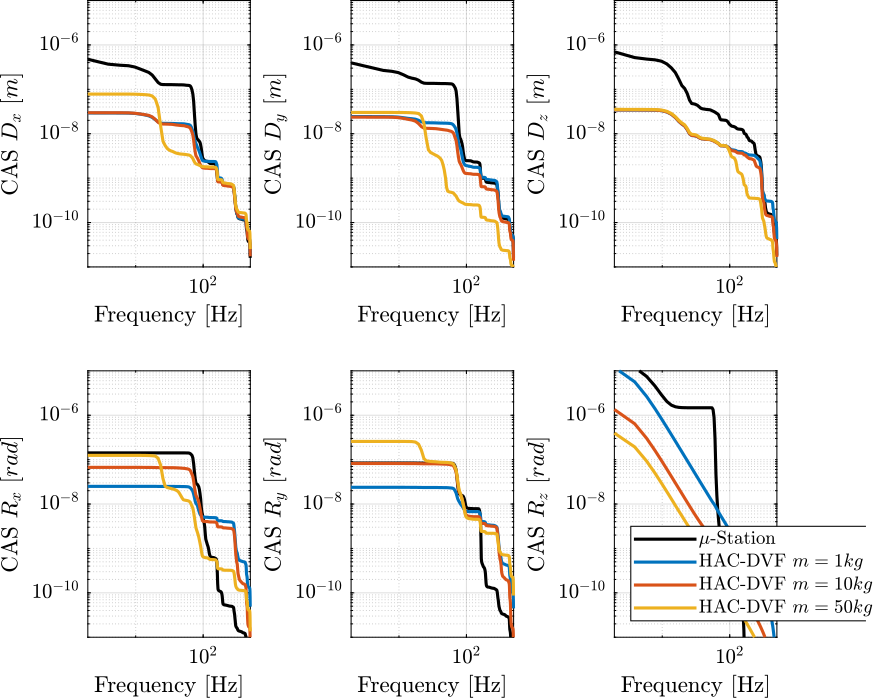
<p><span class="figure-number">Figure 18: </span>Cumulative Amplitude Spectrum of the position error in Open Loop and with the HAC-LAC controller</p>
</div>
<div id="orgf0f1950" class="figure">
<p><img src="figs/opt_stiff_hac_dvf_L_pos_error.png" alt="opt_stiff_hac_dvf_L_pos_error.png" />
</p>
<p><span class="figure-number">Figure 19: </span>Position Error of the sample during a tomography experiment when no control is applied and with the HAC-DVF control architecture</p>
</div>
</div>
</div>
<div id="outline-container-orgd61852c" class="outline-3">
<h3 id="orgd61852c"><span class="section-number-3">2.6</span> Conclusion</h3>
<div class="outline-text-3" id="text-2-6">
<div class="important">
<p>
</p>
</div>
</div>
</div>
</div>
<div id="outline-container-org9bd2bf8" class="outline-2">
<h2 id="org9bd2bf8"><span class="section-number-2">3</span> Primary Control in the task space</h2>
<div class="outline-text-2" id="text-3">
<p>
<a id="orge9c2f9a"></a>
</p>
<p>
In this section, the control architecture shown in Figure <a href="#org7e70ccc">20</a> is applied and consists of:
</p>
<ul class="org-ul">
<li>an inner Low Authority Control loop consisting of a decentralized direct velocity control controller</li>
<li>an outer loop with the primary controller \(\bm{K}_\mathcal{X}\) designed in the task space</li>
</ul>
<div id="org7e70ccc" class="figure">
<p><img src="figs/control_architecture_hac_dvf_pos_X.png" alt="control_architecture_hac_dvf_pos_X.png" />
</p>
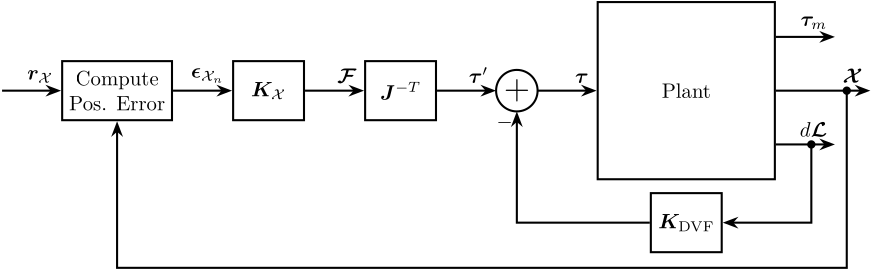
<p><span class="figure-number">Figure 20: </span>HAC-LAC architecture</p>
</div>
</div>
<div id="outline-container-org07b4a9d" class="outline-3">
<h3 id="org07b4a9d"><span class="section-number-3">3.1</span> Plant in the task space</h3>
<div class="outline-text-3" id="text-3-1">
<p>
Let’s look \(\bm{G}_\mathcal{X}(s)\).
</p>
</div>
</div>
<div id="outline-container-org7d888f9" class="outline-3">
<h3 id="org7d888f9"><span class="section-number-3">3.2</span> Control in the task space</h3>
<div class="outline-text-3" id="text-3-2">
<div class="org-src-container">
<pre class="src src-matlab">Kx = tf(zeros(6));
h = 2.5;
Kx<span class="org-type">(1,1) </span>= 3e7 <span class="org-type">*</span> ...
1<span class="org-type">/</span>h<span class="org-type">*</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>100<span class="org-type">/</span>h) <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>100<span class="org-type">*</span>h) <span class="org-type">+</span> 1) <span class="org-type">*</span> ...
(s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>1 <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>1);
Kx<span class="org-type">(2,2) </span>= Kx(1,1);
h = 2.5;
Kx<span class="org-type">(3,3) </span>= 3e7 <span class="org-type">*</span> ...
1<span class="org-type">/</span>h<span class="org-type">*</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>100<span class="org-type">/</span>h) <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>100<span class="org-type">*</span>h) <span class="org-type">+</span> 1) <span class="org-type">*</span> ...
(s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>1 <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>1);
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">h = 1.5;
Kx<span class="org-type">(4,4) </span>= 5e5 <span class="org-type">*</span> ...
1<span class="org-type">/</span>h<span class="org-type">*</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>100<span class="org-type">/</span>h) <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>100<span class="org-type">*</span>h) <span class="org-type">+</span> 1) <span class="org-type">*</span> ...
(s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>1 <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>1);
Kx<span class="org-type">(5,5) </span>= Kx(4,4);
h = 1.5;
Kx<span class="org-type">(6,6) </span>= 5e4 <span class="org-type">*</span> ...
1<span class="org-type">/</span>h<span class="org-type">*</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>30<span class="org-type">/</span>h) <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>(2<span class="org-type">*</span><span class="org-constant">pi</span><span class="org-type">*</span>30<span class="org-type">*</span>h) <span class="org-type">+</span> 1) <span class="org-type">*</span> ...
(s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>1 <span class="org-type">+</span> 1)<span class="org-type">/</span>(s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>1);
</pre>
</div>
</div>
<div id="outline-container-orgb28634b" class="outline-4">
<h4 id="orgb28634b"><span class="section-number-4">3.2.1</span> Stability</h4>
<div class="outline-text-4" id="text-3-2-1">
<div class="org-src-container">
<pre class="src src-matlab"><span class="org-keyword">for</span> <span class="org-variable-name"><span class="org-constant">i</span></span> = <span class="org-constant">1:length(Ms)</span>
isstable(feedback(Gm_x{<span class="org-constant">i</span>}<span class="org-type">*</span>Kx, eye(6), <span class="org-type">-</span>1))
<span class="org-keyword">end</span>
</pre>
</div>
</div>
</div>
</div>
<div id="outline-container-org57e2cfd" class="outline-3">
<h3 id="org57e2cfd"><span class="section-number-3">3.3</span> Simulation</h3>
</div>
<div id="outline-container-org8c0882d" class="outline-3">
<h3 id="org8c0882d"><span class="section-number-3">3.4</span> Conclusion</h3>
<div class="outline-text-3" id="text-3-4">
<div class="important">
<p>
</p>
</div>
</div>
</div>
</div>
</div>
<div id="postamble" class="status">
<p class="author">Author: Dehaeze Thomas</p>
<p class="date">Created: 2020-04-17 ven. 14:10</p>
</div>
</body>
</html>