Compensating the gravity forces to start at steady state
Table of Contents
In this file is shown a technique used to compensate the gravity forces at t=0.
The problem is that in presence of gravity, the system does not start at steady state and experience a transient phase (section 2).
In order to start the simulation at steady state in presence of gravity:
- section 3: first the stages are initialize in such a way that they are rigid, and the forces/torques applied at the location of their joints is measured
- section 4: Then, the equilibrium position of each joint is modified in such a way that at t=0, the forces in each joints exactly compensate the forces due to gravity forces
1 Initialization of the Experimental Conditions
We don’t inject any perturbations and no reference tracking.
initializeReferences(); initializeDisturbances('enable', false); initializeController();
We include the gravity and log all the signals to display.
initializeSimscapeConfiguration('gravity', true); initializeLoggingConfiguration('log', 'all');
2 Without compensation
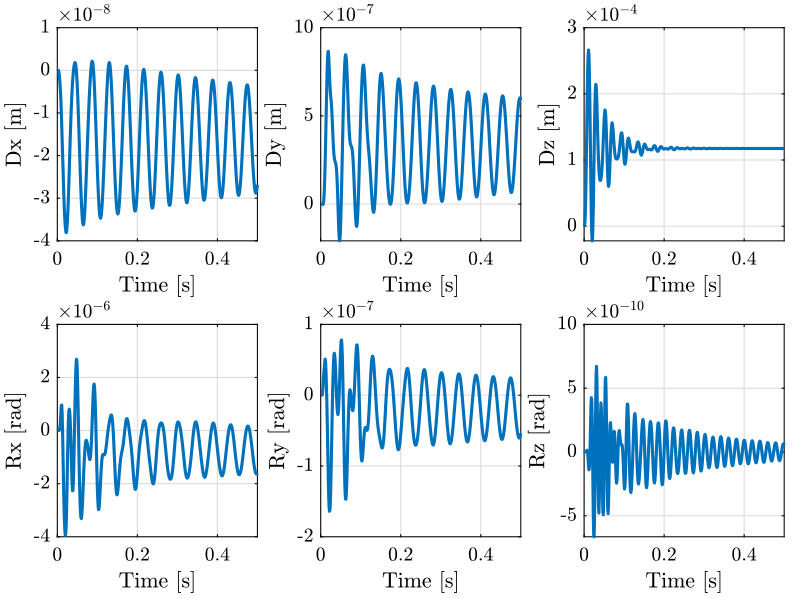
Let’s simulate the system without any compensation of gravity forces.
initializeGround(); initializeGranite(); initializeTy(); initializeRy(); initializeRz(); initializeMicroHexapod(); initializeAxisc(); initializeMirror(); initializeNanoHexapod(); initializeSample();
load('mat/conf_simulink.mat'); set_param(conf_simulink, 'StopTime', '0.5');
sim('nass_model'); sim_no_compensation = simout;
And we can observe on Figure 1 that there are some motion in the system.
3 Simulation to compute the required force in each joint
We here wish to simulate the system in order to compute the required force in each joint to compensate the gravity forces.
initializeGround(); initializeGranite('type', 'init'); initializeTy('type', 'init'); initializeRy('type', 'init'); initializeRz('type', 'init'); initializeMicroHexapod('type', 'init'); initializeAxisc(); initializeMirror(); initializeNanoHexapod('type', 'init'); initializeSample('type', 'init');
We simulate for a short time period (all the bodies are solid, so nothing should move).
load('mat/conf_simulink.mat'); set_param(conf_simulink, 'StopTime', '0.1');
sim('nass_model');
Verification that nothing is moving by looking at the maximum displacement of the sample:
max(max(simout.Em.En.Data))
1.0681e-15
We here show the measured total force/torque applied at the location of each joint.
data2orgtable([Fgm 0 0 0; Ftym; Fym; Fsm], {'Granite', 'Translation Stage', 'Tilt Stage', 'Sample'}, {'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz'}, ' %.1e ');
| Fx | Fy | Fz | Mx | My | Mz | |
|---|---|---|---|---|---|---|
| Granite | -7.6e-12 | 1.2e-11 | -34000.0 | 0.0 | 0.0 | 0.0 |
| Translation Stage | -7.6e-12 | 1.2e-11 | -12000.0 | 31.0 | 2.5 | 6.6e-13 |
| Tilt Stage | -7.6e-12 | 1.2e-11 | -8800.0 | 33.0 | -0.52 | 6.6e-13 |
| Sample | -5.7e-12 | 1.3e-11 | -490.0 | -2.5e-12 | -8.1e-13 | 2.7e-13 |
data2orgtable([Fhm; Fnm], {'Micro-Hexapod', 'Nano-Hexapod'}, {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'}, ' %.1e ');
| F1 | F2 | F3 | F4 | F5 | F6 | |
|---|---|---|---|---|---|---|
| Micro-Hexapod | -180.0 | -180.0 | -180.0 | -180.0 | -180.0 | -180.0 |
| Nano-Hexapod | -160.0 | -160.0 | -160.0 | -160.0 | -160.0 | -160.0 |
We save these forces in Foffset.mat.
save('mat/Foffset.mat', 'Fgm', 'Ftym', 'Fym', 'Fzm', 'Fhm', 'Fnm', 'Fsm');
4 New simulation with compensation of gravity forces
We now initialize the stages with the option Foffset.
initializeGround(); initializeGranite('Foffset', true); initializeTy('Foffset', true); initializeRy('Foffset', true); initializeRz('Foffset', true); initializeMicroHexapod('Foffset', true); initializeAxisc(); initializeMirror(); initializeNanoHexapod('Foffset', true); initializeSample('Foffset', true);
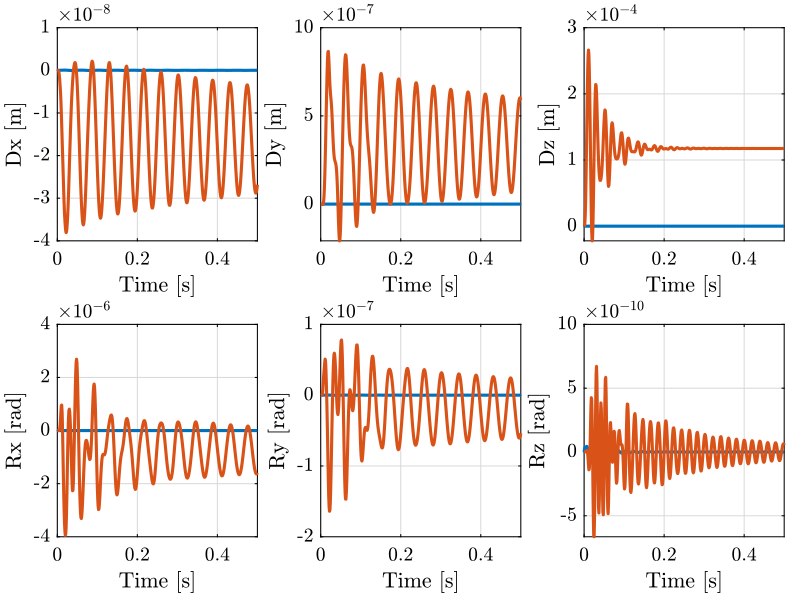
And we simulate the system for 0.5 seconds.
load('mat/conf_simulink.mat'); set_param(conf_simulink, 'StopTime', '0.5');
sim('nass_model'); sim_compensation = simout;
Verification that nothing is moving
5 Conclusion
This initialization technique permits to compute the required forces/torques to be applied in each joint in order to compensate for gravity forces. This initialization should be redone for each configuration (change of sample mass, change of tilt angle), but not when changing the stiffness of joints, for instant when changing from lorentz based nano-hexapod or piezo based.