<?xml version="1.0" encoding="utf-8"?>
<?xml version="1.0" encoding="utf-8"?>
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN"
"http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<!-- 2020-04-05 dim. 19:43 -->
<meta http-equiv="Content-Type" content="text/html;charset=utf-8" />
<meta name="viewport" content="width=device-width, initial-scale=1" />
<title>Determination of the optimal nano-hexapod’s stiffness</title>
<meta name="generator" content="Org mode" />
<meta name="author" content="Dehaeze Thomas" />
<style type="text/css">
<!--/*--><![CDATA[/*><!--*/
.title { text-align: center;
margin-bottom: .2em; }
.subtitle { text-align: center;
font-size: medium;
font-weight: bold;
margin-top:0; }
.todo { font-family: monospace; color: red; }
.done { font-family: monospace; color: green; }
.priority { font-family: monospace; color: orange; }
.tag { background-color: #eee; font-family: monospace;
padding: 2px; font-size: 80%; font-weight: normal; }
.timestamp { color: #bebebe; }
.timestamp-kwd { color: #5f9ea0; }
.org-right { margin-left: auto; margin-right: 0px; text-align: right; }
.org-left { margin-left: 0px; margin-right: auto; text-align: left; }
.org-center { margin-left: auto; margin-right: auto; text-align: center; }
.underline { text-decoration: underline; }
#postamble p, #preamble p { font-size: 90%; margin: .2em; }
p.verse { margin-left: 3%; }
pre {
border: 1px solid #ccc;
box-shadow: 3px 3px 3px #eee;
padding: 8pt;
font-family: monospace;
overflow: auto;
margin: 1.2em;
}
pre.src {
position: relative;
overflow: visible;
padding-top: 1.2em;
}
pre.src:before {
display: none;
position: absolute;
background-color: white;
top: -10px;
right: 10px;
padding: 3px;
border: 1px solid black;
}
pre.src:hover:before { display: inline;}
/* Languages per Org manual */
pre.src-asymptote:before { content: 'Asymptote'; }
pre.src-awk:before { content: 'Awk'; }
pre.src-C:before { content: 'C'; }
/* pre.src-C++ doesn't work in CSS */
pre.src-clojure:before { content: 'Clojure'; }
pre.src-css:before { content: 'CSS'; }
pre.src-D:before { content: 'D'; }
pre.src-ditaa:before { content: 'ditaa'; }
pre.src-dot:before { content: 'Graphviz'; }
pre.src-calc:before { content: 'Emacs Calc'; }
pre.src-emacs-lisp:before { content: 'Emacs Lisp'; }
pre.src-fortran:before { content: 'Fortran'; }
pre.src-gnuplot:before { content: 'gnuplot'; }
pre.src-haskell:before { content: 'Haskell'; }
pre.src-hledger:before { content: 'hledger'; }
pre.src-java:before { content: 'Java'; }
pre.src-js:before { content: 'Javascript'; }
pre.src-latex:before { content: 'LaTeX'; }
pre.src-ledger:before { content: 'Ledger'; }
pre.src-lisp:before { content: 'Lisp'; }
pre.src-lilypond:before { content: 'Lilypond'; }
pre.src-lua:before { content: 'Lua'; }
pre.src-matlab:before { content: 'MATLAB'; }
pre.src-mscgen:before { content: 'Mscgen'; }
pre.src-ocaml:before { content: 'Objective Caml'; }
pre.src-octave:before { content: 'Octave'; }
pre.src-org:before { content: 'Org mode'; }
pre.src-oz:before { content: 'OZ'; }
pre.src-plantuml:before { content: 'Plantuml'; }
pre.src-processing:before { content: 'Processing.js'; }
pre.src-python:before { content: 'Python'; }
pre.src-R:before { content: 'R'; }
pre.src-ruby:before { content: 'Ruby'; }
pre.src-sass:before { content: 'Sass'; }
pre.src-scheme:before { content: 'Scheme'; }
pre.src-screen:before { content: 'Gnu Screen'; }
pre.src-sed:before { content: 'Sed'; }
pre.src-sh:before { content: 'shell'; }
pre.src-sql:before { content: 'SQL'; }
pre.src-sqlite:before { content: 'SQLite'; }
/* additional languages in org.el's org-babel-load-languages alist */
pre.src-forth:before { content: 'Forth'; }
pre.src-io:before { content: 'IO'; }
pre.src-J:before { content: 'J'; }
pre.src-makefile:before { content: 'Makefile'; }
pre.src-maxima:before { content: 'Maxima'; }
pre.src-perl:before { content: 'Perl'; }
pre.src-picolisp:before { content: 'Pico Lisp'; }
pre.src-scala:before { content: 'Scala'; }
pre.src-shell:before { content: 'Shell Script'; }
pre.src-ebnf2ps:before { content: 'ebfn2ps'; }
/* additional language identifiers per "defun org-babel-execute"
in ob-*.el */
pre.src-cpp:before { content: 'C++'; }
pre.src-abc:before { content: 'ABC'; }
pre.src-coq:before { content: 'Coq'; }
pre.src-groovy:before { content: 'Groovy'; }
/* additional language identifiers from org-babel-shell-names in
ob-shell.el: ob-shell is the only babel language using a lambda to put
the execution function name together. */
pre.src-bash:before { content: 'bash'; }
pre.src-csh:before { content: 'csh'; }
pre.src-ash:before { content: 'ash'; }
pre.src-dash:before { content: 'dash'; }
pre.src-ksh:before { content: 'ksh'; }
pre.src-mksh:before { content: 'mksh'; }
pre.src-posh:before { content: 'posh'; }
/* Additional Emacs modes also supported by the LaTeX listings package */
pre.src-ada:before { content: 'Ada'; }
pre.src-asm:before { content: 'Assembler'; }
pre.src-caml:before { content: 'Caml'; }
pre.src-delphi:before { content: 'Delphi'; }
pre.src-html:before { content: 'HTML'; }
pre.src-idl:before { content: 'IDL'; }
pre.src-mercury:before { content: 'Mercury'; }
pre.src-metapost:before { content: 'MetaPost'; }
pre.src-modula-2:before { content: 'Modula-2'; }
pre.src-pascal:before { content: 'Pascal'; }
pre.src-ps:before { content: 'PostScript'; }
pre.src-prolog:before { content: 'Prolog'; }
pre.src-simula:before { content: 'Simula'; }
pre.src-tcl:before { content: 'tcl'; }
pre.src-tex:before { content: 'TeX'; }
pre.src-plain-tex:before { content: 'Plain TeX'; }
pre.src-verilog:before { content: 'Verilog'; }
pre.src-vhdl:before { content: 'VHDL'; }
pre.src-xml:before { content: 'XML'; }
pre.src-nxml:before { content: 'XML'; }
/* add a generic configuration mode; LaTeX export needs an additional
(add-to-list 'org-latex-listings-langs '(conf " ")) in .emacs */
pre.src-conf:before { content: 'Configuration File'; }
table { border-collapse:collapse; }
caption.t-above { caption-side: top; }
caption.t-bottom { caption-side: bottom; }
td, th { vertical-align:top; }
th.org-right { text-align: center; }
th.org-left { text-align: center; }
th.org-center { text-align: center; }
td.org-right { text-align: right; }
td.org-left { text-align: left; }
td.org-center { text-align: center; }
dt { font-weight: bold; }
.footpara { display: inline; }
.footdef { margin-bottom: 1em; }
.figure { padding: 1em; }
.figure p { text-align: center; }
.equation-container {
display: table;
text-align: center;
width: 100%;
}
.equation {
vertical-align: middle;
}
.equation-label {
display: table-cell;
text-align: right;
vertical-align: middle;
}
.inlinetask {
padding: 10px;
border: 2px solid gray;
margin: 10px;
background: #ffffcc;
}
#org-div-home-and-up
{ text-align: right; font-size: 70%; white-space: nowrap; }
textarea { overflow-x: auto; }
.linenr { font-size: smaller }
.code-highlighted { background-color: #ffff00; }
.org-info-js_info-navigation { border-style: none; }
#org-info-js_console-label
{ font-size: 10px; font-weight: bold; white-space: nowrap; }
.org-info-js_search-highlight
{ background-color: #ffff00; color: #000000; font-weight: bold; }
.org-svg { width: 90%; }
/*]]>*/-->
</style>
<link rel="stylesheet" type="text/css" href="./css/htmlize.css"/>
<link rel="stylesheet" type="text/css" href="./css/readtheorg.css"/>
<link rel="stylesheet" type="text/css" href="./css/zenburn.css"/>
<script type="text/javascript" src="./js/jquery.min.js"></script>
<script type="text/javascript" src="./js/bootstrap.min.js"></script>
<script type="text/javascript" src="./js/jquery.stickytableheaders.min.js"></script>
<script type="text/javascript" src="./js/readtheorg.js"></script>
<script type="text/javascript">
// @license magnet:?xt=urn:btih:1f739d935676111cfff4b4693e3816e664797050&dn=gpl-3.0.txt GPL-v3-or-Later
<!--/*--><![CDATA[/*><!--*/
function CodeHighlightOn(elem, id)
{
var target = document.getElementById(id);
if(null != target) {
elem.cacheClassElem = elem.className;
elem.cacheClassTarget = target.className;
target.className = "code-highlighted";
elem.className = "code-highlighted";
}
}
function CodeHighlightOff(elem, id)
{
var target = document.getElementById(id);
if(elem.cacheClassElem)
elem.className = elem.cacheClassElem;
if(elem.cacheClassTarget)
target.className = elem.cacheClassTarget;
}
/*]]>*///-->
// @license-end
</script>
<script>
MathJax = {
tex: { macros: {
bm: ["\\boldsymbol{#1}",1],
}
}
};
</script>
<script type="text/javascript"
src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js"></script>
</head>
<body>
<div id="org-div-home-and-up">
<a accesskey="h" href="index.html"> UP </a>
|
<a accesskey="H" href="index.html"> HOME </a>
</div><div id="content">
<h1 class="title">Determination of the optimal nano-hexapod’s stiffness</h1>
<div id="table-of-contents">
<h2>Table of Contents</h2>
<div id="text-table-of-contents">
<ul>
<li><a href="#org84aa9ce">1. Spindle Rotation Speed</a>
<ul>
<li><a href="#org37d23dd">1.1. Initialization</a></li>
<li><a href="#org75fea48">1.2. Identification when rotating at maximum speed</a></li>
<li><a href="#orgf19758e">1.3. Change of dynamics</a></li>
</ul>
</li>
<li><a href="#org57a0e57">2. Micro-Station Compliance Effect</a>
<ul>
<li><a href="#orgca3001c">2.1. Identification of the micro-station compliance</a></li>
<li><a href="#orgffe89ca">2.2. Identification of the dynamics with a rigid micro-station</a></li>
<li><a href="#org21c0a38">2.3. Identification of the dynamics with a flexible micro-station</a></li>
<li><a href="#orge9344e2">2.4. Obtained Dynamics</a></li>
</ul>
</li>
<li><a href="#orgd6382d8">3. Payload “Impedance” Effect</a>
<ul>
<li><a href="#orgc1416f3">3.1. Initialization</a></li>
<li><a href="#orgc8cd70d">3.2. Identification of the dynamics while change the payload dynamics</a></li>
<li><a href="#org4da36db">3.3. Change of dynamics for the primary controller</a>
<ul>
<li><a href="#org913b8cb">3.3.1. Frequency variation</a></li>
<li><a href="#org906dcba">3.3.2. Mass variation</a></li>
<li><a href="#org632af10">3.3.3. Total variation</a></li>
</ul>
</li>
</ul>
</li>
<li><a href="#orgf0a88c5">4. Total Change of dynamics</a></li>
</ul>
</div>
</div>
<p>
As shown before, many parameters other than the nano-hexapod itself do influence the plant dynamics:
</p>
<ul class="org-ul">
<li>The micro-station compliance (studied <a href="uncertainty_support.html">here</a>)</li>
<li>The payload mass and dynamical properties (studied <a href="uncertainty_payload.html">here</a> and <a href="uncertainty_experiment.html">here</a>)</li>
<li>The experimental conditions, mainly the spindle rotation speed (studied <a href="uncertainty_experiment.html">here</a>)</li>
</ul>
<p>
As seen before, the stiffness of the nano-hexapod greatly influence the effect of such parameters.
</p>
<p>
We wish here to see if we can determine an optimal stiffness of the nano-hexapod such that:
</p>
<ul class="org-ul">
<li>Section <a href="#org1f375bb">1</a>: the change of its dynamics due to the spindle rotation speed is acceptable</li>
<li>Section <a href="#orgcf5798c">2</a>: the support compliance dynamics is not much present in the nano-hexapod dynamics</li>
<li>Section <a href="#org1a9d09c">3</a>: the change of payload impedance has acceptable effect on the plant dynamics</li>
</ul>
<p>
The overall goal is to design a nano-hexapod that will allow the highest possible control bandwidth.
</p>
<div id="outline-container-org84aa9ce" class="outline-2">
<h2 id="org84aa9ce"><span class="section-number-2">1</span> Spindle Rotation Speed</h2>
<div class="outline-text-2" id="text-1">
<p>
<a id="org1f375bb"></a>
</p>
<p>
In this section, we look at the effect of the spindle rotation speed on the plant dynamics.
</p>
<p>
The rotation speed will have an effect due to the Coriolis effect.
</p>
</div>
<div id="outline-container-org37d23dd" class="outline-3">
<h3 id="org37d23dd"><span class="section-number-3">1.1</span> Initialization</h3>
<div class="outline-text-3" id="text-1-1">
<p>
We initialize all the stages with the default parameters.
</p>
<div class="org-src-container">
<pre class="src src-matlab"> initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();
initializeAxisc();
initializeMirror();
</pre>
</div>
<p>
We use a sample mass of 10kg.
</p>
<div class="org-src-container">
<pre class="src src-matlab"> initializeSample(<span class="org-string">'mass'</span>, 10);
</pre>
</div>
<p>
We don’t include disturbances in this model as it adds complexity to the simulations and does not alter the obtained dynamics.
We however include gravity.
</p>
<div class="org-src-container">
<pre class="src src-matlab"> initializeSimscapeConfiguration(<span class="org-string">'gravity'</span>, <span class="org-constant">true</span>);
initializeDisturbances(<span class="org-string">'enable'</span>, <span class="org-constant">false</span>);
initializeLoggingConfiguration(<span class="org-string">'log'</span>, <span class="org-string">'none'</span>);
initializeController();
</pre>
</div>
</div>
</div>
<div id="outline-container-org75fea48" class="outline-3">
<h3 id="org75fea48"><span class="section-number-3">1.2</span> Identification when rotating at maximum speed</h3>
<div class="outline-text-3" id="text-1-2">
<p>
We identify the dynamics for the following spindle rotation speeds <code>Rz_rpm</code>:
</p>
<div class="org-src-container">
<pre class="src src-matlab"> Rz_rpm = linspace(0, 60, 6);
</pre>
</div>
<p>
And for the following nano-hexapod actuator stiffness <code>Ks</code>:
</p>
<div class="org-src-container">
<pre class="src src-matlab"> Ks = logspace(3,9,7); <span class="org-comment">% [N/m]</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-orgf19758e" class="outline-3">
<h3 id="orgf19758e"><span class="section-number-3">1.3</span> Change of dynamics</h3>
<div class="outline-text-3" id="text-1-3">
<p>
We plot the change of dynamics due to the change of the spindle rotation speed (from 0rpm to 60rpm):
</p>
<ul class="org-ul">
<li>Figure <a href="#org2b01fbe">2</a>: from actuator force \(\tau\) to force sensor \(\tau_m\) (IFF plant)</li>
<li>Figure <a href="#org9bfe588">3</a>: from actuator force \(\tau\) to actuator relative displacement \(d\mathcal{L}\) (Decentralized positioning plant)</li>
<li>Figure <a href="#org9f887c8">4</a>: from force in the task space \(\mathcal{F}_x\) to sample displacement \(\mathcal{X}_x\) (Centralized positioning plant)</li>
<li>Figure <a href="#org5926aca">5</a>: from force in the task space \(\mathcal{F}_x\) to sample displacement \(\mathcal{X}_y\) (coupling of the centralized positioning plant)</li>
</ul>
<div id="org3c83afc" class="figure">
<p><img src="figs/opti_stiffness_iff_root_locus.png" alt="opti_stiffness_iff_root_locus.png" />
</p>
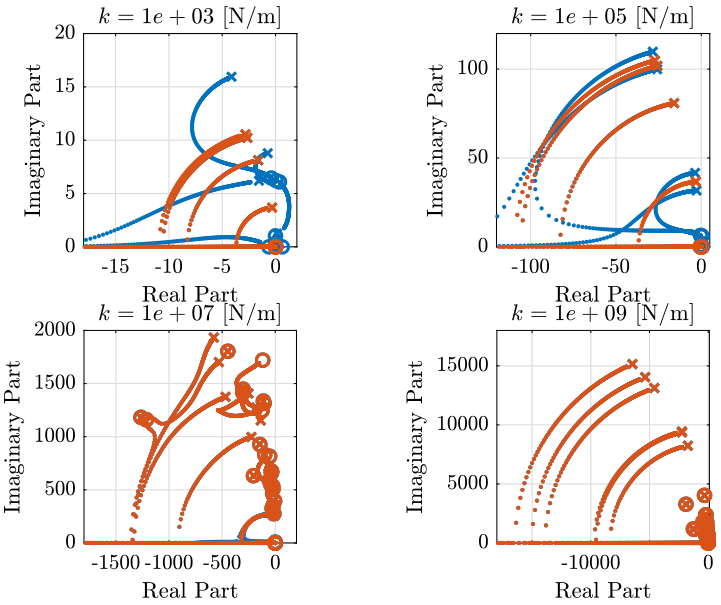
<p><span class="figure-number">Figure 1: </span>Root Locus plot for IFF control when not rotating (in red) and when rotating at 60rpm (in blue) for 4 different nano-hexapod stiffnesses (<a href="./figs/opti_stiffness_iff_root_locus.png">png</a>, <a href="./figs/opti_stiffness_iff_root_locus.pdf">pdf</a>)</p>
</div>
<div id="org2b01fbe" class="figure">
<p><img src="figs/opt_stiffness_wz_iff.png" alt="opt_stiffness_wz_iff.png" />
</p>
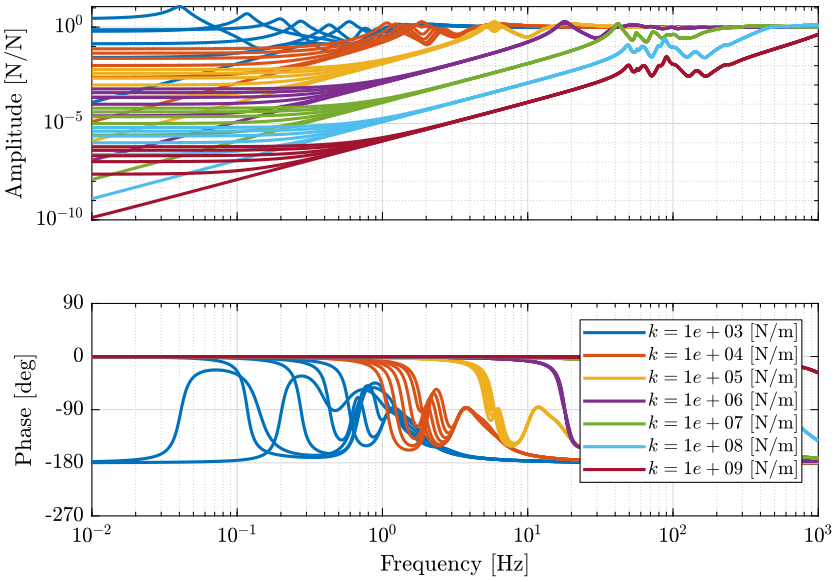
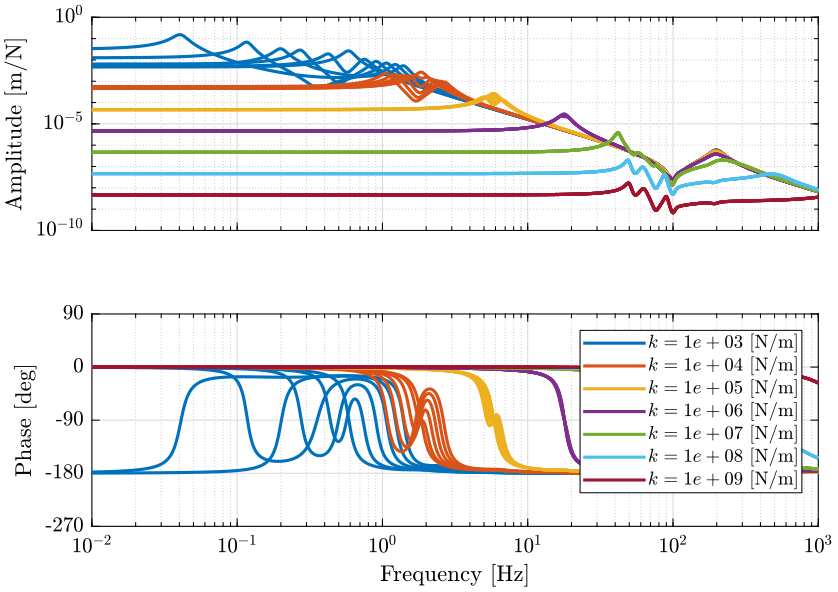
<p><span class="figure-number">Figure 2: </span>Change of dynamics from actuator \(\tau\) to actuator force sensor \(\tau_m\) for a spindle rotation speed from 0rpm to 60rpm (<a href="./figs/opt_stiffness_wz_iff.png">png</a>, <a href="./figs/opt_stiffness_wz_iff.pdf">pdf</a>)</p>
</div>
<div id="org9bfe588" class="figure">
<p><img src="figs/opt_stiffness_wz_dvf.png" alt="opt_stiffness_wz_dvf.png" />
</p>
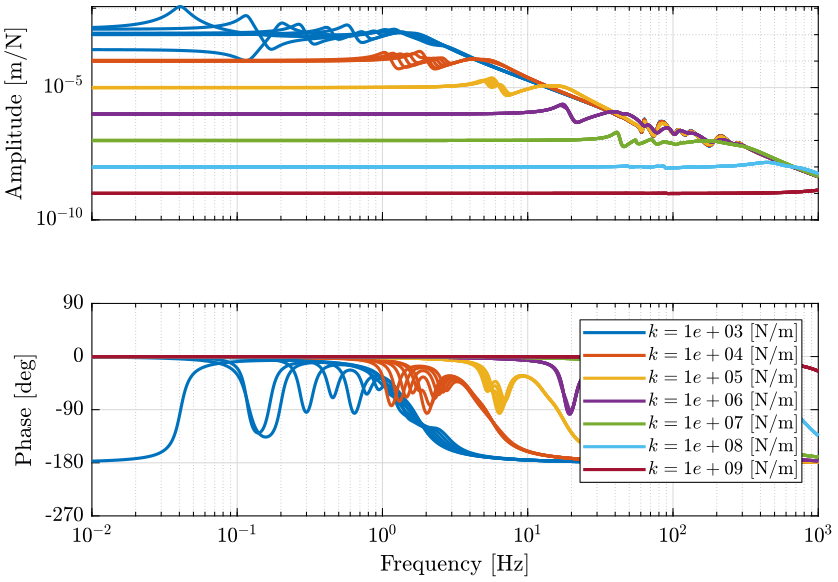
<p><span class="figure-number">Figure 3: </span>Change of dynamics from actuator force \(\tau\) to actuator displacement \(d\mathcal{L}\) for a spindle rotation speed from 0rpm to 60rpm (<a href="./figs/opt_stiffness_wz_dvf.png">png</a>, <a href="./figs/opt_stiffness_wz_dvf.pdf">pdf</a>)</p>
</div>
<div id="org9f887c8" class="figure">
<p><img src="figs/opt_stiffness_wz_fx_dx.png" alt="opt_stiffness_wz_fx_dx.png" />
</p>
<p><span class="figure-number">Figure 4: </span>Change of dynamics from force \(\mathcal{F}_x\) to displacement \(\mathcal{X}_x\) for a spindle rotation speed from 0rpm to 60rpm (<a href="./figs/opt_stiffness_wz_fx_dx.png">png</a>, <a href="./figs/opt_stiffness_wz_fx_dx.pdf">pdf</a>)</p>
</div>
<div id="org5926aca" class="figure">
<p><img src="figs/opt_stiffness_wz_coupling.png" alt="opt_stiffness_wz_coupling.png" />
</p>
<p><span class="figure-number">Figure 5: </span>Change of Coupling from force \(\mathcal{F}_x\) to displacement \(\mathcal{X}_y\) for a spindle rotation speed from 0rpm to 60rpm (<a href="./figs/opt_stiffness_wz_coupling.png">png</a>, <a href="./figs/opt_stiffness_wz_coupling.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div class="outline-text-2" id="text-1">
<div class="important">
<p>
The leg stiffness should be at higher than \(k_i = 10^4\ [N/m]\) such that the main resonance frequency does not shift too much when rotating.
For the coupling, it is more difficult to conclude about the minimum required leg stiffness.
</p>
</div>
<div class="notes">
<p>
Note that we can use very soft nano-hexapod if we limit the spindle rotating speed.
</p>
</div>
</div>
</div>
<div id="outline-container-org57a0e57" class="outline-2">
<h2 id="org57a0e57"><span class="section-number-2">2</span> Micro-Station Compliance Effect</h2>
<div class="outline-text-2" id="text-2">
<p>
<a id="orgcf5798c"></a>
</p>
<ul class="org-ul">
<li>take the 6dof compliance of the micro-station</li>
<li>simple model + uncertainty</li>
</ul>
</div>
<div id="outline-container-orgca3001c" class="outline-3">
<h3 id="orgca3001c"><span class="section-number-3">2.1</span> Identification of the micro-station compliance</h3>
<div class="outline-text-3" id="text-2-1">
<p>
We initialize all the stages with the default parameters.
</p>
<div class="org-src-container">
<pre class="src src-matlab"> initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod(<span class="org-string">'type'</span>, <span class="org-string">'compliance'</span>);
</pre>
</div>
<p>
We put nothing on top of the micro-hexapod.
</p>
<div class="org-src-container">
<pre class="src src-matlab"> initializeAxisc(<span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
initializeMirror(<span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
initializeNanoHexapod(<span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
initializeSample(<span class="org-string">'type'</span>, <span class="org-string">'none'</span>);
</pre>
</div>
<p>
And we identify the dynamics from forces/torques applied on the micro-hexapod top platform to the motion of the micro-hexapod top platform at the same point.
The diagonal element of the identified Micro-Station compliance matrix are shown in Figure <a href="#org15a14d9">6</a>.
</p>
<div id="org15a14d9" class="figure">
<p><img src="figs/opt_stiff_micro_station_compliance.png" alt="opt_stiff_micro_station_compliance.png" />
</p>
<p><span class="figure-number">Figure 6: </span>Identified Compliance of the Micro-Station (<a href="./figs/opt_stiff_micro_station_compliance.png">png</a>, <a href="./figs/opt_stiff_micro_station_compliance.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-orgffe89ca" class="outline-3">
<h3 id="orgffe89ca"><span class="section-number-3">2.2</span> Identification of the dynamics with a rigid micro-station</h3>
<div class="outline-text-3" id="text-2-2">
<p>
We now identify the dynamics when the micro-station is rigid.
This is equivalent of identifying the dynamics of the nano-hexapod when fixed to a rigid ground.
We also choose the sample to be rigid and to have a mass of 10kg.
</p>
<div class="org-src-container">
<pre class="src src-matlab"> initializeSample(<span class="org-string">'type'</span>, <span class="org-string">'rigid'</span>, <span class="org-string">'mass'</span>, 10);
</pre>
</div>
<p>
As before, we identify the dynamics for the following actuator stiffnesses:
</p>
<div class="org-src-container">
<pre class="src src-matlab"> Ks = logspace(3,9,7); <span class="org-comment">% [N/m]</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-org21c0a38" class="outline-3">
<h3 id="org21c0a38"><span class="section-number-3">2.3</span> Identification of the dynamics with a flexible micro-station</h3>
<div class="outline-text-3" id="text-2-3">
<p>
We now initialize all the micro-station stages to be flexible.
And we identify the dynamics of the nano-hexapod.
</p>
</div>
</div>
<div id="outline-container-orge9344e2" class="outline-3">
<h3 id="orge9344e2"><span class="section-number-3">2.4</span> Obtained Dynamics</h3>
<div class="outline-text-3" id="text-2-4">
<p>
We plot the change of dynamics due to the compliance of the Micro-Station.
The solid curves are corresponding to the nano-hexapod without the micro-station, and the dashed curves with the micro-station:
</p>
<ul class="org-ul">
<li>Figure <a href="#org6257db9">7</a>: from actuator force \(\tau\) to force sensor \(\tau_m\) (IFF plant)</li>
<li>Figure <a href="#orgcea6354">8</a>: from actuator force \(\tau\) to actuator relative displacement \(d\mathcal{L}\) (Decentralized positioning plant)</li>
<li>Figure <a href="#org5c6f89c">9</a>: from force in the task space \(\mathcal{F}_x\) to sample displacement \(\mathcal{X}_x\) (Centralized positioning plant)</li>
<li>Figure <a href="#org7f2360c">10</a>: from force in the task space \(\mathcal{F}_z\) to sample displacement \(\mathcal{X}_z\) (Centralized positioning plant)</li>
</ul>
<div id="org6257db9" class="figure">
<p><img src="figs/opt_stiffness_micro_station_iff.png" alt="opt_stiffness_micro_station_iff.png" />
</p>
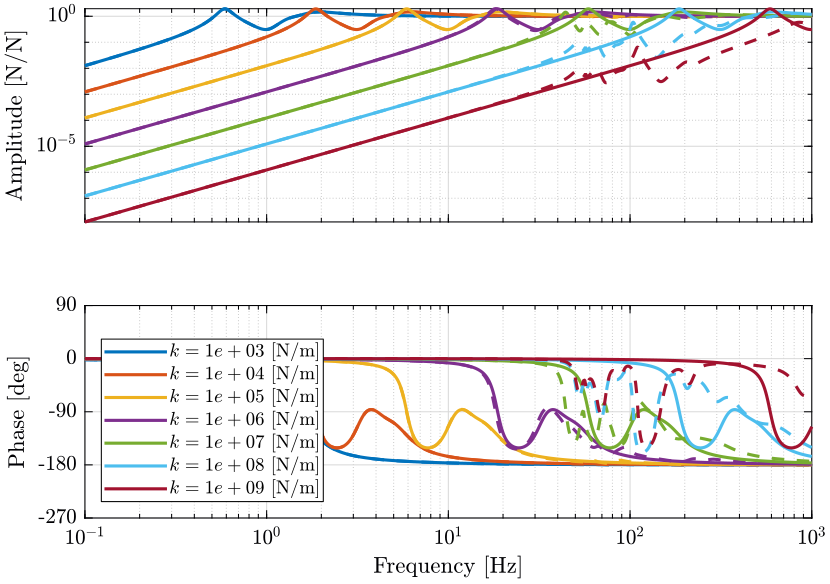
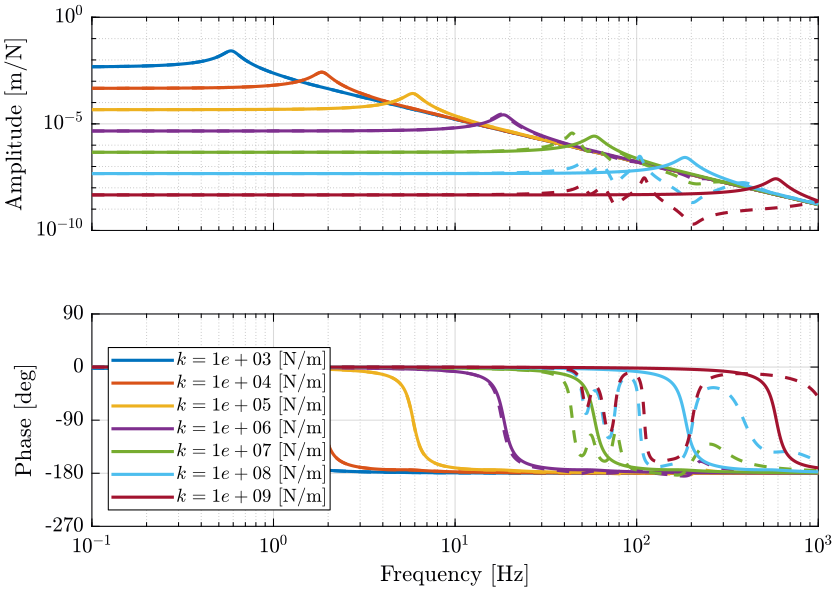
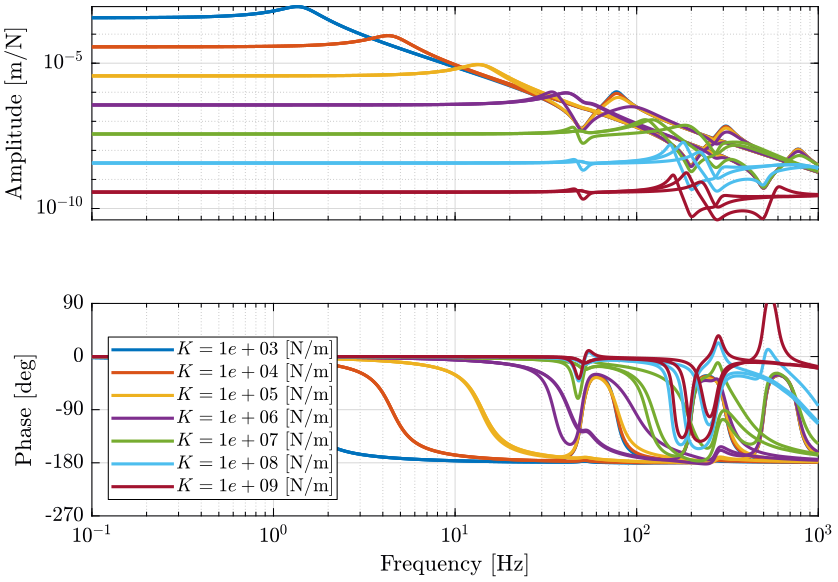
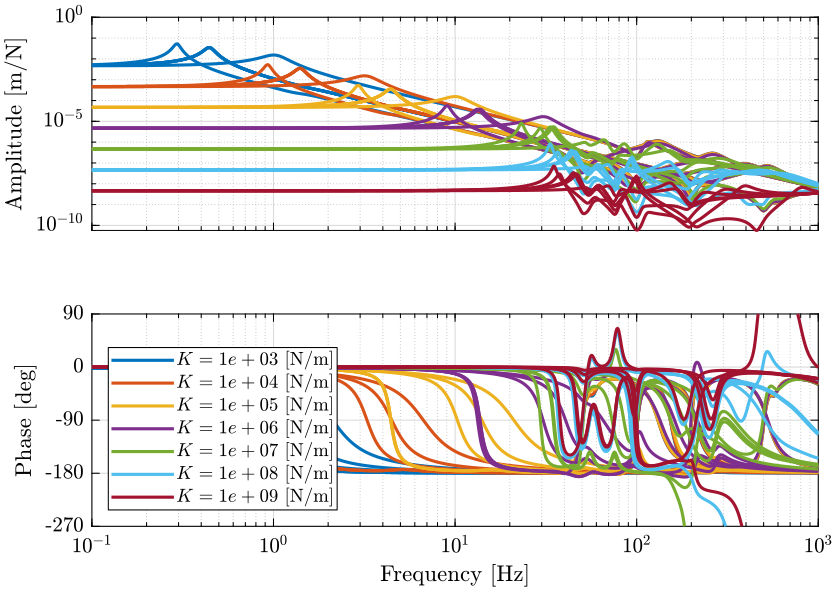
<p><span class="figure-number">Figure 7: </span>Change of dynamics from actuator \(\tau\) to actuator force sensor \(\tau_m\) due to the micro-station compliance (<a href="./figs/opt_stiffness_micro_station_iff.png">png</a>, <a href="./figs/opt_stiffness_micro_station_iff.pdf">pdf</a>)</p>
</div>
<div id="orgcea6354" class="figure">
<p><img src="figs/opt_stiffness_micro_station_dvf.png" alt="opt_stiffness_micro_station_dvf.png" />
</p>
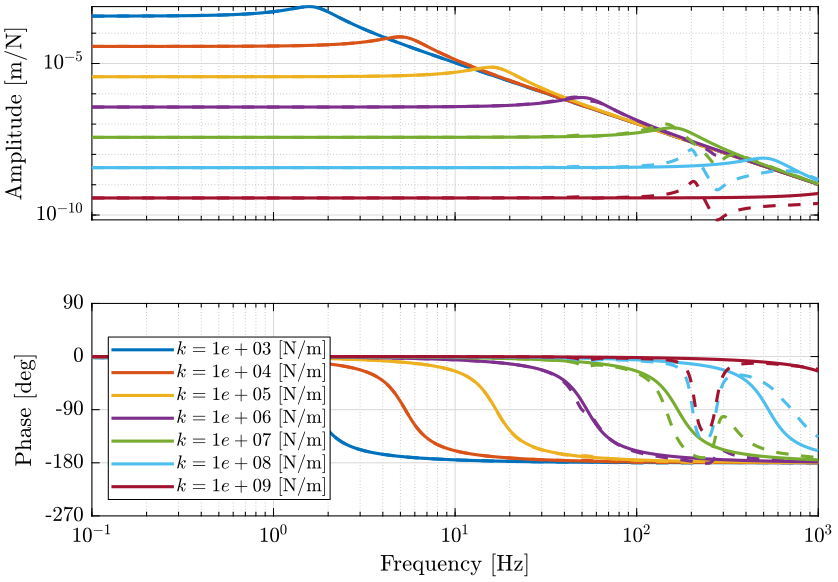
<p><span class="figure-number">Figure 8: </span>Change of dynamics from actuator force \(\tau\) to actuator displacement \(d\mathcal{L}\) due to the micro-station compliance (<a href="./figs/opt_stiffness_micro_station_dvf.png">png</a>, <a href="./figs/opt_stiffness_micro_station_dvf.pdf">pdf</a>)</p>
</div>
<div id="org5c6f89c" class="figure">
<p><img src="figs/opt_stiffness_micro_station_fx_dx.png" alt="opt_stiffness_micro_station_fx_dx.png" />
</p>
<p><span class="figure-number">Figure 9: </span>Change of dynamics from force \(\mathcal{F}_x\) to displacement \(\mathcal{X}_x\) due to the micro-station compliance (<a href="./figs/opt_stiffness_micro_station_fx_dx.png">png</a>, <a href="./figs/opt_stiffness_micro_station_fx_dx.pdf">pdf</a>)</p>
</div>
<div id="org7f2360c" class="figure">
<p><img src="figs/opt_stiffness_micro_station_fz_dz.png" alt="opt_stiffness_micro_station_fz_dz.png" />
</p>
<p><span class="figure-number">Figure 10: </span>Change of dynamics from force \(\mathcal{F}_z\) to displacement \(\mathcal{X}_z\) due to the micro-station compliance (<a href="./figs/opt_stiffness_micro_station_fz_dz.png">png</a>, <a href="./figs/opt_stiffness_micro_station_fz_dz.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div class="outline-text-2" id="text-2">
<div class="important">
<p>
The dynamics of the nano-hexapod is not affected by the micro-station dynamics (compliance) when the stiffness of the legs is less than \(10^6\ [N/m]\).
When the nano-hexapod is stiff (\(k>10^7\ [N/m]\)), the compliance of the micro-station appears in the primary plant.
</p>
</div>
</div>
</div>
<div id="outline-container-orgd6382d8" class="outline-2">
<h2 id="orgd6382d8"><span class="section-number-2">3</span> Payload “Impedance” Effect</h2>
<div class="outline-text-2" id="text-3">
<p>
<a id="org1a9d09c"></a>
</p>
</div>
<div id="outline-container-orgc1416f3" class="outline-3">
<h3 id="orgc1416f3"><span class="section-number-3">3.1</span> Initialization</h3>
<div class="outline-text-3" id="text-3-1">
<p>
We initialize all the stages with the default parameters.
We don’t include disturbances in this model as it adds complexity to the simulations and does not alter the obtained dynamics. :exports none
</p>
<div class="org-src-container">
<pre class="src src-matlab"> initializeDisturbances(<span class="org-string">'enable'</span>, <span class="org-constant">false</span>);
</pre>
</div>
<p>
We set the controller type to Open-Loop, and we do not need to log any signal.
</p>
<div class="org-src-container">
<pre class="src src-matlab"> initializeSimscapeConfiguration(<span class="org-string">'gravity'</span>, <span class="org-constant">true</span>);
initializeController();
initializeLoggingConfiguration(<span class="org-string">'log'</span>, <span class="org-string">'none'</span>);
initializeReferences();
</pre>
</div>
</div>
</div>
<div id="outline-container-orgc8cd70d" class="outline-3">
<h3 id="orgc8cd70d"><span class="section-number-3">3.2</span> Identification of the dynamics while change the payload dynamics</h3>
<div class="outline-text-3" id="text-3-2">
<p>
We make the following change of payload dynamics:
</p>
<ul class="org-ul">
<li>Change of mass: from 1kg to 50kg</li>
<li>Change of resonance frequency: from 50Hz to 500Hz</li>
<li>The damping ratio of the payload is fixed to \(\xi = 0.2\)</li>
</ul>
<p>
We identify the dynamics for the following payload masses <code>Ms</code> and nano-hexapod leg’s stiffnesses <code>Ks</code>:
</p>
<div class="org-src-container">
<pre class="src src-matlab"> Ms = [1, 20, 50]; <span class="org-comment">% [Kg]</span>
Ks = logspace(3,9,7); <span class="org-comment">% [N/m]</span>
</pre>
</div>
<p>
We then identify the dynamics for the following payload resonance frequencies <code>Fs</code>:
</p>
<div class="org-src-container">
<pre class="src src-matlab"> Fs = [50, 200, 500]; <span class="org-comment">% [Hz]</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-org4da36db" class="outline-3">
<h3 id="org4da36db"><span class="section-number-3">3.3</span> Change of dynamics for the primary controller</h3>
<div class="outline-text-3" id="text-3-3">
</div>
<div id="outline-container-org913b8cb" class="outline-4">
<h4 id="org913b8cb"><span class="section-number-4">3.3.1</span> Frequency variation</h4>
<div class="outline-text-4" id="text-3-3-1">
<p>
We here compare the dynamics for the same payload mass, but different stiffness resulting in different resonance frequency of the payload:
</p>
<ul class="org-ul">
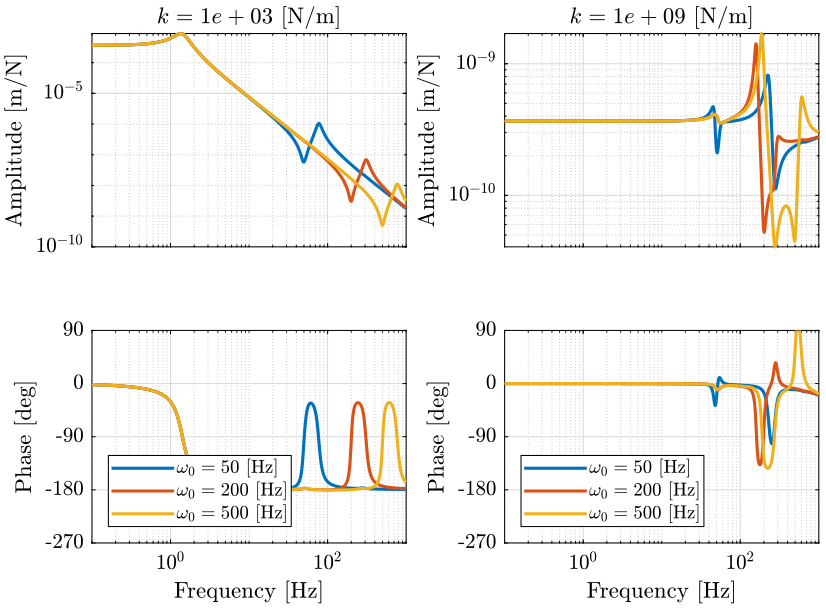
<li>Figure <a href="#orgcce8740">11</a>: dynamics from a force \(\mathcal{F}_z\) applied in the task space in the vertical direction to the vertical displacement of the sample \(\mathcal{X}_z\) for both a very soft and a very stiff nano-hexapod.</li>
<li>Figure <a href="#org87ecfc8">12</a>: same, but for all tested nano-hexapod stiffnesses</li>
</ul>
<p>
We can see two mass lines for the soft nano-hexapod (Figure <a href="#orgcce8740">11</a>):
</p>
<ul class="org-ul">
<li>The first mass line corresponds to \(\frac{1}{(m_n + m_p)s^2}\) where \(m_p = 10\ [kg]\) is the mass of the payload and \(m_n = 15\ [Kg]\) is the mass of the nano-hexapod top platform and attached mirror</li>
<li>The second mass line corresponds to \(\frac{1}{m_n s^2}\)</li>
<li>The zero corresponds to the resonance of the payload alone (fixed nano-hexapod’s top platform)</li>
</ul>
<div id="orgcce8740" class="figure">
<p><img src="figs/opt_stiffness_payload_freq_fz_dz.png" alt="opt_stiffness_payload_freq_fz_dz.png" />
</p>
<p><span class="figure-number">Figure 11: </span>Dynamics from \(\mathcal{F}_z\) to \(\mathcal{X}_z\) for varying payload resonance frequency, both for a soft nano-hexapod and a stiff nano-hexapod (<a href="./figs/opt_stiffness_payload_freq_fz_dz.png">png</a>, <a href="./figs/opt_stiffness_payload_freq_fz_dz.pdf">pdf</a>)</p>
</div>
<div id="org87ecfc8" class="figure">
<p><img src="figs/opt_stiffness_payload_freq_all.png" alt="opt_stiffness_payload_freq_all.png" />
</p>
<p><span class="figure-number">Figure 12: </span>Dynamics from \(\mathcal{F}_z\) to \(\mathcal{X}_z\) for varying payload resonance frequency (<a href="./figs/opt_stiffness_payload_freq_all.png">png</a>, <a href="./figs/opt_stiffness_payload_freq_all.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-org906dcba" class="outline-4">
<h4 id="org906dcba"><span class="section-number-4">3.3.2</span> Mass variation</h4>
<div class="outline-text-4" id="text-3-3-2">
<p>
We here compare the dynamics for different payload mass with the same resonance frequency (100Hz):
</p>
<ul class="org-ul">
<li>Figure <a href="#org4eb6bfc">13</a>: dynamics from a force \(\mathcal{F}_z\) applied in the task space in the vertical direction to the vertical displacement of the sample \(\mathcal{X}_z\) for both a very soft and a very stiff nano-hexapod.</li>
<li>Figure <a href="#org6e013a7">14</a>: same, but for all tested nano-hexapod stiffnesses</li>
</ul>
<p>
We can see here that for the soft nano-hexapod:
</p>
<ul class="org-ul">
<li>the first resonance \(\omega_n\) is changing with the mass of the payload as \(\omega_n = \sqrt{\frac{k_n}{m_p + m_n}}\) with \(k_p\) the stiffness of the nano-hexapod, \(m_p\) the payload’s mass and \(m_n\) the mass of the nano-hexapod top platform</li>
<li>the first mass line corresponding to \(\frac{1}{(m_p + m_n)s^2}\) is changing with the payload mass</li>
<li>the zero at 100Hz is not changing as it corresponds to the resonance of the payload itself</li>
<li>the second mass line does not change</li>
</ul>
<div id="org4eb6bfc" class="figure">
<p><img src="figs/opt_stiffness_payload_mass_fz_dz.png" alt="opt_stiffness_payload_mass_fz_dz.png" />
</p>
<p><span class="figure-number">Figure 13: </span>Dynamics from \(\mathcal{F}_z\) to \(\mathcal{X}_z\) for varying payload mass, both for a soft nano-hexapod and a stiff nano-hexapod (<a href="./figs/opt_stiffness_payload_mass_fz_dz.png">png</a>, <a href="./figs/opt_stiffness_payload_mass_fz_dz.pdf">pdf</a>)</p>
</div>
<div id="org6e013a7" class="figure">
<p><img src="figs/opt_stiffness_payload_mass_all.png" alt="opt_stiffness_payload_mass_all.png" />
</p>
<p><span class="figure-number">Figure 14: </span>Dynamics from \(\mathcal{F}_z\) to \(\mathcal{X}_z\) for varying payload mass (<a href="./figs/opt_stiffness_payload_mass_all.png">png</a>, <a href="./figs/opt_stiffness_payload_mass_all.pdf">pdf</a>)</p>
</div>
</div>
</div>
<div id="outline-container-org632af10" class="outline-4">
<h4 id="org632af10"><span class="section-number-4">3.3.3</span> Total variation</h4>
<div class="outline-text-4" id="text-3-3-3">
<p>
We now plot the total change of dynamics due to change of the payload (Figures <a href="#orgf33beff">15</a> and <a href="#org75c1705">16</a>):
</p>
<ul class="org-ul">
<li>mass from 1kg to 50kg</li>
<li>main resonance from 50Hz to 500Hz</li>
</ul>
<div id="orgf33beff" class="figure">
<p><img src="figs/opt_stiffness_payload_impedance_all_fz_dz.png" alt="opt_stiffness_payload_impedance_all_fz_dz.png" />
</p>
<p><span class="figure-number">Figure 15: </span>Dynamics from \(\mathcal{F}_z\) to \(\mathcal{X}_z\) for varying payload dynamics, both for a soft nano-hexapod and a stiff nano-hexapod (<a href="./figs/opt_stiffness_payload_impedance_all_fz_dz.png">png</a>, <a href="./figs/opt_stiffness_payload_impedance_all_fz_dz.pdf">pdf</a>)</p>
</div>
<div id="org75c1705" class="figure">
<p><img src="figs/opt_stiffness_payload_impedance_fz_dz.png" alt="opt_stiffness_payload_impedance_fz_dz.png" />
</p>
<p><span class="figure-number">Figure 16: </span>Dynamics from \(\mathcal{F}_z\) to \(\mathcal{X}_z\) for varying payload dynamics, both for a soft nano-hexapod and a stiff nano-hexapod (<a href="./figs/opt_stiffness_payload_impedance_fz_dz.png">png</a>, <a href="./figs/opt_stiffness_payload_impedance_fz_dz.pdf">pdf</a>)</p>
</div>
</div>
</div>
</div>
<div class="outline-text-2" id="text-3">
<div class="important">
<p>
</p>
</div>
</div>
</div>
<div id="outline-container-orgf0a88c5" class="outline-2">
<h2 id="orgf0a88c5"><span class="section-number-2">4</span> Total Change of dynamics</h2>
<div class="outline-text-2" id="text-4">
<p>
We now consider the total change of nano-hexapod dynamics due to:
</p>
<ul class="org-ul">
<li><code>Gk_wz_err</code> - Change of spindle rotation speed</li>
<li><code>Gf_err</code> and <code>Gm_err</code> - Change of payload resonance</li>
<li><code>Gmf_err</code> and <code>Gmr_err</code> - Micro-Station compliance</li>
</ul>
<p>
The obtained dynamics are shown:
</p>
<ul class="org-ul">
<li>Figure <a href="#org045955d">17</a> for a stiffness \(k = 10^3\ [N/m]\)</li>
<li>Figure <a href="#orgc2c0741">18</a> for a stiffness \(k = 10^5\ [N/m]\)</li>
<li>Figure <a href="#org7a8f7c3">19</a> for a stiffness \(k = 10^7\ [N/m]\)</li>
<li>Figure <a href="#org4745a60">20</a> for a stiffness \(k = 10^9\ [N/m]\)</li>
</ul>
<p>
And finally, in Figures <a href="#org0a4e875">21</a> and <a href="#orge890242">22</a> are shown an animation of the change of dynamics with the nano-hexapod’s stiffness.
</p>
<div id="org045955d" class="figure">
<p><img src="figs/opt_stiffness_plant_dynamics_fx_dx_k_1e3.png" alt="opt_stiffness_plant_dynamics_fx_dx_k_1e3.png" />
</p>
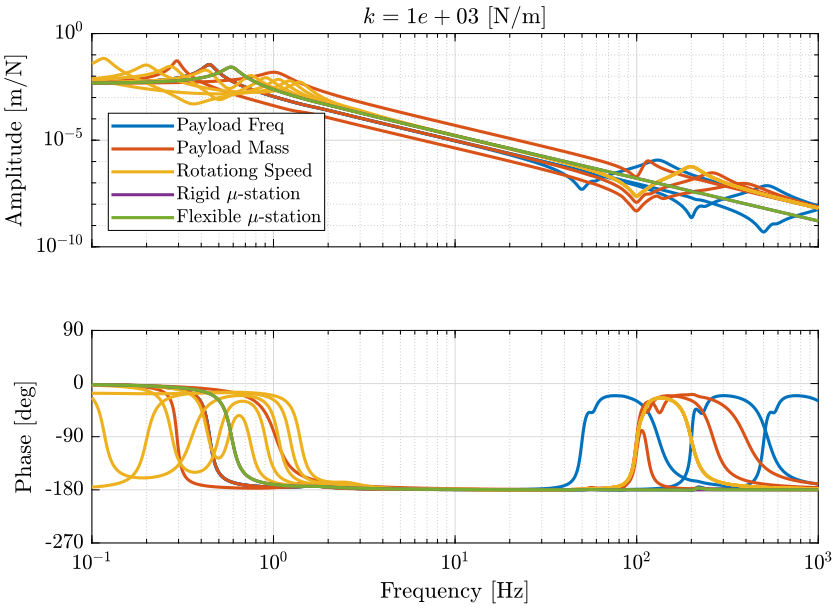
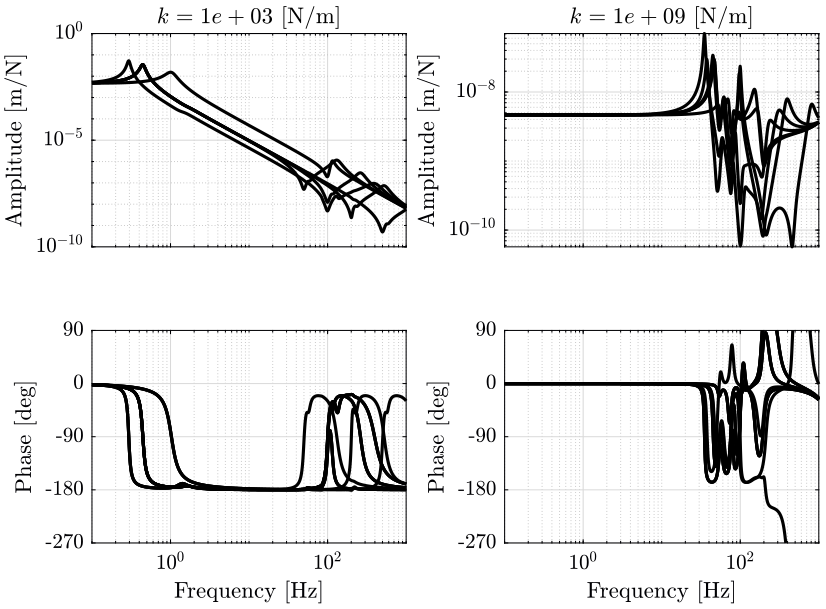
<p><span class="figure-number">Figure 17: </span>Total variation of the dynamics from \(\mathcal{F}_x\) to \(\mathcal{X}_x\). Nano-hexapod leg’s stiffness is equal to \(k = 10^3\ [N/m]\) (<a href="./figs/opt_stiffness_plant_dynamics_fx_dx_k_1e3.png">png</a>, <a href="./figs/opt_stiffness_plant_dynamics_fx_dx_k_1e3.pdf">pdf</a>)</p>
</div>
<div id="orgc2c0741" class="figure">
<p><img src="figs/opt_stiffness_plant_dynamics_fx_dx_k_1e5.png" alt="opt_stiffness_plant_dynamics_fx_dx_k_1e5.png" />
</p>
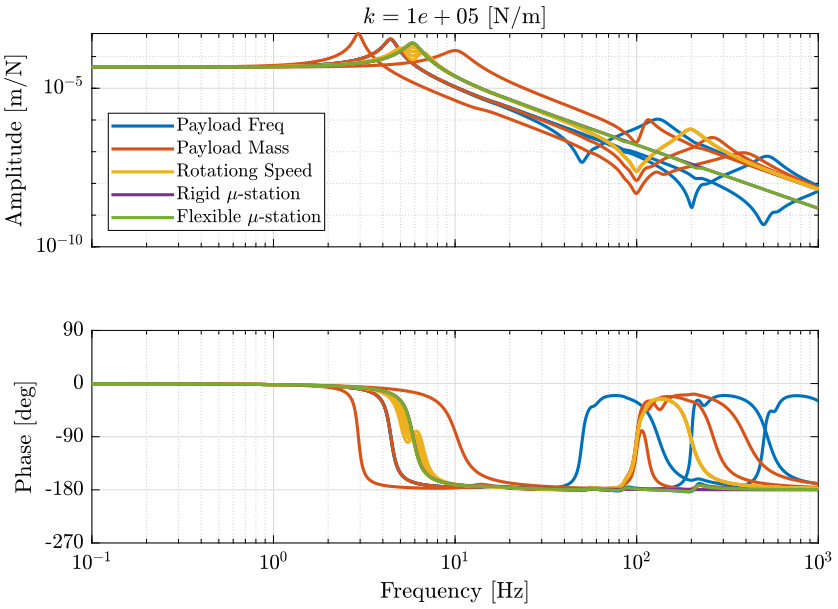
<p><span class="figure-number">Figure 18: </span>Total variation of the dynamics from \(\mathcal{F}_x\) to \(\mathcal{X}_x\). Nano-hexapod leg’s stiffness is equal to \(k = 10^5\ [N/m]\) (<a href="./figs/opt_stiffness_plant_dynamics_fx_dx_k_1e5.png">png</a>, <a href="./figs/opt_stiffness_plant_dynamics_fx_dx_k_1e5.pdf">pdf</a>)</p>
</div>
<div id="org7a8f7c3" class="figure">
<p><img src="figs/opt_stiffness_plant_dynamics_fx_dx_k_1e7.png" alt="opt_stiffness_plant_dynamics_fx_dx_k_1e7.png" />
</p>
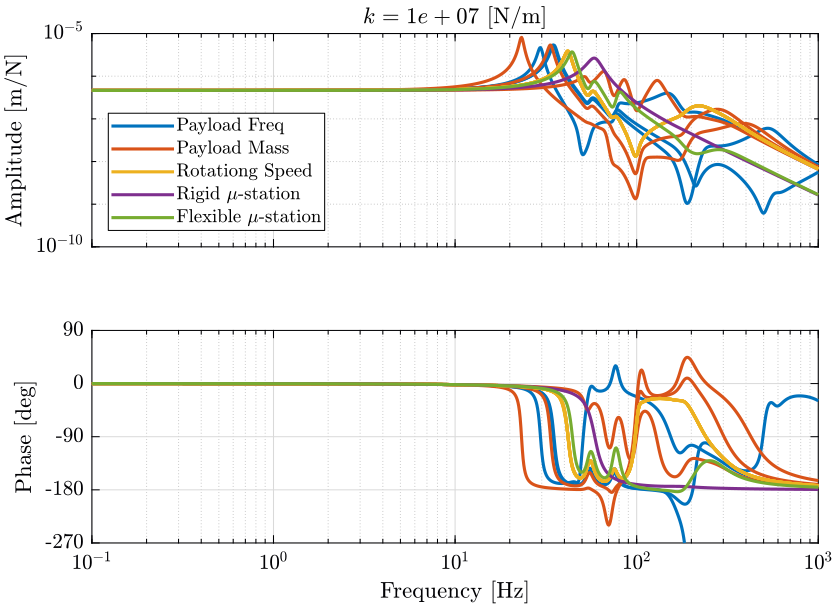
<p><span class="figure-number">Figure 19: </span>Total variation of the dynamics from \(\mathcal{F}_x\) to \(\mathcal{X}_x\). Nano-hexapod leg’s stiffness is equal to \(k = 10^7\ [N/m]\) (<a href="./figs/opt_stiffness_plant_dynamics_fx_dx_k_1e7.png">png</a>, <a href="./figs/opt_stiffness_plant_dynamics_fx_dx_k_1e7.pdf">pdf</a>)</p>
</div>
<div id="org4745a60" class="figure">
<p><img src="figs/opt_stiffness_plant_dynamics_fx_dx_k_1e9.png" alt="opt_stiffness_plant_dynamics_fx_dx_k_1e9.png" />
</p>
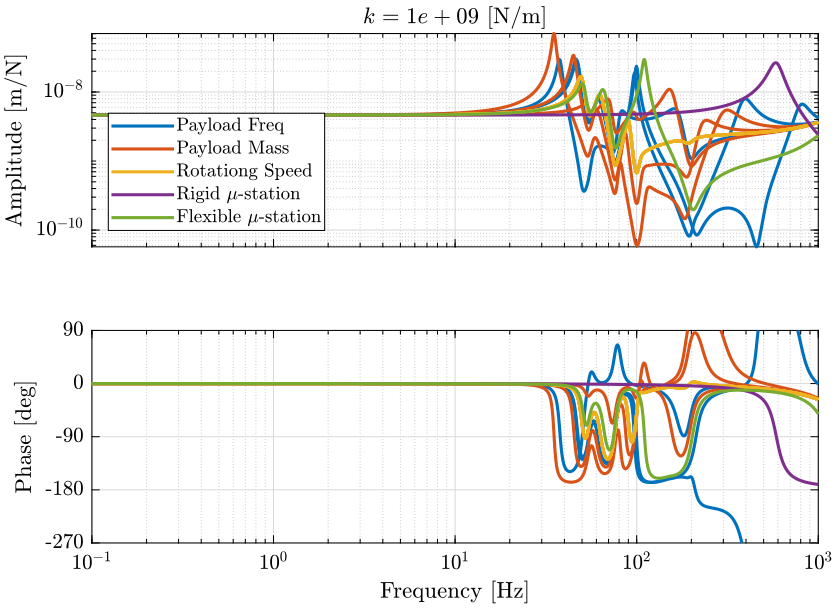
<p><span class="figure-number">Figure 20: </span>Total variation of the dynamics from \(\mathcal{F}_x\) to \(\mathcal{X}_x\). Nano-hexapod leg’s stiffness is equal to \(k = 10^9\ [N/m]\) (<a href="./figs/opt_stiffness_plant_dynamics_fx_dx_k_1e9.png">png</a>, <a href="./figs/opt_stiffness_plant_dynamics_fx_dx_k_1e9.pdf">pdf</a>)</p>
</div>
<div id="org0a4e875" class="figure">
<p><img src="figs/opt_stiffness_plant_dynamics_task_space.gif" alt="opt_stiffness_plant_dynamics_task_space.gif" />
</p>
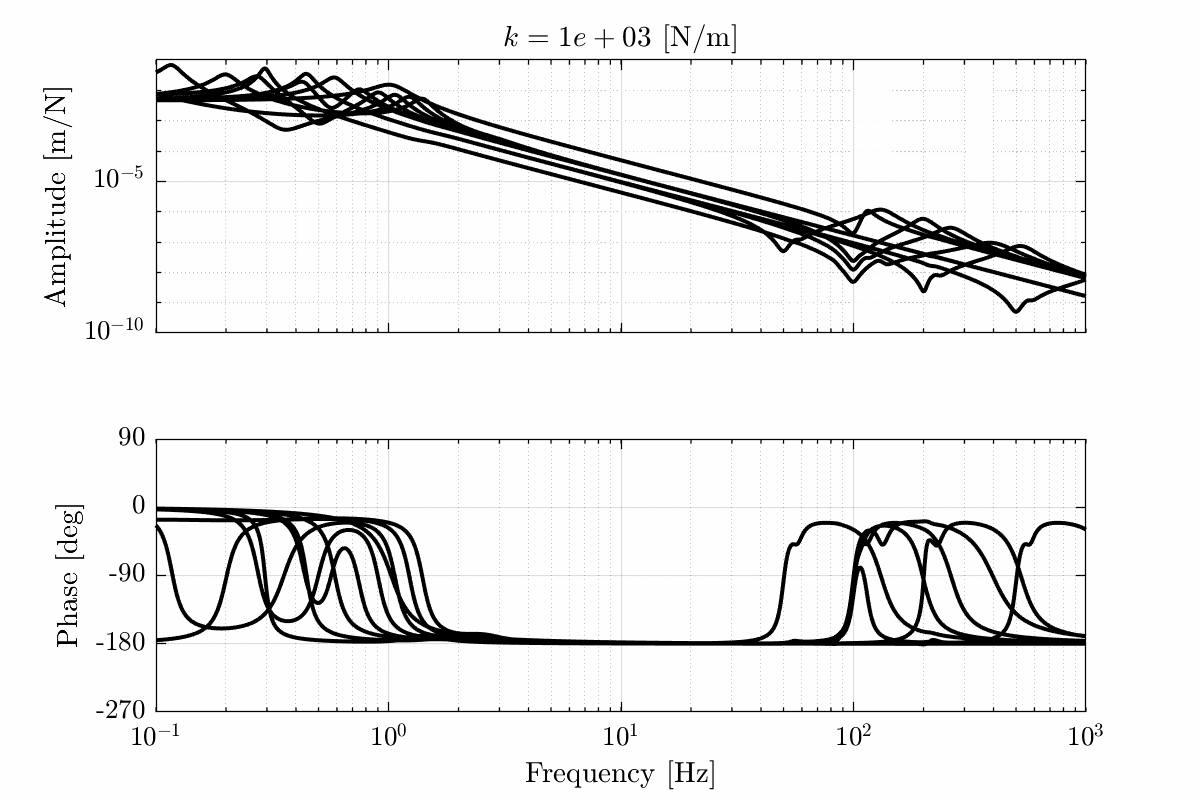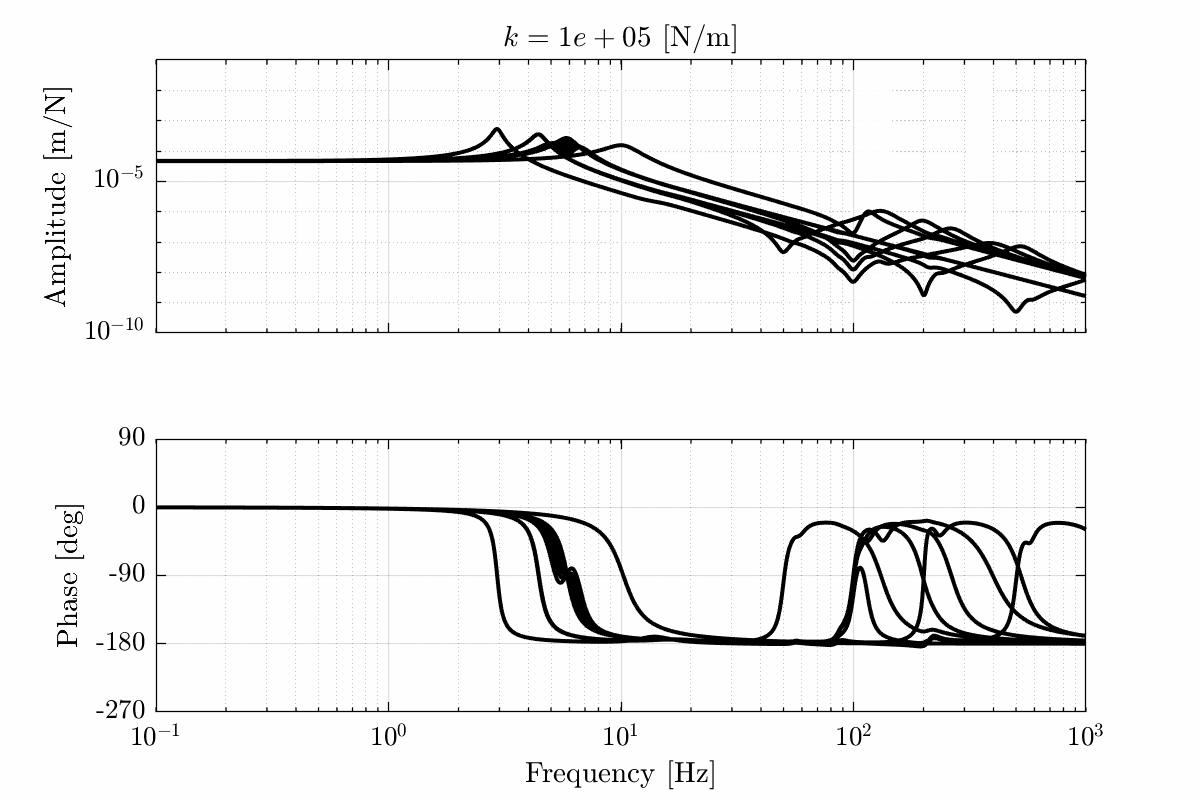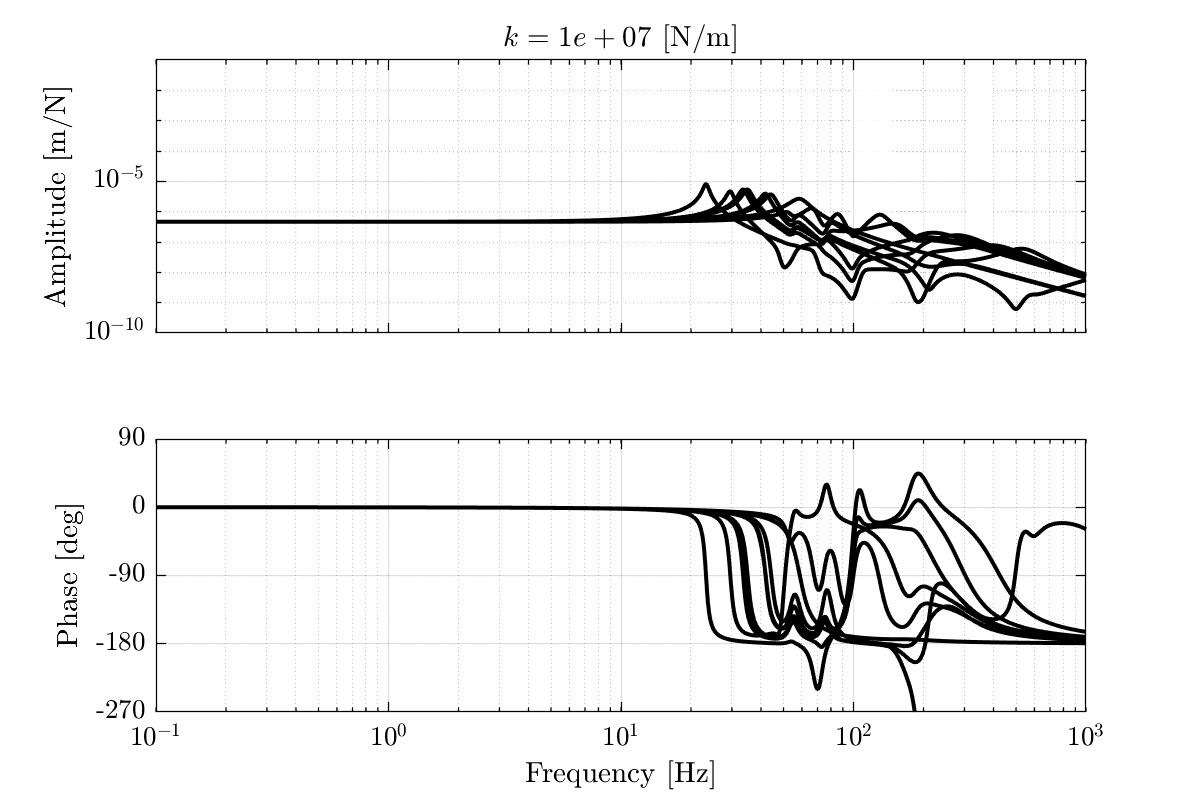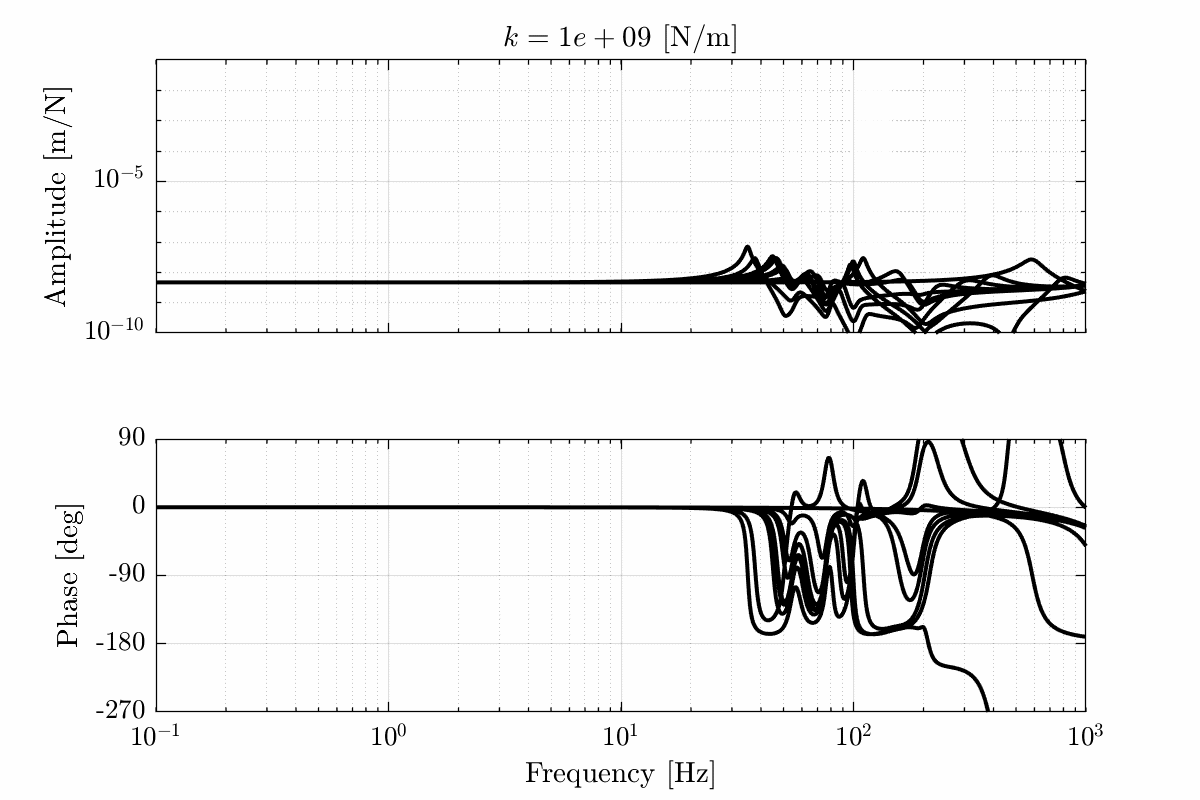
<p><span class="figure-number">Figure 21: </span>Variability of the dynamics from \(\mathcal{F}_x\) to \(\mathcal{X}_x\) with varying nano-hexapod stiffness</p>
</div>
<div id="orge890242" class="figure">
<p><img src="figs/opt_stiffness_plant_dynamics_task_space_colors.gif" alt="opt_stiffness_plant_dynamics_task_space_colors.gif" />
</p>
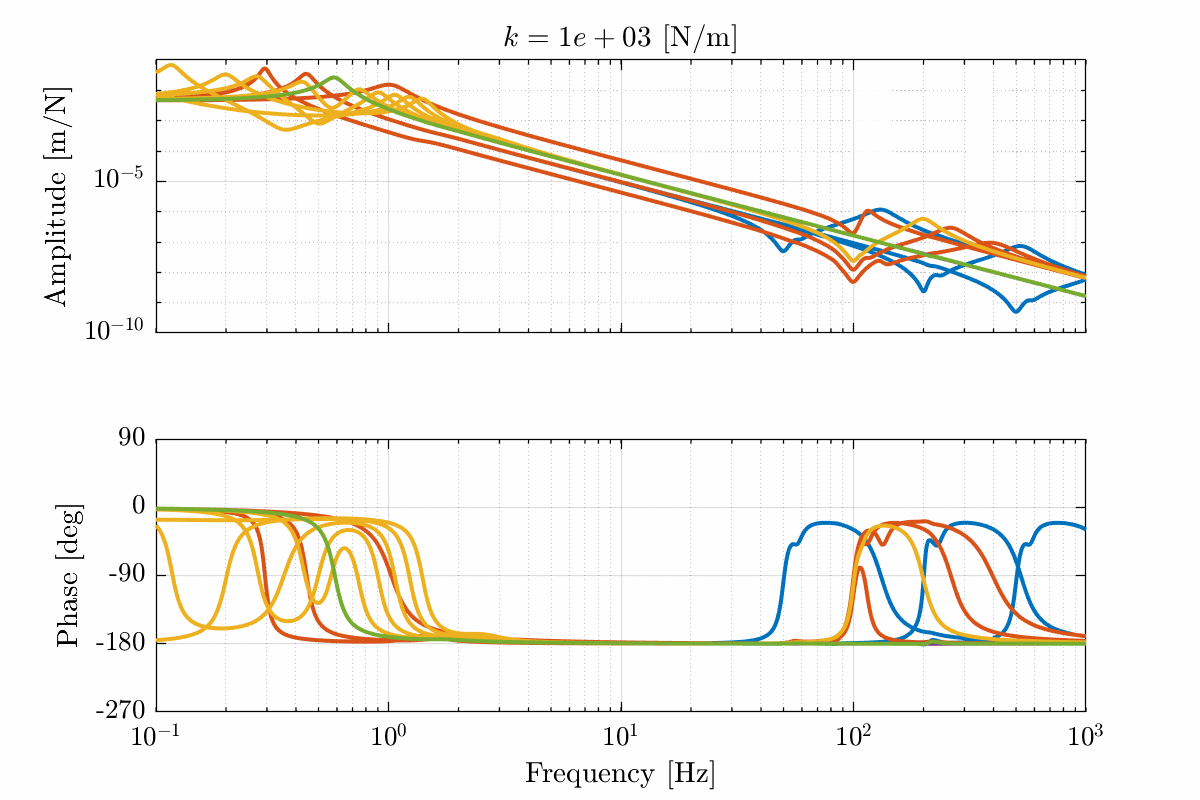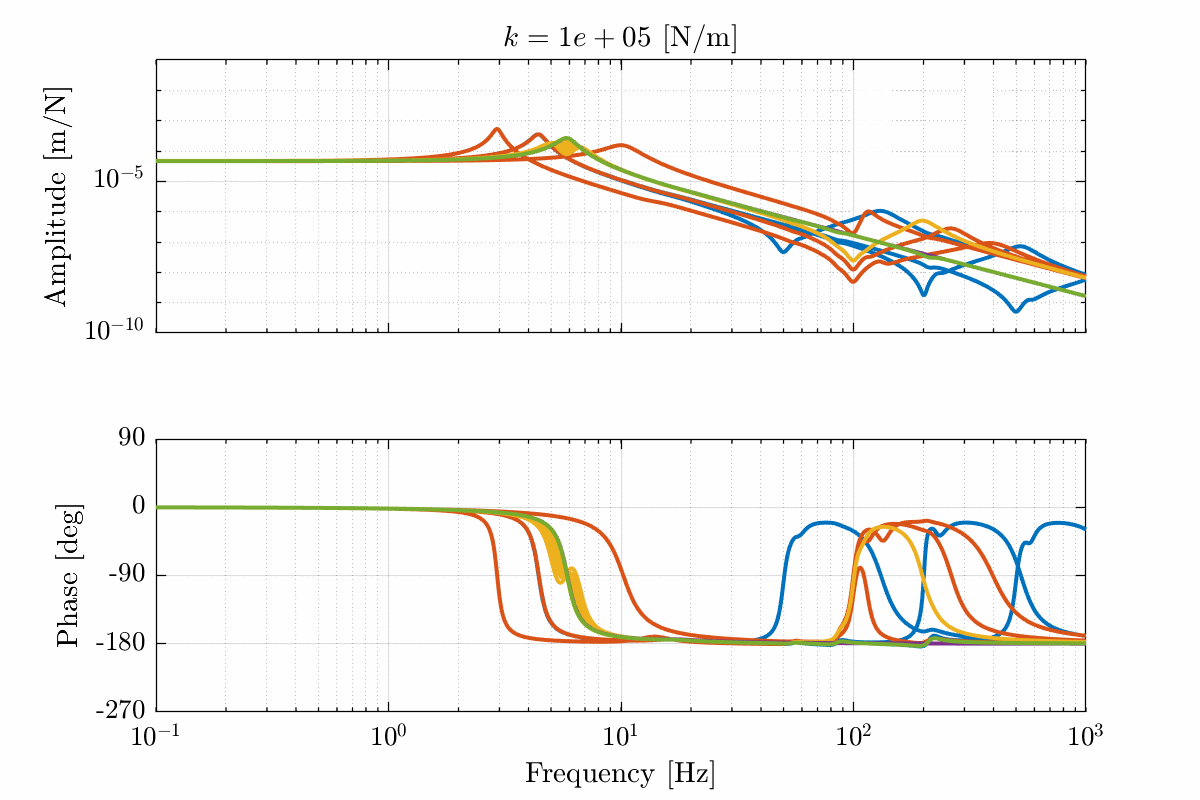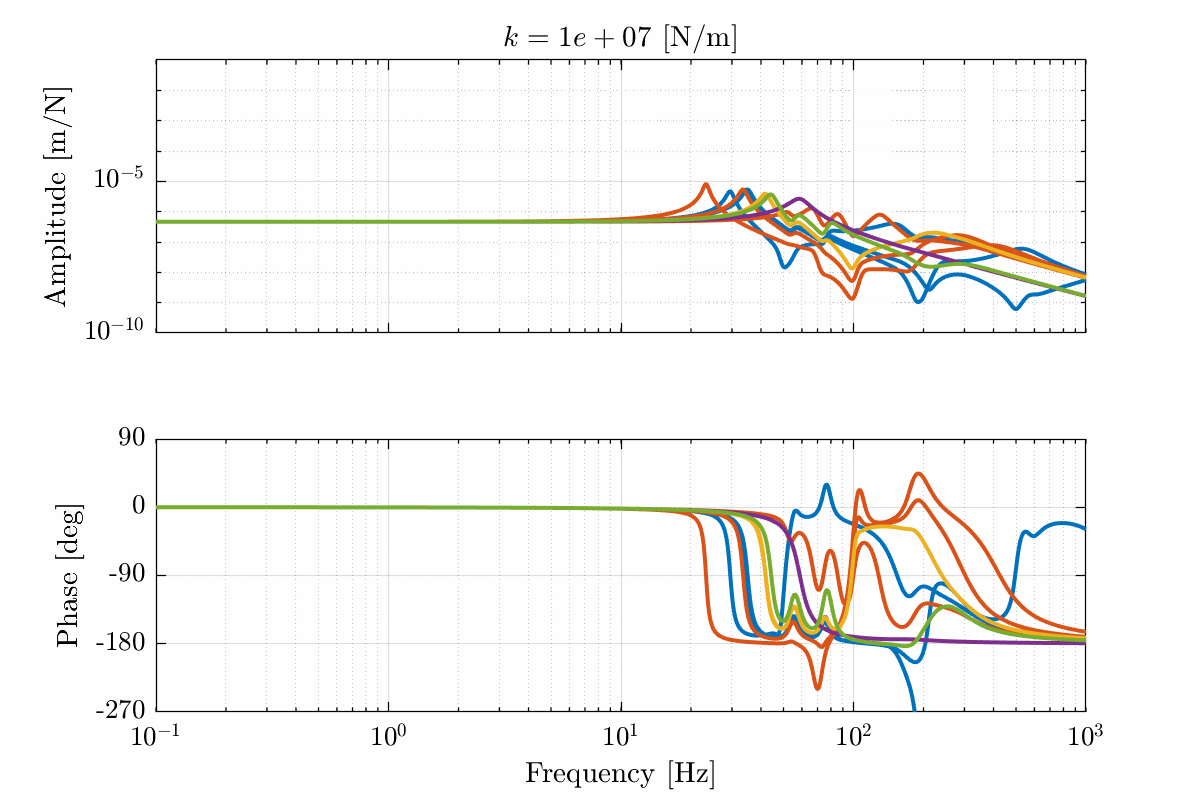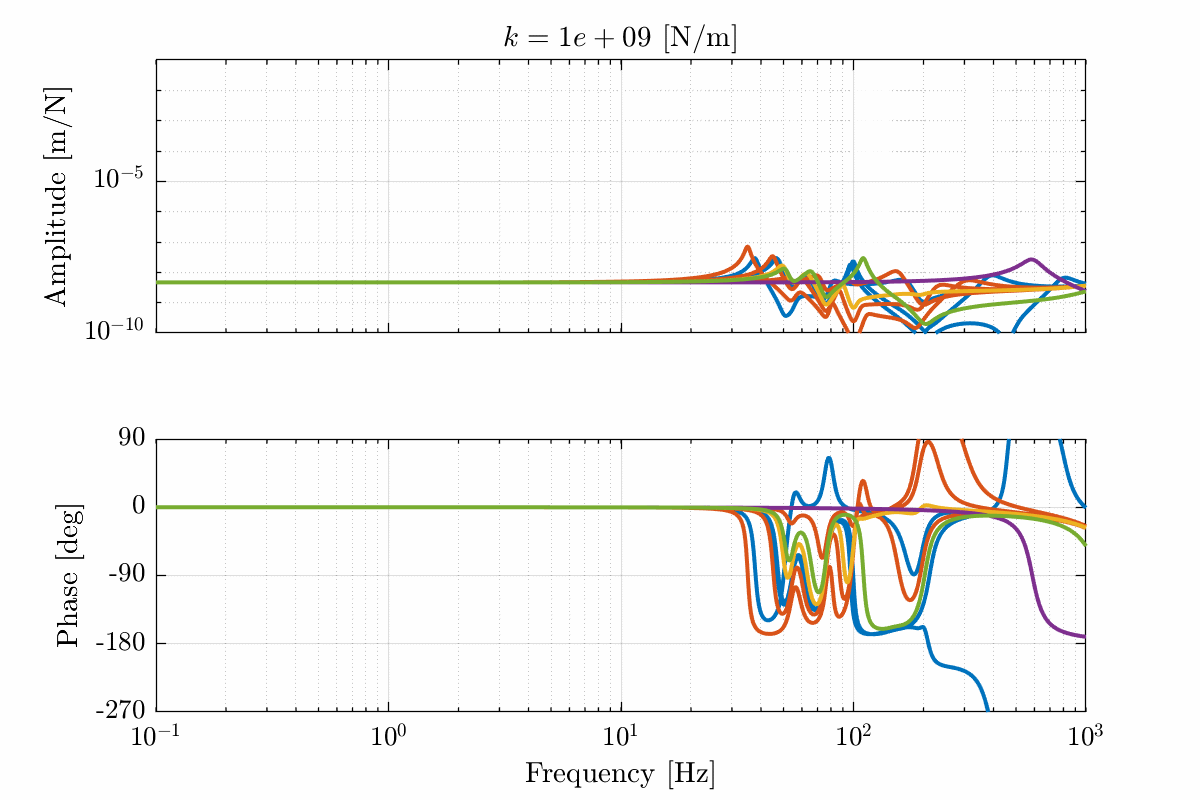
<p><span class="figure-number">Figure 22: </span>Variability of the dynamics from \(\mathcal{F}_x\) to \(\mathcal{X}_x\) with varying nano-hexapod stiffness</p>
</div>
</div>
</div>
</div>
<div id="postamble" class="status">
<p class="author">Author: Dehaeze Thomas</p>
<p class="date">Created: 2020-04-05 dim. 19:43</p>
</div>
</body>
</html>