Determination of the optimal nano-hexapod’s stiffness for reducing the effect of disturbances

1. Disturbances
2. Effect of disturbances on the position error
3. Effect of granite stiffness
4. Open Loop Budget Error
5. Closed Loop Budget Error
- 5.1. Approximation of the effect of feedback on the motion error
- 5.2. Reduction thanks to feedback - Required bandwidth
6. Conclusion

In this document is studied how the stiffness of the nano-hexapod will impact the effect of disturbances on the position error of the sample.

It is divided in the following sections:

Section 1: the disturbances are listed and their Power Spectral Densities (PSD) are shown
Section 2: the transfer functions from disturbances to the position error of the sample are computed for a wide range of nano-hexapod stiffnesses
Section 3:
Section 4: from both the PSD of the disturbances and the transfer function from disturbances to sample’s position errors, we compute the resulting PSD and Cumulative Amplitude Spectrum (CAS)
Section 5: from a simplistic model is computed the required control bandwidth to reduce the position error to acceptable values

1 Disturbances

The main disturbances considered here are:

\(D_w\): Ground displacement in the \(x\), \(y\) and \(z\) directions
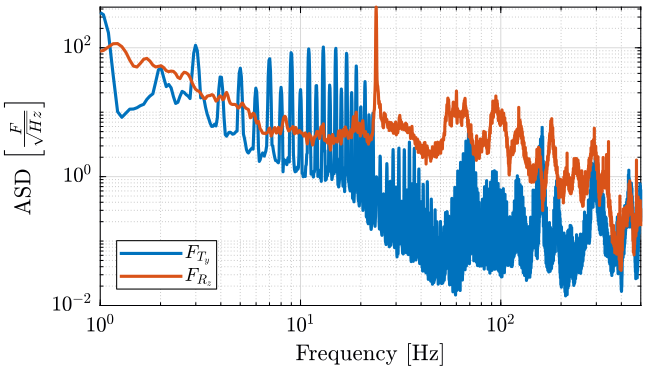
\(F_{ty}\): Forces applied by the Translation stage in the \(x\) and \(z\) directions
\(F_{rz}\): Forces applied by the Spindle in the \(z\) direction
\(F_d\): Direct forces applied at the center of mass of the Payload

The level of these disturbances has been identified form experiments which are detailed in this document.

The measured Amplitude Spectral Densities (ASD) of these forces are shown in Figures 1 and 2.

In this study, the expected frequency content of the direct forces applied to the payload is not considered.

Figure 1: Amplitude Spectral Density of the Ground Displacement (png, pdf)

Figure 2: Amplitude Spectral Density of the “parasitic” forces comming from the Translation stage and the spindle (png, pdf)

2 Effect of disturbances on the position error

In this section, we use the Simscape model to identify the transfer function from disturbances to the position error of the sample. We do that for a wide range of nano-hexapod stiffnesses and we compare the obtained results.

2.1 Initialization

We initialize all the stages with the default parameters.

initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();
initializeAxisc();
initializeMirror();

We use a sample mass of 10kg.

initializeSample('mass', 10);

We include gravity, and we use no controller.

initializeSimscapeConfiguration('gravity', true);
initializeController();
initializeDisturbances('enable', false);
initializeLoggingConfiguration('log', 'none');

2.2 Identification

The considered inputs are:

Dwx: Ground displacement in the \(x\) direction
Dwy: Ground displacement in the \(y\) direction
Dwz: Ground displacement in the \(z\) direction
Fty_x: Forces applied by the Translation stage in the \(x\) direction
Fty_z: Forces applied by the Translation stage in the \(z\) direction
Frz_z: Forces applied by the Spindle in the \(z\) direction
Fd: Direct forces applied at the center of mass of the Payload

The outputs are Ex, Ey, Ez, Erx, Ery, Erz which are the 3 positions and 3 orientations errors of the sample.

We initialize the set of the nano-hexapod stiffnesses, and for each of them, we identify the dynamics from defined inputs to defined outputs.

Ks = logspace(3,9,7); % [N/m]

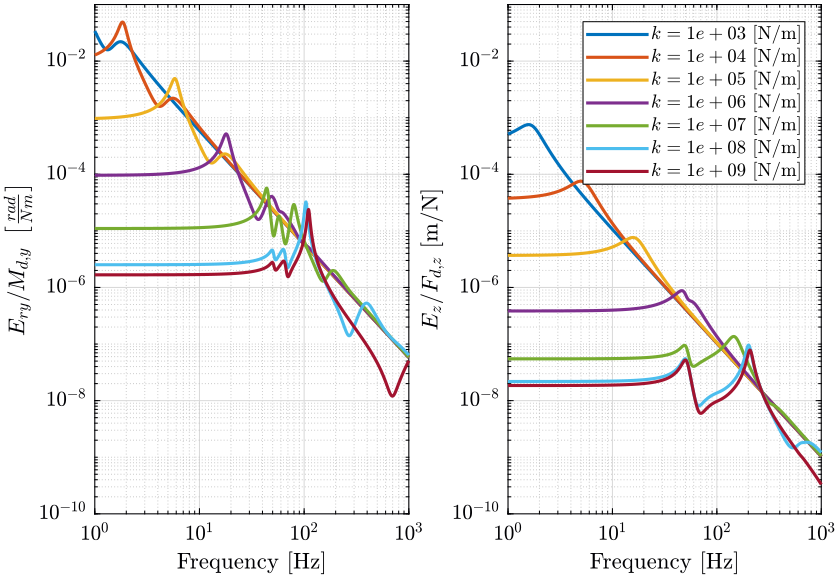
2.3 Sensitivity to Stages vibration (Filtering)

The sensitivity the stage vibrations are displayed:

Figure 3: sensitivity to vertical spindle vibrations
Figure 4: sensitivity to vertical translation stage vibrations
Figure 5: sensitivity to horizontal (x) translation stage vibrations

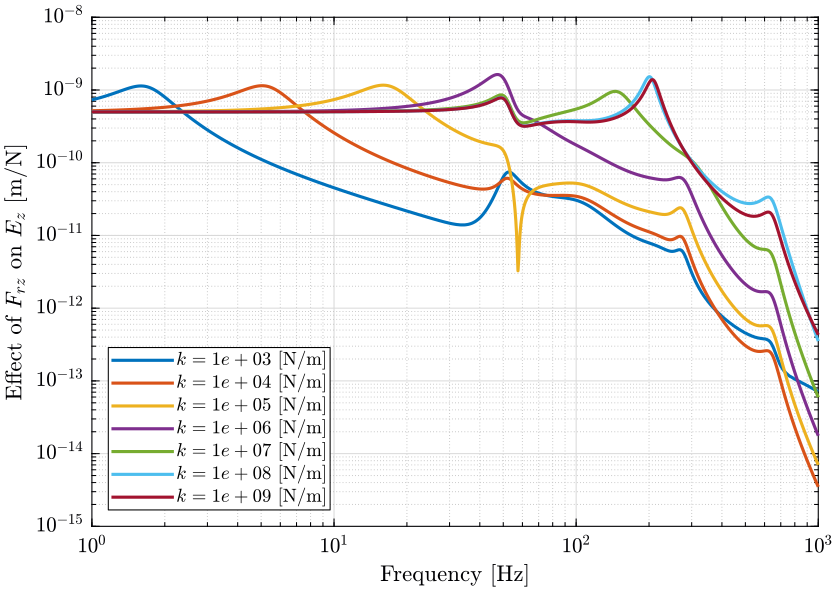
Figure 3: Sensitivity to Spindle vertical motion error (\(F_{rz}\)) to the vertical error position of the sample (\(E_z\)) (png, pdf)

Figure 4: Sensitivity to Translation stage vertical motion error (\(F_{ty,z}\)) to the vertical error position of the sample (\(E_z\)) (png, pdf)

Figure 5: Sensitivity to Translation stage \(x\) motion error (\(F_{ty,x}\)) to the error position of the sample in the \(x\) direction (\(E_x\)) (png, pdf)

2.4 Effect of Ground motion (Transmissibility).

The effect of Ground motion on the position error of the sample is shown in Figure 6.

Figure 6: Sensitivity to Ground motion (\(D_{w}\)) to the position error of the sample (\(E_y\) and \(E_z\)) (png, pdf)

2.5 Direct Forces (Compliance).

The effect of direct forces/torques applied on the sample (cable forces for instance) on the position error of the sample is shown in Figure 7.

Figure 7: Sensitivity to Direct forces and torques applied to the sample (\(F_d\), \(M_d\)) to the position error of the sample (png, pdf)

2.6 Conclusion

Reducing the nano-hexapod stiffness generally lowers the sensitivity to stages vibration but increases the sensitivity to ground motion and direct forces.

In order to conclude on the optimal stiffness that will yield the smallest sample vibration, one has to include the level of disturbances. This is done in Section 4.

3 Effect of granite stiffness

In this section, we wish to see if a soft granite suspension could help in reducing the effect of disturbances on the position error of the sample.

3.1 Analytical Analysis

3.1.1 Simple mass-spring-damper model

Let’s consider the system shown in Figure 8 consisting of two stacked mass-spring-damper systems. The bottom one represents the granite, and the top one all the positioning stages. We want the smallest stage “deformation” \(d = x^\prime - x\) due to ground motion \(w\).

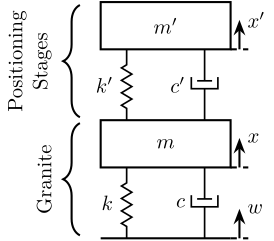
Figure 8: Mass Spring Damper system consisting of a granite and a positioning stage

If we write the equation of motion of the system in Figure 8, we obtain:

\begin{align} m^\prime s^2 x^\prime &= (c^\prime s + k^\prime) (x - x^\prime) \\ ms^2 x &= (c^\prime s + k^\prime) (x^\prime - x) + (cs + k) (w - x) \end{align}

If we note \(d = x^\prime - x\), we obtain:

\begin{equation} \frac{d}{w} = \frac{-m^\prime s^2 (cs + k)}{ (m^\prime s^2 + c^\prime s + k^\prime) (ms^2 + cs + k) + m^\prime s^2(c^\prime s + k^\prime)} \end{equation}

3.1.2 General Case

Let’s now considering a general positioning stage defined by:

\(G^\prime(s) = \frac{F}{x}\): its mechanical “impedance”
\(D^\prime(s) = \frac{d}{x}\): its “deformation” transfer function

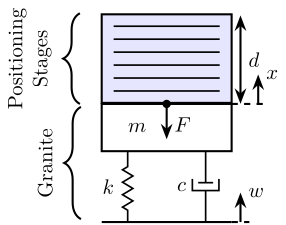
Figure 9: Mass Spring Damper representing the granite and a general representation of positioning stages

The equation of motion are:

\begin{align} ms^2 x &= (cs + k) (x - w) - F \\ F &= G^\prime(s) x \\ d &= D^\prime(s) x \end{align}

where:

\(F\) is the force applied by the position stages on the granite mass

We can express \(d\) as a function of \(w\):

\begin{equation} \frac{d}{w} = \frac{D^\prime(s) (cs + k)}{ms^2 + cs + k + G^\prime(s)} \end{equation}

This is the transfer function that we would like to minimize.

Let’s verify this formula for a simple mass/spring/damper positioning stage. In that case, we have:

\begin{align*} D^\prime(s) &= \frac{d}{x} = \frac{- m^\prime s^2}{m^\prime s^2 + c^\prime s + k^\prime} \\ G^\prime(s) &= \frac{F}{x} = \frac{m^\prime s^2(c^\prime s + k)}{m^\prime s^2 + c^\prime s + k^\prime} \end{align*}

And finally:

\begin{equation} \frac{d}{w} = \frac{-m^\prime s^2 (cs + k)}{ (m^\prime s^2 + c^\prime s + k^\prime) (ms^2 + cs + k) + m^\prime s^2(c^\prime s + k^\prime)} \end{equation}

which is the same as the previously derived equation.

3.2 Soft Granite

Let’s initialize a soft granite and see how the sensitivity to disturbances will change.

initializeGranite('K', 5e5*ones(3,1), 'C', 5e3*ones(3,1));

3.3 Effect of the Granite transfer function

From Figure 10, we can see that having a “soft” granite suspension greatly lowers the sensitivity to ground motion. The sensitivity is indeed lowered starting from the resonance of the granite on its soft suspension (few Hz here).

From Figures 11 and 12, we see that the change of granite suspension does not change a lot the sensitivity to both direct forces and stage vibrations.

Figure 10: Change of sensibility to Ground motion when using a stiff Granite (solid curves) and a soft Granite (dashed curves) (png, pdf)

Figure 11: Change of sensibility to Spindle vibrations when using a stiff Granite (solid curves) and a soft Granite (dashed curves) (png, pdf)

Figure 12: Change of sensibility to direct forces when using a stiff Granite (solid curves) and a soft Granite (dashed curves) (png, pdf)

3.4 Conclusion

Having a soft granite suspension could greatly improve the sensitivity the ground motion and thus the level of sample vibration if it is found that ground motion is the limiting factor.

4 Open Loop Budget Error

Now that the frequency content of disturbances have been estimated (Section 1) and the transfer functions from disturbances to the position error of the sample have been identified (Section 2), we can compute the level of sample vibration due to the disturbances.

We then can conclude and the nano-hexapod stiffness that will lower the sample position error.

4.1 Noise Budgeting - Theory

Let’s consider Figure 13 there \(G_d(s)\) is the transfer function from a signal \(d\) (the perturbation) to a signal \(y\) (the sample’s position error).

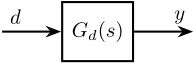
Figure 13: Figure caption

We can compute the Power Spectral Density (PSD) of signal \(y\) from the PSD of \(d\) and the norm of \(G_d(s)\):

\begin{equation} S_{y}(\omega) = \left|G_d(j\omega)\right|^2 S_{d}(\omega) \label{eq:psd_transfer_function} \end{equation}

If we now consider multiple disturbances \(d_1, \dots, d_n\) as shown in Figure 14, we have that:

\begin{equation} S_{y}(\omega) = \left|G_{d_1}(j\omega)\right|^2 S_{d_1}(\omega) + \dots + \left|G_{d_n}(j\omega)\right|^2 S_{d_n}(\omega) \label{eq:sum_psd} \end{equation}

Sometimes, we prefer to compute the Amplitude Spectral Density (ASD) which is related to the PSD by: \[ \Gamma_y(\omega) = \sqrt{S_y(\omega)} \]

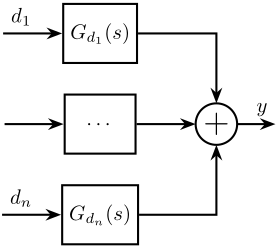
Figure 14: Figure caption

The Cumulative Power Spectrum (CPS) is here defined as:

\begin{equation} \Phi_y(\omega) = \int_\omega^\infty S_y(\nu) d\nu \end{equation}

And the Cumulative Amplitude Spectrum (CAS):

\begin{equation} \Psi(\omega) = \sqrt{\Phi(\omega)} = \sqrt{\int_\omega^\infty S_y(\nu) d\nu} \end{equation}

The CAS evaluation for all frequency corresponds to the rms value of the considered quantity: \[ y_{\text{rms}} = \Psi(\omega = 0) = \sqrt{\int_0^\infty S_y(\nu) d\nu} \]

4.2 Power Spectral Densities

We compute the effect of perturbations on the motion error thanks to Eq. \eqref{eq:psd_transfer_function}.

The result is shown in:

Figure 15: PSD of the vertical sample’s motion error due to vertical ground motion
Figure 16: PSD of the vertical sample’s motion error due to vertical vibrations of the Spindle

Figure 15: Amplitude Spectral Density of the Sample vertical position error due to Ground motion for multiple nano-hexapod stiffnesses (png, pdf)

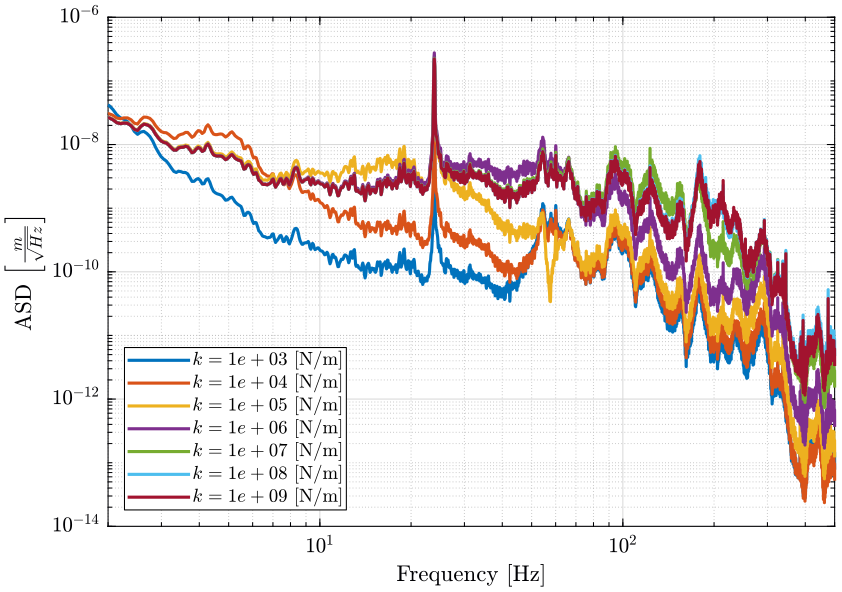
Figure 16: Amplitude Spectral Density of the Sample vertical position error due to Vertical vibration of the Spindle for multiple nano-hexapod stiffnesses (png, pdf)

We compute the effect of all perturbations on the vertical position error using Eq. \eqref{eq:sum_psd} and the resulting PSD is shown in Figure 17.

Figure 17: Amplitude Spectral Density of the Sample vertical position error due to all considered perturbations for multiple nano-hexapod stiffnesses (png, pdf)

4.3 Cumulative Amplitude Spectrum

Similarly, the Cumulative Amplitude Spectrum of the sample vibrations are shown:

Figure 18: due to vertical ground motion
Figure 19: due to vertical vibrations of the Spindle
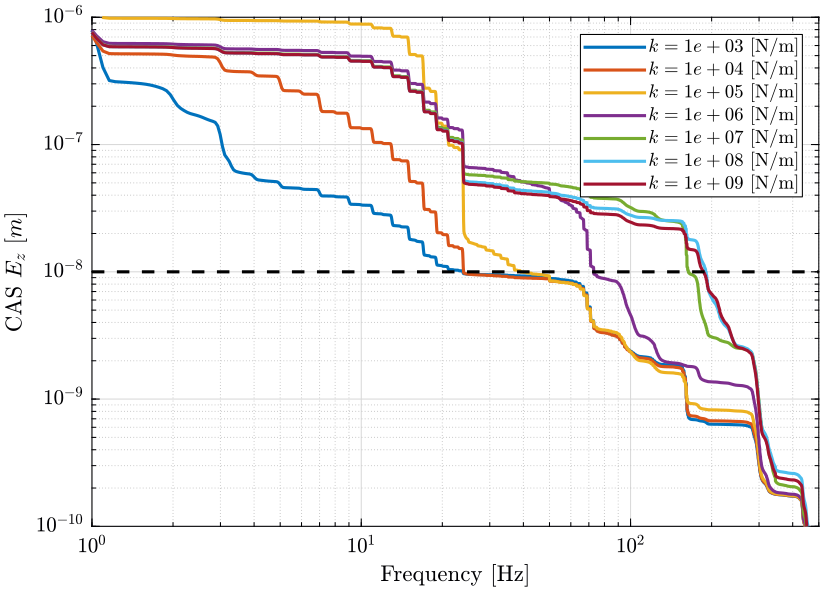
Figure 20: due to all considered perturbations

The black dashed line corresponds to the performance objective of a sample vibration equal to \(10\ nm [rms]\).

freqs = dist_f.f;

figure;
hold on;
for i = 1:length(Ks)
  plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(dist_f.psd_gm.*abs(squeeze(freqresp(Gd{i}('Ez', 'Dwz'), freqs, 'Hz'))).^2)))), '-', ...
         'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i)));
end
plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off');
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('CAS $E_y$ $[m]$')
legend('Location', 'northeast');
xlim([1, 500]); ylim([1e-10 1e-6]);

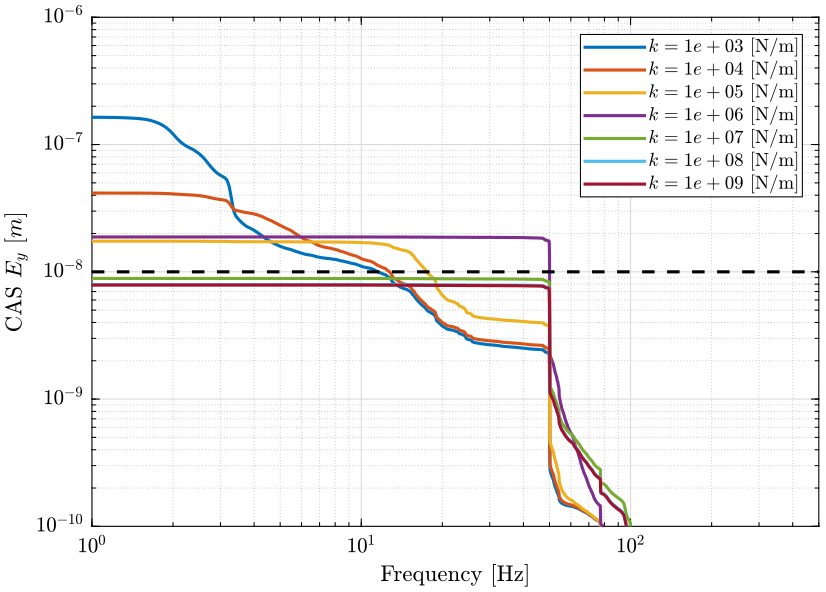
Figure 18: Cumulative Amplitude Spectrum of the Sample vertical position error due to Ground motion for multiple nano-hexapod stiffnesses (png, pdf)

freqs = dist_f.f;

figure;
hold on;
for i = 1:length(Ks)
  plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(dist_f.psd_rz.*abs(squeeze(freqresp(Gd{i}('Ez', 'Frz_z'), freqs, 'Hz'))).^2)))), '-', ...
         'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i)));
end
plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off');
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('CAS $[m]$')
legend('Location', 'southwest');
xlim([1, 500]); ylim([1e-10 1e-6]);

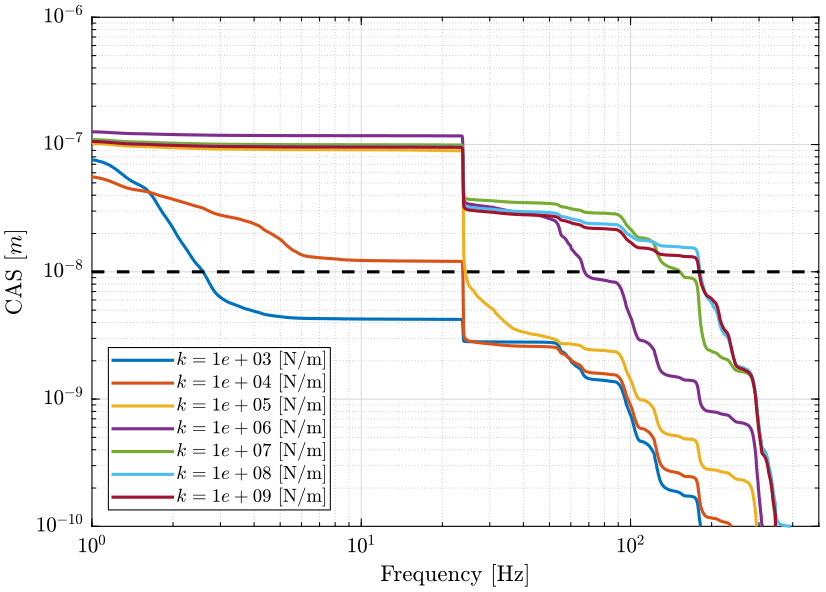
Figure 19: Cumulative Amplitude Spectrum of the Sample vertical position error due to Vertical vibration of the Spindle for multiple nano-hexapod stiffnesses (png, pdf)

freqs = dist_f.f;

figure;
hold on;
for i = 1:length(Ks)
  plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(psd_tot(:,i))))), '-', ...
         'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i)));
end
plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off');
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('CAS $E_z$ $[m]$')
legend('Location', 'northeast');
xlim([1, 500]); ylim([1e-10 1e-6]);

Figure 20: Cumulative Amplitude Spectrum of the Sample vertical position error due to all considered perturbations for multiple nano-hexapod stiffnesses (png, pdf)

4.4 Conclusion

From Figure 20, we can see that a soft nano-hexapod \(k<10^6\ [N/m]\) significantly reduces the effect of perturbations from 20Hz to 300Hz.

5 Closed Loop Budget Error

5.1 Approximation of the effect of feedback on the motion error

Let’s consider Figure 21 where a controller \(K\) is used to reduce the effect of the disturbance \(d\) on the position error \(y\).

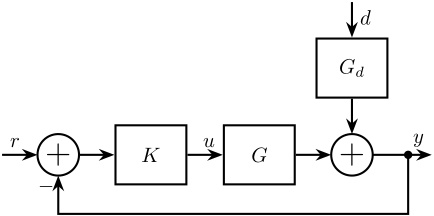
Figure 21: Feedback System

The reduction of the impact of \(d\) on \(y\) thanks to feedback is described by the following equation:

\begin{equation} \frac{y}{d} = \frac{G_d}{1 + KG} \end{equation}

As a first approximation, we can consider that the controller is designed in such a way that the loop gain \(KG\) is a pure integrator: \[ L_1(s) = K_1(s) G(s) = \frac{\omega_c}{s} \] where \(\omega_c\) is the crossover frequency.

We may then consider another controller in such a way that the loop gain corresponds to a double integrator with a lead centered with the crossover frequency \(\omega_c\): \[ L_2(s) = K_2(s) G(s) = \left( \frac{\omega_c}{s} \right)^2 \cdot \frac{1 + \frac{s}{\omega_c/2}}{1 + \frac{s}{2\omega_c}} \]

5.2 Reduction thanks to feedback - Required bandwidth

wc = 1*2*pi; % [rad/s]
xic = 0.5;

S = (s/wc)/(1 + s/wc);

bodeFig({S}, logspace(-1,2,1000))

wc = [1, 5, 10, 20, 50, 100, 200];

S1 = {zeros(length(wc), 1)};
S2 = {zeros(length(wc), 1)};

for j = 1:length(wc)
    L = (2*pi*wc(j))/s; % Simple integrator
    S1{j} = 1/(1 + L);
    L = ((2*pi*wc(j))/s)^2*(1 + s/(2*pi*wc(j)/2))/(1 + s/(2*pi*wc(j)*2));
    S2{j} = 1/(1 + L);
end

freqs = dist_f.f;

figure;
hold on;
i = 6;
for j = 1:length(wc)
    set(gca,'ColorOrderIndex',j);
    plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(abs(squeeze(freqresp(S1{j}, freqs, 'Hz'))).^2.*psd_tot(:,i))))), '-', ...
         'DisplayName', sprintf('$\\omega_c = %.0f$ [Hz]', wc(j)));
end
plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(psd_tot(:,i))))), 'k-', ...
     'DisplayName', 'Open-Loop');
plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off');
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('CAS $E_y$ $[m]$')
legend('Location', 'northeast');
xlim([0.5, 500]); ylim([1e-10 1e-6]);

wc = logspace(0, 3, 100);

Dz1_rms = zeros(length(Ks), length(wc));
Dz2_rms = zeros(length(Ks), length(wc));
for i = 1:length(Ks)
    for j = 1:length(wc)
        L = (2*pi*wc(j))/s;
        Dz1_rms(i, j) = sqrt(trapz(freqs, abs(squeeze(freqresp(1/(1 + L), freqs, 'Hz'))).^2.*psd_tot(:,i)));

        L = ((2*pi*wc(j))/s)^2*(1 + s/(2*pi*wc(j)/2))/(1 + s/(2*pi*wc(j)*2));
        Dz2_rms(i, j) = sqrt(trapz(freqs, abs(squeeze(freqresp(1/(1 + L), freqs, 'Hz'))).^2.*psd_tot(:,i)));
    end
end

freqs = dist_f.f;

figure;
hold on;
for i = 1:length(Ks)
  set(gca,'ColorOrderIndex',i);
  plot(wc, Dz1_rms(i, :), '-', ...
         'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i)))

  set(gca,'ColorOrderIndex',i);
  plot(wc, Dz2_rms(i, :), '--', ...
         'HandleVisibility', 'off')
end
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Control Bandwidth [Hz]'); ylabel('$E_z\ [m, rms]$')
legend('Location', 'southwest');
xlim([1, 500]);