Control in the Frame of the Legs applied on the Simscape Model

1. Decentralized Control
2. HAC-LAC (IFF) Decentralized Control
3. Conclusion

In this document, we apply some decentralized control to the NASS and see what level of performance can be obtained.

1 Decentralized Control

1.1 Control Schematic

The control architecture is shown in Figure 1.

The signals are:

\(\bm{r}_\mathcal{X}\): wanted position of the sample with respect to the granite
\(\bm{r}_{\mathcal{X}_n}\): wanted position of the sample with respect to the nano-hexapod
\(\bm{r}_\mathcal{L}\): wanted length of each of the nano-hexapod’s legs
\(\bm{\tau}\): forces applied in each actuator
\(\bm{\mathcal{L}}\): measured displacement of each leg
\(\bm{\mathcal{X}}\): measured position of the sample with respect to the granite

Figure 1: Decentralized control for reference tracking

1.2 Initialize the Simscape Model

We initialize all the stages with the default parameters.

initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();
initializeAxisc();
initializeMirror();

The nano-hexapod is a piezoelectric hexapod and the sample has a mass of 50kg.

initializeNanoHexapod('actuator', 'piezo');
initializeSample('mass', 1);

We set the references that corresponds to a tomography experiment.

initializeReferences('Rz_type', 'rotating', 'Rz_period', 1);

initializeDisturbances();

Open Loop.

initializeController('type', 'ref-track-L');
Kl = tf(zeros(6));

And we put some gravity.

initializeSimscapeConfiguration('gravity', true);

We log the signals.

initializeLoggingConfiguration('log', 'all');

1.3 Identification of the plant

Let’s identify the transfer function from \(\bm{\tau}\) to \(\bm{\mathcal{L}}\).

%% Name of the Simulink File
mdl = 'nass_model';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Controller'],                          1, 'openinput');  io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Controller/Reference-Tracking-L/Sum'], 1, 'openoutput'); io_i = io_i + 1; % Leg length error

%% Run the linearization
G = linearize(mdl, io, 0);
G.InputName  = {'Fnl1', 'Fnl2', 'Fnl3', 'Fnl4', 'Fnl5', 'Fnl6'};
G.OutputName = {'El1', 'El2', 'El3', 'El4', 'El5', 'El6'};

1.4 Plant Analysis

The diagonal and off-diagonal terms of the plant are shown in Figure 2.

We can see that:

the diagonal terms have similar dynamics
the plant is decoupled at low frequency

Figure 2: Transfer Functions from forces applied in each actuator \(\tau_i\) to the relative motion of each leg \(d\mathcal{L}_i\) (png, pdf)

1.5 Controller Design

The controller consists of:

A pure integrator
An integrator up to little before the crossover
A lead around the crossover
A low pass filter with a cut-off frequency 3 times the crossover to increase the gain margin

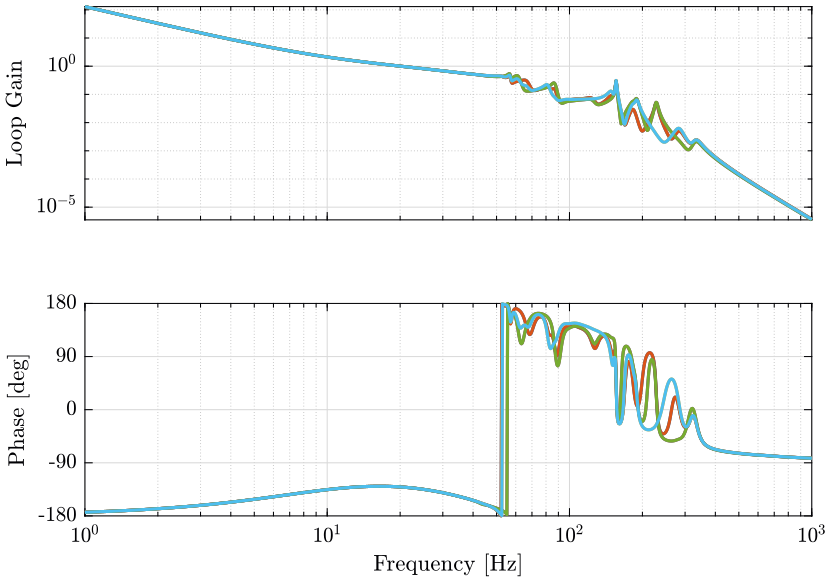
The obtained loop gains corresponding to the diagonal elements are shown in Figure 3.

wc = 2*pi*20;
h = 1.5;

Kl = diag(1./diag(abs(freqresp(G, wc)))) * ...
     wc/s * ... % Pure Integrator
     ((s/wc*2 + 1)/(s/wc*2)) * ... % Integrator up to wc/2
     1/h * (1 + s/wc*h)/(1 + s/wc/h) * ... % Lead
     1/(1 + s/3/wc) * ... % Low pass Filter
     1/(1 + s/3/wc);

Figure 3: Obtained Loop Gain (png, pdf)

We add a minus sign to the controller as it is not included in the Simscape model.

Kl = -Kl;

1.6 Simulation

initializeController('type', 'ref-track-L');

load('mat/conf_simulink.mat');
set_param(conf_simulink, 'StopTime', '2');

sim('nass_model');

decentralized_L = simout;
save('./mat/tomo_exp_decentalized.mat', 'decentralized_L', '-append');

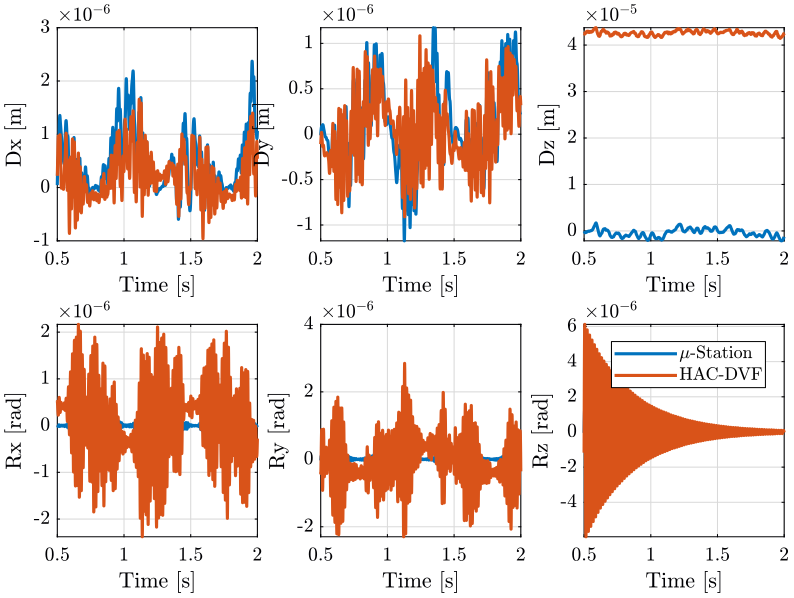
1.7 Results

The reference path and the position of the mobile platform are shown in Figure 4.

load('./mat/experiment_tomography.mat', 'tomo_align_dist');
load('./mat/tomo_exp_decentalized.mat', 'decentralized_L');

Figure 4: Position Errors when using the Decentralized Control Architecture (png, pdf)

2 HAC-LAC (IFF) Decentralized Control

We here add an Active Damping Loop (Integral Force Feedback) prior to using the Decentralized control architecture using \(\bm{\mathcal{L}}\).

2.1 Control Schematic