Study of the Flexible Joints
Table of Contents
In this document is studied the effect of the mechanical behavior of the flexible joints that are located the extremities of each nano-hexapod’s legs.
Ideally, we want the x and y rotations to be free and all the translations to be blocked. However, this is never the case and be have to consider:
This may impose some limitations, also, the goal is to specify the required joints stiffnesses (summarized in Section 3).
1 Bending and Torsional Stiffness
In this section, we wish to study the effect of the rotation flexibility of the nano-hexapod joints.
1.1 Initialization
Let’s initialize all the stages with default parameters.
initializeGround(); initializeGranite(); initializeTy(); initializeRy(); initializeRz(); initializeMicroHexapod(); initializeAxisc(); initializeMirror();
Let’s consider the heaviest mass which should we the most problematic with it comes to the flexible joints.
initializeSample('mass', 50, 'freq', 200*ones(6,1));
initializeReferences('Rz_type', 'rotating-not-filtered', 'Rz_period', 60);
1.2 Realistic Bending Stiffness Values
Let’s compare the ideal case (zero stiffness in rotation and infinite stiffness in translation) with a more realistic case:
- \(K_{\theta, \phi} = 15\,[Nm/rad]\) stiffness in flexion
- \(K_{\psi} = 20\,[Nm/rad]\) stiffness in torsion
Kf_M = 15*ones(6,1); Kf_F = 15*ones(6,1); Kt_M = 20*ones(6,1); Kt_F = 20*ones(6,1);
The stiffness and damping of the nano-hexapod’s legs are:
k_opt = 1e5; % [N/m] c_opt = 2e2; % [N/(m/s)]
This corresponds to the optimal identified stiffness.
1.2.1 Direct Velocity Feedback
We identify the dynamics from actuators force \(\tau_i\) to relative motion sensors \(d\mathcal{L}_i\) with and without considering the flexible joint stiffness.
The obtained dynamics are shown in Figure 1. It is shown that the adding of stiffness for the flexible joints does increase a little bit the frequencies of the mass suspension modes. It stiffen the structure.
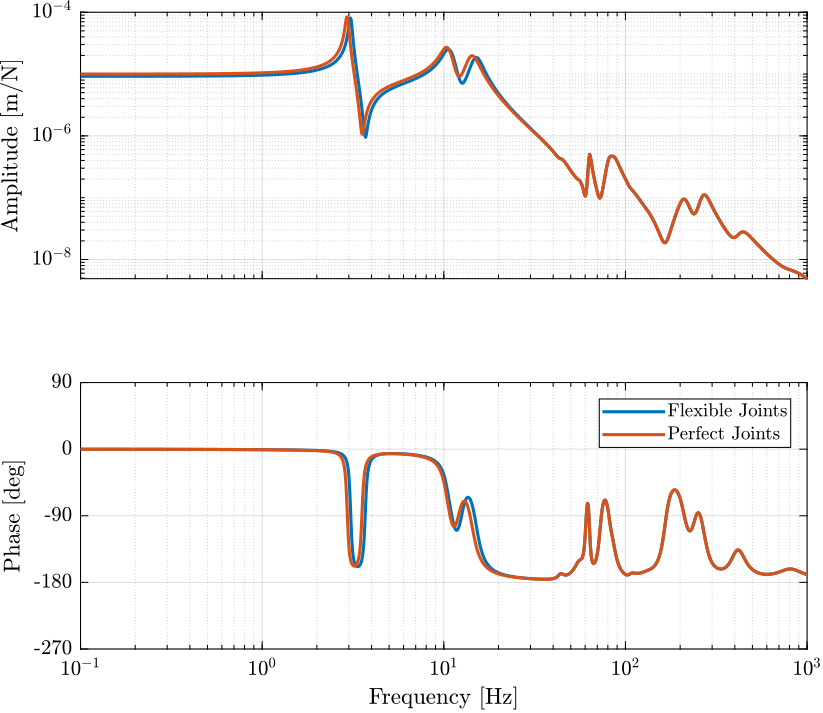
Figure 1: Dynamics from actuators force \(\tau_i\) to relative motion sensors \(d\mathcal{L}_i\) with (blue) and without (red) considering the flexible joint stiffness
1.2.2 Primary Plant
Let’s now identify the dynamics from \(\bm{\tau}^\prime\) to \(\bm{\epsilon}_{\mathcal{X}_n}\) (for the primary controller designed in the frame of the legs).
The dynamics is compare with and without the joint flexibility in Figure 2. The plant dynamics is not found to be changing significantly.

Figure 2: Dynamics from \(\bm{\tau}^\prime_i\) to \(\bm{\epsilon}_{\mathcal{X}_n,i}\) with perfect joints (dashed) and with flexible joints (solid)
1.2.3 Conclusion
Considering realistic flexible joint bending stiffness for the nano-hexapod does not seems to impose any limitation on the DVF control nor on the primary control.
It only increases a little bit the suspension modes of the sample on top of the nano-hexapod.
1.3 Parametric Study
We wish now to see what is the impact of the rotation stiffness of the flexible joints on the dynamics. This will help to determine the requirements on the joint’s stiffness.
Let’s consider the following bending stiffness of the flexible joints:
Ks = [1, 5, 10, 50, 100]; % [Nm/rad]
We also consider here a nano-hexapod with the identified optimal actuator stiffness.
1.3.1 Direct Velocity Feedback
The dynamics from the actuators to the relative displacement sensor in each leg is identified and shown in Figure 3.
The corresponding Root Locus plot is shown in Figure 4.
It is shown that the bending stiffness of the flexible joints does indeed change a little the dynamics, but critical damping is stiff achievable with Direct Velocity Feedback.
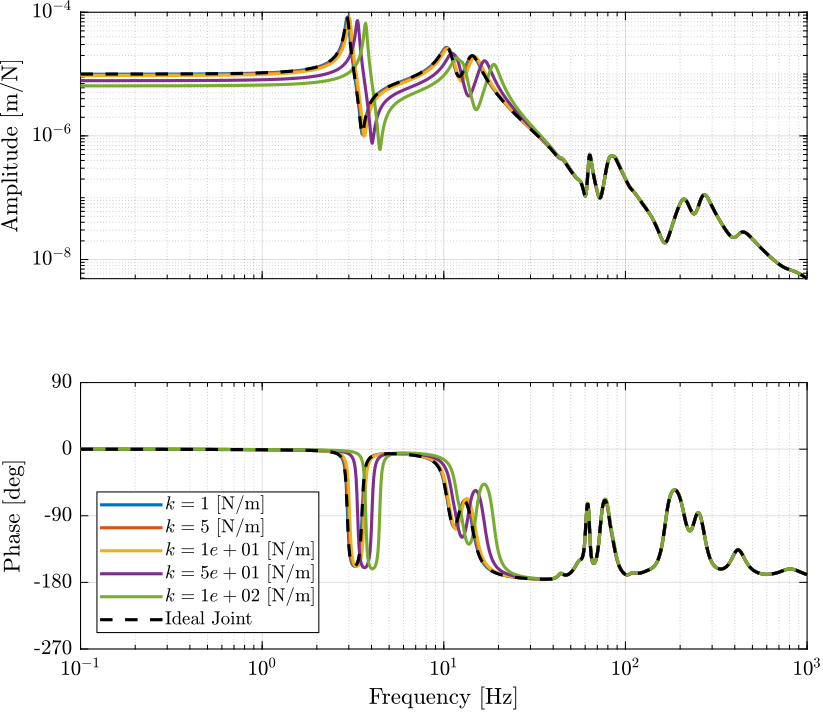
Figure 3: Dynamics from \(\tau_i\) to \(d\mathcal{L}_i\) for all the considered Rotation Stiffnesses
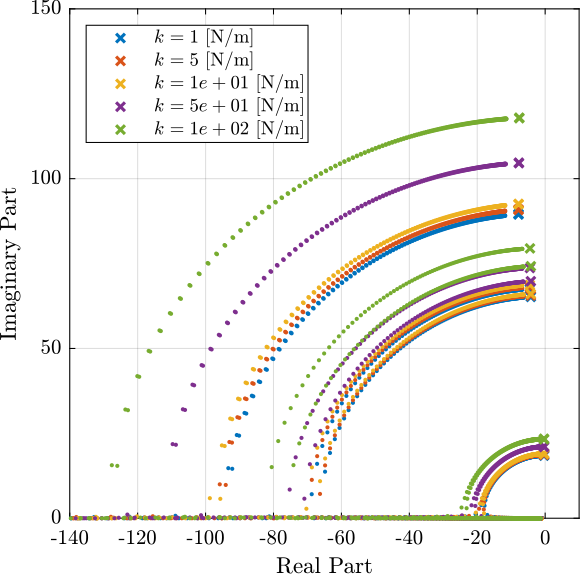
Figure 4: Root Locus for all the considered Rotation Stiffnesses
1.3.2 Primary Control
The dynamics from \(\bm{\tau}^\prime\) to \(\bm{\epsilon}_{\mathcal{X}_n}\) (for the primary controller designed in the frame of the legs) is shown in Figure 5.
It is shown that the bending stiffness of the flexible joints have very little impact on the dynamics.
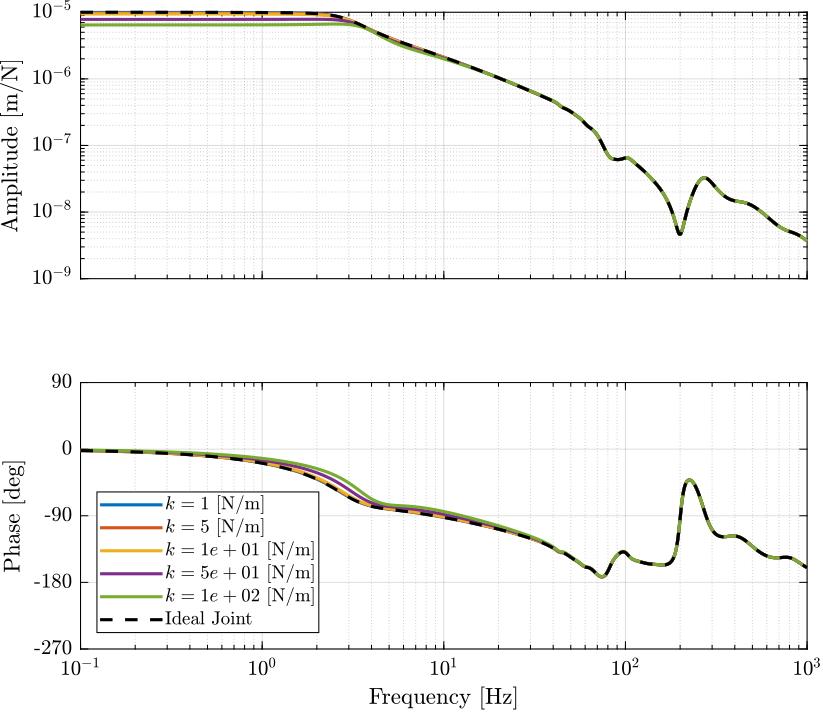
Figure 5: Diagonal elements of the transfer function matrix from \(\bm{\tau}^\prime\) to \(\bm{\epsilon}_{\mathcal{X}_n}\) for the considered bending stiffnesses
1.3.3 Conclusion
The bending stiffness of the flexible joint does not significantly change the dynamics.
2 Translation Stiffness
2.1 Realistic Translation Stiffness Values
We choose realistic values of the axial stiffness of the joints: \[ K_a = 60\,[N/\mu m] \]
Kz_F = 60e6*ones(6,1); % [N/m] Kz_M = 60e6*ones(6,1); % [N/m] Cz_F = 1*ones(6,1); % [N/(m/s)] Cz_M = 1*ones(6,1); % [N/(m/s)]
2.1.1 Initialization
Let’s initialize all the stages with default parameters.
initializeGround(); initializeGranite(); initializeTy(); initializeRy(); initializeRz(); initializeMicroHexapod(); initializeAxisc(); initializeMirror();
Let’s consider the heaviest mass which should we the most problematic with it comes to the flexible joints.
initializeSample('mass', 50, 'freq', 200*ones(6,1));
initializeReferences('Rz_type', 'rotating-not-filtered', 'Rz_period', 60);
2.1.2 Direct Velocity Feedback
The dynamics from actuators force \(\tau_i\) to relative motion sensors \(d\mathcal{L}_i\) with and without considering the flexible joint stiffness are identified.
The obtained dynamics are shown in Figure 6.
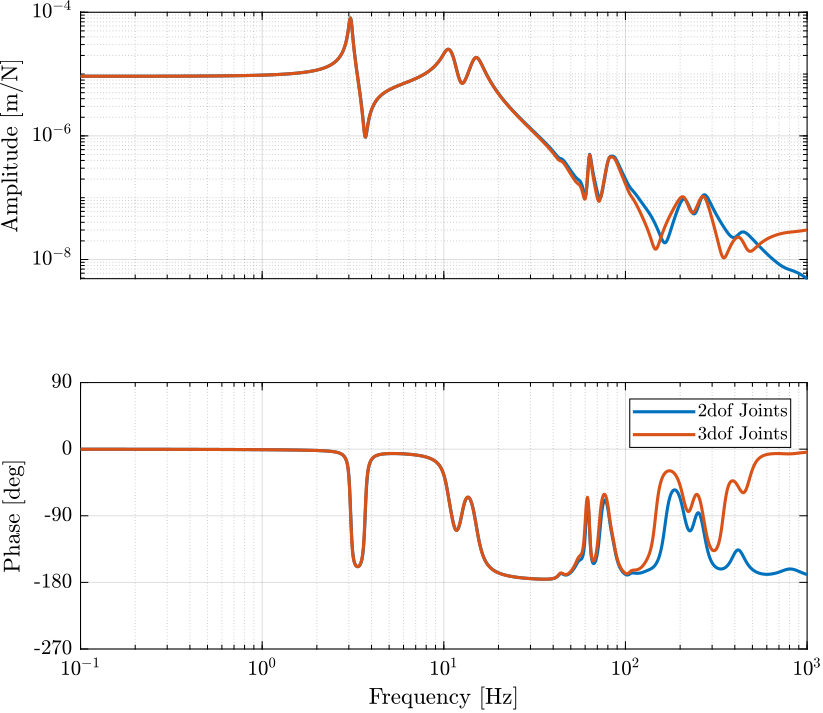
Figure 6: Dynamics from actuators force \(\tau_i\) to relative motion sensors \(d\mathcal{L}_i\) with (blue) and without (red) considering the flexible joint axis stiffness
2.1.3 Primary Plant
Kdvf = 5e3*s/(1+s/2/pi/1e3)*eye(6);
Let’s now identify the dynamics from \(\bm{\tau}^\prime\) to \(\bm{\epsilon}_{\mathcal{X}_n}\) (for the primary controller designed in the frame of the legs).
The dynamics is compare with and without the joint flexibility in Figure 7.
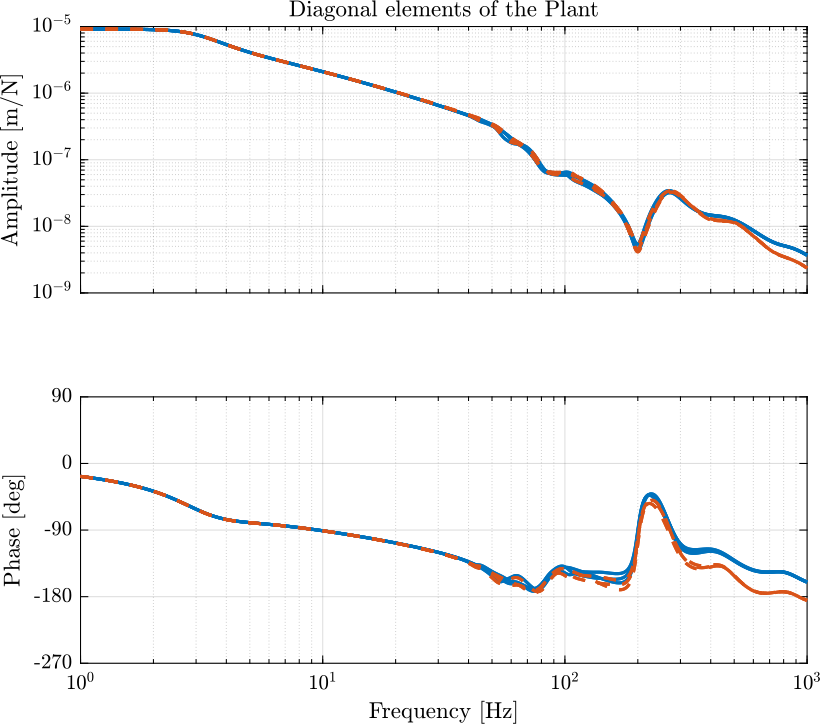
Figure 7: Dynamics from \(\bm{\tau}^\prime_i\) to \(\bm{\epsilon}_{\mathcal{X}_n,i}\) with infinite axis stiffnes (solid) and with realistic axial stiffness (dashed)
2.1.4 Conclusion
For the realistic value of the flexible joint axial stiffness, the dynamics is not much impact, and this should not be a problem for control.
2.2 Parametric study
We wish now to see what is the impact of the axial stiffness of the flexible joints on the dynamics.
Let’s consider the following values for the axial stiffness:
Kzs = [1e4, 1e5, 1e6, 1e7, 1e8, 1e9]; % [N/m]
We also consider here a nano-hexapod with the identified optimal actuator stiffness (\(k = 10^5\,[N/m]\)).
2.2.1 Direct Velocity Feedback
The dynamics from the actuators to the relative displacement sensor in each leg is identified and shown in Figure 8.
It is shown that the axial stiffness of the flexible joints does have a huge impact on the dynamics.
If the axial stiffness of the flexible joints is \(K_a > 10^7\,[N/m]\) (here \(100\) times higher than the actuator stiffness), then the change of dynamics stays reasonably small.
This is more clear by looking at the root locus (Figures 9 and 10). It can be seen that very little active damping can be achieve for axial stiffnesses below \(10^7\,[N/m]\).
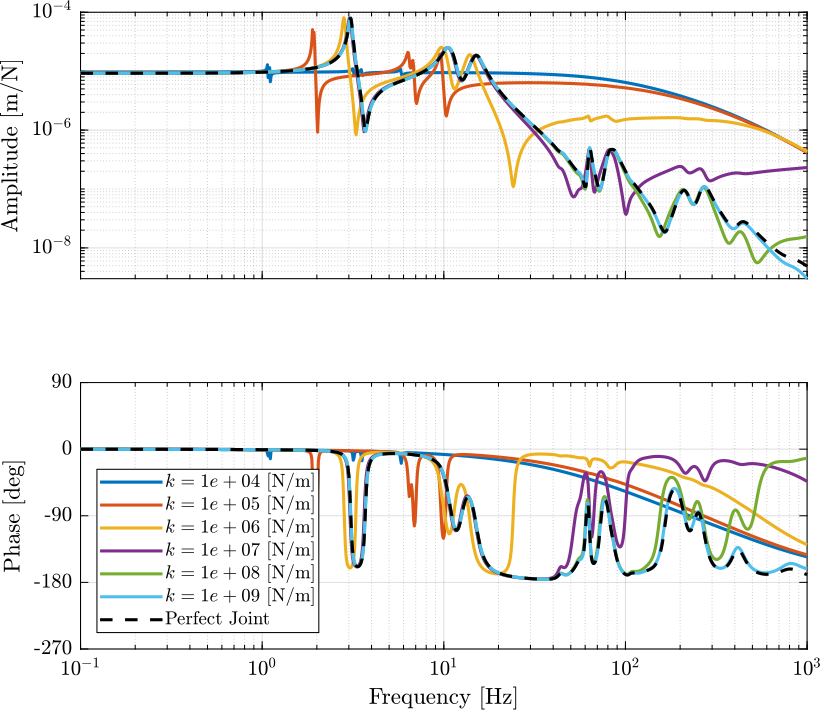
Figure 8: Dynamics from \(\tau_i\) to \(d\mathcal{L}_i\) for all the considered axis Stiffnesses

Figure 9: Root Locus for all the considered axial Stiffnesses
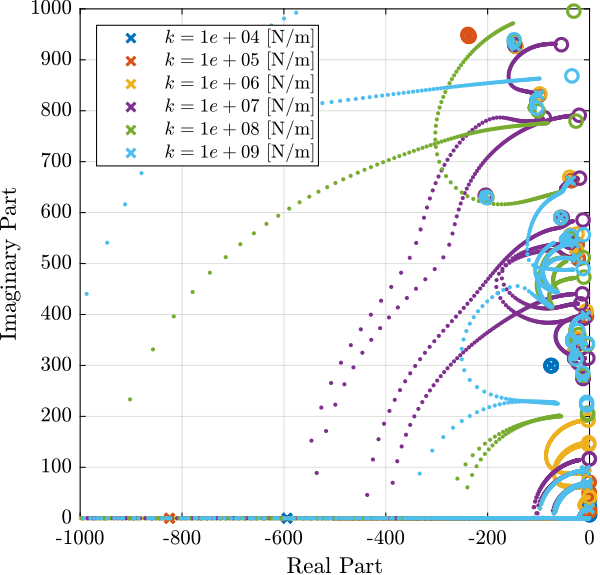
Figure 10: Root Locus (unzoom) for all the considered axial Stiffnesses
2.2.2 Primary Control
The dynamics from \(\bm{\tau}^\prime\) to \(\bm{\epsilon}_{\mathcal{X}_n}\) (for the primary controller designed in the frame of the legs) is shown in Figure 11.

Figure 11: Diagonal elements of the transfer function matrix from \(\bm{\tau}^\prime\) to \(\bm{\epsilon}_{\mathcal{X}_n}\) for the considered axial stiffnesses
2.3 Conclusion
The axial stiffness of the flexible joints should be maximized.
For the considered actuator stiffness \(k = 10^5\,[N/m]\), the axial stiffness of the flexible joints should ideally be above \(10^7\,[N/m]\).
This is a reasonable stiffness value for such joints.
We may interpolate the results and say that the axial joint stiffness should be 100 times higher than the actuator stiffness, but this should be confirmed with further analysis.