Control of the NASS with Voice coil actuators
Table of Contents
- 1. HAC-LAC + Cascade Control Topology
- 1.1. Initialization
- 1.2. Low Authority Control - Integral Force Feedback \(\bm{K}_\text{IFF}\)
- 1.3. High Authority Control in the joint space - \(\bm{K}_\mathcal{L}\)
- 1.4. Primary Controller in the task space - \(\bm{K}_\mathcal{X}\)
- 1.5. Simulation
- 1.6. Results
- 1.7. Compliance of the nano-hexapod
- 1.8. Robustness to Payload Variability
- 2. Other analysis
1 HAC-LAC + Cascade Control Topology
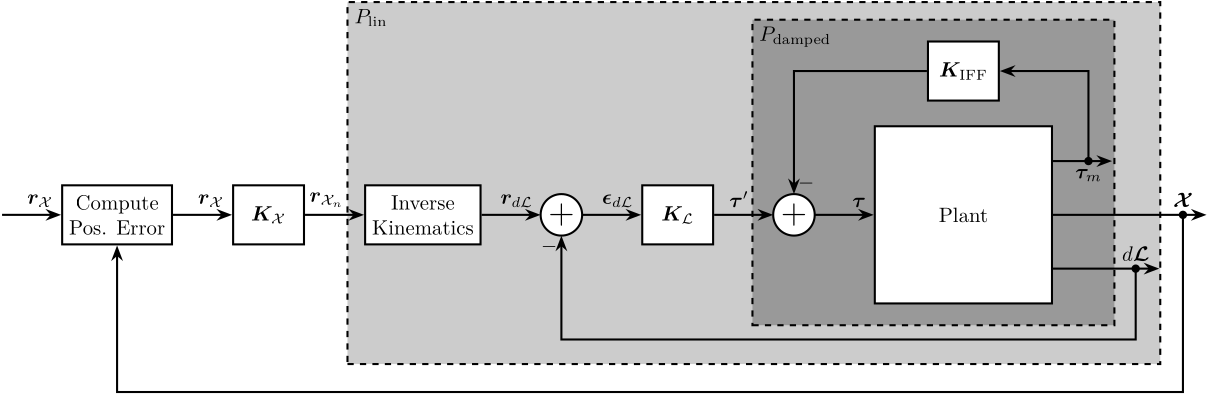
Figure 1: Cascaded Control consisting of (from inner to outer loop): IFF, Linearization Loop, Tracking Control in the frame of the Legs
1.1 Initialization
We initialize all the stages with the default parameters.
initializeGround(); initializeGranite(); initializeTy(); initializeRy(); initializeRz(); initializeMicroHexapod(); initializeAxisc(); initializeMirror();
The nano-hexapod is a voice coil based hexapod and the sample has a mass of 1kg.
initializeNanoHexapod('actuator', 'lorentz'); initializeSample('mass', 1);
We set the references that corresponds to a tomography experiment.
initializeReferences('Rz_type', 'rotating', 'Rz_period', 1);
initializeDisturbances();
initializeController('type', 'cascade-hac-lac');
initializeSimscapeConfiguration('gravity', true);
We log the signals.
initializeLoggingConfiguration('log', 'all');
Kp = tf(zeros(6)); Kl = tf(zeros(6)); Kiff = tf(zeros(6));
1.2 Low Authority Control - Integral Force Feedback \(\bm{K}_\text{IFF}\)
1.2.1 Identification
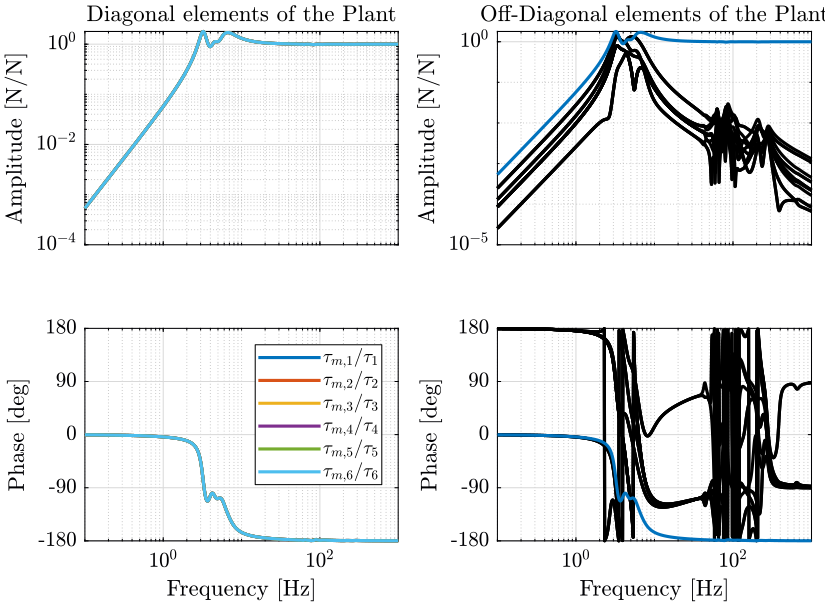
Let’s first identify the plant for the IFF controller.
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Controller'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/Micro-Station'], 3, 'openoutput', [], 'Fnlm'); io_i = io_i + 1; % Force Sensors %% Run the linearization G_iff = linearize(mdl, io, 0); G_iff.InputName = {'Fnl1', 'Fnl2', 'Fnl3', 'Fnl4', 'Fnl5', 'Fnl6'}; G_iff.OutputName = {'Fnlm1', 'Fnlm2', 'Fnlm3', 'Fnlm4', 'Fnlm5', 'Fnlm6'};
1.2.3 Root Locus
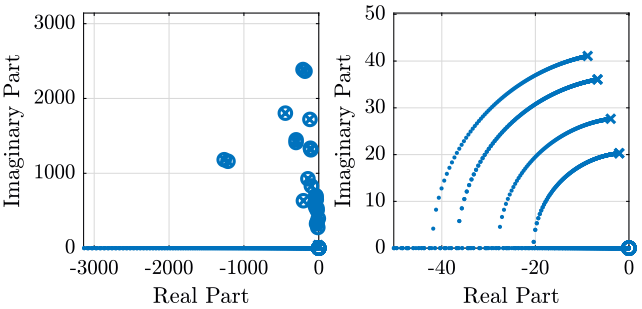
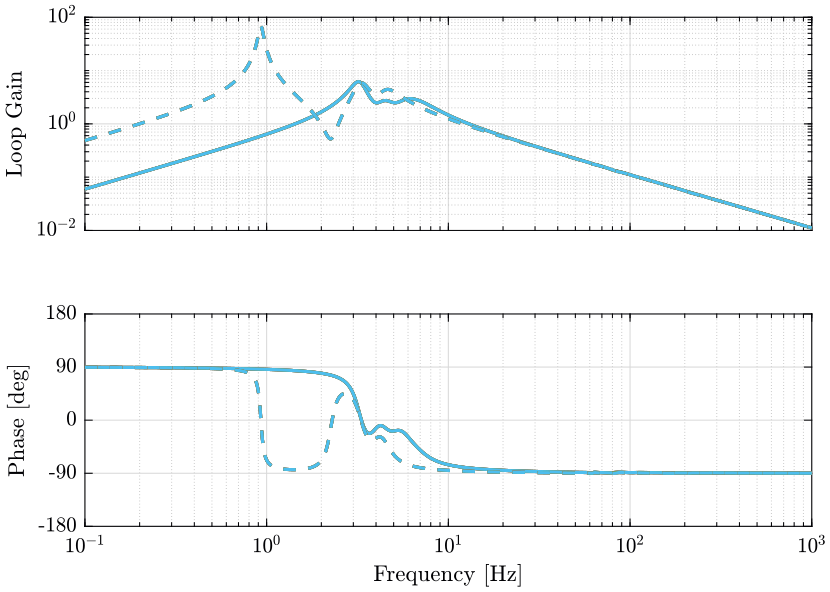
As seen in the root locus (Figure 3, no damping can be added to modes corresponding to the resonance of the micro-station.
However, critical damping can be achieve for the resonances of the nano-hexapod as shown in the zoomed part of the root (Figure 3, left part). The maximum damping is obtained for a control gain of \(\approx 70\).
1.3 High Authority Control in the joint space - \(\bm{K}_\mathcal{L}\)
1.3.1 Identification of the damped plant
Let’s identify the dynamics from \(\bm{\tau}^\prime\) to \(d\bm{\mathcal{L}}\) as shown in Figure 1.
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Controller'], 1, 'input'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/Micro-Station'], 3, 'output', [], 'Dnlm'); io_i = io_i + 1; % Leg Displacement %% Run the linearization Gl = linearize(mdl, io, 0); Gl.InputName = {'Fnl1', 'Fnl2', 'Fnl3', 'Fnl4', 'Fnl5', 'Fnl6'}; Gl.OutputName = {'Dnlm1', 'Dnlm2', 'Dnlm3', 'Dnlm4', 'Dnlm5', 'Dnlm6'};
There are some unstable poles in the Plant with very small imaginary parts. These unstable poles are probably not physical, and they disappear when taking the minimum realization of the plant.
isstable(Gl) Gl = minreal(Gl); isstable(Gl)
1.3.2 Obtained Plant
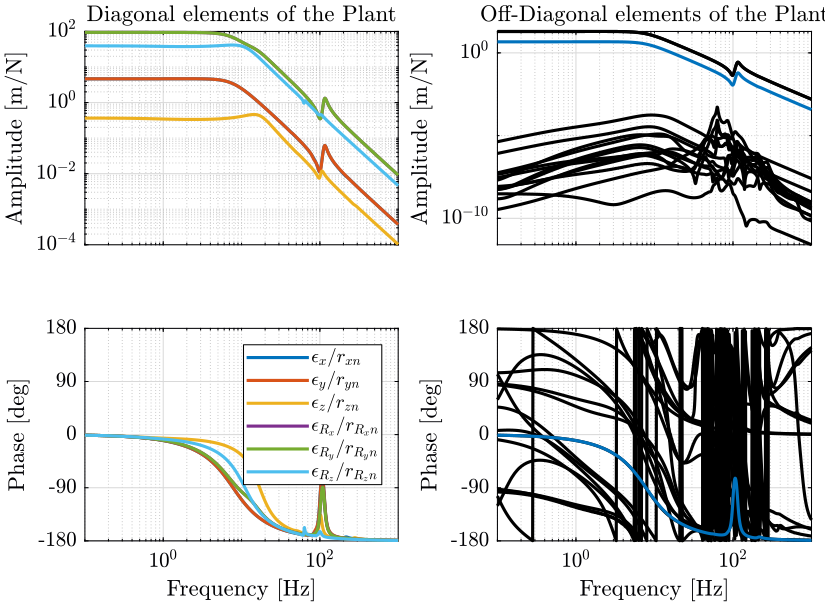
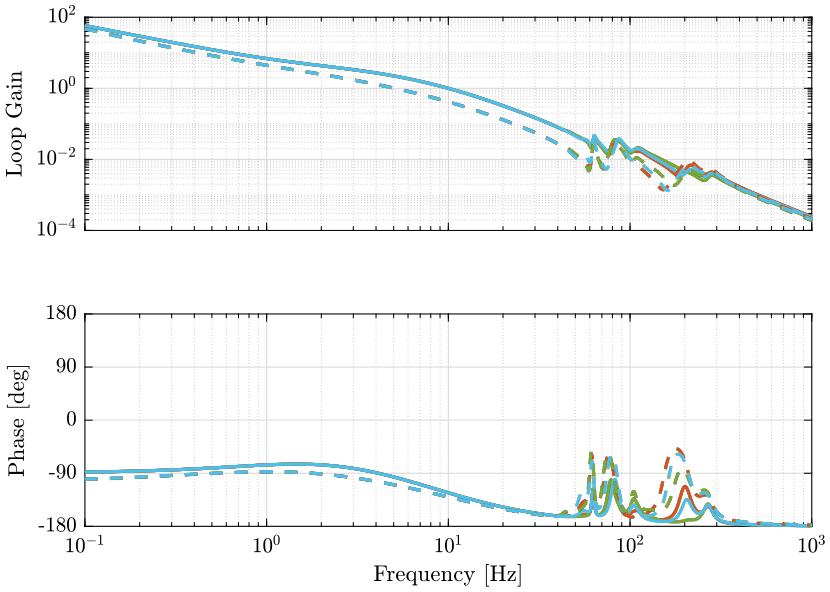
The obtained dynamics is shown in Figure 5.
Few things can be said on the dynamics:
- the dynamics of the diagonal elements are almost all the same
- the system is well decoupled below the resonances of the nano-hexapod (1Hz)
- the dynamics of the diagonal elements are almost equivalent to a critically damped mass-spring-system with some spurious resonances above 50Hz corresponding to the resonances of the micro-station
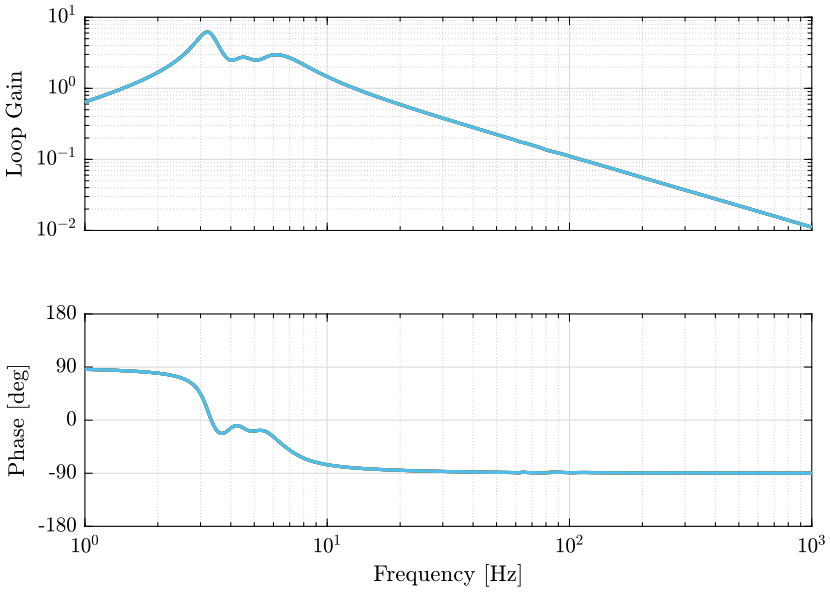
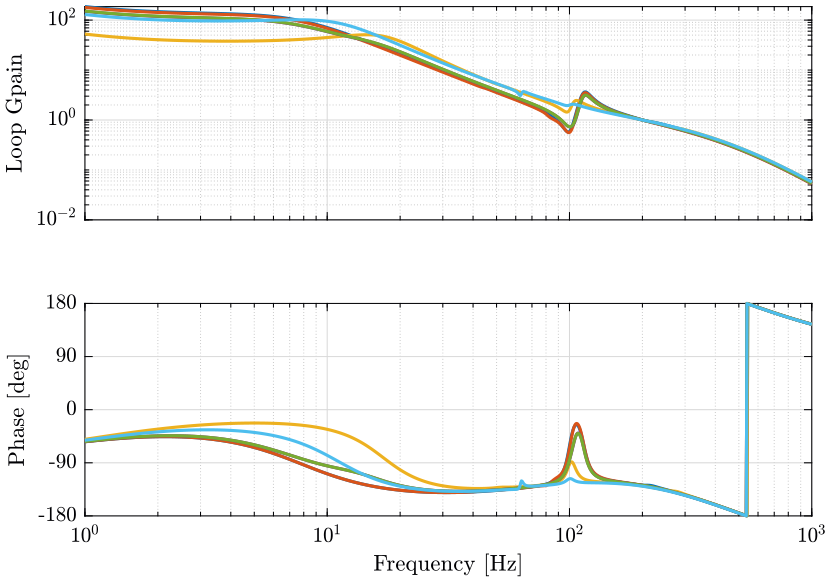
1.3.3 Controller Design and Loop Gain
As the plant is well decoupled, a diagonal plant is designed.
wc = 2*pi*10; % Bandwidth Bandwidth [rad/s] h = 2; % Lead parameter Kl = (s + 2*pi*1)/s; % Normalization of the gain of have a loop gain of 1 at frequency wc Kl = Kl.*diag(1./diag(abs(freqresp(Gl*Kl, wc))));
1.4 Primary Controller in the task space - \(\bm{K}_\mathcal{X}\)
1.4.1 Identification of the linearized plant
We know identify the dynamics between \(\bm{r}_{\mathcal{X}_n}\) and \(\bm{r}_\mathcal{X}\).
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Controller/Cascade-HAC-LAC/Kp'], 1, 'input'); io_i = io_i + 1; io(io_i) = linio([mdl, '/Tracking Error'], 1, 'output', [], 'En'); io_i = io_i + 1; % Position Errror %% Run the linearization Gp = linearize(mdl, io, 0); Gp.InputName = {'rl1', 'rl2', 'rl3', 'rl4', 'rl5', 'rl6'}; Gp.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
A minus sign is added because the minus sign is already included in the plant identification.
isstable(Gp)
Gp = -minreal(Gp);
isstable(Gp)
load('mat/stages.mat', 'nano_hexapod'); Gpx = Gp*inv(nano_hexapod.J'); Gpx.InputName = {'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz'}; Gpl = nano_hexapod.J*Gp; Gpl.OutputName = {'El1', 'El2', 'El3', 'El4', 'El5', 'El6'};
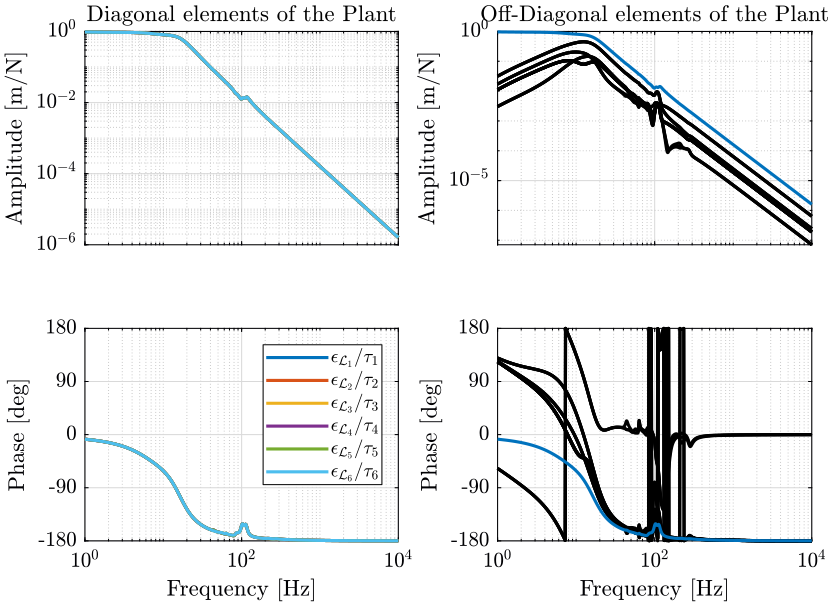
1.4.2 Obtained Plant
1.4.3 Controller Design
wc = 2*pi*200; % Bandwidth Bandwidth [rad/s] h = 2; % Lead parameter Kp = (1/h) * (1 + s/wc*h)/(1 + s/wc/h) * ... (1/h) * (1 + s/wc*h)/(1 + s/wc/h); % For Piezo % Kp = (1/h) * (1 + s/wc*h)/(1 + s/wc/h) * (s + 2*pi*10)/s * (s + 2*pi*1)/s ; % For voice coil % Normalization of the gain of have a loop gain of 1 at frequency wc Kp = Kp.*diag(1./diag(abs(freqresp(Gpx*Kp, wc))));
And now we include the Jacobian inside the controller.
Kp = inv(nano_hexapod.J')*Kp;
1.5 Simulation
Let’s first save the 3 controllers for further analysis:
save('mat/hac_lac_cascade_vc_controllers.mat', 'Kiff', 'Kl', 'Kp')
load('mat/conf_simulink.mat'); set_param(conf_simulink, 'StopTime', '2');
And we simulate the system.
sim('nass_model');
cascade_hac_lac_lorentz = simout; save('./mat/cascade_hac_lac.mat', 'cascade_hac_lac_lorentz', '-append');
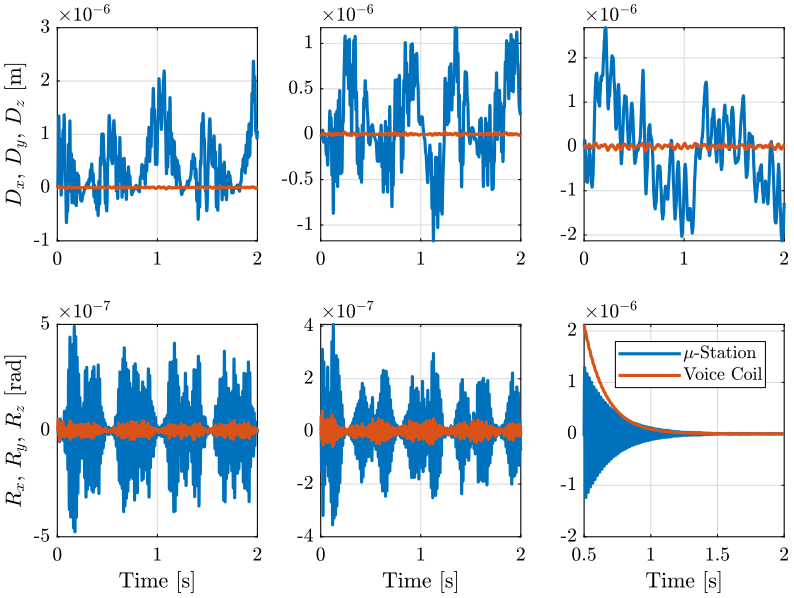
1.6 Results
1.6.1 Load the simulation results
load('./mat/experiment_tomography.mat', 'tomo_align_dist'); load('./mat/cascade_hac_lac.mat', 'cascade_hac_lac', 'cascade_hac_lac_lorentz');
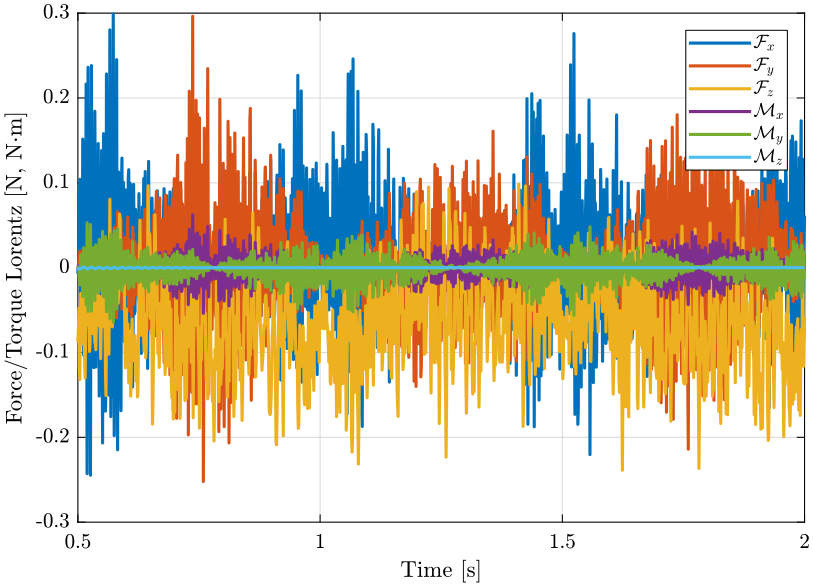
1.6.2 Control effort
1.6.3 Load the simulation results
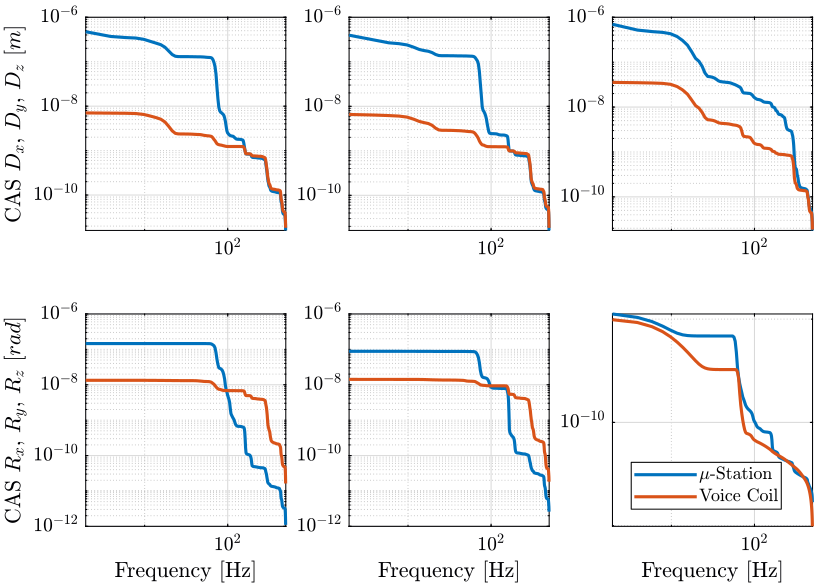
n_av = 4; han_win = hanning(ceil(length(cascade_hac_lac.Em.En.Data(:,1))/n_av));
t = cascade_hac_lac.Em.En.Time; Ts = t(2)-t(1); [pxx_ol, f] = pwelch(tomo_align_dist.Em.En.Data, han_win, [], [], 1/Ts); [pxx_ca, ~] = pwelch(cascade_hac_lac.Em.En.Data, han_win, [], [], 1/Ts); [pxx_vc, ~] = pwelch(cascade_hac_lac_lorentz.Em.En.Data, han_win, [], [], 1/Ts);
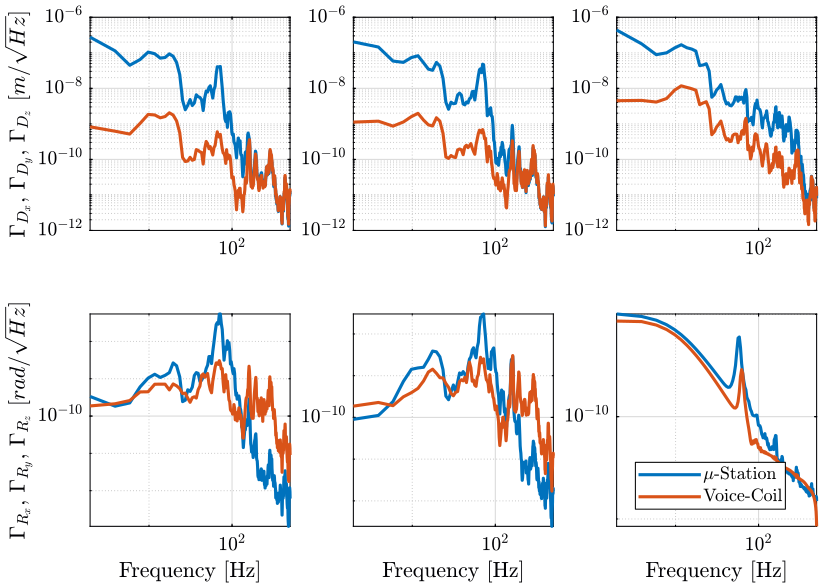
Figure 10: Power Spectral Density of the position error during a tomography experiment when using Voice Coil based nano-hexapod (png, pdf)
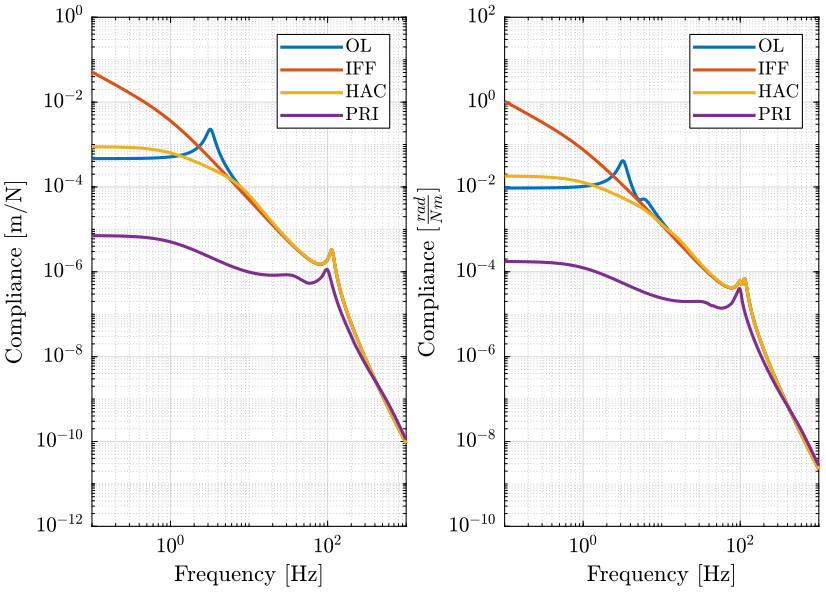
1.7 Compliance of the nano-hexapod
1.7.1 Identification
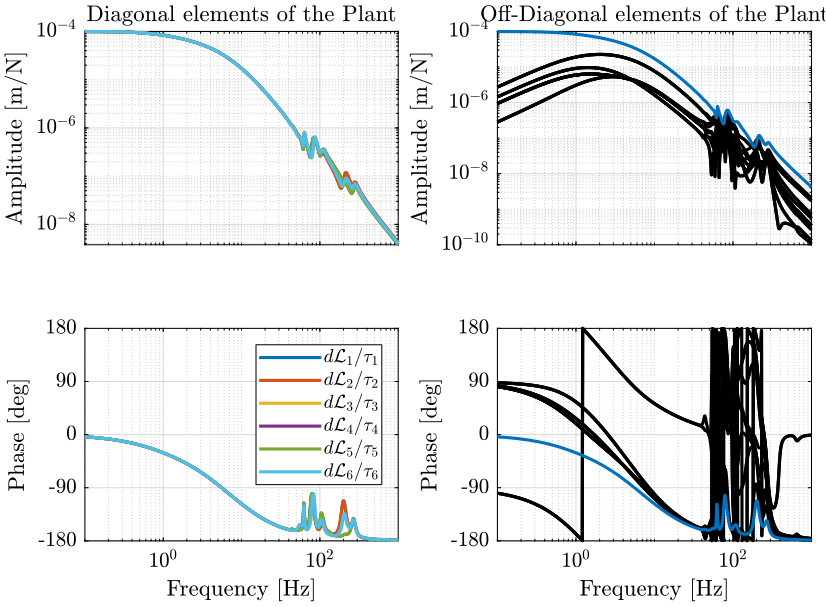
Let’s identify the Compliance of the NASS:
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Disturbances/Fd'], 1, 'openinput'); io_i = io_i + 1; % Direct Forces/Torques applied on the sample io(io_i) = linio([mdl, '/Tracking Error'], 1, 'output', [], 'En'); io_i = io_i + 1; % Position Errror
First in open-loop:
Kp = tf(zeros(6)); Kl = tf(zeros(6)); Kiff = tf(zeros(6));
%% Run the linearization Gc_ol = linearize(mdl, io, 0); Gc_ol.InputName = {'Fdx', 'Fdy', 'Fdz', 'Mdx', 'Mdy', 'Mdz'}; Gc_ol.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
Then with the IFF control.
load('mat/hac_lac_cascade_vc_controllers.mat', 'Kiff')
%% Run the linearization Gc_iff = linearize(mdl, io, 0); Gc_iff.InputName = {'Fdx', 'Fdy', 'Fdz', 'Mdx', 'Mdy', 'Mdz'}; Gc_iff.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
With the HAC control added
load('mat/hac_lac_cascade_vc_controllers.mat', 'Kl')
%% Run the linearization Gc_hac = linearize(mdl, io, 0); Gc_hac.InputName = {'Fdx', 'Fdy', 'Fdz', 'Mdx', 'Mdy', 'Mdz'}; Gc_hac.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
Finally with the primary controller
load('mat/hac_lac_cascade_vc_controllers.mat', 'Kp')
%% Run the linearization Gc_pri = linearize(mdl, io, 0); Gc_pri.InputName = {'Fdx', 'Fdy', 'Fdz', 'Mdx', 'Mdy', 'Mdz'}; Gc_pri.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
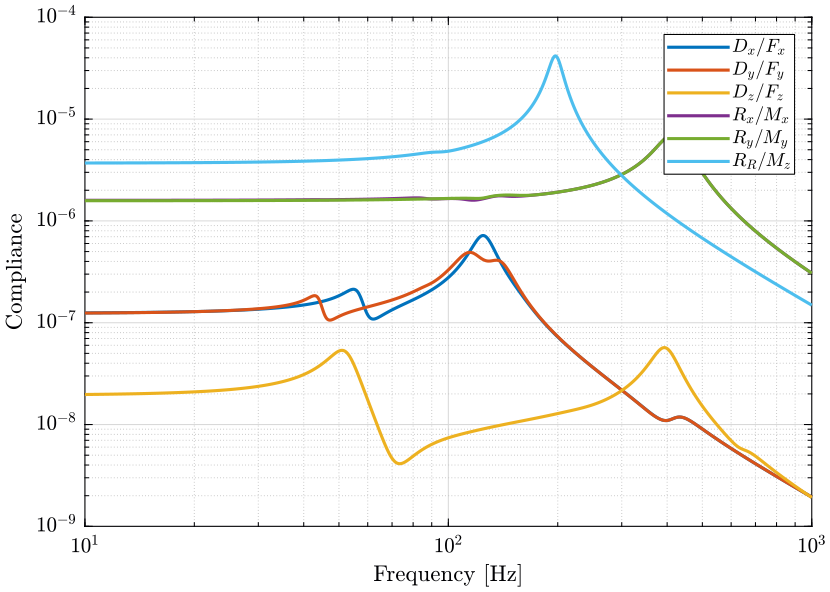
1.7.2 Obtained Compliance
1.7.3 Comparison with Piezo
Let’s initialize a nano-hexapod with piezoelectric actuators.
initializeNanoHexapod('actuator', 'piezo');
We don’t use any controller.
Kp = tf(zeros(6)); Kl = tf(zeros(6)); Kiff = tf(zeros(6));
%% Run the linearization Gc_pz = linearize(mdl, io, 0); Gc_pz.InputName = {'Fdx', 'Fdy', 'Fdz', 'Mdx', 'Mdy', 'Mdz'}; Gc_pz.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
1.8 Robustness to Payload Variability
1.8.1 Initialization
Let’s change the payload mass, and see if the controller design for a payload mass of 1 still gives good performance.
initializeSample('mass', 50);
Kp = tf(zeros(6)); Kl = tf(zeros(6)); Kiff = tf(zeros(6));
1.8.2 Low Authority Control
Let’s first identify the transfer function for the Low Authority control.
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Controller'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/Micro-Station'], 3, 'openoutput', [], 'Fnlm'); io_i = io_i + 1; % Force Sensors %% Run the linearization G_iff_m = linearize(mdl, io, 0); G_iff_m.InputName = {'Fnl1', 'Fnl2', 'Fnl3', 'Fnl4', 'Fnl5', 'Fnl6'}; G_iff_m.OutputName = {'Fnlm1', 'Fnlm2', 'Fnlm3', 'Fnlm4', 'Fnlm5', 'Fnlm6'};
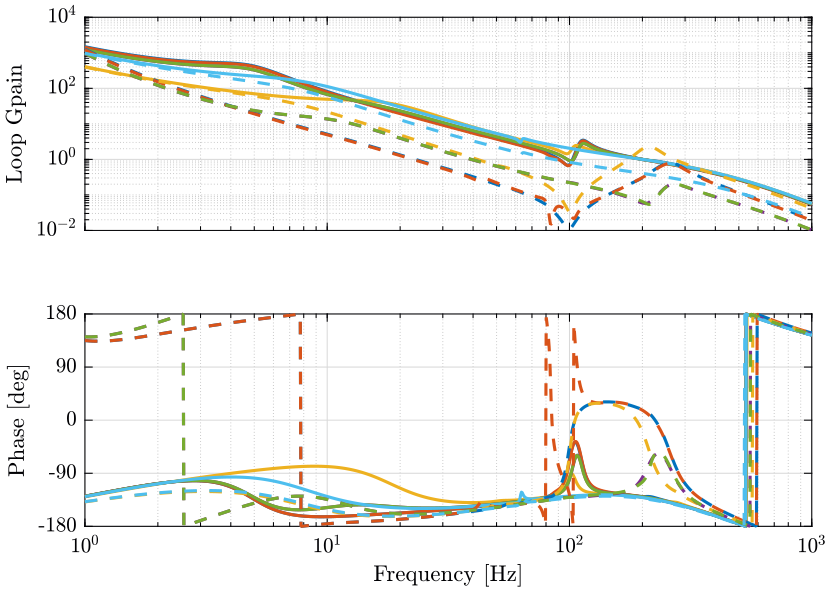
The obtained dynamics is compared when using a payload of 1Kg in Figure 15.
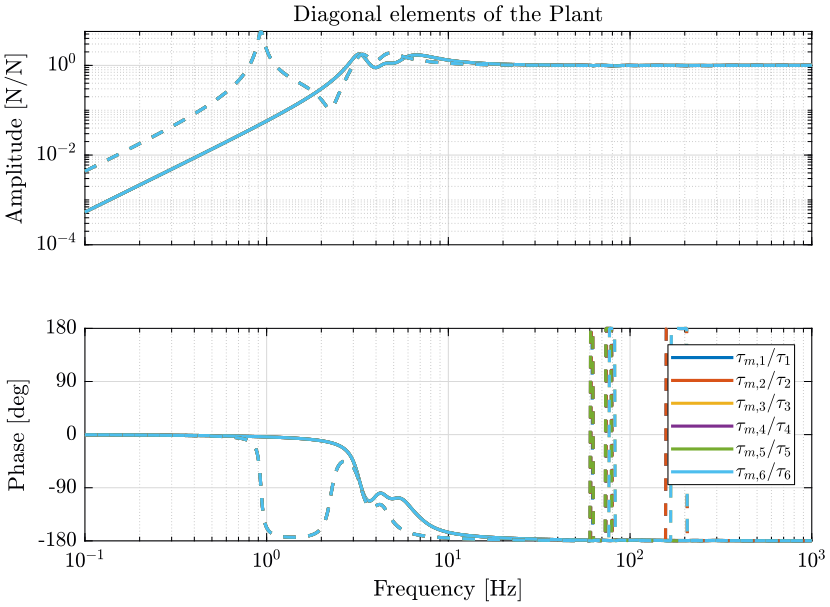
Figure 15: Dynamics of the LAC plant when using a 50Kg payload (dashed) and when using a 1Kg payload (solid) (png, pdf)
A gain of 50 will here suffice to obtain critical damping of the nano-hexapod modes.
Let’s load the IFF controller designed when the payload has a mass of 1Kg.
load('mat/hac_lac_cascade_vc_controllers.mat', 'Kiff')
1.8.3 High Authority Control
We use the Integral Force Feedback developed with a mass of 1Kg and we identify the dynamics for the High Authority Controller in the case of the 50Kg payload
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Controller'], 1, 'input'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/Micro-Station'], 3, 'output', [], 'Dnlm'); io_i = io_i + 1; % Leg Displacement %% Run the linearization Gl_m = linearize(mdl, io, 0); Gl_m.InputName = {'Fnl1', 'Fnl2', 'Fnl3', 'Fnl4', 'Fnl5', 'Fnl6'}; Gl_m.OutputName = {'Dnlm1', 'Dnlm2', 'Dnlm3', 'Dnlm4', 'Dnlm5', 'Dnlm6'}; isstable(Gl_m) Gl_m = minreal(Gl_m); isstable(Gl_m)
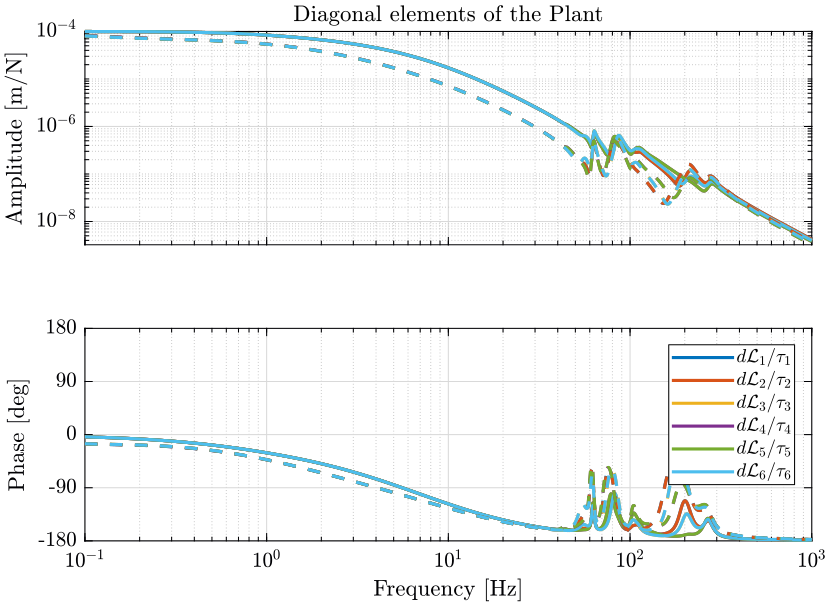
Figure 17: Dynamics of the HAC plant when using a 50Kg payload (dashed) and when using a 1Kg payload (solid) (png, pdf)
We load the HAC controller design when the payload has a mass of 1Kg.
load('mat/hac_lac_cascade_vc_controllers.mat', 'Kl')
1.8.4 Primary Plant
We use the Low Authority Controller developed with a mass of 1Kg and we identify the dynamics for the Primary controller in the case of the 50Kg payload.
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Controller/Cascade-HAC-LAC/Kp'], 1, 'input'); io_i = io_i + 1; io(io_i) = linio([mdl, '/Tracking Error'], 1, 'output', [], 'En'); io_i = io_i + 1; % Position Errror %% Run the linearization Gp_m = linearize(mdl, io, 0); Gp_m.InputName = {'rl1', 'rl2', 'rl3', 'rl4', 'rl5', 'rl6'}; Gp_m.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
A minus sign is added to cancel the minus sign already included in the identified plant.
isstable(Gp_m)
Gp_m = -minreal(Gp_m);
isstable(Gp_m)
load('mat/stages.mat', 'nano_hexapod'); Gpx_m = Gp_m*inv(nano_hexapod.J'); Gpx_m.InputName = {'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz'}; Gpl_m = nano_hexapod.J*Gp_m; Gpl_m.OutputName = {'El1', 'El2', 'El3', 'El4', 'El5', 'El6'};
There are two zeros with positive real part for the plant in the y direction at about 100Hz. This is problematic as it limits the bandwidth to be less than \(\approx 50\ \text{Hz}\).
It is important here to physically understand why such “positive” zero appears.
If we make a “rigid” 50kg paylaod, the positive zero disappears.
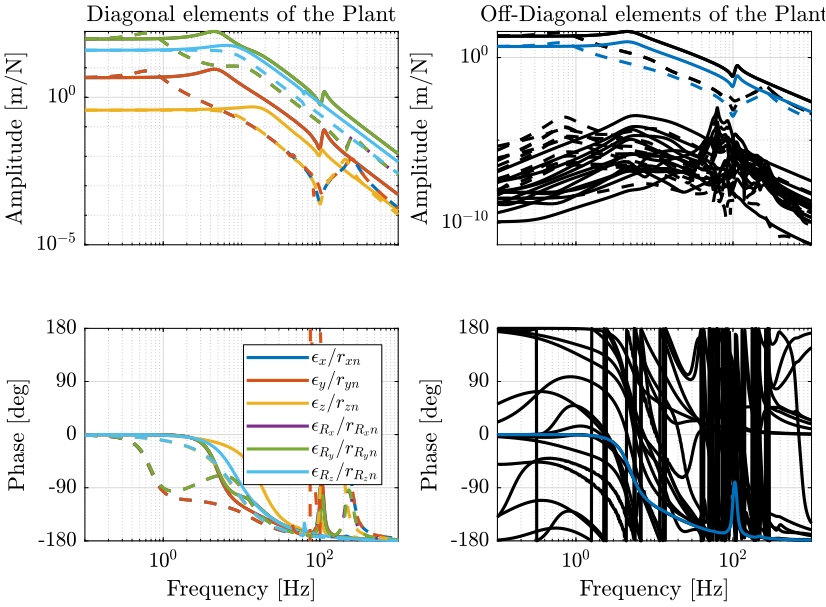
Figure 19: Dynamics of the Primary plant when using a 50Kg payload (dashed) and when using a 1Kg payload (solid) (png, pdf)
We load the primary controller that was design when the payload has a mass of 1Kg.
We load the HAC controller design when the payload has a mass of 1Kg.
load('mat/hac_lac_cascade_vc_controllers.mat', 'Kp') Kp_x = nano_hexapod.J'*Kp;
wc = 2*pi*50; % Bandwidth Bandwidth [rad/s] h = 2; % Lead parameter Kp = (1/h) * (1 + s/wc*h)/(1 + s/wc/h) * ... (1/h) * (1 + s/wc*h)/(1 + s/wc/h) * ... (s + 2*pi*1)/s * ... 1/(1+s/2/wc); % For Piezo % Normalization of the gain of have a loop gain of 1 at frequency wc Kp = Kp.*diag(1./diag(abs(freqresp(Gpx_m*Kp, wc))));
1.8.5 Simulation
load('mat/conf_simulink.mat'); set_param(conf_simulink, 'StopTime', '2');
And we simulate the system.
sim('nass_model');
cascade_hac_lac_lorentz_high_mass = simout; save('./mat/cascade_hac_lac.mat', 'cascade_hac_lac_lorentz_high_mass', '-append');
load('./mat/experiment_tomography.mat', 'tomo_align_dist');
2 Other analysis
2.1 Robustness to Payload Variability
[ ]For 3/masses (1kg, 10kg, 50kg), plot each of the 3 plants
2.2 Direct HAC control in the task space - \(\bm{K}_\mathcal{X}\)
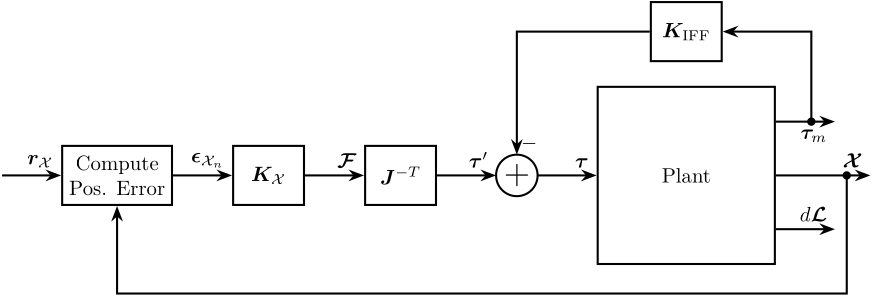
Figure 21: Control Architecture containing an IFF controller and a Controller in the task space
2.2.1 Identification
initializeController('type', 'hac-iff');
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Controller/HAC-IFF/Kx'], 1, 'input'); io_i = io_i + 1; % Control input io(io_i) = linio([mdl, '/Tracking Error'], 1, 'output', [], 'En'); io_i = io_i + 1; % Position Errror %% Run the linearization G = linearize(mdl, io, 0); G.InputName = {'Fnl1', 'Fnl2', 'Fnl3', 'Fnl4', 'Fnl5', 'Fnl6'}; G.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
isstable(G)
G = -minreal(G);
isstable(G)
load('mat/stages.mat', 'nano_hexapod'); Gx = G*inv(nano_hexapod.J'); Gx.InputName = {'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz'}; Gl = nano_hexapod.J*G; Gl.OutputName = {'El1', 'El2', 'El3', 'El4', 'El5', 'El6'};
2.2.2 Obtained Plant in the Task Space
2.2.3 Obtained Plant in the Joint Space
2.2.4 Controller Design in the Joint Space
wc = 2*pi*200; % Bandwidth Bandwidth [rad/s] h = 2; % Lead parameter Kx = (1/h) * (1 + s/wc*h)/(1 + s/wc/h) * ... % Lead (1/h) * (1 + s/wc*h)/(1 + s/wc/h) * ... % Lead (s + 2*pi*10)/s * ... % Pseudo Integrator 1/(1+s/2/pi/500); % Low pass Filter % Normalization of the gain of have a loop gain of 1 at frequency wc Kx = Kx.*diag(1./diag(abs(freqresp(Gx*Kx, wc))));
wc = 2*pi*200; % Bandwidth Bandwidth [rad/s] h = 2; % Lead parameter Kl = (1/h) * (1 + s/wc*h)/(1 + s/wc/h) * ... % Lead (1/h) * (1 + s/wc*h)/(1 + s/wc/h) * ... % Lead (s + 2*pi*1)/s * ... % Pseudo Integrator (s + 2*pi*10)/s * ... % Pseudo Integrator 1/(1+s/2/pi/500); % Low pass Filter % Normalization of the gain of have a loop gain of 1 at frequency wc Kl = Kl.*diag(1./diag(abs(freqresp(Gl*Kl, wc))));
2.3 On the usefulness of the High Authority Control loop / Linearization loop
Let’s see what happens is we omit the HAC loop and we directly try to control the damped plant using the measurement of the sample with respect to the granite \(\bm{\mathcal{X}}\).
We can do that in two different ways:
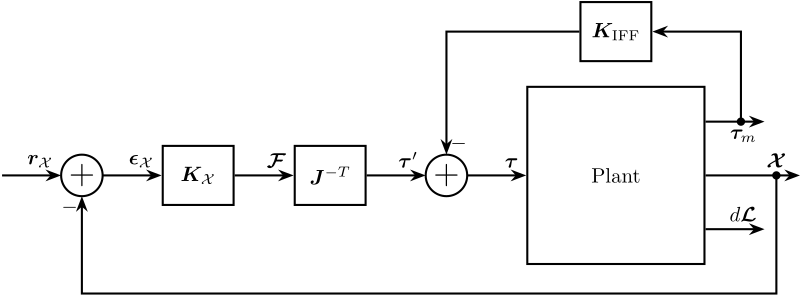
Figure 22: IFF control + primary controller in the task space
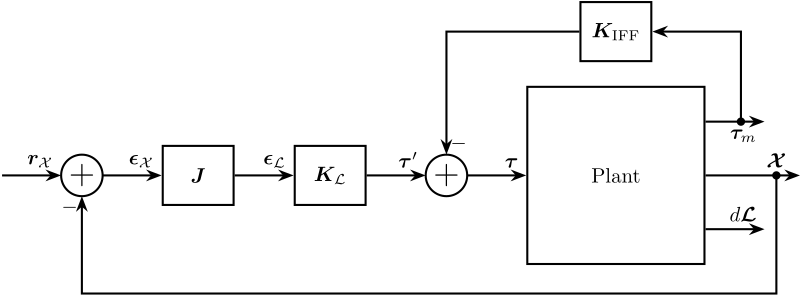
Figure 23: HAC-LAC control architecture in the frame of the legs
2.3.1 Identification
initializeController('type', 'hac-iff');
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Controller/HAC-IFF/Kx'], 1, 'input'); io_i = io_i + 1; io(io_i) = linio([mdl, '/Tracking Error'], 1, 'output', [], 'En'); io_i = io_i + 1; % Position Errror %% Run the linearization G = linearize(mdl, io, 0); G.InputName = {'F1', 'F2', 'F3', 'F4', 'F5', 'F6'}; G.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
isstable(G)
G = -minreal(G);
isstable(G)
2.3.2 Plant in the Task space
The obtained plant is shown in Figure
Gx = G*inv(nano_hexapod.J');
2.3.3 Plant in the Leg’s space
Gl = nano_hexapod.J*G;
2.4 DVF instead of IFF?
2.4.1 Initialization and Identification
initializeController('type', 'hac-dvf'); Kdvf = tf(zeros(6));
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Controller'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs io(io_i) = linio([mdl, '/Micro-Station'], 3, 'openoutput', [], 'Dnlm'); io_i = io_i + 1; % Displacement Sensors %% Run the linearization G_dvf = linearize(mdl, io, 0); G_dvf.InputName = {'Fnl1', 'Fnl2', 'Fnl3', 'Fnl4', 'Fnl5', 'Fnl6'}; G_dvf.OutputName = {'Dlm1', 'Dlm2', 'Dlm3', 'Dlm4', 'Dlm5', 'Dlm6'};
2.4.2 Obtained Plant
2.4.3 Controller
Kdvf = -850*s/(1+s/2/pi/1000)*eye(6);
2.4.4 HAC Identification
%% Name of the Simulink File mdl = 'nass_model'; %% Input/Output definition clear io; io_i = 1; io(io_i) = linio([mdl, '/Controller/HAC-DVF/Kx'], 1, 'input'); io_i = io_i + 1; % Control input io(io_i) = linio([mdl, '/Tracking Error'], 1, 'output', [], 'En'); io_i = io_i + 1; % Position Errror %% Run the linearization G = linearize(mdl, io, 0); G.InputName = {'Fnl1', 'Fnl2', 'Fnl3', 'Fnl4', 'Fnl5', 'Fnl6'}; G.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
isstable(G)
G = -minreal(G);
isstable(G)
load('mat/stages.mat', 'nano_hexapod'); Gx = G*inv(nano_hexapod.J'); Gx.InputName = {'Fx', 'Fy', 'Fz', 'Mx', 'My', 'Mz'}; Gl = nano_hexapod.J*G; Gl.OutputName = {'El1', 'El2', 'El3', 'El4', 'El5', 'El6'};
2.4.5 Conclusion
DVF can be used instead of IFF.