HAC-LAC applied on the Simscape Model

1. Undamped System

1 Undamped System

1.1 Identification of the plant

1.1.1 Initialize the Simulation

We initialize all the stages with the default parameters.

initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();
initializeAxisc();
initializeMirror();

The nano-hexapod is a piezoelectric hexapod and the sample has a mass of 50kg.

initializeNanoHexapod('actuator', 'piezo');
initializeSample('mass', 50);

No disturbances.

initializeDisturbances('enable', false);

We set the references to zero.

initializeReferences();

And all the controllers are set to 0.

initializeController('type', 'open-loop');

1.1.2 Identification

First, we identify the dynamics of the system using the linearize function.

%% Options for Linearized
options = linearizeOptions;
options.SampleTime = 0;

%% Name of the Simulink File
mdl = 'nass_model';

%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/Controller'],     1, 'openinput');            io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/Tracking Error'], 1, 'openoutput', [], 'En'); io_i = io_i + 1; % Metrology Outputs

%% Run the linearization
G = linearize(mdl, io, options);
G.InputName  = {'Fnl1', 'Fnl2', 'Fnl3', 'Fnl4', 'Fnl5', 'Fnl6'};
G.OutputName = {'Edx', 'Edy', 'Edz', 'Erx', 'Ery', 'Erz'};

load('mat/stages.mat', 'nano_hexapod');
G_cart = minreal(G*inv(nano_hexapod.J'));
G_cart.InputName = {'Fnx', 'Fny', 'Fnz', 'Mnx', 'Mny', 'Mnz'};

G_legs = minreal(inv(nano_hexapod.J)*G);
G_legs.OutputName = {'e1', 'e2', 'e3', 'e4', 'e5', 'e6'};

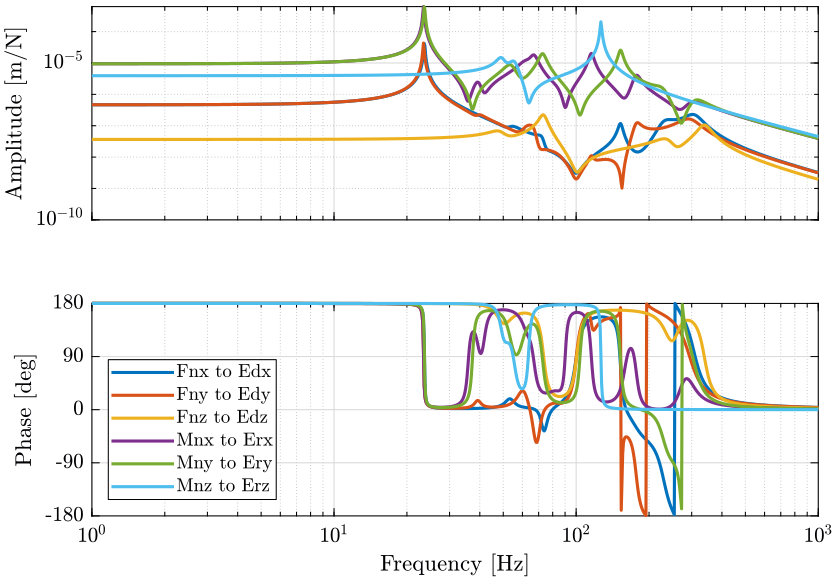
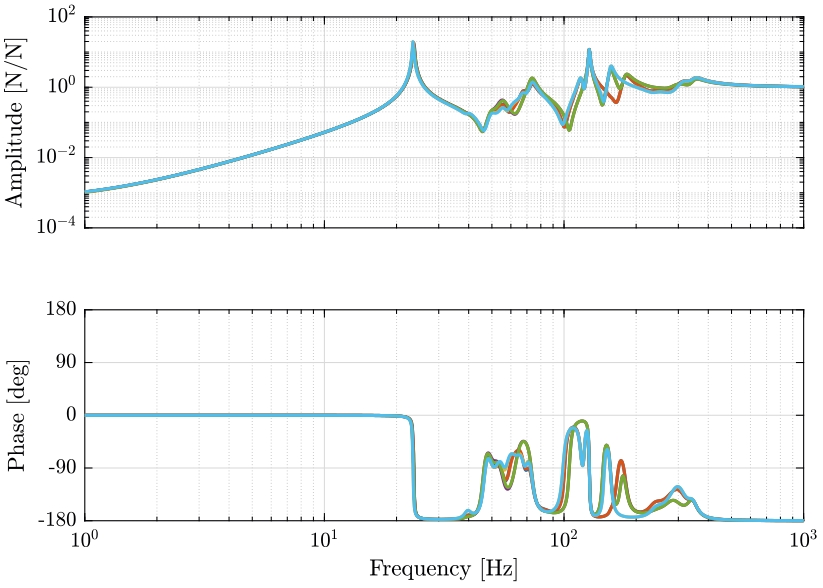
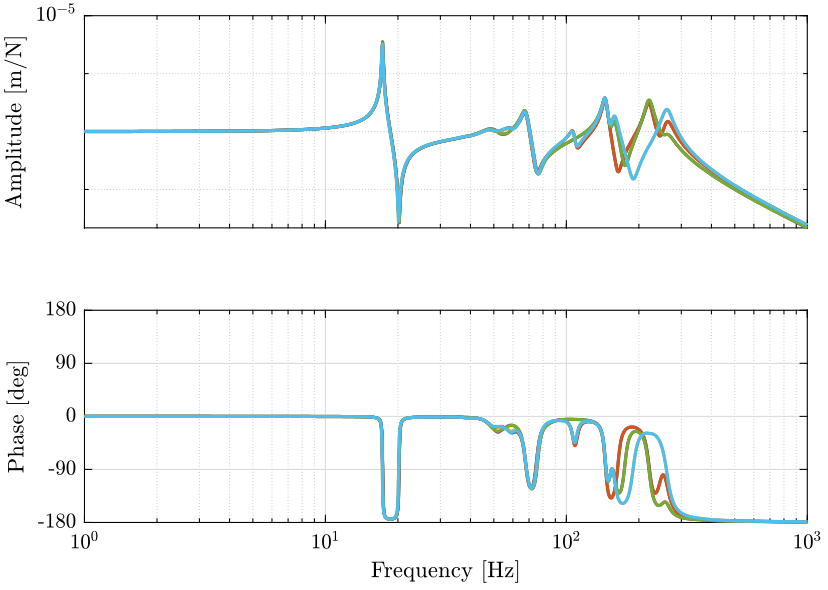
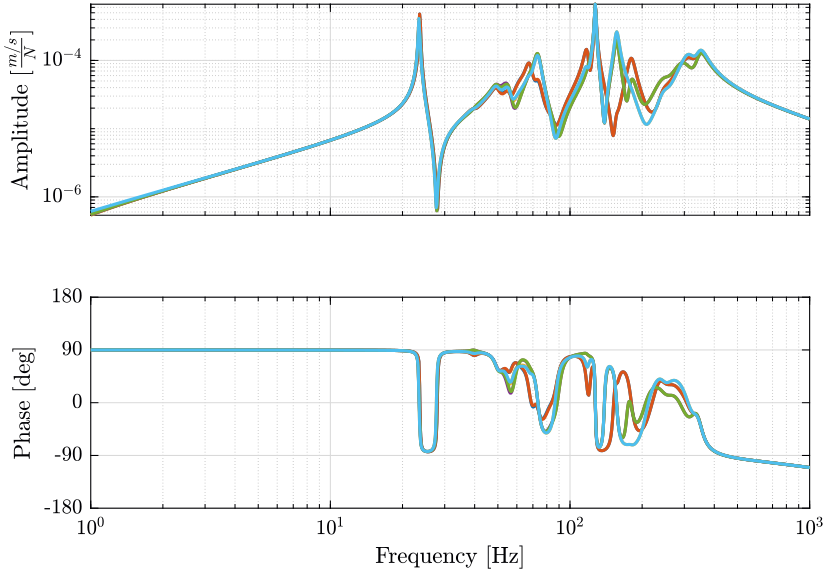
1.1.3 Display TF

Figure 1: Transfer Function from forces applied by the nano-hexapod to position error (png, pdf)

1.1.4 Obtained Plants for Active Damping

Figure 2: G_iff: IFF Plant (png, pdf)

Figure 3: G_dvf: Plant for Direct Velocity Feedback (png, pdf)

Figure 4: Inertial Feedback Plant (png, pdf)

1.2 Tomography Experiment

1.2.1 Simulation

We initialize elements for the tomography experiment.

prepareTomographyExperiment();

We change the simulation stop time.

load('mat/conf_simulink.mat');
set_param(conf_simulink, 'StopTime', '3');

And we simulate the system.

sim('nass_model');

Finally, we save the simulation results for further analysis

save('./active_damping/mat/tomo_exp.mat', 'En', 'Eg', '-append');

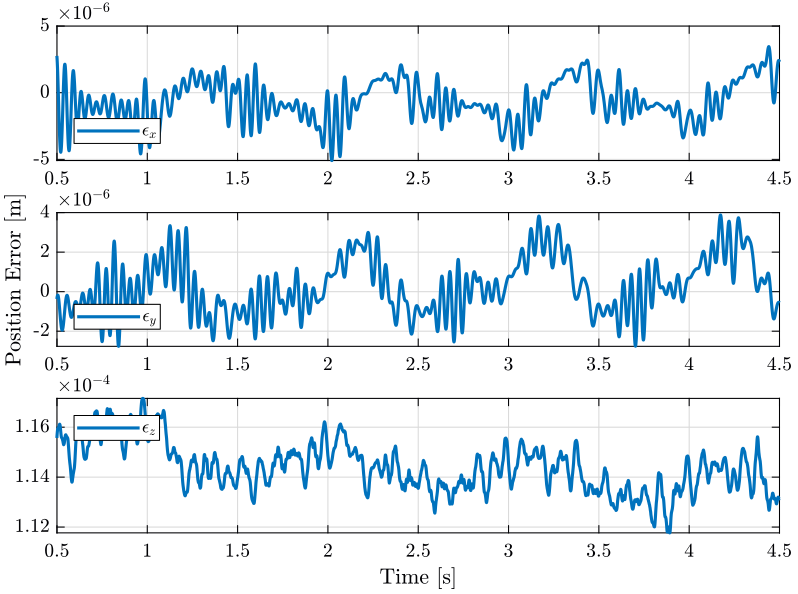
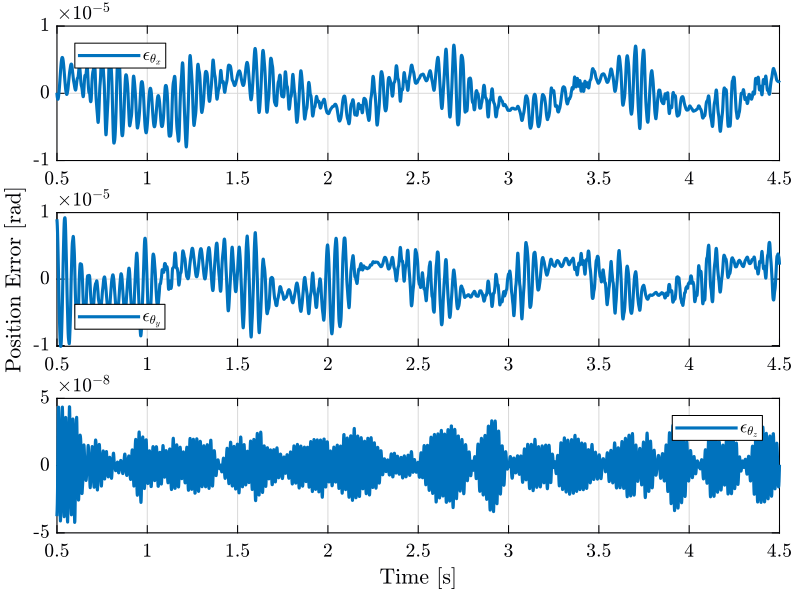
1.2.2 Results

We load the results of tomography experiments.

load('./active_damping/mat/tomo_exp.mat', 'En');
t = linspace(0, 3, length(En(:,1)));

Figure 5: Position Error during tomography experiment - Translations (png, pdf)

Figure 6: Position Error during tomography experiment - Rotations (png, pdf)

1.3 Verification of the transfer function from nano hexapod to metrology

1.3.1 Initialize the Simulation