Determination of the optimal nano-hexapod’s stiffness for reducing the effect of disturbances
Table of Contents
In this document is studied how the stiffness of the nano-hexapod will impact the effect of disturbances on the position error of the sample.
It is divided in the following sections:
- Section 1: the disturbances are listed and their Power Spectral Densities (PSD) are shown
- Section 2: the transfer functions from disturbances to the position error of the sample are computed for a wide range of nano-hexapod stiffnesses
- Section 3:
- Section 4: from both the PSD of the disturbances and the transfer function from disturbances to sample’s position errors, we compute the resulting PSD and Cumulative Amplitude Spectrum (CAS)
- Section 5: from a simplistic model is computed the required control bandwidth to reduce the position error to acceptable values
1 Disturbances
The main disturbances considered here are:
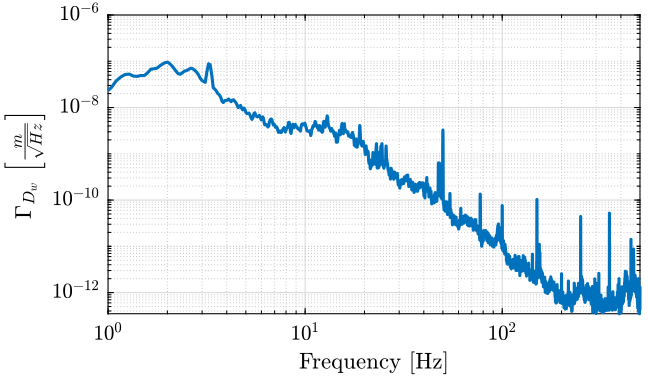
- \(D_w\): Ground displacement in the \(x\), \(y\) and \(z\) directions
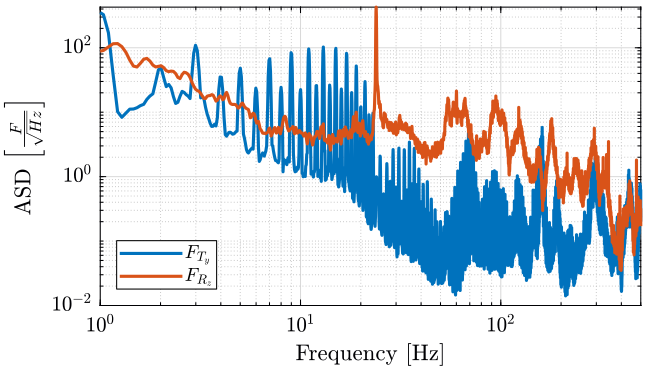
- \(F_{ty}\): Forces applied by the Translation stage in the \(x\) and \(z\) directions
- \(F_{rz}\): Forces applied by the Spindle in the \(z\) direction
- \(F_d\): Direct forces applied at the center of mass of the Payload
The level of these disturbances has been identified form experiments which are detailed in this document.
The measured Amplitude Spectral Densities (ASD) of these forces are shown in Figures 1 and 2.
In this study, the expected frequency content of the direct forces applied to the payload is not considered.
2 Effect of disturbances on the position error
In this section, we use the Simscape model to identify the transfer function from disturbances to the position error of the sample. We do that for a wide range of nano-hexapod stiffnesses and we compare the obtained results.
2.1 Initialization
We initialize all the stages with the default parameters.
initializeGround(); initializeGranite(); initializeTy(); initializeRy(); initializeRz(); initializeMicroHexapod(); initializeAxisc(); initializeMirror();
We use a sample mass of 10kg.
initializeSample('mass', 10);
We include gravity, and we use no controller.
initializeSimscapeConfiguration('gravity', true); initializeController(); initializeDisturbances('enable', false); initializeLoggingConfiguration('log', 'none');
2.2 Identification
The considered inputs are:
Dwx: Ground displacement in the \(x\) directionDwy: Ground displacement in the \(y\) directionDwz: Ground displacement in the \(z\) directionFty_x: Forces applied by the Translation stage in the \(x\) directionFty_z: Forces applied by the Translation stage in the \(z\) directionFrz_z: Forces applied by the Spindle in the \(z\) directionFd: Direct forces applied at the center of mass of the Payload
The outputs are Ex, Ey, Ez, Erx, Ery, Erz which are the 3 positions and 3 orientations errors of the sample.
We initialize the set of the nano-hexapod stiffnesses, and for each of them, we identify the dynamics from defined inputs to defined outputs.
Ks = logspace(3,9,7); % [N/m]
2.3 Sensitivity to Stages vibration (Filtering)
The sensitivity the stage vibrations are displayed:
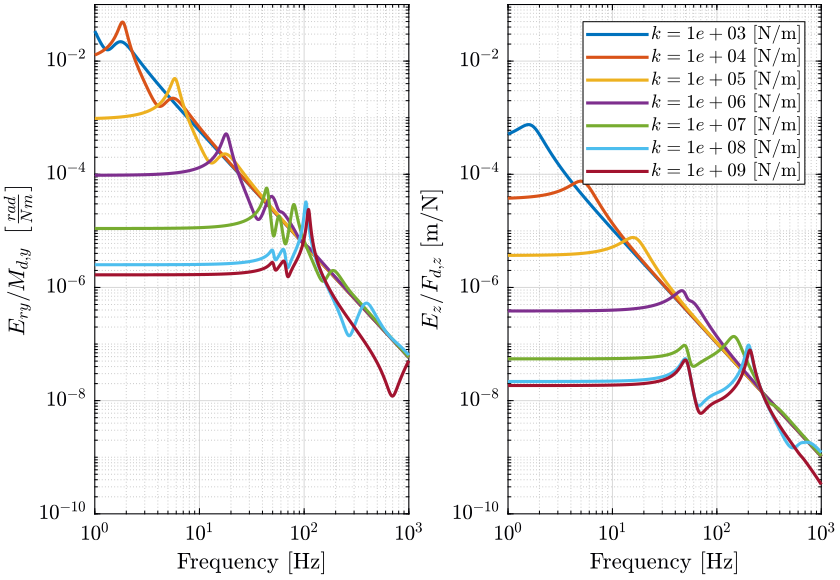
- Figure 3: sensitivity to vertical spindle vibrations
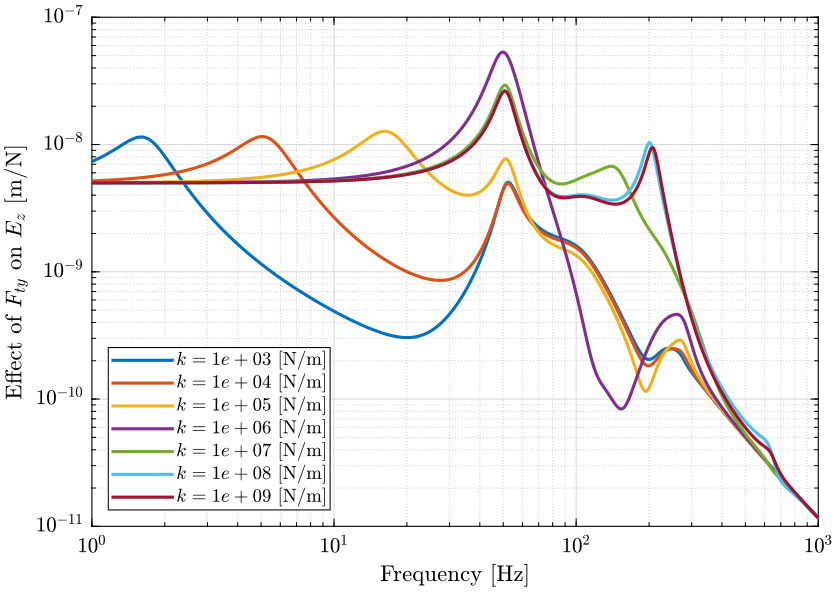
- Figure 4: sensitivity to vertical translation stage vibrations
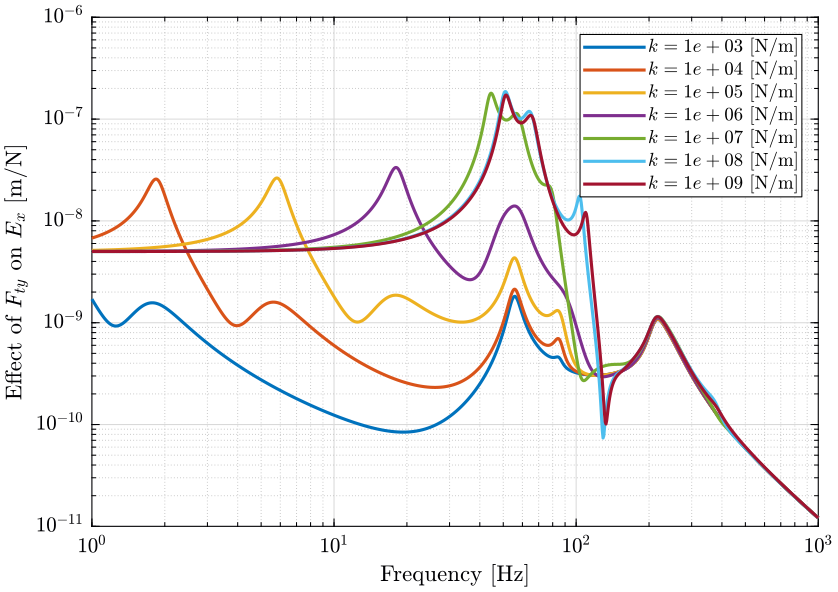
- Figure 5: sensitivity to horizontal (x) translation stage vibrations
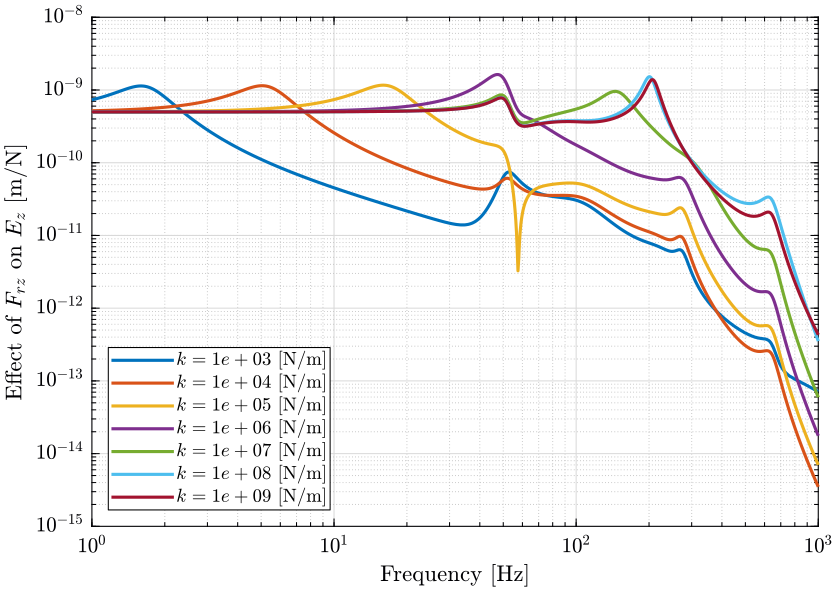
Figure 3: Sensitivity to Spindle vertical motion error (\(F_{rz}\)) to the vertical error position of the sample (\(E_z\)) (png, pdf)
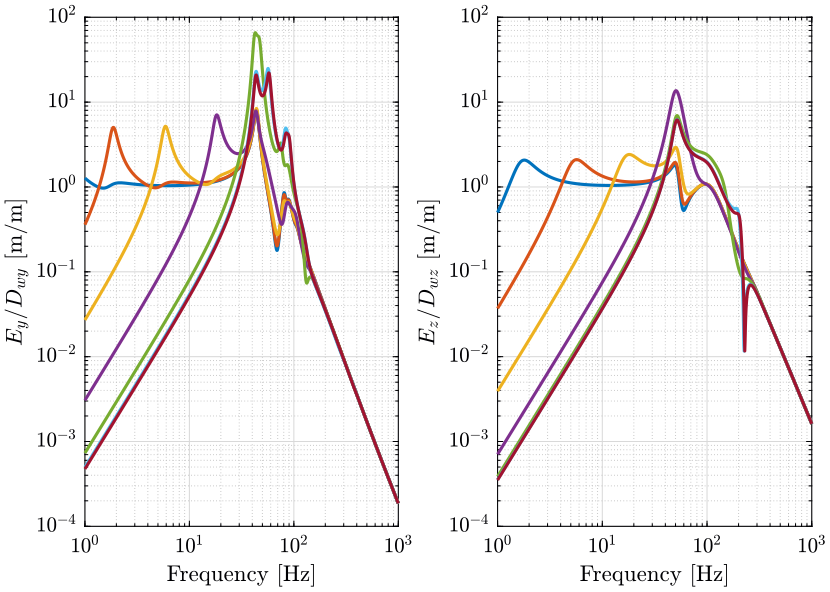
2.4 Effect of Ground motion (Transmissibility).
2.5 Direct Forces (Compliance).
2.6 Conclusion
3 Effect of granite stiffness
3.1 Analytical Analysis
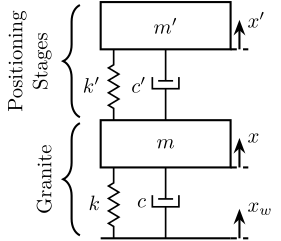
Figure 8: Figure caption
If we write the equation of motion of the system in Figure 8, we obtain:
\begin{align} m^\prime s^2 x^\prime &= (c^\prime s + k^\prime) (x - x^\prime) \\ ms^2 x &= (c^\prime s + k^\prime) (x^\prime - x) + (cs + k) (x_w - x) \end{align}If we note \(d = x^\prime - x\), we obtain:
\begin{equation} \label{org4396920} \frac{d}{x_w} = \frac{-m^\prime s^2 (cs + k)}{ (m^\prime s^2 + c^\prime s + k^\prime) (ms^2 + cs + k) + m^\prime s^2(c^\prime s + k^\prime)} \end{equation}3.2 Soft Granite
Let’s initialize a soft granite that will act as an isolation stage from ground motion.
initializeGranite('K', 5e5*ones(3,1), 'C', 5e3*ones(3,1));
Ks = logspace(3,9,7); % [N/m]
for i = 1:length(Ks) initializeNanoHexapod('k', Ks(i)); G = linearize(mdl, io); G.InputName = {'Dwx', 'Dwy', 'Dwz', 'Fty_x', 'Fty_z', 'Frz_z', 'Fdx', 'Fdy', 'Fdz', 'Mdx', 'Mdy', 'Mdz'}; G.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'}; Gdr(i) = {minreal(G)}; end
3.3 Effect of the Granite transfer function
4 Open Loop Budget Error
4.1 Load of the identified disturbances and transfer functions
load('./mat/dist_psd.mat', 'dist_f'); load('./mat/opt_stiffness_disturbances.mat', 'Gd')
4.2 Equations
4.3 Results
Effect of all disturbances
freqs = dist_f.f; figure; hold on; for i = 1:length(Ks) plot(freqs, sqrt(dist_f.psd_rz).*abs(squeeze(freqresp(Gd{i}('Ez', 'Frz_z'), freqs, 'Hz')))); end hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('ASD $\left[\frac{m}{\sqrt{Hz}}\right]$') legend('Location', 'southwest'); xlim([2, 500]);
4.4 Cumulative Amplitude Spectrum
freqs = dist_f.f; figure; hold on; for i = 1:length(Ks) plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(dist_f.psd_ty.*abs(squeeze(freqresp(Gd{i}('Ez', 'Fty_z'), freqs, 'Hz'))).^2)))), '-', ... 'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i))); end plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off'); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('CAS $[m]$') legend('Location', 'southwest'); xlim([2, 500]); ylim([1e-10 1e-6]);
freqs = dist_f.f; figure; hold on; for i = 1:length(Ks) plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(dist_f.psd_rz.*abs(squeeze(freqresp(Gd{i}('Ez', 'Frz_z'), freqs, 'Hz'))).^2)))), '-', ... 'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i))); end plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off'); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('CAS $[m]$') legend('Location', 'southwest'); xlim([2, 500]); ylim([1e-10 1e-6]);
Ground motion
freqs = dist_f.f; figure; hold on; for i = 1:length(Ks) plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(dist_f.psd_gm.*abs(squeeze(freqresp(Gd{i}('Ez', 'Dwz'), freqs, 'Hz'))).^2)))), '-', ... 'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i))); end plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off'); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('CAS $E_y$ $[m]$') legend('Location', 'northeast'); xlim([2, 500]); ylim([1e-10 1e-6]);
freqs = dist_f.f; figure; hold on; for i = 1:length(Ks) plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(dist_f.psd_gm.*abs(squeeze(freqresp(Gd{i}('Ex', 'Dwx'), freqs, 'Hz'))).^2)))), '-', ... 'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i))); end plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off'); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'lin'); xlabel('Frequency [Hz]'); ylabel('CAS $E_y$ $[m]$') legend('Location', 'northeast'); xlim([2, 500]);
freqs = dist_f.f; figure; hold on; for i = 1:length(Ks) plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(dist_f.psd_gm.*abs(squeeze(freqresp(Gd{i}('Ey', 'Dwy'), freqs, 'Hz'))).^2)))), '-', ... 'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i))); end plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off'); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'lin'); xlabel('Frequency [Hz]'); ylabel('CAS $E_y$ $[m]$') legend('Location', 'northeast'); xlim([2, 500]);
Sum of all perturbations
psd_tot = zeros(length(freqs), length(Ks)); for i = 1:length(Ks) psd_tot(:,i) = dist_f.psd_gm.*abs(squeeze(freqresp(Gd{i}('Ez', 'Dwz' ), freqs, 'Hz'))).^2 + ... dist_f.psd_ty.*abs(squeeze(freqresp(Gd{i}('Ez', 'Fty_z'), freqs, 'Hz'))).^2 + ... dist_f.psd_rz.*abs(squeeze(freqresp(Gd{i}('Ez', 'Frz_z'), freqs, 'Hz'))).^2; end
freqs = dist_f.f; figure; hold on; for i = 1:length(Ks) plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(psd_tot(:,i))))), '-', ... 'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i))); end plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off'); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('CAS $E_z$ $[m]$') legend('Location', 'northeast'); xlim([1, 500]); ylim([1e-10 1e-6]);
5 Closed Loop Budget Error
5.1 Reduction thanks to feedback - Required bandwidth
wc = 1*2*pi; % [rad/s] xic = 0.5; S = (s/wc)/(1 + s/wc); bodeFig({S}, logspace(-1,2,1000))
wc = [1, 5, 10, 20, 50, 100, 200];
S1 = {zeros(length(wc), 1)};
S2 = {zeros(length(wc), 1)};
for j = 1:length(wc)
L = (2*pi*wc(j))/s; % Simple integrator
S1{j} = 1/(1 + L);
L = ((2*pi*wc(j))/s)^2*(1 + s/(2*pi*wc(j)/2))/(1 + s/(2*pi*wc(j)*2));
S2{j} = 1/(1 + L);
end
freqs = dist_f.f; figure; hold on; i = 6; for j = 1:length(wc) set(gca,'ColorOrderIndex',j); plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(abs(squeeze(freqresp(S1{j}, freqs, 'Hz'))).^2.*psd_tot(:,i))))), '-', ... 'DisplayName', sprintf('$\\omega_c = %.0f$ [Hz]', wc(j))); end plot(freqs, sqrt(flip(-cumtrapz(flip(freqs), flip(psd_tot(:,i))))), 'k-', ... 'DisplayName', 'Open-Loop'); plot([freqs(1) freqs(end)], [10e-9 10e-9], 'k--', 'HandleVisibility', 'off'); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('CAS $E_y$ $[m]$') legend('Location', 'northeast'); xlim([0.5, 500]); ylim([1e-10 1e-6]);
wc = logspace(0, 3, 100); Dz1_rms = zeros(length(Ks), length(wc)); Dz2_rms = zeros(length(Ks), length(wc)); for i = 1:length(Ks) for j = 1:length(wc) L = (2*pi*wc(j))/s; Dz1_rms(i, j) = sqrt(trapz(freqs, abs(squeeze(freqresp(1/(1 + L), freqs, 'Hz'))).^2.*psd_tot(:,i))); L = ((2*pi*wc(j))/s)^2*(1 + s/(2*pi*wc(j)/2))/(1 + s/(2*pi*wc(j)*2)); Dz2_rms(i, j) = sqrt(trapz(freqs, abs(squeeze(freqresp(1/(1 + L), freqs, 'Hz'))).^2.*psd_tot(:,i))); end end
freqs = dist_f.f; figure; hold on; for i = 1:length(Ks) set(gca,'ColorOrderIndex',i); plot(wc, Dz1_rms(i, :), '-', ... 'DisplayName', sprintf('$k = %.0g$ [N/m]', Ks(i))) set(gca,'ColorOrderIndex',i); plot(wc, Dz2_rms(i, :), '--', ... 'HandleVisibility', 'off') end hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Control Bandwidth [Hz]'); ylabel('$E_z\ [m, rms]$') legend('Location', 'southwest'); xlim([1, 500]);