<?xml version="1.0" encoding="utf-8"?>
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN"
"http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<!-- 2021-02-20 sam. 23:09 -->
<meta http-equiv="Content-Type" content="text/html;charset=utf-8" />
<title>Decentralize control to add virtual mass</title>
<meta name="generator" content="Org mode" />
<meta name="author" content="Dehaeze Thomas" />
<link rel="stylesheet" type="text/css" href="https://research.tdehaeze.xyz/css/style.css"/>
<script type="text/javascript" src="https://research.tdehaeze.xyz/js/script.js"></script>
<script>
MathJax = {
svg: {
scale: 1,
fontCache: "global"
},
tex: {
tags: "ams",
multlineWidth: "%MULTLINEWIDTH",
tagSide: "right",
macros: {bm: ["\\boldsymbol{#1}",1],},
tagIndent: ".8em"
}
};
</script>
<script id="MathJax-script" async
src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-svg.js"></script>
</head>
<body>
<div id="org-div-home-and-up">
<a accesskey="h" href="./index.html"> UP </a>
|
<a accesskey="H" href="../../index.html"> HOME </a>
</div><div id="content">
<h1 class="title">Decentralize control to add virtual mass</h1>
<div id="table-of-contents">
<h2>Table of Contents</h2>
<div id="text-table-of-contents">
<ul>
<li><a href="#org48b52bd">1. Initialization</a></li>
<li><a href="#org157dc5d">2. Identification</a></li>
<li><a href="#orgd072386">3. Adding Virtual Mass in the Leg’s Space</a>
<ul>
<li><a href="#org147b003">3.1. Plant</a></li>
<li><a href="#orgacd4421">3.2. Controller Design</a></li>
<li><a href="#org4c460cf">3.3. Identification of the Primary Plant</a></li>
</ul>
</li>
<li><a href="#org3c74924">4. Adding Virtual Mass in the Task Space</a>
<ul>
<li><a href="#org3b61568">4.1. Plant</a></li>
<li><a href="#orgf37b1c0">4.2. Controller Design</a></li>
<li><a href="#orgcd22c9f">4.3. Identification of the Primary Plant</a></li>
</ul>
</li>
</ul>
</div>
</div>
<div id="outline-container-org48b52bd" class="outline-2">
<h2 id="org48b52bd"><span class="section-number-2">1</span> Initialization</h2>
<div class="outline-text-2" id="text-1">
<div class="org-src-container">
<pre class="src src-matlab"> initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();
initializeAxisc();
initializeMirror();
initializeSimscapeConfiguration();
initializeDisturbances(<span class="org-string">'enable'</span>, <span class="org-constant">false</span>);
initializeLoggingConfiguration(<span class="org-string">'log'</span>, <span class="org-string">'none'</span>);
initializeController(<span class="org-string">'type'</span>, <span class="org-string">'hac-dvf'</span>);
</pre>
</div>
<p>
The nano-hexapod has the following leg’s stiffness and damping.
</p>
<div class="org-src-container">
<pre class="src src-matlab"> initializeNanoHexapod(<span class="org-string">'k'</span>, 1e5, <span class="org-string">'c'</span>, 2e2);
</pre>
</div>
<p>
We set the stiffness of the payload fixation:
</p>
<div class="org-src-container">
<pre class="src src-matlab"> Kp = 1e8; <span class="org-comment">% [N/m]</span>
</pre>
</div>
</div>
</div>
<div id="outline-container-org157dc5d" class="outline-2">
<h2 id="org157dc5d"><span class="section-number-2">2</span> Identification</h2>
<div class="outline-text-2" id="text-2">
<p>
We identify the system for the following payload masses:
</p>
<div class="org-src-container">
<pre class="src src-matlab"> Ms = [1, 10, 50];
</pre>
</div>
<p>
Identification of the transfer function from \(\tau\) to \(d\mathcal{L}\).
Identification of the Primary plant without virtual add of mass
</p>
</div>
</div>
<div id="outline-container-orgd072386" class="outline-2">
<h2 id="orgd072386"><span class="section-number-2">3</span> Adding Virtual Mass in the Leg’s Space</h2>
<div class="outline-text-2" id="text-3">
</div>
<div id="outline-container-org147b003" class="outline-3">
<h3 id="org147b003"><span class="section-number-3">3.1</span> Plant</h3>
<div class="outline-text-3" id="text-3-1">
<div id="org74dce28" class="figure">
<p><img src="figs/virtual_mass_plant_L.png" alt="virtual_mass_plant_L.png" />
</p>
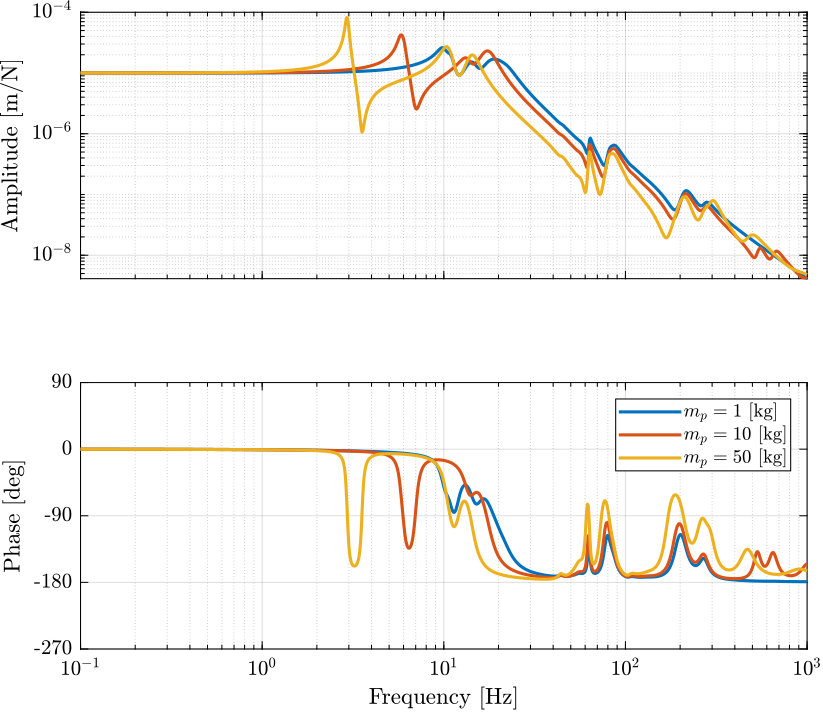
<p><span class="figure-number">Figure 1: </span>Transfer function from \(\tau_i\) to \(d\mathcal{L}_i\) for three payload masses</p>
</div>
</div>
</div>
<div id="outline-container-orgacd4421" class="outline-3">
<h3 id="orgacd4421"><span class="section-number-3">3.2</span> Controller Design</h3>
<div class="outline-text-3" id="text-3-2">
<div class="org-src-container">
<pre class="src src-matlab"> Kdvf = 10<span class="org-type">*</span>s<span class="org-type">^</span>2<span class="org-type">/</span>(1<span class="org-type">+</span>s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>500)<span class="org-type">^</span>2<span class="org-type">*</span>eye(6);
</pre>
</div>
<div id="orgdf2df59" class="figure">
<p><img src="figs/virtual_mass_loop_gain_L.png" alt="virtual_mass_loop_gain_L.png" />
</p>
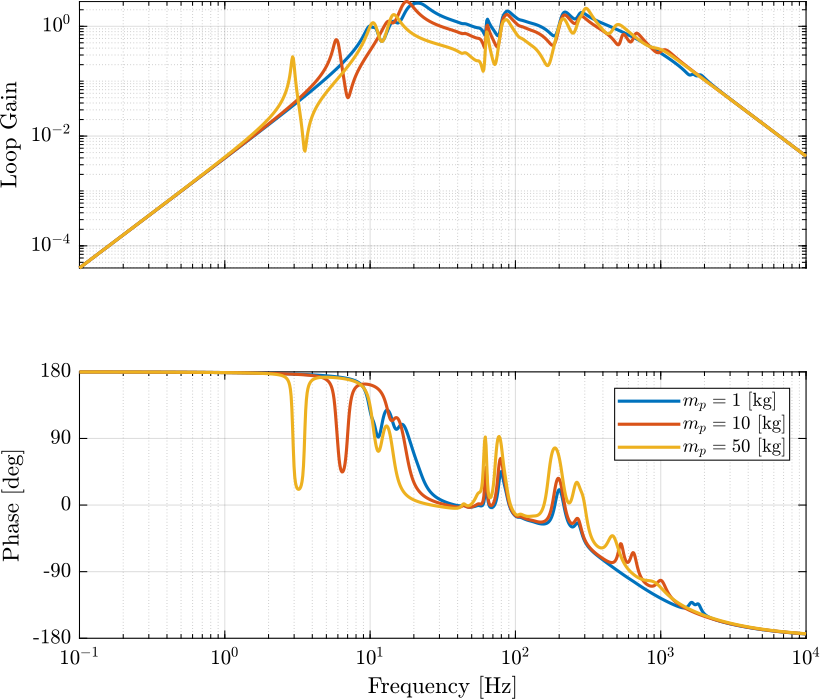
<p><span class="figure-number">Figure 2: </span>Loop Gain for the addition of virtual mass in the leg’s space</p>
</div>
</div>
</div>
<div id="outline-container-org4c460cf" class="outline-3">
<h3 id="org4c460cf"><span class="section-number-3">3.3</span> Identification of the Primary Plant</h3>
<div class="outline-text-3" id="text-3-3">
<div id="org29e9333" class="figure">
<p><img src="figs/virtual_mass_L_primary_plant_X.png" alt="virtual_mass_L_primary_plant_X.png" />
</p>
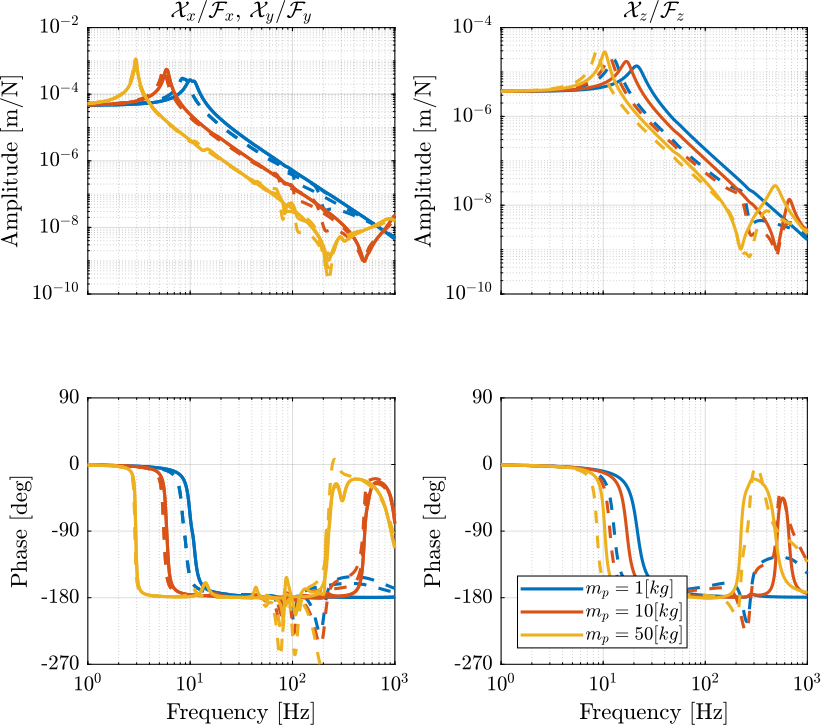
<p><span class="figure-number">Figure 3: </span>Comparison of the transfer function from \(\mathcal{F}_{x,y,z}\) to \(\mathcal{X}_{x,y,z}\) with and without the virtual addition of mass in the leg’s space</p>
</div>
<div id="orgd96256a" class="figure">
<p><img src="figs/virtual_mass_L_primary_plant_L.png" alt="virtual_mass_L_primary_plant_L.png" />
</p>
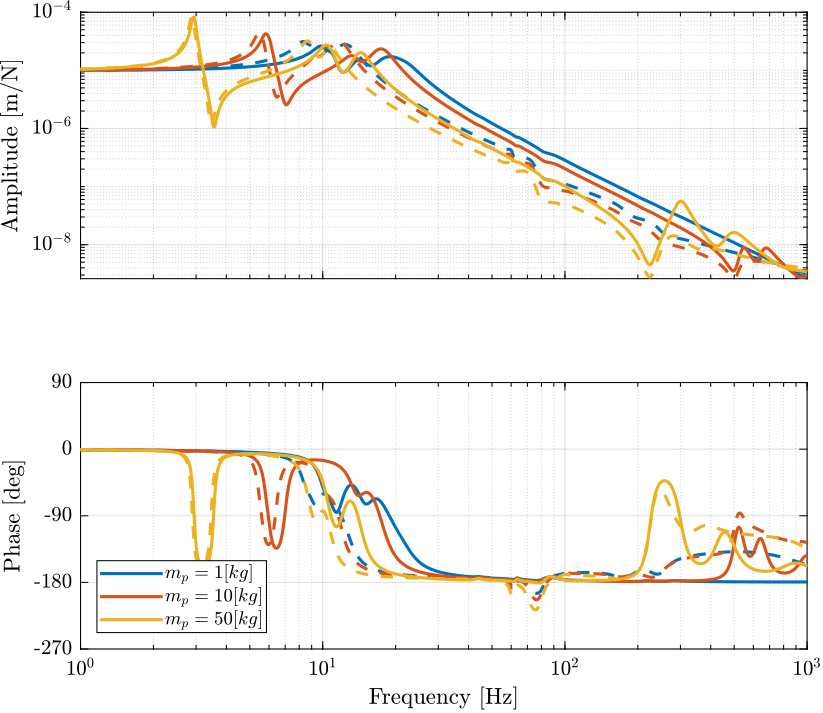
<p><span class="figure-number">Figure 4: </span>Comparison of the transfer function from \(\tau_i\) to \(\mathcal{L}_{i}\) with and without the virtual addition of mass in the leg’s space</p>
</div>
</div>
</div>
</div>
<div id="outline-container-org3c74924" class="outline-2">
<h2 id="org3c74924"><span class="section-number-2">4</span> Adding Virtual Mass in the Task Space</h2>
<div class="outline-text-2" id="text-4">
</div>
<div id="outline-container-org3b61568" class="outline-3">
<h3 id="org3b61568"><span class="section-number-3">4.1</span> Plant</h3>
<div class="outline-text-3" id="text-4-1">
<p>
Let’s look at the transfer function from \(\bm{\mathcal{F}}\) to \(d\bm{\mathcal{X}}\):
\[ \frac{d\bm{\mathcal{L}}}{\bm{\mathcal{F}}} = \bm{J}^{-1} \frac{d\bm{\mathcal{L}}}{\bm{\tau}} \bm{J}^{-T} \]
</p>
<div id="orgb509352" class="figure">
<p><img src="figs/virtual_mass_plant_X.png" alt="virtual_mass_plant_X.png" />
</p>
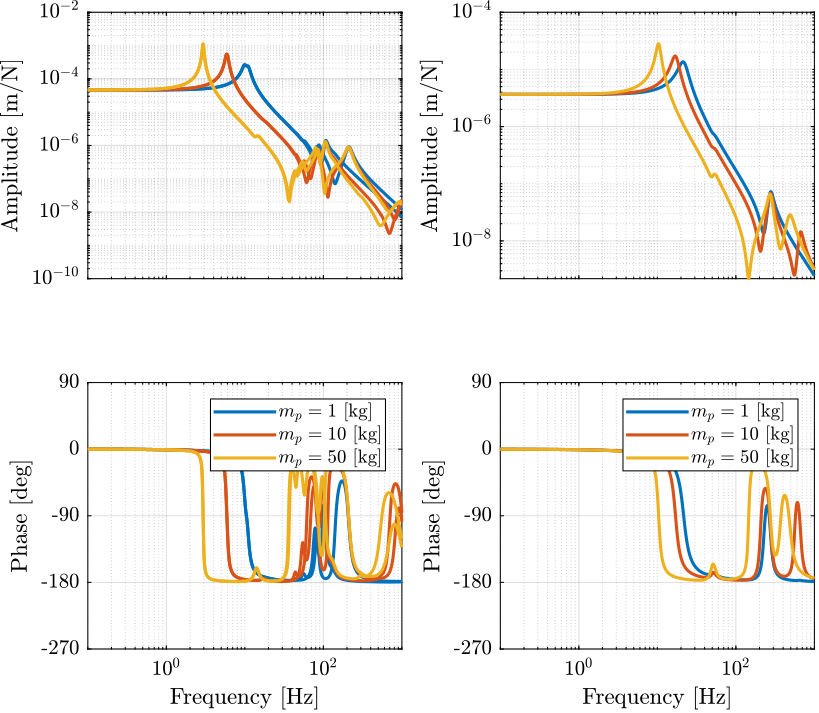
<p><span class="figure-number">Figure 5: </span>Dynamics from \(\mathcal{F}_{x,y,z}\) to \(\mathcal{X}_{x,y,z}\) used for virtual mass addition in the task space</p>
</div>
</div>
</div>
<div id="outline-container-orgf37b1c0" class="outline-3">
<h3 id="orgf37b1c0"><span class="section-number-3">4.2</span> Controller Design</h3>
<div class="outline-text-3" id="text-4-2">
<div class="org-src-container">
<pre class="src src-matlab"> KmX = (s<span class="org-type">^</span>2<span class="org-type">*</span>1<span class="org-type">/</span>(1<span class="org-type">+</span>s<span class="org-type">/</span>2<span class="org-type">/</span><span class="org-constant">pi</span><span class="org-type">/</span>500)<span class="org-type">^</span>2<span class="org-type">*</span>diag([1 1 50 0 0 0]));
</pre>
</div>
<div id="org18b3b14" class="figure">
<p><img src="figs/virtual_mass_loop_gain_X.png" alt="virtual_mass_loop_gain_X.png" />
</p>
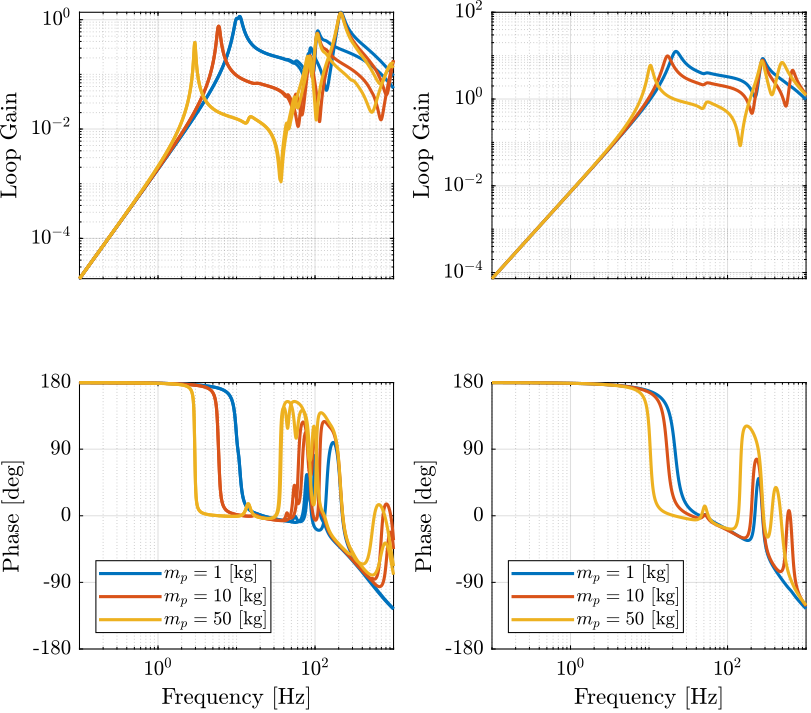
<p><span class="figure-number">Figure 6: </span>Loop gain for virtual mass addition in the task space</p>
</div>
<div class="org-src-container">
<pre class="src src-matlab"> Kdvf = inv(nano_hexapod.kinematics.J<span class="org-type">'</span>)<span class="org-type">*</span>KmX<span class="org-type">*</span>inv(nano_hexapod.kinematics.J);
</pre>
</div>
</div>
</div>
<div id="outline-container-orgcd22c9f" class="outline-3">
<h3 id="orgcd22c9f"><span class="section-number-3">4.3</span> Identification of the Primary Plant</h3>
<div class="outline-text-3" id="text-4-3">
<div id="orgfde1133" class="figure">
<p><img src="figs/virtual_mass_X_primary_plant_X.png" alt="virtual_mass_X_primary_plant_X.png" />
</p>
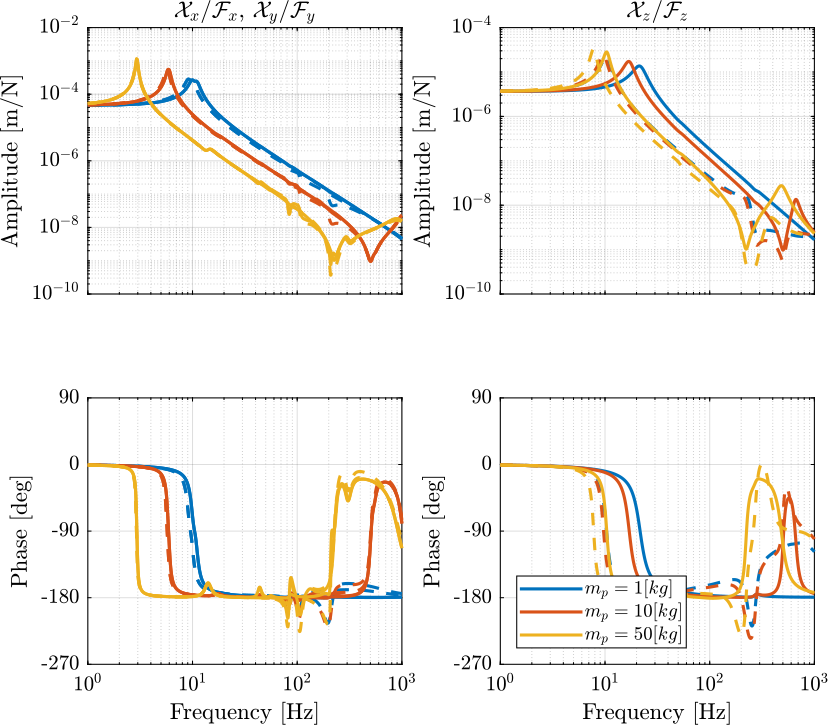
<p><span class="figure-number">Figure 7: </span>Comparison of the transfer function from \(\mathcal{F}_{x,y,z}\) to \(\mathcal{X}_{x,y,z}\) with and without the virtual addition of mass in the task space</p>
</div>
<div id="org095b9cd" class="figure">
<p><img src="figs/virtual_mass_X_primary_plant_L.png" alt="virtual_mass_X_primary_plant_L.png" />
</p>
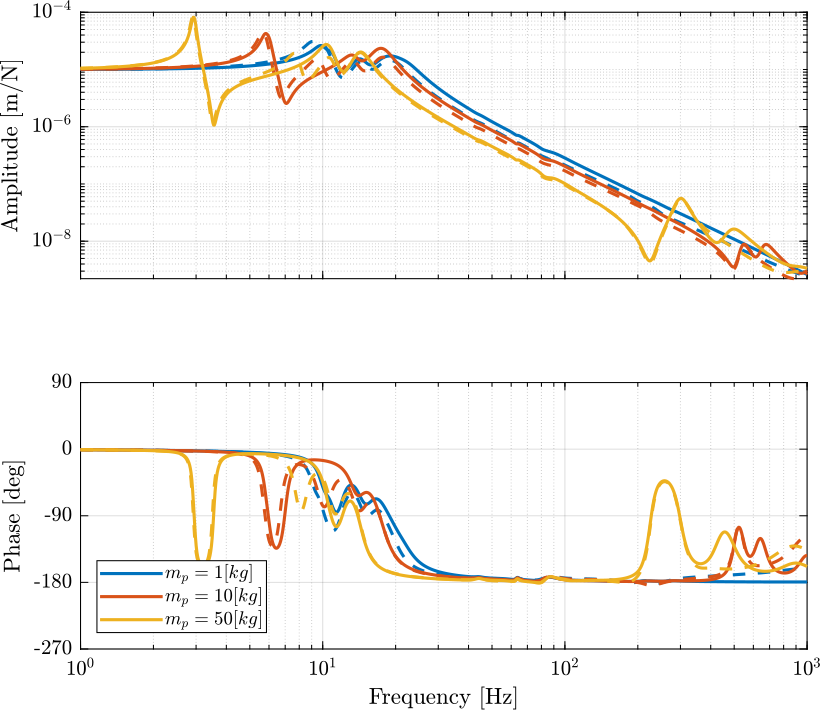
<p><span class="figure-number">Figure 8: </span>Comparison of the transfer function from \(\tau_i\) to \(\mathcal{L}_{i}\) with and without the virtual addition of mass in the task space</p>
</div>
</div>
</div>
</div>
</div>
<div id="postamble" class="status">
<p class="author">Author: Dehaeze Thomas</p>
<p class="date">Created: 2021-02-20 sam. 23:09</p>
</div>
</body>
</html>