<?xml version="1.0" encoding="utf-8"?>
<?xml version="1.0" encoding="utf-8"?>
<?xml version="1.0" encoding="utf-8"?>
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN"
"http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<!-- 2020-05-05 mar. 10:34 -->
<meta http-equiv="Content-Type" content="text/html;charset=utf-8" />
<title>Centrifugal Forces</title>
<meta name="generator" content="Org mode" />
<meta name="author" content="Dehaeze Thomas" />
<link rel="stylesheet" type="text/css" href="./css/htmlize.css"/>
<link rel="stylesheet" type="text/css" href="./css/readtheorg.css"/>
<script src="./js/jquery.min.js"></script>
<script src="./js/bootstrap.min.js"></script>
<script src="./js/jquery.stickytableheaders.min.js"></script>
<script src="./js/readtheorg.js"></script>
<script>MathJax = {
tex: {
tags: 'ams',
macros: {bm: ["\\boldsymbol{#1}",1],}
}
};
</script>
<script type="text/javascript" src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js"></script>
</head>
<body>
<div id="org-div-home-and-up">
<a accesskey="h" href="./index.html"> UP </a>
|
<a accesskey="H" href="./index.html"> HOME </a>
</div><div id="content">
<h1 class="title">Centrifugal Forces</h1>
<div id="table-of-contents">
<h2>Table of Contents</h2>
<div id="text-table-of-contents">
<ul>
<li><a href="#org49834ed">1. Parameters</a></li>
<li><a href="#org4b7747e">2. Centrifugal forces for light and heavy sample</a></li>
<li><a href="#org92c9f54">3. Centrifugal forces as a function of the rotation speed</a></li>
<li><a href="#orgb7f1acf">4. Maximum rotation speed as a function of the mass</a></li>
</ul>
</div>
</div>
<p>
In this document, we wish to estimate the centrifugal forces due to the spindle’s rotation when the sample’s center of mass is off-centered with respect to the rotation axis.
</p>
<p>
This is the case then the sample is moved by the micro-hexapod.
</p>
<p>
The centrifugal forces are defined as represented Figure <a href="#orgd84fe6e">1</a> where:
</p>
<ul class="org-ul">
<li>\(M\) is the total mass of the rotating elements in \([kg]\)</li>
<li>\(\omega\) is the rotation speed in \([rad/s]\)</li>
<li>\(r\) is the distance to the rotation axis in \([m]\)</li>
</ul>
<div id="orgd84fe6e" class="figure">
<p><img src="./figs/centrifugal.png" alt="centrifugal.png" />
</p>
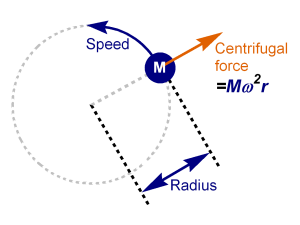
<p><span class="figure-number">Figure 1: </span>Centrifugal forces</p>
</div>
<div id="outline-container-org49834ed" class="outline-2">
<h2 id="org49834ed"><span class="section-number-2">1</span> Parameters</h2>
<div class="outline-text-2" id="text-1">
<p>
We define some parameters for the computation.
</p>
<p>
The mass of the sample can vary from \(1\,kg\) to \(50\,kg\) to which is added to mass of the metrology reflector and the nano-hexapod’s top platform (here set to \(15\,kg\)).
</p>
<div class="org-src-container">
<pre class="src src-matlab">M_light = 16; % mass of excentred parts mooving [kg]
M_heavy = 65; % [kg]
</pre>
</div>
<p>
For the light mass, the rotation speed is 60rpm whereas for the heavy mass, it is equal to 1rpm.
</p>
<div class="org-src-container">
<pre class="src src-matlab">w_light = 2*pi; % rotational speed [rad/s]
w_heavy = 2*pi/60; % rotational speed [rad/s]
</pre>
</div>
<p>
Finally, we consider a mass eccentricity of \(10\,mm\).
</p>
<div class="org-src-container">
<pre class="src src-matlab">R = 0.1; % Excentricity [m]
</pre>
</div>
</div>
</div>
<div id="outline-container-org4b7747e" class="outline-2">
<h2 id="org4b7747e"><span class="section-number-2">2</span> Centrifugal forces for light and heavy sample</h2>
<div class="outline-text-2" id="text-2">
<p>
From the formula \(F_c = m \omega^2 r\), we obtain the values shown below.
</p>
<table border="2" cellspacing="0" cellpadding="6" rules="groups" frame="hsides">
<colgroup>
<col class="org-left" />
<col class="org-right" />
</colgroup>
<thead>
<tr>
<th scope="col" class="org-left"> </th>
<th scope="col" class="org-right">Force [N]</th>
</tr>
</thead>
<tbody>
<tr>
<td class="org-left">light</td>
<td class="org-right">63.2</td>
</tr>
<tr>
<td class="org-left">heavy</td>
<td class="org-right">0.1</td>
</tr>
</tbody>
</table>
</div>
</div>
<div id="outline-container-org92c9f54" class="outline-2">
<h2 id="org92c9f54"><span class="section-number-2">3</span> Centrifugal forces as a function of the rotation speed</h2>
<div class="outline-text-2" id="text-3">
<p>
The centrifugal forces as a function of the rotation speed for light and heavy sample is shown on Figure <a href="#orgfaf795f">2</a>.
</p>
<div id="orgfaf795f" class="figure">
<p><img src="figs/centrifugal_forces_rpm.png" alt="centrifugal_forces_rpm.png" />
</p>
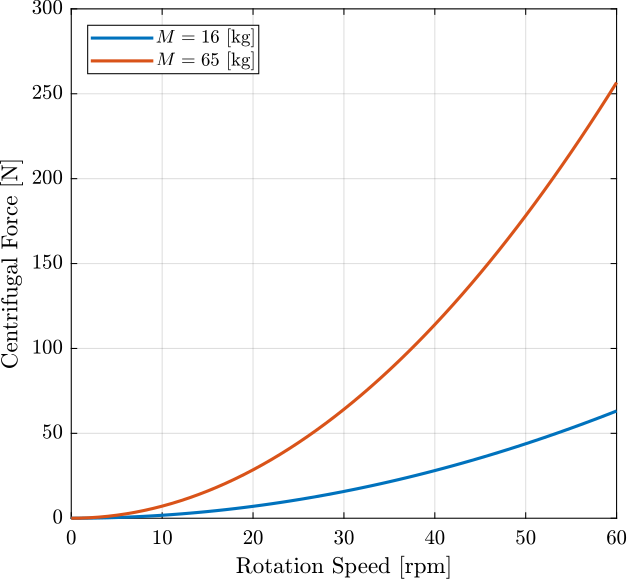
<p><span class="figure-number">Figure 2: </span>Centrifugal forces function of the rotation speed</p>
</div>
</div>
</div>
<div id="outline-container-orgb7f1acf" class="outline-2">
<h2 id="orgb7f1acf"><span class="section-number-2">4</span> Maximum rotation speed as a function of the mass</h2>
<div class="outline-text-2" id="text-4">
<p>
We plot the maximum rotation speed as a function of the mass for different maximum force that we can use to counteract the centrifugal forces (Figure <a href="#org6ee8f38">3</a>).
</p>
<p>
From a specified maximum allowed centrifugal force (here set to \(100\,[N]\)), the maximum rotation speed as a function of the sample’s mass is shown in Figure <a href="#org6ee8f38">3</a>.
</p>
<div class="org-src-container">
<pre class="src src-matlab">F_max = 100; % Maximum accepted centrifugal forces [N]
R = 0.1;
M_sample = 0:1:100;
M_reflector = 15;
</pre>
</div>
<div id="org6ee8f38" class="figure">
<p><img src="figs/max_force_rpm.png" alt="max_force_rpm.png" />
</p>
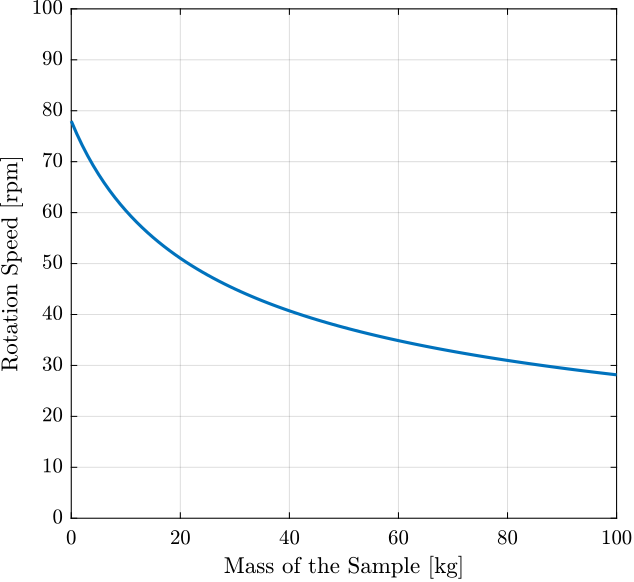
<p><span class="figure-number">Figure 3: </span>Maximum rotation speed as a function of the sample mass for an allowed centrifugal force of \(100\,[N]\)</p>
</div>
</div>
</div>
</div>
<div id="postamble" class="status">
<p class="author">Author: Dehaeze Thomas</p>
<p class="date">Created: 2020-05-05 mar. 10:34</p>
</div>
</body>
</html>