UP | HOME

Stewart Platform - Simscape Model

Table of Contents

Stewart platforms are generated in multiple steps.

We define 4 important frames:

Then, we define the location of the spherical joints:

We define the rest position of the Stewart platform:

From \(\bm{a}_{i}\) and \(\bm{b}_{i}\), we can determine the length and orientation of each strut:

The position of the Spherical joints can be computed using various methods:

For Simscape, we need:

1 initializeStewartPlatform: Initialize the Stewart Platform structure

This Matlab function is accessible here.

Documentation

stewart-frames-position.png

Figure 1: Definition of the position of the frames

Function description

function [stewart] = initializeStewartPlatform()
% initializeStewartPlatform - Initialize the stewart structure
%
% Syntax: [stewart] = initializeStewartPlatform(args)
%
% Outputs:
%    - stewart - A structure with the following sub-structures:
%      - platform_F -
%      - platform_M -
%      - joints_F   -
%      - joints_M   -
%      - struts_F   -
%      - struts_M   -
%      - actuators  -
%      - geometry   -
%      - properties -

Initialize the Stewart structure

stewart = struct();
stewart.platform_F = struct();
stewart.platform_M = struct();
stewart.joints_F   = struct();
stewart.joints_M   = struct();
stewart.struts_F   = struct();
stewart.struts_M   = struct();
stewart.actuators  = struct();
stewart.sensors    = struct();
stewart.sensors.inertial = struct();
stewart.sensors.force    = struct();
stewart.sensors.relative = struct();
stewart.geometry   = struct();
stewart.kinematics = struct();

2 initializeFramesPositions: Initialize the positions of frames {A}, {B}, {F} and {M}

This Matlab function is accessible here.

Documentation

stewart-frames-position.png

Figure 2: Definition of the position of the frames

Function description

function [stewart] = initializeFramesPositions(stewart, args)
% initializeFramesPositions - Initialize the positions of frames {A}, {B}, {F} and {M}
%
% Syntax: [stewart] = initializeFramesPositions(stewart, args)
%
% Inputs:
%    - args - Can have the following fields:
%        - H    [1x1] - Total Height of the Stewart Platform (height from {F} to {M}) [m]
%        - MO_B [1x1] - Height of the frame {B} with respect to {M} [m]
%
% Outputs:
%    - stewart - A structure with the following fields:
%        - geometry.H      [1x1] - Total Height of the Stewart Platform [m]
%        - geometry.FO_M   [3x1] - Position of {M} with respect to {F} [m]
%        - platform_M.MO_B [3x1] - Position of {B} with respect to {M} [m]
%        - platform_F.FO_A [3x1] - Position of {A} with respect to {F} [m]

Optional Parameters

arguments
    stewart
    args.H    (1,1) double {mustBeNumeric, mustBePositive} = 90e-3
    args.MO_B (1,1) double {mustBeNumeric} = 50e-3
end

Compute the position of each frame

H = args.H; % Total Height of the Stewart Platform [m]

FO_M = [0; 0; H]; % Position of {M} with respect to {F} [m]

MO_B = [0; 0; args.MO_B]; % Position of {B} with respect to {M} [m]

FO_A = MO_B + FO_M; % Position of {A} with respect to {F} [m]

Populate the stewart structure

stewart.geometry.H      = H;
stewart.geometry.FO_M   = FO_M;
stewart.platform_M.MO_B = MO_B;
stewart.platform_F.FO_A = FO_A;

3 generateGeneralConfiguration: Generate a Very General Configuration

This Matlab function is accessible here.

Documentation

Joints are positions on a circle centered with the Z axis of {F} and {M} and at a chosen distance from {F} and {M}. The radius of the circles can be chosen as well as the angles where the joints are located (see Figure 3).

stewart_bottom_plate.png

Figure 3: Position of the joints

Function description

function [stewart] = generateGeneralConfiguration(stewart, args)
% generateGeneralConfiguration - Generate a Very General Configuration
%
% Syntax: [stewart] = generateGeneralConfiguration(stewart, args)
%
% Inputs:
%    - args - Can have the following fields:
%        - FH  [1x1] - Height of the position of the fixed joints with respect to the frame {F} [m]
%        - FR  [1x1] - Radius of the position of the fixed joints in the X-Y [m]
%        - FTh [6x1] - Angles of the fixed joints in the X-Y plane with respect to the X axis [rad]
%        - MH  [1x1] - Height of the position of the mobile joints with respect to the frame {M} [m]
%        - FR  [1x1] - Radius of the position of the mobile joints in the X-Y [m]
%        - MTh [6x1] - Angles of the mobile joints in the X-Y plane with respect to the X axis [rad]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%        - platform_F.Fa  [3x6] - Its i'th column is the position vector of joint ai with respect to {F}
%        - platform_M.Mb  [3x6] - Its i'th column is the position vector of joint bi with respect to {M}

Optional Parameters

arguments
    stewart
    args.FH  (1,1) double {mustBeNumeric, mustBePositive} = 15e-3
    args.FR  (1,1) double {mustBeNumeric, mustBePositive} = 115e-3;
    args.FTh (6,1) double {mustBeNumeric} = [-10, 10, 120-10, 120+10, 240-10, 240+10]*(pi/180);
    args.MH  (1,1) double {mustBeNumeric, mustBePositive} = 15e-3
    args.MR  (1,1) double {mustBeNumeric, mustBePositive} = 90e-3;
    args.MTh (6,1) double {mustBeNumeric} = [-60+10, 60-10, 60+10, 180-10, 180+10, -60-10]*(pi/180);
end

Compute the pose

Fa = zeros(3,6);
Mb = zeros(3,6);

for i = 1:6
  Fa(:,i) = [args.FR*cos(args.FTh(i)); args.FR*sin(args.FTh(i));  args.FH];
  Mb(:,i) = [args.MR*cos(args.MTh(i)); args.MR*sin(args.MTh(i)); -args.MH];
end

Populate the stewart structure

stewart.platform_F.Fa = Fa;
stewart.platform_M.Mb = Mb;

4 computeJointsPose: Compute the Pose of the Joints

This Matlab function is accessible here.

Documentation

stewart-struts.png

Figure 4: Position and orientation of the struts

Function description

function [stewart] = computeJointsPose(stewart)
% computeJointsPose -
%
% Syntax: [stewart] = computeJointsPose(stewart)
%
% Inputs:
%    - stewart - A structure with the following fields
%        - platform_F.Fa   [3x6] - Its i'th column is the position vector of joint ai with respect to {F}
%        - platform_M.Mb   [3x6] - Its i'th column is the position vector of joint bi with respect to {M}
%        - platform_F.FO_A [3x1] - Position of {A} with respect to {F}
%        - platform_M.MO_B [3x1] - Position of {B} with respect to {M}
%        - geometry.FO_M   [3x1] - Position of {M} with respect to {F}
%
% Outputs:
%    - stewart - A structure with the following added fields
%        - geometry.Aa    [3x6]   - The i'th column is the position of ai with respect to {A}
%        - geometry.Ab    [3x6]   - The i'th column is the position of bi with respect to {A}
%        - geometry.Ba    [3x6]   - The i'th column is the position of ai with respect to {B}
%        - geometry.Bb    [3x6]   - The i'th column is the position of bi with respect to {B}
%        - geometry.l     [6x1]   - The i'th element is the initial length of strut i
%        - geometry.As    [3x6]   - The i'th column is the unit vector of strut i expressed in {A}
%        - geometry.Bs    [3x6]   - The i'th column is the unit vector of strut i expressed in {B}
%        - struts_F.l     [6x1]   - Length of the Fixed part of the i'th strut
%        - struts_M.l     [6x1]   - Length of the Mobile part of the i'th strut
%        - platform_F.FRa [3x3x6] - The i'th 3x3 array is the rotation matrix to orientate the bottom of the i'th strut from {F}
%        - platform_M.MRb [3x3x6] - The i'th 3x3 array is the rotation matrix to orientate the top of the i'th strut from {M}

Check the stewart structure elements

assert(isfield(stewart.platform_F, 'Fa'),   'stewart.platform_F should have attribute Fa')
Fa = stewart.platform_F.Fa;

assert(isfield(stewart.platform_M, 'Mb'),   'stewart.platform_M should have attribute Mb')
Mb = stewart.platform_M.Mb;

assert(isfield(stewart.platform_F, 'FO_A'), 'stewart.platform_F should have attribute FO_A')
FO_A = stewart.platform_F.FO_A;

assert(isfield(stewart.platform_M, 'MO_B'), 'stewart.platform_M should have attribute MO_B')
MO_B = stewart.platform_M.MO_B;

assert(isfield(stewart.geometry,   'FO_M'), 'stewart.geometry should have attribute FO_M')
FO_M = stewart.geometry.FO_M;

Compute the position of the Joints

Aa = Fa - repmat(FO_A, [1, 6]);
Bb = Mb - repmat(MO_B, [1, 6]);

Ab = Bb - repmat(-MO_B-FO_M+FO_A, [1, 6]);
Ba = Aa - repmat( MO_B+FO_M-FO_A, [1, 6]);

Compute the strut length and orientation

As = (Ab - Aa)./vecnorm(Ab - Aa); % As_i is the i'th vector of As

l = vecnorm(Ab - Aa)';

Bs = (Bb - Ba)./vecnorm(Bb - Ba);

Compute the orientation of the Joints

FRa = zeros(3,3,6);
MRb = zeros(3,3,6);

for i = 1:6
  FRa(:,:,i) = [cross([0;1;0], As(:,i)) , cross(As(:,i), cross([0;1;0], As(:,i))) , As(:,i)];
  FRa(:,:,i) = FRa(:,:,i)./vecnorm(FRa(:,:,i));

  MRb(:,:,i) = [cross([0;1;0], Bs(:,i)) , cross(Bs(:,i), cross([0;1;0], Bs(:,i))) , Bs(:,i)];
  MRb(:,:,i) = MRb(:,:,i)./vecnorm(MRb(:,:,i));
end

Populate the stewart structure

stewart.geometry.Aa = Aa;
stewart.geometry.Ab = Ab;
stewart.geometry.Ba = Ba;
stewart.geometry.Bb = Bb;
stewart.geometry.As = As;
stewart.geometry.Bs = Bs;
stewart.geometry.l  = l;

stewart.struts_F.l  = l/2;
stewart.struts_M.l  = l/2;

stewart.platform_F.FRa = FRa;
stewart.platform_M.MRb = MRb;

5 initializeStewartPose: Determine the initial stroke in each leg to have the wanted pose

This Matlab function is accessible here.

Function description

function [stewart] = initializeStewartPose(stewart, args)
% initializeStewartPose - Determine the initial stroke in each leg to have the wanted pose
%                         It uses the inverse kinematic
%
% Syntax: [stewart] = initializeStewartPose(stewart, args)
%
% Inputs:
%    - stewart - A structure with the following fields
%        - Aa   [3x6] - The positions ai expressed in {A}
%        - Bb   [3x6] - The positions bi expressed in {B}
%    - args - Can have the following fields:
%        - AP   [3x1] - The wanted position of {B} with respect to {A}
%        - ARB  [3x3] - The rotation matrix that gives the wanted orientation of {B} with respect to {A}
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%      - actuators.Leq [6x1] - The 6 needed displacement of the struts from the initial position in [m] to have the wanted pose of {B} w.r.t. {A}

Optional Parameters

arguments
    stewart
    args.AP  (3,1) double {mustBeNumeric} = zeros(3,1)
    args.ARB (3,3) double {mustBeNumeric} = eye(3)
end

Use the Inverse Kinematic function

[Li, dLi] = inverseKinematics(stewart, 'AP', args.AP, 'ARB', args.ARB);

Populate the stewart structure

stewart.actuators.Leq = dLi;

6 initializeCylindricalPlatforms: Initialize the geometry of the Fixed and Mobile Platforms

This Matlab function is accessible here.

Function description

function [stewart] = initializeCylindricalPlatforms(stewart, args)
% initializeCylindricalPlatforms - Initialize the geometry of the Fixed and Mobile Platforms
%
% Syntax: [stewart] = initializeCylindricalPlatforms(args)
%
% Inputs:
%    - args - Structure with the following fields:
%        - Fpm [1x1] - Fixed Platform Mass [kg]
%        - Fph [1x1] - Fixed Platform Height [m]
%        - Fpr [1x1] - Fixed Platform Radius [m]
%        - Mpm [1x1] - Mobile Platform Mass [kg]
%        - Mph [1x1] - Mobile Platform Height [m]
%        - Mpr [1x1] - Mobile Platform Radius [m]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%      - platform_F [struct] - structure with the following fields:
%        - type = 1
%        - M [1x1] - Fixed Platform Mass [kg]
%        - I [3x3] - Fixed Platform Inertia matrix [kg*m^2]
%        - H [1x1] - Fixed Platform Height [m]
%        - R [1x1] - Fixed Platform Radius [m]
%      - platform_M [struct] - structure with the following fields:
%        - M [1x1] - Mobile Platform Mass [kg]
%        - I [3x3] - Mobile Platform Inertia matrix [kg*m^2]
%        - H [1x1] - Mobile Platform Height [m]
%        - R [1x1] - Mobile Platform Radius [m]

Optional Parameters

arguments
    stewart
    args.Fpm (1,1) double {mustBeNumeric, mustBePositive} = 1
    args.Fph (1,1) double {mustBeNumeric, mustBePositive} = 10e-3
    args.Fpr (1,1) double {mustBeNumeric, mustBePositive} = 125e-3
    args.Mpm (1,1) double {mustBeNumeric, mustBePositive} = 1
    args.Mph (1,1) double {mustBeNumeric, mustBePositive} = 10e-3
    args.Mpr (1,1) double {mustBeNumeric, mustBePositive} = 100e-3
end

Compute the Inertia matrices of platforms

I_F = diag([1/12*args.Fpm * (3*args.Fpr^2 + args.Fph^2), ...
            1/12*args.Fpm * (3*args.Fpr^2 + args.Fph^2), ...
            1/2 *args.Fpm * args.Fpr^2]);

I_M = diag([1/12*args.Mpm * (3*args.Mpr^2 + args.Mph^2), ...
            1/12*args.Mpm * (3*args.Mpr^2 + args.Mph^2), ...
            1/2 *args.Mpm * args.Mpr^2]);

Populate the stewart structure

stewart.platform_F.type = 1;

stewart.platform_F.I = I_F;
stewart.platform_F.M = args.Fpm;
stewart.platform_F.R = args.Fpr;
stewart.platform_F.H = args.Fph;

stewart.platform_M.type = 1;

stewart.platform_M.I = I_M;
stewart.platform_M.M = args.Mpm;
stewart.platform_M.R = args.Mpr;
stewart.platform_M.H = args.Mph;

7 initializeCylindricalStruts: Define the inertia of cylindrical struts

This Matlab function is accessible here.

Function description

function [stewart] = initializeCylindricalStruts(stewart, args)
% initializeCylindricalStruts - Define the mass and moment of inertia of cylindrical struts
%
% Syntax: [stewart] = initializeCylindricalStruts(args)
%
% Inputs:
%    - args - Structure with the following fields:
%        - Fsm [1x1] - Mass of the Fixed part of the struts [kg]
%        - Fsh [1x1] - Height of cylinder for the Fixed part of the struts [m]
%        - Fsr [1x1] - Radius of cylinder for the Fixed part of the struts [m]
%        - Msm [1x1] - Mass of the Mobile part of the struts [kg]
%        - Msh [1x1] - Height of cylinder for the Mobile part of the struts [m]
%        - Msr [1x1] - Radius of cylinder for the Mobile part of the struts [m]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%      - struts_F [struct] - structure with the following fields:
%        - M [6x1]   - Mass of the Fixed part of the struts [kg]
%        - I [3x3x6] - Moment of Inertia for the Fixed part of the struts [kg*m^2]
%        - H [6x1]   - Height of cylinder for the Fixed part of the struts [m]
%        - R [6x1]   - Radius of cylinder for the Fixed part of the struts [m]
%      - struts_M [struct] - structure with the following fields:
%        - M [6x1]   - Mass of the Mobile part of the struts [kg]
%        - I [3x3x6] - Moment of Inertia for the Mobile part of the struts [kg*m^2]
%        - H [6x1]   - Height of cylinder for the Mobile part of the struts [m]
%        - R [6x1]   - Radius of cylinder for the Mobile part of the struts [m]

Optional Parameters

arguments
    stewart
    args.Fsm (1,1) double {mustBeNumeric, mustBePositive} = 0.1
    args.Fsh (1,1) double {mustBeNumeric, mustBePositive} = 50e-3
    args.Fsr (1,1) double {mustBeNumeric, mustBePositive} = 5e-3
    args.Msm (1,1) double {mustBeNumeric, mustBePositive} = 0.1
    args.Msh (1,1) double {mustBeNumeric, mustBePositive} = 50e-3
    args.Msr (1,1) double {mustBeNumeric, mustBePositive} = 5e-3
end

Compute the properties of the cylindrical struts

Fsm = ones(6,1).*args.Fsm;
Fsh = ones(6,1).*args.Fsh;
Fsr = ones(6,1).*args.Fsr;

Msm = ones(6,1).*args.Msm;
Msh = ones(6,1).*args.Msh;
Msr = ones(6,1).*args.Msr;

I_F = zeros(3, 3, 6); % Inertia of the "fixed" part of the strut
I_M = zeros(3, 3, 6); % Inertia of the "mobile" part of the strut

for i = 1:6
  I_F(:,:,i) = diag([1/12 * Fsm(i) * (3*Fsr(i)^2 + Fsh(i)^2), ...
                     1/12 * Fsm(i) * (3*Fsr(i)^2 + Fsh(i)^2), ...
                     1/2  * Fsm(i) * Fsr(i)^2]);

  I_M(:,:,i) = diag([1/12 * Msm(i) * (3*Msr(i)^2 + Msh(i)^2), ...
                     1/12 * Msm(i) * (3*Msr(i)^2 + Msh(i)^2), ...
                     1/2  * Msm(i) * Msr(i)^2]);
end

Populate the stewart structure

stewart.struts_M.type = 1;

stewart.struts_M.I = I_M;
stewart.struts_M.M = Msm;
stewart.struts_M.R = Msr;
stewart.struts_M.H = Msh;

stewart.struts_F.type = 1;

stewart.struts_F.I = I_F;
stewart.struts_F.M = Fsm;
stewart.struts_F.R = Fsr;
stewart.struts_F.H = Fsh;

8 initializeStrutDynamics: Add Stiffness and Damping properties of each strut

This Matlab function is accessible here.

Documentation

piezoelectric_stack.jpg

Figure 5: Example of a piezoelectric stach actuator (PI)

A simplistic model of such amplified actuator is shown in Figure 6 where:

  • \(K\) represent the vertical stiffness of the actuator
  • \(C\) represent the vertical damping of the actuator
  • \(F\) represents the force applied by the actuator
  • \(F_{m}\) represents the total measured force
  • \(v_{m}\) represents the absolute velocity of the top part of the actuator
  • \(d_{m}\) represents the total relative displacement of the actuator

actuator_model_simple.png

Figure 6: Simple model of an Actuator

Function description

function [stewart] = initializeStrutDynamics(stewart, args)
% initializeStrutDynamics - Add Stiffness and Damping properties of each strut
%
% Syntax: [stewart] = initializeStrutDynamics(args)
%
% Inputs:
%    - args - Structure with the following fields:
%        - K [6x1] - Stiffness of each strut [N/m]
%        - C [6x1] - Damping of each strut [N/(m/s)]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%      - actuators.type = 1
%      - actuators.K [6x1] - Stiffness of each strut [N/m]
%      - actuators.C [6x1] - Damping of each strut [N/(m/s)]

Optional Parameters

arguments
    stewart
    args.type char {mustBeMember(args.type,{'classical', 'amplified'})} = 'classical'
    args.K (6,1) double {mustBeNumeric, mustBeNonnegative} = 20e6*ones(6,1)
    args.C (6,1) double {mustBeNumeric, mustBeNonnegative} = 2e1*ones(6,1)
    args.k1 (6,1) double {mustBeNumeric} = 1e6
    args.ke (6,1) double {mustBeNumeric} = 5e6
    args.ka (6,1) double {mustBeNumeric} = 60e6
    args.c1 (6,1) double {mustBeNumeric} = 10
    args.ce (6,1) double {mustBeNumeric} = 10
    args.ca (6,1) double {mustBeNumeric} = 10
    args.me (6,1) double {mustBeNumeric} = 0.05
    args.ma (6,1) double {mustBeNumeric} = 0.05
end

Add Stiffness and Damping properties of each strut

if strcmp(args.type, 'classical')
    stewart.actuators.type = 1;
elseif strcmp(args.type, 'amplified')
    stewart.actuators.type = 2;
end

stewart.actuators.K = args.K;
stewart.actuators.C = args.C;

stewart.actuators.k1 = args.k1;
stewart.actuators.c1 = args.c1;

stewart.actuators.ka = args.ka;
stewart.actuators.ca = args.ca;

stewart.actuators.ke = args.ke;
stewart.actuators.ce = args.ce;

stewart.actuators.ma = args.ma;
stewart.actuators.me = args.me;

9 initializeAmplifiedStrutDynamics: Add Stiffness and Damping properties of each strut for an amplified piezoelectric actuator

This Matlab function is accessible here.

Documentation

An amplified piezoelectric actuator is shown in Figure 7.

amplified_piezo_with_displacement_sensor.jpg

Figure 7: Example of an Amplified piezoelectric actuator with an integrated displacement sensor (Cedrat Technologies)

A simplistic model of such amplified actuator is shown in Figure 8 where:

  • \(K_{r}\) represent the vertical stiffness when the piezoelectric stack is removed
  • \(K_{a}\) is the vertical stiffness contribution of the piezoelectric stack
  • \(F_{i}\) represents the part of the piezoelectric stack that is used as a force actuator
  • \(F_{m,i}\) represents the remaining part of the piezoelectric stack that is used as a force sensor
  • \(v_{m,i}\) represents the absolute velocity of the top part of the actuator
  • \(d_{m,i}\) represents the total relative displacement of the actuator

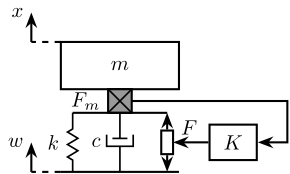
iff_1dof.png

Figure 8: Model of an amplified actuator

Function description

function [stewart] = initializeAmplifiedStrutDynamics(stewart, args)
% initializeAmplifiedStrutDynamics - Add Stiffness and Damping properties of each strut
%
% Syntax: [stewart] = initializeAmplifiedStrutDynamics(args)
%
% Inputs:
%    - args - Structure with the following fields:
%        - Ka [6x1] - Vertical stiffness contribution of the piezoelectric stack [N/m]
%        - Ca [6x1] - Vertical damping contribution of the piezoelectric stack [N/(m/s)]
%        - Kr [6x1] - Vertical (residual) stiffness when the piezoelectric stack is removed [N/m]
%        - Cr [6x1] - Vertical (residual) damping when the piezoelectric stack is removed [N/(m/s)]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%      - actuators.type = 2
%      - actuators.K   [6x1] - Total Stiffness of each strut [N/m]
%      - actuators.C   [6x1] - Total Damping of each strut [N/(m/s)]
%      - actuators.Ka [6x1] - Vertical stiffness contribution of the piezoelectric stack [N/m]
%      - actuators.Ca [6x1] - Vertical damping contribution of the piezoelectric stack [N/(m/s)]
%      - actuators.Kr [6x1] - Vertical stiffness when the piezoelectric stack is removed [N/m]
%      - actuators.Cr [6x1] - Vertical damping when the piezoelectric stack is removed [N/(m/s)]

Optional Parameters

arguments
    stewart
    args.Kr (6,1) double {mustBeNumeric, mustBeNonnegative} = 5e6*ones(6,1)
    args.Cr (6,1) double {mustBeNumeric, mustBeNonnegative} = 1e1*ones(6,1)
    args.Ka (6,1) double {mustBeNumeric, mustBeNonnegative} = 15e6*ones(6,1)
    args.Ca (6,1) double {mustBeNumeric, mustBeNonnegative} = 1e1*ones(6,1)
end

Compute the total stiffness and damping

K = args.Ka + args.Kr;
C = args.Ca + args.Cr;

Populate the stewart structure

stewart.actuators.type = 2;

stewart.actuators.Ka = args.Ka;
stewart.actuators.Ca = args.Ca;

stewart.actuators.Kr = args.Kr;
stewart.actuators.Cr = args.Cr;

stewart.actuators.K = K;
stewart.actuators.C = K;

10 initializeJointDynamics: Add Stiffness and Damping properties for spherical joints

This Matlab function is accessible here.

Function description

function [stewart] = initializeJointDynamics(stewart, args)
% initializeJointDynamics - Add Stiffness and Damping properties for the spherical joints
%
% Syntax: [stewart] = initializeJointDynamics(args)
%
% Inputs:
%    - args - Structure with the following fields:
%        - type_F - 'universal', 'spherical', 'universal_p', 'spherical_p'
%        - type_M - 'universal', 'spherical', 'universal_p', 'spherical_p'
%        - Kf_M [6x1] - Bending (Rx, Ry) Stiffness for each top joints [(N.m)/rad]
%        - Kt_M [6x1] - Torsion (Rz) Stiffness for each top joints [(N.m)/rad]
%        - Cf_M [6x1] - Bending (Rx, Ry) Damping of each top joint [(N.m)/(rad/s)]
%        - Ct_M [6x1] - Torsion (Rz) Damping of each top joint [(N.m)/(rad/s)]
%        - Kz_M [6x1] - Translation (Tz) Stiffness for each top joints [N/m]
%        - Cz_M [6x1] - Translation (Tz) Damping of each top joint [N/m]
%        - Kf_F [6x1] - Bending (Rx, Ry) Stiffness for each bottom joints [(N.m)/rad]
%        - Kt_F [6x1] - Torsion (Rz) Stiffness for each bottom joints [(N.m)/rad]
%        - Cf_F [6x1] - Bending (Rx, Ry) Damping of each bottom joint [(N.m)/(rad/s)]
%        - Cf_F [6x1] - Torsion (Rz) Damping of each bottom joint [(N.m)/(rad/s)]
%        - Kz_F [6x1] - Translation (Tz) Stiffness for each bottom joints [N/m]
%        - Cz_F [6x1] - Translation (Tz) Damping of each bottom joint [N/m]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%      - stewart.joints_F and stewart.joints_M:
%        - type - 1 (universal), 2 (spherical), 3 (universal perfect), 4 (spherical perfect)
%        - Kx, Ky, Kz [6x1] - Translation (Tx, Ty, Tz) Stiffness [N/m]
%        - Kf [6x1] - Flexion (Rx, Ry) Stiffness [(N.m)/rad]
%        - Kt [6x1] - Torsion (Rz) Stiffness [(N.m)/rad]
%        - Cx, Cy, Cz [6x1] - Translation (Rx, Ry) Damping [N/(m/s)]
%        - Cf [6x1] - Flexion (Rx, Ry) Damping [(N.m)/(rad/s)]
%        - Cb [6x1] - Torsion (Rz) Damping [(N.m)/(rad/s)]

Optional Parameters

arguments
    stewart
    args.type_F     char   {mustBeMember(args.type_F,{'universal', 'spherical', 'universal_p', 'spherical_p', 'universal_3dof'})} = 'universal'
    args.type_M     char   {mustBeMember(args.type_M,{'universal', 'spherical', 'universal_p', 'spherical_p', 'spherical_3dof'})} = 'spherical'
    args.Kf_M (6,1) double {mustBeNumeric, mustBeNonnegative} = 15*ones(6,1)
    args.Cf_M (6,1) double {mustBeNumeric, mustBeNonnegative} = 1e-4*ones(6,1)
    args.Kt_M (6,1) double {mustBeNumeric, mustBeNonnegative} = 20*ones(6,1)
    args.Ct_M (6,1) double {mustBeNumeric, mustBeNonnegative} = 1e-3*ones(6,1)
    args.Kz_M (6,1) double {mustBeNumeric, mustBeNonnegative} = 60e6*ones(6,1)
    args.Cz_M (6,1) double {mustBeNumeric, mustBeNonnegative} = 1e2*ones(6,1)
    args.Kf_F (6,1) double {mustBeNumeric, mustBeNonnegative} = 15*ones(6,1)
    args.Cf_F (6,1) double {mustBeNumeric, mustBeNonnegative} = 1e-4*ones(6,1)
    args.Kt_F (6,1) double {mustBeNumeric, mustBeNonnegative} = 20*ones(6,1)
    args.Ct_F (6,1) double {mustBeNumeric, mustBeNonnegative} = 1e-3*ones(6,1)
    args.Kz_F (6,1) double {mustBeNumeric, mustBeNonnegative} = 60e6*ones(6,1)
    args.Cz_F (6,1) double {mustBeNumeric, mustBeNonnegative} = 1e2*ones(6,1)
end

Add Actuator Type

switch args.type_F
  case 'universal'
    stewart.joints_F.type = 1;
  case 'spherical'
    stewart.joints_F.type = 2;
  case 'universal_p'
    stewart.joints_F.type = 1;
  case 'spherical_p'
    stewart.joints_F.type = 2;
  case 'universal_3dof'
    stewart.joints_F.type = 5;
end

switch args.type_M
  case 'universal'
    stewart.joints_M.type = 1;
  case 'spherical'
    stewart.joints_M.type = 2;
  case 'universal_p'
    stewart.joints_M.type = 1;
  case 'spherical_p'
    stewart.joints_M.type = 2;
  case 'spherical_3dof'
    stewart.joints_M.type = 6;
end

10.1 Initialize Stiffness

stewart.joints_M.Kx = zeros(6,1);
stewart.joints_M.Ky = zeros(6,1);
stewart.joints_M.Kz = zeros(6,1);
stewart.joints_F.Kx = zeros(6,1);
stewart.joints_F.Ky = zeros(6,1);
stewart.joints_F.Kz = zeros(6,1);

stewart.joints_M.Kf = zeros(6,1);
stewart.joints_M.Kt = zeros(6,1);
stewart.joints_F.Kf = zeros(6,1);
stewart.joints_F.Kt = zeros(6,1);

stewart.joints_M.Cx = zeros(6,1);
stewart.joints_M.Cy = zeros(6,1);
stewart.joints_M.Cz = zeros(6,1);
stewart.joints_F.Cx = zeros(6,1);
stewart.joints_F.Cy = zeros(6,1);
stewart.joints_F.Cz = zeros(6,1);

stewart.joints_M.Cf = zeros(6,1);
stewart.joints_M.Ct = zeros(6,1);
stewart.joints_F.Cf = zeros(6,1);
stewart.joints_F.Ct = zeros(6,1);

Add Stiffness and Damping in Translation of each strut

Translation Stiffness 

if ~strcmp(args.type_M, 'universal_p') || ~strcmp(args.type_M, 'spherical_p')
    stewart.joints_M.Kz = args.Kz_M;
    stewart.joints_M.Cz = args.Cz_M;
end

if ~strcmp(args.type_F, 'universal_p') || ~strcmp(args.type_F, 'spherical_p')
    stewart.joints_F.Kz = args.Kz_F;
    stewart.joints_F.Cz = args.Cz_F;
end

Add Stiffness and Damping in Rotation of each strut

Rotational Stiffness 

if ~strcmp(args.type_M, 'universal_p') || ~strcmp(args.type_M, 'spherical_p')
    stewart.joints_M.Kf = args.Kf_M;
    stewart.joints_M.Cf = args.Cf_M;

    stewart.joints_M.Kt = args.Kt_M;
    stewart.joints_M.Ct = args.Ct_M;
end

if ~strcmp(args.type_F, 'universal_p') || ~strcmp(args.type_F, 'spherical_p')
    stewart.joints_F.Kf = args.Kf_F;
    stewart.joints_F.Cf = args.Cf_F;

    stewart.joints_F.Kt = args.Kt_F;
    stewart.joints_F.Ct = args.Ct_F;
end

11 initializeInertialSensor: Initialize the inertial sensor in each strut

This Matlab function is accessible here.

Geophone - Working Principle

From the schematic of the Z-axis geophone shown in Figure 9, we can write the transfer function from the support velocity \(\dot{w}\) to the relative velocity of the inertial mass \(\dot{d}\): \[ \frac{\dot{d}}{\dot{w}} = \frac{-\frac{s^2}{{\omega_0}^2}}{\frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1} \] with:

  • \(\omega_0 = \sqrt{\frac{k}{m}}\)
  • \(\xi = \frac{1}{2} \sqrt{\frac{m}{k}}\)

inertial_sensor.png

Figure 9: Schematic of a Z-Axis geophone

We see that at frequencies above \(\omega_0\): \[ \frac{\dot{d}}{\dot{w}} \approx -1 \]

And thus, the measurement of the relative velocity of the mass with respect to its support gives the absolute velocity of the support.

We generally want to have the smallest resonant frequency \(\omega_0\) to measure low frequency absolute velocity, however there is a trade-off between \(\omega_0\) and the mass of the inertial mass.

Accelerometer - Working Principle

From the schematic of the Z-axis accelerometer shown in Figure 10, we can write the transfer function from the support acceleration \(\ddot{w}\) to the relative position of the inertial mass \(d\): \[ \frac{d}{\ddot{w}} = \frac{-\frac{1}{{\omega_0}^2}}{\frac{s^2}{{\omega_0}^2} + 2 \xi \frac{s}{\omega_0} + 1} \] with:

  • \(\omega_0 = \sqrt{\frac{k}{m}}\)
  • \(\xi = \frac{1}{2} \sqrt{\frac{m}{k}}\)

inertial_sensor.png

Figure 10: Schematic of a Z-Axis geophone

We see that at frequencies below \(\omega_0\): \[ \frac{d}{\ddot{w}} \approx -\frac{1}{{\omega_0}^2} \]

And thus, the measurement of the relative displacement of the mass with respect to its support gives the absolute acceleration of the support.

Note that there is trade-off between:

  • the highest measurable acceleration \(\omega_0\)
  • the sensitivity of the accelerometer which is equal to \(-\frac{1}{{\omega_0}^2}\)

Function description

function [stewart] = initializeInertialSensor(stewart, args)
% initializeInertialSensor - Initialize the inertial sensor in each strut
%
% Syntax: [stewart] = initializeInertialSensor(args)
%
% Inputs:
%    - args - Structure with the following fields:
%        - type       - 'geophone', 'accelerometer', 'none'
%        - mass [1x1] - Weight of the inertial mass [kg]
%        - freq [1x1] - Cutoff frequency [Hz]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%      - stewart.sensors.inertial
%        - type    - 1 (geophone), 2 (accelerometer), 3 (none)
%        - K [1x1] - Stiffness [N/m]
%        - C [1x1] - Damping [N/(m/s)]
%        - M [1x1] - Inertial Mass [kg]
%        - G [1x1] - Gain

Optional Parameters

arguments
    stewart
    args.type       char   {mustBeMember(args.type,{'geophone', 'accelerometer', 'none'})} = 'none'
    args.mass (1,1) double {mustBeNumeric, mustBeNonnegative} = 1e-2
    args.freq (1,1) double {mustBeNumeric, mustBeNonnegative} = 1e3
end

Compute the properties of the sensor

sensor = struct();

switch args.type
  case 'geophone'
    sensor.type = 1;

    sensor.M = args.mass;
    sensor.K = sensor.M * (2*pi*args.freq)^2;
    sensor.C = 2*sqrt(sensor.M * sensor.K);
  case 'accelerometer'
    sensor.type = 2;

    sensor.M = args.mass;
    sensor.K = sensor.M * (2*pi*args.freq)^2;
    sensor.C = 2*sqrt(sensor.M * sensor.K);
    sensor.G = -sensor.K/sensor.M;
  case 'none'
    sensor.type = 3;
end

Populate the stewart structure

stewart.sensors.inertial = sensor;

12 displayArchitecture: 3D plot of the Stewart platform architecture

This Matlab function is accessible here.

Function description

function [] = displayArchitecture(stewart, args)
% displayArchitecture - 3D plot of the Stewart platform architecture
%
% Syntax: [] = displayArchitecture(args)
%
% Inputs:
%    - stewart
%    - args - Structure with the following fields:
%        - AP   [3x1] - The wanted position of {B} with respect to {A}
%        - ARB  [3x3] - The rotation matrix that gives the wanted orientation of {B} with respect to {A}
%        - ARB  [3x3] - The rotation matrix that gives the wanted orientation of {B} with respect to {A}
%        - F_color [color] - Color used for the Fixed elements
%        - M_color [color] - Color used for the Mobile elements
%        - L_color [color] - Color used for the Legs elements
%        - frames    [true/false] - Display the Frames
%        - legs      [true/false] - Display the Legs
%        - joints    [true/false] - Display the Joints
%        - labels    [true/false] - Display the Labels
%        - platforms [true/false] - Display the Platforms
%        - views     ['all', 'xy', 'yz', 'xz', 'default'] -
%
% Outputs:

Optional Parameters

arguments
    stewart
    args.AP  (3,1) double {mustBeNumeric} = zeros(3,1)
    args.ARB (3,3) double {mustBeNumeric} = eye(3)
    args.F_color = [0 0.4470 0.7410]
    args.M_color = [0.8500 0.3250 0.0980]
    args.L_color = [0 0 0]
    args.frames    logical {mustBeNumericOrLogical} = true
    args.legs      logical {mustBeNumericOrLogical} = true
    args.joints    logical {mustBeNumericOrLogical} = true
    args.labels    logical {mustBeNumericOrLogical} = true
    args.platforms logical {mustBeNumericOrLogical} = true
    args.views     char    {mustBeMember(args.views,{'all', 'xy', 'xz', 'yz', 'default'})} = 'default'
end

Check the stewart structure elements

assert(isfield(stewart.platform_F, 'FO_A'), 'stewart.platform_F should have attribute FO_A')
FO_A = stewart.platform_F.FO_A;

assert(isfield(stewart.platform_M, 'MO_B'), 'stewart.platform_M should have attribute MO_B')
MO_B = stewart.platform_M.MO_B;

assert(isfield(stewart.geometry, 'H'),   'stewart.geometry should have attribute H')
H = stewart.geometry.H;

assert(isfield(stewart.platform_F, 'Fa'),   'stewart.platform_F should have attribute Fa')
Fa = stewart.platform_F.Fa;

assert(isfield(stewart.platform_M, 'Mb'),   'stewart.platform_M should have attribute Mb')
Mb = stewart.platform_M.Mb;

Figure Creation, Frames and Homogeneous transformations

The reference frame of the 3d plot corresponds to the frame \(\{F\}\). 

if ~strcmp(args.views, 'all')
  figure;
else
  f = figure('visible', 'off');
end

hold on;

We first compute homogeneous matrices that will be useful to position elements on the figure where the reference frame is \(\{F\}\). 

FTa = [eye(3), FO_A; ...
       zeros(1,3), 1];
ATb = [args.ARB, args.AP; ...
       zeros(1,3), 1];
BTm = [eye(3), -MO_B; ...
       zeros(1,3), 1];

FTm = FTa*ATb*BTm;

Let’s define a parameter that define the length of the unit vectors used to display the frames. 

d_unit_vector = H/4;

Let’s define a parameter used to position the labels with respect to the center of the element. 

d_label = H/20;

Fixed Base elements

Let’s first plot the frame \(\{F\}\). 

Ff = [0, 0, 0];
if args.frames
  quiver3(Ff(1)*ones(1,3), Ff(2)*ones(1,3), Ff(3)*ones(1,3), ...
          [d_unit_vector 0 0], [0 d_unit_vector 0], [0 0 d_unit_vector], '-', 'Color', args.F_color)

  if args.labels
    text(Ff(1) + d_label, ...
        Ff(2) + d_label, ...
        Ff(3) + d_label, '$\{F\}$', 'Color', args.F_color);
  end
end

Now plot the frame \(\{A\}\) fixed to the Base. 

if args.frames
  quiver3(FO_A(1)*ones(1,3), FO_A(2)*ones(1,3), FO_A(3)*ones(1,3), ...
          [d_unit_vector 0 0], [0 d_unit_vector 0], [0 0 d_unit_vector], '-', 'Color', args.F_color)

  if args.labels
    text(FO_A(1) + d_label, ...
         FO_A(2) + d_label, ...
         FO_A(3) + d_label, '$\{A\}$', 'Color', args.F_color);
  end
end

Let’s then plot the circle corresponding to the shape of the Fixed base. 

if args.platforms && stewart.platform_F.type == 1
  theta = [0:0.01:2*pi+0.01]; % Angles [rad]
  v = null([0; 0; 1]'); % Two vectors that are perpendicular to the circle normal
  center = [0; 0; 0]; % Center of the circle
  radius = stewart.platform_F.R; % Radius of the circle [m]

  points = center*ones(1, length(theta)) + radius*(v(:,1)*cos(theta) + v(:,2)*sin(theta));

  plot3(points(1,:), ...
        points(2,:), ...
        points(3,:), '-', 'Color', args.F_color);
end

Let’s now plot the position and labels of the Fixed Joints 

if args.joints
  scatter3(Fa(1,:), ...
           Fa(2,:), ...
           Fa(3,:), 'MarkerEdgeColor', args.F_color);
  if args.labels
    for i = 1:size(Fa,2)
      text(Fa(1,i) + d_label, ...
           Fa(2,i), ...
           Fa(3,i), sprintf('$a_{%i}$', i), 'Color', args.F_color);
    end
  end
end

Mobile Platform elements

Plot the frame \(\{M\}\). 

Fm = FTm*[0; 0; 0; 1]; % Get the position of frame {M} w.r.t. {F}

if args.frames
  FM_uv = FTm*[d_unit_vector*eye(3); zeros(1,3)]; % Rotated Unit vectors
  quiver3(Fm(1)*ones(1,3), Fm(2)*ones(1,3), Fm(3)*ones(1,3), ...
          FM_uv(1,1:3), FM_uv(2,1:3), FM_uv(3,1:3), '-', 'Color', args.M_color)

  if args.labels
    text(Fm(1) + d_label, ...
         Fm(2) + d_label, ...
         Fm(3) + d_label, '$\{M\}$', 'Color', args.M_color);
  end
end

Plot the frame \(\{B\}\). 

FB = FO_A + args.AP;

if args.frames
  FB_uv = FTm*[d_unit_vector*eye(3); zeros(1,3)]; % Rotated Unit vectors
  quiver3(FB(1)*ones(1,3), FB(2)*ones(1,3), FB(3)*ones(1,3), ...
          FB_uv(1,1:3), FB_uv(2,1:3), FB_uv(3,1:3), '-', 'Color', args.M_color)

  if args.labels
    text(FB(1) - d_label, ...
         FB(2) + d_label, ...
         FB(3) + d_label, '$\{B\}$', 'Color', args.M_color);
  end
end

Let’s then plot the circle corresponding to the shape of the Mobile platform. 

if args.platforms && stewart.platform_M.type == 1
  theta = [0:0.01:2*pi+0.01]; % Angles [rad]
  v = null((FTm(1:3,1:3)*[0;0;1])'); % Two vectors that are perpendicular to the circle normal
  center = Fm(1:3); % Center of the circle
  radius = stewart.platform_M.R; % Radius of the circle [m]

  points = center*ones(1, length(theta)) + radius*(v(:,1)*cos(theta) + v(:,2)*sin(theta));

  plot3(points(1,:), ...
        points(2,:), ...
        points(3,:), '-', 'Color', args.M_color);
end

Plot the position and labels of the rotation joints fixed to the mobile platform. 

if args.joints
  Fb = FTm*[Mb;ones(1,6)];

  scatter3(Fb(1,:), ...
           Fb(2,:), ...
           Fb(3,:), 'MarkerEdgeColor', args.M_color);

  if args.labels
    for i = 1:size(Fb,2)
      text(Fb(1,i) + d_label, ...
           Fb(2,i), ...
           Fb(3,i), sprintf('$b_{%i}$', i), 'Color', args.M_color);
    end
  end
end

Legs

Plot the legs connecting the joints of the fixed base to the joints of the mobile platform. 

if args.legs
  for i = 1:6
    plot3([Fa(1,i), Fb(1,i)], ...
          [Fa(2,i), Fb(2,i)], ...
          [Fa(3,i), Fb(3,i)], '-', 'Color', args.L_color);

    if args.labels
      text((Fa(1,i)+Fb(1,i))/2 + d_label, ...
           (Fa(2,i)+Fb(2,i))/2, ...
           (Fa(3,i)+Fb(3,i))/2, sprintf('$%i$', i), 'Color', args.L_color);
    end
  end
end

12.1 Figure parameters

switch args.views
  case 'default'
      view([1 -0.6 0.4]);
  case 'xy'
      view([0 0 1]);
  case 'xz'
      view([0 -1 0]);
  case 'yz'
      view([1 0 0]);
end
axis equal;
axis off;

12.2 Subplots

if strcmp(args.views, 'all')
  hAx = findobj('type', 'axes');

  figure;
  s1 = subplot(2,2,1);
  copyobj(get(hAx(1), 'Children'), s1);
  view([0 0 1]);
  axis equal;
  axis off;
  title('Top')

  s2 = subplot(2,2,2);
  copyobj(get(hAx(1), 'Children'), s2);
  view([1 -0.6 0.4]);
  axis equal;
  axis off;

  s3 = subplot(2,2,3);
  copyobj(get(hAx(1), 'Children'), s3);
  view([1 0 0]);
  axis equal;
  axis off;
  title('Front')

  s4 = subplot(2,2,4);
  copyobj(get(hAx(1), 'Children'), s4);
  view([0 -1 0]);
  axis equal;
  axis off;
  title('Side')

  close(f);
end

13 describeStewartPlatform: Display some text describing the current defined Stewart Platform

This Matlab function is accessible here.

Function description

function [] = describeStewartPlatform(stewart)
% describeStewartPlatform - Display some text describing the current defined Stewart Platform
%
% Syntax: [] = describeStewartPlatform(args)
%
% Inputs:
%    - stewart
%
% Outputs:

Optional Parameters

arguments
    stewart
end

13.1 Geometry

fprintf('GEOMETRY:\n')
fprintf('- The height between the fixed based and the top platform is %.3g [mm].\n', 1e3*stewart.geometry.H)

if stewart.platform_M.MO_B(3) > 0
  fprintf('- Frame {A} is located %.3g [mm] above the top platform.\n',  1e3*stewart.platform_M.MO_B(3))
else
  fprintf('- Frame {A} is located %.3g [mm] below the top platform.\n', - 1e3*stewart.platform_M.MO_B(3))
end

fprintf('- The initial length of the struts are:\n')
fprintf('\t %.3g, %.3g, %.3g, %.3g, %.3g, %.3g [mm]\n', 1e3*stewart.geometry.l)
fprintf('\n')

13.2 Actuators

fprintf('ACTUATORS:\n')
if stewart.actuators.type == 1
    fprintf('- The actuators are classical.\n')
    fprintf('- The Stiffness and Damping of each actuators is:\n')
    fprintf('\t k = %.0e [N/m] \t c = %.0e [N/(m/s)]\n', stewart.actuators.K(1), stewart.actuators.C(1))
elseif stewart.actuators.type == 2
    fprintf('- The actuators are mechanicaly amplified.\n')
    fprintf('- The vertical stiffness and damping contribution of the piezoelectric stack is:\n')
    fprintf('\t ka = %.0e [N/m] \t ca = %.0e [N/(m/s)]\n', stewart.actuators.Ka(1), stewart.actuators.Ca(1))
    fprintf('- Vertical stiffness when the piezoelectric stack is removed is:\n')
    fprintf('\t kr = %.0e [N/m] \t cr = %.0e [N/(m/s)]\n', stewart.actuators.Kr(1), stewart.actuators.Cr(1))
end
fprintf('\n')

13.3 Joints

fprintf('JOINTS:\n')

Type of the joints on the fixed base. 

switch stewart.joints_F.type
  case 1
    fprintf('- The joints on the fixed based are universal joints\n')
  case 2
    fprintf('- The joints on the fixed based are spherical joints\n')
  case 3
    fprintf('- The joints on the fixed based are perfect universal joints\n')
  case 4
    fprintf('- The joints on the fixed based are perfect spherical joints\n')
end

Type of the joints on the mobile platform. 

switch stewart.joints_M.type
  case 1
    fprintf('- The joints on the mobile based are universal joints\n')
  case 2
    fprintf('- The joints on the mobile based are spherical joints\n')
  case 3
    fprintf('- The joints on the mobile based are perfect universal joints\n')
  case 4
    fprintf('- The joints on the mobile based are perfect spherical joints\n')
end

Position of the fixed joints 

fprintf('- The position of the joints on the fixed based with respect to {F} are (in [mm]):\n')
fprintf('\t % .3g \t % .3g \t % .3g\n', 1e3*stewart.platform_F.Fa)

Position of the mobile joints 

fprintf('- The position of the joints on the mobile based with respect to {M} are (in [mm]):\n')
fprintf('\t % .3g \t % .3g \t % .3g\n', 1e3*stewart.platform_M.Mb)
fprintf('\n')

13.4 Kinematics

fprintf('KINEMATICS:\n')

if isfield(stewart.kinematics, 'K')
  fprintf('- The Stiffness matrix K is (in [N/m]):\n')
  fprintf('\t % .0e \t % .0e \t % .0e \t % .0e \t % .0e \t % .0e\n', stewart.kinematics.K)
end

if isfield(stewart.kinematics, 'C')
  fprintf('- The Damping matrix C is (in [m/N]):\n')
  fprintf('\t % .0e \t % .0e \t % .0e \t % .0e \t % .0e \t % .0e\n', stewart.kinematics.C)
end

14 generateCubicConfiguration: Generate a Cubic Configuration

This Matlab function is accessible here.

Function description

function [stewart] = generateCubicConfiguration(stewart, args)
% generateCubicConfiguration - Generate a Cubic Configuration
%
% Syntax: [stewart] = generateCubicConfiguration(stewart, args)
%
% Inputs:
%    - stewart - A structure with the following fields
%        - geometry.H [1x1] - Total height of the platform [m]
%    - args - Can have the following fields:
%        - Hc  [1x1] - Height of the "useful" part of the cube [m]
%        - FOc [1x1] - Height of the center of the cube with respect to {F} [m]
%        - FHa [1x1] - Height of the plane joining the points ai with respect to the frame {F} [m]
%        - MHb [1x1] - Height of the plane joining the points bi with respect to the frame {M} [m]
%
% Outputs:
%    - stewart - updated Stewart structure with the added fields:
%        - platform_F.Fa  [3x6] - Its i'th column is the position vector of joint ai with respect to {F}
%        - platform_M.Mb  [3x6] - Its i'th column is the position vector of joint bi with respect to {M}

Documentation

cubic-configuration-definition.png

Figure 11: Cubic Configuration

Optional Parameters

arguments
    stewart
    args.Hc  (1,1) double {mustBeNumeric, mustBePositive} = 60e-3
    args.FOc (1,1) double {mustBeNumeric} = 50e-3
    args.FHa (1,1) double {mustBeNumeric, mustBeNonnegative} = 15e-3
    args.MHb (1,1) double {mustBeNumeric, mustBeNonnegative} = 15e-3
end

Check the stewart structure elements

assert(isfield(stewart.geometry, 'H'),   'stewart.geometry should have attribute H')
H = stewart.geometry.H;

Position of the Cube

We define the useful points of the cube with respect to the Cube’s center. \({}^{C}C\) are the 6 vertices of the cubes expressed in a frame {C} which is located at the center of the cube and aligned with {F} and {M}. 

sx = [ 2; -1; -1];
sy = [ 0;  1; -1];
sz = [ 1;  1;  1];

R = [sx, sy, sz]./vecnorm([sx, sy, sz]);

L = args.Hc*sqrt(3);

Cc = R'*[[0;0;L],[L;0;L],[L;0;0],[L;L;0],[0;L;0],[0;L;L]] - [0;0;1.5*args.Hc];

CCf = [Cc(:,1), Cc(:,3), Cc(:,3), Cc(:,5), Cc(:,5), Cc(:,1)]; % CCf(:,i) corresponds to the bottom cube's vertice corresponding to the i'th leg
CCm = [Cc(:,2), Cc(:,2), Cc(:,4), Cc(:,4), Cc(:,6), Cc(:,6)]; % CCm(:,i) corresponds to the top cube's vertice corresponding to the i'th leg

Compute the pose

We can compute the vector of each leg \({}^{C}\hat{\bm{s}}_{i}\) (unit vector from \({}^{C}C_{f}\) to \({}^{C}C_{m}\)). 

CSi = (CCm - CCf)./vecnorm(CCm - CCf);

We now which to compute the position of the joints \(a_{i}\) and \(b_{i}\). 

Fa = CCf + [0; 0; args.FOc] + ((args.FHa-(args.FOc-args.Hc/2))./CSi(3,:)).*CSi;
Mb = CCf + [0; 0; args.FOc-H] + ((H-args.MHb-(args.FOc-args.Hc/2))./CSi(3,:)).*CSi;

Populate the stewart structure

stewart.platform_F.Fa = Fa;
stewart.platform_M.Mb = Mb;

15 computeJacobian: Compute the Jacobian Matrix

This Matlab function is accessible here.

Function description

function [stewart] = computeJacobian(stewart)
% computeJacobian -
%
% Syntax: [stewart] = computeJacobian(stewart)
%
% Inputs:
%    - stewart - With at least the following fields:
%      - geometry.As [3x6] - The 6 unit vectors for each strut expressed in {A}
%      - geometry.Ab [3x6] - The 6 position of the joints bi expressed in {A}
%      - actuators.K [6x1] - Total stiffness of the actuators
%
% Outputs:
%    - stewart - With the 3 added field:
%        - kinematics.J [6x6] - The Jacobian Matrix
%        - kinematics.K [6x6] - The Stiffness Matrix
%        - kinematics.C [6x6] - The Compliance Matrix

Check the stewart structure elements

assert(isfield(stewart.geometry, 'As'),   'stewart.geometry should have attribute As')
As = stewart.geometry.As;

assert(isfield(stewart.geometry, 'Ab'),   'stewart.geometry should have attribute Ab')
Ab = stewart.geometry.Ab;

assert(isfield(stewart.actuators, 'K'),   'stewart.actuators should have attribute K')
Ki = stewart.actuators.K;

Compute Jacobian Matrix

J = [As' , cross(Ab, As)'];

Compute Stiffness Matrix

K = J'*diag(Ki)*J;

Compute Compliance Matrix

C = inv(K);

Populate the stewart structure

stewart.kinematics.J = J;
stewart.kinematics.K = K;
stewart.kinematics.C = C;

16 inverseKinematics: Compute Inverse Kinematics

This Matlab function is accessible here.

Theory

For inverse kinematic analysis, it is assumed that the position \({}^A\bm{P}\) and orientation of the moving platform \({}^A\bm{R}_B\) are given and the problem is to obtain the joint variables, namely, \(\bm{L} = [l_1, l_2, \dots, l_6]^T\).

From the geometry of the manipulator, the loop closure for each limb, \(i = 1, 2, \dots, 6\) can be written as

\begin{align*} l_i {}^A\hat{\bm{s}}_i &= {}^A\bm{A} + {}^A\bm{b}_i - {}^A\bm{a}_i \\ &= {}^A\bm{A} + {}^A\bm{R}_b {}^B\bm{b}_i - {}^A\bm{a}_i \end{align*}

To obtain the length of each actuator and eliminate \(\hat{\bm{s}}_i\), it is sufficient to dot multiply each side by itself:

\begin{equation} l_i^2 \left[ {}^A\hat{\bm{s}}_i^T {}^A\hat{\bm{s}}_i \right] = \left[ {}^A\bm{P} + {}^A\bm{R}_B {}^B\bm{b}_i - {}^A\bm{a}_i \right]^T \left[ {}^A\bm{P} + {}^A\bm{R}_B {}^B\bm{b}_i - {}^A\bm{a}_i \right] \end{equation}

Hence, for \(i = 1, 2, \dots, 6\), each limb length can be uniquely determined by:

\begin{equation} l_i = \sqrt{{}^A\bm{P}^T {}^A\bm{P} + {}^B\bm{b}_i^T {}^B\bm{b}_i + {}^A\bm{a}_i^T {}^A\bm{a}_i - 2 {}^A\bm{P}^T {}^A\bm{a}_i + 2 {}^A\bm{P}^T \left[{}^A\bm{R}_B {}^B\bm{b}_i\right] - 2 \left[{}^A\bm{R}_B {}^B\bm{b}_i\right]^T {}^A\bm{a}_i} \end{equation}

If the position and orientation of the moving platform lie in the feasible workspace of the manipulator, one unique solution to the limb length is determined by the above equation. Otherwise, when the limbs’ lengths derived yield complex numbers, then the position or orientation of the moving platform is not reachable.

Function description

function [Li, dLi] = inverseKinematics(stewart, args)
% inverseKinematics - Compute the needed length of each strut to have the wanted position and orientation of {B} with respect to {A}
%
% Syntax: [stewart] = inverseKinematics(stewart)
%
% Inputs:
%    - stewart - A structure with the following fields
%        - geometry.Aa   [3x6] - The positions ai expressed in {A}
%        - geometry.Bb   [3x6] - The positions bi expressed in {B}
%        - geometry.l    [6x1] - Length of each strut
%    - args - Can have the following fields:
%        - AP   [3x1] - The wanted position of {B} with respect to {A}
%        - ARB  [3x3] - The rotation matrix that gives the wanted orientation of {B} with respect to {A}
%
% Outputs:
%    - Li   [6x1] - The 6 needed length of the struts in [m] to have the wanted pose of {B} w.r.t. {A}
%    - dLi  [6x1] - The 6 needed displacement of the struts from the initial position in [m] to have the wanted pose of {B} w.r.t. {A}

Optional Parameters

arguments
    stewart
    args.AP  (3,1) double {mustBeNumeric} = zeros(3,1)
    args.ARB (3,3) double {mustBeNumeric} = eye(3)
end

Check the stewart structure elements

assert(isfield(stewart.geometry, 'Aa'),   'stewart.geometry should have attribute Aa')
Aa = stewart.geometry.Aa;

assert(isfield(stewart.geometry, 'Bb'),   'stewart.geometry should have attribute Bb')
Bb = stewart.geometry.Bb;

assert(isfield(stewart.geometry, 'l'),   'stewart.geometry should have attribute l')
l = stewart.geometry.l;

Compute

Li = sqrt(args.AP'*args.AP + diag(Bb'*Bb) + diag(Aa'*Aa) - (2*args.AP'*Aa)' + (2*args.AP'*(args.ARB*Bb))' - diag(2*(args.ARB*Bb)'*Aa));

dLi = Li-l;

17 forwardKinematicsApprox: Compute the Approximate Forward Kinematics

This Matlab function is accessible here.

Function description

function [P, R] = forwardKinematicsApprox(stewart, args)
% forwardKinematicsApprox - Computed the approximate pose of {B} with respect to {A} from the length of each strut and using
%                           the Jacobian Matrix
%
% Syntax: [P, R] = forwardKinematicsApprox(stewart, args)
%
% Inputs:
%    - stewart - A structure with the following fields
%        - kinematics.J  [6x6] - The Jacobian Matrix
%    - args - Can have the following fields:
%        - dL [6x1] - Displacement of each strut [m]
%
% Outputs:
%    - P  [3x1] - The estimated position of {B} with respect to {A}
%    - R  [3x3] - The estimated rotation matrix that gives the orientation of {B} with respect to {A}

Optional Parameters

arguments
    stewart
    args.dL (6,1) double {mustBeNumeric} = zeros(6,1)
end

Check the stewart structure elements

assert(isfield(stewart.kinematics, 'J'),   'stewart.kinematics should have attribute J')
J = stewart.kinematics.J;

Computation

From a small displacement of each strut \(d\bm{\mathcal{L}}\), we can compute the position and orientation of {B} with respect to {A} using the following formula: \[ d \bm{\mathcal{X}} = \bm{J}^{-1} d\bm{\mathcal{L}} \] 

X = J\args.dL;

The position vector corresponds to the first 3 elements. 

P = X(1:3);

The next 3 elements are the orientation of {B} with respect to {A} expressed using the screw axis. 

theta = norm(X(4:6));
s = X(4:6)/theta;

We then compute the corresponding rotation matrix. 

R = [s(1)^2*(1-cos(theta)) + cos(theta) ,        s(1)*s(2)*(1-cos(theta)) - s(3)*sin(theta), s(1)*s(3)*(1-cos(theta)) + s(2)*sin(theta);
     s(2)*s(1)*(1-cos(theta)) + s(3)*sin(theta), s(2)^2*(1-cos(theta)) + cos(theta),         s(2)*s(3)*(1-cos(theta)) - s(1)*sin(theta);
     s(3)*s(1)*(1-cos(theta)) - s(2)*sin(theta), s(3)*s(2)*(1-cos(theta)) + s(1)*sin(theta), s(3)^2*(1-cos(theta)) + cos(theta)];

Author: Dehaeze Thomas

Created: 2020-09-01 mar. 13:48