Amplified Piezoelectric Stack Actuator
Table of Contents
The presented model is based on souleille18_concep_activ_mount_space_applic.
The model represents the amplified piezo APA100M from Cedrat-Technologies (Figure 1). The parameters are shown in the table below.
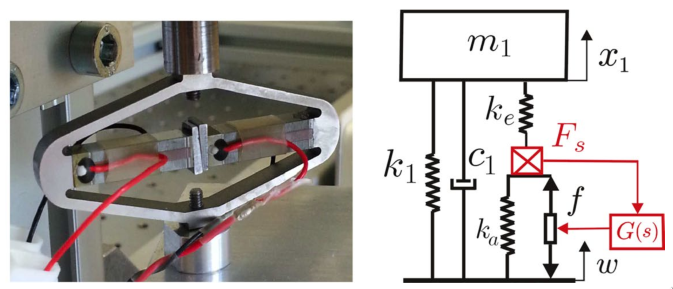
Figure 1: Picture of an APA100M from Cedrat Technologies. Simplified model of a one DoF payload mounted on such isolator
| Value | Meaning | |
|---|---|---|
| \(m\) | \(1\,[kg]\) | Payload mass |
| \(k_e\) | \(4.8\,[N/\mu m]\) | Stiffness used to adjust the pole of the isolator |
| \(k_1\) | \(0.96\,[N/\mu m]\) | Stiffness of the metallic suspension when the stack is removed |
| \(k_a\) | \(65\,[N/\mu m]\) | Stiffness of the actuator |
| \(c_1\) | \(10\,[N/(m/s)]\) | Added viscous damping |
1 Simplified Model
1.1 Parameters
m = 1; % [kg] ke = 4.8e6; % [N/m] ce = 5; % [N/(m/s)] me = 0.001; % [kg] k1 = 0.96e6; % [N/m] c1 = 10; % [N/(m/s)] ka = 65e6; % [N/m] ca = 5; % [N/(m/s)] ma = 0.001; % [kg] h = 0.2; % [m]
IFF Controller:
Kiff = -8000/s;
1.2 Identification
Identification in open-loop.
%% Name of the Simulink File
mdl = 'amplified_piezo_model';
%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/w'], 1, 'openinput'); io_i = io_i + 1; % Base Motion
io(io_i) = linio([mdl, '/f'], 1, 'openinput'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/F'], 1, 'openinput'); io_i = io_i + 1; % External Force
io(io_i) = linio([mdl, '/Fs'], 3, 'openoutput'); io_i = io_i + 1; % Force Sensors
io(io_i) = linio([mdl, '/x1'], 1, 'openoutput'); io_i = io_i + 1; % Mass displacement
G = linearize(mdl, io, 0);
G.InputName = {'w', 'f', 'F'};
G.OutputName = {'Fs', 'x1'};
Identification in closed-loop.
%% Name of the Simulink File
mdl = 'amplified_piezo_model';
%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/w'], 1, 'input'); io_i = io_i + 1; % Base Motion
io(io_i) = linio([mdl, '/f'], 1, 'input'); io_i = io_i + 1; % Actuator Inputs
io(io_i) = linio([mdl, '/F'], 1, 'input'); io_i = io_i + 1; % External Force
io(io_i) = linio([mdl, '/Fs'], 3, 'output'); io_i = io_i + 1; % Force Sensors
io(io_i) = linio([mdl, '/x1'], 1, 'output'); io_i = io_i + 1; % Mass displacement
Giff = linearize(mdl, io, 0);
Giff.InputName = {'w', 'f', 'F'};
Giff.OutputName = {'Fs', 'x1'};
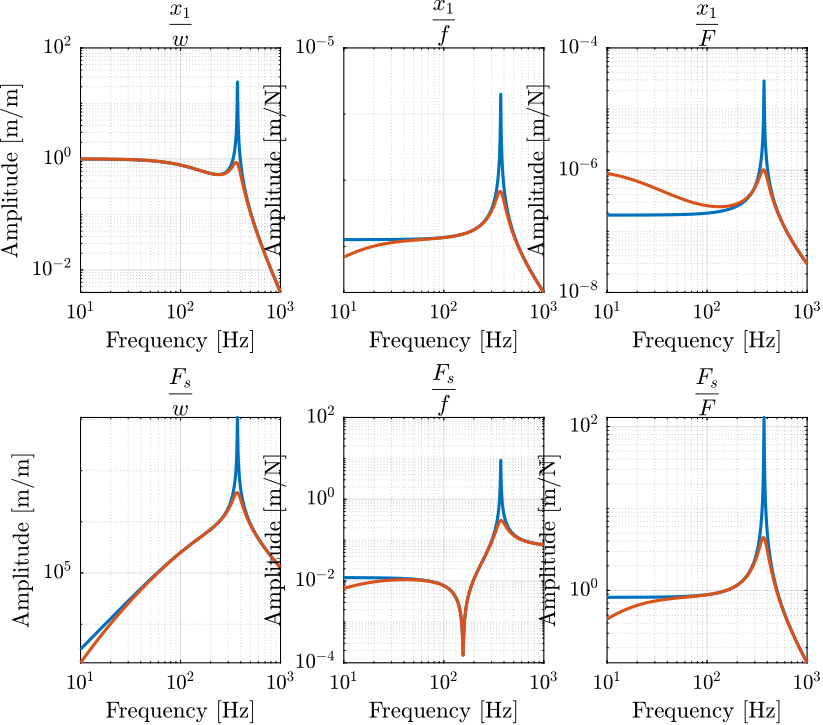
Figure 2: Matrix of transfer functions from input to output in open loop (blue) and closed loop (red)
1.3 Root Locus
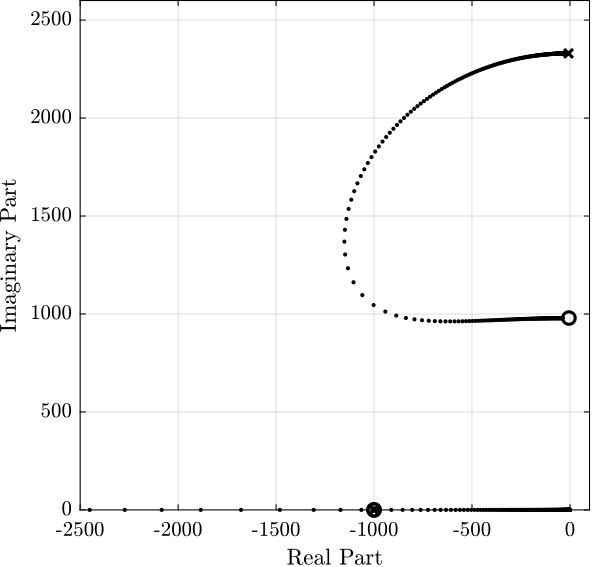
Figure 3: Root Locus
2 Rotating X-Y platform
2.1 Parameters
m = 1; % [kg] ke = 4.8e6; % [N/m] ce = 5; % [N/(m/s)] me = 0.001; % [kg] k1 = 0.96e6; % [N/m] c1 = 10; % [N/(m/s)] ka = 65e6; % [N/m] ca = 5; % [N/(m/s)] ma = 0.001; % [kg] h = 0.2; % [m]
Kiff = tf(0);
2.2 Identification
Rotating speed in rad/s:
Ws = 2*pi*[0, 1, 10, 100];
Gs = {zeros(length(Ws), 1)};
Identification in open-loop.
%% Name of the Simulink File
mdl = 'amplified_piezo_xy_rotating_stage';
%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/fx'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/fy'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Fs'], 1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Fs'], 2, 'openoutput'); io_i = io_i + 1;
for i = 1:length(Ws)
ws = Ws(i);
G = linearize(mdl, io, 0);
G.InputName = {'fx', 'fy'};
G.OutputName = {'Fsx', 'Fsy'};
Gs(i) = {G};
end
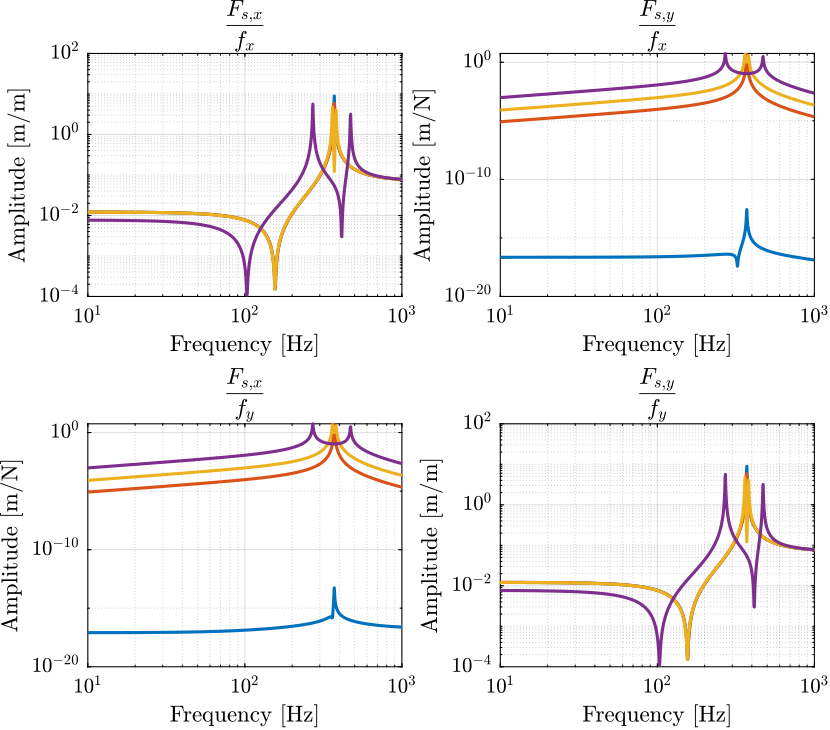
Figure 4: Transfer function matrix from forces to force sensors for multiple rotation speed
2.3 Root Locus
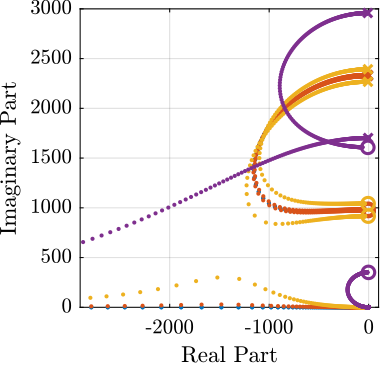
Figure 5: Root locus for 3 rotating speed
2.4 Analysis
The negative stiffness induced by the rotation is equal to \(m \omega_0^2\). Thus, the maximum rotation speed where IFF can be applied is: \[ \omega_\text{max} = \sqrt{\frac{k_1}{m}} \approx 156\,[Hz] \]
Let’s verify that.
Ws = 2*pi*[140, 160];
Identification
%% Name of the Simulink File
mdl = 'amplified_piezo_xy_rotating_stage';
%% Input/Output definition
clear io; io_i = 1;
io(io_i) = linio([mdl, '/fx'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/fy'], 1, 'openinput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Fs'], 1, 'openoutput'); io_i = io_i + 1;
io(io_i) = linio([mdl, '/Fs'], 2, 'openoutput'); io_i = io_i + 1;
for i = 1:length(Ws)
ws = Ws(i);
G = linearize(mdl, io, 0);
G.InputName = {'fx', 'fy'};
G.OutputName = {'Fsx', 'Fsy'};
Gs(i) = {G};
end
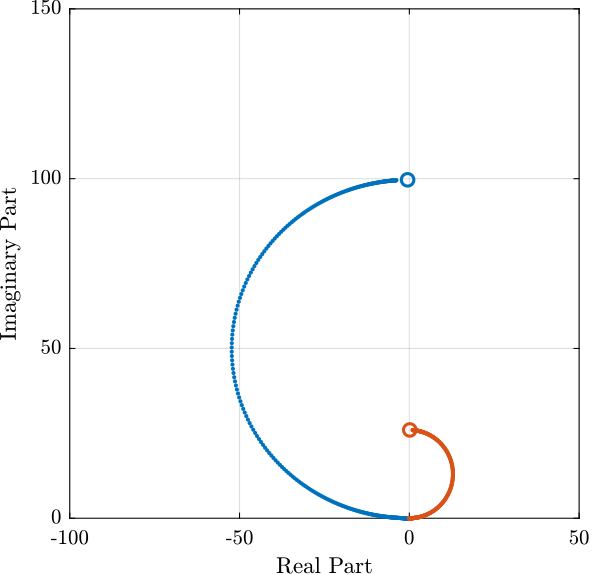
Figure 6: Root Locus for the two considered rotation speed. For the red curve, the system is unstable.
3 Stewart Platform with Amplified Actuators
3.1 Initialization
initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();
initializeAxisc();
initializeMirror();
initializeSimscapeConfiguration();
initializeDisturbances('enable', false);
initializeLoggingConfiguration('log', 'none');
initializeController('type', 'hac-iff');
We set the stiffness of the payload fixation:
Kp = 1e8; % [N/m]
3.2 Identification
K = tf(zeros(6)); Kiff = tf(zeros(6));
We identify the system for the following payload masses:
Ms = [1, 10, 50];
The nano-hexapod has the following leg’s stiffness and damping.
initializeNanoHexapod('actuator', 'amplified');
3.3 Controller Design
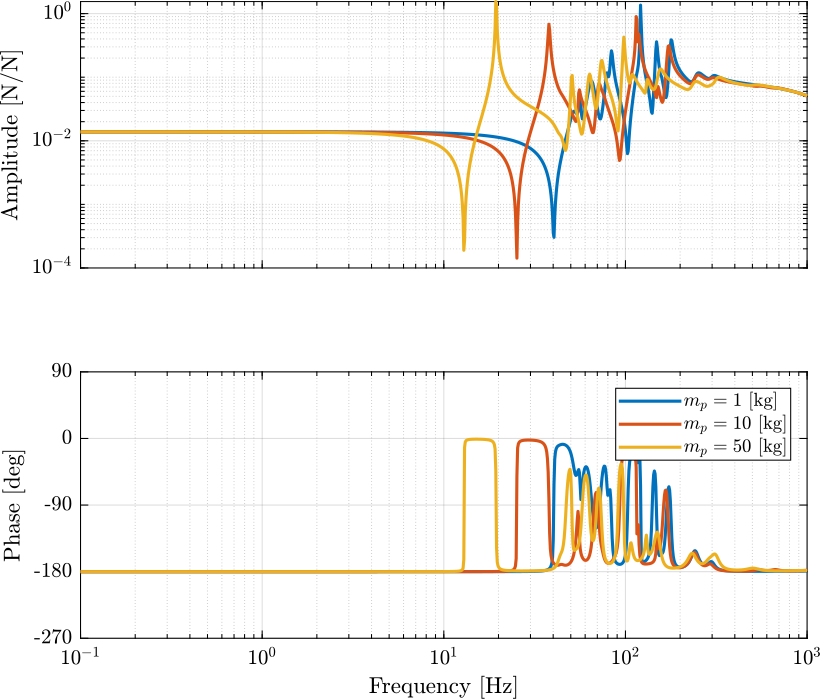
Figure 7: Dynamics for the Integral Force Feedback for three payload masses
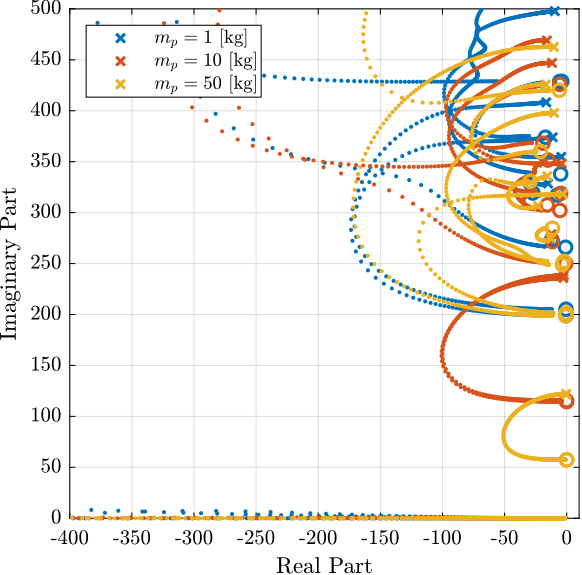
Figure 8: Root Locus for the IFF control for three payload masses
Damping as function of the gain
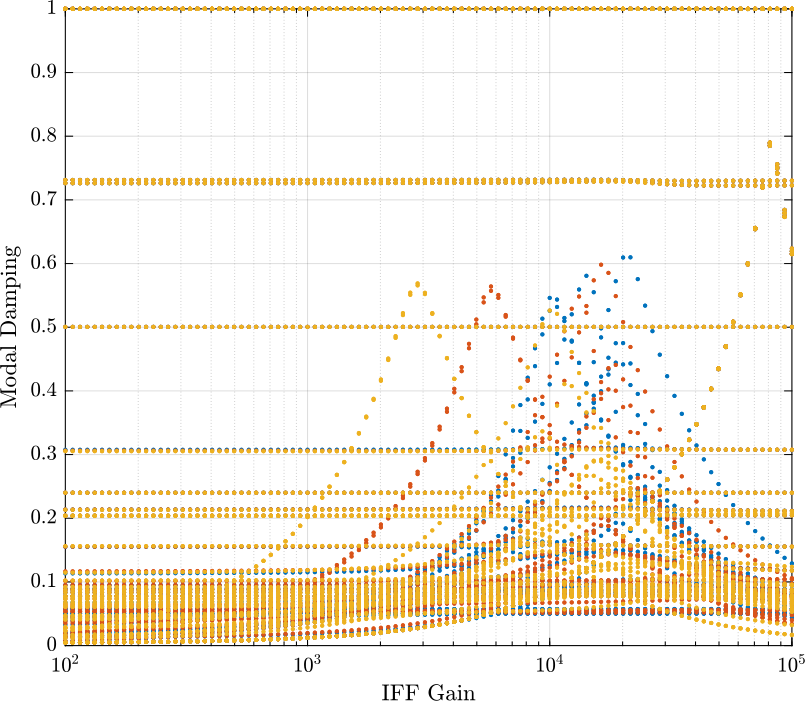
Figure 9: Damping ratio of the poles as a function of the IFF gain
Finally, we use the following controller for the Decentralized Direct Velocity Feedback:
Kiff = -1e4/s*eye(6);