<?xml version="1.0" encoding="utf-8"?>
<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Strict//EN"
"http://www.w3.org/TR/xhtml1/DTD/xhtml1-strict.dtd">
<html xmlns="http://www.w3.org/1999/xhtml" lang="en" xml:lang="en">
<head>
<!-- 2020-07-31 ven. 17:58 -->
<meta http-equiv="Content-Type" content="text/html;charset=utf-8" />
<title>Noise Budgeting</title>
<meta name="generator" content="Org mode" />
<meta name="author" content="Dehaeze Thomas" />
<link rel="stylesheet" type="text/css" href="./css/htmlize.css"/>
<link rel="stylesheet" type="text/css" href="./css/readtheorg.css"/>
<script src="./js/jquery.min.js"></script>
<script src="./js/bootstrap.min.js"></script>
<script src="./js/jquery.stickytableheaders.min.js"></script>
<script src="./js/readtheorg.js"></script>
<script>MathJax = {
tex: {
tags: 'ams',
macros: {bm: ["\\boldsymbol{#1}",1],}
}
};
</script>
<script type="text/javascript" src="https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js"></script>
</head>
<body>
<div id="org-div-home-and-up">
<a accesskey="h" href="./index.html"> UP </a>
|
<a accesskey="H" href="./index.html"> HOME </a>
</div><div id="content">
<h1 class="title">Noise Budgeting</h1>
<div id="table-of-contents">
<h2>Table of Contents</h2>
<div id="text-table-of-contents">
<ul>
<li><a href="#orgc8b5888">1. Maximum Noise of the Relative Motion Sensors</a>
<ul>
<li><a href="#org47d58ae">1.1. Initialization</a></li>
<li><a href="#org9b3405f">1.2. Control System</a></li>
<li><a href="#org4b1b358">1.3. Maximum induced vibration’s ASD</a></li>
<li><a href="#org446dbf5">1.4. Computation of the maximum relative motion sensor noise</a></li>
<li><a href="#org65a9628">1.5. Verification of the induced motion error</a></li>
</ul>
</li>
</ul>
</div>
</div>
<div id="outline-container-orgc8b5888" class="outline-2">
<h2 id="orgc8b5888"><span class="section-number-2">1</span> Maximum Noise of the Relative Motion Sensors</h2>
<div class="outline-text-2" id="text-1">
</div>
<div id="outline-container-org47d58ae" class="outline-3">
<h3 id="org47d58ae"><span class="section-number-3">1.1</span> Initialization</h3>
<div class="outline-text-3" id="text-1-1">
<div class="org-src-container">
<pre class="src src-matlab">open('nass_model.slx');
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">initializeGround();
initializeGranite();
initializeTy();
initializeRy();
initializeRz();
initializeMicroHexapod();
initializeAxisc();
initializeMirror();
initializeSimscapeConfiguration();
initializeDisturbances('enable', false);
initializeLoggingConfiguration('log', 'none');
initializeController('type', 'hac-dvf');
</pre>
</div>
<p>
We set the stiffness of the payload fixation:
</p>
<div class="org-src-container">
<pre class="src src-matlab">Kp = 1e8; % [N/m]
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">initializeNanoHexapod('k', 1e5, 'c', 2e2);
Ms = 50;
initializeSample('mass', Ms, 'freq', sqrt(Kp/Ms)/2/pi*ones(6,1));
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">initializeReferences('Rz_type', 'rotating-not-filtered', 'Rz_period', Ms);
</pre>
</div>
</div>
</div>
<div id="outline-container-org9b3405f" class="outline-3">
<h3 id="org9b3405f"><span class="section-number-3">1.2</span> Control System</h3>
<div class="outline-text-3" id="text-1-2">
<div class="org-src-container">
<pre class="src src-matlab">Kdvf = 5e3*s/(1+s/2/pi/1e3)*eye(6);
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">h = 2.0;
Kl = 2e7 * eye(6) * ...
1/h*(s/(2*pi*100/h) + 1)/(s/(2*pi*100*h) + 1) * ...
1/h*(s/(2*pi*200/h) + 1)/(s/(2*pi*200*h) + 1) * ...
(s/2/pi/10 + 1)/(s/2/pi/10) * ...
1/(1 + s/2/pi/300);
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">load('mat/stages.mat', 'nano_hexapod');
K = Kl*nano_hexapod.kinematics.J*diag([1, 1, 1, 1, 1, 0]);
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">%% Run the linearization
G = linearize(mdl, io);
G.InputName = {'ndL1', 'ndL2', 'ndL3', 'ndL4', 'ndL5', 'ndL6'};
G.OutputName = {'Ex', 'Ey', 'Ez', 'Erx', 'Ery', 'Erz'};
</pre>
</div>
</div>
</div>
<div id="outline-container-org4b1b358" class="outline-3">
<h3 id="org4b1b358"><span class="section-number-3">1.3</span> Maximum induced vibration’s ASD</h3>
<div class="outline-text-3" id="text-1-3">
<p>
Required maximum induced ASD of the sample’s vibration due to the relative motion sensor noise.
\[ \bm{\Gamma}_x(\omega) = \begin{bmatrix} \Gamma_x(\omega) & \Gamma_y(\omega) & \Gamma_{R_x}(\omega) & \Gamma_{R_y}(\omega) \end{bmatrix} \]
</p>
<div class="org-src-container">
<pre class="src src-matlab">Gamma_x = [(1e-9)/(1 + s/2/pi/100); % Dx
(1e-9)/(1 + s/2/pi/100); % Dy
(1e-9)/(1 + s/2/pi/100); % Dz
(2e-8)/(1 + s/2/pi/100); % Rx
(2e-8)/(1 + s/2/pi/100)]; % Ry
</pre>
</div>
<div class="org-src-container">
<pre class="src src-matlab">freqs = logspace(0, 3, 1000);
</pre>
</div>
<p>
Corresponding RMS value in [nm rms, nrad rms]
</p>
<div class="org-src-container">
<pre class="src src-matlab">1e9*sqrt(trapz(freqs, (abs(squeeze(freqresp(Gamma_x, freqs, 'Hz')))').^2))
</pre>
</div>
<table border="2" cellspacing="0" cellpadding="6" rules="groups" frame="hsides">
<colgroup>
<col class="org-left" />
<col class="org-right" />
</colgroup>
<thead>
<tr>
<th scope="col" class="org-left"> </th>
<th scope="col" class="org-right">Specifications</th>
</tr>
</thead>
<tbody>
<tr>
<td class="org-left">Dx [nm]</td>
<td class="org-right">12.1</td>
</tr>
<tr>
<td class="org-left">Dy [nm]</td>
<td class="org-right">12.1</td>
</tr>
<tr>
<td class="org-left">Dz [nm]</td>
<td class="org-right">12.1</td>
</tr>
<tr>
<td class="org-left">Rx [nrad]</td>
<td class="org-right">241.8</td>
</tr>
<tr>
<td class="org-left">Ry [nrad]</td>
<td class="org-right">241.8</td>
</tr>
</tbody>
</table>
</div>
</div>
<div id="outline-container-org446dbf5" class="outline-3">
<h3 id="org446dbf5"><span class="section-number-3">1.4</span> Computation of the maximum relative motion sensor noise</h3>
<div class="outline-text-3" id="text-1-4">
<p>
Let’s note \(G\) the transfer function from the 6 sensor noise \(n\) to the 6dof pose error \(x\).
We have:
\[ x_i = \sum_{j=1}^6 G_{ij}(s) n_j, \quad i = 1 \dots 5 \]
In terms of ASD:
\[ \Gamma_{x_i}(\omega) = \sum_{j=1}^6 |G_{ij}(j\omega)|^2 \Gamma_{n_j}(\omega), \quad i = 1 \dots 5 \]
</p>
<p>
Let’s suppose that the ASD of all the sensor noise are equal:
\[ \Gamma_{n_j} = \Gamma_{n}, \quad j = 1 \dots 6 \]
</p>
<p>
We then have an upper bound of the sensor noise for each of the considered motion errors:
\[ \Gamma_{n_i, \text{max}}(\omega) = \frac{\Gamma_{n_i}(\omega)}{\sum_{j=1}^6 |G_{ij}(j\omega)|^2}, \quad i = 1 \dots 5 \]
</p>
<div class="org-src-container">
<pre class="src src-matlab">Gamma_ndL = zeros(5, length(freqs));
for in = 1:5
Gamma_ndL(in, :) = abs(squeeze(freqresp(Gamma_x(in), freqs, 'Hz')))./sqrt(sum(abs(squeeze(freqresp(G(in, :), freqs, 'Hz'))).^2))';
end
</pre>
</div>
<div id="orgf2f2139" class="figure">
<p><img src="figs/noise_budget_ndL_max_asd.png" alt="noise_budget_ndL_max_asd.png" />
</p>
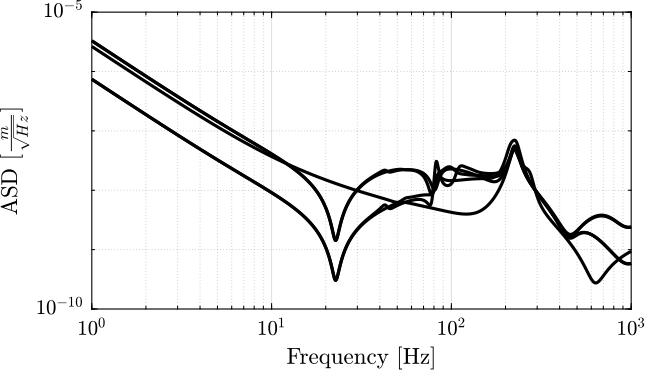
<p><span class="figure-number">Figure 1: </span>Maximum estimated ASD of the relative motion sensor noise</p>
</div>
<p>
If the noise ASD of the relative motion sensor is bellow the maximum specified ASD for all the considered motion:
\[ \Gamma_n < \Gamma_{n_i, \text{max}}, \quad i = 1 \dots 5 \]
Then, the motion error due to sensor noise should be bellow the one specified.
</p>
<div class="org-src-container">
<pre class="src src-matlab">Gamma_ndL_max = min(Gamma_ndL(1:5, :));
</pre>
</div>
<p>
Let’s take a sensor with a white noise up to 1kHz that is bellow the specified one:
</p>
<div class="org-src-container">
<pre class="src src-matlab">Gamma_ndL_ex = abs(squeeze(freqresp(min(Gamma_ndL_max)/(1 + s/2/pi/1e3), freqs, 'Hz')));
</pre>
</div>
<div id="org73ad463" class="figure">
<p><img src="figs/relative_motion_sensor_noise_ASD_example.png" alt="relative_motion_sensor_noise_ASD_example.png" />
</p>
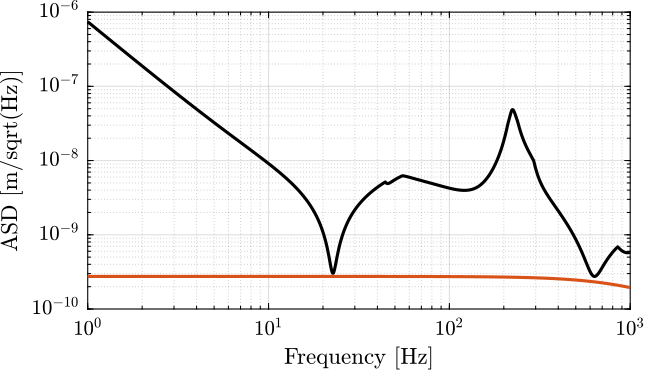
<p><span class="figure-number">Figure 2: </span>Requirement maximum ASD of the sensor noise + example of a sensor validating the requirements</p>
</div>
<p>
The corresponding RMS value of the sensor noise taken as an example is [nm RMS]:
</p>
<div class="org-src-container">
<pre class="src src-matlab">1e9*sqrt(trapz(freqs, Gamma_ndL_max.^2))
</pre>
</div>
<pre class="example">
519.29
</pre>
</div>
</div>
<div id="outline-container-org65a9628" class="outline-3">
<h3 id="org65a9628"><span class="section-number-3">1.5</span> Verification of the induced motion error</h3>
<div class="outline-text-3" id="text-1-5">
<p>
Verify that by taking the sensor noise, we have to wanted displacement error
From the sensor noise PSD \(\Gamma_n(\omega)\), we can estimate the obtained displacement PSD \(\Gamma_x(\omega)\):
\[ \Gamma_{x,i}(\omega) = \sqrt{ \sum_{j=1}^{6} |G_{ij}|^2(j\omega) \Gamma_{n,j}^2(\omega) }, \quad i = 1 \dots 5 \]
</p>
<div class="org-src-container">
<pre class="src src-matlab">Gamma_xest = zeros(5, length(freqs));
for in = 1:5
Gamma_xest(in, :) = sqrt(sum(abs(squeeze(freqresp(G(in, :), freqs, 'Hz'))).^2.*Gamma_ndL_max.^2));
end
</pre>
</div>
<table border="2" cellspacing="0" cellpadding="6" rules="groups" frame="hsides">
<colgroup>
<col class="org-left" />
<col class="org-right" />
<col class="org-right" />
</colgroup>
<thead>
<tr>
<th scope="col" class="org-left"> </th>
<th scope="col" class="org-right">Results</th>
<th scope="col" class="org-right">Specifications</th>
</tr>
</thead>
<tbody>
<tr>
<td class="org-left">Dx [nm]</td>
<td class="org-right">8.9</td>
<td class="org-right">12.1</td>
</tr>
<tr>
<td class="org-left">Dy [nm]</td>
<td class="org-right">9.3</td>
<td class="org-right">12.1</td>
</tr>
<tr>
<td class="org-left">Dz [nm]</td>
<td class="org-right">10.2</td>
<td class="org-right">12.1</td>
</tr>
<tr>
<td class="org-left">Rx [nrad]</td>
<td class="org-right">110.2</td>
<td class="org-right">241.8</td>
</tr>
<tr>
<td class="org-left">Ry [nrad]</td>
<td class="org-right">107.8</td>
<td class="org-right">241.8</td>
</tr>
</tbody>
</table>
</div>
</div>
</div>
</div>
<div id="postamble" class="status">
<p class="author">Author: Dehaeze Thomas</p>
<p class="date">Created: 2020-07-31 ven. 17:58</p>
</div>
</body>
</html>