Compliance Measurement of the Micro Station
Table of Contents
1 Setup
1.1 Position of inertial sensors on top of the micro-hexapod
Orientation is relative to the frame determined by the X-ray
| Num | Position | Orientation | Sensibility | Channels |
|---|---|---|---|---|
| 1 | [0, +A, 0] | [x, y, z] | 1V/g | 1-3 |
| 2 | [-B, 0, 0] | [x, y, z] | 1V/g | 4-6 |
| 3 | [0, -A, 0] | [x, y, z] | 0.1V/g | 7-9 |
| 4 | [+B, 0, 0] | [x, y, z] | 1V/g | 10-12 |
Instrumented Hammer:
- Channel 13
- Sensibility: 230 uV/N
| Acc Number | Dir | Channel Number |
|---|---|---|
| 1 | x | 1 |
| 1 | y | 2 |
| 1 | z | 3 |
| 2 | x | 4 |
| 2 | y | 5 |
| 2 | z | 6 |
| 3 | x | 7 |
| 3 | y | 8 |
| 3 | z | 9 |
| 4 | x | 10 |
| 4 | y | 11 |
| 4 | z | 12 |
| Hammer | 13 |
From the acceleration measurement of the 4 accelerometers, we can compute the translations and rotations:
| Formula | |
|---|---|
| \(D_x\) | (1x + 2x + 3x + 4x)/4 |
| \(D_y\) | (1y + 2y + 3y + 4y)/4 |
| \(D_z\) | (1z + 2z + 3z + 4z)/4 |
| \(R_x\) | (1z - 3z)/A |
| \(R_y\) | (2z - 4z)/B |
| \(R_z\) | (3x - 1x)/A, (4y - 2y)/B |
| Formula | |
|---|---|
| \(D_x\) | (1 + 4 + 7 + 10)/4 |
| \(D_y\) | (2 + 5 + 8 + 11)/4 |
| \(D_z\) | (3 + 6 + 9 + 12)/4 |
| \(R_x\) | (1 - 9)/A |
| \(R_y\) | (6 - 12)/B |
| \(R_z\) | (7 - 1)/A, (11 - 5)/B |
1.2 Hammer blow position/orientation
| Num | Direction | Position |
|---|---|---|
| 1 | -Y | [0, +A, 0] |
| 2 | -Z | [0, +A, 0] |
| 3 | X | [-B, 0, 0] |
| 4 | -Z | [-B, 0, 0] |
| 5 | Y | [0, -A, 0] |
| 6 | -Z | [0, -A, 0] |
| 7 | -X | [+B, 0, 0] |
| 8 | -Z | [+B, 0, 0] |
| 9 | -X | [0, -A, 0] |
| 10 | -X | [0, +A, 0] |
From hammer blows to pure forces / torques:
| Formula | Alternative | |
|---|---|---|
| \(F_x\) | +3 | -7 |
| \(F_y\) | -1 | +5 |
| \(F_z\) | -(2 + 6)/2 | -(4 + 8)/2 |
| \(M_x\) | A/2*(2 - 6) | |
| \(M_y\) | B/2*(8 - 4) | |
| \(M_z\) | A/2*(10 - 9) |
2 Results
2.1 Load Data
m1 = load('data/Measurement1.mat'); m2 = load('data/Measurement2.mat'); m3 = load('data/Measurement3.mat'); m4 = load('data/Measurement4.mat'); m5 = load('data/Measurement5.mat'); m6 = load('data/Measurement6.mat'); m7 = load('data/Measurement7.mat'); m8 = load('data/Measurement8.mat'); m9 = load('data/Measurement9.mat'); m10 = load('data/Measurement10.mat');
2.2 Compute Transfer Functions
freqs = m3.FFT1_H1_1_13_X_Val; w = 2*pi*freqs'; A = 0.14; B = 0.14;
G = zeros(6,6,length(freqs)); % Fx G(1,1,:) = (m3.FFT1_H1_1_13_Y_ReIm + m3.FFT1_H1_4_13_Y_ReIm + m3.FFT1_H1_7_13_Y_ReIm + m3.FFT1_H1_10_13_Y_ReIm)./4; G(2,1,:) = (m3.FFT1_H1_2_13_Y_ReIm + m3.FFT1_H1_5_13_Y_ReIm + m3.FFT1_H1_8_13_Y_ReIm + m3.FFT1_H1_11_13_Y_ReIm)./4; G(3,1,:) = (m3.FFT1_H1_3_13_Y_ReIm + m3.FFT1_H1_6_13_Y_ReIm + m3.FFT1_H1_9_13_Y_ReIm + m3.FFT1_H1_12_13_Y_ReIm)./4; G(4,1,:) = (m3.FFT1_H1_1_13_Y_ReIm - m3.FFT1_H1_9_13_Y_ReIm )./A; G(5,1,:) = (m3.FFT1_H1_6_13_Y_ReIm - m3.FFT1_H1_12_13_Y_ReIm)./B; G(6,1,:) = (m3.FFT1_H1_7_13_Y_ReIm - m3.FFT1_H1_1_13_Y_ReIm )./A; % Fy G(1,2,:) = -(m1.FFT1_H1_2_13_Y_ReIm + m1.FFT1_H1_5_13_Y_ReIm + m1.FFT1_H1_8_13_Y_ReIm + m1.FFT1_H1_11_13_Y_ReIm)./4; G(2,2,:) = -(m1.FFT1_H1_2_13_Y_ReIm + m1.FFT1_H1_5_13_Y_ReIm + m1.FFT1_H1_8_13_Y_ReIm + m1.FFT1_H1_11_13_Y_ReIm)./4; G(3,2,:) = -(m1.FFT1_H1_3_13_Y_ReIm + m1.FFT1_H1_6_13_Y_ReIm + m1.FFT1_H1_9_13_Y_ReIm + m1.FFT1_H1_12_13_Y_ReIm)./4; G(4,2,:) = -(m1.FFT1_H1_1_13_Y_ReIm - m1.FFT1_H1_9_13_Y_ReIm )./A; G(5,2,:) = -(m1.FFT1_H1_6_13_Y_ReIm - m1.FFT1_H1_12_13_Y_ReIm)./B; G(6,2,:) = -(m1.FFT1_H1_7_13_Y_ReIm - m1.FFT1_H1_1_13_Y_ReIm )./A; % Fz G(1,3,:) = -1/2./(1./(m2.FFT1_H1_1_13_Y_ReIm + m2.FFT1_H1_4_13_Y_ReIm + m2.FFT1_H1_7_13_Y_ReIm + m2.FFT1_H1_10_13_Y_ReIm) + ... 1./(m6.FFT1_H1_1_13_Y_ReIm + m6.FFT1_H1_4_13_Y_ReIm + m6.FFT1_H1_7_13_Y_ReIm + m6.FFT1_H1_10_13_Y_ReIm)); G(2,3,:) = -1/2./(1./(m2.FFT1_H1_2_13_Y_ReIm + m2.FFT1_H1_5_13_Y_ReIm + m2.FFT1_H1_8_13_Y_ReIm + m2.FFT1_H1_11_13_Y_ReIm) + ... 1./(m6.FFT1_H1_2_13_Y_ReIm + m6.FFT1_H1_5_13_Y_ReIm + m6.FFT1_H1_8_13_Y_ReIm + m6.FFT1_H1_11_13_Y_ReIm)); G(3,3,:) = -1/2./(1./(m2.FFT1_H1_3_13_Y_ReIm + m2.FFT1_H1_6_13_Y_ReIm + m2.FFT1_H1_9_13_Y_ReIm + m2.FFT1_H1_12_13_Y_ReIm) + ... 1./(m6.FFT1_H1_3_13_Y_ReIm + m6.FFT1_H1_6_13_Y_ReIm + m6.FFT1_H1_9_13_Y_ReIm + m6.FFT1_H1_12_13_Y_ReIm)); G(4,3,:) = -2/A./(1./(m2.FFT1_H1_1_13_Y_ReIm - m2.FFT1_H1_9_13_Y_ReIm) + ... 1./(m6.FFT1_H1_1_13_Y_ReIm - m6.FFT1_H1_9_13_Y_ReIm)); G(5,3,:) = -2/B./(1./(m2.FFT1_H1_6_13_Y_ReIm - m2.FFT1_H1_12_13_Y_ReIm) + ... 1./(m6.FFT1_H1_6_13_Y_ReIm - m6.FFT1_H1_12_13_Y_ReIm)); G(6,3,:) = -2/A./(1./(m2.FFT1_H1_7_13_Y_ReIm - m2.FFT1_H1_1_13_Y_ReIm) + ... 1./(m6.FFT1_H1_7_13_Y_ReIm - m6.FFT1_H1_1_13_Y_ReIm)); % Mx G(1,4,:) = 1/A/2./(1./(m2.FFT1_H1_1_13_Y_ReIm + m2.FFT1_H1_4_13_Y_ReIm + m2.FFT1_H1_7_13_Y_ReIm + m2.FFT1_H1_10_13_Y_ReIm) - ... 1./(m6.FFT1_H1_1_13_Y_ReIm + m6.FFT1_H1_4_13_Y_ReIm + m6.FFT1_H1_7_13_Y_ReIm + m6.FFT1_H1_10_13_Y_ReIm)); G(2,4,:) = 1/A/2./(1./(m2.FFT1_H1_2_13_Y_ReIm + m2.FFT1_H1_5_13_Y_ReIm + m2.FFT1_H1_8_13_Y_ReIm + m2.FFT1_H1_11_13_Y_ReIm) - ... 1./(m6.FFT1_H1_2_13_Y_ReIm + m6.FFT1_H1_5_13_Y_ReIm + m6.FFT1_H1_8_13_Y_ReIm + m6.FFT1_H1_11_13_Y_ReIm)); G(3,4,:) = 1/A/2./(1./(m2.FFT1_H1_3_13_Y_ReIm + m2.FFT1_H1_6_13_Y_ReIm + m2.FFT1_H1_9_13_Y_ReIm + m2.FFT1_H1_12_13_Y_ReIm) - ... 1./(m6.FFT1_H1_3_13_Y_ReIm + m6.FFT1_H1_6_13_Y_ReIm + m6.FFT1_H1_9_13_Y_ReIm + m6.FFT1_H1_12_13_Y_ReIm)); G(4,4,:) = 1/A^2*2./(1./(m2.FFT1_H1_1_13_Y_ReIm - m2.FFT1_H1_9_13_Y_ReIm) - ... 1./(m6.FFT1_H1_1_13_Y_ReIm - m6.FFT1_H1_9_13_Y_ReIm)); G(5,4,:) = 2/A/B./(1./(m2.FFT1_H1_6_13_Y_ReIm - m2.FFT1_H1_12_13_Y_ReIm) - ... 1./(m6.FFT1_H1_6_13_Y_ReIm - m6.FFT1_H1_12_13_Y_ReIm)); G(6,4,:) = 1/A^2*2./(1./(m2.FFT1_H1_7_13_Y_ReIm - m2.FFT1_H1_1_13_Y_ReIm) - ... 1./(m6.FFT1_H1_7_13_Y_ReIm - m6.FFT1_H1_1_13_Y_ReIm)); % My G(1,5,:) = 1/B/2./(1./(m8.FFT1_H1_1_13_Y_ReIm + m8.FFT1_H1_4_13_Y_ReIm + m8.FFT1_H1_7_13_Y_ReIm + m8.FFT1_H1_10_13_Y_ReIm) - ... 1./(m4.FFT1_H1_1_13_Y_ReIm + m4.FFT1_H1_4_13_Y_ReIm + m4.FFT1_H1_7_13_Y_ReIm + m4.FFT1_H1_10_13_Y_ReIm)); G(2,5,:) = 1/B/2./(1./(m8.FFT1_H1_2_13_Y_ReIm + m8.FFT1_H1_5_13_Y_ReIm + m8.FFT1_H1_8_13_Y_ReIm + m8.FFT1_H1_11_13_Y_ReIm) - ... 1./(m4.FFT1_H1_2_13_Y_ReIm + m4.FFT1_H1_5_13_Y_ReIm + m4.FFT1_H1_8_13_Y_ReIm + m4.FFT1_H1_11_13_Y_ReIm)); G(3,5,:) = 1/B/2./(1./(m8.FFT1_H1_3_13_Y_ReIm + m8.FFT1_H1_6_13_Y_ReIm + m8.FFT1_H1_9_13_Y_ReIm + m8.FFT1_H1_12_13_Y_ReIm) - ... 1./(m4.FFT1_H1_3_13_Y_ReIm + m4.FFT1_H1_6_13_Y_ReIm + m4.FFT1_H1_9_13_Y_ReIm + m4.FFT1_H1_12_13_Y_ReIm)); G(4,5,:) = 2/B/A./(1./(m8.FFT1_H1_1_13_Y_ReIm - m8.FFT1_H1_9_13_Y_ReIm) - ... 1./(m4.FFT1_H1_1_13_Y_ReIm - m4.FFT1_H1_9_13_Y_ReIm)); G(5,5,:) = 1/B^2*2./(1./(m8.FFT1_H1_6_13_Y_ReIm - m8.FFT1_H1_12_13_Y_ReIm) - ... 1./(m4.FFT1_H1_6_13_Y_ReIm - m4.FFT1_H1_12_13_Y_ReIm)); G(6,5,:) = 2/B/A./(1./(m8.FFT1_H1_7_13_Y_ReIm - m8.FFT1_H1_1_13_Y_ReIm) - ... 1./(m4.FFT1_H1_7_13_Y_ReIm - m4.FFT1_H1_1_13_Y_ReIm)); % Mz G(1,6,:) = 1/A/2./(1./(m10.FFT1_H1_1_13_Y_ReIm + m10.FFT1_H1_4_13_Y_ReIm + m10.FFT1_H1_7_13_Y_ReIm + m10.FFT1_H1_10_13_Y_ReIm) - ... 1./(m9.FFT1_H1_1_13_Y_ReIm + m9.FFT1_H1_4_13_Y_ReIm + m9.FFT1_H1_7_13_Y_ReIm + m9.FFT1_H1_10_13_Y_ReIm)); G(2,6,:) = 1/A/2./(1./(m10.FFT1_H1_2_13_Y_ReIm + m10.FFT1_H1_5_13_Y_ReIm + m10.FFT1_H1_8_13_Y_ReIm + m10.FFT1_H1_11_13_Y_ReIm) - ... 1./(m9.FFT1_H1_2_13_Y_ReIm + m9.FFT1_H1_5_13_Y_ReIm + m9.FFT1_H1_8_13_Y_ReIm + m9.FFT1_H1_11_13_Y_ReIm)); G(3,6,:) = 1/A/2./(1./(m10.FFT1_H1_3_13_Y_ReIm + m10.FFT1_H1_6_13_Y_ReIm + m10.FFT1_H1_9_13_Y_ReIm + m10.FFT1_H1_12_13_Y_ReIm) - ... 1./(m9.FFT1_H1_3_13_Y_ReIm + m9.FFT1_H1_6_13_Y_ReIm + m9.FFT1_H1_9_13_Y_ReIm + m9.FFT1_H1_12_13_Y_ReIm)); G(4,6,:) = 1/A^2*2./(1./(m10.FFT1_H1_1_13_Y_ReIm - m10.FFT1_H1_9_13_Y_ReIm) - ... 1./(m9.FFT1_H1_1_13_Y_ReIm - m9.FFT1_H1_9_13_Y_ReIm)); G(5,6,:) = 2*A/B./(1./(m10.FFT1_H1_6_13_Y_ReIm - m10.FFT1_H1_12_13_Y_ReIm) - ... 1./(m9.FFT1_H1_6_13_Y_ReIm - m9.FFT1_H1_12_13_Y_ReIm)); G(6,6,:) = 1/A^2*2./(1./(m10.FFT1_H1_7_13_Y_ReIm - m10.FFT1_H1_1_13_Y_ReIm) - ... 1./(m9.FFT1_H1_7_13_Y_ReIm - m9.FFT1_H1_1_13_Y_ReIm));
2.3 Diagonal Dynamics
figure; ax1 = subplot(2,1,1); hold on; plot(freqs, abs(squeeze(G(1,1,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(2,2,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(3,3,:))./(-w.^2)), '.') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); ylabel('Magnitude [m/N]'); set(gca, 'XTickLabel',[]); ylim([1e-9, 2e-6]); ax2 = subplot(2,1,2); hold on; plot(freqs, 180/pi*angle(squeeze(G(1,1,:))./(-w.^2)), '.', 'DisplayName', '$D_x/F_x$') plot(freqs, 180/pi*angle(squeeze(G(2,2,:))./(-w.^2)), '.', 'DisplayName', '$D_y/F_y$') plot(freqs, 180/pi*angle(squeeze(G(3,3,:))./(-w.^2)), '.', 'DisplayName', '$D_z/F_z$') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'lin'); xlabel('Freqency [Hz]'); ylabel('Phase [deg]'); ylim([-180, 180]); yticks([-180, -90, 0, 90, 180]); legend('location', 'southwest'); linkaxes([ax1,ax2],'x'); xlim([30, 300]);
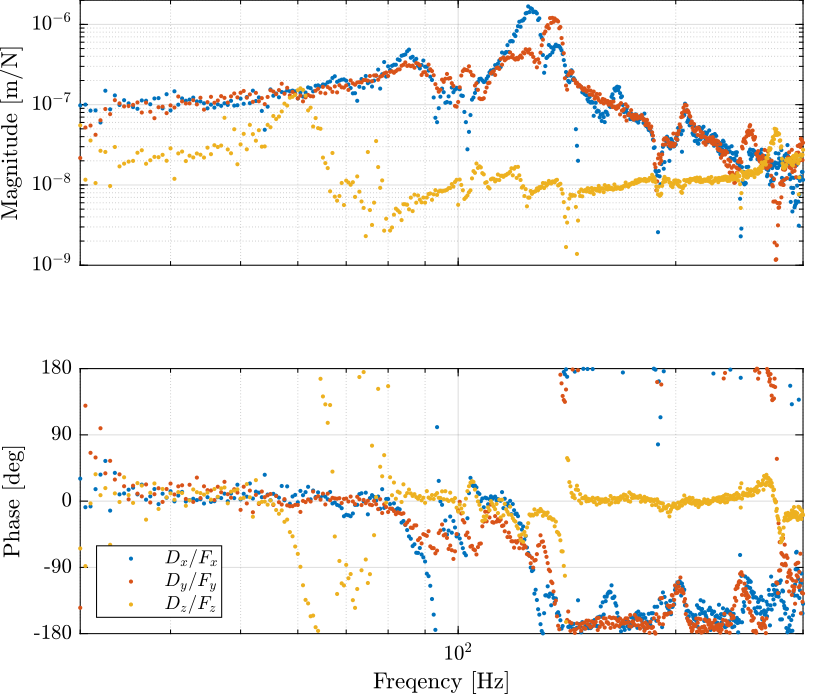
Figure 1: Dynamics from Forces to Translations
figure; ax1 = subplot(2,1,1); hold on; plot(freqs, abs(squeeze(G(4,4,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(5,5,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(6,6,:))./(-w.^2)), '.') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); ylabel('Magnitude [rad/Nm]'); set(gca, 'XTickLabel',[]); ylim([1e-7, 2e-4]); ax2 = subplot(2,1,2); hold on; plot(freqs, 180/pi*angle(squeeze(G(4,4,:))./(-w.^2)), '.', 'DisplayName', '$R_x/M_x$') plot(freqs, 180/pi*angle(squeeze(G(5,5,:))./(-w.^2)), '.', 'DisplayName', '$R_y/M_y$') plot(freqs, 180/pi*angle(squeeze(G(6,6,:))./(-w.^2)), '.', 'DisplayName', '$R_z/M_z$') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'lin'); xlabel('Freqency [Hz]'); ylabel('Phase [deg]'); ylim([-180, 180]); yticks([-180, -90, 0, 90, 180]); legend('location', 'southwest'); linkaxes([ax1,ax2],'x'); xlim([30, 300]);
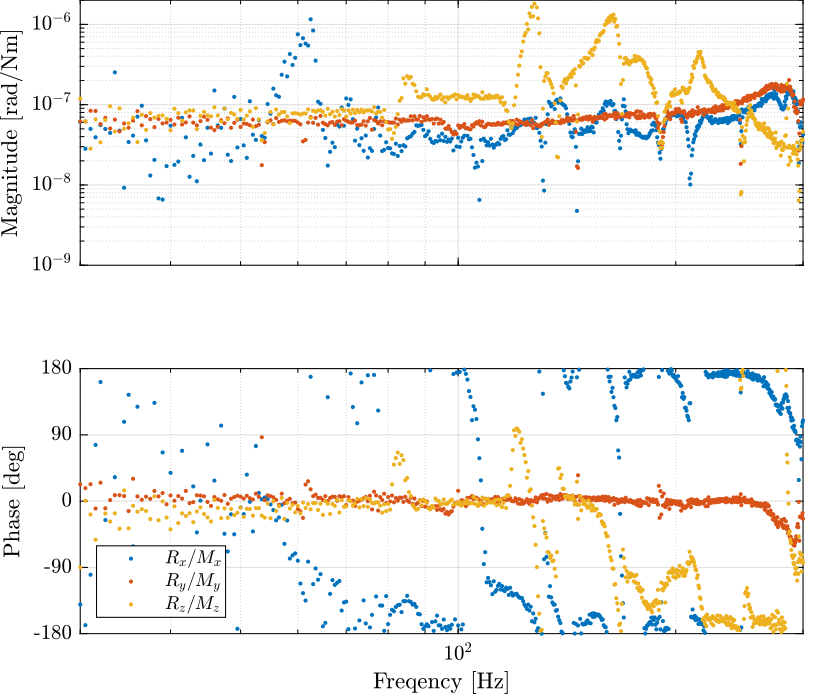
Figure 2: Dynamics from Torques to Rotations
2.4 Equivalent Stiffness and Mass Estimation
K = [1e7, 1e7, 2e8, 5e7, 3e7, 2e7]; f_res = [125, 135, 390, 335, 335, 160];
M = [20, 20, 20, 11, 7, 20]; f_res_est = sqrt(K./M)./(2*pi);
Here is the inertia / stiffness to the granite that can represent the micro-station compliance dynamics:
| Stiffness | Inertia |
|---|---|
| x | 10000000.0 |
| y | 10000000.0 |
| z | 200000000.0 |
| Rx | 50000000.0 |
| Ry | 30000000.0 |
| Rz | 20000000.0 |
2.5 Compare with Model
load('./mat/model.mat', 'Gm');
figure; ax1 = subplot(2,1,1); hold on; plot(freqs, abs(squeeze(G(1,1,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(2,2,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(3,3,:))./(-w.^2)), '.') set(gca,'ColorOrderIndex',1); plot(freqs, abs(squeeze(freqresp(Gm(1,1,:), freqs, 'Hz'))), '-') plot(freqs, abs(squeeze(freqresp(Gm(2,2,:), freqs, 'Hz'))), '-') plot(freqs, abs(squeeze(freqresp(Gm(3,3,:), freqs, 'Hz'))), '-') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); ylabel('Magnitude [m/N]'); set(gca, 'XTickLabel',[]); ylim([1e-9, 2e-6]); ax2 = subplot(2,1,2); hold on; plot(freqs, 180/pi*angle(squeeze(G(1,1,:))./(-w.^2)), '.', 'DisplayName', '$D_x/F_x$') plot(freqs, 180/pi*angle(squeeze(G(2,2,:))./(-w.^2)), '.', 'DisplayName', '$D_y/F_y$') plot(freqs, 180/pi*angle(squeeze(G(3,3,:))./(-w.^2)), '.', 'DisplayName', '$D_z/F_z$') set(gca,'ColorOrderIndex',1); plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(1,1,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(2,2,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(3,3,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'lin'); xlabel('Freqency [Hz]'); ylabel('Phase [deg]'); ylim([-180, 180]); yticks([-180, -90, 0, 90, 180]); legend('location', 'southwest'); linkaxes([ax1,ax2],'x'); xlim([30, 300]);
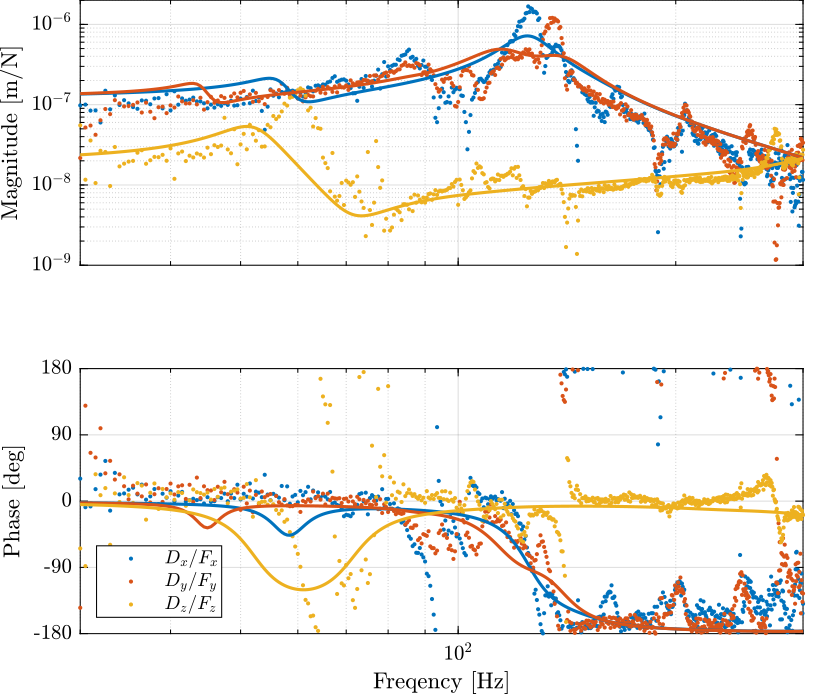
Figure 3: Dynamics from Forces to Translations
figure; ax1 = subplot(2,1,1); hold on; plot(freqs, abs(squeeze(G(4,4,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(5,5,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(6,6,:))./(-w.^2)), '.') set(gca,'ColorOrderIndex',1); plot(freqs, abs(squeeze(freqresp(Gm(4,4,:), freqs, 'Hz'))), '-') plot(freqs, abs(squeeze(freqresp(Gm(5,5,:), freqs, 'Hz'))), '-') plot(freqs, abs(squeeze(freqresp(Gm(6,6,:), freqs, 'Hz'))), '-') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); ylabel('Magnitude [rad/Nm]'); set(gca, 'XTickLabel',[]); % ylim([1e-9, 2e-6]); ax2 = subplot(2,1,2); hold on; plot(freqs, 180/pi*angle(squeeze(G(4,4,:))./(-w.^2)), '.', 'DisplayName', '$R_x/M_x$') plot(freqs, 180/pi*angle(squeeze(G(5,5,:))./(-w.^2)), '.', 'DisplayName', '$R_y/M_y$') plot(freqs, 180/pi*angle(squeeze(G(6,6,:))./(-w.^2)), '.', 'DisplayName', '$R_z/M_z$') set(gca,'ColorOrderIndex',1); plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(4,4,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(5,5,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(6,6,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'lin'); xlabel('Freqency [Hz]'); ylabel('Phase [deg]'); ylim([-180, 180]); yticks([-180, -90, 0, 90, 180]); legend('location', 'southwest'); linkaxes([ax1,ax2],'x'); xlim([30, 300]);
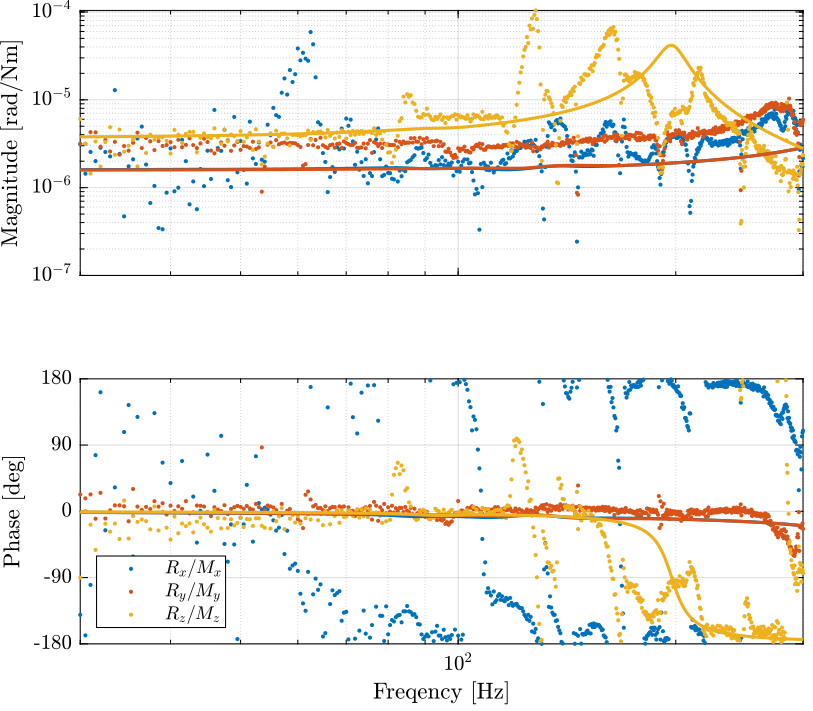
Figure 4: Dynamics from Torques to Rotations
| Stiffness | Unit | |
|---|---|---|
| \(K_x\) | 1e7 | [N/m] |
| \(K_y\) | 1e7 | [N/m] |
| \(K_z\) | 2e8 | [N/m] |
| \(K_{R_x}\) | 5e7 | [Nm/rad] |
| \(K_{R_y}\) | 3e7 | [Nm/rad] |
| \(K_{R_z}\) | 2e7 | [Nm/rad] |
2.6 Coupling Dynamics
figure; ax1 = subplot(2,1,1); hold on; plot(freqs, abs(squeeze(G(1,1,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(2,1,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(3,1,:))./(-w.^2)), '.') set(gca,'ColorOrderIndex',1); plot(freqs, abs(squeeze(freqresp(Gm(1,1,:), freqs, 'Hz'))), '-') plot(freqs, abs(squeeze(freqresp(Gm(2,1,:), freqs, 'Hz'))), '-') plot(freqs, abs(squeeze(freqresp(Gm(3,1,:), freqs, 'Hz'))), '-') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); ylabel('Magnitude [m/N]'); set(gca, 'XTickLabel',[]); ylim([1e-9, 2e-6]); ax2 = subplot(2,1,2); hold on; plot(freqs, 180/pi*angle(squeeze(G(1,1,:))./(-w.^2)), '.', 'DisplayName', '$D_x/F_x$') plot(freqs, 180/pi*angle(squeeze(G(2,1,:))./(-w.^2)), '.', 'DisplayName', '$D_y/F_x$') plot(freqs, 180/pi*angle(squeeze(G(3,1,:))./(-w.^2)), '.', 'DisplayName', '$D_z/F_x$') set(gca,'ColorOrderIndex',1); plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(1,1,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(2,1,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(3,1,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'lin'); xlabel('Freqency [Hz]'); ylabel('Phase [deg]'); ylim([-180, 180]); yticks([-180, -90, 0, 90, 180]); legend('location', 'southwest'); linkaxes([ax1,ax2],'x'); xlim([30, 300]);
figure; ax1 = subplot(2,1,1); hold on; plot(freqs, abs(squeeze(G(5,1,:))./(-w.^2)), '.') plot(freqs, abs(squeeze(G(4,2,:))./(-w.^2)), '.') set(gca,'ColorOrderIndex',1); plot(freqs, abs(squeeze(freqresp(Gm(5,1,:), freqs, 'Hz'))), '-') plot(freqs, abs(squeeze(freqresp(Gm(4,2,:), freqs, 'Hz'))), '-') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); ylabel('Magnitude [m/N]'); set(gca, 'XTickLabel',[]); ylim([1e-9, 2e-6]); ax2 = subplot(2,1,2); hold on; plot(freqs, 180/pi*angle(squeeze(G(5,1,:))./(-w.^2)), '.', 'DisplayName', '$R_y/F_x$') plot(freqs, 180/pi*angle(squeeze(G(4,2,:))./(-w.^2)), '.', 'DisplayName', '$R_x/F_y$') set(gca,'ColorOrderIndex',1); plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(5,1,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') plot(freqs, 180/pi*angle(squeeze(freqresp(Gm(4,2,:), freqs, 'Hz'))), '-', 'HandleVisibility', 'off') hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'lin'); xlabel('Freqency [Hz]'); ylabel('Phase [deg]'); ylim([-180, 180]); yticks([-180, -90, 0, 90, 180]); legend('location', 'southwest'); linkaxes([ax1,ax2],'x'); xlim([30, 300]);