Modal Analysis - Processing of FRF
Table of Contents
- 1. Importation of measured FRF curves
- 2. From accelerometer DOFs to solid body DOFs - Mathematics
- 3. What reference frame to choose?
- 4. From accelerometer DOFs to solid body DOFs - Matlab Implementation
- 5. Analysis of some FRF in the global coordinates
- 6. TODO How to compare the relative motion of solid bodies
- 7. Relative Motion in the global coordinates
- 8. TODO Compare original FRF measurements to transformed FRF in the global frame
- 9. Verify that we find the original FRF from the FRF in the global coordinates
The measurements have been conducted and we have computed the \(n \times p \times q\) Frequency Response Functions Matrix with:
- \(n\): the number of measurements: \(23 \times 3 = 69\) (23 accelerometers measuring 3 directions each)
- \(p\): the number of excitation inputs: \(3\)
- \(q\): the number of frequency points \(\omega_i\)
However, in our model, we only consider 6 solid bodies, namely:
- Bottom Granite
- Top Granite
- Translation Stage
- Tilt Stage
- Spindle
- Hexapod
Thus, we are only interested in \(6 \times 6 = 36\) degrees of freedom.
We here process the FRF matrix to go from the 69 measured DOFs to the wanted 36 DOFs.
1 Importation of measured FRF curves
We load the measured FRF and Coherence matrices. We also load the geometric parameters of the station: solid bodies considered and the position of the accelerometers.
load('./mat/frf_coh_matrices.mat', 'FRFs', 'COHs', 'freqs'); load('mat/geometry.mat', 'solids', 'solid_names', 'acc_pos');
2 From accelerometer DOFs to solid body DOFs - Mathematics
Let's consider the schematic shown on figure 1 where we are measuring the motion of a (supposed) solid body at 4 distinct points in x-y-z.
The goal here is to link these \(4 \times 3 = 12\) measurements to the 6 DOFs of the solid body expressed in the frame \(\{O\}\).
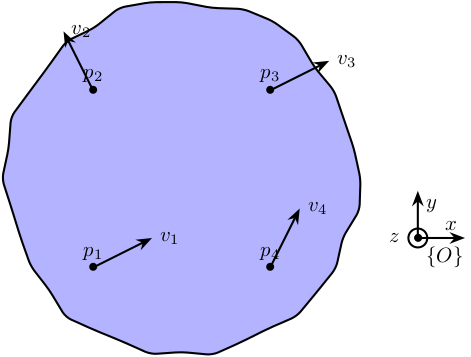
Figure 1: Schematic of the measured motions of a solid body
From the figure 1, we can write:
\begin{align*} \vec{v}_1 &= \vec{v} + \Omega \vec{p}_1\\ \vec{v}_2 &= \vec{v} + \Omega \vec{p}_2\\ \vec{v}_3 &= \vec{v} + \Omega \vec{p}_3\\ \vec{v}_4 &= \vec{v} + \Omega \vec{p}_4 \end{align*}With
\begin{equation} \Omega = \begin{bmatrix} 0 & -\Omega_z & \Omega_y \\ \Omega_z & 0 & -\Omega_x \\ -\Omega_y & \Omega_x & 0 \end{bmatrix} \end{equation}\(\vec{v}\) and \(\Omega\) represent to velocity and rotation of the solid expressed in the frame \(\{O\}\).
We can rearrange the equations in a matrix form:
\begin{equation} \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & 0 & p_{1z} & -p_{1y} \\ 0 & 1 & 0 & -p_{1z} & 0 & p_{1x} \\ 0 & 0 & 1 & p_{1y} & -p_{1x} & 0 \\ \hline & \vdots & & & \vdots & \\ \hline 1 & 0 & 0 & 0 & p_{4z} & -p_{4y} \\ 0 & 1 & 0 & -p_{4z} & 0 & p_{4x} \\ 0 & 0 & 1 & p_{4y} & -p_{4x} & 0 \end{array}\right] \begin{bmatrix} v_x \\ v_y \\ v_z \\ \hline \Omega_x \\ \Omega_y \\ \Omega_z \end{bmatrix} = \begin{bmatrix} v_{1x} \\ v_{1y} \\ v_{1z} \\\hline \vdots \\\hline v_{4x} \\ v_{4y} \\ v_{4z} \end{bmatrix} \end{equation}and then we obtain the velocity and rotation of the solid in the wanted frame \(\{O\}\):
\begin{equation} \begin{bmatrix} v_x \\ v_y \\ v_z \\ \hline \Omega_x \\ \Omega_y \\ \Omega_z \end{bmatrix} = \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & 0 & p_{1z} & -p_{1y} \\ 0 & 1 & 0 & -p_{1z} & 0 & p_{1x} \\ 0 & 0 & 1 & p_{1y} & -p_{1x} & 0 \\ \hline & \vdots & & & \vdots & \\ \hline 1 & 0 & 0 & 0 & p_{4z} & -p_{4y} \\ 0 & 1 & 0 & -p_{4z} & 0 & p_{4x} \\ 0 & 0 & 1 & p_{4y} & -p_{4x} & 0 \end{array}\right]^{-1} \begin{bmatrix} v_{1x} \\ v_{1y} \\ v_{1z} \\\hline \vdots \\\hline v_{4x} \\ v_{4y} \\ v_{4z} \end{bmatrix} \end{equation}This inversion is equivalent to resolving a mean square problem.
3 What reference frame to choose?
The question we wish here to answer is how to choose the reference frame \(\{O\}\) in which the DOFs of the solid bodies are defined.
The goal is to compare the motion of each solid body to see which relative DOFs between solid bodies can be neglected, that is to say, which joint between solid bodies can be regarded as perfect (and this in all the frequency range of interest). Ideally, we would like to have the same number of degrees of freedom than the number of identified modes.
The possibles choices are:
- One frame for each solid body which is located at its center of mass
- One common frame, for instance located at the point of interest (\(270mm\) above the Hexapod)
- Base located at the joint position: this is where we want to see the motion and estimate stiffness
| Chosen Frame | Advantages | Disadvantages |
|---|---|---|
| Frames at CoM | Physically, it makes more sense | How to compare the motion of the solid bodies? |
| Common Frame | We can compare the motion of each solid body | Small \(\theta_{x, y}\) may result in large \(T_{x, y}\) |
| Frames at joint position | Directly gives which joint direction can be blocked | How to choose the joint position? |
As the easiest choice is to choose a common frame, we start with that solution.
4 From accelerometer DOFs to solid body DOFs - Matlab Implementation
First, we initialize a new FRF matrix FRFs_O which is an \(n \times p \times q\) with:
- \(n\) is the number of DOFs of the considered 6 solid-bodies: \(6 \times 6 = 36\)
- \(p\) is the number of excitation inputs: \(3\)
- \(q\) is the number of frequency points \(\omega_i\)
FRFs_O = zeros(length(solid_names)*6, 3, 801);
Then, as we know the positions of the accelerometers on each solid body, and we have the response of those accelerometers, we can use the equations derived in the previous section to determine the response of each solid body expressed in the frame \(\{O\}\).
for solid_i = 1:length(solid_names) solids_i = solids.(solid_names{solid_i}); A = zeros(3*length(solids_i), 6); for i = 1:length(solids_i) acc_i = solids_i(i); A(3*(i-1)+1:3*i, 1:3) = eye(3); A(3*(i-1)+1:3*i, 4:6) = [ 0 acc_pos(acc_i, 3) -acc_pos(acc_i, 2) ; -acc_pos(acc_i, 3) 0 acc_pos(acc_i, 1) ; acc_pos(acc_i, 2) -acc_pos(acc_i, 1) 0]; end for exc_dir = 1:3 FRFs_O((solid_i-1)*6+1:solid_i*6, exc_dir, :) = A\squeeze(FRFs((solids_i(1)-1)*3+1:solids_i(end)*3, exc_dir, :)); end end
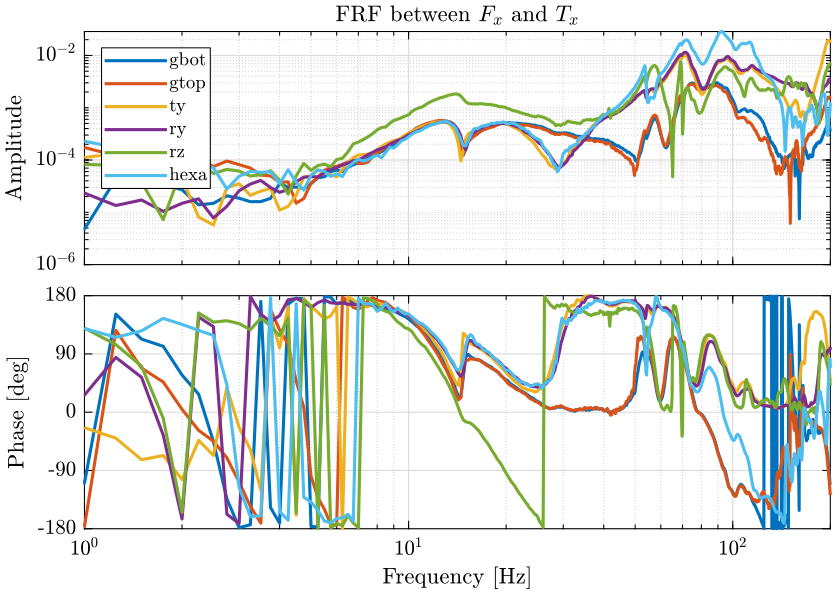
5 Analysis of some FRF in the global coordinates
6 TODO How to compare the relative motion of solid bodies
We have some of elements of the full FRF matrix: \[ \frac{D_{1x}}{F_x},\ \frac{D_{1y}}{F_x},\ \frac{D_{1z}}{F_x},\ \frac{D_{2x}}{F_x},\ \dots \]
\[ \frac{D_{1x}}{D_{2x}} = \frac{\frac{D_{1x}}{F_x}}{\frac{D_{2x}}{F_x}} \] Then, if \(\left| \frac{D_{1x}}{D_{2x}} \right| \approx 1\) in all the frequency band of interest, we can block the \(x\) motion between the solids 1 and 2.
\[ \frac{D_{2x} - D_{1x}}{D_{1x} + D_{2x}} = \frac{\frac{D_{2x}}{F_x} - \frac{D_{1x}}{F_x}}{\frac{D_{1x}}{F_x} + \frac{D_{2x}}{F_x}} \]
Then if \(\left| \frac{D_{2x} - D_{1x}}{D_{1x} + D_{2x}} \right| \ll 1\) in all the frequency band of interest, we can block the \(x\) motion between the solids 1 and 2.
7 Relative Motion in the global coordinates
Below we plot the normalized relative motion between each stage: \[ 0 < \frac{\left| D_{ix} - D_{jx} \right|}{|D_{ix}| + |D_{jx}|} < 1 \]
DOFs = {'$T_x$', '$T_y$', '$T_z$', '$\theta_x$', '$\theta_y$', '$\theta_z$'} dirs_i = 1:6; exc_dir = 1; figure; for i = 2:6 subaxis(3, 2, i); hold on; for dir_i = dirs_i H = (squeeze(FRFs_O((i-1)*6+dir_i, exc_dir, :))-squeeze(FRFs_O((i-2)*6+dir_i, exc_dir, :)))./(abs(squeeze(FRFs_O((i-1)*6+dir_i, exc_dir, :)))+abs(squeeze(FRFs_O((i-2)*6+dir_i, exc_dir, :)))); plot(freqs, abs(H)); end hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'lin'); xlim([1, 200]); ylim([0, 1]); % xlabel('Frequency [Hz]'); ylabel('Relative Motion'); title(sprintf('Normalized motion %s - %s', solid_names{i-1}, solid_names{i})); if i > 4 xlabel('Frequency [Hz]'); else set(gca, 'XTickLabel',[]); end end for i = 1:length(dirs_i) legend_names{i} = DOFs{dirs_i(i)}; end lgd = legend(legend_names); hL = subplot(3, 2, 1); poshL = get(hL,'position'); set(lgd,'position', poshL); axis(hL, 'off');
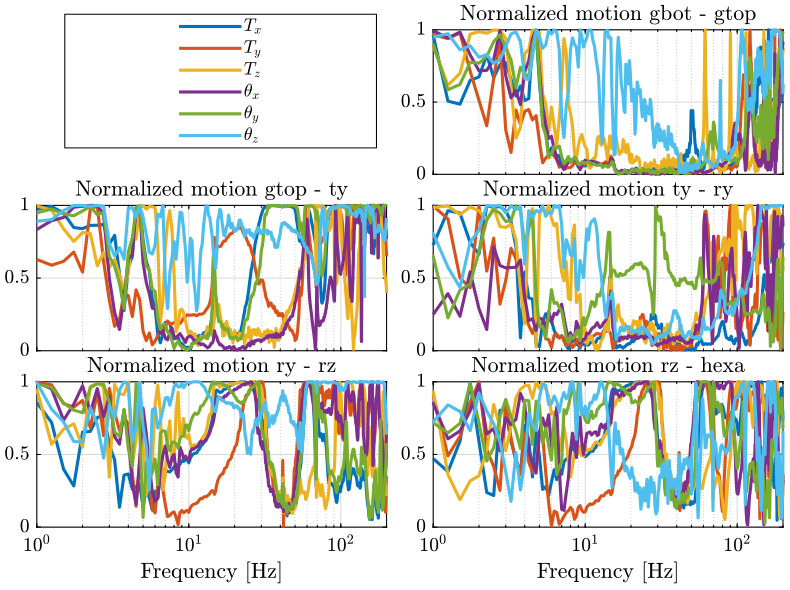
Figure 4: Relative motion between each stage
8 TODO Compare original FRF measurements to transformed FRF in the global frame
We wish here to compare the FRF in order to verify if there is any mistake.
dir_names = {'X', 'Y', 'Z', '$\theta_X$', '$\theta_Y$', '$\theta_Z$'}; solid_i = 6; acc_dir_O = 1; acc_dir = 1; exc_dir = 1; figure; ax1 = subplot(2, 1, 1); hold on; for i = solids.(solid_names{solid_i}) plot(freqs, abs(squeeze(FRFs(acc_dir+3*(i-1), exc_dir, :)))); end plot(freqs, abs(squeeze(FRFs_O((solid_i-1)*6+acc_dir_O, exc_dir, :))), '-k'); hold off; set(gca, 'XScale', 'log'); set(gca, 'YScale', 'log'); set(gca, 'XTickLabel',[]); ylabel('Amplitude'); title(sprintf('%s motion measured by the Acc. vs %s motion computed in the common frame - %s', dir_names{acc_dir}, dir_names{acc_dir_O}, solid_names{solid_i})); ax2 = subplot(2, 1, 2); hold on; for i = solids.(solid_names{solid_i}) plot(freqs, mod(180+180/pi*phase(squeeze(FRFs(acc_dir+3*(i-1), exc_dir, :))), 360)-180); end plot(freqs, mod(180+180/pi*phase(squeeze(FRFs_O((solid_i-1)*6+acc_dir_O, exc_dir, :))), 360)-180, '-k'); hold off; ylim([-180, 180]); yticks(-180:90:180); xlabel('Frequency [Hz]'); ylabel('Phase [deg]'); set(gca, 'xscale', 'log'); linkaxes([ax1,ax2],'x'); xlim([1, 200]);
9 Verify that we find the original FRF from the FRF in the global coordinates
We have computed the Frequency Response Functions Matrix FRFs_O representing the response of the 6 solid bodies in their 6 DOFs.
From the response of one body in its 6 DOFs, we should be able to compute the FRF of each of its accelerometer fixed to it during the measurement.
We can then compare the result with the original measurements. This will help us to determine if:
- the previous inversion used is correct
- the solid body assumption is correct in the frequency band of interest
FRF_recovered = zeros(size(FRFs)); % For each excitation direction for exc_dir = 1:3 % For each solid for solid_i = 1:length(solid_names) v0 = squeeze(FRFs_O((solid_i-1)*6+1:(solid_i-1)*6+3, exc_dir, :)); W0 = squeeze(FRFs_O((solid_i-1)*6+4:(solid_i-1)*6+6, exc_dir, :)); % For each accelerometer attached to the current solid for acc_i = solids.(solid_names{solid_i}) % We get the position of the accelerometer expressed in frame O pos = acc_pos(acc_i, :)'; posX = [0 pos(3) -pos(2); -pos(3) 0 pos(1) ; pos(2) -pos(1) 0]; [0 acc_pos(i, 3) -acc_pos(i, 2) ; -acc_pos(i, 3) 0 acc_pos(i, 1) ; acc_pos(i, 2) -acc_pos(i, 1) 0] FRF_recovered(3*(acc_i-1)+1:3*(acc_i-1)+3, exc_dir, :) = v0 + posX*W0; end end end
We then compare the original FRF measured for each accelerometer with the recovered FRF from the global FRF matrix in the common frame.
The FRF for the 4 accelerometers on the Hexapod are compared on figure 5. All the FRF are matching very well in all the frequency range displayed.
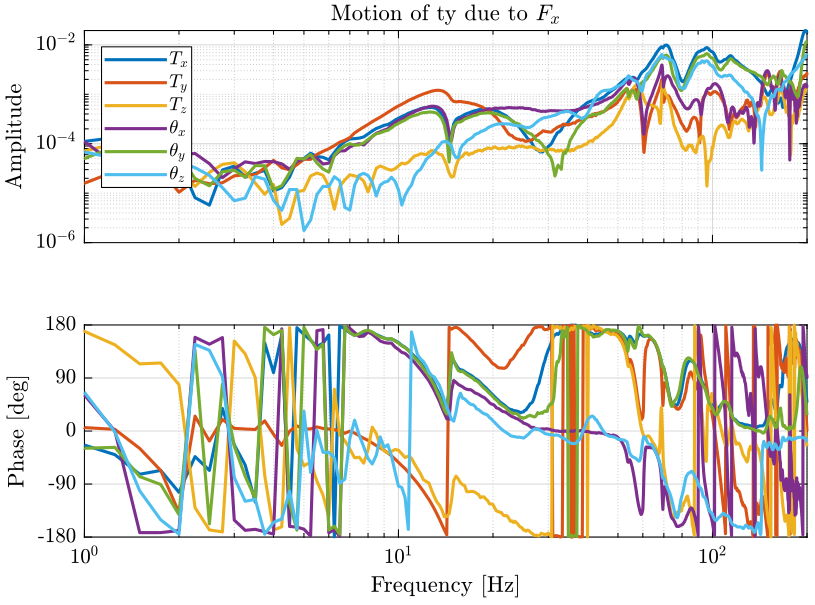
The FRF for accelerometers located on the translation stage are compared on figure 6. The FRF are matching well until 100Hz.

Figure 5: Comparison of the original FRF with the recovered ones - Hexapod
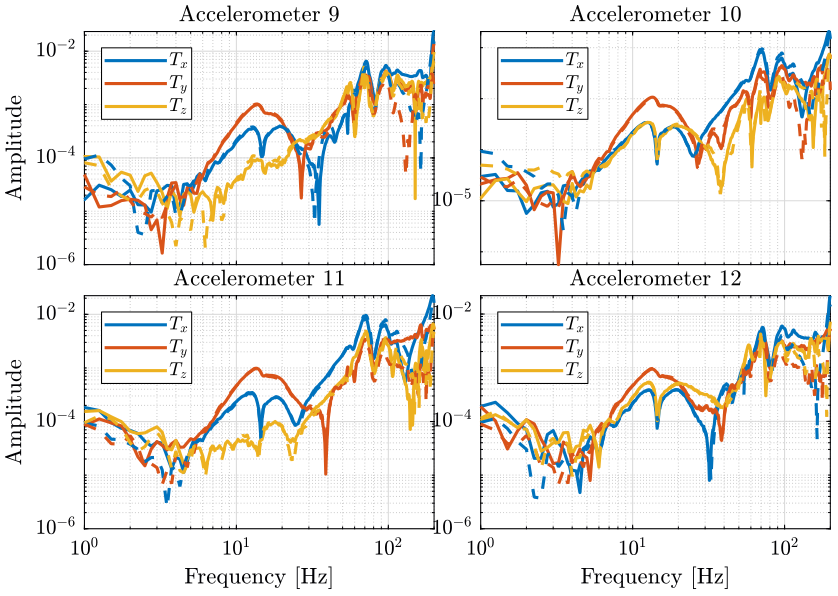
Figure 6: Comparison of the original FRF with the recovered ones - Ty
The reduction of the number of degrees of freedom from 69 (23 accelerometers with each 3DOF) to 36 (6 solid bodies with 6 DOF) seems to work well.
This confirms the fact that the stages are indeed behaving as a solid body in the frequency band of interest. This valid the fact that a multi-body model can be used to represent the dynamics of the micro-station.