Measurement Analysis
Table of Contents
- 1. Measurement Description
- 2. Importation of the data
- 3. Variables for analysis
- 4. Measurement 1 - Effect of Ty stage
- 5. Measurement 2 - Effect of Ry stage
- 6. Measurement 3 - Effect of the Hexapod
- 7. Measurement 4 - Effect of the Splip-Ring and Spindle
- 8. Measurement 5 - Transmission from ground to marble
1 Measurement Description

Figure 1: Picture of the setup for the measurement
Sensors:
- 3 L-4C (Documentation) table
Each motor are turn off and then on.
The goal is to see what noise is injected in the system due to the regulation loop of each stage.
2 Importation of the data
First, load all the measurement files:
meas = {}; meas{1} = load('./mat/Measurement1.mat'); meas{2} = load('./mat/Measurement2.mat'); meas{3} = load('./mat/Measurement3.mat'); meas{4} = load('./mat/Measurement4.mat'); meas{5} = load('./mat/Measurement5.mat');
Change the track name for measurements 3 and 4.
meas{3}.Track1_Name = 'Input 1: Hexa Z'; meas{4}.Track1_Name = 'Input 1: Hexa Z';
For the measurements 1 to 4, the measurement channels are shown table 1.
| Channel 1 | Channel 2 | Channel 3 | |
|---|---|---|---|
| Meas. 1 | Input 1: tilt1 Z | Input 2: tilt2 Z | Input 3: Ty Y |
| Meas. 2 | Input 1: tilt1 Z | Input 2: tilt2 Z | Input 3: Ty Y |
| Meas. 3 | Input 1: Hexa Z | Input 2: tilt2 Z | Input 3: Ty Y |
| Meas. 4 | Input 1: Hexa Z | Input 2: tilt2 Z | Input 3: Ty Y |
For the measurement 5, the channels are shown table 2.
| Channel 1 | Channel 2 | Channel 3 | Channel 4 | |
|---|---|---|---|---|
| Meas. 5 | Input 1: Floor Z | Input 2: Marble Z | Input 3: Floor Y | Input 4: Marble Y |
When using two geophone sensors on the same tilt stage (measurements 1 and 2), we post-process the data to obtain the z displacement and the rotation of the tilt stage:
meas1_z = (meas{1}.Track1+meas{1}.Track2)/2; meas1_tilt = (meas{1}.Track1-meas{1}.Track2)/2; meas{1}.Track1 = meas1_z; meas{1}.Track1_Y_Magnitude = 'Meter / second'; meas{1}.Track1_Name = 'Ry Z'; meas{1}.Track2 = meas1_tilt; meas{1}.Track2_Y_Magnitude = 'Rad / second'; meas{1}.Track2_Name = 'Ry Tilt'; meas2_z = (meas{2}.Track1+meas{2}.Track2)/2; meas2_tilt = (meas{2}.Track1-meas{2}.Track2)/2; meas{2}.Track1 = meas2_z; meas{2}.Track1_Y_Magnitude = 'Meter / second'; meas{2}.Track1_Name = 'Ry Z'; meas{2}.Track2 = meas2_tilt; meas{2}.Track2_Y_Magnitude = 'Rad / second'; meas{2}.Track2_Name = 'Ry Tilt';
3 Variables for analysis
We define the sampling frequency and the time vectors for the plots.
Fs = 256; % [Hz] dt = 1/(Fs); t1 = dt*[1:length(meas{1}.Track1)]; t2 = dt*[1:length(meas{2}.Track1)]; t3 = dt*[1:length(meas{3}.Track1)]; t4 = dt*[1:length(meas{4}.Track1)]; t5 = dt*[1:length(meas{5}.Track1)];
For the frequency analysis, we define the frequency limits for the plot.
fmin = 1; % [Hz] fmax = 100; % [Hz]
Then we define the windows that will be used to average the results.
psd_window = hanning(2*fmin/dt);
4 Measurement 1 - Effect of Ty stage
The configuration for this measurement is shown table 3.
| Time | 0-309 | 309-end |
|---|---|---|
| Ty | OFF | ON |
We then plot the measurements in time domain (figure 2).
We observe strange behavior when the Ty stage is turned on. How can we explain that?
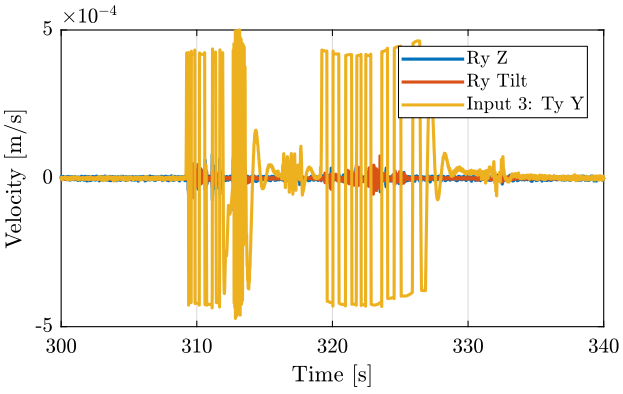
Figure 2: Time domain - measurement 1
To understand what is going on, instead of looking at the velocity, we can look at the displacement by integrating the data. The displacement is computed by integrating the velocity using cumtrapz function.
tdisp = t1(ceil(300/dt):ceil(340/dt)); xdisp = cumtrapz(tdisp, meas{1}.Track3(ceil(300/dt):ceil(340/dt)));
Then we plot the position with respect to time (figure 3).
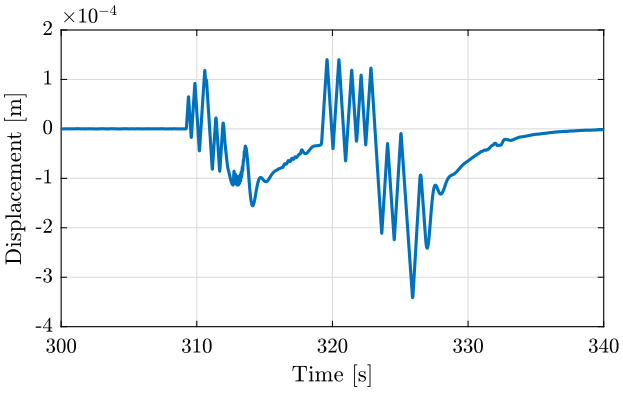
Figure 3: Y displacement of the Ty stage
We when compute the power spectral density of each measurement before and after turning on the stage.
[pxx111, f111] = pwelch(meas{1}.Track1(1:ceil(300/dt)), psd_window, [], [], Fs); [pxx112, f112] = pwelch(meas{1}.Track1(ceil(350/dt):end), psd_window, [], [], Fs); [pxx121, f121] = pwelch(meas{1}.Track2(1:ceil(300/dt)), psd_window, [], [], Fs); [pxx122, f122] = pwelch(meas{1}.Track2(ceil(350/dt):end), psd_window, [], [], Fs); [pxx131, f131] = pwelch(meas{1}.Track3(1:ceil(300/dt)), psd_window, [], [], Fs); [pxx132, f132] = pwelch(meas{1}.Track3(ceil(350/dt):end), psd_window, [], [], Fs);
We finally plot the power spectral density of each track (figures 4, 5, 6).
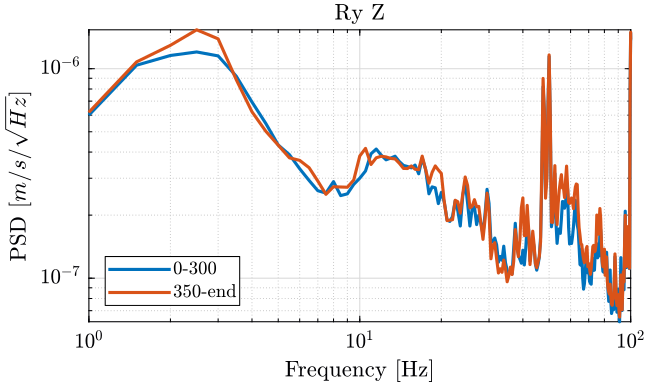
Figure 4: PSD of the Z velocity of Ry stage - measurement 1
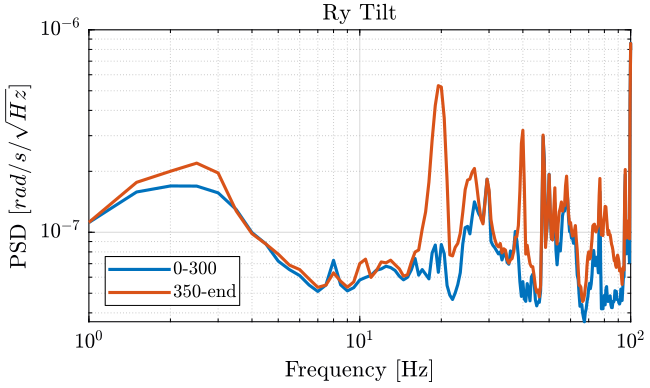
Figure 5: PSD of the Rotation of Ry Stage - measurement 1
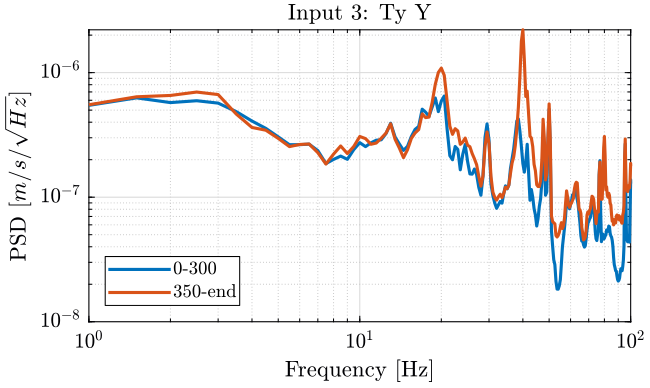
Figure 6: PSD of the Ty velocity in the Y direction - measurement 1
Turning on the Y-translation stage increases the velocity of the Ty stage in the Y direction and the rotation motion of the tilt stage:
- at 20Hz
- at 40Hz
- between 80Hz and 90Hz
It does not seems to have any effect on the Z motion of the tilt stage.
5 Measurement 2 - Effect of Ry stage
The tilt stage is turned ON at around 326 seconds (table 4).
| Time | 0-326 | 326-end |
|---|---|---|
| Tilt | OFF | ON |
We plot the time domain (figure 7) and we don't observe anything special in the time domain.
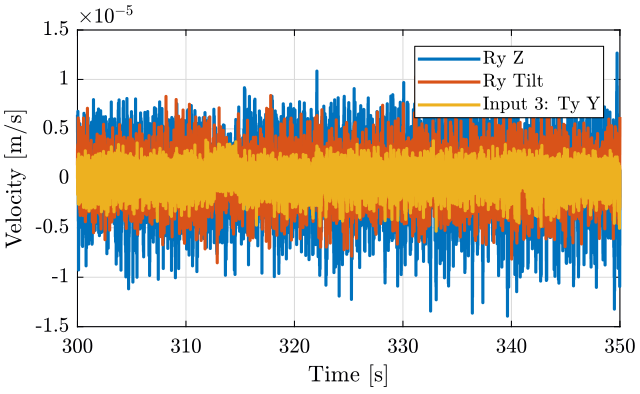
Figure 7: Time domain - measurement 2
We compute the PSD of each track and we plot them (figures 8, 9 and 10 ).
[pxx211, f211] = pwelch(meas{2}.Track1(1:ceil(326/dt)), psd_window, [], [], Fs); [pxx212, f212] = pwelch(meas{2}.Track1(ceil(326/dt):end), psd_window, [], [], Fs); [pxx221, f221] = pwelch(meas{2}.Track2(1:ceil(326/dt)), psd_window, [], [], Fs); [pxx222, f222] = pwelch(meas{2}.Track2(ceil(326/dt):end), psd_window, [], [], Fs); [pxx231, f231] = pwelch(meas{2}.Track3(1:ceil(326/dt)), psd_window, [], [], Fs); [pxx232, f232] = pwelch(meas{2}.Track3(ceil(326/dt):end), psd_window, [], [], Fs);
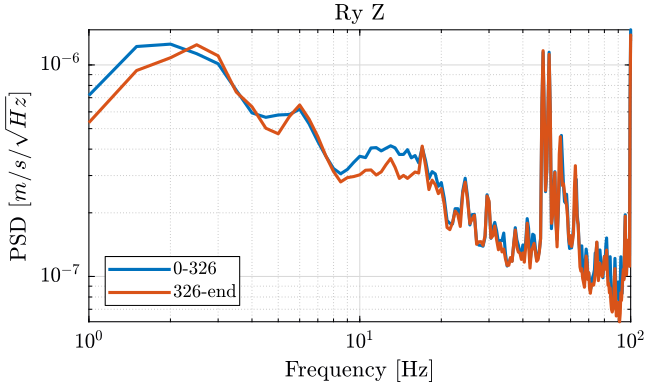
Figure 8: PSD of the Z velocity of Ry Stage - measurement 2
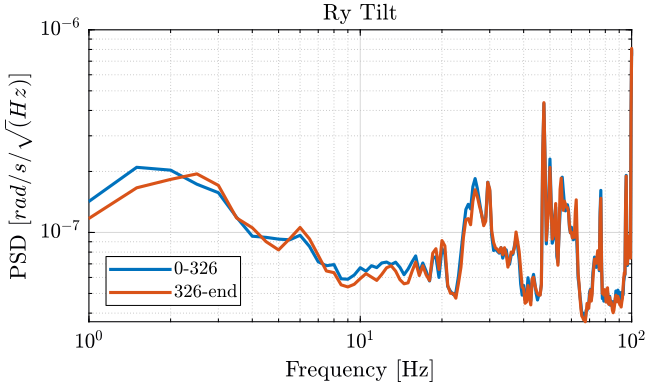
Figure 9: PSD of the Rotation motion of Ry Stage - measurement 2

Figure 10: PSD of the Ty velocity in the Y direction - measurement 2
We observe no noticeable difference when the Tilt-stage is turned ON expect a small decrease of the Z motion of the tilt stage around 10Hz.
6 Measurement 3 - Effect of the Hexapod
The hexapod is turned off after 406 seconds (table 5).
| Time | 0-406 | 406-end |
|---|---|---|
| Tilt | ON | ON |
| Hexa | ON | OFF |
The time domain result is shown figure 11.

Figure 11: Time domain - measurement 3
We then compute the PSD of each track before and after turning off the hexapod and plot the results in the figures 12, 13 and 14.
[pxx311, f311] = pwelch(meas{3}.Track1(1:ceil(400/dt)), psd_window, [], [], Fs); [pxx312, f312] = pwelch(meas{3}.Track1(ceil(420/dt):end), psd_window, [], [], Fs); [pxx321, f321] = pwelch(meas{3}.Track2(1:ceil(400/dt)), psd_window, [], [], Fs); [pxx322, f322] = pwelch(meas{3}.Track2(ceil(420/dt):end), psd_window, [], [], Fs); [pxx331, f331] = pwelch(meas{3}.Track3(1:ceil(400/dt)), psd_window, [], [], Fs); [pxx332, f332] = pwelch(meas{3}.Track3(ceil(420/dt):end), psd_window, [], [], Fs);
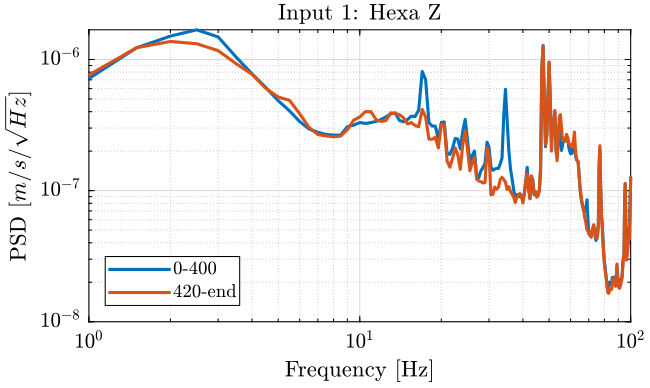
Figure 12: PSD of the Z velocity of the Hexapod - measurement 3
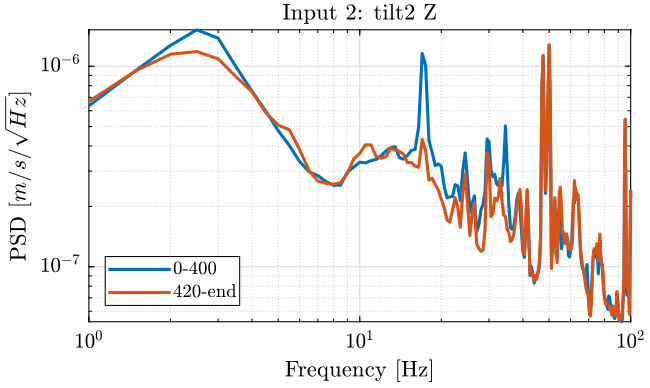
Figure 13: PSD of the Z velocity of the Ry stage - measurement 3
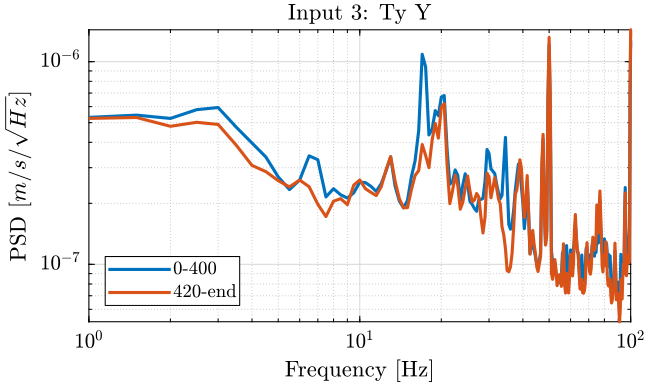
Figure 14: PSD of the Ty velocity in the Y direction - measurement 3
7 Measurement 4 - Effect of the Splip-Ring and Spindle
The slip ring is turned on at 300s, then the spindle is turned on at 620s (table 6). The time domain signals are shown figure 15.
| Time | 0-300 | 300-620 | 620-end |
|---|---|---|---|
| SlipRing | OFF | ON | ON |
| Hexa | OFF | OFF | OFF |
| Spindle | OFF | OFF | ON |
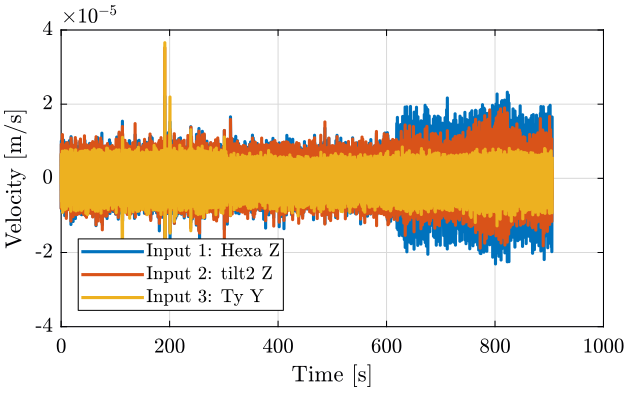
Figure 15: Time domain - measurement 4
The PSD of each track are computed using the code below.
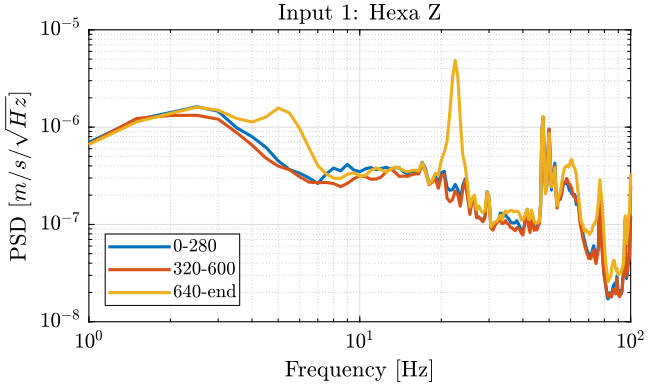
Figure 16: PSD of the Z velocity of the Hexapod - measurement 4

Figure 17: PSD of the Ry rotation in the Y direction - measurement 4
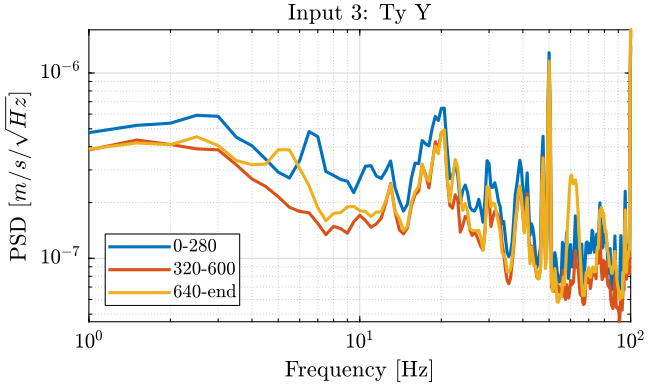
Figure 18: PSD of the Ty velocity in the Y direction - measurement 4
Turning ON the splipring seems to not add motions on the stages measured. It even seems to lower the motion of the Ty stage (figure 18): does that make any sense?
Turning ON the spindle induces motions:
- at 5Hz on each motion measured
- at 22.5Hz on the Z motion of the Hexapod. Can this is due to some 50Hz?
- at 62Hz on each motion measured
8 Measurement 5 - Transmission from ground to marble
This measurement just consists of measurement of Y-Z motion of the ground and the marble.
The time domain signals are shown on figure 19.
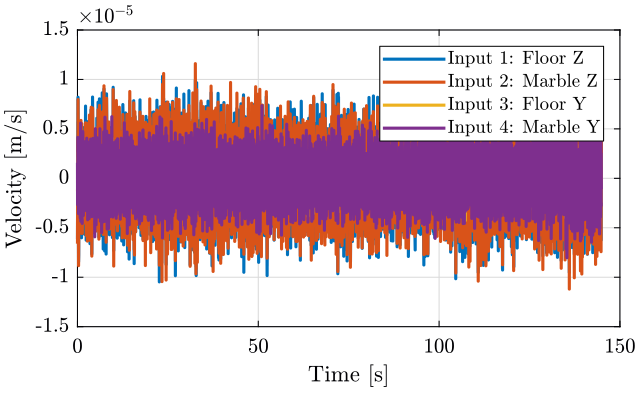
Figure 19: Time domain - measurement 5
We compute the PSD of each track and we plot the PSD of the Z motion for the ground and marble on figure 20 and for the Y motion on figure 21.
[pxx51, f51] = pwelch(meas{5}.Track1(:), psd_window, [], [], Fs); [pxx52, f52] = pwelch(meas{5}.Track2(:), psd_window, [], [], Fs); [pxx53, f53] = pwelch(meas{5}.Track3(:), psd_window, [], [], Fs); [pxx54, f54] = pwelch(meas{5}.Track4(:), psd_window, [], [], Fs);
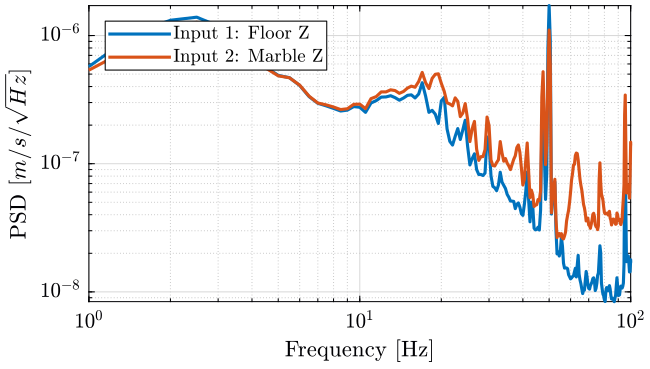
Figure 20: PSD of the ground and marble in the Z direction
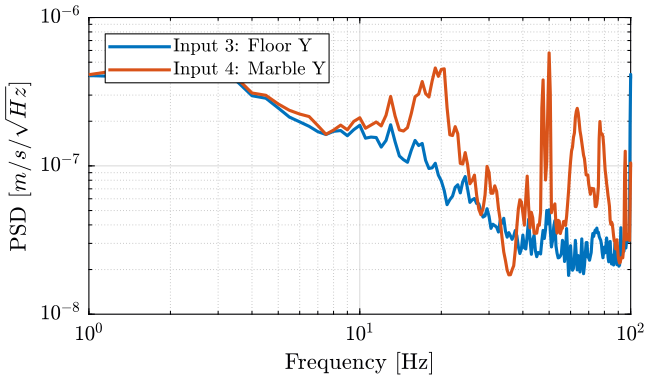
Figure 21: PSD of the ground and marble in the Y direction
Then, instead of looking at the Power Spectral Density, we can try to estimate the transfer function from a ground motion to the motion of the marble. The transfer functions are shown on figure 22 and the coherence on figure 23.
[tfz, fz] = tfestimate(meas{5}.Track1(:), meas{5}.Track2(:), psd_window, [], [], Fs); [tfy, fy] = tfestimate(meas{5}.Track3(:), meas{5}.Track4(:), psd_window, [], [], Fs);
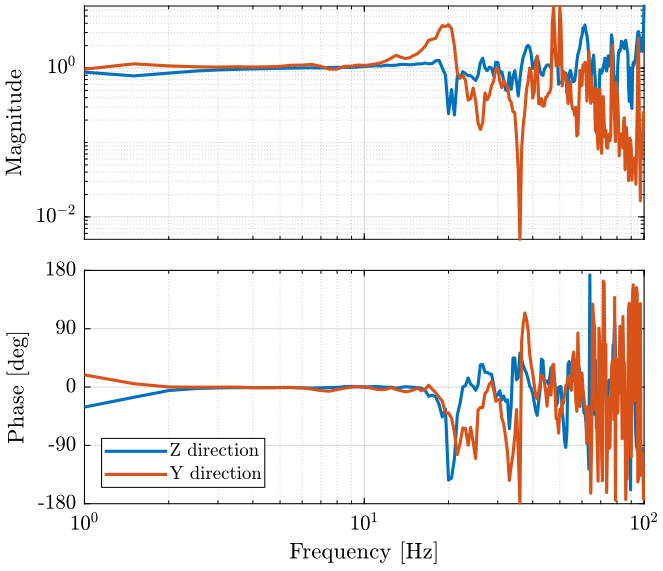
Figure 22: Transfer function estimation - measurement 5
[cohz, fz] = mscohere(meas{5}.Track1(:), meas{5}.Track2(:), psd_window, [], [], Fs); [cohy, fy] = mscohere(meas{5}.Track3(:), meas{5}.Track4(:), psd_window, [], [], Fs);

Figure 23: Coherence - measurement 5
The marble seems to have a resonance at around 20Hz on the Y direction. But the coherence is not good above 20Hz, so it is difficult to estimate resonances.