Measurements

1. Effect of the rotation of the Slip-Ring
2. Measure of the noise of the Voltage Amplifier
3. Measure of the noise induced by the Slip-Ring
4. Measure of the noise induced by the slip ring when using a geophone
5. Measure of the influence of the AC/DC option on the voltage amplifiers
6. Measure of the Low Pass Filter

1 Effect of the rotation of the Slip-Ring

The data and matlab files are accessible here.

1.1 Measurement Description

Random Signal is generated by one DAC of the SpeedGoat.

The signal going out of the DAC is split into two:

one BNC cable is directly connected to one ADC of the SpeedGoat
one BNC cable goes two times in the Slip-Ring (from bottom to top and then from top to bottom) and then is connected to one ADC of the SpeedGoat

Two measurements are done.

Data File	Description
`mat/data_001.mat`	Slip-ring not turning
`mat/data_002.mat`	Slip-ring turning

For each measurement, the measured signals are:

Data File	Description
`t`	Time vector
`x1`	Direct signal
`x2`	Signal going through the Slip-Ring

The goal is to determine is the signal is altered when the spindle is rotating.

Here, the rotation speed of the Slip-Ring is set to 1rpm.

1.2 Load data

We load the data of the z axis of two geophones.

sr_off = load('mat/data_001.mat', 't', 'x1', 'x2');
sr_on  = load('mat/data_002.mat', 't', 'x1', 'x2');

1.3 Analysis

Let's first look at the signal produced by the DAC (figure 1).

figure;
hold on;
plot(sr_on.t,  sr_on.x1);
hold off;
xlabel('Time [s]'); ylabel('Voltage [V]');
xlim([0 10]);

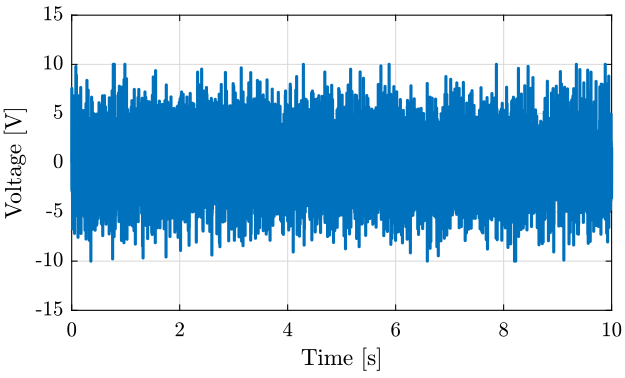
Figure 1: Random signal produced by the DAC

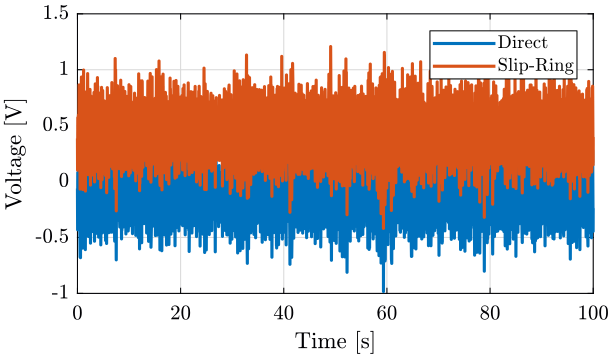
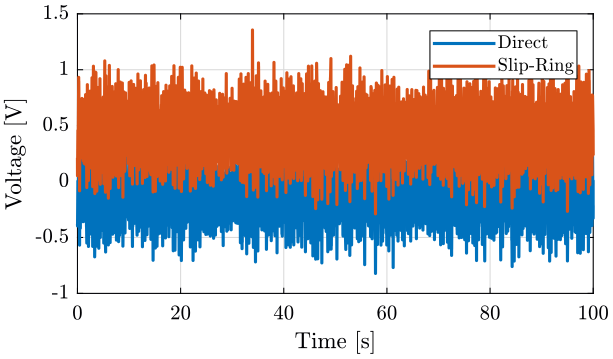
We now look at the difference between the signal directly measured by the ADC and the signal that goes through the slip-ring (figure 2).

figure;
hold on;
plot(sr_on.t,  sr_on.x1  -  sr_on.x2,  'DisplayName', 'Slip-Ring - $\omega = 1rpm$');
plot(sr_off.t, sr_off.x1 - sr_off.x2,'DisplayName', 'Slip-Ring off');
hold off;
xlabel('Time [s]'); ylabel('Voltage [V]');
xlim([0 10]);
legend('Location', 'northeast');

Figure 2: Alteration of the signal when the slip-ring is turning

dt = sr_on.t(2) - sr_on.t(1);
Fs = 1/dt; % [Hz]

win = hanning(ceil(1*Fs));

[pxx_on,  f] = pwelch(sr_on.x1  - sr_on.x2,  win, [], [], Fs);
[pxx_off, ~] = pwelch(sr_off.x1 - sr_off.x2, win, [], [], Fs);

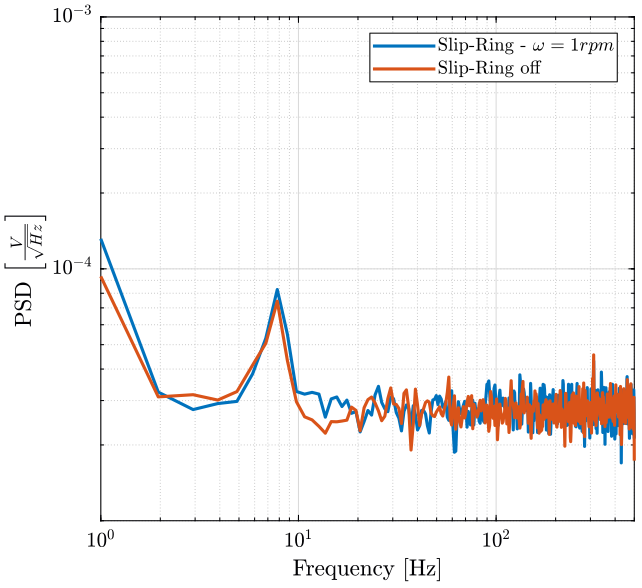
Figure 3: ASD of the measured noise

1.4 Conclusion

Remaining questions:

Should the measurement be redone using voltage amplifiers?
Use higher rotation speed and measure for longer periods (to have multiple revolutions) ?

2 Measure of the noise of the Voltage Amplifier

The data and matlab files are accessible here.

2.1 Measurement Description

Goal:

Determine the Voltage Amplifier noise

Setup:

The two inputs (differential) of the voltage amplifier are shunted with 50Ohms
The AC/DC option of the Voltage amplifier is on AC
The low pass filter is set to 1hHz
We measure the output of the voltage amplifier with a 16bits ADC of the Speedgoat

Measurements:

data_003: Ampli OFF
data_004: Ampli ON set to 20dB
data_005: Ampli ON set to 40dB
data_006: Ampli ON set to 60dB

2.2 Load data

amp_off = load('mat/data_003.mat', 'data'); amp_off = amp_off.data(:, [1,3]);
amp_20d = load('mat/data_004.mat', 'data'); amp_20d = amp_20d.data(:, [1,3]);
amp_40d = load('mat/data_005.mat', 'data'); amp_40d = amp_40d.data(:, [1,3]);
amp_60d = load('mat/data_006.mat', 'data'); amp_60d = amp_60d.data(:, [1,3]);

2.3 Time Domain

The time domain signals are shown on figure 4.

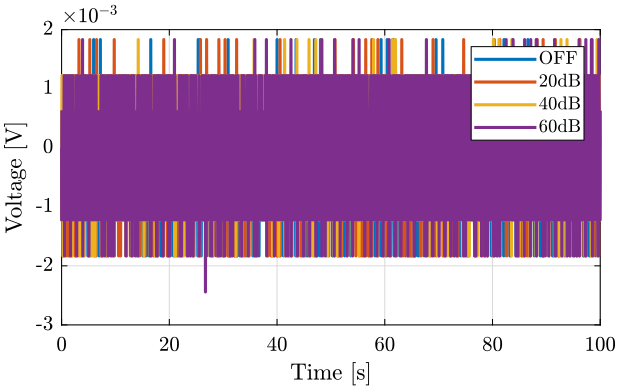
Figure 4: Output of the amplifier

2.4 Frequency Domain

We first compute some parameters that will be used for the PSD computation.

dt = amp_off(2, 2)-amp_off(1, 2);

Fs = 1/dt; % [Hz]

win = hanning(ceil(10*Fs));

Then we compute the Power Spectral Density using pwelch function.

[pxoff, f] = pwelch(amp_off(:,1), win, [], [], Fs);
[px20d, ~] = pwelch(amp_20d(:,1), win, [], [], Fs);
[px40d, ~] = pwelch(amp_40d(:,1), win, [], [], Fs);
[px60d, ~] = pwelch(amp_60d(:,1), win, [], [], Fs);

We compute the theoretical ADC noise.

q = 20/2^16; % quantization
Sq = q^2/12/1000; % PSD of the ADC noise

Finally, the ASD is shown on figure 5.

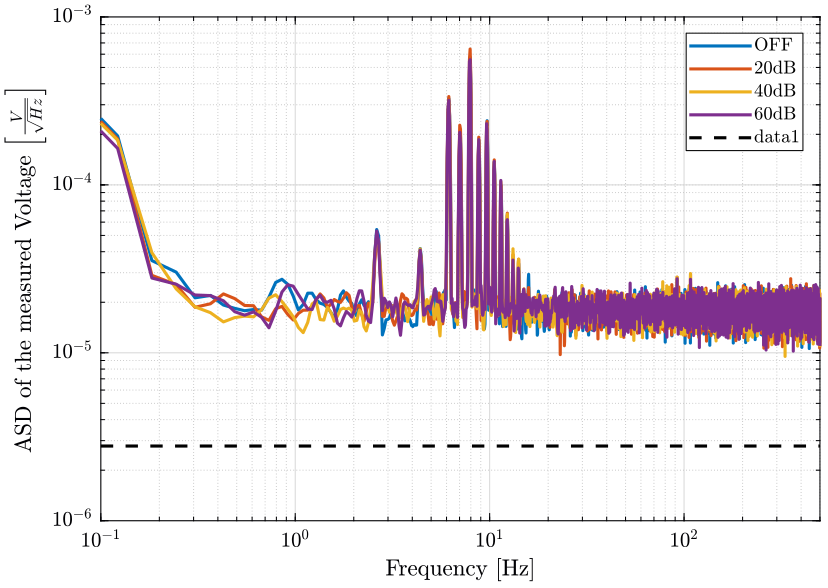
Figure 5: Amplitude Spectral Density of the measured voltage at the output of the voltage amplifier

2.5 Conclusion

Noise induced by the voltage amplifiers is not a limiting factor.

3 Measure of the noise induced by the Slip-Ring

The data and matlab files are accessible here.

3.1 Measurement Description

Goal:

Determine the noise induced by the slip-ring

Setup:

0V is generated by the DAC of the Speedgoat
Using a T, one part goes directly to the ADC
The other part goes to the slip-ring 2 times and then to the ADC
The parameters of the Voltage Amplifier are: 80dB, AC, 1kHz
Every stage of the station is OFF

First column: Direct measure Second column: Slip-ring measure

Measurements:

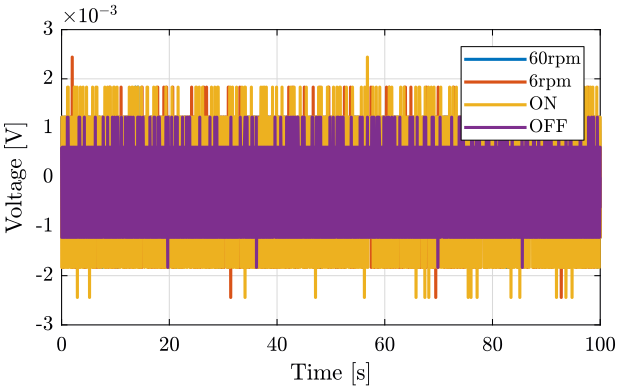
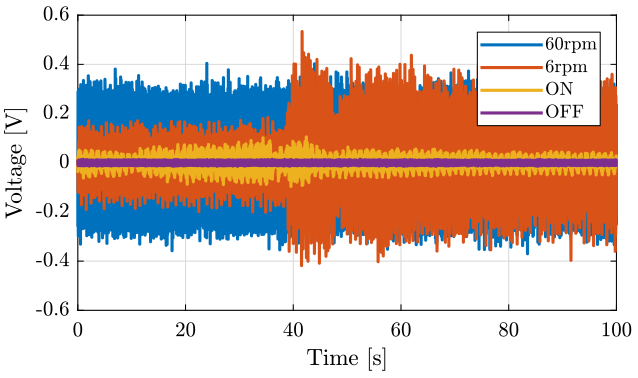
data_008: Slip-Ring OFF
data_009: Slip-Ring ON
data_010: Slip-Ring ON and omega=6rpm
data_011: Slip-Ring ON and omega=60rpm

Figure 6: Slip-Ring rotating at 6rpm

Figure 7: Slip-Ring rotating at 60rpm

3.2 Load data

We load the data of the z axis of two geophones.

sr_off = load('mat/data_008.mat', 'data'); sr_off = sr_off.data;
sr_on  = load('mat/data_009.mat', 'data'); sr_on  = sr_on.data;
sr_6r  = load('mat/data_010.mat', 'data'); sr_6r  = sr_6r.data;
sr_60r = load('mat/data_011.mat', 'data'); sr_60r = sr_60r.data;

3.3 Time Domain

We plot the time domain data for the direct measurement (figure 8) and for the signal going through the slip-ring (figure 9);

Figure 8: Direct measurement

Figure 9: Measurement of the signal going through the Slip-Ring

3.4 Frequency Domain

We first compute some parameters that will be used for the PSD computation.

dt = sr_off(2, 3)-sr_off(1, 3);

Fs = 1/dt; % [Hz]

win = hanning(ceil(10*Fs));

Then we compute the Power Spectral Density using pwelch function.

[pxdir, f] = pwelch(sr_off(:, 1), win, [], [], Fs);
[pxoff, ~] = pwelch(sr_off(:, 2), win, [], [], Fs);
[pxon,  ~] = pwelch(sr_on(:, 2),  win, [], [], Fs);
[px6r,  ~] = pwelch(sr_6r(:, 2),  win, [], [], Fs);
[px60r, ~] = pwelch(sr_60r(:, 2), win, [], [], Fs);

And we plot the ASD of the measured signals (figure 10);

figure;
hold on;
plot(f, sqrt(pxoff), 'DisplayName', 'OFF');
plot(f, sqrt(pxon),  'DisplayName', 'ON');
plot(f, sqrt(px6r),  'DisplayName', '6rpm');
plot(f, sqrt(px60r), 'DisplayName', '60rpm');
plot(f, sqrt(pxdir), 'k-', 'DisplayName', 'Direct');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'northeast');
xlim([0.1, 500]);

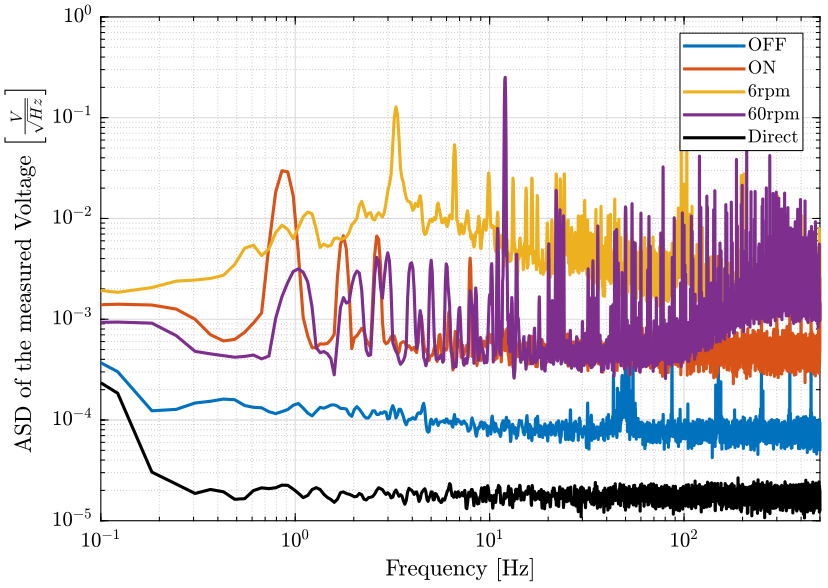
Figure 10: Comparison of the ASD of the measured signals when the slip-ring is ON, OFF and turning

3.5 Conclusion

4 Measure of the noise induced by the slip ring when using a geophone

The data and matlab files are accessible here.

4.1 First Measurement without LPF

4.1.1 Measurement Description

Goal:

Determine if the noise induced by the slip-ring is a limiting factor when measuring the signal coming from a geophone

Setup:

The geophone is located at the sample location
The two Voltage amplifiers have the same following settings:
- AC
- 60dB
- 1kHz
The signal from the geophone is split into two using a T-BNC:
- One part goes directly to the voltage amplifier and then to the ADC.
- The other part goes to the slip-ring=>voltage amplifier=>ADC.

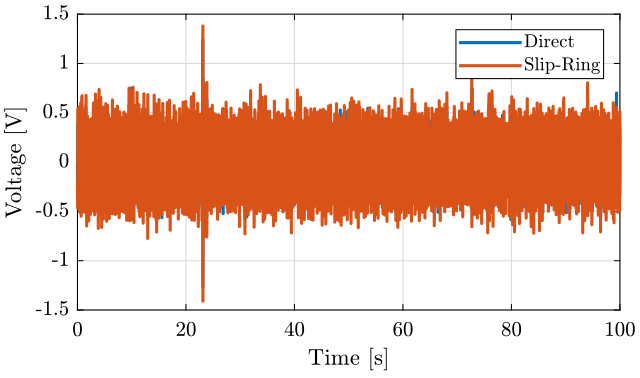
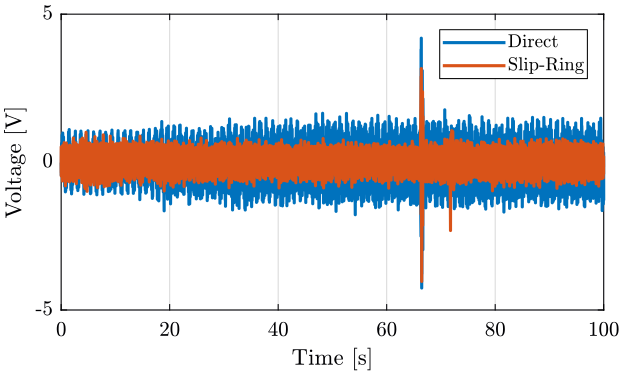
First column: Direct measure Second column: Slip-ring measure

Measurements:

data_012: Slip-Ring OFF
data_013: Slip-Ring ON

4.1.2 Load data

We load the data of the z axis of two geophones.

sr_off = load('mat/data_012.mat', 'data'); sr_off = sr_off.data;
sr_on  = load('mat/data_013.mat', 'data'); sr_on  = sr_on.data;

4.1.3 Time Domain

We compare the signal when the Slip-Ring is OFF (figure 11) and when it is ON (figure 12).

Figure 11: Comparison of the time domain signals when the slip-ring is OFF

Figure 12: Comparison of the time domain signals when the slip-ring is ON

4.1.4 Frequency Domain

We first compute some parameters that will be used for the PSD computation.

dt = sr_off(2, 3)-sr_off(1, 3);

Fs = 1/dt; % [Hz]

win = hanning(ceil(10*Fs));

Then we compute the Power Spectral Density using pwelch function.

% Direct measure
[pxdoff, ~] = pwelch(sr_off(:, 1), win, [], [], Fs);
[pxdon,  ~] = pwelch(sr_on(:, 1),  win, [], [], Fs);

% Slip-Ring measure
[pxsroff, f] = pwelch(sr_off(:, 2), win, [], [], Fs);
[pxsron,  ~] = pwelch(sr_on(:, 2),  win, [], [], Fs);

Finally, we compare the Amplitude Spectral Density of the signals (figure 13);

figure;
hold on;
plot(f, sqrt(pxdoff), 'DisplayName', 'Direct - OFF');
plot(f, sqrt(pxsroff), 'DisplayName', 'Slip-Ring - OFF');
plot(f, sqrt(pxdon),  'DisplayName', 'Direct - ON');
plot(f, sqrt(pxsron),  'DisplayName', 'Slip-Ring - ON');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'northeast');
xlim([0.1, 500]);

Figure 13: Comparison of the Amplitude Spectral Sensity

Figure 14: Comparison of the Amplitude Spectral Sensity - Zoom

4.1.5 Conclusion

The fact that the Slip-Ring is turned ON adds some noise to the signal.
The signal going through the Slip-Ring is less noisy than the one going directly to the ADC.
This could be due to less good electromagnetic isolation.

Questions:

Can the sharp peak on figure 14 be due to the Aliasing?

4.2 Measurement using an oscilloscope

4.2.1 Measurement Setup

Know we are measuring the same signals but using an oscilloscope instead of the Speedgoat ADC.

4.2.2 Observations

Then the Slip-Ring is ON (figure 15), we observe a signal at 40kHz with a peak-to-peak amplitude of 200mV for the direct measure and 100mV for the signal going through the Slip-Ring.

Then the Slip-Ring is OFF, we don't observe this 40kHz anymore (figure 16).

Figure 15: Signals measured by the oscilloscope - Slip-Ring ON - Yellow: Direct measure - Blue: Through Slip-Ring

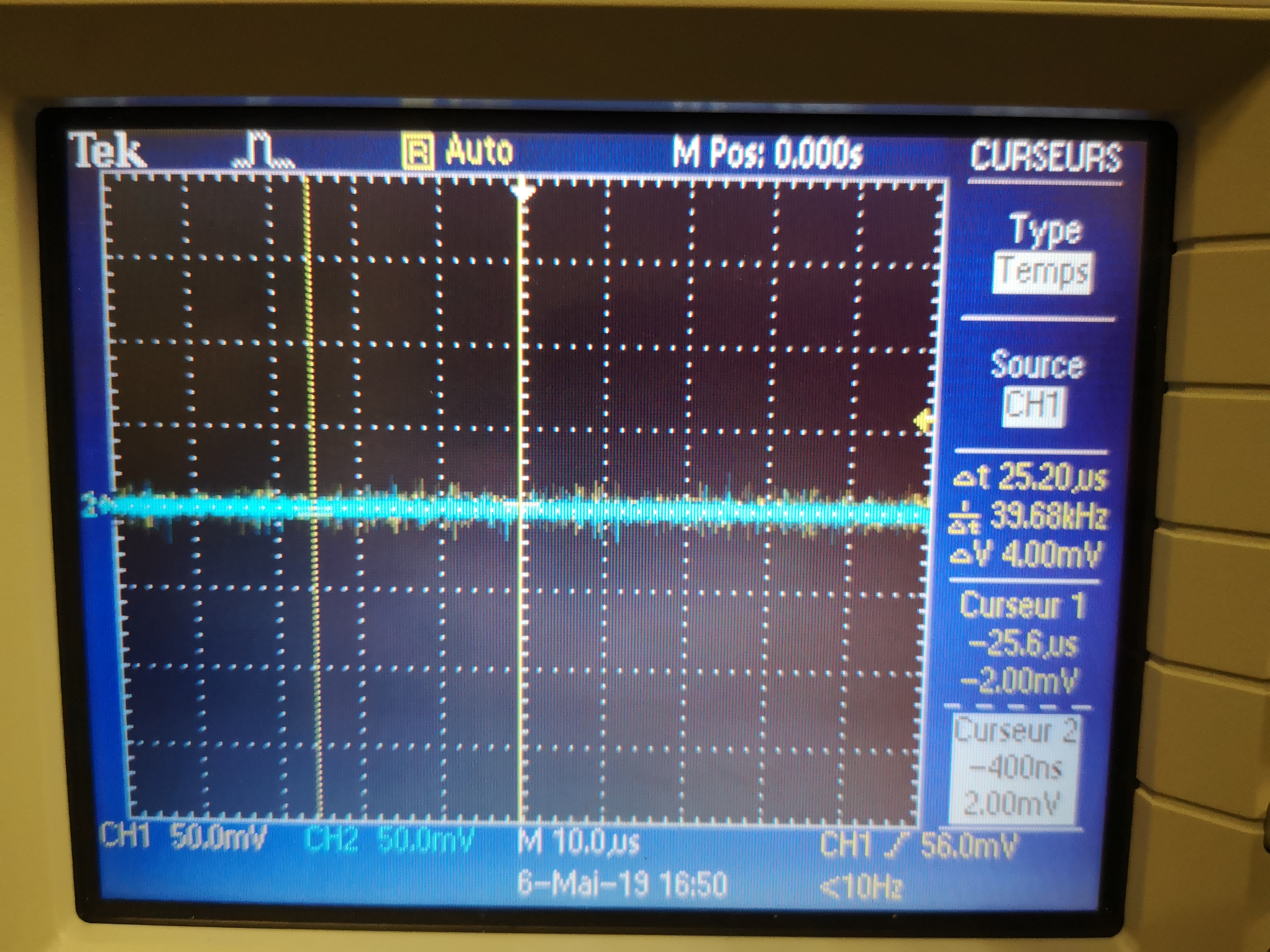
Figure 16: Signals measured by the oscilloscope - Slip-Ring OFF - Yellow: Direct measure - Blue: Through Slip-Ring

4.2.3 Conclusion

By looking at the signals using an oscilloscope, there is a lot of high frequency noise when turning on the Slip-Ring
This can eventually saturate the voltage amplifiers (seen by a led indicating saturation)
The choice is to add a Low pass filter before the voltage amplifiers to not saturate them and filter the noise.

4.3 New measurements with a LPF before the Voltage Amplifiers

4.3.1 Setup description

A first order low pass filter is added before the Voltage Amplifiers with the following values:

\begin{aligned} R &= 1k\Omega \\ C &= 1\mu F \end{aligned}

And we have a cut-off frequency of \(f_c = \frac{1}{RC} = 160Hz\).

We are measuring the signal from a geophone put on the marble with and without the added LPF:

with the slip ring OFF: mat/data_016.mat
with the slip ring ON: mat/data_017.mat

4.3.2 Load data

We load the data of the z axis of two geophones.

sr_lpf_off = load('mat/data_016.mat', 'data'); sr_lpf_off = sr_lpf_off.data;
sr_lpf_on  = load('mat/data_017.mat', 'data'); sr_lpf_on  = sr_lpf_on.data;

4.3.3 Time Domain

We compare the signal when the Slip-Ring is OFF (figure 17) and when it is ON (figure 18).

Figure 17: Comparison of the time domain signals when the slip-ring is OFF

Figure 18: Comparison of the time domain signals when the slip-ring is ON

4.3.4 Frequency Domain

We first compute some parameters that will be used for the PSD computation.

dt = sr_lpf_off(2, 3)-sr_lpf_off(1, 3);

Fs = 1/dt; % [Hz]

win = hanning(ceil(10*Fs));

Then we compute the Power Spectral Density using pwelch function.

% Direct measure
[pxd_lpf_off, ~] = pwelch(sr_lpf_off(:, 1), win, [], [], Fs);
[pxd_lpf_on,  ~] = pwelch(sr_lpf_on(:, 1),  win, [], [], Fs);

% Slip-Ring measure
[pxsr_lpf_off, f] = pwelch(sr_lpf_off(:, 2), win, [], [], Fs);
[pxsr_lpf_on,  ~] = pwelch(sr_lpf_on(:, 2),  win, [], [], Fs);

Finally, we compare the Amplitude Spectral Density of the signals (figure 19);

figure;
hold on;
plot(f, sqrt(pxd_lpf_off), 'DisplayName', 'Direct - OFF');
plot(f, sqrt(pxsr_lpf_off), 'DisplayName', 'Slip-Ring - OFF');
plot(f, sqrt(pxd_lpf_on),  'DisplayName', 'Direct - ON');
plot(f, sqrt(pxsr_lpf_on),  'DisplayName', 'Slip-Ring - ON');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'northeast');
xlim([0.1, 500]);

Figure 19: Comparison of the Amplitude Spectral Sensity

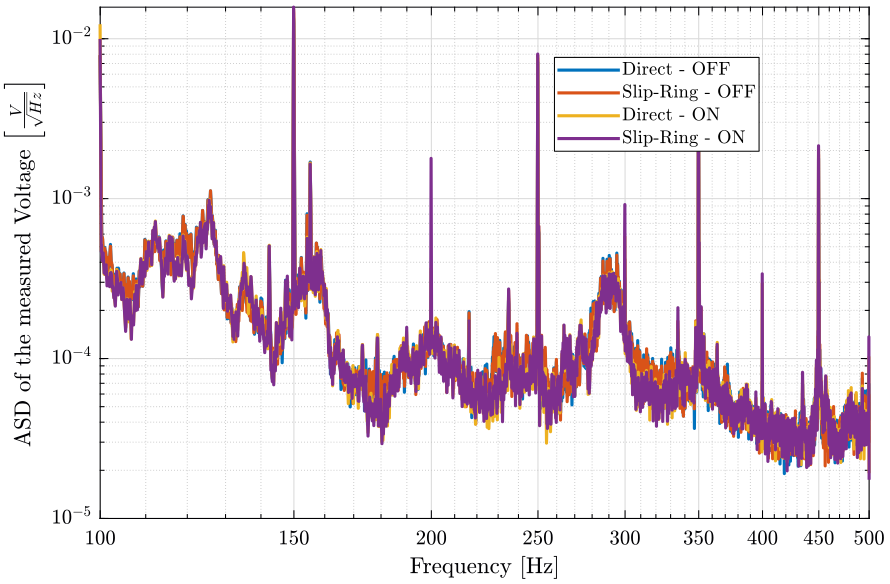
Figure 20: Comparison of the Amplitude Spectral Sensity - Zoom

4.3.5 Comparison of with and without LPF

figure;
hold on;
plot(f, sqrt(pxdon),  'DisplayName', 'Direct - ON');
plot(f, sqrt(pxsron),  'DisplayName', 'Slip-Ring - ON');
plot(f, sqrt(pxd_lpf_on),  'DisplayName', 'Direct - ON - LPF');
plot(f, sqrt(pxsr_lpf_on),  'DisplayName', 'Slip-Ring - ON - LPF');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'northeast');
xlim([0.1, 500]);

Figure 21: Comparison of the measured signals with and without LPF

4.3.6 Conclusion

Using the LPF, we don't have any perturbation coming from the slip-ring when it is on.
However, we will use a smaller value of the capacitor to have a cut-off frequency at \(1kHz\).

5 Measure of the influence of the AC/DC option on the voltage amplifiers

The data and matlab files are accessible here.

5.1 Measurement Description

Goal:

Measure the influence of the high-pass filter option of the voltage amplifiers

Setup:

One geophone is located on the marble.
It's signal goes to two voltage amplifiers with a gain of 60dB.
One voltage amplifier is on the AC option, the other is on the DC option.

Measurements: First measurement (mat/data_014.mat file):

Column	Signal
1	Amplifier 1 with AC option
2	Amplifier 2 with DC option
3	Time

Second measurement (mat/data_015.mat file):

Column	Signal
1	Amplifier 1 with DC option
2	Amplifier 2 with AC option
3	Time

Figure 22: Picture of the two voltages amplifiers

5.2 Load data

We load the data of the z axis of two geophones.

meas14 = load('mat/data_014.mat', 'data'); meas14 = meas14.data;
meas15 = load('mat/data_015.mat', 'data'); meas15 = meas15.data;

5.3 Time Domain

The signals are shown on figure 23.

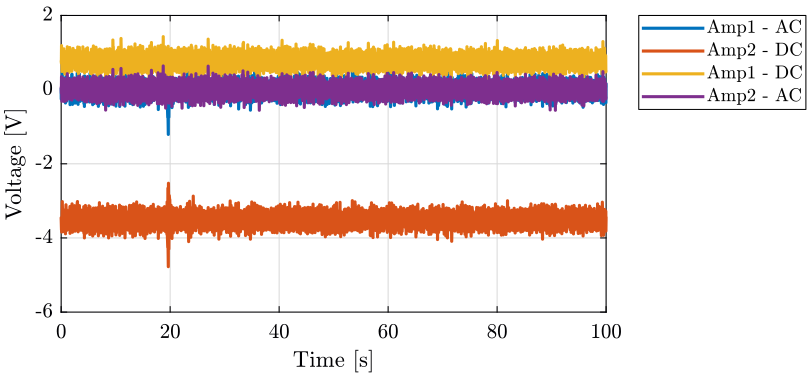
Figure 23: Comparison of the signals going through the Voltage amplifiers

5.4 Frequency Domain

We first compute some parameters that will be used for the PSD computation.

dt = meas14(2, 3)-meas14(1, 3);

Fs = 1/dt; % [Hz]

win = hanning(ceil(10*Fs));

Then we compute the Power Spectral Density using pwelch function.

[pxamp1ac, f] = pwelch(meas14(:, 1), win, [], [], Fs);
[pxamp2dc, ~] = pwelch(meas14(:, 2), win, [], [], Fs);

[pxamp1dc, ~] = pwelch(meas15(:, 1), win, [], [], Fs);
[pxamp2ac, ~] = pwelch(meas15(:, 2), win, [], [], Fs);

The ASD of the signals are compare on figure 24.

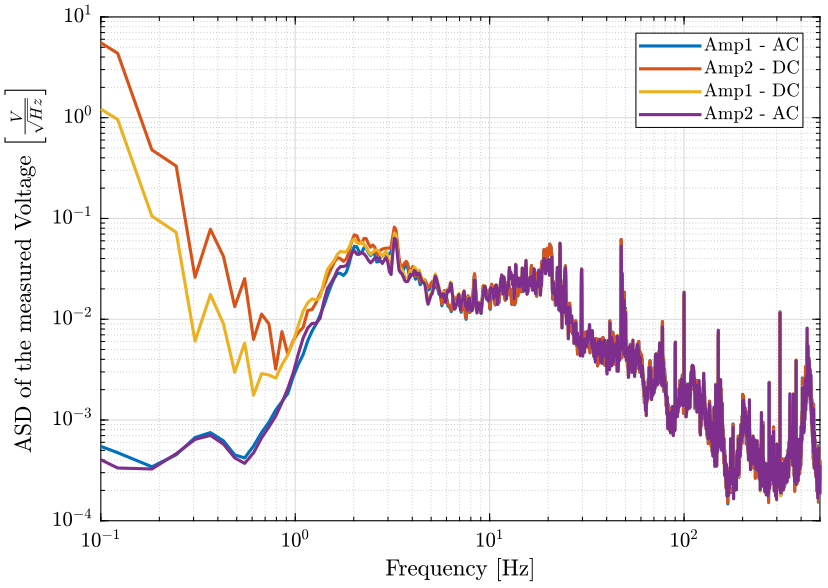
Figure 24: Amplitude Spectral Density of the measured signals

5.5 Conclusion

The voltage amplifiers include some very sharp high pass filters at 1.5Hz (maybe 4th order)
There is a DC offset on the time domain signal because the DC-offset knob was not set to zero

Questions:

What option should be used for the measurements?

6 Measure of the Low Pass Filter

6.1 Measurement Description

Goal:

Measure the Low Pass Filter Transfer Function

The values of the components are:

\begin{aligned} R &= 1k\Omega \\ C &= 1\mu F \end{aligned}

Which makes a cut-off frequency of \(f_c = \frac{1}{RC} = 1000 rad/s = 160Hz\).

\begin{tikzpicture}
  \draw (0,2) node[circ]
        to [R=\(R\)] ++(2,0)
        to ++(2,0)  node[circ]
        ++(-2,0)  node[circ]
        to [C=\(C\)] ++(0,-2)
        ++(-2,0) node[circ]
        to ++(2,0) node[circ]
        to ++(2,0) node[circ];
\end{tikzpicture}

Figure 25: Schematic of the Low Pass Filter used

Setup:

We are measuring the signal from from Geophone with a BNC T
On part goes to column 1 through the LPF
The other part goes to column 2 without the LPF

Measurements: mat/data_018.mat:

Column	Signal
1	Amplifier 1 with LPF
2	Amplifier 2
3	Time

6.2 Load data

We load the data of the z axis of two geophones.

data = load('mat/data_018.mat', 'data'); data = data.data;

6.3 Transfer function of the LPF

We compute the transfer function from the signal without the LPF to the signal measured with the LPF.

dt = data(2, 3)-data(1, 3);

Fs = 1/dt; % [Hz]

win = hanning(ceil(10*Fs));

[Glpf, f] = tfestimate(data(:, 2), data(:, 1), win, [], [], Fs);

We compare this transfer function with a transfer function corresponding to an ideal first order LPF with a cut-off frequency of \(1000rad/s\). We obtain the result on figure 26.

Gth = 1/(1+s/1000)

figure;
ax1 = subplot(2, 1, 1);
hold on;
plot(f, abs(Glpf));
plot(f, abs(squeeze(freqresp(Gth, f, 'Hz'))));
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
set(gca, 'XTickLabel',[]);
ylabel('Magnitude');

ax2 = subplot(2, 1, 2);
hold on;
plot(f, mod(180+180/pi*phase(Glpf), 360)-180);
plot(f, 180/pi*unwrap(angle(squeeze(freqresp(Gth, f, 'Hz')))));
hold off;
set(gca, 'xscale', 'log');
ylim([-180, 180]);
yticks([-180, -90, 0, 90, 180]);
xlabel('Frequency [Hz]'); ylabel('Phase');

linkaxes([ax1,ax2],'x');
xlim([1, 500]);

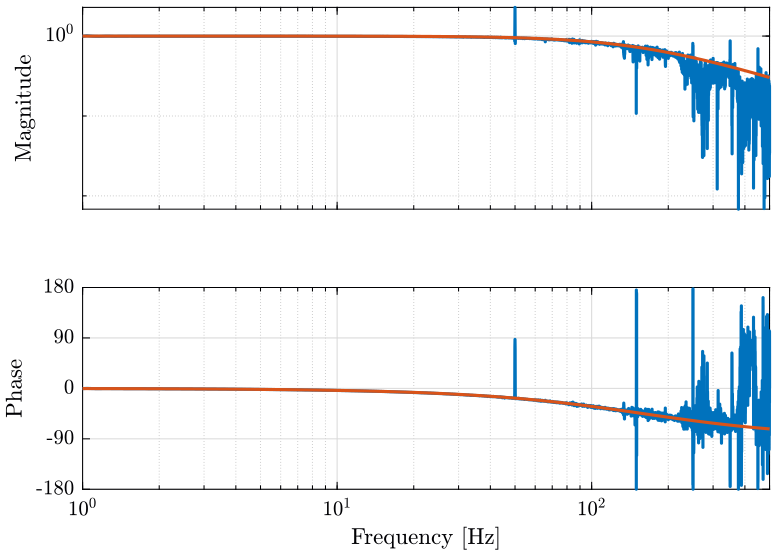
Figure 26: Bode Diagram of the measured Low Pass filter and the theoritical one

6.4 Conclusion

As we want to measure things up to \(500Hz\), we chose to change the value of the capacitor to obtain a cut-off frequency of \(1kHz\).

6.5 TODO Low Pass Filter with a cut-off frequency of 1kHz

This time, the value are

\begin{aligned} R &= 1k\Omega \\ C &= 150nF \end{aligned}

Which makes a low pass filter with a cut-off frequency of \(f_c = 1060Hz\).

Measurements

Table of Contents

1 Effect of the rotation of the Slip-Ring

1.1 Measurement Description

1.2 Load data

1.3 Analysis

1.4 Conclusion

2 Measure of the noise of the Voltage Amplifier

2.1 Measurement Description

2.2 Load data

2.3 Time Domain

2.4 Frequency Domain

2.5 Conclusion

3 Measure of the noise induced by the Slip-Ring

3.1 Measurement Description

3.2 Load data

3.3 Time Domain

3.4 Frequency Domain

3.5 Conclusion

4 Measure of the noise induced by the slip ring when using a geophone

4.1 First Measurement without LPF

4.1.1 Measurement Description

4.1.2 Load data

4.1.3 Time Domain

4.1.4 Frequency Domain

4.1.5 Conclusion

4.2 Measurement using an oscilloscope

4.2.1 Measurement Setup

4.2.2 Observations

4.2.3 Conclusion

4.3 New measurements with a LPF before the Voltage Amplifiers

4.3.1 Setup description

4.3.2 Load data

4.3.3 Time Domain

4.3.4 Frequency Domain

4.3.5 Comparison of with and without LPF

4.3.6 Conclusion

5 Measure of the influence of the AC/DC option on the voltage amplifiers

5.1 Measurement Description

5.2 Load data

5.3 Time Domain

5.4 Frequency Domain

5.5 Conclusion

6 Measure of the Low Pass Filter

6.1 Measurement Description

6.2 Load data

6.3 Transfer function of the LPF

6.4 Conclusion

6.5 TODO Low Pass Filter with a cut-off frequency of 1kHz