SpeedGoat

Table of Contents

1 Experimental Setup

Two L22 geophones are used. They are placed on the ID31 granite. They are leveled.

The signals are amplified using voltage amplifier with a gain of 60dB. The voltage amplifiers include a low pass filter with a cut-off frequency at 1kHz.

setup.jpg

Figure 1: Setup

geophones.jpg

Figure 2: Geophones

2 Signal Processing

The Matlab computing file for this part is accessible here. The mat file containing the measurement data is accessible here.

2.1 Load data

We load the data of the z axis of two geophones. 

load('mat/data_001.mat', 't', 'x1', 'x2');
dt = t(2) - t(1);

2.2 Time Domain Data

figure;
hold on;
plot(t, x1);
plot(t, x2);
hold off;
xlabel('Time [s]');
ylabel('Voltage [V]');
xlim([t(1), t(end)]);

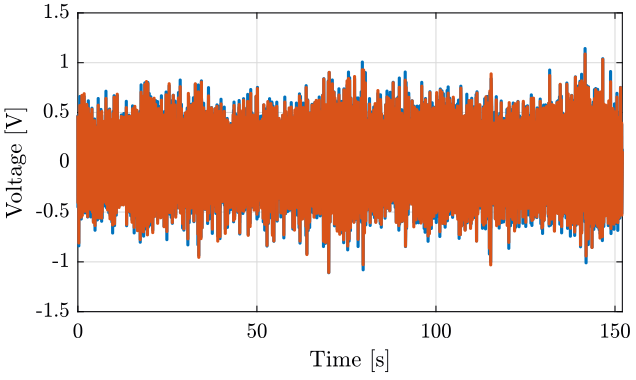
data_time_domain.png

Figure 3: Time domain Data

figure;
hold on;
plot(t, x1);
plot(t, x2);
hold off;
xlabel('Time [s]');
ylabel('Voltage [V]');
xlim([0 1]);

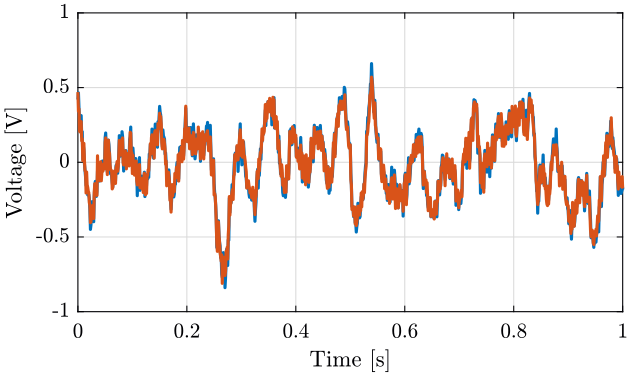
data_time_domain_zoom.png

Figure 4: Time domain Data - Zoom

2.3 Computation of the ASD of the measured voltage

We first define the parameters for the frequency domain analysis. 

win = hanning(ceil(length(x1)/100));
Fs = 1/dt;

[pxx1, f] = pwelch(x1, win, [], [], Fs);
[pxx2, ~] = pwelch(x2, win, [], [], Fs);

2.4 Scaling to take into account the sensibility of the geophone and the voltage amplifier

The Geophone used are L22. Their sensibility are shown on figure 5. 

S0 = 88; % Sensitivity [V/(m/s)]
f0 = 2; % Cut-off frequnecy [Hz]
S = (s/2/pi/f0)/(1+s/2/pi/f0);

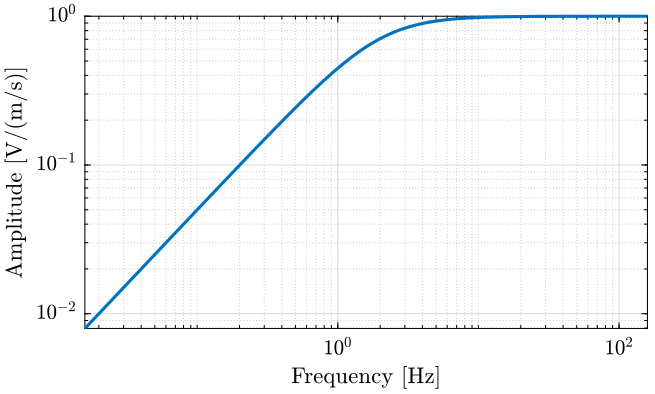
geophone_sensibility.png

Figure 5: Sensibility of the Geophone

We also take into account the gain of the electronics which is here set to be \(60dB\). The amplifiers also include a low pass filter with a cut-off frequency set at 1kHz. 

G0 = 60; % [dB]

G = G0/(1+s/2/pi/1000);

We divide the ASD measured (in \(\text{V}/\sqrt{\text{Hz}}\)) by the transfer function of the voltage amplifier to obtain the ASD of the voltage across the geophone. We further divide the result by the sensibility of the Geophone to obtain the ASD of the velocity in \(m/s/\sqrt{Hz}\). 

scaling = 1./squeeze(abs(freqresp(G, f, 'Hz')))./squeeze(abs(freqresp(S, f, 'Hz')));

2.5 Computation of the ASD of the velocity

The ASD of the measured velocity is shown on figure 6. 

figure;
hold on;
plot(f, sqrt(pxx1)./scaling);
plot(f, sqrt(pxx2)./scaling);
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('PSD [m/s/sqrt(Hz)]')
xlim([2, 500]);

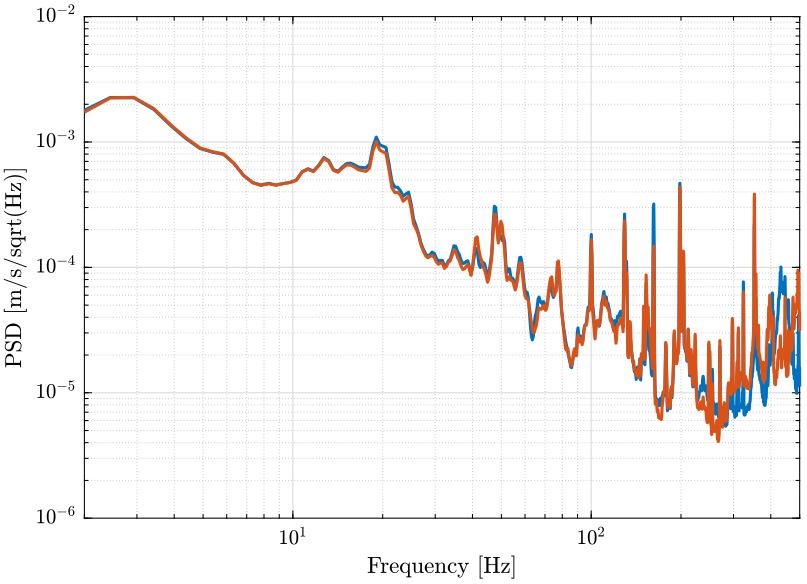
psd_velocity.png

Figure 6: Spectral density of the velocity

2.6 Transfer function between the two geophones

We here compute the transfer function from one geophone to the other. The result is shown on figure 7.

We also compute the coherence between the two signals (figure 8). 

[T12, ~] = tfestimate(x1, x2, win, [], [], Fs);

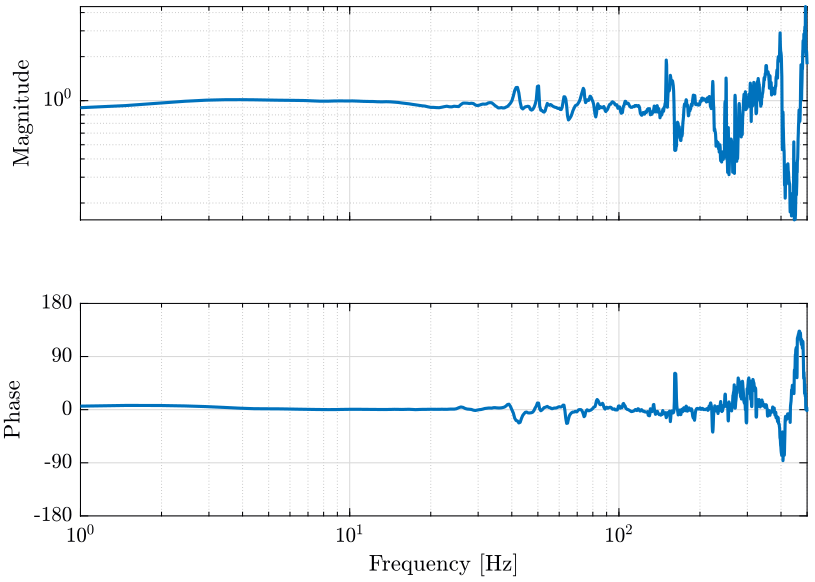
tf_geophones.png

Figure 7: Estimated transfer function between the two geophones

[coh12, ~] = mscohere(x1, x2, win, [], [], Fs);

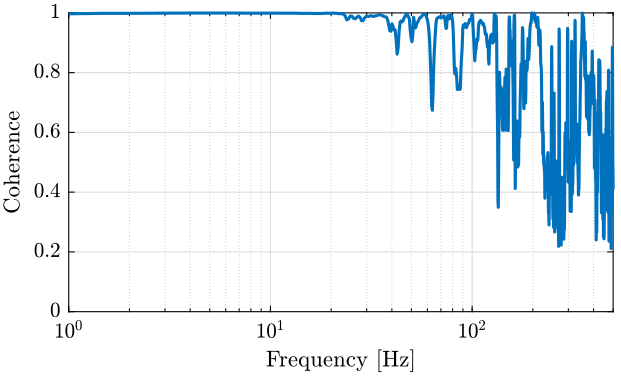
coh_geophones.png

Figure 8: Cohererence between the signals of the two geophones

2.7 Estimation of the sensor noise

The technique to estimate the sensor noise is taken from barzilai98_techn_measur_noise_sensor_presen.

The coherence between signals \(X\) and \(Y\) is defined as follow \[ \gamma^2_{XY}(\omega) = \frac{|G_{XY}(\omega)|^2}{|G_{X}(\omega)| |G_{Y}(\omega)|} \] where \(|G_X(\omega)|\) is the output Power Spectral Density (PSD) of signal \(X\) and \(|G_{XY}(\omega)|\) is the Cross Spectral Density (CSD) of signal \(X\) and \(Y\).

The PSD and CSD are defined as follow:

\begin{align} |G_X(\omega)| &= \frac{2}{n_d T} \sum^{n_d}_{n=1} \left| X_k(\omega, T) \right|^2 \\ |G_{XY}(\omega)| &= \frac{2}{n_d T} \sum^{n_d}_{n=1} [ X_k^*(\omega, T) ] [ Y_k(\omega, T) ] \end{align}

where:

  • \(n_d\) is the number for records averaged
  • \(T\) is the length of each record
  • \(X_k(\omega, T)\) is the finite Fourier transform of the kth record
  • \(X_k^*(\omega, T)\) is its complex conjugate

The mscohere function is compared with this formula on Appendix (section 4.1), it is shown that it is identical.

Figure 9 illustrate a block diagram model of the system used to determine the sensor noise of the geophone.

Two geophones are mounted side by side to ensure that they are exposed by the same motion input \(U\).

Each sensor has noise \(N\) and \(M\).

huddle-test.png

Figure 9: Huddle test block diagram

We here assume that each sensor has the same magnitude of instrumental noise (\(N = M\)). We also assume that \(H_1 = H_2 = 1\).

We then obtain:

\begin{equation} \label{org65b3ddf} \gamma_{XY}^2(\omega) = \frac{1}{1 + 2 \left( \frac{|G_N(\omega)|}{|G_U(\omega)|} \right) + \left( \frac{|G_N(\omega)|}{|G_U(\omega)|} \right)^2} \end{equation}

Since the input signal \(U\) and the instrumental noise \(N\) are incoherent:

\begin{equation} \label{org14038cd} |G_X(\omega)| = |G_N(\omega)| + |G_U(\omega)| \end{equation}

From equations \eqref{org65b3ddf} and \eqref{org14038cd}, we finally obtain

\begin{equation} \label{org84c455c} |G_N(\omega)| = |G_X(\omega)| \left( 1 - \sqrt{\gamma_{XY}^2(\omega)} \right) \end{equation}

The instrumental noise is computed below. The result in V2/Hz is shown on figure 10. 

pxxN = pxx1.*(1 - coh12);

figure;
hold on;
plot(f, pxx1, '-');
plot(f, pxx2, '-');
plot(f, pxxN, 'k--');
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('PSD [$V^2/Hz$]');
xlim([1, 500]);

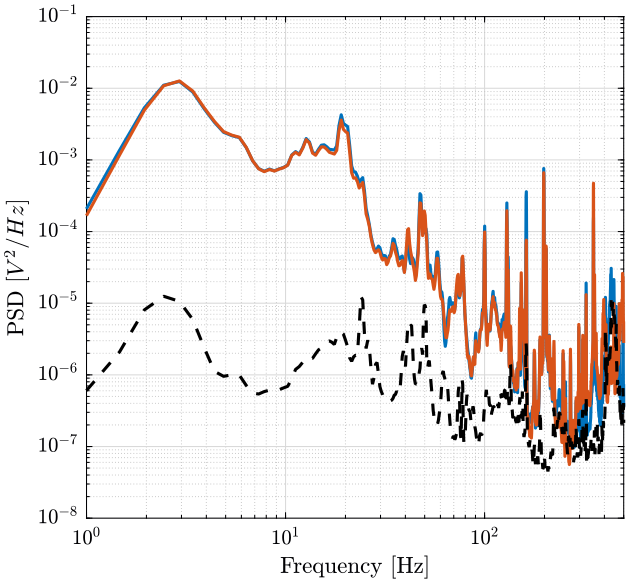
intrumental_noise_V.png

Figure 10: Instrumental Noise and Measurement in \(V^2/Hz\)

This is then further converted into velocity and compared with the ground velocity measurement. (figure 11) 

figure;
hold on;
plot(f, sqrt(pxx1).*scaling, '-');
plot(f, sqrt(pxx2).*scaling, '-');
plot(f, sqrt(pxxN).*scaling, 'k--');
hold off;
set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('PSD [$m/s/\sqrt{Hz}$]');
xlim([1, 500]);

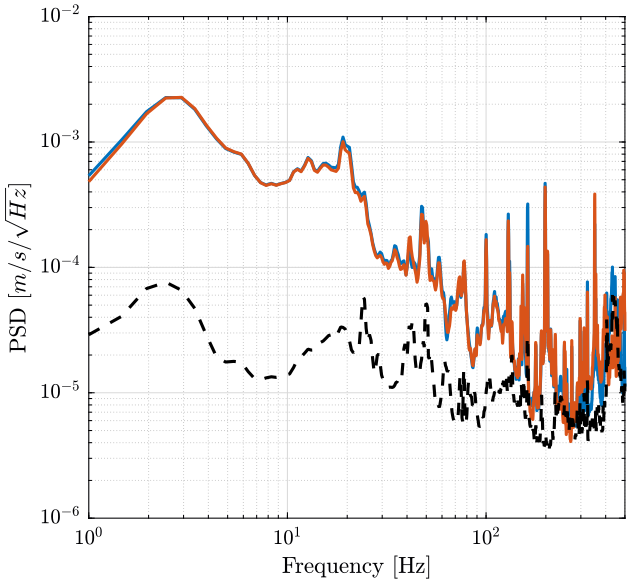
intrumental_noise_velocity.png

Figure 11: Instrumental Noise and Measurement in \(m/s/\sqrt{Hz}\)

3 Compare axis

The Matlab computing file for this part is accessible here. The mat files containing the measurement data are accessible with the following links:

3.1 Load data

We first load the data for the three axis. 

z     = load('mat/data_001.mat', 't', 'x1', 'x2');
east  = load('mat/data_002.mat', 't', 'x1', 'x2');
north = load('mat/data_003.mat', 't', 'x1', 'x2');

3.2 Compare PSD

The PSD for each axis of the two geophones are computed. 

[pz1, fz] = pwelch(z.x1, hanning(ceil(length(z.x1)/100)), [], [], 1/(z.t(2)-z.t(1)));
[pz2, ~]  = pwelch(z.x2, hanning(ceil(length(z.x2)/100)), [], [], 1/(z.t(2)-z.t(1)));

[pe1, fe] = pwelch(east.x1, hanning(ceil(length(east.x1)/100)), [], [], 1/(east.t(2)-east.t(1)));
[pe2, ~]  = pwelch(east.x2, hanning(ceil(length(east.x2)/100)), [], [], 1/(east.t(2)-east.t(1)));

[pn1, fn] = pwelch(north.x1, hanning(ceil(length(north.x1)/100)), [], [], 1/(north.t(2)-north.t(1)));
[pn2, ~]  = pwelch(north.x2, hanning(ceil(length(north.x2)/100)), [], [], 1/(north.t(2)-north.t(1)));

We compare them. The result is shown on figure 12.

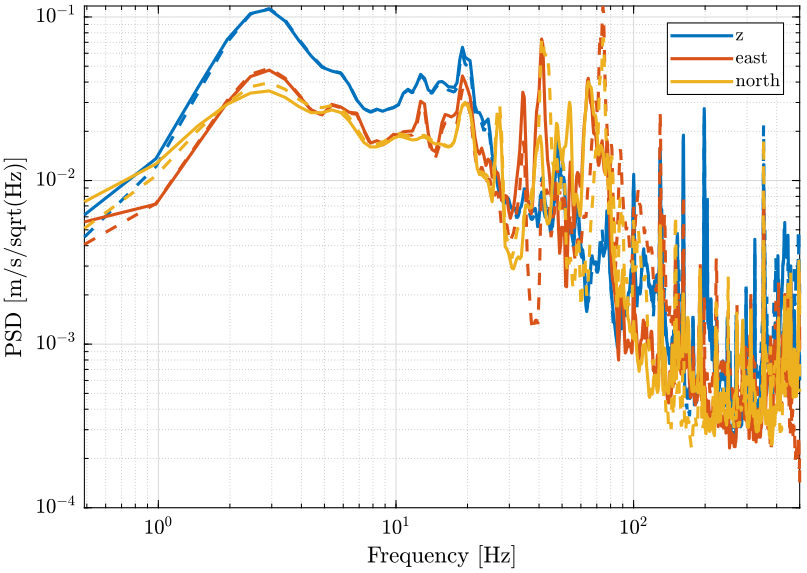
compare_axis_psd.png

Figure 12: Compare the measure PSD of the two geophones for the three axis

3.3 Compare TF

The transfer functions from one geophone to the other are also computed for each axis. The result is shown on figure 13. 

[Tz, fz] = tfestimate(z.x1, z.x2, hanning(ceil(length(z.x1)/100)), [], [], 1/(z.t(2)-z.t(1)));
[Te, fe] = tfestimate(east.x1, east.x2, hanning(ceil(length(east.x1)/100)), [], [], 1/(east.t(2)-east.t(1)));
[Tn, fn] = tfestimate(north.x1, north.x2, hanning(ceil(length(north.x1)/100)), [], [], 1/(north.t(2)-north.t(1)));

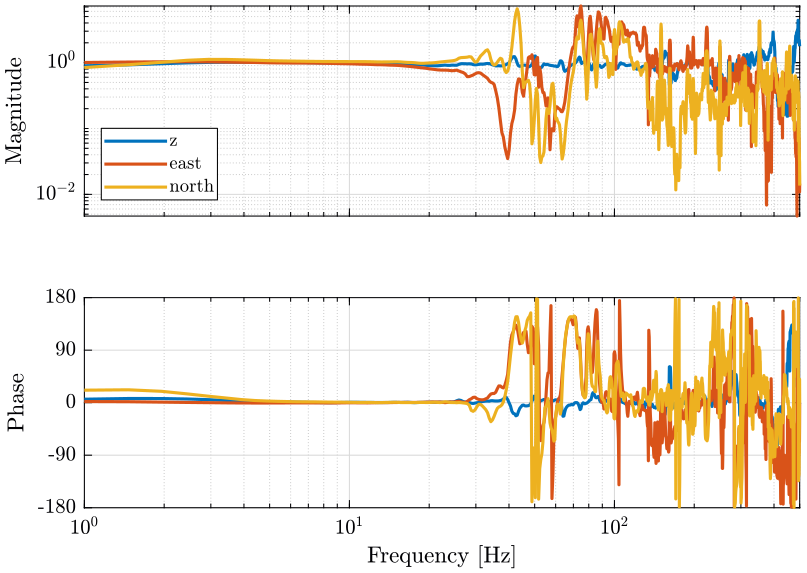
compare_tf_axis.png

Figure 13: Compare the transfer function from one geophone to the other for the 3 axis

4 Appendix

4.1 Computation of coherence from PSD and CSD

load('mat/data_001.mat', 't', 'x1', 'x2');
dt = t(2) - t(1);
Fs = 1/dt;
win = hanning(ceil(length(x1)/100));

pxy = cpsd(x1, x2, win, [], [], Fs);
pxx = pwelch(x1, win, [], [], Fs);
pyy = pwelch(x2, win, [], [], Fs);
coh = mscohere(x1, x2, win, [], [], Fs);

figure;
hold on;
plot(f, abs(pxy).^2./abs(pxx)./abs(pyy), '-');
plot(f, coh, '--');
hold off;
set(gca, 'xscale', 'log');
xlabel('Frequency'); ylabel('Coherence');
xlim([1, 500]);

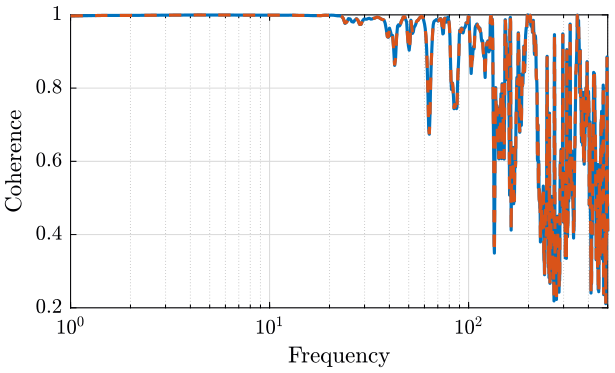
comp_coherence_formula.png

Figure 14: Comparison of mscohere and manual computation

Bibliography

Author: Thomas Dehaeze

Created: 2019-04-18 jeu. 17:11

Validate