Vibrations induced by the Slip-Ring and the Spindle

1. Experimental Setup
2. Data Analysis

1 Experimental Setup

All the stages are OFF.

Two geophone are use:

One on the marble (corresponding to the first column in the data)
One at the sample location (corresponding to the second column in the data)

Two voltage amplifiers are used, their setup is:

gain of 60dB
AC/DC switch on AC
Low pass filter at 1kHz

A first order low pass filter is also added at the input of the voltage amplifiers.

Goal:

Identify the vibrations induced by the rotation of the Slip-Ring and Spindle

Three measurements are done:

mat/data_024.mat: All the stages are OFF
mat/data_025.mat: The slip-ring is ON and rotates at 6rpm. The spindle is OFF
mat/data_026.mat: The slip-ring and spindle are both ON. They are both turning at 6rpm

A movie showing the experiment is shown on figure 1.

Figure 1: Movie of the experiment, rotation speed is 6rpm

2 Data Analysis

All the files (data and Matlab scripts) are accessible here.

2.1 Load data

of = load('mat/data_024.mat', 'data'); of = of.data;
sr = load('mat/data_025.mat', 'data'); sr = sr.data;
sp = load('mat/data_026.mat', 'data'); sp = sp.data;

2.2 Time domain plots

figure;
hold on;
plot(sp(:, 3), sp(:, 1), 'DisplayName', 'Spindle - 6rpm');
plot(sr(:, 3), sr(:, 1), 'DisplayName', 'Slip-Ring - 6rpm');
plot(of(:, 3), of(:, 1), 'DisplayName', 'OFF');
hold off;
xlabel('Time [s]'); ylabel('Voltage [V]');
xlim([0, 100]); ylim([-10 10]);
legend('Location', 'northeast');

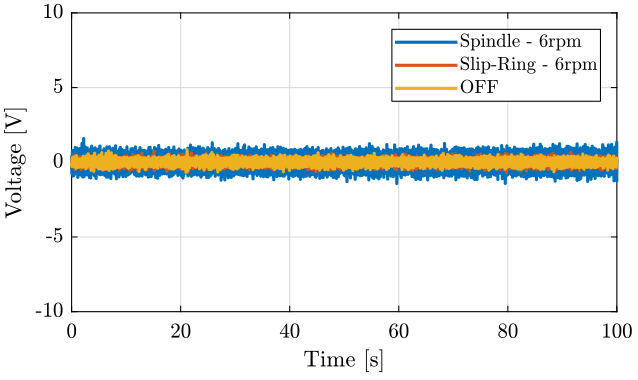
Figure 2: Measurement of the geophone located on the marble - Time domain

figure;
hold on;
plot(sp(:, 3), sp(:, 2), 'DisplayName', 'Spindle and Slip-Ring');
plot(sr(:, 3), sr(:, 2), 'DisplayName', 'Only Slip-Ring');
plot(of(:, 3), of(:, 2), 'DisplayName', 'OFF');
hold off;
xlabel('Time [s]'); ylabel('Voltage [V]');
xlim([0, 100]); ylim([-10 10]);
legend('Location', 'northeast');

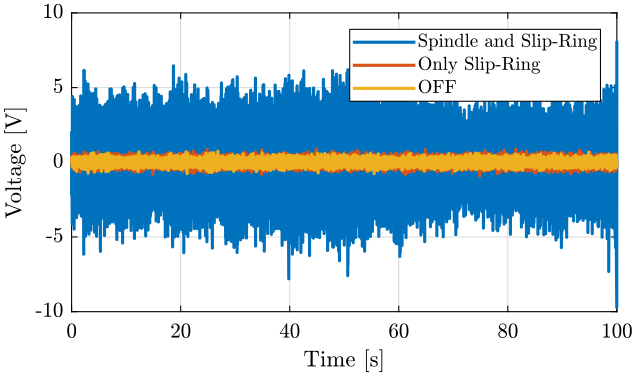
Figure 3: Measurement of the geophone at the sample location - Time domain

2.3 Frequency Domain

We first compute some parameters that will be used for the PSD computation.

dt = of(2, 3)-of(1, 3);

Fs = 1/dt; % [Hz]

win = hanning(ceil(10*Fs));

Then we compute the Power Spectral Density using pwelch function.

First for the geophone located on the marble

[pxof_m, f] = pwelch(of(:, 1), win, [], [], Fs);
[pxsr_m, ~] = pwelch(sr(:, 1), win, [], [], Fs);
[pxsp_m, ~] = pwelch(sp(:, 1), win, [], [], Fs);

And for the geophone located at the sample position.

[pxof_s, f] = pwelch(of(:, 2), win, [], [], Fs);
[pxsr_s, ~] = pwelch(sr(:, 2), win, [], [], Fs);
[pxsp_s, ~] = pwelch(sp(:, 2), win, [], [], Fs);

And we plot the ASD of the measured signals:

figure 4 for the geophone located on the marble
figure 5 for the geophone at the sample position

figure;
hold on;
plot(f, sqrt(pxsp_m), 'DisplayName', 'Spindle - 6rpm');
plot(f, sqrt(pxsr_m), 'DisplayName', 'Slip-Ring - 6rpm');
plot(f, sqrt(pxof_m), 'DisplayName', 'OFF');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'southwest');
xlim([0.1, 500]);

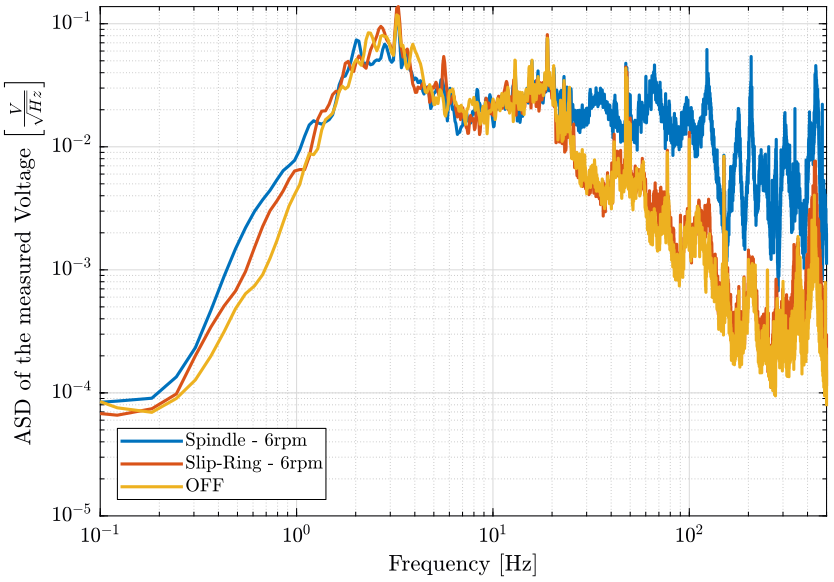
Figure 4: Comparison of the ASD of the measured voltage from the Geophone on the marble

figure;
hold on;
plot(f, sqrt(pxsp_s), 'DisplayName', 'Spindle - 6rpm');
plot(f, sqrt(pxsr_s), 'DisplayName', 'Slip-Ring - 6rpm');
plot(f, sqrt(pxof_s), 'DisplayName', 'OFF');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'southwest');
xlim([0.1, 500]);

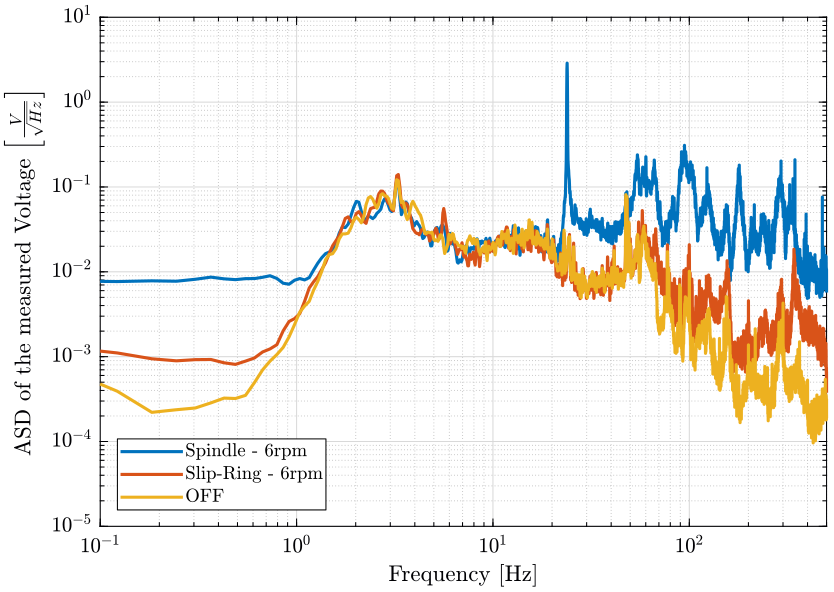
Figure 5: Comparison of the ASD of the measured voltage from the Geophone at the sample location

2.4 Conclusion

The slip-ring rotation induces almost no vibrations on the marble, and only a little vibrations on the sample above 100Hz.

The spindle rotation induces a lot of vibrations of the sample as well as on the granite. There is a huge peak at 24Hz on the sample vibration but not on the granite vibration.