UP | HOME

Measurement Analysis

Table of Contents

All the files (data and Matlab scripts) are accessible here.

1 Measurement Description

setup_picture.png

Figure 1: Picture of the setup for the measurement

The sensor used are 3 L-4C geophones (Documentation).

Each motor are turn off and then on.

The goal is to see what noise is injected in the system due to the regulation loop of each stage.

2 Importation of the data

First, load all the measurement files: 

meas = {};
meas{1} = load('./mat/Measurement1.mat');
meas{2} = load('./mat/Measurement2.mat');
meas{3} = load('./mat/Measurement3.mat');
meas{4} = load('./mat/Measurement4.mat');
meas{5} = load('./mat/Measurement5.mat');

Change the track name for measurements 3 and 4. 

meas{3}.Track1_Name = 'Input 1: Hexa Z';
meas{4}.Track1_Name = 'Input 1: Hexa Z';

For the measurements 1 to 4, the measurement channels are shown table 1.

Table 1: Channels for measurements 1 to 4
  Channel 1 Channel 2 Channel 3
Meas. 1 Input 1: tilt1 Z Input 2: tilt2 Z Input 3: Ty Y
Meas. 2 Input 1: tilt1 Z Input 2: tilt2 Z Input 3: Ty Y
Meas. 3 Input 1: Hexa Z Input 2: tilt2 Z Input 3: Ty Y
Meas. 4 Input 1: Hexa Z Input 2: tilt2 Z Input 3: Ty Y

For the measurement 5, the channels are shown table 2.

Table 2: Channels for measurement 5
  Channel 1 Channel 2 Channel 3 Channel 4
Meas. 5 Input 1: Floor Z Input 2: Marble Z Input 3: Floor Y Input 4: Marble Y

3 Variables for analysis

We define the sampling frequency and the time vectors for the plots. 

Fs = 256; % [Hz]
dt = 1/(Fs);
t1  = dt*(0:length(meas{1}.Track1)-1);
t2  = dt*(0:length(meas{2}.Track1)-1);
t3  = dt*(0:length(meas{3}.Track1)-1);
t4  = dt*(0:length(meas{4}.Track1)-1);
t5  = dt*(0:length(meas{5}.Track1)-1);

For the frequency analysis, we define the frequency limits for the plot. 

fmin = 1; % [Hz]
fmax = 100; % [Hz]

Then we define the windows that will be used to average the results. 

psd_window = hanning(2*fmin/dt);

4 Coherence between the two vertical geophones on the Tilt Stage

We first compute the coherence between the two geophones located on the tilt stage. The result is shown on figure 2. 

[coh, f] = mscohere(meas{1}.Track1(:), meas{1}.Track2(:), psd_window, [], [], Fs);

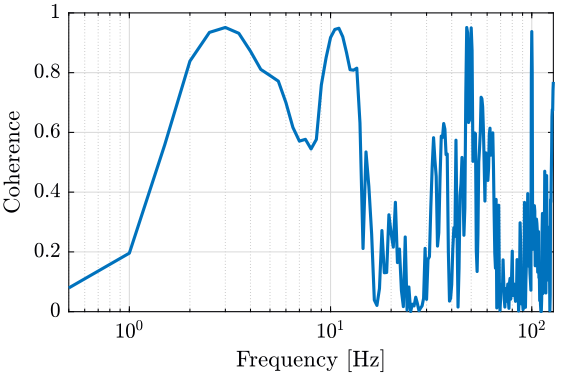
coherence_vertical_tilt_sensors.png

Figure 2: Coherence between the two vertical sensors positionned on the Tilt Stage

We then compute the transfer function from one sensor to the other (figure 3). 

[tf23, f] = tfestimate(meas{1}.Track1(:), meas{1}.Track2(:), psd_window, [], [], Fs);

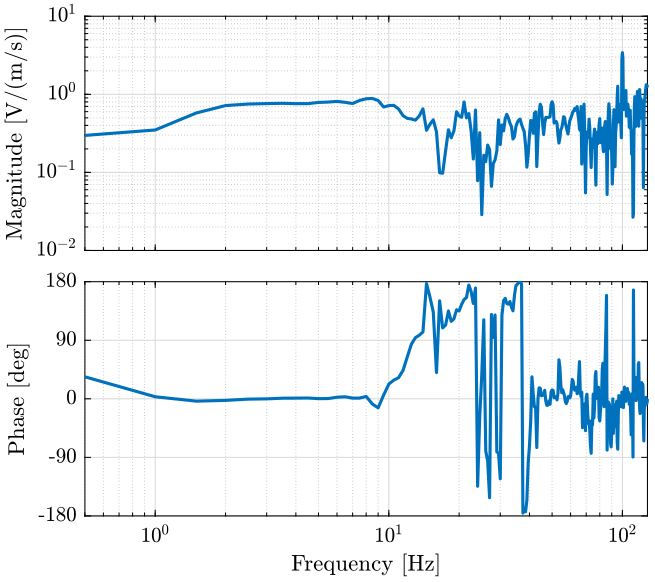
tf_vertical_tilt_sensors.png

Figure 3: Transfer function from one vertical geophone on the tilt stage to the other vertical geophone on the tilt stage

Even though the coherence is not very good, we observe no resonance between the two sensors.

5 Data Post Processing

When using two geophone sensors on the same tilt stage (measurements 1 and 2), we post-process the data to obtain the z displacement and the rotation of the tilt stage: 

meas1_z    = (meas{1}.Track1+meas{1}.Track2)/2;
meas1_tilt = (meas{1}.Track1-meas{1}.Track2)/2;

meas{1}.Track1 = meas1_z;
meas{1}.Track1_Y_Magnitude = 'Meter / second';
meas{1}.Track1_Name = 'Ry Z';
meas{1}.Track2 = meas1_tilt;
meas{1}.Track2_Y_Magnitude = 'Rad / second';
meas{1}.Track2_Name = 'Ry Tilt';

meas2_z    = (meas{2}.Track1+meas{2}.Track2)/2;
meas2_tilt = (meas{2}.Track1-meas{2}.Track2)/2;
meas{2}.Track1 = meas2_z;
meas{2}.Track1_Y_Magnitude = 'Meter / second';
meas{2}.Track1_Name = 'Ry Z';
meas{2}.Track2 = meas2_tilt;
meas{2}.Track2_Y_Magnitude = 'Rad / second';
meas{2}.Track2_Name = 'Ry Tilt';

6 Normalization

Parameters of the geophone are defined below. The transfer function from geophone velocity to measured voltage is shown on figure 4.

Measurements will be normalized by the inverse of this transfer function in order to go from voltage measurement to velocity measurement. 

L4C_w0 = 2*pi; % [rad/s]
L4C_ksi = 0.28;
L4C_G0 = 276.8; % [V/(m/s)]
L4C_G = L4C_G0*(s/L4C_w0)^2/((s/L4C_w0)^2 + 2*L4C_ksi*(s/L4C_w0) + 1);

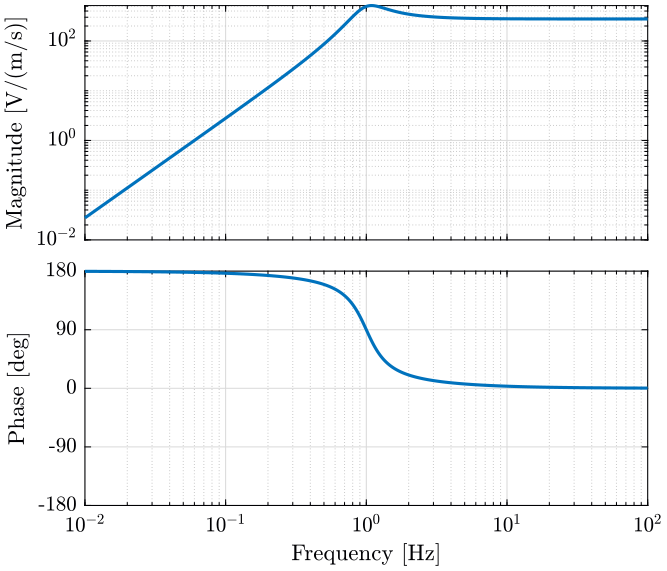
L4C_bode_plot.png

Figure 4: Bode plot of the L4C Geophone

meas{1}.Track1 = (meas{1}.Track1)./276.8;
meas{1}.Track2 = (meas{1}.Track2)./276.8;
meas{1}.Track3 = (meas{1}.Track3)./276.8;

meas{2}.Track1 = (meas{2}.Track1)./276.8;
meas{2}.Track2 = (meas{2}.Track2)./276.8;
meas{2}.Track3 = (meas{2}.Track3)./276.8;

meas{3}.Track1 = (meas{3}.Track1)./276.8;
meas{3}.Track2 = (meas{3}.Track2)./276.8;
meas{3}.Track3 = (meas{3}.Track3)./276.8;

meas{4}.Track1 = (meas{4}.Track1)./276.8;
meas{4}.Track2 = (meas{4}.Track2)./276.8;
meas{4}.Track3 = (meas{4}.Track3)./276.8;

meas{5}.Track1 = (meas{5}.Track1)./276.8;
meas{5}.Track2 = (meas{5}.Track2)./276.8;
meas{5}.Track3 = (meas{5}.Track3)./276.8;
meas{5}.Track4 = (meas{5}.Track4)./276.8;

meas{1}.Track1_norm = lsim(inv(L4C_G), meas{1}.Track1, t1);
meas{1}.Track2_norm = lsim(inv(L4C_G), meas{1}.Track2, t1);
meas{1}.Track3_norm = lsim(inv(L4C_G), meas{1}.Track3, t1);

meas{2}.Track1_norm = lsim(inv(L4C_G), meas{2}.Track1, t2);
meas{2}.Track2_norm = lsim(inv(L4C_G), meas{2}.Track2, t2);
meas{2}.Track3_norm = lsim(inv(L4C_G), meas{2}.Track3, t2);

meas{3}.Track1_norm = lsim(inv(L4C_G), meas{3}.Track1, t3);
meas{3}.Track2_norm = lsim(inv(L4C_G), meas{3}.Track2, t3);
meas{3}.Track3_norm = lsim(inv(L4C_G), meas{3}.Track3, t3);

meas{4}.Track1_norm = lsim(inv(L4C_G), meas{4}.Track1, t4);
meas{4}.Track2_norm = lsim(inv(L4C_G), meas{4}.Track2, t4);
meas{4}.Track3_norm = lsim(inv(L4C_G), meas{4}.Track3, t4);

meas{5}.Track1_norm = lsim(inv(L4C_G), meas{5}.Track1, t5);
meas{5}.Track2_norm = lsim(inv(L4C_G), meas{5}.Track2, t5);
meas{5}.Track3_norm = lsim(inv(L4C_G), meas{5}.Track3, t5);
meas{5}.Track4_norm = lsim(inv(L4C_G), meas{5}.Track4, t5);

7 Measurement 1 - Effect of Ty stage

The configuration for this measurement is shown table 3.

Table 3: Stages configuration - Measurement 1
Time 0-309 309-end
Ty OFF ON
Ry OFF OFF
SlipRing OFF OFF
Spindle OFF OFF
Hexa OFF OFF

We then plot the measurements in time domain (figure 5).

We observe strange behavior when the Ty stage is turned on. How can we explain that?

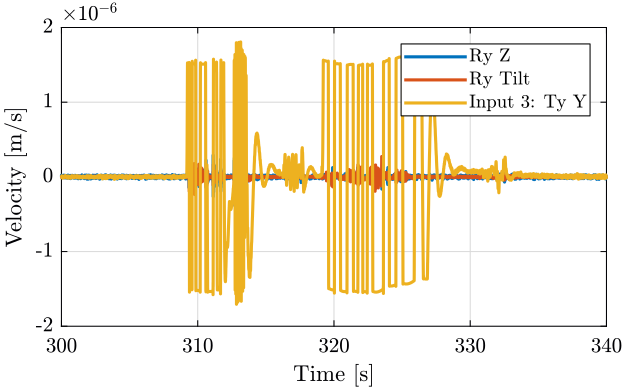
meas1.png

Figure 5: Time domain - measurement 1

To understand what is going on, instead of looking at the velocity, we can look at the displacement by integrating the data. The displacement is computed by integrating the velocity using cumtrapz function.

Then we plot the position with respect to time (figure 6).

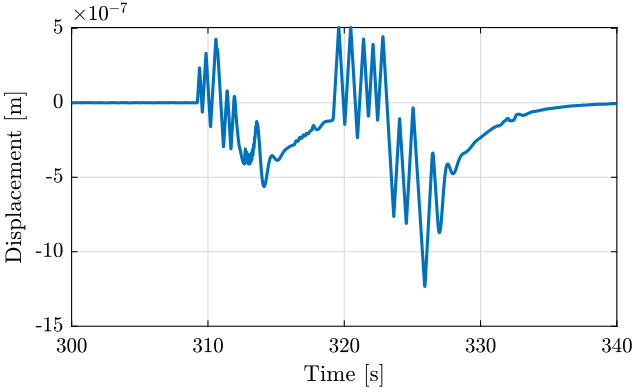
meas1_disp.png

Figure 6: Y displacement of the Ty stage

We when compute the power spectral density of each measurement before and after turning on the stage. 

[pxx111, f11] = pwelch(meas{1}.Track1(1:ceil(300/dt)),   psd_window, [], [], Fs);
[pxx112, f12] = pwelch(meas{1}.Track1(ceil(350/dt):end), psd_window, [], [], Fs);

[pxx121, ~] = pwelch(meas{1}.Track2(1:ceil(300/dt)),   psd_window, [], [], Fs);
[pxx122, ~] = pwelch(meas{1}.Track2(ceil(350/dt):end), psd_window, [], [], Fs);

[pxx131, ~] = pwelch(meas{1}.Track3(1:ceil(300/dt)),   psd_window, [], [], Fs);
[pxx132, ~] = pwelch(meas{1}.Track3(ceil(350/dt):end), psd_window, [], [], Fs);

We finally plot the power spectral density of each track (figures 7, 8, 9).

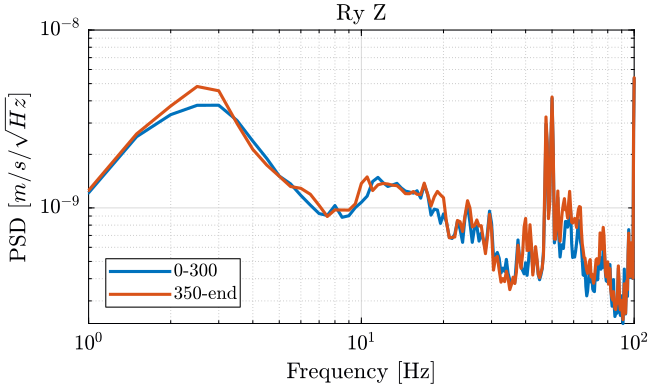
meas1_ry_z_psd.png

Figure 7: PSD of the Z velocity of Ry stage - measurement 1

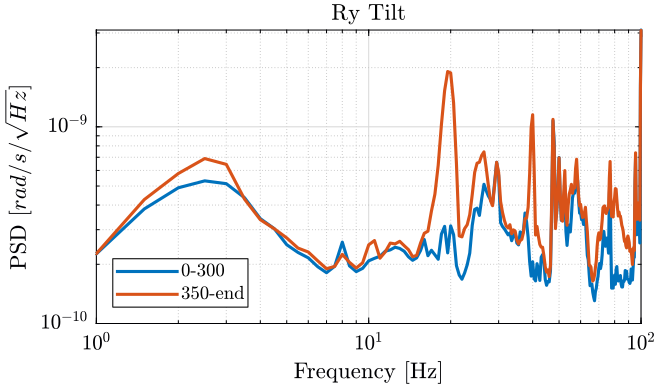
meas1_ry_tilt_psd.png

Figure 8: PSD of the Rotation of Ry Stage - measurement 1

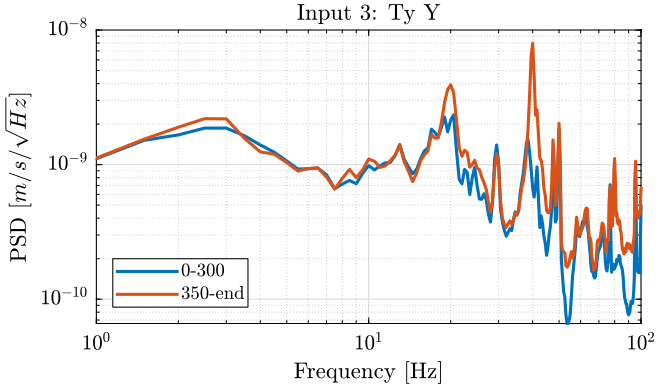
meas1_ty_y_psd.png

Figure 9: PSD of the Ty velocity in the Y direction - measurement 1

Turning on the Y-translation stage increases the velocity of the Ty stage in the Y direction and the rotation motion of the tilt stage:

  • at 20Hz
  • at 40Hz
  • between 80Hz and 90Hz

It does not seems to have any effect on the Z motion of the tilt stage.

8 Measurement 2 - Effect of Ry stage

The tilt stage is turned ON at around 326 seconds (table 4).

Table 4: Stages configuration - Measurement 2
Time 0-326 326-end
Ty OFF OFF
Ry OFF ON
SlipRing OFF OFF
Spindle OFF OFF
Hexa OFF OFF

We plot the time domain (figure 10) and we don’t observe anything special in the time domain.

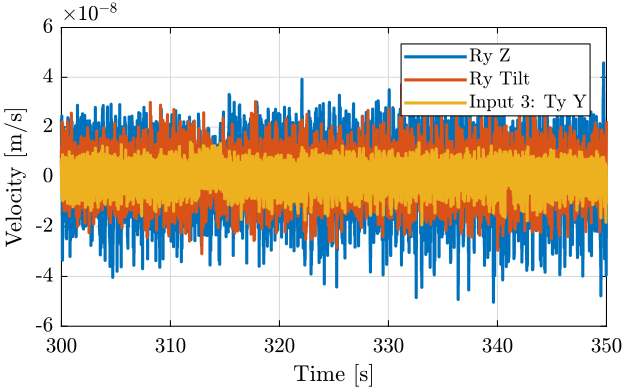
meas2.png

Figure 10: Time domain - measurement 2

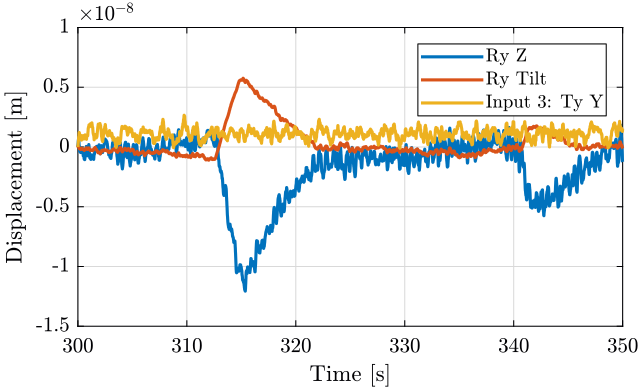
meas2_disp.png

Figure 11: Time domain - measurement 2

We compute the PSD of each track and we plot them (figures 12, 13 and 14 ). 

[pxx211, f21] = pwelch(meas{2}.Track1(1:ceil(326/dt)),   psd_window, [], [], Fs);
[pxx212, f22] = pwelch(meas{2}.Track1(ceil(326/dt):end), psd_window, [], [], Fs);

[pxx221, ~] = pwelch(meas{2}.Track2(1:ceil(326/dt)),   psd_window, [], [], Fs);
[pxx222, ~] = pwelch(meas{2}.Track2(ceil(326/dt):end), psd_window, [], [], Fs);

[pxx231, ~] = pwelch(meas{2}.Track3(1:ceil(326/dt)),   psd_window, [], [], Fs);
[pxx232, ~] = pwelch(meas{2}.Track3(ceil(326/dt):end), psd_window, [], [], Fs);

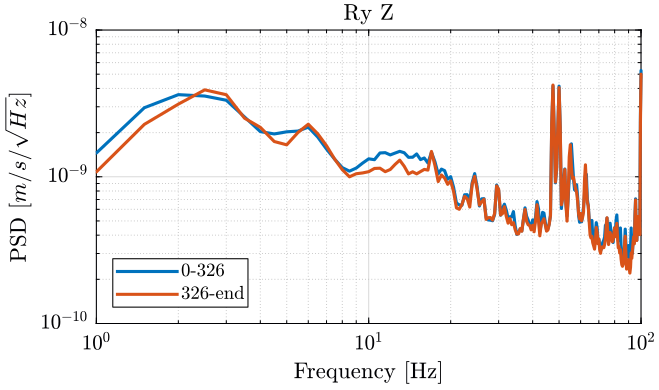
meas2_ry_z_psd.png

Figure 12: PSD of the Z velocity of Ry Stage - measurement 2

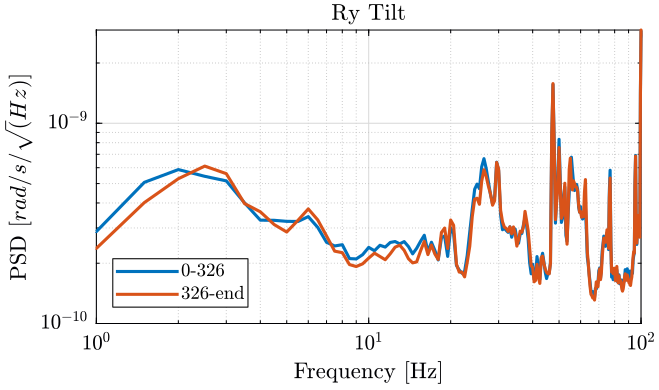
meas2_ry_tilt_psd.png

Figure 13: PSD of the Rotation motion of Ry Stage - measurement 2

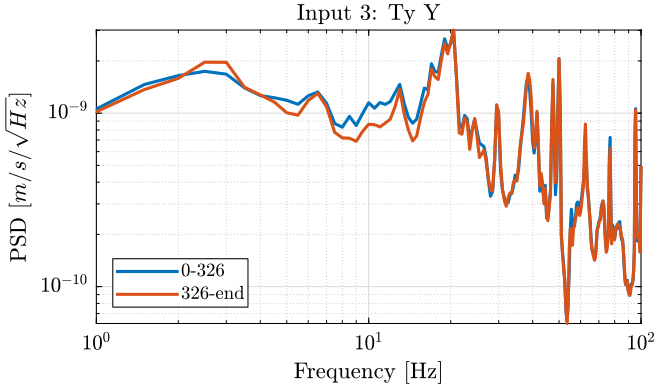
meas2_ty_y_psd.png

Figure 14: PSD of the Ty velocity in the Y direction - measurement 2

We observe no noticeable difference when the Tilt-stage is turned ON expect a small decrease of the Z motion of the tilt stage around 10Hz.

9 Measurement 3 - Effect of the Hexapod

The hexapod is turned off after 406 seconds (table 5).

Table 5: Stages configuration - Measurement 3
Time 0-406 406-end
Ty OFF OFF
Ry ON ON
SlipRing OFF OFF
Spindle OFF OFF
Hexa ON OFF

The time domain result is shown figure 15.

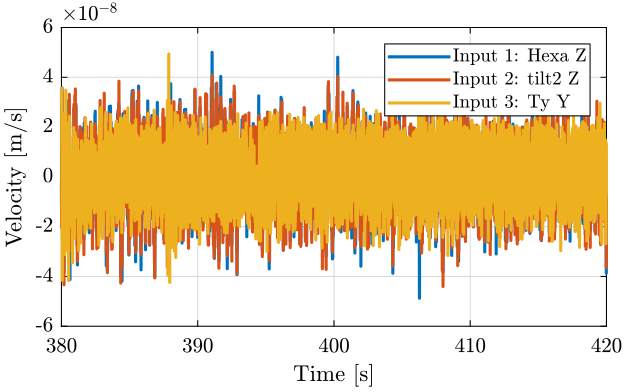
meas3.png

Figure 15: Time domain - measurement 3

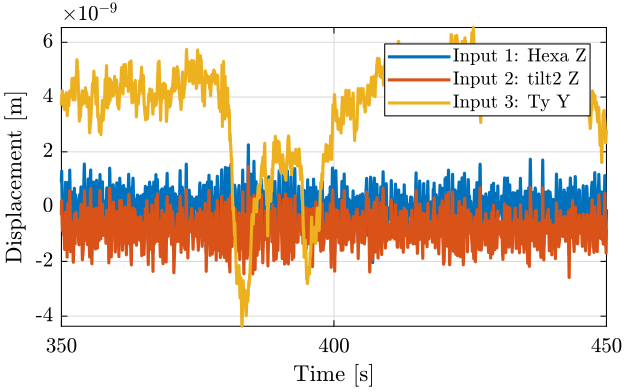
meas3_disp.png

Figure 16: Time domain - measurement 3

We then compute the PSD of each track before and after turning off the hexapod and plot the results in the figures 17, 18 and 19. 

[pxx311, f31] = pwelch(meas{3}.Track1(1:ceil(400/dt)),   psd_window, [], [], Fs);
[pxx312, f32] = pwelch(meas{3}.Track1(ceil(420/dt):end), psd_window, [], [], Fs);

[pxx321, ~] = pwelch(meas{3}.Track2(1:ceil(400/dt)),   psd_window, [], [], Fs);
[pxx322, ~] = pwelch(meas{3}.Track2(ceil(420/dt):end), psd_window, [], [], Fs);

[pxx331, ~] = pwelch(meas{3}.Track3(1:ceil(400/dt)),   psd_window, [], [], Fs);
[pxx332, ~] = pwelch(meas{3}.Track3(ceil(420/dt):end), psd_window, [], [], Fs);

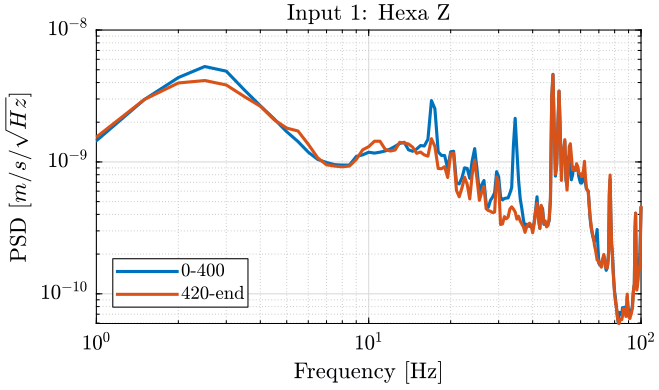
meas3_hexa_z_psd.png

Figure 17: PSD of the Z velocity of the Hexapod - measurement 3

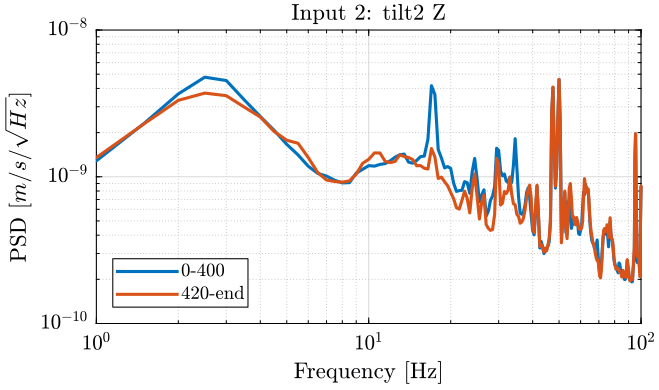
meas3_ry_z_psd.png

Figure 18: PSD of the Z velocity of the Ry stage - measurement 3

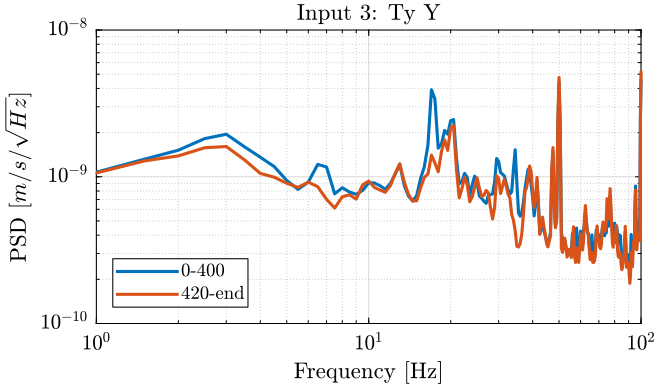
meas3_ty_y_psd.png

Figure 19: PSD of the Ty velocity in the Y direction - measurement 3

Turning ON induces some motion on the hexapod in the z direction (figure 17), on the tilt stage in the z direction (figure 18) and on the y motion of the Ty stage (figure 19):

  • at 17Hz
  • at 34Hz

10 Measurement 4 - Effect of the Splip-Ring and Spindle

The slip ring is turned on at 300s, then the spindle is turned on at 620s (table 6). The time domain signals are shown figure 20.

Table 6: Stages configuration - Measurement 4
Time 0-300 300-620 620-end
Ty OFF OFF OFF
Ry OFF OFF OFF
SlipRing OFF ON ON
Spindle OFF OFF ON
Hexa OFF OFF OFF

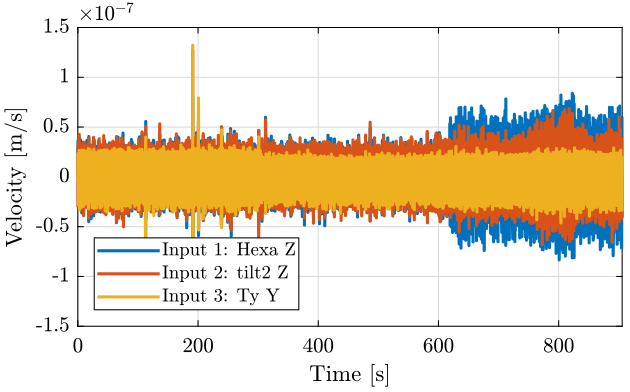
meas4.png

Figure 20: Time domain - measurement 4

If we integrate this signal, we obtain Figure 21.

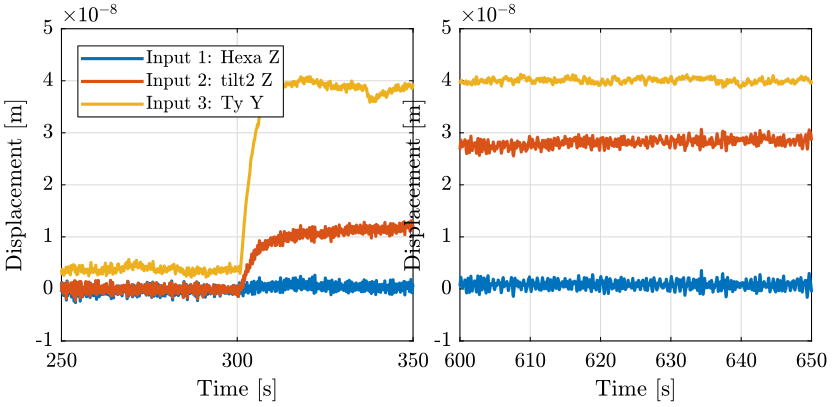
meas4_int.png

Figure 21: Time domain - measurement 4

The PSD of each track are computed using the code below.

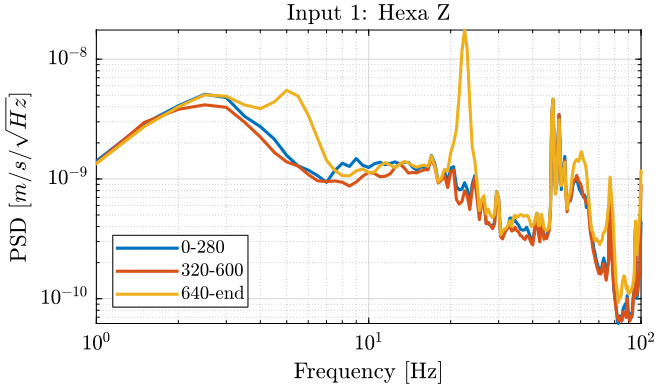
meas4_hexa_z_psd.png

Figure 22: PSD of the Z velocity of the Hexapod - measurement 4

We plot the PSD of the displacement.

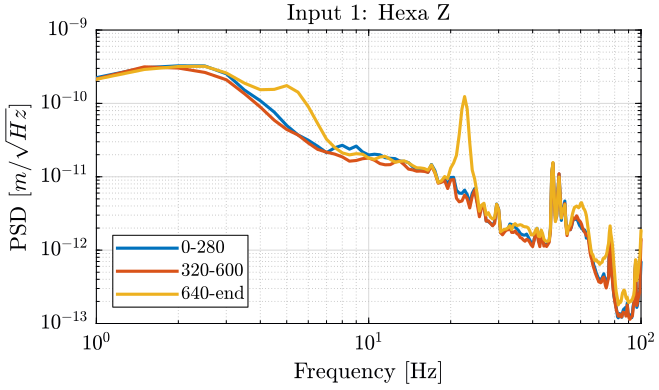
meas4_hexa_z_psd_int.png

Figure 23: PSD_INT of the Z velocity of the Hexapod - measurement 4

And we compute the Cumulative amplitude spectrum.

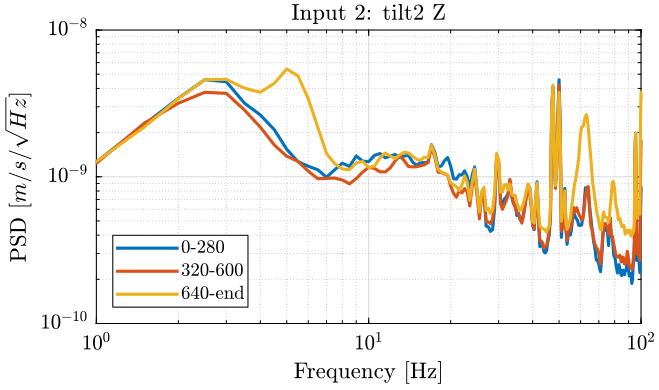
meas4_ry_z_psd.png

Figure 24: PSD of the Ry rotation in the Y direction - measurement 4

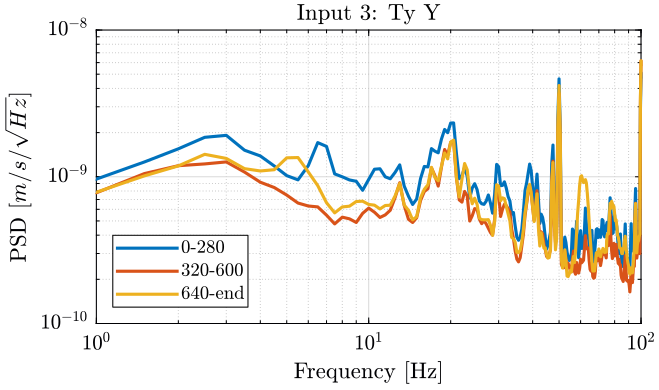
meas4_ty_y_psd.png

Figure 25: PSD of the Ty velocity in the Y direction - measurement 4

Turning ON the splipring seems to not add motions on the stages measured. It even seems to lower the motion of the Ty stage (figure 25): does that make any sense?

Turning ON the spindle induces motions:

  • at 5Hz on each motion measured
  • at 22.5Hz on the Z motion of the Hexapod. Can this is due to some 50Hz?
  • at 62Hz on each motion measured

11 Measurement 5 - Transmission from ground to marble

This measurement just consists of measurement of Y-Z motion of the ground and the marble.

The time domain signals are shown on figure 26.

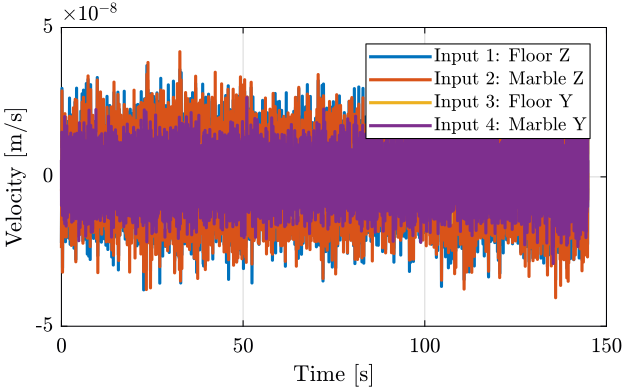
meas5.png

Figure 26: Time domain - measurement 5

We compute the PSD of each track and we plot the PSD of the Z motion for the ground and marble on figure 27 and for the Y motion on figure 28. 

[pxx51, f51] = pwelch(meas{5}.Track1(:), psd_window, [], [], Fs);
[pxx52, f52] = pwelch(meas{5}.Track2(:), psd_window, [], [], Fs);
[pxx53, f53] = pwelch(meas{5}.Track3(:), psd_window, [], [], Fs);
[pxx54, f54] = pwelch(meas{5}.Track4(:), psd_window, [], [], Fs);

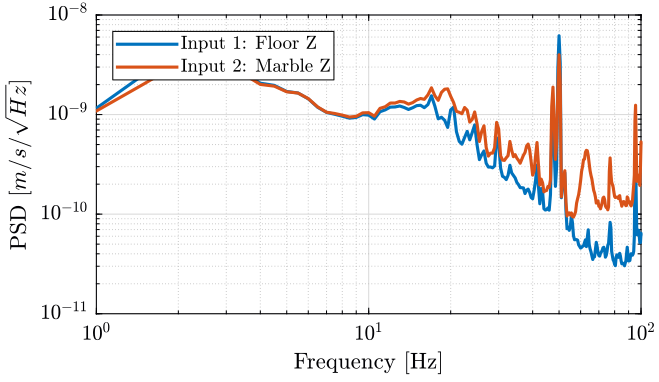
meas5_z_psd.png

Figure 27: PSD of the ground and marble in the Z direction

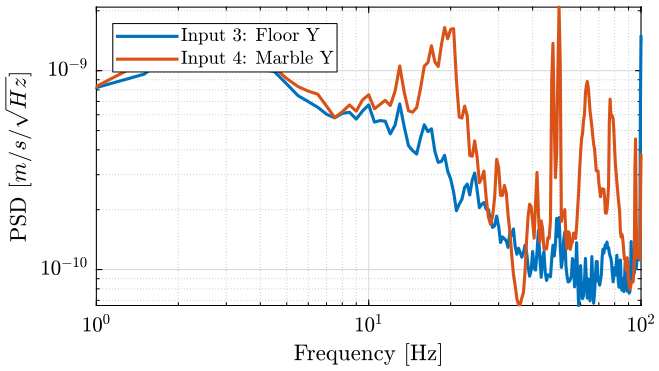
meas5_y_psd.png

Figure 28: PSD of the ground and marble in the Y direction

Then, instead of looking at the Power Spectral Density, we can try to estimate the transfer function from a ground motion to the motion of the marble. The transfer functions are shown on figure 29 and the coherence on figure 30. 

[tfz, fz] = tfestimate(meas{5}.Track1(:), meas{5}.Track2(:), psd_window, [], [], Fs);
[tfy, fy] = tfestimate(meas{5}.Track3(:), meas{5}.Track4(:), psd_window, [], [], Fs);

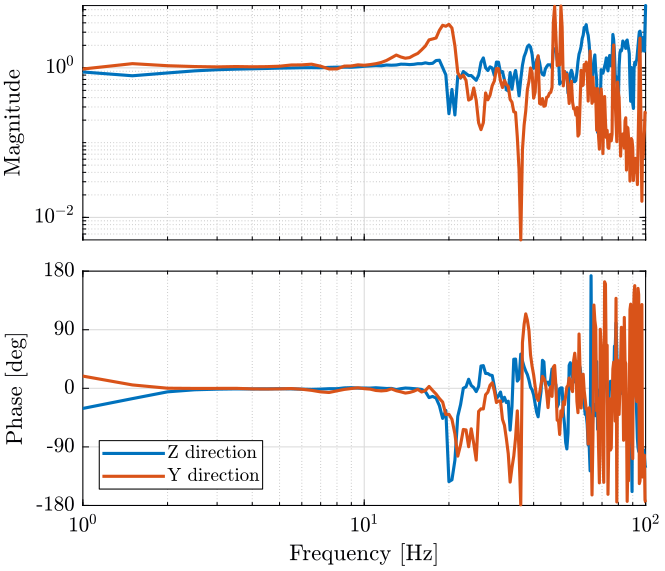
meas5_tf.png

Figure 29: Transfer function estimation - measurement 5

[cohz, fz] = mscohere(meas{5}.Track1(:), meas{5}.Track2(:), psd_window, [], [], Fs);
[cohy, fy] = mscohere(meas{5}.Track3(:), meas{5}.Track4(:), psd_window, [], [], Fs);

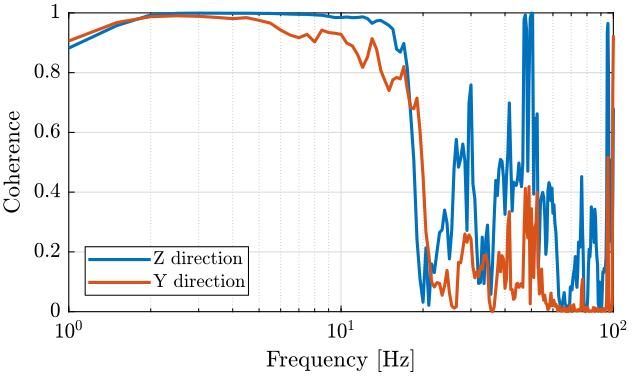
meas5_coh.png

Figure 30: Coherence - measurement 5

The marble seems to have a resonance at around 20Hz on the Y direction. But the coherence is not good above 20Hz, so it is difficult to estimate resonances.

Author: Dehaeze Thomas

Created: 2020-11-12 jeu. 10:27