Vibrations induced by the translation stage motion

1. Measurement description
2. Measurement Analysis

1 Measurement description

Setup: Two geophone are use:

One is on the marble (corresponding to the first column in the data)
One at the sample location (corresponding to the second column in the data)

Two voltage amplifiers are used, their setup is:

gain of 40dB (the gain at the be lowered from 60dB to 40dB to not saturate the voltage amplifiers)
AC/DC switch on AC
Low pass filter at 1kHz

A first order low pass filter is also added at the input of the voltage amplifiers.

Scans are done with the translation stage following sinus reference at 1Hz with amplitude of 600 000 cnt (= 3mm) The scans are done with the ELMO software.

The North of the Geophones corresponds to the +Y direction and the East of the Geophones to the +X direction (see figure 1).

The spindle and slip-ring are turned ON. The Hexapod and the tilt-stage are OFF.

Goal:

Determine the disturbances induced by the translation stage in the Z and X directions when scanning along the Y direction

Measurements: Three measurements are done:

Measurement File	Description
`mat/data_040.mat`	Z direction
`mat/data_041.mat`	E direction
`mat/data_042.mat`	E direction without any motion (Ty OFF)

Each of the measurement mat file contains one data array with 3 columns:

Column number	Description
1	Geophone - Marble
2	Geophone - Sample
3	Time

Figure 1: Picture of the experimental setup

2 Measurement Analysis

All the files (data and Matlab scripts) are accessible here.

2.1 Load data

z_ty = load('mat/data_040.mat', 'data'); z_ty = z_ty.data;
e_ty = load('mat/data_041.mat', 'data'); e_ty = e_ty.data;
e_of = load('mat/data_042.mat', 'data'); e_of = e_of.data;

2.2 Time domain plots

figure;
hold on;
plot(z_ty(:, 3), z_ty(:, 1), 'DisplayName', 'Marble - Z');
plot(z_ty(:, 3), z_ty(:, 2), 'DisplayName', 'Sample - Z');
hold off;
xlabel('Time [s]'); ylabel('Voltage [V]');
xlim([0, 100]); ylim([-5, 5]);
legend('Location', 'northeast');

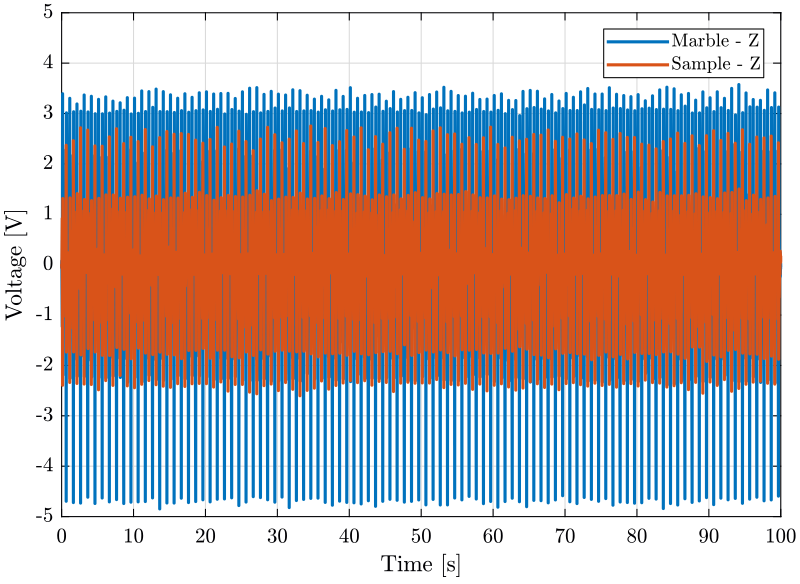
Figure 2: Z motion of the sample and marble when scanning with the translation stage

Figure 3: Z motion of the sample and marble when scanning with the translation stage - Zoom

figure;
hold on;
plot(e_ty(:, 3), e_ty(:, 1), 'DisplayName', 'Marble - X');
plot(e_ty(:, 3), e_ty(:, 2), 'DisplayName', 'Sample - X');
hold off;
xlabel('Time [s]'); ylabel('Voltage [V]');
xlim([0, 100]); ylim([-10, 10]);
legend('Location', 'northeast');

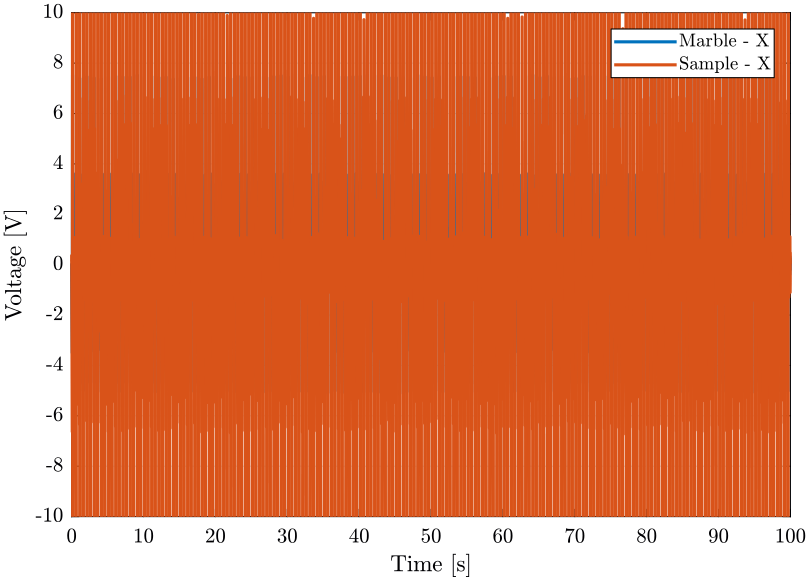
Figure 4: Motion of the sample and marble in the east direction when scanning with the translation stage

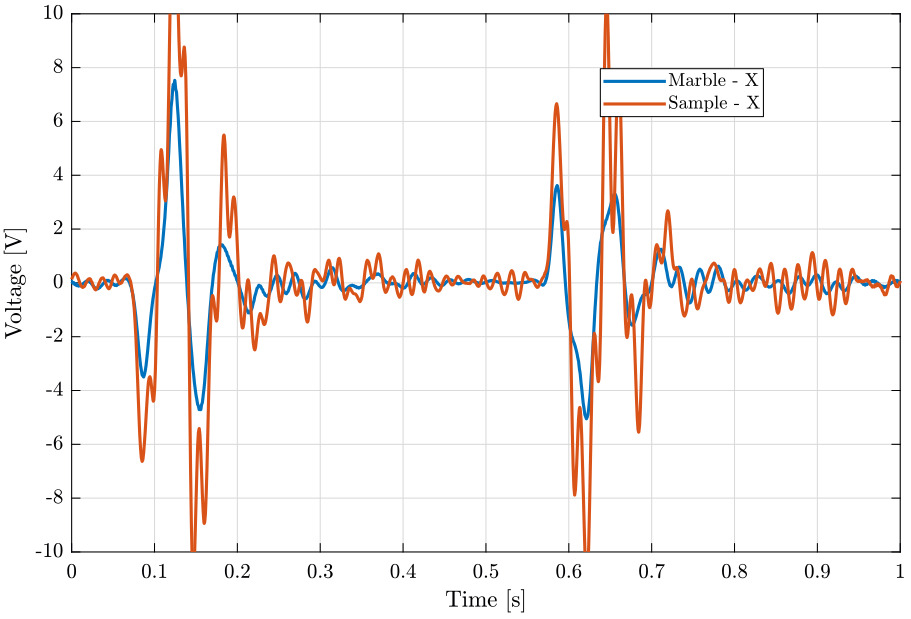
Figure 5: Motion of the sample and marble in the east direction when scanning with the translation stage - Zoom

2.3 Frequency Domain analysis

We first compute some parameters that will be used for the PSD computation.

dt = z_ty(2, 3)-z_ty(1, 3);

Fs = 1/dt; % [Hz]

win = hanning(ceil(10*Fs));

Then we compute the Power Spectral Density using pwelch function.

First for the geophone located on the marble

[pxz_ty_m, f] = pwelch(z_ty(:, 1), win, [], [], Fs);
[pxe_ty_m, ~] = pwelch(e_ty(:, 1), win, [], [], Fs);
[pxe_of_m, ~] = pwelch(e_of(:, 1), win, [], [], Fs);

And for the geophone located at the sample position.

[pxz_ty_s, f] = pwelch(z_ty(:, 2), win, [], [], Fs);
[pxe_ty_s, ~] = pwelch(e_ty(:, 2), win, [], [], Fs);
[pxe_of_s, ~] = pwelch(e_of(:, 2), win, [], [], Fs);

And we plot the ASD of the measured signals:

figure 6 compares the marble motion in the east direction when scanning and when Ty is OFF
figure 7 compares the sample motion in the east direction when scanning and when Ty is OFF
figure 8 shows the marble and sample motion in the Z direction when scanning with the translation stage

figure;
hold on;
plot(f, sqrt(pxe_ty_m), 'DisplayName', 'Ty 1Hz - Marble - X');
plot(f, sqrt(pxe_of_m), 'DisplayName', 'Ty OFF - Marble - X');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'northwest');
xlim([0.1, 500]); ylim([1e-5, 1e1]);

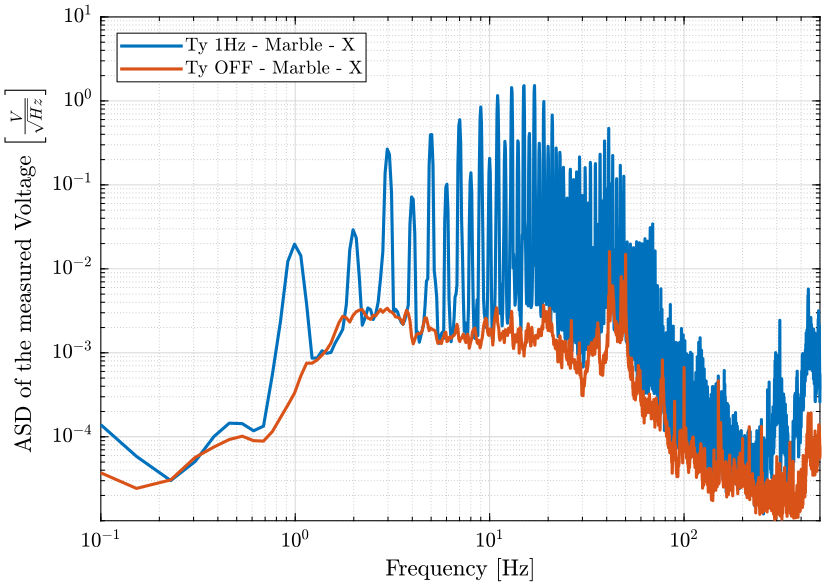
Figure 6: Amplitude spectral density of the measure voltage corresponding to the geophone in the east direction located on the marble when the translation stage is OFF and when it is scanning at 1Hz

figure;
hold on;
plot(f, sqrt(pxe_ty_s), 'DisplayName', 'Ty 1Hz - Sample - X');
plot(f, sqrt(pxe_of_s), 'DisplayName', 'Ty OFF - Sample - X');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'northwest');
xlim([0.1, 500]); ylim([1e-5, 1e1]);

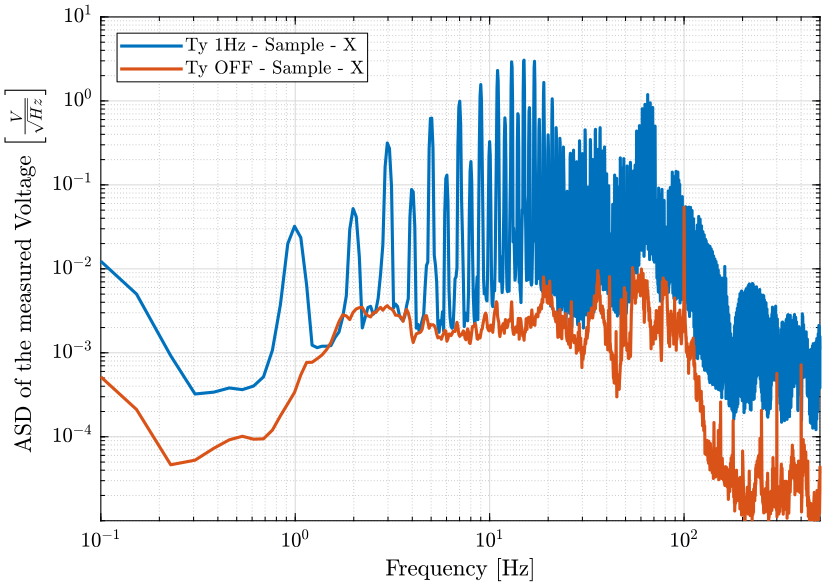
Figure 7: Amplitude spectral density of the measure voltage corresponding to the geophone in the east direction located at the sample location when the translation stage is OFF and when it is scanning at 1Hz

figure;
hold on;
plot(f, sqrt(pxz_ty_m), 'DisplayName', 'Ty 1Hz - Marble - Z');
plot(f, sqrt(pxz_ty_s), 'DisplayName', 'Ty 1Hz - Sample - Z');
hold off;
set(gca, 'xscale', 'log');
set(gca, 'yscale', 'log');
xlabel('Frequency [Hz]'); ylabel('ASD of the measured Voltage $\left[\frac{V}{\sqrt{Hz}}\right]$')
legend('Location', 'northwest');
xlim([0.1, 500]); ylim([1e-5, 1e1]);

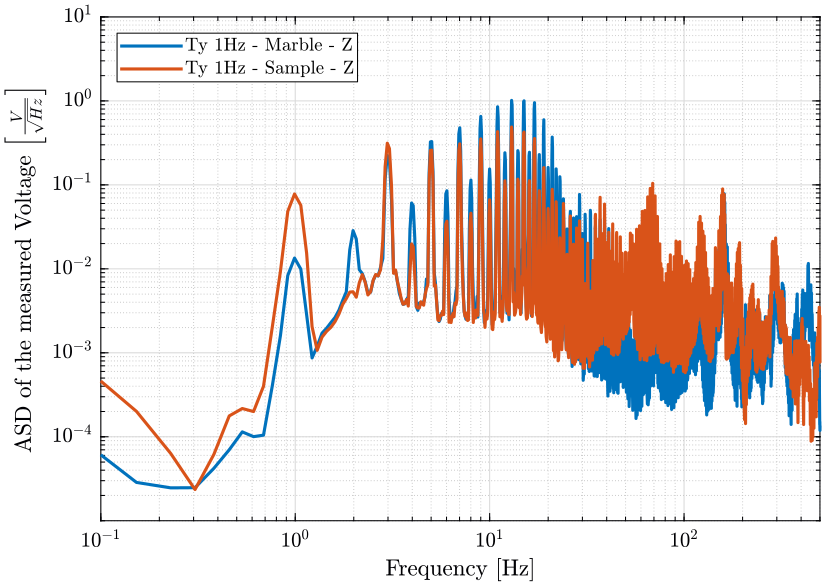
Figure 8: Amplitude spectral density of the measure voltage corresponding to the geophone in the vertical direction located on the granite and at the sample location when the translation stage is scanning at 1Hz

2.4 Transfer function from marble motion in the East direction to sample motion in the East direction

Let's compute the transfer function for the marble motion in the east direction to the sample motion in the east direction.

We first plot the time domain motions when every stage is off (figure 9).

figure;
hold on;
plot(e_of(:, 3), e_of(:, 2), 'DisplayName', 'Sample - X');
plot(e_of(:, 3), e_of(:, 1), 'DisplayName', 'Marble - X');
hold off;
xlabel('Time [s]'); ylabel('Voltage [V]');
xlim([0, 100]); ylim([-1, 1]);
legend('Location', 'northeast');

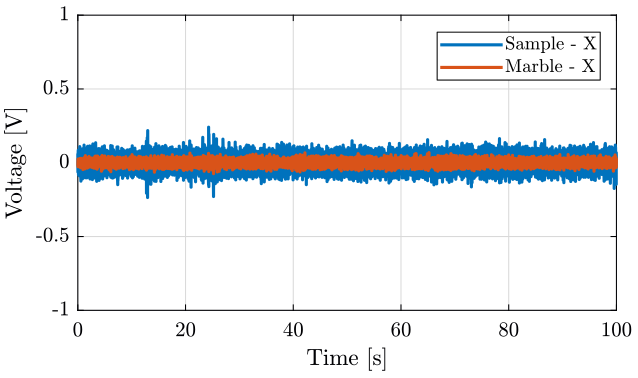
Figure 9: East motion of the marble and sample when all the stages are OFF

We then compute the transfer function using tfestimate.

dt = e_of(2, 3)-e_of(1, 3);
Fs = 1/dt; % [Hz]
win = hanning(ceil(10*Fs));

[T, f] = tfestimate(e_of(:, 1), e_of(:, 2), win, [], [], Fs);

The result is shown on figure 10.

Figure 10: Estimation of the transfer function from marble motion in the east direction to sample motion in the east direction

2.5 Position of the translation stage and Current

The position of the translation and current flowing in its actuator are measured using the elmo software and saved as an csv file.

2.5.1 Data pre-processing

Let's look at at the start of the csv file.

sed -n 1,30p mat/sin_elmo.csv | nl -ba -

The real data starts at line 29. We then load this cvs file starting at line 29.

data = csvread("mat/sin_elmo.csv", 29, 0);

2.5.2 Time domain data

We plot the position of the translation stage measured by the encoders. There is 200000 encoder count for each mm, we then divide by 200000 to obtain mm. The result is shown on figure 11.

figure;
hold on;
plot(data(:, 1), data(:, 2)/200000);
hold off;
xlim([0, 5]);
xlabel('Time [s]'); ylabel('Position [mm]');

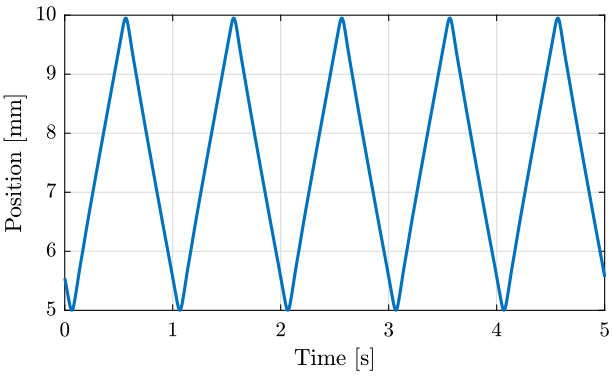
Figure 11: Y position of the translation stage measured by the encoders

Figure 12: Y position of the translation stage measured by the encoders - Zoom

We also plot the current as function of the time on figure 13.

figure;
hold on;
plot(data(:, 1), data(:, 3));
hold off;
xlim([0, 5]); ylim([-10, 10]);
xlabel('Time [s]'); ylabel('Current [A]');

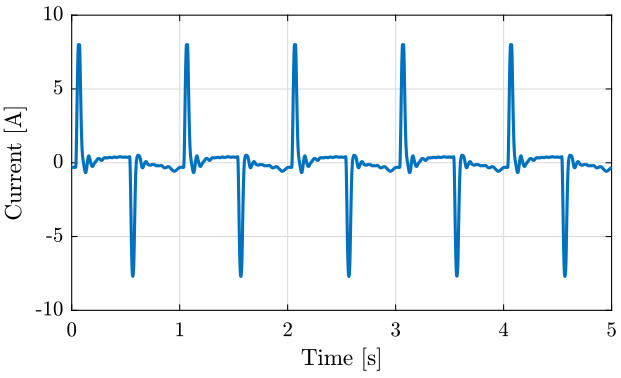
Figure 13: Current going through the actuator of the translation stage

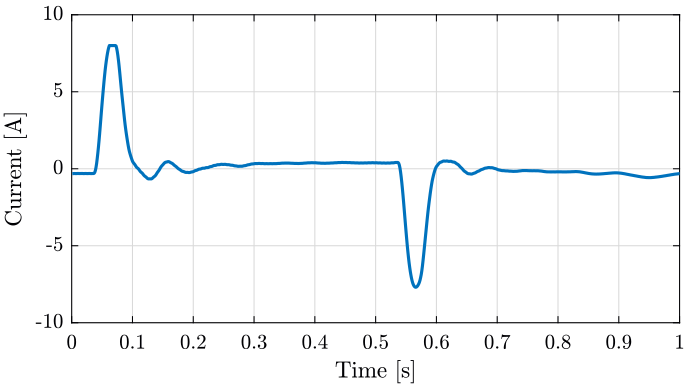
Figure 14: Current going through the actuator of the translation stage - Zoom

2.6 Conclusion

The acquisition is done using the Speedgoat as well as using ELMO. The two acquisition are not synchronize
The value of the translation stage encoder can also be read with the speedgoat, this could permit to synchronize the measurements