SpeedGoat
Table of Contents
1 Setup
Two L22 geophones are used. They are placed on the ID31 granite. They are leveled.
The signals are amplified using voltage amplifier with a gain of 60dB. The voltage amplifiers include a low pass filter with a cut-off frequency at 1kHz.

Figure 1: Setup

Figure 2: Geophones
2 Signal Processing
2.1 Load data
load('mat/data_001.mat', 't', 'x1', 'x2'); dt = t(2) - t(1);
2.2 Time Domain Data
figure; hold on; plot(t, x1); plot(t, x2); hold off; xlabel('Time [s]'); ylabel('Voltage [V]'); xlim([t(1), t(end)]);

Figure 3: Time domain Data
figure; hold on; plot(t, x1); plot(t, x2); hold off; xlabel('Time [s]'); ylabel('Voltage [V]'); xlim([0 1]);
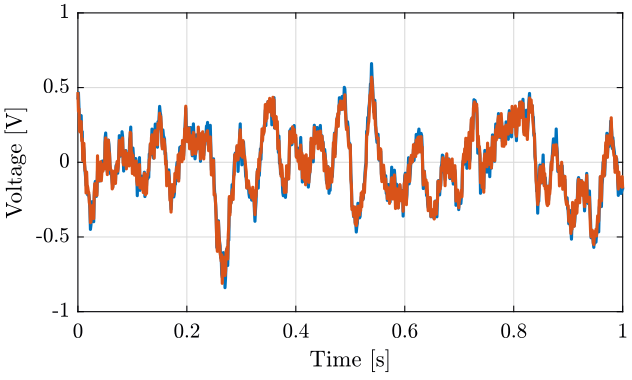
Figure 4: Time domain Data - Zoom
2.3 Compute PSD
[pxx1, f1] = pwelch(x1, hanning(ceil(1/dt)), 0, [], 1/dt); [pxx2, f2] = pwelch(x2, hanning(ceil(1/dt)), 0, [], 1/dt);
2.4 Take into account sensibility of Geophone
The Geophone used are L22.
S0 = 88; % Sensitivity [V/(m/s)] f0 = 2; % Cut-off frequnecy [Hz] S = (s/2/pi/f0)/(1+s/2/pi/f0);
figure; bodeFig({S}); ylabel('Amplitude [V/(m/s)]')
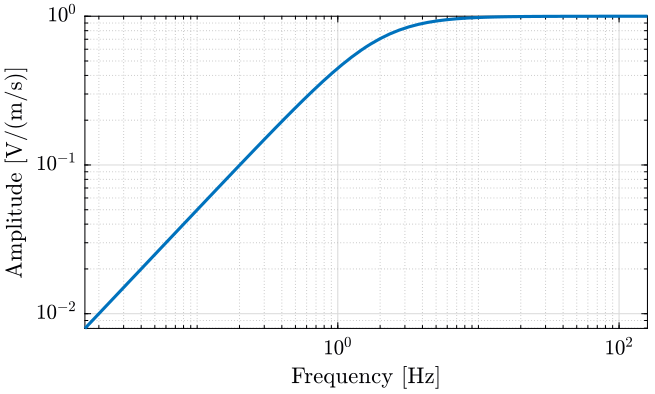
Figure 5: Sensibility of the Geophone
We take into account the gain of the electronics. The cut-off frequency is set at 1kHz.
[ ]Check what is the order of the filter[ ]Maybe I should not use this filter as there is no high frequencies anyway?
G0 = 60; % [dB] G = G0/(1+s/2/pi/1000);
figure; hold on; plot(f1, sqrt(pxx1)./squeeze(abs(freqresp(G, f1, 'Hz')))./squeeze(abs(freqresp(S, f1, 'Hz')))); plot(f2, sqrt(pxx2)./squeeze(abs(freqresp(G, f2, 'Hz')))./squeeze(abs(freqresp(S, f2, 'Hz')))); hold off; set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); xlabel('Frequency [Hz]'); ylabel('PSD [m/s/sqrt(Hz)]') xlim([2, 500]);

Figure 6: Spectral density of the velocity
2.5 Transfer function between the two geophones
[T12, f12] = tfestimate(x1, x2, hanning(ceil(length(x1)/100)), [], [], 1/dt);
figure; ax1 = subplot(2, 1, 1); plot(f12, abs(T12)); set(gca, 'xscale', 'log'); set(gca, 'yscale', 'log'); set(gca, 'XTickLabel',[]); ylabel('Magnitude'); ax2 = subplot(2, 1, 2); plot(f12, mod(180+180/pi*phase(T12), 360)-180); set(gca, 'xscale', 'log'); ylim([-180, 180]); yticks([-180, -90, 0, 90, 180]); xlabel('Frequency [Hz]'); ylabel('Phase'); linkaxes([ax1,ax2],'x'); xlim([1, 500]);
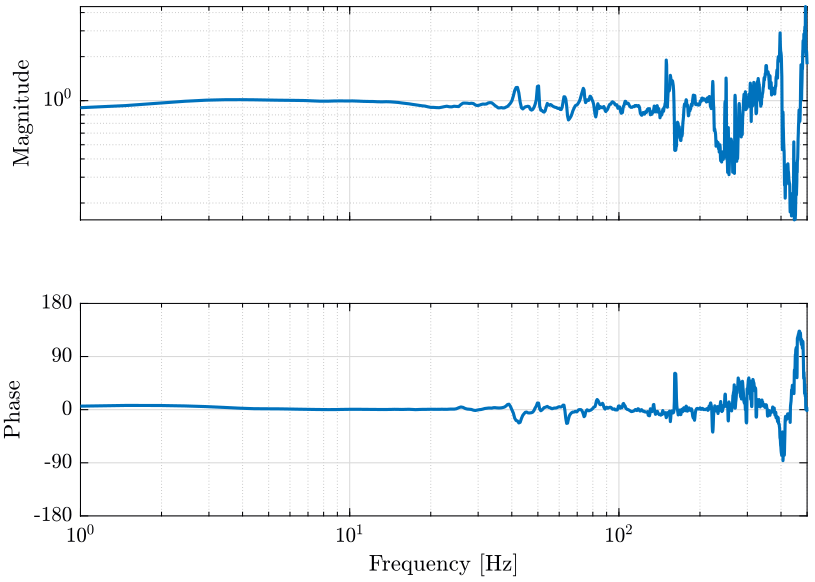
Figure 7: Estimated transfer function between the two geophones