Cercalo Test Bench
Table of Contents
1 Identification
All the files (data and Matlab scripts) are accessible here.
1.1 Excitation Data
fs = 1e4; Ts = 1/fs;
We generate white noise with the "random number" simulink block, and we filter that noise.
Gi = (1)/(1+s/2/pi/100);
c2d(Gi, Ts, 'tustin')
c2d(Gi, Ts, 'tustin')
ans =
0.030459 (z+1)
--------------
(z-0.9391)
Sample time: 0.0001 seconds
Discrete-time zero/pole/gain model.
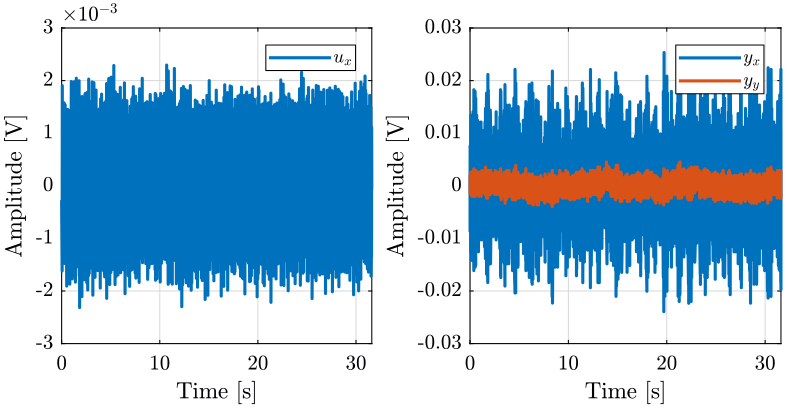
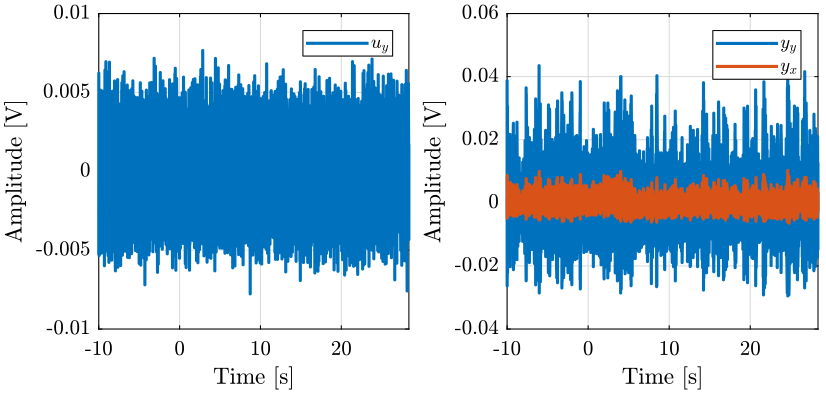
1.2 Input / Output data
The identification data is loaded
ux = load('mat/data_ux.mat', 't', 'ux', 'yx', 'yy'); uy = load('mat/data_uy.mat', 't', 'uy', 'yx', 'yy');
We remove the first seconds where the Cercalo is turned on.
i0x = 20*fs; i0y = 10*fs; ux.t = ux.t( i0x:end) - ux.t(i0x); ux.ux = ux.ux(i0x:end); ux.yx = ux.yx(i0x:end); ux.yy = ux.yy(i0x:end); uy.t = uy.t( i0y:end) - uy.t(i0x); uy.uy = uy.uy(i0y:end); uy.yx = uy.yx(i0y:end); uy.yy = uy.yy(i0y:end);
ux.ux = ux.ux-mean(ux.ux); ux.yx = ux.yx-mean(ux.yx); ux.yy = ux.yy-mean(ux.yy); uy.ux = uy.ux-mean(uy.ux); uy.yx = uy.yx-mean(uy.yx); uy.yy = uy.yy-mean(uy.yy);
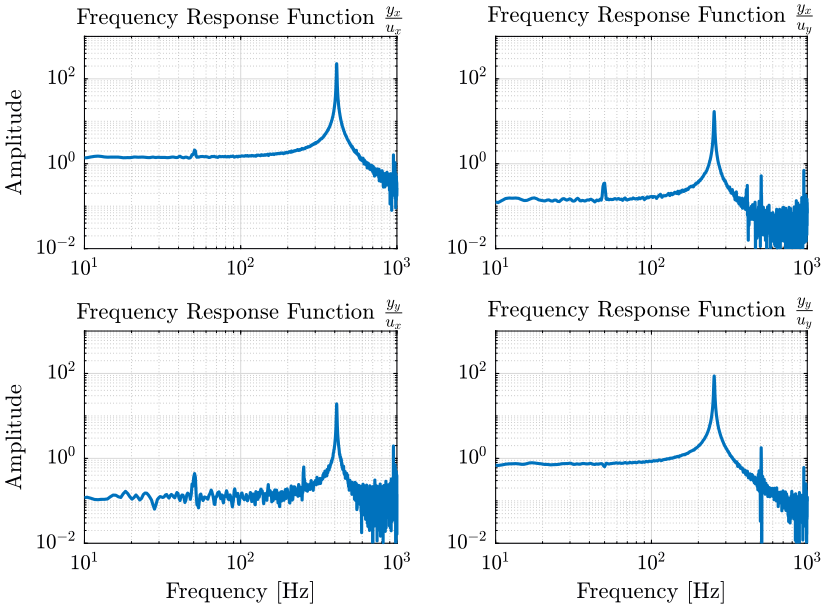
1.3 Estimation of the Frequency Response Function Matrix
We compute an estimate of the transfer functions.
[tf_ux_yx, f] = tfestimate(ux.ux, ux.yx, hanning(ceil(1*fs)), [], [], fs); [tf_ux_yy, ~] = tfestimate(ux.ux, ux.yy, hanning(ceil(1*fs)), [], [], fs); [tf_uy_yx, ~] = tfestimate(uy.uy, uy.yx, hanning(ceil(1*fs)), [], [], fs); [tf_uy_yy, ~] = tfestimate(uy.uy, uy.yy, hanning(ceil(1*fs)), [], [], fs);
1.4 Coherence
[coh_ux_yx, f] = mscohere(ux.ux, ux.yx, hanning(ceil(1*fs)), [], [], fs); [coh_ux_yy, ~] = mscohere(ux.ux, ux.yy, hanning(ceil(1*fs)), [], [], fs); [coh_uy_yx, ~] = mscohere(uy.uy, uy.yx, hanning(ceil(1*fs)), [], [], fs); [coh_uy_yy, ~] = mscohere(uy.uy, uy.yy, hanning(ceil(1*fs)), [], [], fs);
1.5 Extraction of a transfer function matrix
First we define the initial guess for the resonance frequencies and the weights associated.
freqs_res = [410, 250]; % [Hz] freqs_res_weights = [10, 10]; % [Hz]
From the number of resonance frequency we want to fit, we define the order N of the system we want to obtain.
N = 2*length(freqs_res);
We then make an initial guess on the complex values of the poles.
xi = 0.001; % Approximate modal damping poles = [2*pi*freqs_res*(xi + 1i), 2*pi*freqs_res*(xi - 1i)];
We then define the weight that will be used for the fitting. Basically, we want more weight around the resonance and at low frequency (below the first resonance). Also, we want more importance where we have a better coherence.
weight = ones(1, length(f)); % weight = G_coh'; % alpha = 0.1; % for freq_i = 1:length(freqs_res) % weight(f>(1-alpha)*freqs_res(freq_i) & omega<(1 + alpha)*2*pi*freqs_res(freq_i)) = freqs_res_weights(freq_i); % end
Ignore data above some frequency.
weight(f>1000) = 0;
When we set some options for vfit3.
opts = struct(); opts.stable = 1; % Enforce stable poles opts.asymp = 1; % Force D matrix to be null opts.relax = 1; % Use vector fitting with relaxed non-triviality constraint opts.skip_pole = 0; % Do NOT skip pole identification opts.skip_res = 0; % Do NOT skip identification of residues (C,D,E) opts.cmplx_ss = 0; % Create real state space model with block diagonal A opts.spy1 = 0; % No plotting for first stage of vector fitting opts.spy2 = 0; % Create magnitude plot for fitting of f(s)
We define the number of iteration.
Niter = 5;
An we run the vectfit3 algorithm.
for iter = 1:Niter [SER_ux_yx, poles, ~, fit_ux_yx] = vectfit3(tf_ux_yx.', 1i*2*pi*f, poles, weight, opts); end for iter = 1:Niter [SER_uy_yx, poles, ~, fit_uy_yx] = vectfit3(tf_uy_yx.', 1i*2*pi*f, poles, weight, opts); end for iter = 1:Niter [SER_ux_yy, poles, ~, fit_ux_yy] = vectfit3(tf_ux_yy.', 1i*2*pi*f, poles, weight, opts); end for iter = 1:Niter [SER_uy_yy, poles, ~, fit_uy_yy] = vectfit3(tf_uy_yy.', 1i*2*pi*f, poles, weight, opts); end
And finally, we create the identified state space model:
G_ux_yx = minreal(ss(full(SER_ux_yx.A),SER_ux_yx.B,SER_ux_yx.C,SER_ux_yx.D)); G_uy_yx = minreal(ss(full(SER_uy_yx.A),SER_uy_yx.B,SER_uy_yx.C,SER_uy_yx.D)); G_ux_yy = minreal(ss(full(SER_ux_yy.A),SER_ux_yy.B,SER_ux_yy.C,SER_ux_yy.D)); G_uy_yy = minreal(ss(full(SER_uy_yy.A),SER_uy_yy.B,SER_uy_yy.C,SER_uy_yy.D)); G = [G_ux_yx, G_uy_yx; G_ux_yy, G_uy_yy];
save('mat/plant.mat', 'G');