Robust Control - \(\mathcal{H}_\infty\) Synthesis
Table of Contents
- 1. Introduction to the Control Methodology - Model Based Control
- 2. Classical Open Loop Shaping
- 3. The \(\mathcal{H}_\infty\) Norm
- 4. \(\mathcal{H}_\infty\) Synthesis
- 5. The Generalized Plant
- 6. Problem Formulation
- 7. Classical feedback control and closed loop transfer functions
- 8. From a Classical Feedback Architecture to a Generalized Plant
- 9. Modern Interpretation of the Control Specifications
- 10. Resources
1 Introduction to the Control Methodology - Model Based Control
1.1 Control Methodology
The typical methodology when applying Model Based Control to a plant is schematically shown in Figure 1. It consists of three steps:
- Identification or modeling: \(\Longrightarrow\) mathematical model
- Translate the specifications into mathematical criteria:
- Specifications: Response Time, Noise Rejection, Maximum input amplitude, Robustness, …
- Mathematical Criteria: Cost Function, Shape of TF
- Synthesis: research of \(K\) that satisfies the specifications for the model of the system
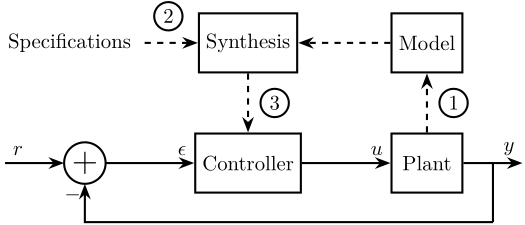
Figure 1: Typical Methodoly for Model Based Control
In this document, we will mainly focus on steps 2 and 3.
1.2 Some Background: From Classical Control to Robust Control
Classical Control (1930)
- Tools:
- TF (input-output)
- Nyquist, Bode, Black, \ldots
- P-PI-PID, Phase lead-lag, \ldots
- Advantages:
- Stability
- Performances
- Robustness
- Disadvantages:
- Manual Method
- Only SISO
Modern Control (1960)
- Tools:
- State Space
- Optimal Command
- LQR, LQG
- Advantages:
- Automatic Synthesis
- MIMO
- Optimisation problem
- Disadvantages:
- Robustness
- Rejection of Perturbations
Robust Control (1980)
- Tools:
- Disk Margin
- Systems and Signals norms (\(\mathcal{H}_\infty\) and \(\mathcal{H}_2\) norms)
- Closed Loop Transfer Functions
- Loop Shaping
- Advantages:
- Stability
- Performances
- Robustness
- Automatic Synthesis
- MIMO
- Optimization Problem
- Disadvantages:
- Requires the knowledge of specific tools
- Need a reasonably good model of the system
1.3 Example System
Let’s consider the test-system shown in Figure 2. The notations used are listed in Table 1.

Figure 2: Test System consisting of a payload with a mass \(m\) on top of an active system with a stiffness \(k\), damping \(c\) and an actuator.
| Notation | Description | Value | Unit |
|---|---|---|---|
| \(m\) | Payload’s mass to position / isolate | [kg] | |
| \(k\) | Stiffness of the suspension system | [N/m] | |
| \(c\) | Damping coefficient of the suspension system | [N/(m/s)] | |
| \(y\) | Payload absolute displacement (measured by an inertial sensor) | [m] | |
| \(d\) | Ground displacement, it acts as a disturbance | [m] | |
| \(u\) | Actuator force | [N] | |
| \(r\) | Wanted position of the mass (the reference) | [m] | |
| \(\epsilon = r - y\) | Position error | [m] | |
| \(K\) | Feedback controller | to be designed | [N/m] |
Derive the following open-loop transfer functions:
\begin{align} G(s) &= \frac{y}{u} \\ G_d(s) &= \frac{y}{d} \end{align}Hint: You can follow this generic procedure:
- List all applied forces ot the mass: Actuator force, Stiffness force (Hooke’s law), …
- Apply the Newton’s Second Law on the payload \[ m \ddot{y} = \Sigma F \]
- Transform the differential equations into the Laplace domain: \[ \frac{d\ \cdot}{dt} \Leftrightarrow \cdot \times s \]
- Write \(y(s)\) as a function of \(u(s)\) and \(w(s)\)
Having obtained \(G(s)\) and \(G_d(s)\), we can transform the system shown in Figure 2 into a classical feedback form as shown in Figure 4.

Figure 3: Block diagram corresponding to the example system
2 Classical Open Loop Shaping
2.1 Introduction ot Open Loop Shaping
Usually, the controller \(K(s)\) is designed such that the loop gain \(L(s)\) has desirable shape. This technique is called Open Loop Shaping.
For instance example all the specifications can usually be explained in terms of the open loop gain.

Figure 4: Classical Feedback Architecture
This is usually done manually has the loop gain \(L(s)\) depends linearly of \(K(s)\):
\begin{equation} L(s) = G(s) K(s) \end{equation}- where \(L(s)\) is called the Loop Gain Transfer Function
\(K(s)\) then consists of a combination of leads, lags, notches, etc. such that its product with \(G(s)\) has wanted shape.
2.2 Example of Open Loop Shaping
k = 1e-6;
m = 10;
c = 10;
G =
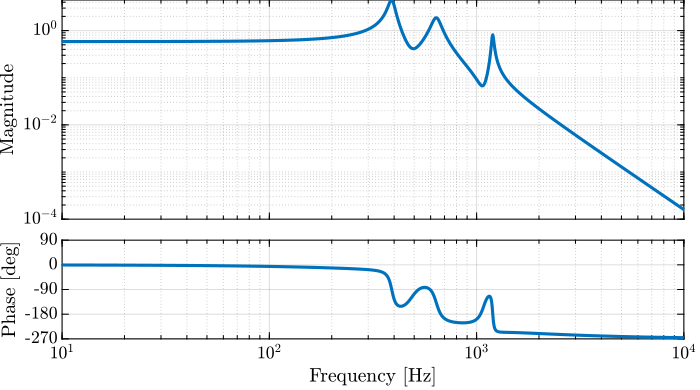
Figure 5: Bode plot of the plant \(G(s)\)
Specifications:
- Performance: Bandwidth of approximately 50Hz
- Noise Attenuation: Roll-off of -40dB/decade past 250Hz
- Robustness: Gain margin > 5dB and Phase margin > 40 deg
Using SISOTOOL, design a controller that fulfill the specifications.
sisotool(G)
In order to have the wanted Roll-off, two integrators are used, a lead is also added to have sufficient phase margin.
The obtained controller is shown below, and the bode plot of the Loop Gain is shown in Figure 6.
K = 6e4 * ... % Gain 1/(s^2) * ... % Double Integrator (1 + s/111)/(1 + s/888); % Lead
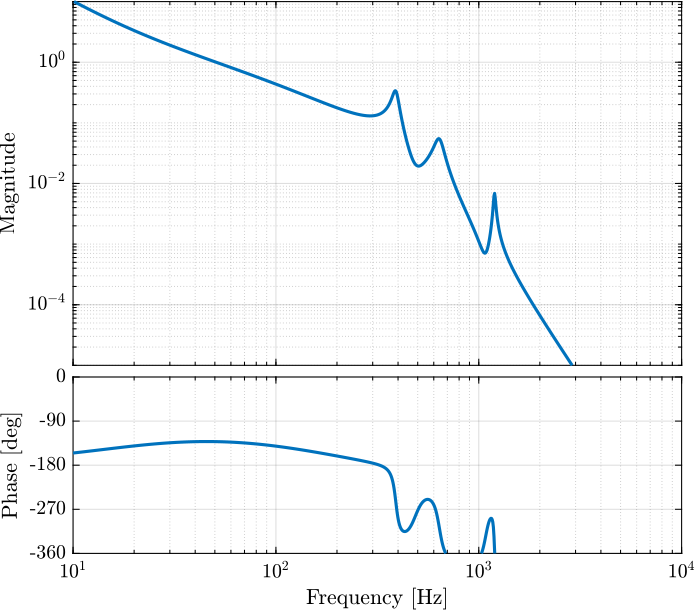
Figure 6: Bode Plot of the obtained Loop Gain \(L(s) = G(s) K(s)\)
And we can verify that we have the wanted stability margins:
[Gm, Pm, ~, Wc] = margin(G*K)
| Value | |
|---|---|
| Gain Margin [dB] | 7.2 |
| Phase Margin [deg] | 48.1 |
| Crossover [Hz] | 50.7 |
2.3 \(\mathcal{H}_\infty\) Loop Shaping Synthesis
The Open Loop Shaping synthesis can be performed using the \(\mathcal{H}_\infty\) Synthesis.
Even though we will not go into details, we will provide one example.
Using Matlab, the \(\mathcal{H}_\infty\) synthesis of a controller based on the wanted open loop shape can be performed using the loopsyn command:
K = loopsyn(G, Gd);
where:
Gis the (LTI) plantGdis the wanted loop shapeKis the synthesize controller
Matlab documentation of loopsyn (link).
2.4 Example of the \(\mathcal{H}_\infty\) Loop Shaping Synthesis
Let’s re-use the previous plant.
Translate the specification into the wanted shape of the open loop gain.
G = tf(16,[1 0.16 16]); Gd = 3.7e4*1/s*(1 + s/2/pi/20)/(1 + s/2/pi/220)*1/(s + s/2/pi/500);
[K,CL,GAM,INFO] = loopsyn(G, Gd);
bodeFig({K})
3 The \(\mathcal{H}_\infty\) Norm
The \(\mathcal{H}_\infty\) norm is defined as the peak of the maximum singular value of the frequency response
\begin{equation} \|G(s)\|_\infty = \max_\omega \bar{\sigma}\big( G(j\omega) \big) \end{equation}For a SISO system \(G(s)\), it is simply the peak value of \(|G(j\omega)|\) as a function of frequency:
\begin{equation} \|G(s)\|_\infty = \max_{\omega} |G(j\omega)| \label{eq:hinf_norm_siso} \end{equation}Let’s define a plant dynamics:
w0 = 2*pi; k = 1e6; xi = 0.04; G = 1/k/(s^2/w0^2 + 2*xi*s/w0 + 1);
And compute its \(\mathcal{H}_\infty\) norm using the hinfnorm function:
hinfnorm(G)
1.0013e-05
The magnitude \(|G(j\omega)|\) of the plant \(G(s)\) as a function of frequency is shown in Figure 7. The maximum value of the magnitude over all frequencies does correspond to the \(\mathcal{H}_\infty\) norm of \(G(s)\) as Equation \eqref{eq:hinf_norm_siso} implies.

Figure 7: Example of the \(\mathcal{H}_\infty\) norm of a SISO system
4 \(\mathcal{H}_\infty\) Synthesis
Optimization problem: \(\mathcal{H}_\infty\) synthesis is a method that uses an algorithm (LMI optimization, Riccati equation) to find a controller of the same order as the system so that the \(\mathcal{H}_\infty\) norms of defined transfer functions are minimized.
Engineer work:
- Write the problem as standard \(\mathcal{H}_\infty\) problem
- Translate the specifications as \(\mathcal{H}_\infty\) norms
- Make the synthesis and analyze the obtain controller
- Reduce the order of the controller for implementation
Many ways to use the \(\mathcal{H}_\infty\) Synthesis:
- Traditional \(\mathcal{H}_\infty\) Synthesis
- Mixed Sensitivity Loop Shaping
- Fixed-Structure \(\mathcal{H}_\infty\) Synthesis
- Signal Based \(\mathcal{H}_\infty\) Synthesis
5 The Generalized Plant

| Notation | Meaning |
|---|---|
| \(P\) | Generalized plant model |
| \(w\) | Exogenous inputs: commands, disturbances, noise |
| \(z\) | Exogenous outputs: signals to be minimized |
| \(v\) | Controller inputs: measurements |
| \(u\) | Control signals |
6 Problem Formulation
The \(\mathcal{H}_\infty\) Synthesis objective is to find all stabilizing controllers \(K\) which minimize
\begin{equation} \| F_l(P, K) \|_\infty = \max_{\omega} \overline{\sigma} \big( F_l(P, K)(j\omega) \big) \end{equation}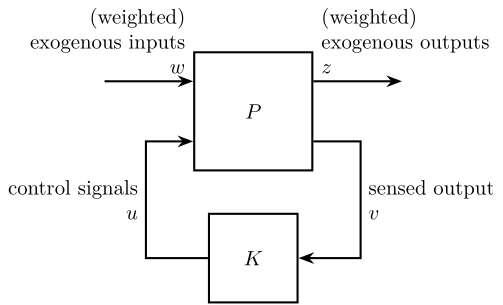
Figure 9: General Control Configuration
7 Classical feedback control and closed loop transfer functions
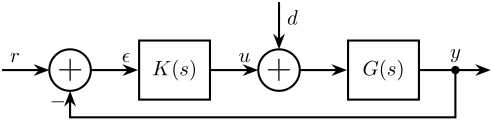
Figure 10: Classical Feedback Architecture
| Notation | Meaning |
|---|---|
| \(G\) | Plant model |
| \(K\) | Controller |
| \(r\) | Reference inputs |
| \(y\) | Plant outputs |
| \(u\) | Control signals |
| \(d\) | Input Disturbance |
| \(\epsilon\) | Tracking Error |
8 From a Classical Feedback Architecture to a Generalized Plant
The procedure is:
- define signals of the generalized plant
- Remove \(K\) and rearrange the inputs and outputs
Let’s find the Generalized plant of corresponding to the tracking control architecture shown in Figure 11
![]()
Figure 11: Classical Feedback Control Architecture (Tracking)
First, define the signals of the generalized plant:
- Exogenous inputs: \(w = r\)
- Signals to be minimized: \(z_1 = \epsilon\), \(z_2 = u\)
- Control signals: \(v = y\)
- Control inputs: \(u\)
Then, Remove \(K\) and rearrange the inputs and outputs. We obtain the generalized plant shown in Figure 12.
![]()
Figure 12: Generalized plant of the Classical Feedback Control Architecture (Tracking)
Using Matlab, the generalized plant can be defined as follows:
P = [1 -G; 0 1; 1 -G]
9 Modern Interpretation of the Control Specifications
9.1 Introduction
- Reference tracking Overshoot, Static error, Setling time
- \(S(s) = T_{r \rightarrow \epsilon}\)
- Disturbances rejection
- \(G(s) S(s) = T_{d \rightarrow \epsilon}\)
- Measurement noise filtering
- \(T(s) = T_{n \rightarrow \epsilon}\)
- Small command amplitude
- \(K(s) S(s) = T_{r \rightarrow u}\)
- Stability
- \(S(s)\), \(T(s)\), \(K(s)S(s)\), \(G(s)S(s)\)
- Robustness to plant uncertainty (stability margins)
- Controller implementation
**
10 Resources