A brief and practical introduction to \(\mathcal{H}_\infty\) Control
Table of Contents
- 1. Introduction to Model Based Control
- 2. Classical Open Loop Shaping
- 3. A first Step into the \(\mathcal{H}_\infty\) world
- 4. Modern Interpretation of Control Specifications
- 5. \(\mathcal{H}_\infty\) Shaping of closed-loop transfer functions
- 6. Mixed-Sensitivity \(\mathcal{H}_\infty\) Control - Example
- 7. Conclusion
The purpose of this document is to give a practical introduction to the wonderful world of \(\mathcal{H}_\infty\) Control.
No attend is made to provide an exhaustive treatment of the subject. \(\mathcal{H}_\infty\) Control is a very broad topic and entire books are written on it. Therefore, for more advanced discussion, please have a look at the recommended references at the bottom of this document.
When possible, Matlab scripts used for the example/exercises are provided such that you can easily test them on your computer.
The general structure of this document is as follows:
- A short introduction to model based control is given in Section 1
- Classical open loop shaping method is presented in Section 2. It is also shown that \(\mathcal{H}_\infty\) synthesis can be used for open loop shaping
- Important concepts indispensable for \(\mathcal{H}_\infty\) control such as the \(\mathcal{H}_\infty\) norm and the generalized plant are introduced in Section 3
- A very important step in \(\mathcal{H}_\infty\) control is to express the control specifications (performances, robustness, etc.) as an \(\mathcal{H}_\infty\) optimization problem. Such procedure is described in Section 4
- One of the most useful use of the \(\mathcal{H}_\infty\) control is the shaping of closed-loop transfer functions. Such technique is presented in Section 5
- Finally, complete examples of the use of \(\mathcal{H}_\infty\) Control for practical problems are provided in Section 6.
1 Introduction to Model Based Control
1.1 Model Based Control - Methodology
The typical methodology for Model Based Control techniques is schematically shown in Figure 1.
It consists of three steps:
- Identification or modeling: a mathematical model \(G(s)\) representing the plant dynamics is obtained
- Translate the specifications into mathematical criteria:
- Specifications: Response Time, Noise Rejection, Maximum input amplitude, Robustness, …
- Mathematical Criteria: Cost Function, Shape of transfer function, Phase/Gain margin, Roll-Off, …
- Synthesis: research of a controller \(K(s)\) that satisfies the specifications for the model of the system
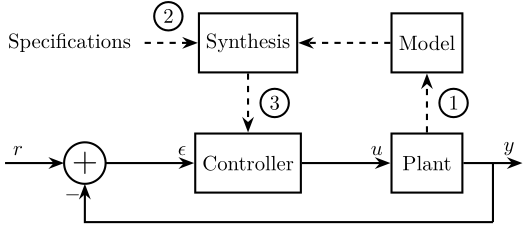
Figure 1: Typical Methodoly for Model Based Control
In this document, we will suppose a model of the plant is available (step 1 already performed), and we will focus on steps 2 and 3.
In Section 2, steps 2 and 3 will be described for a control techniques called classical (open-)loop shaping.
Then, steps 2 and 3 for the \(\mathcal{H}_\infty\) Loop Shaping of closed-loop transfer functions will be discussed in Sections 4, 5 and 6.
1.2 From Classical Control to Robust Control
Many different model based control techniques have been developed since the birth of classical control theory in the ’30s.
Classical control methods were developed starting from 1930 based on tools such as the Laplace and Fourier transforms. It was then natural to study systems in the frequency domain using tools such as the Bode and Nyquist plots. Controllers were manually tuned to optimize criteria such as control bandwidth, gain and phase margins.
The ’60s saw the development of control techniques based on a state-space. Linear algebra and matrices were used instead of the frequency domain tool of the class control theory. This allows multi-inputs multi-outputs systems to be easily treated. Kalman introduced the well known Kalman estimator as well the notion of optimality by minimizing quadratic cost functions. This set of developments is loosely termed Modern Control theory.
By the 1980’s, modern control theory was shown to have some robustness issues and to lack the intuitive tools that the classical control methods were offering. This lead to a new control theory called Robust control that blends the best features of classical and modern techniques. This robust control theory is the subject of this document.
The three presented control methods are compared in Table 1.
Note that in parallel, there have been numerous other developments, including non-linear control, adaptive control, machine-learning control just to name a few.
| Classical Control | Modern Control | Robust Control | |
|---|---|---|---|
| Date | 1930- | 1960- | 1980- |
| Tools | Transfer Functions | State Space formulation | Systems and Signals Norms (\(\mathcal{H}_\infty\), \(\mathcal{H}_2\) Norms) |
| Nyquist Plots | Riccati Equations | Closed Loop Transfer Functions | |
| Bode Plots | Open/Closed Loop Shaping | ||
| Phase and Gain margins | Weighting Functions | ||
| Disk margin | |||
| Singular Value Decomposition | |||
| Control Architectures | Proportional, Integral, Derivative | Full State Feedback, LQR | General Control Configuration |
| Leads, Lags | Kalman Filters, LQG | Generalized Plant | |
| Advantages | Study Stability | Automatic Synthesis | Automatic Synthesis |
| Simple | MIMO | MIMO | |
| Natural | Optimization Problem | Optimization Problem | |
| Guaranteed Robustness | |||
| Easy specification of performances | |||
| Disadvantages | Manual Method | No Guaranteed Robustness | Required knowledge of specific tools |
| Only SISO | Difficult Rejection of Perturbations | Need a reasonably good model of the system | |
| No clear way to limit input usage |
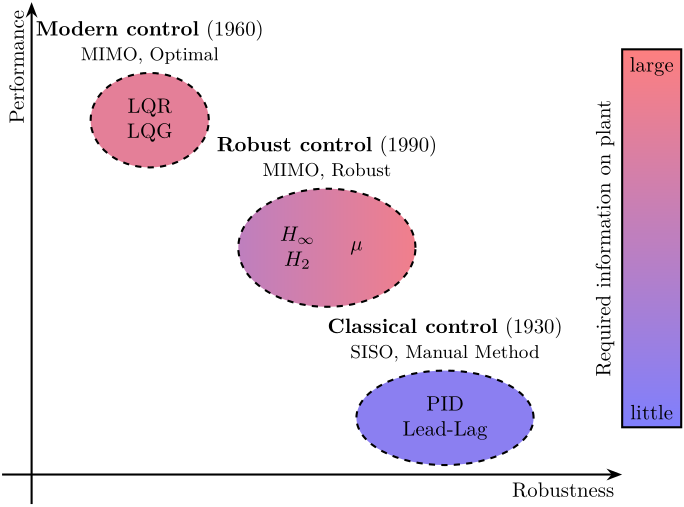
Figure 2: Comparison of the performance and robustness of classical control methods, modern control methods and robust control methods. The required information on the plant to succesfuly apply each of the control methods are indicated by the colors.
1.3 Example System
Let’s consider the model shown in Figure 3. It could represent a suspension system with a payload to position or isolate using an force actuator and an inertial sensor. The notations used are listed in Table 2.
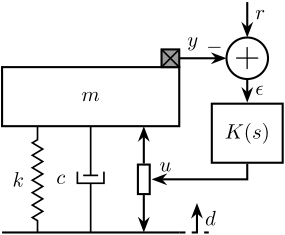
Figure 3: Test System consisting of a payload with a mass \(m\) on top of an active system with a stiffness \(k\), damping \(c\) and an actuator. A feedback controller \(K(s)\) is added to position / isolate the payload.
| Notation | Description | Value | Unit |
|---|---|---|---|
| \(m\) | Payload’s mass to position / isolate | \(10\) | [kg] |
| \(k\) | Stiffness of the suspension system | \(10^6\) | [N/m] |
| \(c\) | Damping coefficient of the suspension system | \(400\) | [N/(m/s)] |
| \(y\) | Payload absolute displacement (measured by an inertial sensor) | [m] | |
| \(d\) | Ground displacement, it acts as a disturbance | [m] | |
| \(u\) | Actuator force | [N] | |
| \(r\) | Wanted position of the mass (the reference) | [m] | |
| \(\epsilon = r - y\) | Position error | [m] | |
| \(K\) | Feedback controller | to be designed | [N/m] |
Derive the following open-loop transfer functions:
\begin{align} G(s) &= \frac{y}{u} \\ G_d(s) &= \frac{y}{d} \end{align}Hint
You can follow this generic procedure:
- List all applied forces ot the mass: Actuator force, Stiffness force (Hooke’s law), …
- Apply the Newton’s Second Law on the payload \[ m \ddot{y} = \Sigma F \]
- Transform the differential equations into the Laplace domain: \[ \frac{d\ \cdot}{dt} \Leftrightarrow \cdot \times s \]
- Write \(y(s)\) as a function of \(u(s)\) and \(w(s)\)
Results
\begin{align} G(s) &= \frac{1}{m s^2 + cs + k} \\ G_d(s) &= \frac{cs + k}{m s^2 + cs + k} \end{align}Having obtained \(G(s)\) and \(G_d(s)\), we can transform the system shown in Figure 3 into a classical feedback form as shown in Figure 7.
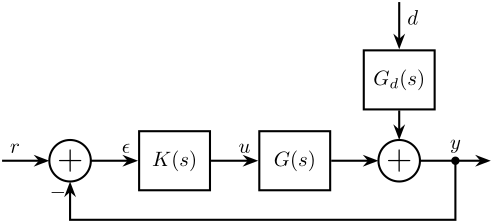
Figure 4: Block diagram corresponding to the example system
Let’s define the system parameters on Matlab.
1: k = 1e6; % Stiffness [N/m] 2: c = 4e2; % Damping [N/(m/s)] 3: m = 10; % Mass [kg]
And now the system dynamics \(G(s)\) and \(G_d(s)\) (their bode plots are shown in Figures 5 and 6).
4: G = 1/(m*s^2 + c*s + k); % Plant 5: Gd = (c*s + k)/(m*s^2 + c*s + k); % Disturbance
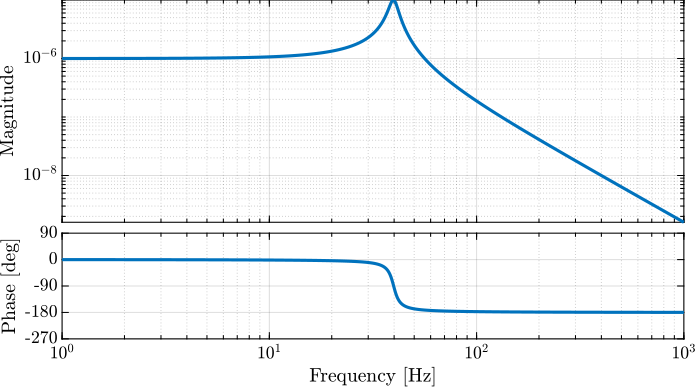
Figure 5: Bode plot of the plant \(G(s)\)
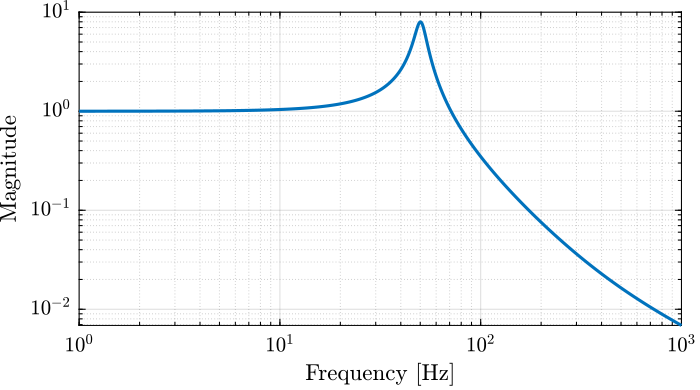
Figure 6: Magnitude of the disturbance transfer function \(G_d(s)\)
2 Classical Open Loop Shaping
2.1 Introduction to Loop Shaping
Loop Shaping refers to a design procedure that involves explicitly shaping the magnitude of the Loop Transfer Function \(L(s)\).
The Loop Gain \(L(s)\) usually refers to as the product of the controller and the plant (“Gain around the loop”, see Figure 7):
\begin{equation} L(s) = G(s) \cdot K(s) \label{eq:loop_gain} \end{equation}
Figure 7: Classical Feedback Architecture
This synthesis method is widely used as many characteristics of the closed-loop system depend on the shape of the open loop gain \(L(s)\) such as:
- Performance: \(L\) large
- Good disturbance rejection: \(L\) large
- Limitation of measurement noise on plant output: \(L\) small
- Small magnitude of input signal: \(K\) and \(L\) small
- Nominal stability: \(L\) small (RHP zeros and time delays)
- Robust stability: \(L\) small (neglected dynamics)
The Open Loop shape is usually done manually has the loop gain \(L(s)\) depends linearly on \(K(s)\) \eqref{eq:loop_gain}.
\(K(s)\) then consists of a combination of leads, lags, notches, etc. such that \(L(s)\) has the wanted shape (an example is shown in Figure 8).

Figure 8: Typical Wanted Shape for the Loop Gain \(L(s)\)
2.2 Example of Open Loop Shaping
Let’s take our example system and try to apply the Open-Loop shaping strategy to design a controller that fulfils the following specifications:
- Performance: Bandwidth of approximately 10Hz
- Noise Attenuation: Roll-off of -40dB/decade past 30Hz
- Robustness: Gain margin > 3dB and Phase margin > 30 deg
Using SISOTOOL, design a controller that fulfill the specifications.
sisotool(G)
In order to have the wanted Roll-off, two integrators are used, a lead is also added to have sufficient phase margin.
The obtained controller is shown below, and the bode plot of the Loop Gain is shown in Figure 9.
K = 14e8 * ... % Gain 1/(s^2) * ... % Double Integrator 1/(1 + s/2/pi/40) * ... % Low Pass Filter (1 + s/(2*pi*10/sqrt(8)))/(1 + s/(2*pi*10*sqrt(8))); % Lead
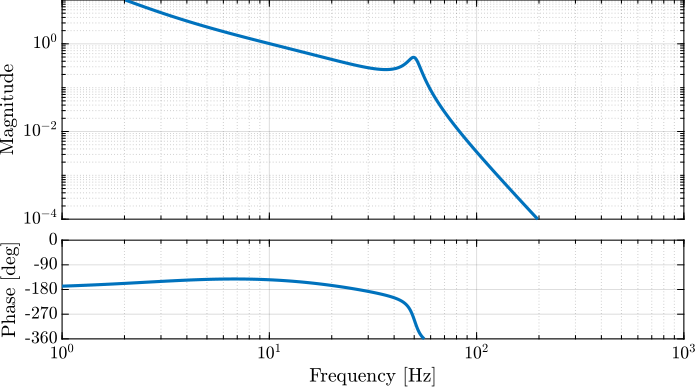
Figure 9: Bode Plot of the obtained Loop Gain \(L(s) = G(s) K(s)\)
And we can verify that we have the wanted stability margins:
[Gm, Pm, ~, Wc] = margin(G*K)
| Requirements | Manual Method |
|---|---|
| Gain Margin \(> 3\) [dB] | 3.1 |
| Phase Margin \(> 30\) [deg] | 35.4 |
| Crossover \(\approx 10\) [Hz] | 10.1 |
2.3 \(\mathcal{H}_\infty\) Loop Shaping Synthesis
The Open Loop Shaping synthesis can be performed using the \(\mathcal{H}_\infty\) Synthesis.
Even though we will not go into details, we will provide one example.
Using Matlab, the \(\mathcal{H}_\infty\) Loop Shaping Synthesis can be performed using the loopsyn command:
K = loopsyn(G, Gd);
where:
Gis the (LTI) plantGdis the wanted loop shapeKis the synthesize controller
Matlab documentation of loopsyn (link).
2.4 Example of the \(\mathcal{H}_\infty\) Loop Shaping Synthesis
Let’s reuse the previous plant.
Translate the specification into the wanted shape of the open loop gain.
- Performance: Bandwidth of approximately 10Hz: \(|L_w(j2 \pi 10)| = 1\)
- Noise Attenuation: Roll-off of -40dB/decade past 30Hz
- Robustness: Gain margin > 3dB and Phase margin > 30 deg
Lw = 2.3e3 * ... 1/(s^2) * ... % Double Integrator (1 + s/(2*pi*10/sqrt(3)))/(1 + s/(2*pi*10*sqrt(3))); % Lead
The \(\mathcal{H}_\infty\) optimal open loop shaping synthesis is performed using the loopsyn command:
[K, ~, GAM] = loopsyn(G, Lw);
It is always important to analyze the controller after the synthesis is performed.
In the end, a synthesize controller is just a combination of low pass filters, high pass filters, notches, leads, etc.
Let’s briefly analyze the obtained controller which bode plot is shown in Figure 10:
- two integrators are used at low frequency to have the wanted low frequency high gain
- a lead is added centered with the crossover frequency to increase the phase margin
- a notch is added at the resonance of the plant to increase the gain margin (this is very typical of \(\mathcal{H}_\infty\) controllers, and can be an issue, more info on that latter)
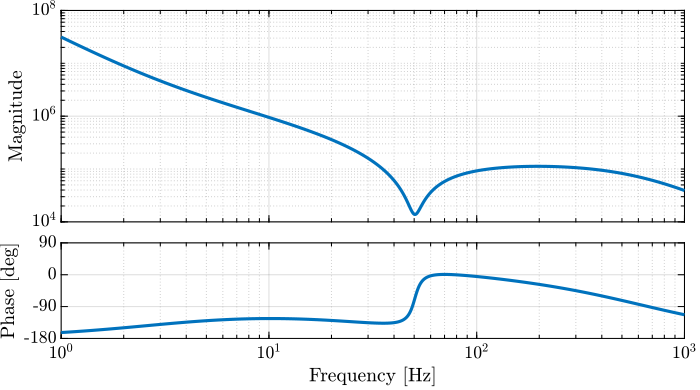
Figure 10: Obtained controller \(K\) using the open-loop \(\mathcal{H}_\infty\) shaping
The obtained Loop Gain is shown in Figure 11 and matches the specified one by a factor \(\gamma\).
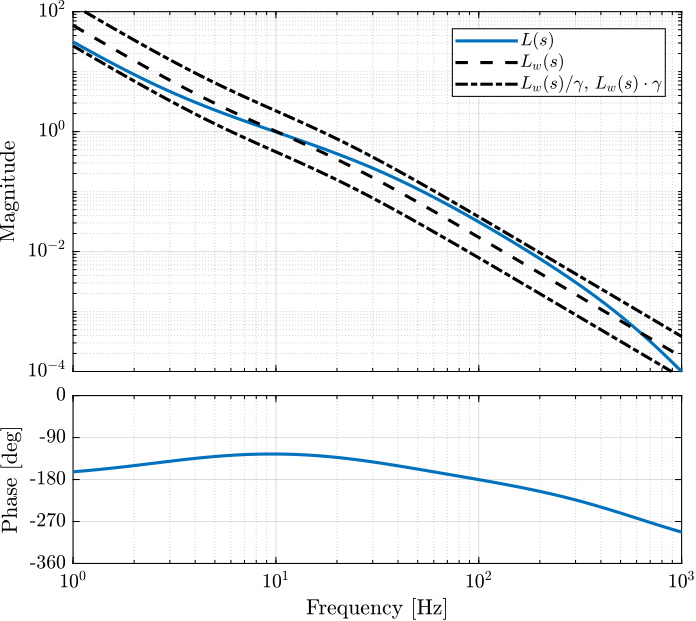
Figure 11: Obtained Open Loop Gain \(L(s) = G(s) K(s)\) and comparison with the wanted Loop gain \(L_w\)
Let’s now compare the obtained stability margins of the \(\mathcal{H}_\infty\) controller and of the manually developed controller in Table 3.
| Specifications | Manual Method | \(\mathcal{H}_\infty\) Method |
|---|---|---|
| Gain Margin \(> 3\) [dB] | 3.1 | 31.7 |
| Phase Margin \(> 30\) [deg] | 35.4 | 54.7 |
| Crossover \(\approx 10\) [Hz] | 10.1 | 9.9 |
3 A first Step into the \(\mathcal{H}_\infty\) world
3.1 The \(\mathcal{H}_\infty\) Norm
The \(\mathcal{H}_\infty\) norm is defined as the peak of the maximum singular value of the frequency response
\begin{equation} \|G(s)\|_\infty = \max_\omega \bar{\sigma}\big( G(j\omega) \big) \end{equation}For a SISO system \(G(s)\), it is simply the peak value of \(|G(j\omega)|\) as a function of frequency:
\begin{equation} \|G(s)\|_\infty = \max_{\omega} |G(j\omega)| \label{eq:hinf_norm_siso} \end{equation}
Let’s compute the \(\mathcal{H}_\infty\) norm of our test plant \(G(s)\) using the hinfnorm function:
hinfnorm(G)
7.9216e-06
We can see that the \(\mathcal{H}_\infty\) norm of \(G(s)\) does corresponds to the peak value of \(|G(j\omega)|\) as a function of frequency as shown in Figure 12.
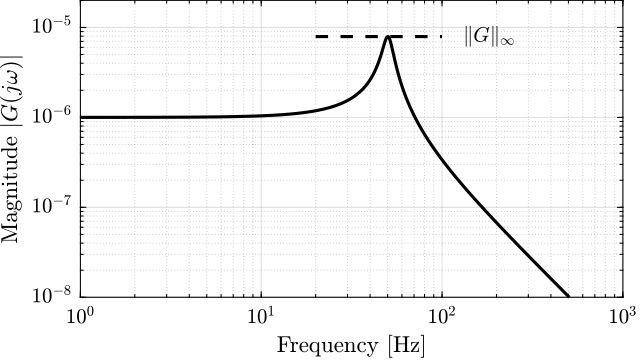
Figure 12: Example of the \(\mathcal{H}_\infty\) norm of a SISO system
3.2 \(\mathcal{H}_\infty\) Synthesis
\(\mathcal{H}_\infty\) synthesis is a method that uses an algorithm (LMI optimization, Riccati equation) to find a controller that stabilize the system and that minimizes the \(\mathcal{H}_\infty\) norms of defined transfer functions.
Why optimizing the \(\mathcal{H}_\infty\) norm of transfer functions is a pertinent choice will become clear when we will translate the typical control specifications into the \(\mathcal{H}_\infty\) norm of transfer functions.
Then applying the \(\mathcal{H}_\infty\) synthesis to a plant, the engineer work usually consists of the following steps
- Write the problem as standard \(\mathcal{H}_\infty\) problem
- Translate the specifications as \(\mathcal{H}_\infty\) norms of transfer functions
- Make the synthesis and analyze the obtain controller
- Reduce the order of the controller for implementation
Note that there are many ways to use the \(\mathcal{H}_\infty\) Synthesis:
3.3 The Generalized Plant
The first step when applying the \(\mathcal{H}_\infty\) synthesis is usually to write the problem as a standard \(\mathcal{H}_\infty\) problem. This consist of deriving the Generalized Plant for the current problem. It makes things much easier for the following steps.
The generalized plant, usually noted \(P(s)\), is shown in Figure 13. It has two inputs and two outputs (both could contains many signals). The meaning of the inputs and outputs are summarized in Table 4.
Note that this generalized plant is as its name implies, quite general. It can indeed represent feedback as well as feedforward control architectures.
\begin{equation} \begin{bmatrix} z \\ v \end{bmatrix} = P \begin{bmatrix} w \\ u \end{bmatrix} = \begin{bmatrix} P_{11} & P_{12} \\ P_{21} & P_{22} \end{bmatrix} \begin{bmatrix} w \\ u \end{bmatrix} \end{equation}
Figure 13: Inputs and Outputs of the generalized Plant
| Notation | Meaning |
|---|---|
| \(P\) | Generalized plant model |
| \(w\) | Exogenous inputs: commands, disturbances, noise |
| \(z\) | Exogenous outputs: signals to be minimized |
| \(v\) | Controller inputs: measurements |
| \(u\) | Control signals |
3.4 The \(\mathcal{H}_\infty\) Synthesis applied on the Generalized plant
Once the generalized plant is obtained, the \(\mathcal{H}_\infty\) synthesis problem can be stated as follows:
- \(\mathcal{H}_\infty\) Synthesis applied on the generalized plant
Find a stabilizing controller \(K\) that, using the sensed output \(v\), generates a control signal \(u\) such that the \(\mathcal{H}_\infty\) norm of the closed-loop transfer function from \(w\) to \(z\) is minimized.
After \(K\) is found, the system is robustified by adjusting the response around the unity gain frequency to increase stability margins.

Figure 14: General Control Configuration
Note that the closed-loop transfer function from \(w\) to \(z\) is:
\begin{equation} \frac{z}{w} = P_{11} + P_{12} K \big( I - P_{22} K \big)^{-1} P_{21} \triangleq F_l(P, K) \end{equation}
Using Matlab, the \(\mathcal{H}_\infty\) Synthesis applied on a Generalized plant can be applied using the hinfsyn command (documentation):
K = hinfsyn(P, nmeas, ncont);
where:
Pis the generalized plant transfer function matrixnmeasis the number of sensed output (size of \(v\))ncontis the number of control signals (size of \(u\))Kobtained controller that minimized the \(\mathcal{H}_\infty\) norm from \(w\) to \(z\)
3.5 From a Classical Feedback Architecture to a Generalized Plant
The procedure to convert a typical control architecture as the one shown in Figure 15 to a generalized Plant is as follows:
- Define signals (\(w\), \(z\), \(u\) and \(v\)) of the generalized plant
- Remove \(K\) and rearrange the inputs and outputs to match the generalized configuration shown in Figure 13
- Convert the tracking control architecture shown in Figure 15 to a generalized configuration
- Compute the transfer function matrix using Matlab as a function or \(K\) and \(G\)
![]()
Figure 15: Classical Feedback Control Architecture (Tracking)
Hint
First, define the signals of the generalized plant:
- Exogenous inputs: \(w = r\)
- Signals to be minimized: Usually, we want to minimize the tracking errors \(\epsilon\) and the control signal \(u\): \(z = [\epsilon,\ u]\)
- Controller inputs: this is the signal at the input of the controller: \(v = \epsilon\)
- Control inputs: signal generated by the controller: \(u\)
Then, Remove \(K\) and rearrange the inputs and outputs as in Figure 13.
Answer
The obtained generalized plant shown in Figure 16.
![]()
Figure 16: Generalized plant of the Classical Feedback Control Architecture (Tracking)
Using Matlab, the generalized plant can be defined as follows:
P = [1 -G; 0 1; 1 -G] P.InputName = {'w', 'u'}; P.OutputName = {'e', 'u', 'v'};
4 Modern Interpretation of Control Specifications
As shown in Section 2, the loop gain \(L(s) = G(s) K(s)\) is a useful and easy tool when manually designing controllers. This is mainly due to the fact that \(L(s)\) is very easy to shape as it depends linearly on \(K(s)\). Moreover, important quantities such as the stability margins and the control bandwidth can be estimated from the shape/phase of \(L(s)\).
However, the loop gain \(L(s)\) does not directly give the performances of the closed-loop system, which are determined by the closed-loop transfer functions.
If we consider the feedback system shown in Figure 17, we can link to the following specifications to closed-loop transfer functions. This is summarized in Table 5.
| Specification | Closed-Loop Transfer Function |
|---|---|
| Reference Tracking | From \(r\) to \(\epsilon\) |
| Disturbance Rejection | From \(d\) to \(y\) |
| Measurement Noise Filtering | From \(n\) to \(y\) |
| Small Command Amplitude | From \(n,r,d\) to \(u\) |
| Stability | All closed-loop transfer function |
| Robustness (stability margins) | Module margin (see Section 4.3) |

Figure 17: Simple Feedback Architecture
4.1 Closed Loop Transfer Functions
As the performances of a controlled system depend on the closed loop transfer functions, it is very important to derive these closed-loop transfer functions as a function of the plant \(G(s)\) and controller \(K(s)\).
Write the output signals \([\epsilon, u, y]\) as a function of the systems \(K(s), G(s)\) and of the input signals \([r, d, n]\) as shown in Figure 17.
Hint
Take one of the output (e.g. \(y\)), and write it as a function of the inputs \([d, r, n]\) going step by step around the loop:
\begin{aligned} y &= G u \\ &= G (d + K \epsilon) \\ &= G \big(d + K (r - n - y) \big) \\ &= G d + GK r - GK n - GK y \end{aligned}Isolate \(y\) at the right hand side, and finally obtain: \[ y = \frac{GK}{1+ GK} r + \frac{G}{1 + GK} d - \frac{GK}{1 + GK} n \]
Do the same procedure for \(u\) and \(\epsilon\)
Answer
The following equations should be obtained:
\begin{align} y &= \frac{GK}{1 + GK} r + \frac{G}{1 + GK} d - \frac{GK}{1 + GK} n \\ \epsilon &= \frac{1 }{1 + GK} r - \frac{G}{1 + GK} d - \frac{G }{1 + GK} n \\ u &= \frac{K }{1 + GK} r - \frac{1}{1 + GK} d - \frac{K }{1 + GK} n \end{align}We can see that they are 4 different transfer functions describing the behavior of the system in Figure 17. These called the Gang of Four:
\begin{align} S &= \frac{1 }{1 + GK}, \quad \text{the sensitivity function} \\ T &= \frac{GK}{1 + GK}, \quad \text{the complementary sensitivity function} \\ GS &= \frac{G }{1 + GK}, \quad \text{the load disturbance sensitivity function} \\ KS &= \frac{K }{1 + GK}, \quad \text{the noise sensitivity function} \end{align}If a feedforward controller is included, a Gang of Six transfer functions can be defined. More on that in this short video.
And we have:
\begin{align} \epsilon &= S r - GS d - GS n \\ y &= T r + GS d - T n \\ u &= KS r - S d - KS n \end{align}Thus, for reference tracking, we have to shape the closed-loop transfer function from \(r\) to \(\epsilon\), that is the sensitivity function \(S(s)\). Similarly, to reduce the effect of measurement noise \(n\) on the output \(y\), we have to act on the complementary sensitivity function \(T(s)\).
4.2 Sensitivity Function
The sensitivity function is indisputably the most important closed-loop transfer function of a feedback system. In this section, we will see how the shape of the sensitivity function will impact the performances of the closed-loop system.
Suppose we have developed a “reference” controller \(K_r(s)\) and made three small changes to obtained three controllers \(K_1(s)\), \(K_2(s)\) and \(K_3(s)\). The obtained sensitivity functions are shown in Figure 18 and the corresponding step responses are shown in Figure 19.
The comparison of the sensitivity functions shapes and their effect on the step response is summarized in Table 6.
| Controller | Sensitivity Function Shape | Change of the Step Response |
|---|---|---|
| \(K_1(s)\) | Larger bandwidth \(\omega_b\) | Faster rise time |
| \(K_2(s)\) | Larger peak value \(\Vert S\Vert_\infty\) | Large overshoot and oscillations |
| \(K_3(s)\) | Larger low frequency gain \(\vert S(j\cdot 0)\vert\) | Larger static error |
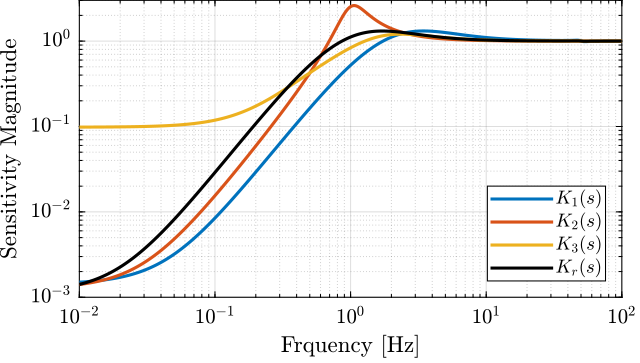
Figure 18: Sensitivity function magnitude \(|S(j\omega)|\) corresponding to the reference controller \(K_r(s)\) and the three modified controllers \(K_i(s)\)
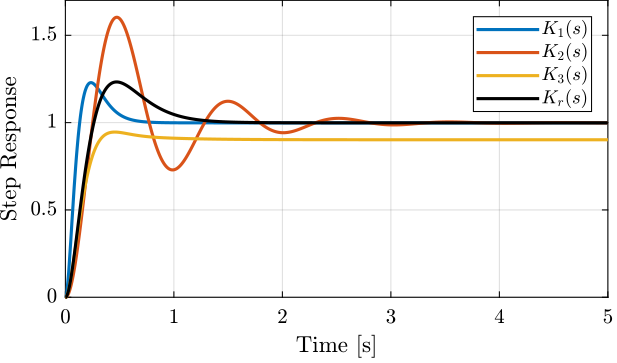
Figure 19: Step response (response from \(r\) to \(y\)) for the different controllers
- Closed-Loop Bandwidth
The closed-loop bandwidth \(\omega_b\) is the frequency where \(|S(j\omega)|\) first crosses \(1/\sqrt{2} = -3dB\) from below.
In general, a large bandwidth corresponds to a faster rise time.
From the simple analysis above, we can draw a first estimation of the wanted shape for the sensitivity function in Figure 20.
The wanted characteristics on the magnitude of the sensitivity function are then:
- A small magnitude at low frequency to make the static errors small
- A wanted minimum closed-loop bandwidth in order to have fast rise time and good rejection of perturbations
- A small peak value in order to limit large overshoot and oscillations. This generally means higher robustness. This will become clear in the next section about the module margin.
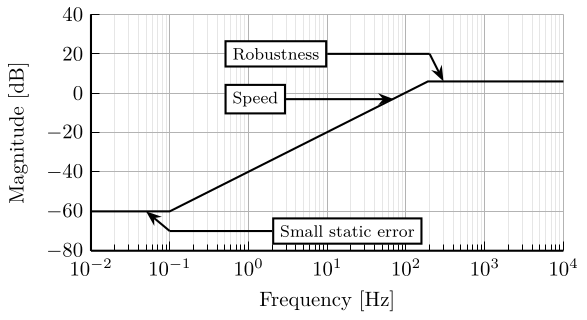
Figure 20: Typical wanted shape of the Sensitivity transfer function
4.3 Robustness: Module Margin
Let’s start by an example demonstrating why the phase and gain margins might not be good indicators of robustness.
Let’s consider the following plant \(G_t(s)\):
w0 = 2*pi*100; xi = 0.1; k = 1e7; Gt = 1/k*(s/w0/4 + 1)/(s^2/w0^2 + 2*xi*s/w0 + 1);
Let’s say we have designed a controller \(K_t(s)\) that gives the loop gain shown in Figure 21.
Kt = 1.2e6*(s + w0)/s;
The following characteristics can be determined from Figure 21:
- bandwidth of \(\approx 10\, \text{Hz}\)
- infinite gain margin (the phase of the loop-gain never reaches -180 degrees
- more than 90 degrees of phase margin
This might indicate very good robustness properties of the closed-loop system.
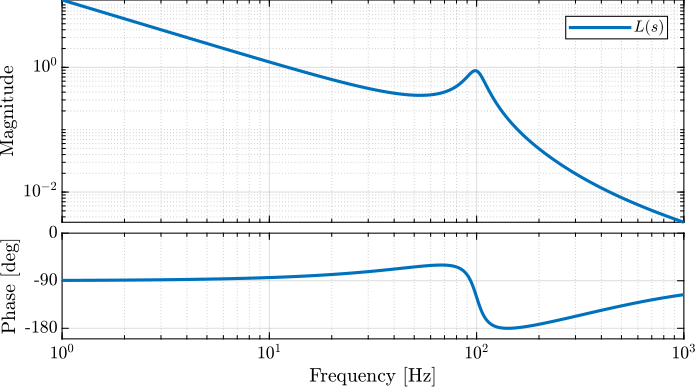
Figure 21: Bode plot of the obtained Loop Gain \(L(s)\)
Now let’s suppose the “real” plant \(G_r(s)\) as a slightly lower damping factor:
xi = 0.03;
The obtained “real” loop gain is shown in Figure 22. At a frequency little bit above 100Hz, the phase of the loop gain reaches -180 degrees while its magnitude is more than one which indicated instability.
It is confirmed by checking the stability of the closed loop system:
isstable(feedback(Gr,K))
0
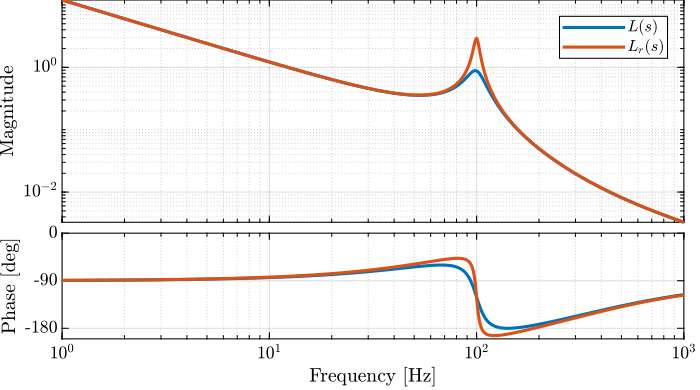
Figure 22: Bode plots of \(L(s)\) (loop gain corresponding the nominal plant) and \(L_r(s)\) (loop gain corresponding to the real plant)
Therefore, even a small change of the plant parameter makes the system unstable even though both the gain margin and the phase margin for the nominal plant are excellent.
This is due to the fact that the gain and phase margin are robustness indicators for a pure change or gain or a pure change of phase but not a combination of both.
Let’s now determine a new robustness indicator based on the Nyquist Stability Criteria.
- Nyquist Stability Criteria (for stable systems)
- If the open-loop transfer function \(L(s)\) is stable, then the closed-loop system is unstable for any encirclement of the point \(−1\) on the Nyquist plot.
- Nyquist Plot
- The Nyquist plot shows the evolution of \(L(j\omega)\) in the complex plane from \(\omega = 0 \to \infty\).
For more information about the general Nyquist Stability Criteria, you may want to look at this video.
From the Nyquist stability criteria, it is clear that we want \(L(j\omega)\) to be as far as possible from the \(-1\) point (called the unstable point) in the complex plane. This minimum distance is called the module margin.
- Module Margin
- The Module Margin \(\Delta M\) is defined as the minimum distance between the point \(-1\) and the loop gain \(L(j\omega)\) in the complex plane.
A typical Nyquist plot is shown in Figure 23. The gain, phase and module margins are graphically shown to have an idea of what they represent.
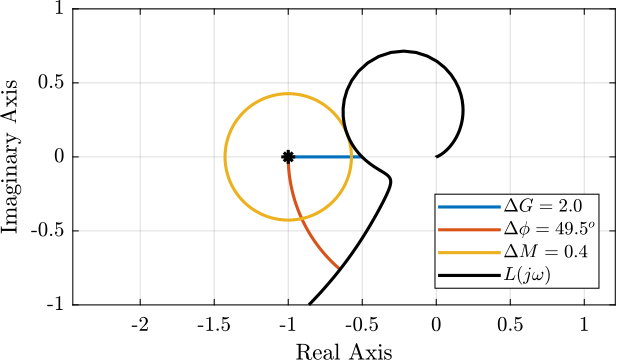
Figure 23: Nyquist plot with visual indication of the Gain margin \(\Delta G\), Phase margin \(\Delta \phi\) and Module margin \(\Delta M\)
As expected from Figure 23, there is a close relationship between the module margin and the gain and phase margins. We can indeed show that for a given value of the module margin \(\Delta M\), we have:
\begin{equation} \Delta G \ge \frac{\Delta M}{\Delta M - 1}; \quad \Delta \phi \ge \frac{1}{\Delta M} \end{equation}Let’s now try to express the Module margin \(\Delta M\) as an \(\mathcal{H}_\infty\) norm of a closed-loop transfer function:
\begin{align*} \Delta M &= \text{minimum distance between } L(j\omega) \text{ and point } (-1) \\ &= \min_\omega |L(j\omega) - (-1)| \\ &= \min_\omega |1 + L(j\omega)| \\ &= \frac{1}{\max_\omega \frac{1}{|1 + L(j\omega)|}} \\ &= \frac{1}{\|S\|_\infty} \end{align*}The \(\mathcal{H}_\infty\) norm of the sensitivity function \(\|S\|_\infty\) is a measure of the Module margin \(\Delta M\) and therefore an indicator of the system robustness.
\begin{equation} \Delta M = \frac{1}{\|S\|_\infty} \label{eq:module_margin_S} \end{equation}The wanted robustness of the closed-loop system can be specified by setting a maximum value on \(\|S\|_\infty\).
Note that this is why large peak value of \(|S(j\omega)|\) usually indicate robustness problems. And we know understand why setting an upper bound on the magnitude of \(S\) is generally a good idea.
Typical, we require \(\|S\|_\infty < 2 (6dB)\) which implies \(\Delta G \ge 2\) and \(\Delta \phi \ge 29^o\)
To learn more about module/disk margin, you can check out this video.
4.4 Other Requirements
Interpretation of the \(\mathcal{H}_\infty\) norm of systems:
- frequency by frequency attenuation / amplification
Let’s note \(G_t(s)\) the closed-loop transfer function from \(w\) to \(z\).
Consider an input sinusoidal signal \(w(t) = \sin\left( \omega_0 t \right)\), then the output signal \(z(t)\) will be equal to: \[ z(t) = A \sin\left( \omega_0 t + \phi \right) \] with:
- \(A = |G_t(j\omega_0)|\) is the magnitude of \(G_t(s)\) at \(\omega_0\)
- \(\phi = \angle G_t(j\omega_0)\) is the phase of \(G_t(s)\) at \(\omega_0\)
Noise Attenuation: typical wanted shape for \(T\)
| Open-Loop Shaping | Closed-Loop Shaping | |
|---|---|---|
| Reference Tracking | \(L\) large | \(S\) small |
| Disturbance Rejection | \(L\) large | \(GS\) small |
| Measurement Noise Filtering | \(L\) small | \(T\) small |
| Small Command Amplitude | \(K\) and \(L\) small | \(KS\) small |
| Robustness | Phase/Gain margins | Module margin: \(\Vert S\Vert_\infty\) small |
5 \(\mathcal{H}_\infty\) Shaping of closed-loop transfer functions
In the previous sections, we have seen that the performances of the system depends on the shape of the closed-loop transfer function.
Therefore, the synthesis problem is to design \(K(s)\) such that closed-loop system is stable and such that various closed-loop transfer functions such as \(S\), \(KS\) and \(T\) are shaped as wanted. This is clearly not simple as these closed-loop transfer functions does not depend linearly on \(K\).
But don’t worry, the \(\mathcal{H}_\infty\) synthesis will do this job for us!
5.1 How to Shape closed-loop transfer function? Using Weighting Functions!
If the \(\mathcal{H}_\infty\) synthesis is applied on the generalized plant \(P(s)\) shown in Figure 24, it will generate a controller \(K(s)\) such that the \(\mathcal{H}_\infty\) norm of closed-loop transfer function from \(r\) to \(\epsilon\) is minimized. This closed-loop transfer function actually correspond to the sensitivity function. Therefore, it will minimize the the \(\mathcal{H}_\infty\) norm of the sensitivity function: \(\|S\|_\infty\).
However, as the \(\mathcal{H}_\infty\) norm is the maximum peak value of the transfer function’s magnitude, this synthesis is quite useless and clearly does not allow to shape the norm of \(S(j\omega)\) over all frequencies.
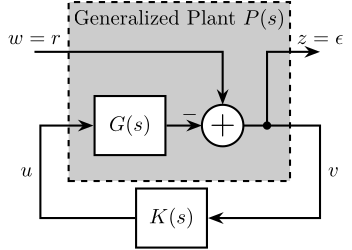
Figure 24: Generalized Plant
The trick is to include a weighting function \(W_S(s)\) in the generalized plant as shown in Figure 25.
Now, the closed-loop transfer function from \(w\) to \(z\) is equal to \(W_s(s)S(s)\) and applying the \(\mathcal{H}_\infty\) synthesis to the weighted generalized plant \(\tilde{P}(s)\) will generate a controller \(K(s)\) such that \(\|W_s(s)S(s)\|_\infty\) is minimized.
Let’s now show how this is equivalent as shaping the sensitivity function:
\begin{align} & \left\| W_s(s) S(s) \right\|_\infty < 1\nonumber \\ \Leftrightarrow & \left| W_s(j\omega) S(j\omega) \right| < 1 \quad \forall \omega\nonumber \\ \Leftrightarrow & \left| S(j\omega) \right| < \frac{1}{\left| W_s(j\omega) \right|} \quad \forall \omega \label{eq:sensitivity_shaping} \end{align}As shown in Equation \eqref{eq:sensitivity_shaping}, the \(\mathcal{H}_\infty\) synthesis applying on the weighted generalized plant allows to shape the magnitude of the sensitivity transfer function.
Therefore, the choice of the weighting function \(W_s(s)\) is very important: its inverse magnitude will define the wanted upper bound of the sensitivity function magnitude.
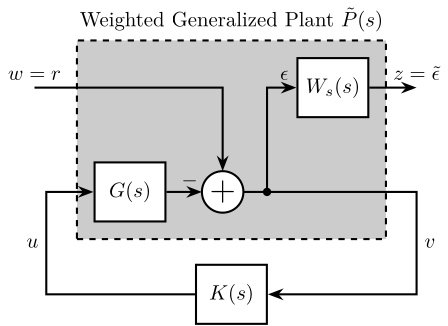
Figure 25: Weighted Generalized Plant
Using matlab, compute the weighted generalized plant shown in Figure 26 as a function of \(G(s)\) and \(W_S(s)\).
Hint
The weighted generalized plant can be defined in Matlab using two techniques:
- by writing manually the 4 transfer functions from \([w, u]\) to \([\tilde{\epsilon}, v]\)
- by pre-multiplying the (non-weighted) generalized plant by a block-diagonal transfer function matrix containing the weights for the outputs \(z\) and
1for the outputs \(v\)
Answer
The two solutions below can be used.
Pw = [Ws -Ws*G; 1 -G];
Pw = blkdiag(Ws, 1)*P;
The second solution is however more general, and can also be used when weights are added at the inputs by post-multiplying instead of pre-multiplying.
5.2 Design of Weighting Functions
Weighting function included in the generalized plant must be proper, stable and minimum phase transfer functions.
- proper
- more poles than zeros, this implies \(\lim_{\omega \to \infty} |W(j\omega)| < \infty\)
- stable
- no poles in the right half plane
- minimum phase
- no zeros in the right half plane
Matlab is providing the makeweight function that allows to design first-order weights by specifying the low frequency gain, high frequency gain, and the gain at a specific frequency:
W = makeweight(dcgain,[freq,mag],hfgain)
with:
dcgain: low frequency gain[freq,mag]: frequencyfreqat which the gain ismaghfgain: high frequency gain
The Matlab code below produces a weighting function with the following characteristics (Figure 26):
- Low frequency gain of 100
- Gain of 1 at 10Hz
- High frequency gain of 0.5
Ws = makeweight(1e2, [2*pi*10, 1], 1/2);
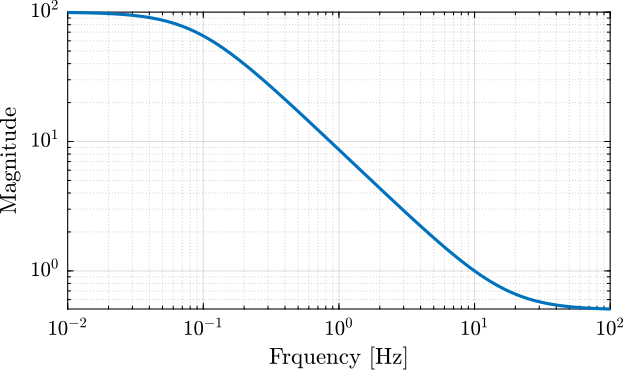
Figure 26: Obtained Magnitude of the Weighting Function
Quite often, higher orders weights are required.
In such case, the following formula can be used:
\begin{equation} W(s) = \left( \frac{ \frac{1}{\omega_0} \sqrt{\frac{1 - \left(\frac{G_0}{G_c}\right)^{\frac{2}{n}}}{1 - \left(\frac{G_c}{G_\infty}\right)^{\frac{2}{n}}}} s + \left(\frac{G_0}{G_c}\right)^{\frac{1}{n}} }{ \left(\frac{1}{G_\infty}\right)^{\frac{1}{n}} \frac{1}{\omega_0} \sqrt{\frac{1 - \left(\frac{G_0}{G_c}\right)^{\frac{2}{n}}}{1 - \left(\frac{G_c}{G_\infty}\right)^{\frac{2}{n}}}} s + \left(\frac{1}{G_c}\right)^{\frac{1}{n}} }\right)^n \label{eq:weight_formula_advanced} \end{equation}The parameters permit to specify:
- the low frequency gain: \(G_0 = lim_{\omega \to 0} |W(j\omega)|\)
- the high frequency gain: \(G_\infty = lim_{\omega \to \infty} |W(j\omega)|\)
- the absolute gain at \(\omega_0\): \(G_c = |W(j\omega_0)|\)
- the absolute slope between high and low frequency: \(n\)
A Matlab function implementing Equation \eqref{eq:weight_formula_advanced} is shown below:
function [W] = generateWeight(args) arguments args.G0 (1,1) double {mustBeNumeric, mustBePositive} = 0.1 args.G1 (1,1) double {mustBeNumeric, mustBePositive} = 10 args.Gc (1,1) double {mustBeNumeric, mustBePositive} = 1 args.wc (1,1) double {mustBeNumeric, mustBePositive} = 2*pi args.n (1,1) double {mustBeInteger, mustBePositive} = 1 end if (args.Gc <= args.G0 && args.Gc <= args.G1) || (args.Gc >= args.G0 && args.Gc >= args.G1) eid = 'value:range'; msg = 'Gc must be between G0 and G1'; throwAsCaller(MException(eid,msg)) end s = zpk('s'); W = (((1/args.wc)*sqrt((1-(args.G0/args.Gc)^(2/args.n))/(1-(args.Gc/args.G1)^(2/args.n)))*s + (args.G0/args.Gc)^(1/args.n))/((1/args.G1)^(1/args.n)*(1/args.wc)*sqrt((1-(args.G0/args.Gc)^(2/args.n))/(1-(args.Gc/args.G1)^(2/args.n)))*s + (1/args.Gc)^(1/args.n)))^args.n; end
Let’s use this function to generate three weights with the same high and low frequency gains, but but different slopes.
W1 = generateWeight('G0', 1e2, 'G1', 1/2, 'Gc', 1, 'wc', 2*pi*10, 'n', 1); W2 = generateWeight('G0', 1e2, 'G1', 1/2, 'Gc', 1, 'wc', 2*pi*10, 'n', 2); W3 = generateWeight('G0', 1e2, 'G1', 1/2, 'Gc', 1, 'wc', 2*pi*10, 'n', 3);
The obtained shapes are shown in Figure 27.
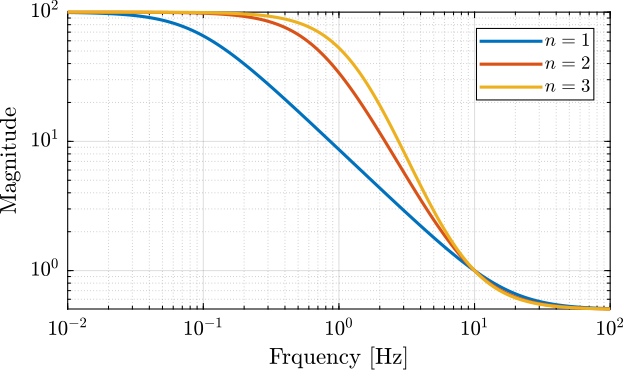
Figure 27: Higher order weights using Equation \eqref{eq:weight_formula_advanced}
5.3 Shaping the Sensitivity Function
Let’s design a controller using the \(\mathcal{H}_\infty\) synthesis that fulfils the following requirements:
- Bandwidth of at least 10Hz
- Small static errors for step responses
- Robustness: Large module margin \(\Delta M > 0.5\) (\(\Rightarrow \Delta G > 2\) and \(\Delta \phi > 29^o\))
As usual, the plant used is the one presented in Section 1.3.
Translate the requirements as upper bounds on the Sensitivity function and design the corresponding Weight using Matlab.
Hint
The typical wanted upper bound of the sensitivity function is shown in Figure 28.
More precisely:
- Recall that the closed-loop bandwidth is defined as the frequency \(|S(j\omega)|\) first crosses \(1/\sqrt{2} = -3dB\) from below
- For the small static error, -60dB is usually enough as other factors (measurement noise, disturbances) will anyhow limit the performances
- Recall that the module margin is equal to the inverse of the \(\mathcal{H}_\infty\) norm of the sensitivity function: \[ \Delta M = \frac{1}{\|S\|_\infty} \]
Remember that the wanted upper bound of the sensitivity function is defined by the inverse magnitude of the weight.

Figure 28: Typical wanted shape of the Sensitivity transfer function
Answer
- \(|W_s(j \cdot 2 \pi 10)| = \sqrt{2}\)
- \(|W_s(j \cdot 0)| = 10^3\)
- \(\|W_s\|_\infty = 0.5\)
Using Matlab, such weighting function can be generated using the makeweight function as shown below:
Ws = makeweight(1e3, [2*pi*10, sqrt(2)], 1/2);
Or using the generateWeight function:
Ws = generateWeight('G0', 1e3, ... 'G1', 1/2, ... 'Gc', sqrt(2), 'wc', 2*pi*10, ... 'n', 2);
Let’s say we came up with the following weighting function:
Ws = generateWeight('G0', 1e3, ... 'G1', 1/2, ... 'Gc', sqrt(2), 'wc', 2*pi*10, ... 'n', 2);
The weighting function is then added to the generalized plant.
P = [1 -G; 1 -G]; Pw = blkdiag(Ws, 1)*P;
And the \(\mathcal{H}_\infty\) synthesis is performed on the weighted generalized plant.
K = hinfsyn(Pw, 1, 1, 'Display', 'on');
Test bounds: 0.5 <= gamma <= 0.51 gamma X>=0 Y>=0 rho(XY)<1 p/f 5.05e-01 0.0e+00 0.0e+00 3.000e-16 p Limiting gains... 5.05e-01 0.0e+00 0.0e+00 3.461e-16 p 5.05e-01 -3.5e+01 # -4.9e-14 1.732e-26 f Best performance (actual): 0.503
\(\gamma \approx 0.5\) means that the \(\mathcal{H}_\infty\) synthesis generated a controller \(K(s)\) that stabilizes the closed-loop system, and such that:
\begin{aligned} & \| W_s(s) S(s) \|_\infty \approx 0.5 \\ & \Leftrightarrow |S(j\omega)| < \frac{0.5}{|W_s(j\omega)|} \quad \forall \omega \end{aligned}This is indeed what we can see by comparing \(|S|\) and \(|W_S|\) in Figure 29.
Having \(\gamma < 1\) means that the \(\mathcal{H}_\infty\) synthesis found a controller such that the specified closed-loop transfer functions are bellow the specified upper bounds.
Having \(\gamma\) slightly above one does not necessary means the obtained controller is not “good”. It just means that at some frequency, one of the closed-loop transfer functions is above the specified upper bound by a factor \(\gamma\).
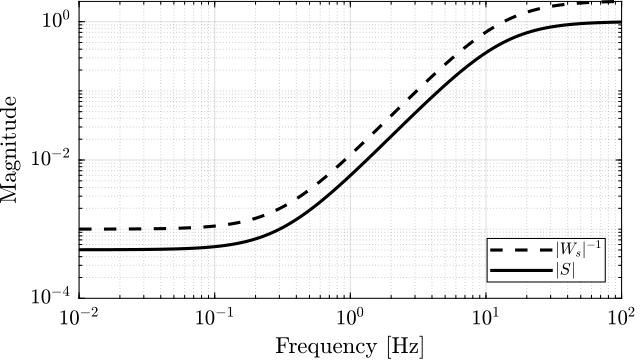
Figure 29: Weighting function and obtained closed-loop sensitivity
5.4 Shaping multiple closed-loop transfer functions
As was shown in Section 4, depending on the specifications, up to four closed-loop transfer function may be shaped (the Gang of four). This was summarized in Table 7.
For instance to limit the control input \(u\), \(KS\) should be shaped while to filter measurement noise, \(T\) should be shaped.
When multiple closed-loop transfer function are shaped at the same time, it is refereed to as “Mixed-Sensitivity \(\mathcal{H}_\infty\) Control” and is the subject of Section 6.
Depending on the closed-loop transfer function being shaped, different general control configuration are used and are described below.
Shaping of S and KS

Figure 30: Generalized Plant to shape \(S\) and \(KS\)
P = [W1 -G*W1 0 W2 1 -G];
- \(W_1(s)\) is used to shape \(S\)
- \(W_2(s)\) is used to shape \(KS\)
Shaping of S and T

Figure 31: Generalized Plant to shape \(S\) and \(T\)
P = [W1 -G*W1 0 G*W2 1 -G];
- \(W_1\) is used to shape \(S\)
- \(W_2\) is used to shape \(T\)
Shaping of S and GS
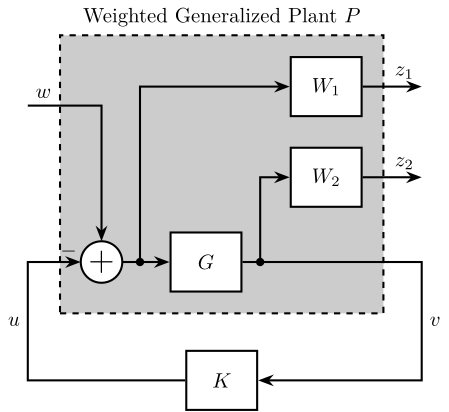
Figure 32: Generalized Plant to shape \(S\) and \(GS\)
P = [W1 -W1 G*W2 -G*W2 G -G];
- \(W_1\) is used to shape \(S\)
- \(W_2\) is used to shape \(GS\)
Shaping of S, T and KS
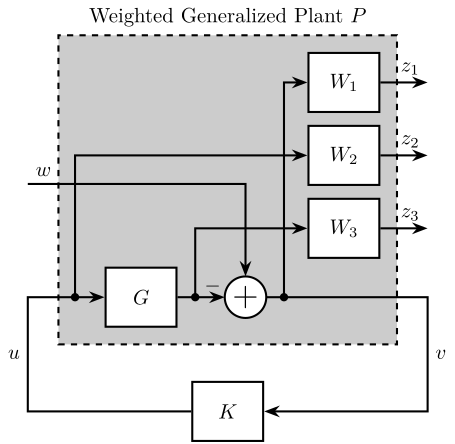
Figure 33: Generalized Plant to shape \(S\), \(T\) and \(KS\)
P = [W1 -G*W1 0 W2 0 G*W3 1 -G];
- \(W_1\) is used to shape \(S\)
- \(W_2\) is used to shape \(KS\)
- \(W_3\) is used to shape \(T\)
Shaping of S, T and GS
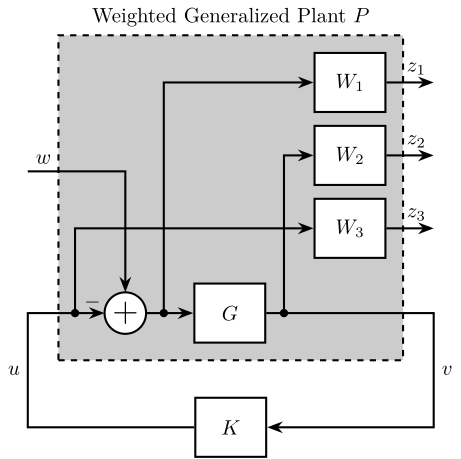
Figure 34: Generalized Plant to shape \(S\), \(T\) and \(GS\)
P = [W1 -W1 G*W2 -G*W2 0 W3 G -G];
- \(W_1\) is used to shape \(S\)
- \(W_2\) is used to shape \(GS\)
- \(W_3\) is used to shape \(T\)
Shaping of S, T, KS and GS

Figure 35: Generalized Plant to shape \(S\), \(T\), \(KS\) and \(GS\)
P = [ W1 -W1*G*W3 -G*W1 0 0 W2 1 -G*W3 -G];
- \(W_1\) is used to shape \(S\)
- \(W_2\) is used to shape \(KS\)
- \(W_1W_3\) is used to shape \(GS\)
- \(W_2W_3\) is used to shape \(T\)
When shaping multiple closed-loop transfer functions, one should be verify careful about the three following points that are further discussed:
- The shaped closed-loop transfer functions are linked by mathematical relations and cannot be shaped
- Closed-loop transfer function can only be shaped in certain frequency range.
- The size of the obtained controller may be very large and not implementable in practice
Mathematical relations are linking the closed-loop transfer functions. For instance, the sensitivity function \(S(s)\) and the complementary sensitivity function \(T(s)\) as link by the following well known relation:
\begin{equation} S(s) + T(s) = 1 \end{equation}This means that \(|S(j\omega)|\) and \(|T(j\omega)|\) cannot be made small at the same time!
It is therefore not possible to shape the four closed-loop transfer functions independently. The weighting function should be carefully design such as these fundamental relations are not violated.
The control bandwidth is clearly limited by physical constrains such as sampling frequency, electronics bandwidth,
\begin{align*} &|G(j\omega) K(j\omega)| \ll 1 \Longrightarrow |S(j\omega)| = \frac{1}{1 + |G(j\omega)K(j\omega)|} \approx 1 \\ &|G(j\omega) K(j\omega)| \gg 1 \Longrightarrow |S(j\omega)| = \frac{1}{1 + |G(j\omega)K(j\omega)|} \approx \frac{1}{|G(j\omega)K(j\omega)|} \end{align*}Similar relationship can be found for \(T\), \(KS\) and \(GS\).
Determine the approximate norms of \(T\), \(KS\) and \(GS\) for large loop gains (\(|G(j\omega) K(j\omega)| \gg 1\)) and small loop gains (\(|G(j\omega) K(j\omega)| \ll 1\)).
Hint
You can follows this procedure for \(T\), \(KS\) and \(GS\):
- Write the closed-loop transfer function \(T(s)\) as a function of \(K(s)\) and \(G(s)\)
- Take \(|K(j\omega)G(j\omega)| \gg 1\) and conclude on \(|T(j\omega)|\)
- Take \(|K(j\omega)G(j\omega)| \ll 1\) and conclude on \(|T(j\omega)|\)
Answer
The obtained constrains are shown in Figure 36.
Depending on the frequency band, the norms of the closed-loop transfer functions depend on the controller \(K\) and therefore can be shaped. However, in some frequency bands, the norms do not depend on the controller and therefore cannot be shaped.
Therefore the weighting functions should only focus on certainty frequency range depending on the transfer function being shaped. These regions are summarized in Figure 36.
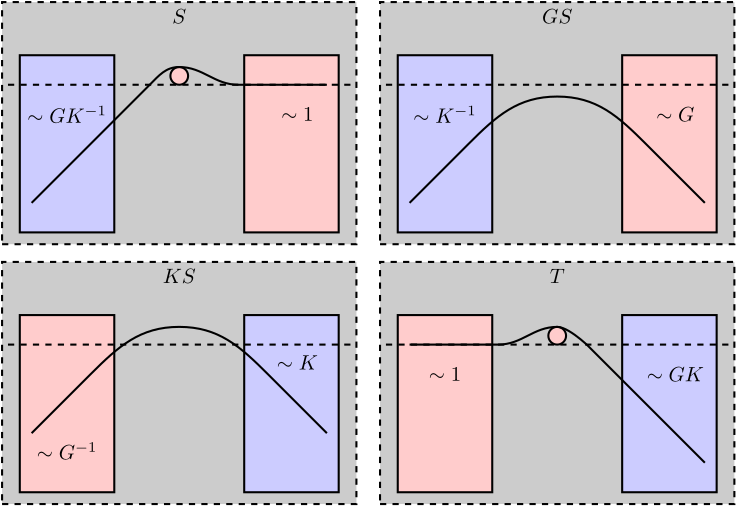
Figure 36: Shaping the Gang of Four: Limitations
The order (resp. number of state) of the controller given by the \(\mathcal{H}_\infty\) synthesis is equal to the order (resp. number of state) of the weighted generalized plant. It is thus equal to the sum of the number of state of the non-weighted generalized plant and the number of state of all the weighting functions.
Two approaches can be used to obtain controllers with reasonable order:
- use simple weights (usually first order)
- perform a model reduction on the obtained high order controller
6 Mixed-Sensitivity \(\mathcal{H}_\infty\) Control - Example
6.1 Control Problem
[ ]Control Diagram
- Inputs Signals
- Reference steps of 1mm
- Measurement noise is considered to be a white noise with a power spectral density of …
- Specifications
- Follow reference steps with a response time of 0.1s and static error less than \(1 \mu m\)
- Maximum control signal of 10N
- Robustness
- Reduce the effect of measurement noise on the position
k = 1e6; % Stiffness [N/m] c = 4e2; % Damping [N/(m/s)] m = 10; % Mass [kg] G = 1/(m*s^2 + c*s + k); % Plant Gd = (c*s + k)/(m*s^2 + c*s + k); % Disturbance
% Generate Input Signals t = 0:1e-3:1; r = zeros(size(t)); r(t>0.1) = 1e-3; Fs = 1e3; % Sampling Frequency [Hz] Ts = 1/Fs; % Sampling Time [s] n = sqrt(Fs/2)*randn(1, length(t)); % Signal with an ASD equal to one n = n*1e-6; d = zeros(size(t)); d(t>0.5) = 5e-4;
6.2 Control Design Procedure
| Response Time | ||
| Robustness | ||
| Limitation of the Command Amplitude | ||
| Filtering of the measurement noise |
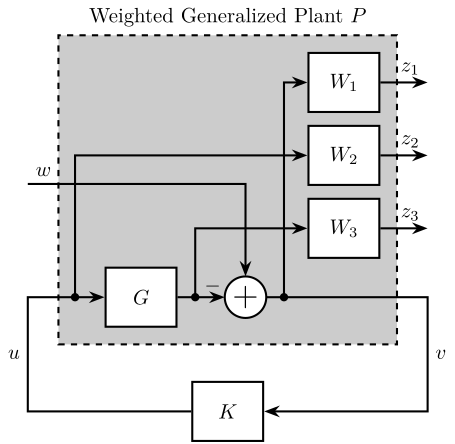
Figure 37: Generalized Plant used for the Mixed Sensitivity Synthesis
- \(W_1\) is used to shape \(S\)
- \(W_2\) is used to shape \(KS\)
- \(W_3\) is used to shape \(T\)
P = [1 -G 0 1 0 G 1 -G];
6.3 Step 1 - Shaping of \(S\)
We start with the shaping of \(S\) alone. To not constrain \(KS\) and \(T\), we set small values for \(W_2\) and \(W_3\)
W2 = tf(1e-8);
W3 = tf(0.1);
W1 = generateWeight('G0', 1e3, ... 'G1', 1/2, ... 'Gc', sqrt(2), 'wc', 2*pi*10, ... 'n', 1);
Pw = blkdiag(W1, W2, W3, 1)*P;
K1 = hinfsyn(Pw, 1, 1, 'Display', 'on');
K1 = hinfsyn(Pw, 1, 1, 'Display', 'on');
Test bounds: 0.5 <= gamma <= 0.552
gamma X>=0 Y>=0 rho(XY)<1 p/f
5.25e-01 0.0e+00 0.0e+00 6.061e-16 p
5.13e-01 0.0e+00 0.0e+00 0.000e+00 p
5.06e-01 -2.5e+00 # -6.4e-14 1.440e-15 f
5.09e-01 -5.5e+00 # -4.1e-14 9.510e-16 f
Limiting gains...
5.14e-01 0.0e+00 0.0e+00 1.039e-25 p
5.14e-01 0.0e+00 0.0e+00 1.040e-25 p
Best performance (actual): 0.514
'org_babel_eoe'
ans =
'org_babel_eoe'
Z1 = lft(P, K1);
% Create model with r and n as inputs and y and u as outputs Psim = [0 0 Gd G 0 0 0 1 1 -1 -Gd -G]; Z1sim = lft(Psim, K1);
z = lsim(Z1sim, [r;n;d], t); y1 = z(:,1); u1 = z(:,2);
figure; tiledlayout(1, 2, 'TileSpacing', 'None', 'Padding', 'None'); nexttile; hold on; plot(t, y1); hold off; xlabel('Time [s]'); ylabel('Output $y$ [m]'); nexttile; hold on; plot(t, u1); hold off; xlabel('Time [s]'); ylabel('Control Input $u$ [N]');
6.4 Step 2 - Shaping of \(KS\)
W2 = generateWeight('G0', 5e-7, ... 'G1', 1e-3, ... 'Gc', 1e-6, 'wc', 2*pi*100, ... 'n', 1);
Pw = blkdiag(W1, W2, W3, 1)*P;
K2 = hinfsyn(Pw, 1, 1, 'Display', 'on');
K1 = hinfsyn(Pw, 1, 1, 'Display', 'on');
Test bounds: 0.51 <= gamma <= 1.2
gamma X>=0 Y>=0 rho(XY)<1 p/f
7.82e-01 0.0e+00 0.0e+00 0.000e+00 p
6.32e-01 -2.2e+00 # -3.0e-14 -1.136e-32 f
7.03e-01 -5.1e+00 # -2.9e-14 5.128e-17 f
7.41e-01 -1.1e+01 # -1.0e-14 1.431e-22 f
7.61e-01 -2.6e+01 # -9.1e-15 1.215e-21 f
7.72e-01 -6.9e+01 # -1.9e-14 2.828e-16 f
7.77e-01 -3.6e+02 # -1.2e-14 1.213e-15 f
Best performance (actual): 0.782
'org_babel_eoe'
ans =
'org_babel_eoe'
Z2 = lft(P, K2);
Z2sim = lft(Psim, K2);
z = lsim(Z2sim, [r;n;d], t); y2 = z(:,1); u2 = z(:,2);
figure; tiledlayout(1, 2, 'TileSpacing', 'None', 'Padding', 'None'); nexttile; hold on; plot(t, y1); plot(t, y2); hold off; xlabel('Time [s]'); ylabel('Output $y$ [m]'); nexttile; hold on; plot(t, u1); plot(t, u2); hold off; xlabel('Time [s]'); ylabel('Control Input $u$ [N]');
6.5 Step 3 - Shaping of \(T\)
W3 = generateWeight('G0', 1e-1, ... 'G1', 1e4, ... 'Gc', 1, 'wc', 2*pi*30, ... 'n', 3);
Pw = blkdiag(W1, W2, W3, 1)*P;
K3 = hinfsyn(Pw, 1, 1, 'Display', 'on');
K3 = hinfsyn(Pw, 1, 1, 'Display', 'on');
Test bounds: 0.578 <= gamma <= 1.66
gamma X>=0 Y>=0 rho(XY)<1 p/f
9.78e-01 -1.3e+01 # -6.2e-15 1.141e-18 f
1.27e+00 0.0e+00 0.0e+00 1.524e-15 p
1.12e+00 0.0e+00 0.0e+00 4.481e-15 p
1.04e+00 -4.0e+01 # -1.0e-13 1.102e-42 f
1.08e+00 -6.6e+02 # -4.4e-15 3.641e-18 f
1.10e+00 0.0e+00 0.0e+00 6.052e-21 p
1.09e+00 0.0e+00 0.0e+00 5.005e-15 p
Best performance (actual): 1.09
'org_babel_eoe'
ans =
'org_babel_eoe'
Z3 = lft(P, K3);
Z3sim = lft(Psim, K3);
z = lsim(Z3sim, [r;n;d], t); y3 = z(:,1); u3 = z(:,2);
figure; tiledlayout(1, 2, 'TileSpacing', 'None', 'Padding', 'None'); nexttile; hold on; plot(t, y1); plot(t, y2); plot(t, y3); hold off; xlabel('Time [s]'); ylabel('Output $y$ [m]'); nexttile; hold on; plot(t, u1); plot(t, u2); plot(t, u3); hold off; xlabel('Time [s]'); ylabel('Control Input $u$ [N]');
Resources